1 Introduction

Most of the biological, chemical and physical phenomena are governed by nonlinear partial differential equations (NLPDEs). The research on NLPDEs becomes increasingly important with the development of nonlinear dynamics. Exact solutions of NLPDEs are of great importance to investigate the dynamics of such equations. These solutions are more relevant in the fields of applied mathematics, mathematical physics and engineering sciences. The exact solutions play a significant role to understand the various complex dynamical models. The results are also capable of improving the accuracy and efficiency of the relevant dynamical systems.

The aim of this research is to obtain some new group-invariant solutions of Konopelchenko–Dubrovsky (KD) equation. Hence, we consider the following (2 + 1)-dimensional KD equation:

$$\begin{aligned}&2u_t-12b\,u\,u_x+ 3a^2\,u^2\,u_x-6v_y+6a\,u_x v\nonumber \\&-2{u_{xxx}}=0,u_y= v_x. \end{aligned}$$
(1)

where \(u = u(x,y, t)\) and \(v = v(x,y, t)\); a and b are the real parameters. Subscripts stand for the partial derivatives with respect to the subscript variables throughout the article.

Konopelchenko and Dubrovsky [1] derived the KD equation in 1984 during the study of integrable nonlinear evolution equations (NLEEs) through the inverse scattering transform (IST) method. The equation reduces into the Gardner equation for \(u_y = 0\), and it also converts into the Kadomtsev–Petviashvili equation for \(a =0\). Moreover, it turns into the modified Kadomtsev–Petviashvili equation for \(b=0\), which is useful in soliton theory.

The KD system has been studied in detail by a diverse group of researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14] across the globe and presented some effective methods for its exact solutions. Lin et al. [2] derived multisoliton solutions of the KD equations by applying Bäcklund transformation. Wang et al. [3] derived exact solutions of the equations in terms of Jacobi elliptic functions through an improved form of the extended F-expansion method, while Zhang et al. [4] presented some wave solutions of the KD equation by using generalized F-expansion method with Mathematica. Furthermore, Wazwaz [5] attained exact solutions of the equation with solitons, kink and periodic wave nature. Song et al. [6] obtained exact solutions of the equation by applying extended Riccati equation rational expansion method.

On the other hand, He [7] constructed bounded traveling wave solutions by using the bifurcation theory method of planar dynamical system. Hongyan [8] studied Lie point symmetry of the KD equations through the classical Lie group method. Ultimately, he derived soliton solutions by applying the tanh function method. Feng et al. [9] obtained exact solutions by applying the improved mapping approach and variable separation method. Hongyan [10] found that the KD equation and its Lax pair admits the same symmetry transformations of the independent variables. Zhang [11] used Riccati equation and its generalized solitary wave solutions constructed through the Exp-function method and derived exact solutions. Ren et al. [12] derived nonlocal symmetries by applying the truncated Painlevé method and the conformal invariant form. Furthermore, they obtained finite symmetry by solving the initial value problem of the prolonged systems and studied symmetry reductions through Lie point symmetry. Ultimately, they obtained multisolitary wave solutions of the KD equation. Moreover, Kumar et al. [13, 14] derived various invariant solutions by employing the group theoretical method.

Motivated by the rich treasure of the KD equation available in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14] specially from Kumar et al. [13, 14] derived many exact solutions through similarity transformation method (STM) with particular choices of the functions of t. In this research , we have obtain exact solutions of the KD equation by using the similarity transformation method with arbitrary choice of function. The methodology and applications of similarity transformation method have been given in the literature [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

This research paper is organized as follows: A brief introduction of the KD equation is presented in Sect. 1; Sect. 2 furnishes with infinite-dimensional Lie algebra and commutation relations of the KD equation; Sect. 3 deals with derived group-invariant solutions of the equation; Sect. 4 depicts analysis and discussions of the exact solutions; finally, some concluding remarks are drawn in Sect. 5.

2 Lie symmetry analysis for the KD equation

Let us consider a one-parameter Lie group of transformation

$$\begin{aligned} x^*&= x + \epsilon ~\xi (x, y, t, u, v)+ O(\epsilon ^2),\\ y^*&= y + \epsilon ~\eta (x, y, t, u, v)+ O(\epsilon ^2),\\ t^*&= t + \epsilon ~\tau (x, y, t, u, v)+ O(\epsilon ^2 ),\\ u^*&= u + \epsilon ~\phi (x, y, t, u, v)+ O(\epsilon ^2 ),\\ v^*&= v + \epsilon \,\psi (x, y, t, u, v)+ O(\epsilon ^2 ). \end{aligned}$$

The vector field associated with the above group of transformations can be written as:

$$\begin{aligned} \mathbf{V} = \xi \frac{\partial }{\partial x}+\eta \frac{\partial }{\partial y}+\tau \frac{\partial }{\partial t} +\phi \frac{\partial }{\partial u}+\psi \frac{\partial }{\partial v}. \end{aligned}$$
(2)

Lie invariance condition for KD equation with respect to vector field Eq. (2) read as [15, 16]:

$$\begin{aligned}&\text{ pr }^{(3)}{} \mathbf V [2u_t-12b\,u\,u_x+ 3a^2\,u^2\,u_x-6v_y\nonumber \\&+6a\,u_x\,v-2{u_{xxx}}]=0, \text{ pr }^{(1)}{} \mathbf V [u_y-v_x]=0. \end{aligned}$$
(3)

The symbol \(\text{ pr }^{(n)}{} \mathbf V \) is the usual nth-order prolongation operator; therefore,

$$\begin{aligned} \text{ pr }^{(1)}{} \mathbf V&= \mathbf V +\phi ^{y}\frac{\partial }{\partial u_y}+\psi ^{x}\frac{\partial }{\partial v_x},\\ \text{ pr }^{(3)}{} \mathbf V&= \mathbf V {+}\phi ^{t}\frac{\partial }{\partial u_t}{+}\phi ^{x}\frac{\partial }{\partial u_x} {+}\psi ^{y}\frac{\partial }{\partial v_y}{+}\phi ^{xxx}\frac{\partial }{\partial u_{xxx}}, \end{aligned}$$

where \({\phi }^t\), \({\phi }^x\), \({\phi }^y\), \({\phi }^{xxx}\), \({\psi }^x\) and \({\psi }^y\) are the coefficients in \( \text{ pr }^{(1)}{} \mathbf V \) and \( \text{ pr }^{(3)}{} \mathbf V \) defined as

$$\begin{aligned} {\phi }^t&=D_t\phi -u_x\,D_t\xi -u_y\,D_t\eta -u_t\,D_t\tau ,\\ {\phi }^x&=D_x\,\phi -u_x\,D_x\xi -u_y\,D_x\eta -u_t\,D_x\tau ,\\ {\phi }^y&=D_y\phi -u_x\,D_y\xi -u_y\,D_y\eta -u_t\,D_y\tau ,\\ {\psi }^x&=D_x\,\psi -v_x\,D_x\xi -v_y\,D_x\eta -v_t\,D_x\tau ,\\ {\psi }^y&=D_y\,\psi -v_x\,D_y\xi -v_y\,D_y\eta -v_t\,D_y\tau ,\\&\quad \quad \quad {\cdots \cdots \cdots \cdots \cdots \cdots }, \end{aligned}$$

and \(D_t, D_x\) and \(D_y\) stand for the total derivative operators, for example,

$$\begin{aligned} D_t&=\frac{\partial }{\partial t}+u_t\frac{\partial }{\partial u}+v_t\frac{\partial }{\partial v}+u_{tx}\frac{\partial }{\partial u_x}+v_{tx}\frac{\partial }{\partial v_x}\\&\quad +u_{tt}\frac{\partial }{\partial u_ t}+v_{tt}\frac{\partial }{\partial v_ t}+{\cdots }. \end{aligned}$$

Applying the prolongations \( \text{ pr }^{(1)}{} \mathbf V \) and \( \text{ pr }^{(3)}{} \mathbf V \) to Eq. (3), we have derived following system of the equations:

$$\begin{aligned}&\tau _{x}=0,\quad \tau _{y}=0,\quad \tau _{u}=0,\quad \tau _{v}=0,\\&\tau _{tt}=0,\quad \xi _u=0,\\&\xi _v=0,\quad \xi _{x}=\frac{1}{3}\tau _{t},\quad \xi _{y}=0,\quad \eta _{x}=0,\\&\eta _{u}=0,\quad \eta _{v}=0,\\&\eta _y=\frac{2}{3}\tau _{t},\quad \eta _{tt}=0,\quad \phi =\frac{1}{3}\left( \frac{2b}{a^2}-u\right) \tau _{t}+\frac{1}{3a}\, \eta _{t},\\&\psi =\frac{2}{3}\left( \frac{2b^2}{a^3}-v\right) \tau _{t}+\frac{1}{3}\left( \frac{2b}{a^2}-u\right) \, \eta _{t}-\frac{1}{3a}\xi _{t}. \end{aligned}$$

Solving above system of the equations, we get

$$\begin{aligned} \xi&= 18x{\bar{f_1}}+3y^2\bar{\bar{f_1}}+3y\bar{f_2}+3f_3,\\ \eta&= 36y\bar{f_1}+18f_2+1, \\ \tau&=54f_1, \\ \phi&=\frac{6y}{a} \bar{\bar{f_1}}+18\left( \frac{2b}{a^2}-u\right) \bar{f_1}+\frac{3}{a}\bar{f_2},\\ \psi&=\frac{y^2}{a}\bar{\bar{\bar{f_1}}}+6\left( \frac{x}{a}-uy+\frac{2by}{a^2}\right) \bar{\bar{f_1}}\\&\quad +36\left( \frac{2b^2}{a^3}-v\right) \bar{f_1}\\&\quad +\frac{y}{a}\bar{\bar{f_2}}+3\left( \frac{2b}{a^2}-u\right) \bar{f_2}+\frac{\bar{f_3}}{a}, \end{aligned}$$

where \(f_{1}\), \(f_{2}\) and \(f_{3}\) are arbitrary smooth functions of t and bar is used for the derivative throughout the article. The spanned vector field of Eq. (1) can be written as

$$\begin{aligned} \mathbf V =\mathbf{V_1}(f_1)+\mathbf{V_2}(f_2)+\mathbf{V_3}(f_3)+\mathbf{V_4}, \end{aligned}$$

where

$$\begin{aligned} \mathbf{V_1}(f_1)&= (18\,x\,\bar{f_1} +3\,y^2\bar{\bar{f_1}})\frac{\partial }{\partial x}+36\,y\bar{f_1}\frac{\partial }{\partial y}+54f_1\frac{\partial }{\partial t}\\&\quad +\,\left( \frac{6y}{a}\bar{\bar{f_1}}+\frac{36\,b}{a^2}\bar{f_1}-18\,u\bar{f_1}\right) \frac{\partial }{\partial u}+\left( \frac{y^2}{a}\bar{\bar{\bar{f_1}}}+\frac{6\,}{a}x\bar{\bar{f_1}}\right. \\&\quad \left. +\,\frac{12\,b\,y}{a^2}\bar{\bar{f_1}}-6\,y\,u\bar{\bar{f_1}}+\frac{72\,b^2}{a^3}\bar{f_1}-36\,v\,\bar{f_1}\right) \frac{\partial }{\partial v},\\ \mathbf{V_2}(f_2)&= 3y\bar{f_2}\frac{\partial }{\partial x}+18\,f_2\frac{\partial }{\partial y}+\frac{\bar{3\,f_3}}{a}\frac{\partial }{\partial u}\\&\quad +\,\left( \frac{y}{a}\bar{\bar{f_2}}+\frac{6\,b}{a^2}\bar{f_2}-3\,u\bar{f_2}\right) \frac{\partial }{\partial v},\\\mathbf{V_3}(f_3)&= 3\,f_3 \frac{\partial }{\partial x}+\frac{\bar{f_3}}{a}\frac{\partial }{\partial v},\quad \quad \mathbf{V_4}= \frac{\partial }{\partial y}. \end{aligned}$$

The associated Lie algebra between these vector fields becomes:

$$\begin{aligned} {[}{} \mathbf{V_i}, \mathbf{V_i}]= & {} 0,\quad i=1,2,3\\ {[}{} \mathbf{V_1}, \mathbf{V_2}]= & {} \mathbf{V_2}(54\,f_1\,\bar{f_{2}}-36\,f_2\,\bar{f_{1}}),\\ {[}{} \mathbf{V_1}, \mathbf{V_3}]= & {} \mathbf{V_3}(54\,f_1\,\bar{f_{3}}-18\,f_3\,\bar{f_{1}}),\\ {[}{} \mathbf{V_1}, \mathbf{V_4}]= & {} \mathbf{V_2}(-2\bar{f_{1}}),\\ {[}{} \mathbf{V_2}, \mathbf{V_3}]= & {} 0,\\ {[}{} \mathbf{V_2}, \mathbf{V_4}]= & {} \mathbf{V_3}(-\bar{f_{2}}), \\ {[}{} \mathbf{V_3}, \mathbf{V_4}]= & {} 0,\\ {[}{} \mathbf{V_1} (g_1), \mathbf{V_1}(h_1)]= & {} \mathbf{V_1}(54g_1\bar{h_{1}}-54 h_1\bar{g_{1}}),\\ {[}{} \mathbf{V_2}(g_2), \mathbf{V_2}(h_2)]= & {} \mathbf{V_3}(18g_2\bar{h_{2}}-18h_2\bar{g_{2}}),\\ {[}{} \mathbf{V_3}(g_3), \mathbf{V_3}(h_3)]= & {} 0. \end{aligned}$$
Table 1 Commutator table of Lie algebra
Full size table

3 Group-invariant solutions of the KD equation

Authors considered a particular choices of the functions \(f_2=2a_0 \bar{f_1}-\frac{1}{18}\) and \(f_3=a^2_0\bar{\bar{f_1}}\) (\(a_0\) is a constant). Consequently, Lie symmetry supplies following Lagrange system to generate various forms of the invariant solutions (Tables 1, 2).

$$\begin{aligned}&\frac{\hbox {d}x}{18x{\bar{f_1}}+3(y+a_0)^2\bar{\bar{f_1}}} = \frac{\hbox {d}y}{36(y+a_0)\bar{f_1}} =\frac{\hbox {d}t}{54f_1}=\frac{\hbox {d}u}{\frac{6}{a}(y+a_0) \bar{\bar{f_1}}+18\left( \frac{2b}{a^2}-u\right) \bar{f_1}}\nonumber \\&\quad =\frac{\hbox {d}v}{\left[ \frac{(y+a_0)^2}{a}\bar{\bar{\bar{f_1}}}+\frac{6x}{a}\bar{\bar{f_1}}+6(y+a_0)\left( \frac{2b}{a^2}-u\right) \bar{\bar{f_1}}+36\left( \frac{2b^2}{a^3}-v\right) \bar{f_1}\right] }. \end{aligned}$$
(4)
Table 2 Adjoint table of Lie algebra
Full size table

The solution of Eq. (4) can be written as

$$\begin{aligned} u&=\frac{(y+a_0)\bar{f_1}}{9af_1}+\frac{2b}{a^2}+\frac{U(X,Y)}{f_1^\frac{1}{3}}, \end{aligned}$$
(5)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad -\frac{(y+a_0)\bar{f_1}\,U(X,Y)}{9f_1^{\frac{4}{3}}}+\frac{V(X,Y)}{f_1^{\frac{2}{3}}}. \end{aligned}$$
(6)

Obviously, U(X, Y) and V(X, Y) are the similarity functions of the similarity variables X, Y as

$$\begin{aligned} X=\frac{x}{f_1^\frac{1}{3}}-\frac{(y+a_0)^2\bar{f_1}}{18f_1^{\frac{4}{3}}},\quad Y=\frac{(y+a_0)}{f_1^\frac{2}{3}}. \end{aligned}$$
(7)

The functions U(X, Y), V(X, Y) can be calculated by the following system

$$\begin{aligned} 2U_{XXX}-{3a^2}U^2U_X{+}6V_Y{-}6aV U_X{=}0, U_Y{=}V_X. \end{aligned}$$
(8)

Furthermore, the above system provides

$$\begin{aligned} {\hat{\xi }}&=a_1+\frac{a_2}{2}X,\quad {\hat{\eta }}=a_3+a_2 Y,\nonumber \\ {\hat{\phi }}&=-\frac{a_2}{2}U,\quad {\hat{\psi }}=-a_2V, \end{aligned}$$
(9)

where \(a_1\), \(a_2\) and \(a_3\) are arbitrary constants. Hence, the spanned vector field of Eq. (8) can be written as:

$$\begin{aligned} \mathbf{W}=a_1\mathbf{W_1}+a_2 \mathbf{W_2}+a_3 \mathbf{W_3}, \end{aligned}$$

where

$$\begin{aligned}&\mathbf{W_1}=\frac{\partial }{\partial X},\quad \mathbf{W_2}=\frac{X}{2}\frac{\partial }{\partial X}+Y\frac{\partial }{\partial Y}-\frac{U}{2}\frac{\partial }{\partial U}-V\frac{\partial }{\partial V},\\&\mathbf{W_3}=\frac{\partial }{\partial Y}. \end{aligned}$$

To compute the adjoint representation, following Lie series can be written as:

$$\begin{aligned} Ad[\exp (\epsilon \,W_i)]W_j&= Wj- \epsilon [W_i, W_j ]\\&\quad +\frac{1}{2}\epsilon ^2[W_i,[W_i,W_j]]-\cdots , \end{aligned}$$

Further processing of the problem results in the following cases:

Case (I): \(a_2\ne 0\), yields

$$\begin{aligned}&\frac{\hbox {d}X}{A_1+\frac{1}{2}X}=\frac{\hbox {d}Y}{A_2+Y}=\frac{\hbox {d}U}{-\frac{1}{2}U}=\frac{\hbox {d}V}{-V}, \end{aligned}$$
(10)

where \(A_1=\frac{a_1}{a_2} \), \( A_2=\frac{a_3}{a_2} \).

The above Lagrange system further proceeds as

$$\begin{aligned}&U=\frac{U_1(X_1)}{(A_2+Y)^\frac{1}{2}},\, V=\frac{V_1(X_1)}{A_2+Y}\nonumber \\&\text{ with }\,\, X_1=\frac{(2A_1+X)}{(A_2+Y)^{\frac{1}{2}}}. \end{aligned}$$
(11)

The above system is responsible to evaluate the unknown functions \(U_1\) and \(V_1\) from the following equations

$$\begin{aligned}&2\bar{\bar{\bar{U_1}}}-{3a^2}U_1^2\bar{U_1}-6aV_1\bar{U_1}-3X_1\bar{V_1}-6V_1=0,\nonumber \\&X_1\bar{U_1}+U_1+2\bar{V_1}=0. \end{aligned}$$
(12)

Equation (12) is a nonlinear ordinary differential equation. We could not find its general solution. However, some particular solutions can be found as:

$$\begin{aligned} \mathbf{Case (Ia):} ~~&U_1=\pm \frac{2}{aX_1}-\frac{X_1}{a},\,\, V_1=\frac{X_1^2}{2a}\pm \frac{1}{a}. \end{aligned}$$

Ultimately, the solution of KD equation can be read as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}-\frac{(2A_1+X)}{a\,f^\frac{1}{3}(A_2+Y)}+\frac{2b}{a^2}\nonumber \\&\quad \pm \frac{2}{a\,f^\frac{1}{3}(2A_1+X)}, \end{aligned}$$
(13)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad \mp \frac{2(y+a_0)\bar{f_1}}{9\,a\,f_1^{\frac{4}{3}}(2A_1+X)}+\frac{(y+a_0)\bar{f_1}}{9\,a\,f_1^{\frac{4}{3}}}\frac{(2A_1+X)}{(A_2+Y)}\nonumber \\&\quad +\frac{(2A_1+X)^2}{2\,a\,f_1^{\frac{2}{3}}(A_2+Y)^2}\pm \frac{1}{a\,f_1^{\frac{2}{3}}(A_2+Y)} . \end{aligned}$$
(14)
$$\begin{aligned} \mathbf{Case (Ib):}\quad&U_1=-\frac{X_1}{a}\,\,\, \text{ and }\,\,\, V_1=\frac{X_1^2}{2a}+c_1. \end{aligned}$$

where \(c_1\) is an arbitrary constant. Consequently, the solution of KD equation can be furnished as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}-\frac{(2A_1+X)}{a\,f^\frac{1}{3}(A_2+Y)}+\frac{2b}{a^2}, \end{aligned}$$
(15)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}\nonumber \\&\quad +\frac{c_1}{\,f_1^{\frac{2}{3}}(A_2+Y)}+\frac{(y+a_0)(2A_1+X)\bar{f_1}}{9\,a\,f_1^{\frac{4}{3}}(A_2+Y)}\nonumber \\&\quad +\frac{(2A_1+X)^2}{2\,a\,f_1^{\frac{2}{3}}(A_2+Y)^2}+\frac{2b^2}{a^3} . \end{aligned}$$
(16)
$$\begin{aligned} \mathbf{Case (Ic):} \quad&U_1=\frac{2X_1}{a}\quad \text{ and } \quad V_1=-\frac{X_1^2}{a}. \end{aligned}$$

Hence, complete solution of the KD equation can be furnished as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{2(2A_1+X)}{a\,f^\frac{1}{3}(A_2+Y)}+\frac{2b}{a^2}, \end{aligned}$$
(17)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad -\frac{2(y+a_0)(2A_1+X)\bar{f_1}}{9\,a\,f_1^{\frac{4}{3}}(A_2+Y)}-\frac{(2A_1+X)^2}{\,a\,f_1^{\frac{2}{3}}(A_2+Y)^2} . \end{aligned}$$
(18)

Case (II): \(a_2=0\) and \(a_3\ne 0\), then Lagrange system for (8) is

$$\begin{aligned}&\frac{\hbox {d}X}{A_3}=\frac{\hbox {d}Y}{1}=\frac{\hbox {d}U}{0}=\frac{\hbox {d}V}{0},\quad \text{ where } ~A_3= \frac{a_1}{a_3}. \end{aligned}$$
(19)

Thus, similarity reduction of Eq. (8) can be obtained as

$$\begin{aligned} U=U_2(X_2) \quad \text{ and } \quad V=V_2(X_2), \end{aligned}$$
(20)

with similarity variable \(X_2=X-A_3Y\).

On inserting the values of U and V from Eq. (20) into (8), one can get

$$\begin{aligned}&2\bar{\bar{\bar{U_2}}}-{3a^2}U_2^2\bar{U_2}-6aV_2\bar{U_2}-6A_3\bar{V_2}=0,\nonumber \\ {}&A_3\bar{U_2}+\bar{V_2}=0. \end{aligned}$$
(21)

Equation(21) can be reduced in the following form:

$$\begin{aligned}&2\bar{\bar{\bar{U_2}}}-{3a^2}U_2^2\bar{U_2}+6(A_3^2-a c_2+a A_3U_2)\bar{U_2}=0, \end{aligned}$$
(22)
$$\begin{aligned}&A_3U_2+V_2= c_2. \end{aligned}$$
(23)

Twice integration of Eq. (22) gives

$$\begin{aligned}&\bar{U_2}^2-\frac{a^2}{4}U_2^4+aA_3U_2^3+3(A_3^2-ac_2)U_2^2\nonumber \\&\quad =c_3U_2+c_4, \end{aligned}$$
(24)

where \(c_2,~c_3\) and \(c_4\) are constants of integration.

Equation (24) is a nonlinear ordinary differential. We could not find its general solution. However, some particular solutions are found by adjusting the various constants.

Case (IIa): By setting \(c_2=\frac{a^3}{6}\), \(c_3= 0\), \(c_4= \frac{a^6}{4}\) and \(A_3= 0\), the solution of Eq. (24) is given by

$$\begin{aligned} U_2&=a\tan (ac_5\pm \frac{a^2}{2}X), \quad V_2=\frac{a^3}{6}. \end{aligned}$$
(25)

Combining Eqs. (5)–(6), (20) and (25), solution of the KD equation is attained as

$$\begin{aligned} u=\,&\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{a\,\tan \left( ac_5\pm \frac{a^2}{2}X\right) }{f^\frac{1}{3}}+\frac{2b}{a^2}, \end{aligned}$$
(26)
$$\begin{aligned} v=\,&\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\ {}&-\frac{a\,\bar{f_1}\,(y+a_0)\tan \left( a\,c_5\pm \frac{a^2}{2}X\right) }{9\,f_1^{\frac{4}{3}}}+\frac{a^3}{6\,f_1^{\frac{2}{3}}} . \end{aligned}$$
(27)

Case (IIb): By assuming \(c_2=-\frac{a^3}{12}\), \(c_3= 0\), \(c_4= 0\) and \(A_3= 0\), the solution of Eq. (24) can be obtained as

$$\begin{aligned} U_2&=a\sec \left( ac_6\pm \frac{a^2}{2}X\right) ,\quad V_2=-\frac{a^3}{12}. \end{aligned}$$
(28)

Comprising Eqs. (5)–(6), (20) and (28), solution of the KD equation yields as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{a\,\sec \left( ac_6\pm \frac{a^2}{2}X\right) }{f^\frac{1}{3}}+\frac{2b}{a^2}, \end{aligned}$$
(29)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad -\frac{a\,\bar{f_1}\,\left( y+a_0\right) \sec \left( a\,c_6\pm \frac{a^2}{2}X\right) }{9\,f_1^{\frac{4}{3}}}-\frac{a^3}{12\,f_1^{\frac{2}{3}}} . \end{aligned}$$
(30)

Case (IIc): Let \(c_2=\frac{3a^3}{2}\), \(c_3= a^5\), \(c_4= \frac{a^6}{4}\) and \(A_3= -a^2\), the solution of Eq. (24) can be derived as

$$\begin{aligned} U_2&=-a -\frac{1}{\left( c_7\pm \frac{a}{2}X_2\right) },\,\, V_2=\frac{a^3}{2}-\frac{a^2}{\left( c_7\pm \frac{a}{2}X_2\right) }. \end{aligned}$$
(31)

Incorporating Eqs. (5)–(6), (20) and (31), solution of the KD equation is obtained as follows

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}-\frac{a}{f^\frac{1}{3}}+\frac{2b}{a^2}\nonumber \\ {}&-\frac{2}{f^\frac{1}{3}\{2c_7\pm (aX+a^3Y)\}}, \end{aligned}$$
(32)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad +\frac{\,a (y+a_0)\bar{f_1}}{9\,f_1^{\frac{4}{3}}} +\frac{2 (y+a_0)\bar{f_1}}{9\,f_1^{\frac{4}{3}}\left\{ 2c_7\pm a\left( X+a^2Y\right) \right\} }\nonumber \\&\quad +\frac{a^3}{2\,f_1^{\frac{2}{3}}}-\frac{2a^2}{{\,f_1^{\frac{2}{3}}\left\{ 2c_7\pm a(X+a^2 Y)\right\} }} . \end{aligned}$$
(33)

Case (IId): If \(c_2=\frac{-a^3}{6}\), \(c_3= 0\), \(c_4= \frac{a^6}{4}\) and \(A_3= 0\), then solution of Eq. (24) can be obtained as

$$\begin{aligned} U_2&=a\coth \left( ac_8\pm \frac{a^2}{2}X\right) ,\quad V_2=-\frac{a^3}{6}. \end{aligned}$$
(34)

Comprising Eqs. (5)–(6), (20) and (34), we have explicit solution of the KD equation as

$$\begin{aligned} u=\,&\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{a\,\coth \left( ac_8\pm \frac{a^2}{2}X\right) }{f^\frac{1}{3}}+\frac{2b}{a^2}, \end{aligned}$$
(35)
$$\begin{aligned} v=\,&\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\ {}&-\frac{a\,\bar{f_1}\,(y+a_0)\coth \left( a\,c_8\pm \frac{a^2}{2}X\right) }{9\,f_1^{\frac{4}{3}}}-\frac{a^3}{6\,f_1^{\frac{2}{3}}}. \end{aligned}$$
(36)

Case (IIe): When \(c_2=\frac{a^3}{12}\), \(c_3= 0\), \(c_4= 0\) and \(A_3= 0\), the solution of Eq. (24) can be read as

$$\begin{aligned} U_2&=a\,Csch\left( ac_9\pm \frac{a^2}{2}X\right) , \quad V_2=\frac{a^3}{12}. \end{aligned}$$
(37)

Thus from Eqs. (5)–(6), (20) and (37), we derived solution of the KD equation as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{a\,Csch\left( ac_9\pm \frac{a^2}{2}X\right) }{f^\frac{1}{3}}+\frac{2b}{a^2}, \end{aligned}$$
(38)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\ {}&+\frac{a^3}{12\,f_1^{\frac{2}{3}}}-\frac{a\,\bar{f_1}\,(y+a_0)Csch\left( a\,c_8\pm \frac{a^2}{2}X\right) }{9\,f_1^{\frac{4}{3}}}. \end{aligned}$$
(39)

Case (IIf): By considering \(c_2=\frac{a^3}{3}\), \(c_3= 0\), \(c_4= 0\) and \(A_3= -\frac{a^2}{2}\), the solution of Eq. (24) is given as

$$\begin{aligned}&U_2=\frac{a\,c_{10}\,e^{\pm \frac{a^2}{2}X_2}}{\left\{ 1-\,c_{10}\,e^{\pm \frac{a^2}{2}X_2}\right\} },\nonumber \\ {}&V_2=\frac{a^3}{3}+\frac{a^3\,c_{10}\,e^{\pm \frac{a^2}{2}X_2}}{2\left( 1-\,c_{10}\,e^{\pm \frac{a^2}{2}X_2}\right) }. \end{aligned}$$
(40)

Comprising Eqs. (5)–(6), (20) and (40), we have explicit solution of the KD equation as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{2b}{a^2}\nonumber \\&\quad +\frac{a\,c_{10}\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }}{f^\frac{1}{3}\left[ 1-\,c_{10}\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }\right] } , \end{aligned}$$
(41)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}\nonumber \\&\quad -\frac{a\,c_{10}\,\bar{f_1}\,(y+a_0)\,\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }}{9\,f_1^{\frac{4}{3}}\left[ 1-\,c_{10}\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }\right] }+\frac{2b^2}{a^3}\nonumber \\&\quad +\frac{a^3\,c_{10}\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }}{2\,f_1^{\frac{2}{3}}\left[ 1-\,c_{10}\,e^{\left\{ \pm \frac{a^2}{2}\left( X+\frac{a^2}{2}Y\right) \right\} }\right] }+\frac{a^3}{3\,f_1^{\frac{2}{3}}} . \end{aligned}$$
(42)

Case (IIg): By taking \(c_2=\frac{A_3^2}{a}-\frac{a}{12}\), \(c_3= 0\) and \(c_4= 0\), the solution of Eq. (24) can be derived as

$$\begin{aligned}&U_2=\frac{a}{\left[ \sqrt{a^2+4 A^2_3} \sin \left\{ \frac{a}{2}\left( c_{11}\pm X_2\right) \right\} -2A_3\right] }, \nonumber \\&V_2=c_2-\frac{a A_3}{\left[ \sqrt{a^2+4 A^2_3} \sin \left\{ \frac{a}{2}\left( c_{11}\pm X_2\right) \right\} -2A_3\right] }. \end{aligned}$$
(43)
Fig. 1
figure 1

Multisoliton wave profiles of u, v via Eqs. (13)–(14) at time \(t = 1.6\)

Full size image

Incorporating Eqs. (5)–(6), (20) and (43), solution of the KD equation can be attained as

$$\begin{aligned} u&= \frac{af_1^{-{\frac{1}{3}}}}{\left[ \sqrt{a^2+4 A^2_3} \sin \left\{ \frac{a}{2}\left( c_{11}\pm (X-A_3Y)\right) \right\} -2A_3\right] }\nonumber \\ {}&+\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1} +\frac{2b}{a^2}, \end{aligned}$$
(44)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}\nonumber \\&\quad -\frac{af_1^{-{\frac{4}{3}}}\bar{f_1}(y+a_0)}{9\left[ \sqrt{a^2+4 A^2_3} \sin \left\{ \frac{a}{2}\left( c_{11}\pm (X-A_3Y)\right) \right\} -2A_3\right] }\nonumber \\&\quad -\frac{af_1^{-{\frac{2}{3}}}A_3}{\left[ \sqrt{a^2+4 A^2_3} \sin \left\{ \frac{a}{2}\left( c_{11}\pm (X-A_3Y)\right) \right\} -2A_3\right] }\nonumber \\&\quad +\frac{c_2}{f_1^{\frac{2}{3}}}+\frac{2b^2}{a^3}. \end{aligned}$$
(45)

Case (IIh): By setting \(c_2=\frac{\sqrt{c_4}}{3}+\frac{c_3^2}{3ac_4}\), \(A_3= -\frac{c_3}{2\sqrt{c_4}}\) and \(c_4 > 0\), the solution of Eq. (24) can be read as

$$\begin{aligned}&U_2=\frac{4c_4}{\left[ 4kc_4^{\frac{1}{2} }\tan \left\{ k\left( c_{12}\pm X_2\right) \right\} -c_3\right] }, \nonumber \\ {}&V_2=c_2-\frac{4c_4A_3}{\left[ 4kc_4^{\frac{1}{2} }\tan \left\{ k\left( c_{12}\pm X_2\right) \right\} -c_3\right] }, \end{aligned}$$
(46)

where \(k= \frac{1}{4}\sqrt{(8ac_4^{\frac{1}{2} }-\frac{c_3^2}{c_4})}\) with \(c_3^2\le 8ac_4^{\frac{3}{2}}\) .

Making use of Eqs. (5)–(6), (20) and (46), solution of the KD equation can be obtained as

$$\begin{aligned} u&=\frac{(y+a_0)^2\bar{f_1}}{9\,a\,f_1}+\frac{2b}{a^2}\nonumber \\&\quad +\frac{4c_4f_1^{-{\frac{1}{3}}}}{\left[ 4kc_4^{\frac{1}{2}} \tan \left\{ k\left( c_{12}\pm (X-A_3Y)\right) \right\} -c_3\right] } , \end{aligned}$$
(47)
$$\begin{aligned} v&=\frac{x\bar{f_1}}{9af_1}+\frac{(y+a_0)^2\bar{\bar{f_1}}}{54af_1}-\frac{(y+a_0)^2\bar{f_1}^2}{54af^2_1}+\frac{2b^2}{a^3}\nonumber \\&\quad -\frac{4c_4 f_1^{-{\frac{4}{3}}}\bar{f_1}(y+a_0)}{9\left[ 4kc_4^{\frac{1}{2}} \tan \left\{ k\left( c_{12}\pm (X-A_3Y)\right) \right\} -c_3\right] }+\frac{c_2}{f_1^{\frac{2}{3}}}\nonumber \\&\quad -\frac{4c_4 A_3f^{-{\frac{2}{3}}}}{\left[ 4kc_4^{\frac{1}{2}} \tan \left\{ k\left( c_{12}\pm (X-A_3Y)\right) \right\} -c_3\right] } . \end{aligned}$$
(48)

where \(c_{i}'s~{(5 \le i \le 12)}\) are arbitrary constants of integration and X, Y can be read from Eq. (7).

Fig. 2
figure 2

Multisoliton and doubly solitons wave profiles of u, v via Eqs. (15)–(16) at time \(t = 0\)

Full size image
Fig. 3
figure 3

Multisoliton and doubly solitons wave profiles of u, v via Eqs. (17)–(18) at time \(t = 0\)

Full size image
Fig. 4
figure 4

Periodic multisoliton wave profiles for Eqs. (26)–(27) treating at time \(t = 0.1869\)

Full size image
Fig. 5
figure 5

Periodic multisoliton wave profiles for Eqs. (29)–(30) at time \(t = 0.88777\)

Full size image
Fig. 6
figure 6

Multisoliton wave profiles for Eqs. (32)–(33) at time \(t = 0.0598\)

Full size image
Fig. 7
figure 7

Multisoliton wave profiles for Eqs. (35)–(36) at time \(t = 0.4820\)

Full size image
Fig. 8
figure 8

Multisoliton wave profiles for Eqs. (38)–(39) at time \(t = 0.8331\)

Full size image
Fig. 9
figure 9

Parabolic wave profiles for Eqs. (41)–(42) at time \(t = 0\)

Full size image
Fig. 10
figure 10

Multiple wavefront profiles for Eqs. (44)–(45) at time \(t = 0.9631\)

Full size image
Fig. 11
figure 11

Multisoliton wave interaction profiles of u, v via Eqs. (47)–(48) at time \(t = 0.3008\)

Full size image

4 Analysis and discussion

A variety of eleven group-invariant solutions of the KD equation are followed by Eqs. (13)–(14), (15)–(16), (17)–(18), (26)–(27), (29)–(30), (32)–(33), (35)–(36), (38)–(39), (41)–(42), (44)–(45) and (47)–(48). Nature of each result has been identified through their evolutionary profiles. Consequently, dynamical behavior of the results such as multisoliton, doubly solitons, periodic multisoliton, multiple wavefront, parabolic, solitons interactions and stationary wave has been found by their graphical structures.

Solitons theory is very useful to explain the various phenomena in nonlinear dynamics such as optical switching in slab wave guides, optical bistability, propagation of light in fibers, surface waves in nonlinear dielectrics and many other phenomena in plasma and fluid dynamics [33, 34].

The surface plots of the results have been traced between the spaces range \( -\,5\le x,y \le 5\) with particular choices of arbitrary function \(f_1(t)\) such as \(a_4\,\exp (a_5t+a_6)\), \((a_7t+a_8)\) and \((a_7t+a_8)^2\). The values of arbitrary constants have been taken randomly from numerical simulations to trace physically meaningful profile. The process has been followed by computational software MATLAB. The physical nature of the results is analyzed in the following manner:

Figure 1: The solution of the KD equation represented by Eqs. (13)–(14) shows multisoliton wave nature at time \(t=1.6\). The profiles have been traced with the function \(f_1(t)=a_4\,\exp ({a_5t+a_6})\), while arbitrary constants recorded from MATLAB simulations as: \(a= 0.8772\), \(b= 0.7849\), \(a_0= 0.4650\), \(a_1= 0.8140\), \(a_2= 0.8984\), \(a_3= 0.4292\), \(a_4= 0.3343\), \(a_5= 0.5966\) and \(a_6= 0.9020\). Furthermore, we have observed through numerical simulations that multisoliton wave nature of the solution turns into stationary wave nature after time \(t = 4.7096\).

Figure 2: The evolution profiles of Eqs. (15)–(16) show multisoliton and doubly soliton wave nature. These profiles have been traced at \(t=0\) with arbitrary function \((a_7t+a_8)^2\). The values of constants taken through numerical simulation as \(a_7= 0.7021\), \(a_8= 0.3775\), \(c_1=0.5777\) and remaining kept same as in Fig. 1.

Figure 3: The profiles of Eqs. (17)–(18) reveal multisoliton and doubly soliton nature. We have traced the surface plots at time \(t=0\) for arbitrary function \(f_1(t)=(a_7t+a_8)\), while values of arbitrary constant are taken the same as in previous profiles.

Figures 4 and 5: The results represented by Eqs. (26)–(27), (29)–(30) describe periodic multisoliton nature. Figures are traced for \(c_5=0.6987\) and \(c_6= 0.1500\), while other values of constants are used from above profiles. Furthermore, we have used function \(f_1(t)= (a_7t+a_8)^2\) for Fig. 4 and \(f_1(t)= (a_7t+a_8)\) for Fig. 5.

Figures 6, 7 and 8: The multisoliton wave profiles of solutions followed by Eqs. (32)–(33), (35)–(36) and (38)–(39) are shown in Figs. 6-8. The values of the arbitrary constants are taken as \(c_7=0.1386\), \(c_8=0.7482\), \(c_9=0.4453\) while remaining constants kept same as in previous profiles. We have used arbitrary function \(a_4\,\exp (a_5t+a_6)\) in Figs. 6 and 7, while Fig. 8 is traced for the function \((a_7t+a_8)\).

Figure 9: Expressions (41)–(42) show parabolic nature at \(t=0\). The surface plots are traced by taking \(c_{10}=0.3037\) and function \(f_1(t)=(a_7t+a_8)^2\) . The values of other constants are used from previous figures.

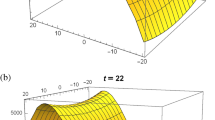
Figure 10: The results given by expressions (44)–(45) are described graphically in this figure. We have presented the physical nature at \(t=0.9631\), which show multiple wavefront nature. The profiles are plotted by taking the values of constants \(A_3=1.8966\), \(c_2=4.0276\), \(c_{11}=0.5108\) for the function \((a_7t+a_8)^2\), while other values of the constants kept the same as in previous figures.

Figure 11: Interactions of solitons can be viewed in this figure. The surfaces are traced for Eqs. (47)–(48) for the function \((a_7t+a_8)\) at \(t=0.3008\). The values of constants are taken as \(a=3.1980\), \(c_2=1.7120\), \(c_3=-\,2.4149\), \(c_4=0.4053\), \(c_{12}=0.1048\), \(k=0.3445\), and remaining are the same as in previous profiles.

5 Conclusions

In this paper, we have obtained some group-invariant solutions of Konopelchenko–Dubrovsky equation by using Lie symmetry approach. Furthermore, we have presented infinite-dimensional Lie algebra and commutation relations for the equation. The solutions followed by Eqs. (13)–(14), (15)–(16), (17)–(18), (26)–(27), (29)–(30), (32)–(33), (35)–(36), (38)–(39), (41)–(42), (44)–(45) and (47)–(48) are analyzed physically. Consequently, results show multisoliton, doubly solitons periodic multisoliton, multiple wavefront, parabolic, solitons interactions and stationary behavior of the waves. The solutions obtained in this research are more general and may have richer physical structures than previous findings [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. These results may provide a future research scope to validate the various numerical scheme and their accuracy.