1 Introduction

Chaotic systems play a critical role in numerous fields such as, for example, information processing, secure communications, and high-performance circuit design for telecommunications [1]. Chaos is a very attractive subject from a theoretical point of view; however, it is quite challenging technically [2]. Over the last decade, many techniques have been proposed to control chaos, and many excellent results have been reported [3–27]. In 2005, Qi et al. [28] investigated the complex dynamical behaviors (e.g., familiar period-doubling route to chaos, Hopf bifurcation) of the following Qi system:

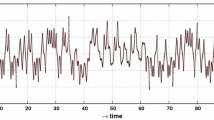
$$\begin{aligned} \dot{x}_1&= a(x_2-x_1)+x_2x_3x_4,\nonumber \\ \dot{x}_2&= b(x_1+x_2)-x_1x_3x_4,\nonumber \\ \dot{x}_3&= -cx_3+x_1x_2x_4,\\ \dot{x}_4&= -dx_4+x_1x_2x_3,\nonumber \end{aligned}$$
(1)

where \(x_1,x_2,x_3\), and \(x_4\) are the state variables of the system and \(a,b,c\), and \(d\) are all positive real constants. Interestingly, system (2) can generate chaotic phenomena (Fig. 1) given the system parameters \(a=30,b=10,c=1\), and \(d=10\).

Fig. 1
figure 1

Chaotic attractor of system (2) with \(a=30,b=10,c=1\), and \(d=10\)

Full size image

Since chaos can cause irregular behaviors that are sometimes undesirable in practical systems, in many cases, it is preferable to avoid or eliminate them. Control mechanisms that enable a chaotic system to achieve and maintain a desired dynamical behavior have potential applications in various disciplines [29]. In 2009, Niah and Sunday [29] investigated the chaos control of system (2) by applying a recursive backstepping nonlinear controller. The aim of this paper is to investigate the dynamics of a four-dimensional (4D) chaotic Qi system by considering the effect of delayed feedback. Analyzing the characteristic equation of a linearized system of the Qi model, we theoretically prove that under some suitable conditions, a Hopf bifurcation will occur. Numerical results support theoretical predictions.

2 Controlling chaos via feedback control methods

In this section, we shall apply a conventional feedback method to the dynamical system (2). Our aim is to drag the chaotic trajectories to the equilibria or the periodic orbits. To reflect the dynamical behaviors of the model depending on past information, it is reasonable to incorporate a time delay into this system. The signal error of the current and past states of the continuous time system will be given as feedback to the system itself. Following the idea of Pyragas [30], we consider two cases.

Case I Add the time-delayed force \(k_1[x_2-x_2(t-\tau _1)]\) to the second equation of system (2). In this case, system (2) takes the form

$$\begin{aligned} \dot{x}_1&= a(x_2-x_1)+x_2x_3x_4,\nonumber \\ \dot{x}_2&= b(x_1+x_2)-x_1x_3x_4+k_1[x_2(t)-x_2(t-\tau _1)],\nonumber \\ \dot{x}_3&= -cx_3+x_1x_2x_4,\\ \dot{x}_4&= -dx_4+x_1x_2x_3.\nonumber \end{aligned}$$
(2)

Case II Add the time-delayed forces \(k_2[x_2(t)-x_2(t-\tau _2)]\) and \(k_3[x_3(t)-x_3(t-\tau _2)]\) to the second and third equations of system (2), respectively. In this case, system (2) becomes

$$\begin{aligned} \dot{x}_1&= a(x_2-x_1)+x_2x_3x_4,\nonumber \\ \dot{x}_2&= b(x_1+x_2)-x_1x_3x_4+k_2[x_2(t)-x_2(t-\tau _2)],\nonumber \\ \dot{x}_3&= -cx_3+x_1x_2x_4+k_3[x_3(t)-x_3(t-\tau _2)],\\ \dot{x}_4&= -dx_4+x_1x_2x_3.\nonumber \end{aligned}$$
(3)

Let \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) be the equilibrium of systems (2) and (3).

Case 1 Delayed feedback on the first equation [system (2)]:

The linearized system of Eq. (2) around \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) is given by

$$\begin{aligned} \dot{x}_1&= -ax_1+(a+x_3^*x_4^*)x_2+x_2^*x_4^*x_3+x_2^*x_3^*x_4,\nonumber \\ \dot{x}_2&= (b+x_3^*x_4^*)x_1+k_1x_2+x_1^*x_4^*x_3+x_1^*x_3^*x_4-k_1x_2(t-\tau _1),\nonumber \\ \dot{x}_3&= x_2^*x_4^*x_1+x_1^*x_4^*x_2-cx_3+x_1^*x_2^*x_4,\\ \dot{x}_4&= x_2^*x_3^*x_1+x_1^*x_3^*x_2+x_1^*x_2^*x_3-dx_4.\nonumber \end{aligned}$$
(4)

The characteristic equation of (4) takes the form

$$\begin{aligned} \det \left( \begin{array}{cccc} \lambda +a &{}\quad -(a+x_3^*x_4^*) &{}\quad -x_2^*x_4^* &{}\quad -x_2^*x_3^* \\ -(b+x_3^*x_4^*) &{} \quad \lambda -k_1+k_1\text {e}^{-\lambda \tau _1} &{}\quad -x_1^*x_4^* &{}\quad -x_1^*x_3^* \\ -x_2^*x_4^* &{} \quad -x_1^*x_4^* &{} \lambda +c &{}\quad -x_1^*x_2^* \\ -x_2^*x_3^* &{} \quad -x_1^*x_3^* &{} \quad -x_1^*x_2^* &{}\quad \lambda +d\\ \end{array} \right) =0, \end{aligned}$$
(5)

that is,

$$\begin{aligned} \lambda ^4+a_3\lambda ^3+a_2\lambda ^2+a_1\lambda +a_0+(b_3\lambda ^3+b_2 \lambda ^2+b_1\lambda +b_0)\text {e}^{-\lambda \tau _1}=0, \end{aligned}$$
(6)

where

$$\begin{aligned} a_0&= cdk_1+2(x_1^*)^2x_2^*x_3^*x_4^*+c(x_1^*x_3^*)^2+d(x_1^*x_4^*)^2+k_1(x_1^*x_2^*)^2\\&+(b+x_3^*x_4^*)[cd(a+x_3^*x_4^*)-2(x_1^*x_2^*)^2x_3^*x_4^*-cx_1^*x_2^*(x_3^*)^2\\&-dx_1^*x_2^*(x_4^*)^2-(a+x_3^*x_4^*)(x_1^*x_2^*)^2]-x_2^*x_4^*[(a+x_3^*x_4^*)x_1^*x_4^*d\\&+(x_1^*x_3^*)^2x_2^*x_4^*-k_1x_1^*x_4^*(x_2^*)^2+(x_1^*)^2x_2^*x_3^*(a+x_3^*x_4^*)]\\&-x_2^*x_4^*[(a+x_3^*x_4^*)(x_1^*x_4^*)^2+(x_1^*x_4^*)^2x_2^*x_3^*-k_1x_2^*x_3^*\\&-(x_1^*x_4^*)^2x_2^*x_3^*+k_1x_1^*x_2^*(x_4^*)^2+c(a+x_3^*x_4^*)x_1^*x_3^*],\\ a_1&= a[cd-k_1(c+d)-(x_1^*x_3^*)^2-(x_1^*x_4^*)^2-(x_1^*x_2^*)^2]\\&-[cdk_1+2(x_1^*)^2x_2^*x_3^*x_4^*+c(x_1^*x_3^*)^2+d(x_1^*x_4^*)^2+k_1(x_1^*x_2^*)^2]\\&+(b+x_3^*x_4^*)[(c+d)(a+x_3^*x_4^*)-x_1^*x_2^*((x_3^*)^2+(x_4^*)^2)]\\&-x_2^*x_4^*[(a+x_3^*x_4^*)x_1^*x_4^*+x_1^*x_4^*(x_2^*)^2+(d-k_1)x_2^*x_4^*]\\&-x_2^*x_3^*[((c-k_1)x_2^*x_3^*+(a+x_3^*x_4^*)x_1^*x_3^*+x_1^*x_2^*(x_4^*)^2],\\ a_2&= a(c+d-k_1)+cd-k_1(c+d) -(x_1^*x_3^*)^2-(x_1^*x_4^*)^2-(x_1^*x_2^*)^2\\&-(a+x_3^*x_4^*)(b+x_3^*x_4^*)-(x_2^*x_4^*)^2-(x_2^*x_3^*)^2,\\ a_3&= a+c+d-k_1,\\ b_0&= k_1acd-k_1a(x_1^*x_4^*)^2-k_1x_1^*(x_4^*)^3(x_2^*)^3 -k_1d(x_2^*x_4^*)^2-x_2^*x_3^*[x_2^*x_3^*k_1c+x_1^*x_2^*(x_4^*)^2k_1],\\ b_1&= k_1a(c+d)+k_1cd-k_1(x_1^*x_2^*)^2-(x_2^*x_4^*)^2k_1,\\ b_2&= k_1(c+d+a),\\ b_3&= k_3. \end{aligned}$$

Next, we will discuss the distribution of the roots of the transcendental equation (6).

Lemma 1

[31] For the transcendental equation

$$\begin{aligned} P(\lambda ,\mathrm{e}^{-\lambda \tau _1},\ldots ,\mathrm{e}^{-\lambda \tau _m})&= \lambda ^n+p_1^{(0)} \lambda ^{n-1}+\cdots +p_{n-1}^{(0)}\lambda +p_n^{(0)} +\left[ p_1^{(1)}\lambda ^{n-1}+\cdots +p_{n-1}^{(1)}\lambda +p_{n}^{(1)}\right] \mathrm{e}^{-\lambda \tau _1}+\cdots \\&+\left[ p_1^{(m)}\lambda ^{n-1}+\cdots +p_{n-1}^{(m)}\lambda +p_{n}^{(m)}\right] \mathrm{e}^{-\lambda \tau _m}=0, \end{aligned}$$

as \((\tau _1,\tau _2,\tau _3,\ldots ,\tau _m)\) vary, the sum of orders of the zeros of \(P(\lambda , \mathrm{e}^{-\lambda \tau _1},\ldots ,\mathrm{e}^{-\lambda \tau _m})\) in the open right half-plane can change, and only a zero appears on or crosses the imaginary axis.

When \(\tau _1=0,\) equation (6) becomes

$$\begin{aligned} \lambda ^4+(a_3+b_3)\lambda ^3+(a_2+b_2)\lambda ^2+(a_1+b_1) \lambda +(a_0+b_0)=0. \end{aligned}$$
(7)

We can easily know that all the roots of (7) have a negative real part if the following conditions hold:

$$\begin{aligned} D_1&= a_3+b_3>0,\end{aligned}$$
(8)
$$\begin{aligned} D_2&= \det \left( \begin{array}{cc} a_3+b_3 &{} \quad a_1+b_1 \\ 1 &{}\quad a_2+b_2 \\ \end{array} \right) =(a_2+b_2)(a_3+b_3)-(a_1+b_1)>0,\end{aligned}$$
(9)
$$\begin{aligned} D_3&= \det \left( \begin{array}{ccc} a_3+b_3 &{}\quad a_1+b_1 &{} 0 \\ 1 &{} a_2+b_2 &{}\quad a_0+b_0 \\ 0 &{} a_3+b_3 &{}\quad a_1+b_1 \\ \end{array} \right) \nonumber \\&= (a_3+b_3)[(a_2+b_2)(a_1+b_1)-(a_3+b_3)(a_0+b_0)]-(a_1+b_1)^2>0,\end{aligned}$$
(10)
$$\begin{aligned} D_4&= \det \left( \begin{array}{cccc} a_3+b_3 &{}\quad a_1+b_1 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad a_2+b_2 &{}\quad a_0+b_0 &{} \quad 0 \\ 0 &{}\quad a_3+b_3 &{}\quad a_1+b_1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad a_2+b_2 &{}\quad a_0+b_0 \\ \end{array} \right) =(a_0+b_0)D_3>0. \end{aligned}$$
(11)

Then the equilibrium point \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) is locally asymptotically stable when (8)–(11) hold.

We assume that

$$\begin{aligned} (\hbox {H}1)\qquad (8){-}(11)~\hbox {hold}. \end{aligned}$$

For \(\omega >0,\mathrm{i}\omega \) is a root of (6) if and only if

$$\begin{aligned} \omega ^4-a_3\omega ^3\mathrm{i}-a_2\omega ^2+a_1\omega {\mathrm{i}}+a_0+(-b_3 \omega ^3\mathrm{i}-b_2\omega ^2+b_1\omega {\mathrm{i}}+b_0)\mathrm{e}^{-\omega \tau _1{\mathrm{i}}}=0. \end{aligned}$$

Separating the real and imaginary parts gives

$$\begin{aligned} (b_0-b_2\omega ^2)\cos \omega \tau _1+(b_1\omega -b_3\omega ^3)\sin \omega \tau _1&= a_2\omega ^2-\omega ^4-a_0,\nonumber \\ (b_1\omega -b_3\omega ^3)\cos \omega \tau _1-(b_0-b_2\omega ^2)\sin \omega \tau _1&= a_3\omega ^3-a_1\omega . \end{aligned}$$
(12)

It follows from (12) that

$$\begin{aligned} (b_0-b_2\omega ^2)^2+(b_1\omega -b_3\omega ^3)^2 =(a_2\omega ^2-\omega ^4-a_0)^2+(a_3\omega ^3-a_1\omega )^2, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \omega ^8+p_3\omega ^6+p_2\omega ^4+p_1\omega ^2+p_0=0, \end{aligned}$$
(13)

where

$$\begin{aligned}&p_0=a_0^2-b_0^2, \quad p_1=a_1^2-2a_0a_2+2b_0b_2-b_1^2,\\&p_2=a_0^2-2a_1a_3+2b_1b_3+2a_0-b_2^2,\quad p_3=a_3^2-2a_2-b_3^2. \end{aligned}$$

Use the notation \(z=\omega ^2\); then (13) takes the following form:

$$\begin{aligned} z^4+p_3z^3+p_2z^2+p_1z+p_0=0. \end{aligned}$$
(14)

Let

$$\begin{aligned} h(z)=z^4+p_3z^3+p_2z^2+p_1z+p_0. \end{aligned}$$
(15)

Suppose

$$\begin{aligned} (\hbox {H}2)\qquad (14) \, \hbox {has at least one positive real root}. \end{aligned}$$

If all the coefficients of system (2) are given, then we can easily calculate the roots of (14). Since \(\lim _{z\rightarrow {\infty }}h(z)=\infty \), we can conclude that if \(p_0<0\), then (14) has at least one positive real root. Without loss of generality, we assume that (14) has four positive real roots, defined by \(z_1,z_2,z_3,z_4\). Then (13) has four positive roots:

$$\begin{aligned} \omega _1=\sqrt{z_1}, \quad \omega _2=\sqrt{z_2},\quad \omega _3 =\sqrt{z_3},\quad \omega _4=\sqrt{z_4}. \end{aligned}$$

By (12), we derive

$$\begin{aligned} \cos \omega _k\tau _1=\frac{(a_2\omega _k^2-\omega _k^4-a_0)(b_0-b_2\omega _k^2) +(a_3\omega _k^3-a_1\omega _k)(b_1\omega _k-b_3\omega _k^3)}{(b_0-b_2\omega _k^2)^2+(b_1\omega _k-b_3\omega _k^3)^2}. \end{aligned}$$

Thus, if we use the notation

$$\begin{aligned} \tau _{1k}^{(j)}=\frac{1}{\omega _k}\Bigg \{\arccos \left( \frac{(a_2\omega _k^2-\omega _k^4-a_0)(b_0-b_2\omega _k^2) +(a_3\omega _k^3-a_1\omega _k)(b_1\omega _k-b_3\omega _k^3)}{(b_0-b_2\omega _k^2)^2+(b_1\omega _k-b_3\omega _k^3)^2}\right) +2j\pi \Bigg \}, \end{aligned}$$
(16)

where \(k=1,2,3,4; j=0,1,2,\ldots \), then \(\pm {\mathrm{i}\omega _k}\) are a pair of imaginary roots of Eq. (6) when \(\tau _1=\tau _{1k}^{(j)}\). Define

$$\begin{aligned} \tau _{1_0}=\tau _{1k0}^{(0)}=\min _{k\in \{1,2,3,4\}}\{\tau _{1k}^{(0)}\}, \quad \omega _0=\omega _{k0}. \end{aligned}$$
(17)

Let \(\lambda (\tau _1)=\alpha (\tau _1)+\mathrm{i}\omega (\tau _1)\) be a root of (6) around \(\tau _1=\tau _{1k}^{(j)}\), where \(\alpha (\tau _1)\) and \(\omega (\tau _1)\) satisfy \(\alpha (\tau _{1k}^{(j)})=0\) and \( \omega (\tau _{1k}^{(j)})=\omega _k.\) Differentiating both sides of (6) with respect to \(\tau _1\) yields

$$\begin{aligned} \left[ \frac{\mathrm{d}\lambda }{\mathrm{d}\tau _1}\right] ^{-1}= -\frac{(4\lambda ^3+3a_3\lambda ^2+2a_2\lambda +a_0) \text {e}^{\lambda \tau _1}}{\lambda (b_3\lambda ^3+b_2\lambda ^2+b_1\lambda +b_0)} +\frac{3b_3\lambda ^2+2b_2\lambda +b_1}{\lambda (b_3\lambda ^3+b_2\lambda ^2+b_1\lambda +b_0)}-\frac{\tau _1}{\lambda }. \end{aligned}$$

Letting \(\lambda =\mathrm{i}\omega _k, \tau _1=\tau _{1k}^{(j)}\), we have

$$\begin{aligned} \hbox {Re}\Bigg \{\left[ \frac{\mathrm{d}\lambda }{\mathrm{d}\tau _1}\right] ^{-1}\Bigg |_{\lambda =i\omega _k,\tau _1=\tau _{1k}^{(j)}}\Bigg \} =\frac{\rho _1\cos \omega _k\tau _{1k}^{(j)}+\rho _2\sin \omega _k\tau _{1k}^{(j)}+\rho _3}{\Lambda }, \end{aligned}$$

where

$$\begin{aligned} \rho _1&= (a_0-3a_3\omega _k^2)(b_3\omega _k-b_1)+(4\omega _k^2+2a_0) (b_0-b_2\omega _k^2),\\ \rho _2&= (a_0-3a_3\omega _k^2)(b_0-b_2\omega _k^2) -(4\omega _k^3+2a_2\omega _k)(b_3\omega _k-b_1),\\ \rho _3&= (b_1-3b_3\omega _k^2)(b_3\omega _k^2-b_1)+2b_2(b_0-b_2\omega _k^2)\\ \Lambda&= (b_3\omega _k^2-b_1\omega _k)^2+(b_0-b_2\omega _k^2)^2. \end{aligned}$$

Suppose that the following condition holds:

$$\begin{aligned} (\hbox {H}3)\qquad \rho _1\cos \omega _k\tau _{1k0}^{(j)} +\rho _2\sin \omega _k\tau _{1k}^{(j)}+\rho _3\ne {0}. \end{aligned}$$

According to the preceding analysis and the results of Kuang [32] and Hale [33], we have the following theorem.

Theorem 2

If (H1) and (H2) hold, then the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) of system (2) is asymptotically stable when \(\tau _1\in [0,\tau _{1_0})\). In addition to (H1) and (H2), if (H3) holds, then system (2) undergoes a Hopf bifurcation at the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) when \(\tau _1=\tau _{1k}^{(j)}, k=1,2,3,4, j=0,1,2,\ldots \).

Remark 3

It is shown that if (H1) and (H2) are fulfilled, then the states \(x_i(i=1,2,3,4)\) of system (2) will tend to \(x_i^*\) when \(\tau _1\in [0,\tau _{1_0})\). If (H1), (H2), and (H3) hold, then the states \(x_i(i=1,2,3,4)\) of system (2) may coexist and remain in an oscillatory mode near the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\). Thus, chaos vanishes, which means that chaos can be controlled.

Case 2 Delayed feedback on second and third equations [system (3)]

The linearized system of Eq. (3) around \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) is given by

$$\begin{aligned} \dot{x}_1&= -ax_1+(a+x_3^*x_4^*)x_2+x_2^*x_4^*x_3+x_2^*x_3^*x_4,\nonumber \\ \dot{x}_2&= (b+x_3^*x_4^*)x_1+k_2x_2+x_1^*x_4^*x_3+x_1^*x_3^*x_4-k_2x_2(t-\tau _2),\nonumber \\ \dot{x}_3&= x_2^*x_4^*x_1+x_1^*x_4^*x_2+(k_3-c)x_3+x_1^*x_2^*x_4-k_3x_3(t-\tau _2),\\ \dot{x}_4&= x_2^*x_3^*x_1+x_1^*x_3^*x_2+x_1^*x_2^*x_3-dx_4.\nonumber \end{aligned}$$
(18)

The characteristic equation of (19) takes the form

$$\begin{aligned} \det \left( \begin{array}{cccc} \lambda +a &{} \quad -(a+x_3^*x_4^*) &{} \quad -x_2^*x_4^* &{}\quad -x_2^*x_3^* \\ -(b+x_3^*x_4^*) &{} \quad \lambda -k_2+k_2\text {e}^{-\lambda \tau _2} &{}\quad -x_1^*x_4^* &{}\quad -x_1^*x_3^* \\ -x_2^*x_4^* &{}\quad -x_1^*x_4^* &{}\quad \lambda -k_2+c+k_2\text {e}^{\lambda \tau _2} &{}\quad -x_1^*x_2^* \\ -x_2^*x_3^* &{}\quad -x_1^*x_3^* &{}\quad -x_1^*x_2^* &{} \quad \lambda +d\\ \end{array} \right) =0, \end{aligned}$$
(19)

that is,

$$\begin{aligned} \lambda ^4+c_3\lambda ^3+c_2\lambda ^2+c_1\lambda +c_0+(d_3\lambda ^3+d_2 \lambda ^2+d_1\lambda +d_0)\text {e}^{-\lambda \tau _2}+e_0\text {e}^{-2\lambda \tau _2}=0, \end{aligned}$$
(20)

where

$$\begin{aligned} c_0&= a[dk_2(c-k_2)-2x_2^*x_3^*x_4^*(x_1^*)^2+(x_1^*x_3^*)^2(c-k_2)+(x_1^*x_4^*)^2d\\&-k_2(x_1^*x_2^*)^2]+(b+x_3^*x_4^*)[d(a+x_3^*x_4^*)(k_2-c)-x_1^*(x_2^*)^2x_3^*x_4^*\\&-(x_1^*x_2^*)^2x_3^*x_4^*-(c-k_2)x_1^*x_2^*(x_3^*)^2+dx_1^*x_2^*(x_4^*)^2-(a+x_3^*x_4^*)(x_1^*x_2^*)^2]\\&+x_2^*x_4^*[(a+x_3^*x_4^*)x_1^*x_4^*d-(x_1^*x_3^*)^2x_2^*x_4^*+k_2x_1^*x_3^*(x_2^*)^2+(x_1^*x_3^*)^2x_2^*x_4^*\\&-dk_2x_2^*x_4^*+(x_1^*)^2x_2^*x_3^*(a+x_3^*x_4^*)]-x_2^*x_3^*[(a+x_3^*x_4^*)(x_1^*)^2x_2^*x_4^*\\&-k_2x_2^*x_3^*(c-k_2)-k_2x_1^*(x_2^*)^2x_4^*+(c-k_2)(a+x_3^*x_4^*)x_1^*x_3^*,\\ c_1&= dk_2(c-k_2)-2(x_1^*)^2x_2^*x_3^*x_4^*+(x_1^*x_3^*)(c-k_2)+d(x_1^*x_4^*)-k_2(x_1^*x_2^*)^2\\&+a[k_2(c-k_2)+d(c-2k_2)-(x_1^*x_3^*)^2+(x_1^*x_4^*)^2+(x_1^*x_2^*)^2]\\&-(b+x_3^*x_4^*)[(a+x_3^*x_4^*)(c+d-k_2)+x_1^*x_2^*(x_3^*)^2-x_1^*x_2^*(x_4^*)^2]\\&+x_2^*x_4^*[(a+x_3^*x_4^*)x_1^*x_4^*-x_1^*x_4^*(x_2^*)^2+(d-k_2)x_2^*x_4^*]\\&+x_2^*x_3^*[(2k_2-c)x_2^*x_3^*-x_1^*x_4^*(x_2^*)^2-(a+x_3^*x_4^*)x_1^*x_3^*],\\ c_2&= k_2(c-k_2)+d(c-2k_2)-(x_1^*x_3^*)^2+(x_1^*x_4^*)^2+a(d+c-2k_2)\\&-(b+x_3^*x_4^*)(a+x_3^*x_4^*)-(x_2^*x_2^*)^2-(x_2^*x_3^*)^2,\\ c_3&= a+b+c-2k_2,\\ d_0&= a(ck_2-k_2^2)d-ak_2(x_1^*x_3^*)^2+ak_2(x_1^*x_2^*)^2,\\&-(b+x_3^*x_4^*)[dk_2(a+x_3^*x_4^*)+x_1^*x_2^*(x_3^*)^2k_2]\\&+x_2^*x_4^*[dk_2x_2^*x_4^*-k_2x_1^*x_3^*(x_2^*)^2]+x_2^*x_3^*[ck_2-k_2x_1^*(x_2^*)^2x_4^* +k_2(a+x_3^*x_4^*)x_1^*x_3^*],\\ d_1&= (k_2-2k_2^2)d-k_2(x_1^*x_3^*)^2+k_2(x_1^*x_2^*)^2+a(ck_2-2k_2^2+2k_2d)\\&-(b+x_3^*x_4^*)(a+x_3^*x_4^*)k_2+x_2^*x_4^*(k_2x_2^*x_4^*-k_2x_1^*x_3^*(x_2^*)^2) -2k_2(x_2^*x_3^*),\\ d_2&= ck_2-2k_2^2+2k_2d+2k_2a,\\ d_3&= 2k_3,\\ e_0&= ak_2^2. \end{aligned}$$

Multiplying \(\text {e}^{\lambda \tau _2}\) on both sides of (20), we have

$$\begin{aligned} (\lambda ^4+c_3\lambda ^3+c_2\lambda ^2+c_1\lambda +c_0)\text {e}^{\lambda \tau _2} +(d_3\lambda ^3+d_2\lambda ^2+d_1\lambda +d_0)+e_0\mathrm{e}^{-\lambda \tau _2}=0. \end{aligned}$$
(21)

Next, we will focus on the distribution of the roots of the transcendental equation (21).

When \(\tau _2=0,\) (21) reads as

$$\begin{aligned} \lambda ^4+(c_3+d_3)\lambda ^3+(c_2+d_2)\lambda ^2+(c_1+d_1) \lambda +c_0+d_0+e_0=0. \end{aligned}$$
(22)

All the roots of (22) have a negative real part if the following conditions hold:

$$\begin{aligned} \bar{D}_1&= c_3+d_3>0,\end{aligned}$$
(23)
$$\begin{aligned} \bar{D}_2&= \det \left( \begin{array}{c@{\quad }c} c_3+d_3 &{} c_1+d_1 \\ 1 &{} c_2+d_2 \\ \end{array} \right) =(c_2+d_2)(c_3+d_3)-(c_1+d_1)>0,\end{aligned}$$
(24)
$$\begin{aligned} \bar{D}_3&= \det \left( \begin{array}{c@{\quad }c@{\quad }c} c_3+d_3 &{} \quad c_1+d_1 &{}\quad 0 \\ 1 &{}\quad c_2+d_2 &{}\quad c_0+d_0+e_0 \\ 0 &{}\quad c_3+c_3 &{}\quad c_1+c_1 \\ \end{array} \right) \nonumber \\&=(c_3+d_3)[(c_2+d_2)(c_1+d_1) -(c_3+d_3)(c_0+d_0+e_0)]-(c_1+d_1)^2>0,\end{aligned}$$
(25)
$$\begin{aligned} \bar{D}_4&= \det \left( \begin{array}{cccc} c_3+d_3 &{}\quad c_1+d_1 &{} \quad 0 &{}\quad 0 \\ 1 &{}\quad c_2+d_2 &{}\quad c_0+d_0+e_0 &{}\quad 0 \\ 0 &{} \quad c_3+d_3 &{}\quad c_1+d_1 &{} \quad 0 \\ 0 &{}\quad 1 &{} \quad c_2+d_2 &{}\quad c_0+d_0+e_0 \\ \end{array} \right) =(c_0+d_0+e_0)D_3>0. \end{aligned}$$
(26)

Then the equilibrium point \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) is locally asymptotically stable when (23)–(26) hold.

We assume that

$$\begin{aligned} (\hbox {H}4)\qquad (23){-}(26) ~\hbox {hold}. \end{aligned}$$

For \(\tilde{\omega }>0,\mathrm{i}\tilde{\omega }\) is a root of (21) if and only if

$$\begin{aligned} (-\tilde{\omega }^4-c_3\tilde{\omega }^3\mathrm{i}-c_2\tilde{\omega }^2 +c_1\tilde{\omega }{\mathrm{i}}c_0)\mathrm{e}^{\tilde{\omega }\tau _2} +(-d_3\tilde{\omega }^3\mathrm{i}-d_2\tilde{\omega }^2+d_1\tilde{\omega }\mathrm{i}+d_0) +e_0\mathrm{e}^{-\tilde{\omega }\tau _2}=0. \end{aligned}$$

Separating the real and imaginary parts gives

$$\begin{aligned} (\tilde{\omega }^4-c_2\tilde{\omega }^2+c_0+e_0)\cos \tilde{\omega }\tau _2 +(c_3\tilde{\omega }^3-c_1\tilde{\omega })\sin \tilde{\omega } \tau _2=d_2\tilde{\omega }^2-d_0,\nonumber \\ (c_1\tilde{\omega }-c_3\tilde{\omega }^3)\cos \tilde{\omega } \tau _2+(\tilde{\omega }^4-c_2\tilde{\omega }^2+c_0-e_0) \sin \tilde{\omega }\tau _2=d_3\tilde{\omega }^3-d_1\tilde{\omega }. \end{aligned}$$
(27)

It follows from (27) that

$$\begin{aligned} \cos \tilde{\omega }\tau _2&= \frac{(d_2\tilde{\omega }_k^2-d_0) (\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0-e_0) -(d_3\tilde{\omega }_k^3-d_1\tilde{\omega }_k) (c_3\tilde{\omega }_k^3-c_1\tilde{\omega }_k)}{(\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0)^2-e_0^2 +(c_3\tilde{\omega }_k^3-c_1\tilde{\omega }_k^2)^2},\\ \sin \tilde{\omega }\tau _2&= \frac{(d_3\tilde{\omega }_k^2 -d_1\tilde{\omega }_k)(\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0+e_0) -(d_2\tilde{\omega }_k^2-d_0)(c_1\tilde{\omega }_k-c_3\tilde{\omega }_k^3)}{(\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0)^2-e_0^2 +(c_3\tilde{\omega }_k^3-c_1\tilde{\omega }_k^2)^2}, \end{aligned}$$

which leads to

$$\begin{aligned} \delta _{12}\tilde{\omega }^{12}+\delta _{11}\tilde{\omega }^{11} +\delta _{10}\tilde{\omega }^{10}+\delta _{9}\tilde{\omega }^{9} +\delta _{8}\tilde{\omega }^{8}+\delta _{7}\tilde{\omega }^{7} +\delta _{6}\tilde{\omega }^{6}+\delta _{5}\tilde{\omega }^{5} +\delta _{4}\tilde{\omega }^{4}+\delta _{3}\tilde{\omega }^{3} +\delta _{2}\tilde{\omega }^{2}+\delta _{1}=0, \end{aligned}$$
(28)

where

$$\begin{aligned} \delta _1&= d_0^2(e_0-c_0)^2-c_0^2,\\ \delta _2&= 2d_0(c_0d_2-e_0d_2+c_2d_0-c_1d_1)(e_0-c_0) +2_0c_2+(c_1d_0-c_0d_1-e_0d_1)^2,\\ \delta _3&= 2d_3(c_0+e_0)(c_1d_0-c_0d_1-e_0d_1),\\ \delta _4&= (c_0d_2-e_0d_2+c_2d_0-c_1d_1)^2+2d_0(e_0-c_0) (c_1d_3-c_2d_2+c_1d_1-d_0)\\&+2(c_2d_1-d_2c_1-c_3d_0)(c_1d_0-c_0d_1-e_0d_1)+(c_0+d_0)^2d_3^2 -2c_0-c_1^2-c_2^2,\\ \delta _5&= 2d_3(c_2d_1-d_2c_1-c_3d_0)(c_0+e_0)-2c_2d_3(c_1d_0-c_0d_1-e_0d_1) +2c_1c_3,\\ \delta _6&= 2d_0(d_2-c_3d_3)(e_0-c_0)+(c_2d_1-d_2c_1-c_3d_0)^2+2c_2-c-3^2\\&+2(c_1d_3-c-2d_2+c_3d_1-d_0)(c_0d_2-e_0d_2+c_2d_0-c_1d_1)-2c_2d_3^2 (c_0+e_0),\\ \delta _7&= 2d_3(c_1d_0-c_0d_1-e_0d_1)+2d_3(d_2c_3-d_1)(c_0+e_0) -2c_2d_3(c_2d_1-d_2c_1-c_3d_0),\\ \delta _8&= (c_1d_3-c_2d_2+c_3d_1-d_0)^2+2(d_2-c_3d_3) (c_0d_2-e_0d_2+c_2d_0-c_1d_1)\\&+(c_2d_3)^2+2d_3^2(c_0+e_0)+2(d_2c_3-d_1)(c_2d_1-d_2c_1-c_3d_0)-1,\\ \delta _9&= 2d_3(c_2d_1-d_2c_1-c_3d_0)-2c_2d_3(d_2c_3-d_1),\\ \delta _{10}&= 2(d_2-c_3d_3)(c_1d_3-c_2d_2+c_3d_1-d_0) +(d_2c_3-d_1)^2-2c_2d_3^2,\\ \delta _{11}&= 2d_3(d_2c_3-d_1),\\ \delta _{12}&= (d_2-c_3d_3)^2+d_3^2. \end{aligned}$$

Let

$$\begin{aligned} \tilde{h}(\tilde{\omega })=\delta _{12}\tilde{\omega }^{12} +\delta _{11}\tilde{\omega }^{11}+\delta _{10}\tilde{\omega }^{10} +\delta _{9}\tilde{\omega }^{9} +\delta _{8}\tilde{\omega }^{8}+\delta _{7}\tilde{\omega }^{7} +\delta _{6}\tilde{\omega }^{6}+\delta _{5}\tilde{\omega }^{5} +\delta _{4}\tilde{\omega }^{4}+\delta _{3}\tilde{\omega }^{3} +\delta _{2}\tilde{\omega }^{2}+\delta _{1}. \end{aligned}$$

We assume that

$$\begin{aligned} (\hbox {H}5)\qquad (28) ~ \hbox {has at least one positive real root}. \end{aligned}$$

If all the coefficients of system (3) are given, it is not difficult to calculate the roots of (28). Since \(\lim _{\tilde{\omega }\rightarrow {\infty }}\tilde{h}(\tilde{\omega })=\infty ,\) we can conclude that if \(\delta _1<0\), then (28) has at least one positive real root.

Suppose that Eq. (28) has positive roots. Without loss of generality, we assume that it has 12 positive roots, denoted by \(\tilde{\omega }_k(k=1,2,3\ldots ,12).\) If we use the notation

$$\begin{aligned} \tau _{2k}^{(j)}=\frac{1}{\tilde{\omega }_k} \left\{ \arccos \left( \frac{(d_2\tilde{\omega }_k^2-d_0) (\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0-e_0) -(d_3\tilde{\omega }_k^3-d_1\tilde{\omega }_k)(c_3\tilde{\omega }_k^3 -c_1\tilde{\omega }_k)}{(\tilde{\omega }_k^4-c_2\tilde{\omega }_k^2+c_0)^2 -e_0^2+(c_3\tilde{\omega }_k^3-c_1\tilde{\omega }_k^2)^2}\right) +2j\pi \right\} , \end{aligned}$$
(29)

where \(k=1,2,\ldots ,12, j=0,1,2,\ldots \), then \(\pm {\mathrm{i}\tilde{\omega }_k}\) are a pair of imaginary roots of Eq. (21) when \(\tau _2=\tau _{2k}^{(j)}\). Define

$$\begin{aligned} \tau _{2_0}=\tau _{2k0}^{(0)}=\min _{k\in \{1,2,3,\ldots ,12\}} \Big \{\tau _{2k}^{(0)}\Big \}, \tilde{\omega }_0=\tilde{\omega }_{k0}. \end{aligned}$$
(30)

Let \(\lambda (\tau _2)=\tilde{\alpha }(\tau _2)+\mathrm{i}\tilde{\omega }(\tau _2)\) be a root of (21) around \(\tau _2=\tau _{2k}^{(j)}\), and let \(\tilde{\alpha }(\tau _{2k}^{(j)})=0\) and \( \tilde{\omega }(\tau _{2k}^{(j)})=\tilde{\omega }_k.\) Differentiating both sides of (21) with respect to \(\tau _2\) yields

$$\begin{aligned} \left[ \frac{d\lambda }{d\tau _2}\right] ^{-1} =\frac{(4\lambda ^3+3c_3\lambda ^2+2c_2\lambda +c_1) \text {e}^{\lambda \tau _2}+3d_3\lambda ^2+2d_2\lambda +d_1}{\lambda [e_0\text {e}^{-\lambda \tau _2}-\text {e}^{\lambda \tau _2} (\lambda ^4+c_3\lambda ^3+c_2\lambda ^2+c_1\lambda +c_0)]} -\frac{\tau _2}{\lambda }. \end{aligned}$$

Letting \(\lambda =\mathrm{i}\tilde{\omega }_k, \tau _2=\tau _{2k}^{(j)}\), we obtain

$$\begin{aligned} \hbox {Re}\Bigg \{\left[ \frac{\mathrm{d}\lambda }{\mathrm{d}\tau _2}\right] ^{-1} \Bigg |_{\lambda =i\tilde{\omega }_k,\tau _2=\tau _{2k}^{(j)}}\Bigg \} =\frac{\theta _1+i\theta _2}{\theta _3+i\theta _4} =\frac{\theta _1\theta _3+\theta _2\theta _4}{\theta _3^3+\theta _4^3}, \end{aligned}$$

where

$$\begin{aligned} \theta _1&= (c_1-3c_3\tilde{\omega }_k^2)\cos \tilde{\omega }_k\tau _{2_0}^{(j)} +(4\tilde{\omega }_k^3-2c_2\tilde{\omega }_k)\sin \tilde{\omega }_k\tau _{2_0}^{(j)} +d_1-3d_3\tilde{\omega }_k^2,\\ \theta _2&= (c_1-3c_3\tilde{\omega }_k^2)\sin \tilde{\omega }_k\tau _{2_0}^{(j)} +(2c_2\tilde{\omega }_k-4\tilde{\omega }_k^3)\cos \tilde{\omega }_k\tau _{2_0}^{(j)}+2d_2\tilde{\omega }_k,\\ \theta _3&= (c_1-c_3\tilde{\omega }_k^2)\tilde{\omega }_k^2 \cos \tilde{\omega }_k\tau _{2_0}^{(j)}+(e_0-c_0+c_2\tilde{\omega }_k^2 -\tilde{\omega }_k^4)\tilde{\omega }_k\sin \tilde{\omega }_k\tau _{2_0}^{(j)},\\ \theta _4&= (e_0-c_0+c_2\tilde{\omega }_k^2-\tilde{\omega }_k^4) \tilde{\omega }_k\cos \tilde{\omega }_k\tau _{2_0}^{(j)} (c_1\tilde{\omega }_k-c_3\tilde{\omega }_k^3) \omega _k\cos \tilde{\omega }_k\tau _{2_0}^{(j)}. \end{aligned}$$

Assume that the following condition holds:

$$\begin{aligned} (\hbox {H}6)\qquad \theta _1\theta _3+\theta _2\theta _4\ne {0}. \end{aligned}$$

Based on the foregoing analysis and the results of Kuang [32] and Hale [33], we obtain the following theorem.

Theorem 4

If (H4) and (H5) hold, then the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) of system (3) is asymptotically stable when \(\tau _2\in [0,\tau _{2_0})\). In addition to (H4) and (H5), if (H6) holds, then system (3) undergoes a Hopf bifurcation at the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) when \(\tau _2=\tau _{2k}^{(j)}, k=1,2,\ldots ,12, j=0,1,2,\ldots \).

Remark 5

It is shown that if (H4) and (H5) are satisfied, then the states \(x_i(i=1,2,3,4)\) of system (2) will tend to \(x_i^*\) when \(\tau _2\in [0,\tau _{2_0})\). If (H4), (H5), and (H6) hold, then the states \(x_i(i=1,2,3,4)\) of system (2) may coexist and remain in an oscillatory mode near the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\). Thus, chaos vanishes, which means that chaos can be controlled.

3 Computer simulations

In this section, we present some numerical results of systems (2) and (3) to verify the analytical predictions obtained in the previous section. Let us consider the following two systems:

$$\begin{aligned} \dot{x}_1&= 30(x_2-x_1)+x_2x_3x_4,\nonumber \\ \dot{x}_2&= 10(x_1+x_2)-x_1x_3x_4-5[x_2(t)-x_2(t-\tau _1)],\nonumber \\ \dot{x}_3&= -x_3+x_1x_2x_4,\\ \dot{x}_4&= -10x_4+x_1x_2x_3\nonumber \end{aligned}$$
(31)

and

$$\begin{aligned} \dot{x}_1&= 30(x_2-x_1)+x_2x_3x_4,\nonumber \\ \dot{x}_2&= 10(x_1+x_2)-x_1x_3x_4-6[x_2(t)-x_2(t-\tau _2)],\nonumber \\ \dot{x}_3&= -x_3+x_1x_2x_4-4[x_3(t)-x_3(t-\tau _2)],\\ \dot{x}_4&= -10x_4+x_1x_2x_3,\nonumber \end{aligned}$$
(32)

respectively. We can easily obtain that systems (33) and (33) have an equilibrium \(E(-2.2129,-1.4290,7.2141,\) \(2.2813)\).

For system (32), we can easily check that (H1)–(H3) are satisfied. We let \(j=0\), and, using MATLAB 7.0 software, we derive \(\omega _{0}\approx 0.7004, \tau _{1_0}\approx 0.162\). Thus, the equilibrium \(E(-2.2129,-1.4290,7.2141,2.2813)\) is asymptotically stable when \(\tau _1<\tau _{1_0}\approx 0.162\), which is illustrated in Fig. 2. When \(\tau _1=\tau _{1_0}\approx 0.162\), Eq. (32) undergoes a Hopf bifurcation at the equilibrium \(E(-2.2129,-1.4290,7.2141,2.2813)\), i.e., a small-amplitude periodic solution occurs near \(E(-2.2129,-1.4290,7.2141,2.2813)\) when \(\tau _1\) is close to \(\tau _{1_0}\approx 0.162\), which can be shown in Fig. 3.

Fig. 2
figure 2

Chaos vanishes when \(\tau _1= 0.1<\tau _{1_0}\approx 0.162\). The equilibrium \(E(-2.2129, -1.4290, 7.2141, 2.2813)\) is asymptotically stable; the initial value is (\(-\)0.5, \(-\)1, 6.5, 1)

Full size image
Fig. 3
figure 3

Chaos vanishes when \(\tau _1 = 0.2>\tau _{1_0}\approx 0.162\). The Hopf bifurcation occurs from the equilibrium \(E(-2.2129, -1.4290, 7.2141, 2.2813)\); the initial value is (\(-0.5, -1, 6.5, 1\))

Full size image

For system (33), we can check that (H4)–(H6) are satisfied. Then \(\tilde{\omega }_0\approx 0.6809, \tau _{2_0}\approx 0.164\). Thus, the equilibrium \(E(-2.2129,-1.4290,7.2141,2.2813)\) is asymptotically stable when \(\tau _2<\tau _{2_0}\approx 0.164\), which is illustrated in Fig. 4. When \(\tau _2=\tau _{2_0}\approx 0.164\), Eq. (33) undergoes a Hopf bifurcation around the equilibrium \(E(-2.2129,-1.4290,7.2141,2.2813)\) when \(\tau _2\) is close to \(\tau _{2_0}\approx 0.164\), which is shown in Fig. 5.

Fig. 4
figure 4

Chaos vanishes when \(\tau _2= 0.1<\tau _{2_0}\approx 0.164\). The equilibrium \(E(-2.2129, -1.4290, 7.2141, 2.2813)\) is asymptotically stable; the initial value is (\(-\)0.5, \(-\)1, 6.5, 1)

Full size image
Fig. 5
figure 5

The chaos vanishes when \(\tau _2 =0.2>\tau _{2_0}\approx 0.164.\) The Hopf bifurcation occurs from the equilibrium \(E(-2.2129, -1.4290, 7.2141, 2.2813)\). The initial value is (\(-\)0.5, \(-\)1, 6.5, 1)

Full size image

Remark 6

Since the original system (2) is chaotic, there is no stabilized orbit. When we add feedback perturbations to the original system (2), then under some suitable conditions, stabilized orbits will occur. Thus, we can conclude that the stabilized orbits of the original system (2) are delay-induced.

4 Conclusions

In this paper, a feedback control method was applied to suppress the chaotic behavior of a 4D chaotic Qi system. By adding a time-delayed force to the second equation of the 4D chaotic Qi system, we focused on the local stability of the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) and local Hopf bifurcation of the 4D delayed chaotic Qi system. It was shown that if (H1) is satisfied, then the 4D delayed chaotic Qi system is asymptotically stable when \(\tau _1\in [0, \tau _{1_0})\). If (H1)–(H3) hold, a sequence of Hopf bifurcations occur around the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\), that is, a family of periodic orbits bifurcate from the equilibrium \(E(x^*,y^*,z^*)\). Adding a time-delayed force to the second and third equations of the 4D chaotic Qi system, we analyzed the local stability of the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\) and local Hopf bifurcation of the 4D delayed chaotic Qi system. We found that if (H4) is satisfied, then the 4D delayed chaotic Qi system is asymptotically stable when \(\tau _2\in [0, \tau _{2_0})\). If (H4)–(H6) hold, a sequence of Hopf bifurcations occurs around the equilibrium \(E(x_1^*,x_2^*,x_3^*,x_4^*)\). All the cases showed that chaos vanishes and can be suppressed. Some numerical simulations were carried out to visualize the theoretical findings.