Adaptive nonlinear model-based control scheme implemented on the nonlinear processes

Abstract

In this work, two adaptive nonlinear model-based control schemes have been proposed and implemented on the simulated model of the nonlinear benchmark processes. The servo performance of the proposed control schemes was found satisfactory. In order to improve the servo-regulatory performance of one of the proposed control schemes, the model state and parameters have been estimated simultaneously online with the help of a derivative-free Kalman filter and the predicted values of model states have been used in the proposed control law. The performances have been compared between two proposed control schemes with conventional adaptive PI control scheme. From the extensive simulation studies, it has been found that proposed control schemes implemented on nonlinear processes are having better performance over conventional adaptive PI control scheme. It was also found that proposed control schemes are able to eliminate measurement noise and having good robustness features.

1 Introduction

P/PI/PID, MPC, IMC are the most commonly used control schemes in industries over past few decades. Most of the industrial processes exhibit inherent nonlinearity; hence, nonlinear controller would be a better choice in order to control nonlinear process variables rather than conventional linear controllers, which needs re-linearizing the plant model, when it moves to new operating point. In the case of adaptive nonlinear system, process states need to be updated with time to cope up with process uncertainty [1]. Different kinds of adaptive control schemes such as gain-scheduled adaptive controller, self-tuning controller and model reference adaptive controller are widely used control techniques for various types of processes whose parameters are varying with time [2]. The design plethora of formulating control law on the basis of different performance and robustness criteria has been discussed in the literature [1, 2].

Due to difficulties of achieving exact values of process parameters from real plant, a nonlinear model-based control (NMBC) law needs to be employed for the convergence with true process parameter value [1]. As a well-recognized example of feedback control loop, NMBC scheme was improvised for nonlinear process. However, NMBC scheme specifies output/state variable feedback to formulate driving action for generating proper manipulated variable to control the plant output [1]. The noteworthy phenomenon of MBC technique deals with trade-off between robustness and performances as well [3]. Several articles have already been discussed about various way of approaches for NMBC schemes like neural network model-based control scheme [4], fuzzy model-based control scheme [5], Hammerstein model-based control scheme [6], IMC-based PID scheme [7], IMC on the basis of multiple linear discrete transfer function models [8], minimum–maximum-based MPC scheme [9] and so on. An easiest way of adaptive NMBC scheme has been introduced by Economou, which relies on first principle model-based scheme [3, 10]. He had proposed a nonlinear control scheme where nonlinear partition inverse was imposed by means of nonlinear operator theory. A linear model-based filter has been considered to reduce the critically damped behavior in case of plant and model mismatch. Controller stability and causality has also been focused in his work. This work highlighted on designing an unconstrained NMBC scheme. But most of the citations refer direct way of adaption incorporated in MBC technique. In addition, direct synthesization of NMBC control schemes redraws cumbersome computation, which needs to be avoided. The practical utility of NMBC using Volterra model has been presented in [11]. Furthermore, the need of adaptation mechanism in NMBC techniques has been explained by Michael and Costas [12], which shows significant improvement in feedback control performances. An event-based state and output feedback control techniques were discussed in [13], whereas state and output feedback control using NMPC was developed in [14]. The difficulties of achieving true process parameter from the real plant have been mentioned in article [15] by Hu and Rangaiah, and it still persists in several nonlinear complex processes. They also suggested an approach to measure true value of process parameter in order to improve plant output. The methodology deals with input–output linearization technique based on certain constraints imposed on it. PI-like model-based control scheme used for linear system has been deployed in [16], whereas an indirect way of adaption using NMBC techniques with having comparison study with NMPC implemented on nonlinear processes was discussed in [17]. An experimental validation of NMBC control algorithm on experimental rigs (benchmark conical tank system) has been mentioned in article [18].

The foremost drawback of designing model-based controller faces real problem, especially in case of sudden changes in process parameters or load disturbances [7]. Hence, model structure needs to cope up with uncertainty associated with process or in the case of load disturbances. A typical structural characteristics-based models have been studied and considered in this proposed work.

Thus, the objective of this simulation study employs adaptation in NMBC scheme. In this proposed work, we have implemented combination of state feedback- and output feedback-based control schemes. To achieve true value of process parameters in the case of regulatory response, model states and parameters need to be estimated to cope up with process uncertainties.

A first principle model-based control scheme has been considered in this work. A nonlinear model has been incorporated to compute process gain, which in term calculates controller output to obtain desired output. The motivation of the proposed control scheme1 leads to development of an accurate nonlinear controller which would be able to track desired value and would be able to eliminate load disturbances. Performance of the proposed scheme shows significant improvement in uncertainties associated with process/load disturbance.

The motivation of another proposed control scheme was formulated based on the model states which need to be estimated as dynamics of system changes from time to time. In servo response model, states have been estimated on line and with the help of estimated model outputs controller gain has been calculated. It should be noted that UKF-based estimation technique has been used to estimate model states. In servo–regulatory response, process parameter has also been estimated in addition to model states. The objective of this proposed work leads to develop an accurate nonlinear controller design where model states and parameters have been estimated to eliminate load disturbances. Performance of the proposed scheme was found satisfactory.

In this work, a comparison study has been made between proposed control schemes with conventional adaptive PI control technique. From the extensive simulation study, performances like integral square error (ISE) and control effort (CE) for the mentioned control schemes have been calculated. The robustness of both the controllers has also been discussed in this study. To the best of our knowledge, both the proposed control schemes were not addressed in the literature.

The organization of the paper is as follows: Sect. 1 discusses the literature survey and motivation of the proposed work. Section 2 deals with different control schemes. Details of the processes as well as simulation results related to servo response, load disturbance, introduction of measurement noise and performance comparison study of various control schemes have been offered in Sect. 3. Section 4 explains conclusion of the proposed work.

2 Control schemes

2.1 Conventional adaptive PI control scheme

The adaptive conventional PI control law has been described by the general equation as [18, 19]:

$$\begin{aligned} u(k)=u(k-1)+(k_{c1} \,*\,\partial e_1 (k))+(T_\mathrm{s} \,*\,(k_{c1} /T_\mathrm{i} )\,*\, e(k)) \end{aligned}$$

(1)

where $k_{c1}$ and $T_\mathrm{i}$ are proportional gain and integral time constant of the conventional adaptive PI control scheme, respectively. $T_\mathrm{s}$ is the sampling time. e is the process error which can be described as:

$$\begin{aligned}&e(k)=y_\mathrm{sp} (k)-y(k) \end{aligned}$$

(2)

$$\begin{aligned}&\partial e(k)=e(k)-e(k-1) \end{aligned}$$

(3)

In this simulation study, conventional adaptive PI controller tuning parameters $(k_{c1} ;T_\mathrm{i} )$ have been estimated by UKF algorithm. The system equations for the controller parameters of the conventional adaptive PI controller are as follows [20,21,22]:

$$\begin{aligned}&\theta (k)=\theta (k-1)+w(k-1) \end{aligned}$$

(4)

$$\begin{aligned}&\theta (k)=[k_{c1} ;T_\mathrm{i} ] \end{aligned}$$

(5)

$$\begin{aligned}&pv(k)=f[pv(k-1),q_c (k-1),\theta (k-1)]+v(k)\nonumber \\ \end{aligned}$$

(6)

pv is the measured value (of process variable) obtained from the plant. The predicted controller parameters estimation are obtained as

$$\begin{aligned} \hat{{\theta }}(k|k-1)=\hat{{\theta }}(k-1|k-1) \end{aligned}$$

(7)

The covariance matrix of estimation errors in the predicted controller parameters estimation is obtained as follows:

$$\begin{aligned} P_\theta (k|k-1)=P_\theta (k|k-1)+Q \end{aligned}$$

(8)

A set of $(2L+1)$ sigma points with the associated weights w(i) are chosen symmetrically about $\hat{{\theta }}(k|k-1)$ as follows:

Fig. 1

Schematic diagram of proposed control schemes1

Fig. 2

Schematic diagram of proposed control schemes2

$$\begin{aligned} \theta _s= & {} \left[ \hat{{\theta }}(k|k-1),\hat{{\theta }}(k|k-1)+\,\sqrt{(L+\kappa )P_\theta (k|k-1)},\right. \nonumber \\&\left. \hat{{\theta }}(k|k-1)-\sqrt{(L+\kappa )P_\theta (k|k-1)}\right] \end{aligned}$$

(9)

The measurement prediction $(\hat{{p}}v(k|k-1))$, computation of innovation $(e_{k|k-1} )$, covariance matrix of innovation $(P_{ee} (k))$, the cross-covariance matrix between the predicted model parameter estimation errors and innovation $(P_{\theta e} (k))$ are computed as follows:

$$\begin{aligned}&\hat{{p}}v^{i}(k|k-1)=f(pv(k-1),u(k-1),\theta ^{i}(k|k-1)) \nonumber \\\end{aligned}$$

(10)

$$\begin{aligned}&\hat{{p}}v(k|k-1)=\sum _0^{2L} {\hat{{p}}v(k|k-1)} \end{aligned}$$

(11)

$$\begin{aligned}&e_{k|k-1} =\hat{{p}}v(k)-pv(k) \end{aligned}$$

(12)

$$\begin{aligned}&P_{ee} (k)=\sum _{i=0}^{2L} w_i \left( \hat{{p}}v^{i}(k|k-1)-pv_r (k|k-1) \right) \nonumber \\&\left( pv_r^i (k|k-1)-pv_r (k|k-1))^\mathrm{T}+R \right. \end{aligned}$$

(13)

$$\begin{aligned}&P_{\theta e} (k)=\sum _{i=0}^{2L} w_i \left( \hat{{\theta }}_s^i (k|k-1)-\,\hat{{\theta }}(k|k-1) \right) \nonumber \\&\left( \hat{{p}}v^{i}(k|k-1)-\,pv_r(k|k-1)\right) ^\mathrm{T} \end{aligned}$$

(14)

where $w_0 =\kappa /(L+\kappa )$ and $w_i =\kappa /(2(L+\kappa ))$. The Kalman gain is computed using the equation

$$\begin{aligned} K=P_{\theta e} \left( P_{ee} ^{-1}\right) \end{aligned}$$

(15)

The updated model parameter estimates are obtained using the equation:

$$\begin{aligned} \hat{{\theta }}(k|k)=\hat{{\theta }}(k|k-1)+Ke_{k|k-1} \end{aligned}$$

(16)

The covariance matrix of estimation errors in the updated model parameter estimation is obtained as:

$$\begin{aligned} P_\theta (k|k)=P_\theta (k|k-1)-KP_{ee} K^\mathrm{T} \end{aligned}$$

(17)

2.2 Proposed control scheme1

An adaptive nonlinear model-based control scheme implemented on conical tank and pH processes has been proposed. The proposed control law for the above-mentioned systems is as follows:

$$\begin{aligned}&u(k)= \alpha \,*\, k_{c2} (k)(y_\mathrm{sp} (k)-y(k))+u_d (k) \end{aligned}$$

(18)

$$\begin{aligned}&k_{c2} (k)=u_d (k)/y_\mathrm{m} (k) \end{aligned}$$

(19)

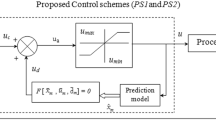
where $y_\mathrm{sp}$ is the set point. $y_\mathrm{m}$ is the model state. Controller gain $(k_{c2} )$, bias $(u_d )$ and numerical multiplier $(\alpha )$ are considered to be the tuning parameters of the proposed control scheme. The schematic diagram of the proposed control scheme is shown in Fig. 1.

2.3 Proposed control scheme2

Firstly, an adaptive nonlinear model-based control scheme implemented on conical tank and pH processes has been proposed. As an example of derivative-free Kalman filter, UKF has been considered for estimating all the states. The values of the predicted states have been used to formulate proposed adaptive NMBC scheme (see Fig. 2). It should be noted that adaptive NMBC scheme has been denoted as proposed scheme2 in the figures. In case of servo–regulatory response, $x_{{1i}}$ has been estimated in addition with available process state variable (i.e., Augmented UKF/AUKF). The proposed control law for the above-mentioned systems is as follows:

$$\begin{aligned}&u(k)=\alpha \,*\,\hat{{k}}_{c2} (k/k-1)(y_\mathrm{sp} (k)-y(k))\nonumber \\&\qquad \qquad +\,\hat{{u}}(k/k-1) \end{aligned}$$

(20)

$$\begin{aligned}&\hat{{k}}_{c2} (k/k-1)=\hat{{u}}(k/k-1)/\hat{{y}}(k/k-1) \end{aligned}$$

(21)

where controller gain $(\hat{{k}}_{c2} (k/k-1))$ or $(k_{c2} )$, bias $(\hat{{u}}(k/k-1))$ or $(u_d )$ and numerical multiplier $(\alpha )$ are considered to be the tuning parameters of the proposed control scheme. The schematic diagram of the proposed control scheme is shown in Fig. 2. The states of the system can be represented as [16, 20,21,22]:

$$\begin{aligned} x(k)&=x(k-1)+\left[ {\int \limits _{(k-1)T}^{kT} f [x(\tau ),u(k-1)]\mathrm{d}\tau } \right] \nonumber \\&\quad +w(k) \end{aligned}$$

(22)

Measurement equation can be described as:

$$\begin{aligned} y(k)=h[x(k)]+v(k) \end{aligned}$$

(23)

where x(k) denotes the system state vector $(x\in R^{L})$ and $q_c (k)$ is the process input $(q_c \in R^{m})$. w(k) is the process noise $(w\in R^{L})$ and y(k) is the measured state variable $(y\in R^{r})$. v(k) is the measurement disturbance $(v\in R^{r})$. k is the sampling instances. f[.] and h[.] are nonlinear process and measurement model, respectively.

A set of $(2L+1)$ sigma points $\chi (k-1/k-1,i)$ with the associated weights w(i) are chosen symmetrically about $\hat{{\chi }}(k-1/k-1)$ as follows:

$$\begin{aligned}&\chi (k-1/k-1,i)=\hat{{\chi }}(k-1/k-1) \end{aligned}$$

(24)

$$\begin{aligned}&\chi (k-1/k-1,i)=\hat{{\chi }}(k-1/k-1)\nonumber \\&\quad +\left( {\sqrt{(L+\lambda )P(k-1/k-1}} \right) _i\quad i=1,\ldots ,L \end{aligned}$$

(25)

$$\begin{aligned}&\chi (k-1/k-1,i)=\hat{{\chi }}(k-1/k-1)\nonumber \\&\quad -\left( {\sqrt{(L+\lambda )P(k-1/k-1}} \right) _{i-L}\nonumber \\&\quad i=L+1,\ldots ,2L \end{aligned}$$

(26)

$$\begin{aligned}&W^{m}(0)=\lambda /(L+\lambda ); \end{aligned}$$

(27)

$$\begin{aligned}&W^{c}(0)=\lambda /(L+\lambda )+(1-\alpha _1 ^{2}+\beta ); \end{aligned}$$

(28)

$$\begin{aligned}&\lambda =\alpha _1 ^{2}(L+\kappa )-L; \end{aligned}$$

(29)

$$\begin{aligned}&W^{c}(i)=W^{m}(i)=1/(2(L+\lambda ));\quad i=1,\ldots ,2L\nonumber \\ \end{aligned}$$

(30)

where $\kappa$ is a secondary scaling parameter. $(\alpha _1 )$ is the factor determining by spread of sigma points around $\hat{{\chi }}(k-1/k-1)$ and is usually set between $(1\hbox {e}{-}4)$ to 1. The parameter $\beta$ is used to incorporate prior knowledge of distribution of x and for Gaussian distribution. Its optimum value is 2. $(2L+1)$sigma points have been derived from the state $\hat{{x}}(k-1/k-1)$ and covariance of the state vector $P(k-1/k-1).$ Here L is the dimension of the state vector. In case of prediction step, sigma points are propagated through nonlinear differential equation for obtaining predicted set of sigma points as mentioned below:

$$\begin{aligned}&\chi (k/k-1,i) =\hat{{\chi }}(k-1/k-1,i)\nonumber \\&\quad +\int \limits _{(k-1)T}^{kT} f [\chi (\tau ,i),u(k-1)]\mathrm{d}\tau ;\quad i=0,\ldots ,2L.\nonumber \\ \end{aligned}$$

(31)

Predicted state estimates $\hat{{x}}(k/k-1)$ are obtained from predicted sigma points as:

$$\begin{aligned} \hat{{x}}(k/k-1)=\sum _0^{2L} {W^{m}(i)} \chi (k/k-1,i) \end{aligned}$$

(32)

Error covariance matrix $P(k-1/k-1)$ can be obtained from predicted sigma points as:

$$\begin{aligned} P(k/k-1,i)= & {} \sum _0^{2L} {W^{c}(i)} \{\chi (k/k-1,i)\nonumber \\&-\,\hat{{x}}(k/k-1,i)\}\,*\,\{\chi (k/k-1,i)\nonumber \\&-\,\hat{{x}}(k/k-1,i)\}^\mathrm{T}+Q \end{aligned}$$

(33)

Sigma points are re-drawn using the predicted state estimate as given as:

$$\begin{aligned}&\chi ^{*}(k/k-1,i)=\hat{{x}}(k-1/k-1); \end{aligned}$$

(34)

$$\begin{aligned}&\chi ^{*}(k/k-1,i)=\hat{{x}}(k/k-1)\nonumber \\&\quad +\left( {\sqrt{(L+\lambda )P(k/k-1}} \right) _i\quad i=1,\ldots ,L; \end{aligned}$$

(35)

$$\begin{aligned}&\chi ^{*}(k/k-1,i)=\hat{{x}}(k/k-1)\nonumber \\&\quad -\left( {\sqrt{(L+\lambda )P(k/k-1}} \right) _i\quad i=L+1,\ldots ,2L;\nonumber \\ \end{aligned}$$

(36)

Re-drawn sigma points are propagated through nonlinear measurement equation to obtain predicted measurement as

$$\begin{aligned} \hat{{y}}(k/k-1)=\sum _0^{2L} {W^{m}(i)*[} \chi (k/k-1,i)] \end{aligned}$$

(37)

The covariance matrix of innovation $P_{yy} (k)$ and cross-covariance matrix between the predicted states estimation errors and innovation $P_{xy} (k)$ are computed as follows:

$$\begin{aligned} P_{yy} (k)= & {} \sum _0^{2L} \left[ W^{c}(i)\{h[\chi ^{*}(k/k-1,i)]\right. \nonumber \\&-\,\hat{{y}}(k/k-1)\}\,*\,\{h[\chi ^{*}(k/k-1,i)]\nonumber \\&\left. -\,\hat{{y}}(k/k-1)\}^\mathrm{T} \right] +R \end{aligned}$$

(38)

$$\begin{aligned} P_{xy} (k)= & {} \sum _{0}^{2L} \left[ W^{c}(i)\{\chi ^{*}(k/k-1,i)\right. \nonumber \\&-\,\hat{{x}}(k/k-1)\}\,*\,\{h[\chi ^{*}(k/k-1,i)]\nonumber \\&\left. -\,\hat{{y}}(k/k-1)\}^\mathrm{T} \right] \end{aligned}$$

(39)

The residual can be calculated as follows:

$$\begin{aligned} \gamma (k)=y(k)-\hat{{y}}(k/k-1) \end{aligned}$$

(40)

The Kalman gain matrix can be obtained as

$$\begin{aligned} K(k)=P_{xy} (k)P_{yy}^{-1} (k) \end{aligned}$$

(41)

The updated state can be determined as mentioned below:

$$\begin{aligned} \hat{{x}}(k/k)=\hat{{x}}(k/k-1)+K(k)\,*\,\gamma (k) \end{aligned}$$

(42)

The covariance matrix of error in the updated state estimates can be computed by the equation

$$\begin{aligned} P(k/k)=P(k/k-1)-K(k)\,*\,P_{yy} (k)\,*\,K^\mathrm{T}(k) \end{aligned}$$

(43)

In case of servo–regulatory response, we have estimated process parameter (Causes disturbance) in addition to process states.

In this proposed work, a performance comparison study (ISE and CE) has been made between proposed control schemes with conventional adaptive PI control technique. The ISE and CE can be derived as follows [16]:

$$\begin{aligned} \hbox {ISE}= & {} \int \limits _0^\tau {(y_\mathrm{sp} (k)-y(k))^{2}\mathrm{d}k} \end{aligned}$$

(44)

$$\begin{aligned} \hbox {CE}= & {} \sum _{i=1}^k {|u(k)-u(k-1)|} \end{aligned}$$

(45)

3 Process description and simulation results

The processes considered for the simulation study are conical tank and pH processes.

Table 1 Values of the process parameters and variables associated with conical tank system

3.1 Conical tank system

Table 1 shows the process parameter values for benchmark conical tank system. The material balance equation for the conical tank system is as follows [18]:

$$\begin{aligned} A(h)\frac{\mathrm{d}h}{\mathrm{d}t}=f_\mathrm{in} -f_\mathrm{out} \end{aligned}$$

(46)

where A(h) is the area of the tank. $f_\mathrm{in}$ (cc/s) and $f_\mathrm{out}$ (cc/s) are inflow and outflow rate of the tank, respectively. $h \hbox { (cm)}$ is the water level in the conical tank system. The relationship between outflow rate ($f_\mathrm{out} )$ and the water level (h) in the tank is as follows:

$$\begin{aligned} f_\mathrm{out} = c_\mathrm{v} \sqrt{2gh} \end{aligned}$$

(47)

where $c_\mathrm{v}$ is the discharge coefficient. It should be noted that the area of the conical tank varies with water level in the tank. In case of conical tank, the area of the tank can be calculated using following relations.

$$\begin{aligned} A(h)= \frac{\pi \,*\,{R_\mathrm{max }}^{{2}}\,*\,h^{2}}{{H_\mathrm{max }} ^{2}} \end{aligned}$$

(48)

where $R_\mathrm{max}$ is the maximum radius and $H_\mathrm{max}$ is the maximum height of conical tank.

All the simulations were executed by considering first principle model mentioned in Eqs. (46–48). True state variable is obtained by solving differential equation using MATLAB 7.2 toolboxes. In the entire simulation studies, sampling time has been considered as 0.0833 min. A constrained on the manipulated variable $(0.01<f_\mathrm{in} <20\hbox { cc/s} )$ has been imposed. Following operating point has been taken for entire simulation studies $(\bar{{h}}=30,f_\mathrm{in} =2.7386)$. The controller performances (ISE and CE computation) of all mentioned control schemes at servo level, servo-regulatory performance and in the presence of measurement noise are reported in Tables 3 and 4, respectively.

3.1.1 Open-loop study

In order to assess the open-loop study of the conical tank system, a sequence of step changes (combination of positive and negative steps) in the manipulated variable has been introduced. Figure 3a represents the steps changes in the input ($f_\mathrm{in} )$. The variation of process output (h) is reported in Fig. 3b.

Fig. 3

Open-loop response of the conical tank processes. a Variation of input, b process output

Fig. 4

Servo response of the conical tank process with various control schemes. a Process output, b variation of controller output

Table 2 Parameters associated with UKF-based state estimation scheme

Fig. 5

Evolution of controller parameters in various control schemes for servo response. a $k_{c1}$, b $T_\mathrm{i}$, c $k_{c2}$, d $u{}_d$

3.1.2 Servo response

In order to assess the tracking capability of all the above-mentioned control schemes, set point variation as shown in Fig. 4a has been introduced. In the case of conventional adaptive PI control scheme, controller tuning parameters $(k_{c1} ;T_\mathrm{i} )$ have been updated by UKF estimation technique. For proposed control scheme2, only model state [h] has been estimated by UKF algorithm, which in term updated controller parameters. Table 2 mentions parameters associated with UKF-based state estimation scheme implemented on conical tank system. Simulation studies were made based on the set point variation of 30–35, 35–30 and finally 30–25. From Fig. 4a, it can be inferred that the all the controllers are able to maintain the set point at desired level. The variation of controller output is reported in Fig. 4b. The evolution of the conventional adaptive PI controller tuning parameters $(k_{c1} ;T_\mathrm{i} )$ and proposed controllers tuning parameters $(k_{c2} ;u_d )$ is shown in Fig. 5a–d, respectively. From the simulation study, it can be concluded that conventional adaptive PI control scheme is very sluggish and oscillatory in nature. However, it can be stated that controller is having poor robustness. From the extensive simulation study, it was found that initialization of the adaptive PI controller tuning parameters should be considered as perfect as possible. Even little bit deviation from accurate initialization of the controller tuning parameters causes system to become unstable. The robustness of both the proposed controllers was found satisfactory. In order to achieve desired level quickly at the time of set point variation, controller tuning parameter $(\alpha )$ needs to be increased. From the observations, it was found that significant increase of $(\alpha )$, robustness of the controller, would have negligible impacts.

Fig. 6

Regulatory response of the conical tank process with various control schemes. a Process output, b variation of controller output

Fig. 7

Evolution of controller parameters in various control schemes for regulatory response. a Disturbance pattern—variation of downstream valve ($c_\mathrm{v})$, b $k_{c1}$, c $T_\mathrm{i}$, d evolution of downstream valve (true $c{ }_\mathrm{v}$ and estimated $c{ }_\mathrm{v})$, e $k_{c2}$, f $u{ }_d$

Fig. 8

Servo and regulatory response of the conical tank process with various control schemes in the presence of measurement noise. a Process output—servo response, b variation of controller output—servo response, c process output—regulatory response, d variation of controller output—regulatory response

3.1.3 Regulatory response

In order to assess the disturbance rejection capability of all the mentioned control schemes, step-like changes in the downstream valve position as shown in Fig. 7a have been introduced. In case of regulatory response, with proposed control scheme2, both model states with process parameter $[c_\mathrm{v} ]$ have been estimated by UKF algorithm (AUKF), which in term updated controller parameters. In this simulation study, set point was maintained at 30 cm. It should be noted that a positive step change in the downstream valve position of magnitude 0.05 (from 0.5 to 0.55) has been introduced at 501th sampling instance and the same value has been maintained up to 1200th and again negative step change in the downstream valve position of magnitude 0.05 (from 0.55 to 0.5) has been introduced at 1201th sampling instance and the same value has been maintained up to 3000th sampling instance. From Fig. 6a, it can be inferred that the conventional adaptive PI controller is able to reject disturbance and bring back process variable to the desired level. The variation of controller output is reported in Fig. 6b. The evolution of conventional adaptive PI controller tuning parameters $(k_{c1} ;T_\mathrm{i} )$ and proposed controllers tuning parameters $(k_{c2} ;u_d )$ is shown in Fig. 7. Variation of downstream value position (true $[c_\mathrm{v} ]$ and estimated $[c_\mathrm{v} ])$ is reported in Fig. 7d. From the simulation study, it can be concluded that eliminating disturbances with conventional adaptive PI control scheme is oscillatory in nature and taking longer time to settle. It can be inferred that controller is having poor robustness. In case of conventional adaptive PI controller, changes in downstream valve position $[c_\mathrm{v} ]$ more than 10% resulted in the failure of UKF to estimate controller parameters, whereas in case of proposed controller2, large variation of downstream valve position does not have any impact on the UKF to estimate model parameters. The merit of the proposed schemes also leads to the robustness feature of the controller.

3.1.4 Measurement noise elimination

Real-time processes exhibit measurement noise; hence, effectiveness of the controller can be identified by checking the ability to track at desired value in the presence of measurement noise [1]. In order to introduce measurement noise into the system, white random noise has been added into the process output. The efficacy of the proposed control schemes in the presence of measurement noise has been measured and compared with conventional adaptive PI control scheme.

It should be noted that, for introduction of measurement noise, NSR (noise-to-signal ratio) has been taken as 0.02. From Fig. 8, it can be inferred that the proposed control schemes are able to eliminate the measurement noise and bring the process variable back to the desired level, whereas introducing measurement noise (NSR $=$ 0.02) with conventional adaptive PI controller, system becomes unstable. The evolution of controller outputs is reported in Fig. 8.

3.1.5 Robustness of the controller

To assess the robustness criteria for the proposed control schemes, changes of parameters (downstream valve coefficient $[c_\mathrm{v} ])$ at different point of time between plant and model have been introduced (shown in Fig. 7a). From Fig. 6a, it can be concluded that all the control schemes are able to maintain the water level at the desired setpoint in the presence of plant and model mismatch. The variations of controller outputs are shown in Fig. 6b. The ISE and CE values of all the control schemes in the absence and presence of plant and model mismatch (10% deviation of discharge coefficient) are reported in Tables 3 and 4. From Tables 3 and 4, it can be inferred that there is deterioration in performances for all the control schemes in the presence of plant and model mismatch.

Table 3 ISE chart for servo, servo–regulatory responses and in the presence of measurement noise (NSR $=$ 0.015) for various control schemes implemented on conical tank system

Table 4 CE chart for servo, servo–regulatory responses and in the presence of measurement noise (NSR $=$ 0.015) for various control schemes implemented on conical tank system

3.1.6 Performance measurement of different control schemes

In order to assess the performances of different control schemes for servo, regulatory response and in the presence of measurement noise, ISE and CE computation have been reported. Tables 3 and 4 represent ISE and CE calculations for conical tank process, respectively. Servo performance was made based on set point variation as shown in Fig. 4a. For computation of regulatory performance, Fig. 6a has been considered. It was observed that the performance of proposed schemes (ISE and CE value) is better than conventional adaptive PI scheme. From Tables 3 and 4, it can be inferred that there is deterioration in performances for all the control schemes in the presence of measurement noise and in the presence of plant and model mismatch. It has been observed that, introducing measurement noise (NSR $=$ 0.02) with conventional adaptive PI control scheme, system becomes unstable. From overall comparison study (both ISE and CE as shown in Table 9), it can be stated that control scheme1 has better performances over other control schemes.

3.2 pH process

The material balance equation of the pH process mentioned in [8, 23] has been considered in this work. pH is the desired output. Disturbance was introduced through changes in the acid composition in acid flow rate ($x_{{{1i}}} )$. Table 5 mentions the process parameter data for pH. The first principle-based model equation for pH process can be described by [8, 23]:

$$\begin{aligned}&\mathop {{X}_1 }\limits ^{\cdot } =\frac{1}{\theta }({X}_{{1i}} -{X}_1 )-\frac{1}{\theta }{X}_1 {u} \end{aligned}$$

(49)

$$\begin{aligned}&\mathop {{X}_{2} }\limits ^{{\cdot }} =\frac{{1}}{{\theta }}{(X}_{{{2i}}} {-X}_{2} {){u}-}\frac{{1}}{{\theta }}{X}_{2} \end{aligned}$$

(50)

$$\begin{aligned}&\mathop {{X}_{3} }\limits ^{{\cdot }} =\frac{{1}}{{\theta }}{(X}_{{{3i}}} {-X}_{3} {){u}-}\frac{{1}}{{\theta }}{X}_{3} \end{aligned}$$

(51)

$$\begin{aligned}&{h(X,y)}=\xi +{X}_{2} +{X}_{3} -{X}_{1}\nonumber \\&\qquad \quad \quad \quad \quad -\frac{{K}_{\mathrm{w}} }{{\xi }}-\frac{{X}_{3} }{{1+}{{K}_\mathrm{x} {\xi }}/{{K}_\mathrm{w} }}=0 \end{aligned}$$

(52)

where

$$\begin{aligned} {\xi =10}^{{{-y}}} ;\quad \theta ={V}\big /{{{q}}_{\mathrm{a}} }{ ; \quad {u}}=\frac{{q}_{\mathrm{b}} }{{q}_{\mathrm{a}} } \end{aligned}$$

(53)

Table 5 Steady-state values of the process parameters and variables associated with pH Process

Fig. 9

Open-loop response of pH processes. a Variation of input, b process output—pH

Fig. 10

Servo response of the pH process with various control schemes. a Process output, b variation of controller output

All the simulations were executed by considering Eqs. (49–53). True state variables are obtained by solving differential equation using MATLAB 7.2 toolboxes. In the entire simulation studies for pH process, sampling time has been considered as 0.083 min. A constraint on the process output $(0<\textit{pH}<14)$ has been imposed. Following operating point has been taken for entire simulation studies ($\bar{{x}}_1 =8.3537 \, *\,\hbox {e}{-}004;\bar{{x}}_2 =6.0771 \,*\,\hbox {e}{-}004;\bar{{x}}_3 =7.5964 \,*\, \hbox {e}{-}004$) (see [8, 23]).

Table 6 Parameters associated with UKF-based state estimation scheme

Fig. 11

Evolution of controller parameters in various control schemes for servo response. a $k_{c1}$, b $T_\mathrm{i}$, c $k_{c2}$ (proposed scheme1), d $u{ }_d$ (proposed scheme1), e $k_{c2}$ (proposed scheme2), f $u{ }_d$ (proposed scheme2)

3.2.1 Open-loop study

In order to assess the open-loop study of the pH process, a sequence of step changes (combination of positive and negative steps) in the manipulated variable (u) has been introduced. Figure 9a represents the steps changes introduced in the input (u). The variation of process output ($\textit{pH}$) is reported in Fig. 9b.

Fig. 12

Regulatory response of pH process with various control schemes. a Evolution of $x_{i1}$, b process output—pH, c variation of controller output

3.2.2 Servo response

In order to assess the tracking capability of all the above-mentioned control schemes, set point variation as shown in Fig. 10a has been introduced. In case of conventional adaptive PI control scheme, controller tuning parameter $(k_{c1} ;T_\mathrm{i} )$ has been updated by UKF estimation technique. For proposed control scheme2, only model states $[x_1 ;x_2 ;x_3 ]$ have been estimated by UKF algorithm, which in term updated controller parameters. Table 6 mentions parameters associated with UKF-based state estimation scheme implemented on pH process. Simulation studies were made based on the set point variation of 7.37–9, 9–7 and finally 7–4.5. From Fig. 10a, it can be inferred that all the controllers are able to bring back the process variable at desired value. The variation of controller output is reported in Fig. 10b. The evolution of conventional adaptive PI tuning parameters $(k_{c1} ;T_\mathrm{i} )$ and proposed controller tuning parameters $(k_{c2} ;u_d )$ is shown in Fig. 11. From the simulation study, it can be concluded that conventional adaptive PI control scheme is sluggish in nature compared to the proposed control schemes. It was also observed that proposed controller1 is aggressive in nature at the time of set point variation. Performance of proposed schemes can further be improved by adjusting $(\alpha )$. It was found that significant increase of $(\alpha )$, robustness of both proposed schemes, would have negligible impacts. The robustness of the proposed control schemes is found better than conventional PI control scheme.

3.2.3 Regulatory response

In order to assess the disturbance rejection capability of all the control schemes, ramp-based step-wise changes (see Fig. 12a) in the acid composition in acid flow rate ($x_{{{1i}}} )$ have been introduced at different sampling instance (see Fig. 12a). In this simulation study, set point was maintained at 7 throughout simulation study. From Fig. 12b, it can be inferred that all the above-mentioned controllers are able to reject disturbance and bring back process variable to the desired value. The variations of controller outputs are reported in Fig. 12c. The evolution of conventional adaptive PI tuning parameters $(k_{c1} ;T_\mathrm{i} )$ and proposed controller tuning parameters $(k_{c2} ;u_d )$ has been shown in Fig. 13. It was found that conventional adaptive PI is taking almost same time like proposed control schemes to eliminate disturbances.

Fig. 13

Evolution of controller parameters for various control schemes at servo–regulatory response. a $k_{c1}$, b $T_\mathrm{i}$, c $k_{c2}$(proposed scheme1), b $k_{c2}$ (proposed scheme2), e $u_d$(proposed scheme1), f $u_d$ (proposed scheme2)

Fig. 14

Servo and regulatory response of the pH process with various control schemes in presence of measurement noise. a Process output—servo response, b variation of controller output—servo response, c process output—regulatory response, d variation of controller output—regulatory response

3.2.4 Measurement noise elimination

In order to assess the tracking capability and disturbance rejection capability of various control schemes in the presence of measurement noise, white random noise has been added into the process. It should be noted that for introduction of measurement noise, NSR has been taken as 0.03. In case of servo response, similar kind of set point variation as mentioned in Fig. 10 has been considered and for regulatory response similar kind of disturbance as well as set point variation as mentioned in Fig. 12 has been maintained in this simulation study. From Fig. 14a, it can be inferred that all the control schemes are able to maintain the set point at desired value. The variation of controller outputs at servo response is reported in Fig. 14b. From Fig. 14c, it can be inferred that all the control schemes are able to eliminate disturbance and bring back process variable at set point. The variation of all the controller outputs at regulatory level is reported in Fig. 14d. From the simulation study, it can be inferred that both proposed control schemes are able to settle quickly over conventional adaptive PI controller at the time of set point variation. It was noticed that conventional adaptive PI is taking almost same time like proposed control schemes to eliminate disturbances.

Fig. 15

Closed-loop response of the pH process in case of parameter mismatch between process and model in the presence of measurement noise. a Introduction of step changes of $x_{1i}$, b introduction of step changes of $x_{2i}$, c process output—pH, d variation of controller output

Table 7 ISE chart of servo, servo–regulatory responses in the absence and presence of measurement noise (NSR $=$ 0.015) for various control schemes implemented on pH process

Table 8 CE chart of servo, servo–regulatory responses and in the presence of measurement noise (NSR $=$ 0.015) for various control schemes implemented on pH process

Table 9 Comparison of overall closed-loop performance (ISE $+$ CE) for conical tank and pH process

Fig. 16

Performance measure (J) as a function of $(\alpha )$

3.2.5 Robustness of the controllers

To assess the robustness criteria for the proposed control schemes, step changes of different parameters [acid composition in acid flow rate ($x_{{{1i}}} )$ and base composition in base flow rate ($x_{{{2i}}} )$] at different points of time have been introduced (shown in Fig. 15a, b, respectively). It should be noted that for checking robustness of the controller, white random noise has been taken as NSR $=$ 0.03. From Fig. 15c, it can be concluded that all the control schemes are able to maintain the desired level even in case of plant and model mismatch. The evolution of controller outputs is shown in Fig. 15d.

3.2.6 Performance measurement of different control schemes

In order to assess the performances of different control schemes for servo, regulatory response and in the presence of measurement noise, ISE and CE computation have been reported. Tables 7 and 8 represent ISE and CE computation of pH process, respectively. Servo performance of pH process was made based on set point variation as shown in Fig. 8a. For regulatory performance calculation, Fig. 12 has been considered. From the simulation study, it can be inferred that conventional adaptive PI control scheme is sluggish in nature and taking longer time to settle compared to proposed control schemes. It was observed that servo performance of proposed schemes (ISE and CE value) is better than of conventional adaptive PI scheme, whereas conventional adaptive PI scheme performs better in regulatory level over proposed control schemes. From overall comparison study (both performance of ISE and CE as shown in Table 9), it can be inferred that control scheme1 provides better performances over other control schemes.

Table 10 Performance (J) measured on pH process for different control parameter

Table 11 Performance (J) measured on conical tank system for different control parameter

3.3 Guidelines of choosing $(\alpha )$

The proposed NMBC control schemes have tuning parameters, namely $K_{c2}$, $u_d$ and numerical multiplier $(\alpha )$. Hence, optimization of $K_{c2}$ for any process can be determined by minimizing the performance measure in terms of integral square error J(ISE).

$$\begin{aligned} J(\hbox {ISE}) = \mathop {(\alpha \, *\,{K}_{{c2}} })\sum _{{{k}}=1}^{{N}_0 } {{w}_0 {e}^{2}({k})} \end{aligned}$$

(54)

where output error $e(k)=y_\mathrm{sp} (k)-y(k)$ and ${w}_0$ is the weighting factor associated with output error. $N_0$ signifies the length of the simulation trail. Here $(\alpha )$ can be derived as:

$$\begin{aligned} \alpha =(1/K_{c2} )\,*\,\left[ {\frac{u_p (k)}{y_\mathrm{m} (k)}} \right] =(1/K_{c2} )\,*\,\left[ {\frac{u_p (k)}{{{{\varvec{C}}}}_\mathrm{m} {{{\varvec{x}}}}_\mathrm{m} (k)}} \right] \end{aligned}$$

(55)

Hence, $(\alpha )$ can be determined by minimizing the performance measure as follows:

$$\begin{aligned} {J} = \mathop \alpha \sum _{{k}=1}^{{N}_0 } {{w}_0 {e}^{2}({k})} \end{aligned}$$

(56)

Figure 16a, b shows the variation of J with respect to $(\alpha )$ for pH process and conical tank system, respectively. From Tables 10 and 11, it can easily be concluded that optimal value of $(\alpha )$ can be determined based on minimal range of J. From the extensive simulation study, it can also be inferred that minimal range of J can be obtained either on a wider range or on a narrow region of $(\alpha )$ variation. It was observed that with the increase in $(\alpha )$ system takes lesser time to reach set point, resulting minimal performance value. We have to keep on increasing $(\alpha )$. A point will be reached where performance will be started degrading. Please be noted that, with having lesser values of $(\alpha )$, system becomes sluggish in nature. Hence, there exists a trade-off.

4 Conclusion

In this paper, a successful design and implementation of proposed adaptive nonlinear model-based control schemes has been discussed. From the simulation study, it can be concluded that servo and regulatory performances of proposed control schemes (both the presence and absence of measurement noise) implemented on conical tank and pH processes were found satisfactory. From the comparison study, it can be inferred that proposed control schemes take very less time to settle over conventional adaptive PI controller at the time of set point variation. It was also observed that conventional adaptive PI control scheme is having poor robustness compared to proposed control schemes. From the controller performances chart (ISE and CE computation), it can be inferred that proposed controllers are having better performance over conventional adaptive PI control schemes, whereas for pH process, proposed control schemes are having poorer ISE and CE value in regulatory level. It was also noticed that proposed control schemes are good to eliminate measurement noise compared to conventional adaptive PI control scheme. From overall performance of all the mentioned control schemes, it can be concluded that proposed control schemes perform better over conventional adaptive PI control law.