Generalized synchronization of fractional-order hyperchaotic systems and its DSP implementation

Abstract

In this paper, we investigate synchronization and its DSP implementation of fractional-order simplified Lorenz hyperchaotic systems by employing the Adomian decomposition method. The active controller and linear feedback controller are designed. Numerical simulation of the synchronized systems is carried out, and it is found that the synchronization phenomenon can be observed in both state variables and intermediate variables. Moreover, the synchronized systems are implemented in two TMS320F2-8335 DSP boards which are connected by a serial port and the output signals are exhibited by an oscilloscope. The experiment results show that the proposed implementation method works well on DSP.

1 Introduction

Recently, dynamical analysis, synchronization and secure communication applications of fractional-order chaotic systems have become hot topics. Rich dynamics has been found in these systems [1,2,3,4,5]. For example, Li et al. [1] numerically investigated chaotic behaviors in the fractional-order R$\ddot{o}$ssler system and the fractional-order R$\ddot{o}$ssler hyperchaotic system, and they found the minimum order for chaos is less than three and less than four, respectively. Also, Jia et al. [2] analyzed the dynamics of fractional-order Lorenz system and implemented the system in analog circuit. Meanwhile, some fractional-order models with rich dynamics are reported by researchers. For instance, Xu et al. [6] investigated a novel nonlinear fractional-order mathematical model by introducing a fractional-order damping force, a fractional-order oil-film force, an asymmetric magnetic pull and a hydraulic-asymmetric force.

Synchronization of chaotic systems has aroused much interest of scholars [7], and it is found that fractional-order chaotic systems can also be synchronized. A variety of approaches have been proposed for the synchronization of fractional-order chaotic systems which include lag synchronization [8], active control [9], fuzzy sliding mode control [10], active sliding mode control [11], robust observer [12]. Meanwhile, circuit implementation of synchronization in fractional-order chaotic systems also aroused the scholars interest [13,14,15]. For instance, Zhang et al. [13] analyzed synchronization and its circuit experiment simulation of two fractional-order generalized Lorenz chaotic systems by utilizing a single-variable feedback method. Since signals generated by fractional-order chaotic systems are chaotic, broadband, noise like and sensitive to initial condition, synchronization-based secure communication of fractional-order chaotic systems has high security and was widely reported by scholars [16, 17]. However, numerical solutions of the above reports are obtained by employing the Adams–Bashforth–Moulton algorithm (ABM) [18] and frequency method [19], and these two methods are not suitable for digital circuit implementation of fractional-order chaotic systems.

Compared with analog circuit implementation, digital circuit implementation of fractional-order chaos including the system and synchronization scheme has more advantages such as better design flexibility, easier to modify parameters, better repeatability and stronger anti-interference capacity. Meanwhile, digital signal processor (DSP) is popularized in engineering since it has fast computation speed and strong ability in processing data. Actually, digital implementation of integer-order chaotic systems is not a difficult thing and many reports illustrated this [20,21,22], and DSP digital circuit implementation of fractional-order chaotic systems is reported in References [23,24,25] by applying Adomian decomposition method (ADM) [26]. However, investigation about digital circuit implementation of fractional-order synchronization scheme was rarely reported.

Motivated by the above discussion, in this paper, a synchronization scheme of fractional-order simplified Lorenz hyperchaotic systems with active controller and linear feedback controller is firstly proposed. Since numerical solution of fractional-order chaotic system obtained by ADM works well in DSP [23,24,25], ADM is applied to solve the synchronized systems for the first time. Moreover, the synchronization phenomenon of the state variables and intermediate variables generated by ADM is analyzed. With the numerical solution, digital circuit implementation of fractional-order chaotic systems is achieved by employing DSP technology for the first time.

The rest of this article is organized as follows. In Sec.2, the proposed synchronization scheme and Adomian decomposition method are given. In Sect.3, synchronization analysis in fractional-order simplified Lorenz hyperchaotic systems is carried out. In Sect.4, DSP implementation of the proposed synchronization scheme is achieved. Finally, a concluding remark is presented in Sect.5.

2 Synchronization scheme and numerical solution method

2.1 Synchronization scheme

Consider the following master fractional-order chaotic system

$$\begin{aligned} D_{{t_0}}^q\mathbf{{x}} = f(\mathbf{{x}}), \end{aligned}$$

(1)

where $\mathbf x \in \mathbf{{R}}^n$ is the state vector, $f: \mathbf{{R}}^n-\mathbf{{R}}^n$ is a continuous nonlinear vector function and $D_{{t_0}}^q$ is the Caputo fractional-order derivative [27], which is defined by

$$\begin{aligned} D_{{t_0}}^qx(t) = \left\{ \begin{array}{l} \frac{1}{{\Gamma (1 - q)}}\int _{{t_0}}^t {\frac{1}{{{{(t - \tau )}^q}}}\dot{x}(\tau ){\hbox {d}}\tau } , \quad 0< q < 1\\ \frac{\hbox {d}}{{\hbox {d}t}}x(t), \quad q = 1 \end{array} .\right. \end{aligned}$$

(2)

Then, the slave system can be presented as

$$\begin{aligned} D_{{t_0}}^q\mathbf{{y}} = f(\mathbf{{y}}) + \mathbf{{U}}, \end{aligned}$$

(3)

where U is the controller. We define the error system $\mathrm{e}(t)$ as

$$\begin{aligned} \mathbf{{e}} = \mathbf{{y}} - {\varvec{\Phi x}}. \end{aligned}$$

(4)

Here, ${\varvec{\Phi }}$ is a $n \times n$ constant matrix. The fractional-order error system can be denoted as

$$\begin{aligned} D_{{t_0}}^q\mathbf{{e}} = D_{{t_0}}^q\mathbf{{y}} - {\varvec{\Phi }}D_{{t_0}}^q\mathbf{{x}} = f(\mathbf{{y}}) - {\varvec{\Phi }}f(\mathbf{{x}}) + \mathbf{{U}} . \end{aligned}$$

(5)

In this paper, let

$$\begin{aligned} \mathbf{{U}}(t) = \mathbf{{u}}(t) + {\varvec{\Psi }}(t), \end{aligned}$$

(6)

where $\mathbf {u}(t)$ is the active controller and $\varvec{\Psi }(t)$ is the linear feedback controller. They can be defined as

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf{{u}}(t) = {\varvec{\Phi }}f(\mathbf{{x}}) - f(\mathbf{{y}})\\ {\varvec{\Psi }}(t) = -\,\,\kappa \mathbf{{e}} \end{array} \right. , \end{aligned}$$

(7)

where $\kappa$ is $n\times 1$ constant matrix, denoted as $[ \kappa _1, \kappa _2, ..., \kappa _n]$. Thus, the error system can be presented as

$$\begin{aligned} D_{{t_0}}^q\mathbf{{e}} = - \kappa \mathbf{{e}}. \end{aligned}$$

(8)

When $\kappa >0$, this error system is convergent. It means that the two identical systems are synchronized.

2.2 Adomian decomposition method

In this paper, Adomian decomposition method (ADM) algorithm is employed to solve the master and slave systems. Compared with ABM and frequency method, ADM can get a more exact solution of the fractional-order system as it preserves the system nonlinearities. Let $\mathbf{{x}}(t)$ = $[x_1(t), x_2(t), ..., x_n(t)]^\mathrm{T}$ be the vector of state variables. The fractional-order chaotic system is separated into two parts [28],

$$\begin{aligned} \left\{ \begin{array}{l} D_{{t_0}}^q\mathbf{{x}}(t) = L\mathbf{{x}} + N\mathbf{{x}}\\ {\mathbf{{x}}^{(k)}}(t_0^ + ) = {\mathbf{{b}}_k},k = 0, \ldots ,m - 1 \end{array} \right. . \end{aligned}$$

(9)

Here, $m= \left\lceil q \right\rceil$ , $\mathbf{b}_k$ is a specified constant matrix relating to the initial values. $L\mathbf{{x}}$ and $N\mathbf{{x}}$ represent the linear part and nonlinear part of system, respectively. By applying the fractional integral operator $J_{{t_0}}^q$, which is denoted by [27]

$$\begin{aligned} J_{{t_0}}^qx(t) = \frac{1}{{\Gamma (q)}}\int _{{t_0}}^t {\frac{1}{{{{(t - \tau )}^{1 - q}}}}x(\tau )\mathrm{d}\tau } , \end{aligned}$$

(10)

to both sides of Eq.(9), the solution of system (9) is given by [27, 28]

$$\begin{aligned} \mathbf{{x}}\left( t \right) = J_{{t_0}}^qL\mathbf{{x}} + J_{{t_0}}^qN\mathbf{{x}} + \sum \limits _{k = 0}^{m - 1} {{\mathbf{{b}}_k}\frac{{{{(t - {t_0})}^k}}}{{k!}}} . \end{aligned}$$

(11)

According to [28], the nonlinear terms can be decomposed according to

$$\begin{aligned} A_{}^i({\mathbf{{x}}^0},{\mathbf{{x}}^1}, \cdots ,{\mathbf{{x}}^i})= & {} \frac{1}{{i!}}{\left[ \frac{{{\mathrm{d}^i}}}{{\mathrm{d}{\lambda ^i}}}N(\mathbf{{v}}_{}^i(\lambda ))\right] _{\lambda = 0}} \mathbf{{v}}_{}^i(\lambda )\nonumber \\= & {} \sum \nolimits _{k = 0}^i {{{(\lambda )}^k}{} \mathbf{{x}}_{}^k}, \end{aligned}$$

(12)

where $i=0, 1, ...$; then, the nonlinear terms can be expressed as

$$\begin{aligned} N\mathbf{{x}} = \sum \limits _{i = 0}^\infty {{A^i}\left( {{\mathbf{{x}}^0},{\mathbf{{x}}^1}, \cdots ,{\mathbf{{x}}^i}} \right) } . \end{aligned}$$

(13)

According to [27, 28], the solution of Eq.(11) is derived by

$$\begin{aligned} {\mathbf{{x}}^0}= & {} \sum \limits _{k = 0}^{m - 1} {{\mathbf{{b}}_k}\frac{{{{(t - {t_0})}^k}}}{{k!}}} \nonumber \\ {\mathbf{{x}}^1}= & {} J_{{t_0}}^qL{\mathbf{{x}}^0} + J_{{t_0}}^q{A^0}({\mathbf{{x}}^0})\nonumber \\ {\mathbf{{x}}^2}= & {} J_{{t_0}}^qL{\mathbf{{x}}^1} + J_{{t_0}}^q{A^1}({\mathbf{{x}}^0},{\mathbf{{x}}^1})\nonumber \\&\cdots&\nonumber \\ {\mathbf{{x}}^i}= & {} J_{{t_0}}^qL{\mathbf{{x}}^{i - 1}} + J_{{t_0}}^q{A^{i - 1}}({\mathbf{{x}}^0},{\mathbf{{x}}^1}, \cdots ,{\mathbf{{x}}^{i - 1}})\nonumber \\&\cdots&. \end{aligned}$$

(14)

The analytical solution of the fractional-order system is presented by

$$\begin{aligned} \mathbf{{x}}(t) = \sum \limits _{i = 0}^\infty {{\mathbf{{x}}^i}} = F(\mathbf{{x}}({t_0})) . \end{aligned}$$

(15)

Dividing the time interval $[t_0, t]$, we get subintervals $[t_m, t_{m+1}]$ with equal step size of $h=t_{m+1}-t_m=(t-t_0)/N$. Then, we get the value of $\mathbf{{x}}(t_{m+1})$ according to $F(\mathbf{{x}}(t_m))$. Finally, the numerical solution of the fractional-order chaotic system is denoted as a discrete map $\mathbf{{x}}(m+1)=F(\mathbf{{x}}(m))$.

3 Numerical simulation of the synchronization scheme

In this section, synchronization between two identical fractional-order simplified Lorenz hyperchaotic systems is carried out based on ADM.

3.1 Solution of two simplified Lorenz hyperchaotic systems

The simplified Lorenz hyperchaotic system is proposed in Reference [29], which is presented by

$$\begin{aligned} {{\dot{x}}_1}= & {} 10({x_2} - {x_1}),\nonumber \\ {{\dot{x}}_2}= & {} (24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4},\nonumber \\ {{\dot{x}}_3}= & {} {x_1}{x_2} - 8{x_3}/3,\nonumber \\ {{\dot{x}}_4}= & {} -\,\,k{x_1}, \end{aligned}$$

(16)

where c and k are bifurcation parameters and $[x_1$, $x_2$, $x_3$, $x_4]$ are state variables. Consider that the derivational order of system (16) is fractional and the fractional-order hyperchaotic simplified Lorenz [30] has the form of

$$\begin{aligned} D_{{t_0}}^q{x_1}= & {} 10({x_2} - {x_1}),\nonumber \\ D_{{t_0}}^q{x_2}= & {} (24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4},\nonumber \\ D_{{t_0}}^q{x_3}= & {} {x_1}{x_2} - 8{x_3}/3, \nonumber \\ D_{{t_0}}^q{x_4}= & {} -\,\,k{x_1}, \end{aligned}$$

(17)

where $D_{{t_0}}^q$ is the Caputo derivation. According to ADM, system (17) can be solved as

$$\begin{aligned} {x_{1}}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {c_{1}^j{{{h^{jq}}} \big / {\Gamma (jq + 1)}}}, \nonumber \\ {x_{2}}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {c_2^j{{{h^{jq}}} \big /{\Gamma (jq + 1)}}}, \nonumber \\ {x_{3}}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {c_{3}^j{{{h^{jq}}} \big / {\Gamma (jq + 1)}}}, \nonumber \\ {x_{4}}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {c_{4}^j{{{h^{jq}}} \big /{\Gamma (jq + 1)}}}, \end{aligned}$$

(18)

where the intermediate variables are defined as

$$\begin{aligned} c_1^0= & {} {x_1}(m),c_2^0 = {x_2}(m),c_3^0 = {x_3}(m),c_4^0 = {x_4}(m). \nonumber \\ \end{aligned}$$

(19)

$$\begin{aligned} c_1^1= & {} 10\left( c_2^0 - c_1^0\right) \nonumber \\ c_2^1= & {} (24 - 4c)c_1^0 - c_1^0c_3^0 + cc_2^0 + c_4^0\nonumber \\ c_3^1= & {} c_1^0c_2^0 - 8c_3^0/3\nonumber \\ c_4^1= & {} -\,\,kc_1^0. \end{aligned}$$

(20)

$$\begin{aligned} c_1^2= & {} 10\left( c_2^1 - c_1^1\right) \nonumber \\ c_2^2= & {} (24 - 4c)c_1^1 - c_1^0c_3^1 - c_1^1c_3^0 + c \cdot c_2^1 + c_4^1\nonumber \\ c_3^2= & {} c_1^1c_2^0 + c_1^0c_2^1 - 8c_3^1/3\nonumber \\ c_4^2= & {} -\,\,kc_1^1. \end{aligned}$$

(21)

$$\begin{aligned} c_1^3= & {} 10\left( c_2^0 - c_1^0\right) \nonumber \\ c_2^3= & {} (24 - 4c)c_1^2 - c_1^0c_3^2 - c_1^1c_3^1\frac{{\Gamma (2q + 1)}}{{{\Gamma ^2}(q + 1)}} \nonumber \\&-\,\,c_1^2c_3^0 + c \cdot c_2^2 + c_4^2\nonumber \\ c_3^3= & {} c_1^0c_2^2 + c_1^1c_2^1\frac{{\Gamma (2q + 1)}}{{{\Gamma ^2}(q + 1)}}\nonumber \\&+\,\,c_1^2c_2^0 - 8c_3^2/3\nonumber \\ c_4^3= & {} - kc_1^2. \end{aligned}$$

(22)

$$\begin{aligned} c_1^4= & {} 10\left( c_2^3 - c_1^3\right) \nonumber \\ c_2^4= & {} (24 - 4c)c_1^3 - c_1^0c_3^3 - c_1^3c_3^0 + c \cdot c_2^3 + c_4^3\nonumber \\&- \left( c_1^2c_3^1 + c_1^1c_3^2\right) \frac{{\Gamma (3q + 1)}}{{\Gamma (q + 1)\Gamma (2q + 1)}}\nonumber \\ c_3^4= & {} c_1^0c_2^3 + \left( c_1^2c_2^1 + c_1^1c_2^2\right) \frac{{\Gamma (3q + 1)}}{{\Gamma (q + 1)\Gamma (2q + 1)}}\nonumber \\&+\,\,c_1^3c_2^0 + 8c_3^3/3\nonumber \\ c_4^4= & {} -\,\,kc_1^3. \end{aligned}$$

(23)

$$\begin{aligned} c_1^5= & {} 10\left( c_2^4 - c_1^4\right) \nonumber \\ c_2^5= & {} (24 - 4c)c_1^4\nonumber \\&-\,\,c_1^0c_3^4 - \left( c_1^3c_3^1 + c_1^1c_3^3\right) \frac{{\Gamma (4q + 1)}}{{\Gamma (q + 1)\Gamma (3q + 1)}} \nonumber \\&-\,\,c_1^2c_3^2\frac{{\Gamma (4q + 1)}}{{{\Gamma ^2}(2q + 1)}}\nonumber \\&-\,\,c_1^4c_3^0 + cc_2^4 + c_4^4\nonumber \\ c_3^5= & {} c_1^0c_2^4\nonumber \\&+ \left( c_1^3c_2^1 + c_1^1c_2^3\right) \frac{{\Gamma (4q + 1)}}{{\Gamma (q + 1)\Gamma (3q + 1)}}\nonumber \\&+\,\,c_1^2c_2^2\frac{{\Gamma (4q + 1)}}{{{\Gamma ^2}(2q + 1)}} \nonumber \\&+\,\,c_1^4c_2^0 - 8c_3^4/3\nonumber \\ c_4^5= & {} -\, kc_1^4 \end{aligned}$$

(24)

Dynamics of this system was investigated in Reference [30], and it shows that this system has high complexity for real application. Specifically, when $k = 5$, $c = -2$, $q = 0.98$ and $\mathbf{{x}}_0 = [0.1, 0.2, 0.3, 0.4]$, Lyapunov character exponents (LCEs) of system (17) are $\lambda _i$ (i = 1, 2, 3, 4)=(0.3901, 0.3583, 0, −  16.9756), which implies the system is hyperchaotic. The phase portraits are shown in Fig. 1a–d, while its LCEs diagram is illustrated in Fig. 1e.

Fig. 1

Phase diagram of the fractional-order simplified Lorenz hyperchaotic system a $x_1-x_2$; b $x_1-x_3$; c $x_2-x_3$; d $x_1-x_4$; e Lyapunov exponents

The response system with controllers $u_1$, $u_2$, $u_3$ and $u_4$ is presented as

$$\begin{aligned} D_{{t_0}}^q{y_1}= & {} 10({y_2} - {y_1}) + {u_1}\nonumber \\ D_{{t_0}}^q{y_2}= & {} (24 - 4c){y_1} - {y_1}{y_3}\nonumber \\&+\,\,c{y_2} + {y_4} + {u_2}\nonumber \\ D_{{t_0}}^q{y_3}= & {} {y_1}{y_2} - 8{y_3}/3 + {u_3}\nonumber \\ D_{{t_0}}^q{y_4}= & {} -\,\,k{y_1} + {u_4}. \end{aligned}$$

(25)

According to Eqs. (5) and (6), if $\Phi$ = [$\alpha _{11}$, $\alpha _{12}$, $\alpha _{13}$, $\alpha _{14}$; $\alpha _{21}$, $\alpha _{22}$, $\alpha _{23}$, $\alpha _{24}$; $\alpha _{31}$, $\alpha _{32}$, $\alpha _{33}$, $\alpha _{34}$; $\alpha _{41}$, $\alpha _{42}$, $\alpha _{43}$, $\alpha _{44}$], then the controllers are denoted by

$$\begin{aligned} {u_1}= & {} -\,\,\kappa \left( {{y_1} - {\alpha _{11}}{x_1} - {\alpha _{12}}{x_2} - {\alpha _{13}}{x_3} - {\alpha _{14}}{x_4}} \right) \nonumber \\&+\,\,{\alpha _{11}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{12}}\left( {(24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}} \right) \nonumber \\&+\,\,{\alpha _{13}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) \nonumber \\&-\,\,{\alpha _{14}}k{x_1}- 10({y_2} - {y_1}). \end{aligned}$$

(26)

$$\begin{aligned} {u_2}= & {} -\,\,\kappa ({y_2} - {\alpha _{21}}{x_1} - {\alpha _{22}}{x_2} - {\alpha _{23}}{x_3} - {\alpha _{24}}{x_4}) \nonumber \\&-\,\,(24 - 4c){y_1} + {y_1}{y_3} - c{y_2} - {y_4}\nonumber \\&+\,\,{\alpha _{21}}10({x_2} - {x_1}) \nonumber \\&+\,\,{\alpha _{22}}((24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}) \nonumber \\&+\,\,{\alpha _{23}}({x_1}{x_2} - 8{x_3}/3) \nonumber \\&-\,\,{\alpha _{24}}k{x_1}. \end{aligned}$$

(27)

$$\begin{aligned} {u_3}= & {} -\,\,\kappa \left( {{y_3} - {\alpha _{31}}{x_1} - {\alpha _{32}}{x_2} - {\alpha _{33}}{x_3} - {\alpha _{34}}{x_4}} \right) \nonumber \\&- {y_1}{y_2} + 8{y_3}/3 \nonumber \\&+\,\,{\alpha _{31}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{32}}((24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}) \nonumber \\&+\,\,{\alpha _{33}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) \nonumber \\&-\,\,{\alpha _{34}}k{x_1}. \end{aligned}$$

(28)

$$\begin{aligned} {u_4}= & {} -\,\,\kappa \left( {{y_1} - {\alpha _{41}}{x_1} - {\alpha _{42}}{x_2} - {\alpha _{43}}{x_3} - {\alpha _{44}}{x_4}} \right) \nonumber \\&+\,\,k{y_1}+ {\alpha _{41}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{42}}((24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}) \nonumber \\&+\,\,{\alpha _{43}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) \nonumber \\&-\,\,{\alpha _{44}}k{x_1}. \end{aligned}$$

(29)

Thus the response system can also be defined as

$$\begin{aligned} D_{{t_0}}^q{y_1}= & {} -\,\,\kappa \left( {{y_1} - {\alpha _{11}}{x_1} - {\alpha _{12}}{x_2} - {\alpha _{13}}{x_3} - {\alpha _{14}}{x_4}} \right) \nonumber \\&+\,\,{\alpha _{11}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{12}}\left( {(24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}} \right) \nonumber \\&+\,\,{\alpha _{13}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) - {\alpha _{14}}k{x_1}\nonumber \\ D_{{t_0}}^q{y_2}= & {} \kappa \left( {{y_2} - {\alpha _{21}}{x_1} - {\alpha _{22}}{x_2} - {\alpha _{23}}{x_3} - {\alpha _{24}}{x_4}} \right) \nonumber \\&+\,\,{\alpha _{21}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{22}}\left( {(24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}} \right) \nonumber \\&+ {\alpha _{23}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) - {\alpha _{24}}k{x_1}\nonumber \\ D_{{t_0}}^q{y_3}= & {} -\,\,\kappa \left( {{y_3} - {\alpha _{31}}{x_1} -{\alpha _{32}}{x_2} - {\alpha _{33}}{x_3} - {\alpha _{34}}{x_4}} \right) \nonumber \\&+\,\,{\alpha _{31}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{32}}\left( {(24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}} \right) \nonumber \\&+\,\,{\alpha _{33}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) - {\alpha _{34}}k{x_1}\nonumber \\ D_{{t_0}}^q{y_4}= & {} - \kappa \left( {{y_1} - {\alpha _{41}}{x_1} -{\alpha _{42}}{x_2} - {\alpha _{43}}{x_3} - {\alpha _{44}}{x_4}} \right) \nonumber \\&+\,\,{\alpha _{41}}\left( {10({x_2} - {x_1})} \right) \nonumber \\&+\,\,{\alpha _{42}}\left( {(24 - 4c){x_1} - {x_1}{x_3} + c{x_2} + {x_4}} \right) \nonumber \\&+\,\,{\alpha _{43}}\left( {{x_1}{x_2} - 8{x_3}/3} \right) - {\alpha _{44}}k{x_1}. \end{aligned}$$

(30)

By applying ADM, the solution of the response system is given by

$$\begin{aligned} {y_1}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {\zeta _1^j{{{h^{jq}}} \big / {\Gamma (jq + 1)}}}, \nonumber \\ {y_2}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {\zeta _2^j{{{h^{jq}}} \big / {\Gamma (jq + 1)}}}, \nonumber \\ {y_3}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {\zeta _3^j{{{h^{jq}}} \big /{\Gamma (jq + 1)}}}, \nonumber \\ {y_4}(m + 1)= & {} \sum \nolimits _{j = 0}^5 {\zeta _4^j{{{h^{jq}}} \big /{\Gamma (jq + 1)}}}, \end{aligned}$$

(31)

in which the intermediate variables are defined as

$$\begin{aligned} \zeta _1^0= & {} {y_1}(m),\zeta _2^0 = {y_2}(m),\zeta _3^0 = {y_3}(m),\zeta _4^0 = {y_4}(m) .\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} \zeta _1^j= & {} -\,\,\kappa \left( \zeta _1^{j - 1} - {\alpha _{11}}c_1^{j - 1} - {\alpha _{12}}c_2^{j - 1} - {\alpha _{13}}c_3^{j - 1} \right. \nonumber \\&\left. -\,\,{\alpha _{14}}c_4^{j - 1} \right) + {\alpha _{11}}c_1^j + {\alpha _{12}}c_2^j + {\alpha _{13}}c_3^j + {\alpha _{14}}c_4^j \nonumber \\ \zeta _2^j= & {} -\,\,\kappa \left( \zeta _2^{j - 1} - {\alpha _{21}}c_1^{j - 1} -\,\,{\alpha _{22}}c_2^{j - 1} - {\alpha _{23}}c_3^{j - 1} \right. \nonumber \\&\left. - {\alpha _{24}}c_4^{j - 1}\right) + {\alpha _{21}}c_1^j + {\alpha _{22}}c_2^j + {\alpha _{23}}c_3^j + {\alpha _{24}}c_4^j \nonumber \\ \zeta _3^j= & {} -\,\,\kappa \left( \zeta _3^{j - 1} - {\alpha _{31}}c_1^{j - 1} -\,\,{\alpha _{32}}c_2^{j - 1} - {\alpha _{33}}c_3^{j - 1} \right. \nonumber \\&\left. -\, {\alpha _{34}}c_4^{j - 1}\right) + {\alpha _{31}}c_1^j + {\alpha _{32}}c_2^j + {\alpha _{33}}c_3^j + {\alpha _{34}}c_4^j\nonumber \\ \zeta _4^j= & {} -\,\,\kappa \left( \zeta _4^{j - 1} - {\alpha _{41}}c_1^{j - 1} -\,\,{\alpha _{42}}c_2^{j - 1} - {\alpha _{43}}c_3^{j - 1} \right. \nonumber \\&\left. -\, {\alpha _{44}}c_4^{j - 1}\right) + {\alpha _{41}}c_1^j + {\alpha _{42}}c_2^j + {\alpha _{43}}c_3^j + {\alpha _{44}}c_4^j,\nonumber \\ \end{aligned}$$

(33)

where j = 1, 2, 3, 4, 5. According to Eq. (31), the chaotic sequences of the response system can be obtained with appropriate initial values.

3.2 Synchronization simulation of simplified Lorenz hyperchaotic system

Numerical simulations are presented to demonstrate the effectiveness of the proposed synchronization controller. The time step size is $h = 0.01$. The parameters are chosen to be $q = 0.98$, $c = -\,\,2$, $k = 5$ and $k=[2, 2, 2, 2]$ in all simulations so that the simplified Lorenz hyperchaotic system exhibits hyperchaos. The initial condition of the master system is [0.1, 0.2, 0.3, 0.4], and the initial values of the slave system are [5, 6, 7, 8]. Two cases are analyzed.

Case 1 Generalized dislocated synchronization

Let $\Phi =\alpha _{ij}\delta _{ij}$, where $\alpha _{ij}$ is the scaling factor and $\delta _{ij}$ is zero or one. It means there is only one nonzero number in each row and each column. As the dimension of the system is 4, thus there are 4!-1=23 possible kinds of $\Phi$. Let

$$\begin{aligned} {\varvec{\Phi }} = \left[ {\begin{array}{*{20}{c}} 0&{}{0.5}&{}0&{}0\\ { - 0.5}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{1.5}\\ 0&{}0&{}{ - 1.5}&{}0 \end{array}} \right] . \end{aligned}$$

(34)

Then, the errors between two systems can be expressed as

$$\begin{aligned} {e_1}= & {} {y_1} - 0.5{x_2}\nonumber \\ {e_2}= & {} {y_2} + 0.5{x_1}\nonumber \\ {e_3}= & {} {y_3} - 1.5{x_4}\nonumber \\ {e_4}= & {} {y_4} + 1.5{x_3}. \end{aligned}$$

(35)

Obviously, dislocated synchronization is the special case of the proposed synchronization scheme.

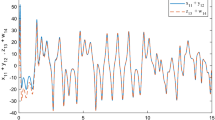
Numerical results of the generalized dislocated synchronization are shown in Fig. 2. According to (32), $y_1$, $y_2$, $y_3$ and $y_4$ synchronize with 0.5$x_2$, −0.5$x_1$, −1.5$x_4$ and 1.5$x_3$, respectively. The time series for four pairs of variables ($y_1$, $x_2$), ($y_2$, $x_1$), ($y_3$, $x_4$) and ($y_4$, $x_3$) are illustrated in Fig. 2a, c, e and g, respectively, where the blue lines are plotted from the response system and the red lines are obtained in the master system. Synchronization plots are correspondingly drawn in Figs 2b, d–f. It shows that the two fractional-order hyperchaotic systems are synchronized.

Fig. 2

Simulation results of generalized dislocated synchronization a time series $y_1$ and $x_2$; b synchronization plot of $y_1-x_2$; c time series $y_2$ and $x_1$; d synchronization line $y_2-x_1$; e time series $y_3$ and $x_4$; f synchronization plot of $y_3-x_4$; g time series $y_4$ and $x_3$; h synchronization plot of $y_4$-$x_3$

Case 2 Generalized linear synchronization, Let $\Phi =\alpha _{ij}(i, j=1, 2,..., n)$, where $\alpha _{ij}$ represent real numbers. We can treat Case 1 as a particular case of this proposed synchronization scheme. Case 2 is the general case of the scheme. Particularly, we choose matrix $\varPhi$ as

$$\begin{aligned} {\varvec{\Phi }} = \left[ {\begin{array}{*{20}{l}} {0.1}&{}{0.2}&{}{0.3}&{}{0.4}\\ {0.25}&{}{0.25}&{}{0.25}&{}{0.25}\\ {0.1}&{}{0.4}&{}{0.4}&{}{0.1}\\ {0.3}&{}{0.2}&{}{0.2}&{}{0.3} \end{array}} \right] . \end{aligned}$$

(36)

Thus, the error system becomes

$$\begin{aligned} {e_1}= & {} {y_1} - 0.1{x_1} - 0.2{x_2} - 0.3{x_3} - 0.4{x_4}\nonumber \\ {e_2}= & {} {y_2} - 0.25{x_1} - 0.25{x_2} - 0.25{x_3} - 0.25{x_4}\nonumber \\ {e_3}= & {} {y_3} - 0.1{x_1} - 0.4{x_2} - 0.4{x_3} - 0.1{x_4}\nonumber \\ {e_4}= & {} {y_4} - 0.3{x_1} - 0.2{x_2} - 0.2{x_3} - 0.3{x_4}. \end{aligned}$$

(37)

By applying ADM, the simulation results are presented in Fig. 3. The time series of $x_1$ and $y_1$ are plotted in Fig. 3a, where the red line represents the $x_1$ and the blue line is $y_1$. Phase diagrams of $x_1-y_1$ and $y_1-y_2$ are shown in Fig. 3b, c. It can be seen from these two phase diagrams that there are no correlations between $x_1$ and $y_1$ and between $y_1$ and $y_2$. Let

$$\begin{aligned} {\varphi _1}= & {} 0.1{x_1} + 0.2{x_2} + 0.3{x_3} + 0.4{x_4}\nonumber \\ {\varphi _2}= & {} 0.25{x_1} + 0.25{x_2} + 0.25{x_3} + 0.25{x_4}\nonumber \\ {\varphi _3}= & {} 0.1{x_1} + 0.4{x_2} + 0.4{x_3} + 0.1{x_4}\nonumber \\ {\varphi _4}= & {} 0.3{x_1} + 0.2{x_2} + 0.2{x_3} + 0.3{x_4} . \end{aligned}$$

(38)

The synchronization results between $y_1-\varphi _1$, $y_2-\varphi _2$, $y_3-\varphi _3$ and $y_4-\varphi _4$ are illustrated in Fig. 3d–g, respectively. Thus, the simulation results verify that the two systems are synchronized.

Fig. 3

Simulation results of the generalized linear synchronization a time series $x_1$ (red line) and $y_1$ (blue line); b phase diagram $x_1-y_1$; c phase diagram $y_1-y_2$; d synchronization plot of $y_1-\varphi _1$; e synchronization plot of $y_2-\varphi _2$; f synchronization plot of $y_3-\varphi _3$; g synchronization plot of $y_4-\varphi _4$. (Color figure online)

3.3 Synchronization performance analysis

Taking Case 2 as an example, the synchronization setup time with different q is obtained as displayed in Fig. 4a. The error between master system and slave system is defined as

$$\begin{aligned} \mathrm{Error} = \sum \limits _{i = 1}^4 {\left| {{y_i} - {\alpha _{i1}}{x_1} - {\alpha _{i2}}{x_2} - {\alpha _{i3}}{x_3} - {\alpha _{i4}}{x_4}} \right| } . \end{aligned}$$

(39)

It indicates in Fig. 4 that the synchronization setup time is increasing with the increasing derivative order q. In addition, if we fix $q = 0.98$, the control parameter k also affects the synchronization setup time. As shown in Fig. 4b, the larger the k is, the shorter the synchronization setup time is.

Fig. 4

The synchronization simulation results a result with different q; b result with different $\kappa$. (Color figure online)

Fig. 5

Synchronization result between intermediate variables a $E^0$; b $E^1$; c $E^2$; d $E^3$

As can be seen from Eq. (33), the intermediate variables ($c_i^j$: i = 1, 2, 3, 4; $j = 0$, 1, 2..., 5) of the master system are used in the numerical solution of the slave system. Define the error of intermediate variables between the two synchronized systems as

$$\begin{aligned} {E^j} = \sum \limits _{i = 1}^4 {\left| {\zeta _i^j - {\alpha _{i1}}c_i^j - {\alpha _{i2}}c_i^j - {\alpha _{i3}}c_i^j - {\alpha _{i4}}c_i^j} \right| }, \end{aligned}$$

(40)

in which $\zeta _i^j$(i = 1, 2, 3, 4; j=0, 1, 2, ..., 4) are intermediate variables of the response system. It shows in Fig. 5 that synchronization exists between the intermediate variables. The corresponding time series of these intermediate variables are illustrated in Fig. 6. Since these intermediate variables are obtained from the state variables, they are also chaotic. In summary, the intermediate variables can also be used in practical applications.

Fig. 6

Time series of intermediate variables a $c_1^0\left( {{x_1}} \right)$; b $c_1^1$; c $c_1^2$; d $c_1^3$

Fig. 7

Synchronization setup time with different intermediate variables. a $c_i^5 = 0$ (i = 1, 2, 3, 4); b $c_i^j = 0$ (i = 1, 2, 3, 4; j=4, 5); c $c_i^j = 0$ (i = 1, 2, 3, 4; j = 3, 4, 5); d $c_i^j = 0$ (i=1, 2, 3, 4; j=2, 3, 4, 5)

The impact of intermediate variables to the synchronization should be investigated. If we just send $c_i^j$ (i = 1, 2, 3, 4; j=0, 1, 2 3) to the slave system, that is to say, let $c_i^4 = 0$ (i = 1, 2, 3, 4), the two systems are synchronized as shown in Fig. 7a. Similarly, Fig. 7b shows that the two systems can also be synchronized when $c_i^j = 0$ (i = 1, 2, 3, 4; j = 3, 4). However, if we just send $c_i^j$ (i = 1, 2, 3, 4; j =0, 1, 2) or $c_i^j$ (i = 1, 2, 3, 4; j = 0, 1) to the slave system, according to Fig. 7c, d, the two systems cannot synchronize. It means that, to achieve synchronization, we should send at least $c_i^j$ (i = 1, 2, 3, 4; j = 0, 1, 2, 3) to the slave system.

4 Synchronization implementation on DSP

4.1 DSP implementation scheme

In this section, the synchronization scheme for fractional-order chaotic systems is implemented in the DSP digital circuit. The hardware block diagram for synchronization of fractional-order chaotic systems is shown in Fig. 8, where the oscilloscope is used to capture the synchronization phenomenon. In our experiment, the floating point DSP TMS320F28335 is used to calculate the fractional -order systems. Between the two DSP boards, we introduce a UART port. Thus, the intermediate variables of the master system can be sent to the slave system, and the iteration information as a response of the slave system can be derived to the master system to control the iteration of both systems. Two correspondent state variables are sent to a D/A chip (DAC8552), so the synchronization phenomenon can be observed in the oscilloscope. The DSP board used to perform the digital implementation is shown in Fig. 9.

Fig. 8

Hardware block diagram for synchronization of fractional-order chaotic systems

Fig. 9

DSP platform for synchronization of fractional-order chaotic systems

Fig. 10

Flow diagram for the DSP implementation of the master system

Flow diagrams for DSP implementation of master system and slave system are illustrated in Figs. 10 and 11, respectively. In the calculation preparation step, some variables such as $h^q$, $\Gamma (q+1)$, $h^q/\Gamma (q+1)$ and $h^{2q}$ are computed for further iteration. In the data processing step, a large enough number is added to the states variable to make sure it is greater than zero. Then, the data are rescaled and truncated to adjust the scale of the D/A converter. To control the iteration of both systems, the following method is designed. Firstly, the master system iterates once, then we get state variables $\mathbf{{x}}$ = $[x_1, x_2, x_3, x_4]$ and intermediate variables $c_i^j$ (i = 1, 2, 3, 4; j = 0, 1, 2). Next, we push the state variables to register as the initial value of the next iteration. As the calculation of the slave system needs the intermediate variables, they are sent to the slave system by the serial port. With these intermediate variables, the slave system iterates once and sends a response message to the master system. After receiving the response message, the next round goes on. In the next section, the experiment results are presented to show the effectiveness of the proposed DSP implementation scheme.

Fig. 11

Flow diagram for the DSP implementation of slave system

4.2 DSP implementation result

We set the step size $h =0.01$, the initial state of master system as $(x_1(t_0)$, $x_2(t_0)$, $x_3(t_0)$, $x_4(t_0))$ = (1, 2, 3, 4) and the initial state of slave system as $(y_1(t_0)$, $y_2(t_0)$, $y_3(t_0)$, $y_4(t_0))$ = (0.1, 0.2, 0.3, 0.4). Generalized dislocated synchronization is implemented on the DSP board. Let series one be $y_1$ and series two be $x_2$. The synchronization line of $x_2-y_1$ with

$$\begin{aligned} {\varvec{\Phi }} = \left[ {\begin{array}{*{20}{c}} 0&{}{0.5}&{}0&{}0\\ { - 0.5}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{1.5}\\ 0&{}0&{}{ - 1.5}&{}0 \end{array}} \right] \end{aligned}$$

(41)

is shown in Fig. 12a, where $\alpha _{12} = 0.5$ and the two time series captured are illustrated in the oscilloscope Fig. 12b, which shows that the systems are synchronized on the DSP board. Moreover, we also let

$$\begin{aligned} {\varvec{\Phi }} = \left[ {\begin{array}{*{20}{c}} 0&{}{2}&{}0&{}0\\ { - 0.5}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{1.5}\\ 0&{}0&{}{ - 1.5}&{}0 \end{array}} \right] \end{aligned}$$

(42)

and

$$\begin{aligned} {\varvec{\Phi }} = \left[ {\begin{array}{*{20}{c}} 0&{}{1}&{}0&{}0\\ { - 0.5}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{1.5}\\ 0&{}0&{}{ - 1.5}&{}0 \end{array}} \right] , \end{aligned}$$

(43)

where $\alpha _{12} = 2$ and $\alpha _{12} = 1$; thus, $y_1 = 2x_2$ and $y_1 = x_2$, respectively. The captured results are illustrated in Fig. 12c–f, and it can be seen that synchronization is established.

According to our test results, the error between $y_1$ and $\alpha _{12}x_2$ is smaller than $10^{-6}$. Although it is not the complete synchronization, it can be used in real applications. This section indicates that synchronization of the two fractional-order chaotic systems is successfully realized in the digital circuit.

Fig. 12

Synchronization results by DSP implementation a synchronization plot of $x_2-y_1$ with $\alpha _{12} = 0.5$; b time series of $x_2$ and $y_1$ with $\alpha _{12} = 0.5$; c synchronization plot of $x_2-y_1$ with $\alpha _{12}$ =2; d time series of $x_2$ and $y_1$ with $\alpha _{12}$ = 2; e synchronization plot of $x_2-y_1$ when $\alpha _{12}$ = 1; f time series of $x_2$ and $y_1$ with $\alpha _{12}$ = 1

5 Conclusion

In this paper, generalized synchronization of fractional-order simplified Lorenz hyperchaotic systems is investigated where the active controller and linear feedback controller are designed. By employing the Adomian decomposition method (ADM), numerical solutions of the two synchronized systems are obtained. Then, we numerically analyzed the synchronization phenomenon with two cases including the generalized dislocated synchronization and the generalized linear synchronization, and some new results are found. By employing the DSP technique, the proposed synchronization scheme is realized in the DSP developing boards in which the chip is TMS320F28335. The conclusions of this article are drawn as follows.

• (1) Numerical solutions obtained by ADM have fast speed for numerical simulation and work well in the DSP board, which shows that the solutions are good for real applications.

• (2) The synchronization setup time is decreasing with the increasing derivative order q and decreases with the increase in control parameter k.

• (3) The synchronization phenomenon is observed in the intermediate variables, and it shows that the intermediate variables can also be used in real applications.

• (4) The synchronization results captured in the oscilloscope are consistent with the simulation results. It shows that synchronization of fractional-order chaotic systems can be used in the engineering field.