Deployment dynamics modeling and analysis for mesh reflector antennas considering the motion feasibility

Abstract

Mesh reflector antennas have been widely used in space satellites for their characteristics of large aperture, low levels of total mass, stowed volume, surface distortion, etc. The antenna turns from a stowed state to a fully deployed configuration and finally forms a required functional surface, and this deployment process affects the performances of antennas on orbit. The dynamic modeling and analysis for the deployment of mesh reflector antennas considering the rigid body rotation of rods, the geometric nonlinearity of the cable net, and the rigid-flexible coupling of the truss and the cable net are presented in this paper. Instead of the previous lumped mass model, the mass of hinges is concentrated on their centroids and the longerons, battens, and diagonals are regarded as homogeneous rods in the study. By this model, the rigid body motion of rods can be well considered in the calculation of kinetic energies rather than be ignored in previous researches. Then, the cable net is discretized into multiple cable elements that are modeled by springs. The slacked and tensioned state of cable elements during deployment are captured by updating the stiffness matrix real-timely. The elastic energy of the cable net is derived by solving systematic equilibrium equations. The dynamic model is established by using Lagrange equation, and then the driving force under the predesigned motion is derived. The “ideal deployment motion” and “feasible deployment motion” are proposed and discussed through several numerical examples. Simulation results match well with experimental data in previous literature.

1 Introduction

Space antennas play an indispensable role in the aerospace communication, military reconnaissance, deep-space probes, global broadcasting, remote sensing and climate forecasting. Due to the volume and weight constraints of launch vehicles, the deployable antennas are widely used for their easy storage and transportation [1,2,3]. They are stowed in the fairing at the launch stage, and then start to deploy after entering the orbit and finally form the parabolic reflective surfaces. The stable and reliable deployment of the antenna concerns the success of the space mission greatly.

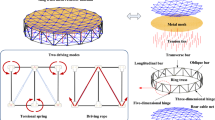
Since the late 1960’s, mesh reflectors have been favored for their potential to fill large apertures with extremely lightweight hardware. At present, the AstroMesh reflector antenna is the most advanced and reliable deployable mesh antenna available [4]. As shown in Fig. 1, it is composed of an articulated ring truss, a knitted lightweight metallic mesh, two cable nets (front and rear nets) and tension ties. The deployable truss includes several cable-actuated, synchronized parallelograms. The driving cable connected with a motor goes through the diagonal rods and drives the truss to deploy by contracting the sleeves. After the reflector is released from a stowed state, the slacked cable net is pulled by the truss to stretch and then the stretched cable net begins to resist the further deployment of the truss. At the end, the driving cable transfers significant energy to the cable net to develop the high overall pre-stress condition. The deployment completes with the latching of the truss and the formation of the required parabolic reflecting surface.

Fig. 1

AstroMesh reflector antenna [5]

As the deployment is irreversible and there are no effective ways for maintenance and active adjustment on orbit, it is essential to study and simulate the deployment process in the design stage to gain a deep insight into the deployment dynamics [6]. The complex kinematic and dynamic behaviors of trusses, high nonlinear tensions and various topologies of cable nets, as well as the dissipation of energy caused by friction, damping and clearance lead to non-ignorable influences on the deployment of mesh reflector antennas. In the field of aerospace, dynamic modeling methods for space devices with flexible appendages are proposed [7, 8], and the deployment/retrieval of tethered satellite system is researched [9,10,11]; these research ideas for the nonlinear dynamic problems provide references for the deployment modeling and analysis of mesh reflector antennas.

Among the researches about the deployment process of deployable antennas, Li [12] establishes the dynamic model of a ring truss antenna based on Lagrange equation and obtains the driving force under a predesigned deployment motion. But as he uses the lumped mass model for the kinematic analysis, the rigid body motion characteristics of rods (longerons, battens and diagonal rods in Fig. 1) are not considered. In fact, as the motion of rods is the combination of translation and rotation, the Euler rotation should not be ignored in the calculation of kinematic energy. Li et al. [13] study the deployment dynamics of a novel ring mechanism and propose a modified deployment motion planning method. However, the cable net tensions are calculated based on a simplified model which cannot depict the potential energy of the cable net accurately. Mitsugi [14] researches the required driving force and the cable tensions of a mesh reflector during the deployment process using the flexible multi-body dynamics approach, and validates the results by experiments. He has concluded that the reflector should be designed such that the deployment driving force is larger than the mesh tensions at any stage of the deployment. Furthermore, it has been verified by experiments that the complex nonlinear forces generated mainly by cable nets will lead to non-negligible influences on the deployment process [15].

In previous studies, the influences of cable tensions on the deployment are mostly ignored or estimated using equivalent spring models. These models are built based on the assumptions that all the cable segments are stretched simultaneous at a certain moment. Furthermore, the cable tensions are simply described by Hooke’s law [12, 13, 15, 17, 18]. Nevertheless, it has been proved by experiments that the cable net is stretched gradually from a completely slacked state to a partly slacked/tensioned state and finally attains a completely tensioned state [14, 15]. Cable tensions are dependent on characteristics of the truss’ deployment as well as on the parameters and topology of the cable nets. Zhang et al. [15, 16] uses catenary elements to simulate cable elements of mesh reflector antennas. Nevertheless, this approach is not general for cable tensions with varying topologies and parameters. Once the topology or parameters are changed, the modeling and calculation have to be revised.

Many researchers try to analyze the deployment process by inverse dynamics, and the main goal is to find the required driving force for a predesigned deployment motion. But the actual motion feasibility is not considered in these researches [12, 13, 15,16,17]. The driving cable cannot offer a negative force for the decelerated deployment, because cables can only be tensioned but not be compressed. So, if the deployment motion is designed to decelerate while the potential energy of the cable net decreases, the released potential energy will be transferred to the kinetic energy and leads to unexpected acceleration. In this case, the antennas cannot be deployed as the predesigned motion. Therefore, the motion feasibility should be considered in the inverse dynamics analysis to ensure a realizable deployment process.

In this paper, the dynamic modeling and analysis for the deployment of mesh reflector antennas considering the motion feasibility are proposed. Firstly, the mass of hinges is concentrated on their centroids and the rods are considered to be homogeneous in the modeling. The homogeneous transformation method is consulted in the kinematic analysis, and then the kinetic energy of the truss is derived. Secondly, the cable net is discretized into multiple cable elements which are modeled by spring elements. The stiffness matrix of the cable net is updated real-timely according to the slacked or tensioned state of cable elements. After the systematic equilibrium equations are formulated and solved, the elastic energy of the cable net can be obtained. The dynamic model of the reflector antennas is built based on the Lagrange equations. Finally, several numerical case studies are provided and the feasibility of the predesigned motion is discussed. Simulation results agree with experiment data in previous literature. On the basis of these simulations, it can be concluded that the topology and design parameters of cable nets well as the motion planning should be combined in the design stage to guarantee the smoothness and feasibility of the deployment motion.

2 Kinematic analysis of the truss

In the truss model, the mass of hinges is concentrated on the nodes in Fig. 2, and the red nodes represent the five-dimensional hinges, while the black and hollow nodes represent three-dimensional hinges and sleeves, respectively. The mass of rods is regarded as uniformly distributed along longitudinal direction. Suppose there are n parallelograms in the truss ($n\ge 4$ and n is an even number), and these parallelograms are deployed synchronously. The local coordinate frames of these parallelograms are defined as in Fig. 2 and the origins are fixed on the node in each parallelogram. During the deployment, the hinges and rods in the same parallelogram always stay in the same plane $(x_j O_j y_j)$, and the angle between the two adjacent parallelograms is constant.

Fig. 2

Equivalent model of the truss

Figure 3 shows two arbitrary adjacent parallelograms, and $A_i,B_i,C_i,D_i$ represent the nodes in the $i\hbox {th}$ parallelograms. The angle between the two parallelograms is $\theta \left( {\theta ={2\pi }/n} \right)$, and the angle $\varphi$ between the longeron and the batten represents the degree of the deployment.

Fig. 3

Two arbitrary adjacent parallelograms

For an arbitrary point P in parallelogram j, its position vector ${{\varvec{r}}}^{j}$ in local coordinate frame $(x_j ,y_j ,z_j)$ can be transformed to frame $(x_i ,y_i ,z_i)$ by homogeneous transformation, as shown in Eqs. (1) and (2).

$$\begin{aligned} {{\varvec{r}}}^{i}= & {} {{\varvec{A}}}^{{\textit{ij}}}{{\varvec{r}}}^{j} \end{aligned}$$

(1)

$$\begin{aligned} {{\varvec{A}}}^{{\textit{ij}}}= & {} \left[ {{\begin{array}{ccccc} {\cos \left[ {\left( {j-i} \right) \theta } \right] }&{} 0&{} {\sin \left[ {\left( {j-i} \right) \theta } \right] }&{} {\left\{ {\sum \limits _{k=i+1}^j {\cos \left[ {\left( {k-i-1} \right) \theta } \right] } } \right\} R_2 \cos \left( {\frac{1}{2}\pi -\varphi } \right) } \\ 0&{} 1&{} 0&{} {\frac{\left[ {1-(-1)^{j-1}} \right] R_2 \sin \left( {\frac{1}{2}\pi -\varphi } \right) }{2}} \\ {-\sin \left[ {\left( {j-i} \right) \theta } \right] }&{} 0&{} {\cos \left[ {\left( {j-i} \right) \theta } \right] }&{} {\left\{ {-\sum \limits _{k=i+1}^j {\sin \left[ {\left( {k-i-1} \right) \theta } \right] } } \right\} R_2 \cos \left( {\frac{1}{2}\pi -\varphi } \right) } \\ 0&{} 0&{} 0&{} 1 \\ \end{array} }} \right] \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(2)

where $j>i,\,i\ge 1,\,j\ge 2$; ${{\varvec{A}}}^{{\textit{ij}}}$ is the homogenous transformation matrix; $R_2$ is the length of the longeron.

The velocity of the arbitrary point P in frame $(x_i ,y_i ,z_i)$ can be obtained by

$$\begin{aligned} {{\varvec{v}}}^{i}=\dot{{{\varvec{A}}}}^{\left( {{\textit{ij}}}\right) } {{\varvec{r}}}^{j}+{{\varvec{A}}}^{\left( {{\textit{ij}}} \right) }\dot{{{\varvec{r}}}}^{j} \end{aligned}$$

(3)

The position vectors of point $A_j$ and $B_j$ in frame $(x_j ,y_j ,z_j)$ are as follows

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{r}}}_{A_j }^j =\left( {0,R_1 ,0,1} \right) ^{T} \\ {{\varvec{r}}}_{B_j }^j =\left( {0,0,0,1} \right) ^{T} \\ \end{array}} \right. \end{aligned}$$

(4)

where $R_1$ is the length of the batten.

Suppose the batten $A_{1}B_{1}$ is fixed during the deployment, that is ${{\varvec{v}}}_{{A_{1}}}^1 ={{\varvec{v}}}_{{B_{1}}}^1 =0$, so the local coordinate frame $(x_1 ,y_1 ,z_1 )$ is chosen as the global coordinate frame. Then the velocity of point $A_j$ and $B_j (j\ge 2)$ in global frame can be derived

$$\begin{aligned} {{\varvec{v}}}_{{A_{j}}}^1= & {} {{\varvec{v}}}_{{B_{j}}}^1\nonumber \\= & {} \left[ {{\begin{array}{l} {\left\{ {\sum \nolimits _{k=2}^j {\cos \left[ {\left( {k-2} \right) \theta } \right] } } \right\} R_2 \sin \left( {\frac{1}{2}\pi -\varphi } \right) \dot{\varphi }} \\ {\frac{\left[ {(-1)^{j-1}-1} \right] R_2 \cos \left( {\frac{1}{2}\pi -\varphi } \right) \dot{\varphi }}{2}} \\ {{\begin{array}{c} {\left\{ {-\sum \nolimits _{k=2}^j {\sin \left[ {\left( {k-2} \right) \theta } \right] } } \right\} R_2 \sin \left( {\frac{1}{2}\pi -\varphi } \right) \dot{\varphi }} \\ 1 \\ \end{array} }} \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(5)

The velocity of point $D_j$ and $C_j$ is equal to the velocity of point $A_{j+1}$ and $B_{j+1}$, as follows

$$\begin{aligned} {{\varvec{v}}}_{{D_{j}}}^1 ={{\varvec{v}}}_{{A_{j+1}}}^1 , {{\varvec{v}}}_{{C_{j}}}^1 ={{\varvec{v}}}_{B_{j+1}}^1 \end{aligned}$$

(6)

For arbitrary rods in the truss (longerons, battens or diagonal rods), their motion is the superposition of translation and rotation. So, the centroid velocity of the batten $A_j B_j$ is

$$\begin{aligned} {{\varvec{v}}}_{{A_{j} B_{j}}}^1 =\frac{\left( {{{\varvec{v}}}_{{A_{j}}}^1 +{{\varvec{v}}}_{{B_{j}} }^1 } \right) }{2} \end{aligned}$$

(7)

The angular velocity of the batten $A_j B_j$ is

$$\begin{aligned} {\varvec{\omega }}_{{A_{j} B_{j}} }^1 =\frac{{{\varvec{v}}}_{{B_{j}}}^1 -{{\varvec{v}}}_{{A_{j}}}^1 }{R_1 } \end{aligned}$$

(8)

The velocity and angular velocity of the longeron $A_j D_j$ are

$$\begin{aligned} {{\varvec{v}}}_{{A_{j} D_{j}} }^1= & {} \frac{\left( {{{\varvec{v}}}_{{A_{j}}}^1 +{{\varvec{v}}}_{{A_{j+1}} }^1 } \right) }{2} \end{aligned}$$

(9)

$$\begin{aligned} {\varvec{\omega }}_{{A_{j} D_{j}}}^1= & {} \frac{{{\varvec{v}}}_{{A_{j+1}}}^1 -{{\varvec{v}}}_{{A_{j}} }^1}{R_2 } \end{aligned}$$

(10)

The velocity and angular velocity of the longeron $B_j C_j$ can be obtained by the same way.

The length of the diagonal rods varies with the deployment angle $\varphi$, so the velocity and angular velocity of diagonal rods are

$$\begin{aligned} \left\{ {\begin{array}{l} {{\varvec{v}}}_{{\mathrm{d}_j}}^1 =\frac{\left( {{{\varvec{v}}}_{{B_j} }^1 +{{\varvec{v}}}_{A_{j+1}}^1 } \right) }{2},\;{\varvec{\omega }} _{{\mathrm{d}_{j}} }^1 =\frac{{{\varvec{v}}}_{A_{j+1}}^1 -{{\varvec{v}}}_{{B_{j}} }^1 }{\sqrt{R_1^2 +R_2^2 -2R_1 R_2 \cos \left( {\pi -\varphi } \right) }}\hbox { }j=2k-1,k=1,2,\ldots ,n/2\hbox { } \\ {{\varvec{v}}}_{{\mathrm{d}_{j}}}^1 =\frac{\left( {{{\varvec{v}}}_{{A_{j}}}^1 +{{\varvec{v}}}_{B_{j+1}}^1 } \right) }{2},\;{\varvec{\omega }} _{{\mathrm{d}_{j}}}^1 =\frac{{{\varvec{v}}}_{{B_{j+1}}}^1 -{{\varvec{v}}}_{{A_{j}}}^1 }{\sqrt{R_1^2 +R_2^2 -2R_1 R_2 \cos \left( {\pi -\varphi } \right) }}\qquad j=2k,k=1,2,\ldots ,n/2 \\ \end{array}} \right. \end{aligned}$$

(11)

3 Dynamic modeling

The curve of the deployment angle $\varphi$ is generally predesigned to do the inverse dynamics analysis. In this section, this angle is chosen as the generalized coordinate to build the dynamic model of mesh reflector antennas. Kinematic and potential energy during the deployment is analyzed and formulated in Sects. 3.1 and 3.2. Then the corresponding driving force is derived in Sect. 3.3 based on the Lagrange equation of the second kind.

3.1 Kinetic energy

According to the kinematic analysis in Sect. 2, the kinetic energy of all rods can be derived that

$$\begin{aligned} T_\mathrm{b} =\frac{1}{2}\sum _{j=1}^n {\left\{ {\begin{array}{l} m_1 \left( {{{\varvec{v}}}_{A_{j} B_{j} }^1 } \right) ^{2}+J_1 \left( {{\varvec{\omega }}_{{A_{j} B_{j}}}^1 } \right) ^{2}+m_2 \left[ {\left( {{{\varvec{v}}}_{A_{j} D_{j} }^1} \right) ^{2}+\left( {{{\varvec{v}}}_{B_{j} C_{j}}^1}\right) ^{2}} \right] +J_2 \times \\ \left[ {\left( {{\varvec{\omega }} _{{A_j D_{j}}}^1}\right) ^{2} +\left( {{\varvec{\omega }} _{{B_{j} C_{j}}}^1 } \right) ^{2}} \right] +m_3 \left( {{{\varvec{v}}}_{{\mathrm{d}_{j}}}^1}\right) ^{2} +J_3 \left( {{\varvec{\omega }} _{{d_{j}}}^1 } \right) ^{2} \\ \end{array}} \right\} } \end{aligned}$$

(12)

where $m_1$ is the mass of the batten; $m_2$ is the mass of the lengeron; $m_3$ is the mass of the diagonal rod; $J_1$ is the moment of inertia of the longeron, $J_1 =\frac{1}{12}m_1 R_1^2;J_2$ is the moment of inertia of the batten, $J_2 =\frac{1}{12}m_2 R_2^2 ;J_3$ is moment of inertia of the diagonal rod which can be calculated by Eq. (13).

$$\begin{aligned} J_3 =\frac{1}{12}m_3 \left[ {R_1^2 +R_2^2 -2R_1 R_2 \cos \left( {\pi -\varphi } \right) } \right] \end{aligned}$$

(13)

The kinetic energy of all hinges is

$$\begin{aligned} T_\mathrm{h} =\frac{1}{2}\sum _{j=1}^n {\left[ {m_\mathrm{t} \left( {{{\varvec{v}}}_{\mathrm{A}_j }^1 } \right) ^{2}+m_\mathrm{f} \left( {{{\varvec{v}}}_{\mathrm{B}_j }^1 } \right) ^{2}+m_\mathrm{d} \left( {{{\varvec{v}}}_{{\mathrm{d}_{j}}}^1 } \right) ^{2}} \right] } \end{aligned}$$

(14)

where $m_\mathrm{t}$ is the mass of the three-dimensional hinge; $m_\mathrm{f}$ is the mass of the five-dimensional hinge; $m_\mathrm{d}$ is the mass of the sleeve.

Then the kinetic energy of the truss during the deployment can be obtained by Eq. (15).

$$\begin{aligned} T=T_\mathrm{b} +T_\mathrm{h} \end{aligned}$$

(15)

3.2 Potential energy

The potential energy mainly consists of the elastic potential energy of the cable net and the gravitational potential energy of the truss. As the cable net is lightweight, the mass can be ignored in the calculation of the potential energy. To establish the equivalent model, the cable net is discretized into multiple cable elements, and each element is modeled by the spring, as shown in Fig. 4.

Fig. 4

Equivalent model of the cable net

For the cable net with m cable elements and $n^{\prime }$ nodes $(n_{\mathrm{f}}^{\prime }$ free nodes and $n_{\mathrm{b}}^{\prime }$ boundary nodes), at any time t during the deployment, the coordinate-difference vector of the arbitrary cable element $i^{\prime }$ is defined as follows

$$\begin{aligned} C_{{i^{\prime }}} =\left( {\Delta x_{i^{\prime }} (t),\Delta y_{i^{\prime }} (t),\Delta z_{i^{\prime }} (t)} \right) \end{aligned}$$

(16)

The elements in the coordinate-difference vectors can be obtained by

$$\begin{aligned} \left\{ {\begin{array}{l} {\varvec{\Delta }}{} \mathbf{x}(t)=\mathbf{Tx}(t),\hbox { }{\varvec{\Delta }} \mathbf{x}(t)=[{{\Delta }} x_1 (t),\hbox { }\ldots ,\hbox { }{{\Delta }} x_{i^{\prime }} (t)\cdots {{\Delta }} x_m (t)] \\ {\varvec{\Delta }}{} \mathbf{y}(t)=\mathbf{Ty}(t),\hbox { } {\varvec{\Delta }}{} \mathbf{y}(t)=[{{\Delta }} y_1 (t),\hbox { }\ldots ,\hbox { } {{\Delta }} y_{i^{\prime }} (t)\cdots {{\Delta }} y_m (t)] \\ {\varvec{\Delta }}{} \mathbf{z}(t)=\mathbf{Tz}(t),\hbox { } {\varvec{\Delta }} \mathbf{z}(t)=[{{\Delta }} z_1 (t),\hbox { }\ldots , \hbox { }{{\Delta }} z_{i^{\prime }} (t)\cdots {{\Delta }} z_m (t)] \\ \end{array}} \right. \end{aligned}$$

(17)

where $\mathbf{x}(t)$, $\mathbf{y}(t)$ and $\mathbf{z}(t)$ are the coordinate values of nodes at time t in x, y and z direction. $\mathbf{T}(\in {\mathbb {R}}^{m\times n^{\prime }})$ is the topological matrix, refer to our companion paper [19].

The elongation matrix ${\varvec{\delta }}{} \mathbf{l} \left( t \right) \left( {\in {\mathbb {R}}^{m\times 1}} \right)$ is defined as follows

$$\begin{aligned}&{\varvec{\delta }}{} \mathbf{l}\left( t \right) =[\delta l_1 \left( t \right) ,\hbox { }\ldots ,\hbox { }\delta l_{i^{\prime }} \left( t \right) \hbox { }\ldots \hbox { }\delta l_m \left( t \right) ] \end{aligned}$$

(18)

$$\begin{aligned}&\delta l_{i^{\prime }} \left( t \right) =\left\{ {\begin{array}{c} {\left( {\left| {C_{i^{\prime }} } \right| -l_{i^{\prime }} } \right) }/{\left| {C_{i^{\prime }} } \right| },\quad \left| {C_{i^{\prime }} } \right| >l_{i^{\prime }} \\ \hbox { }0\quad ,\quad \left| {C_{i^{\prime }} } \right| \le l_{i^{\prime }} \\ \end{array}} \right. \end{aligned}$$

(19)

where $l_{i^{\prime }}$ is the original length of the cable element $i^{\prime }$.

The system stiffness coefficient matrix $\mathbf{K}\left( t \right) \left( {\in {\mathbb {R}}^{m\times 1}} \right)$ is given by Eqs. (20) and (21)

$$\begin{aligned}&\mathbf{K}\left( t \right) =[k_1 \left( t \right) ,\hbox { }\ldots ,\hbox { }k_{i^{\prime }} \left( t \right) \hbox {, }\ldots \hbox { }k_m \left( t \right) ] \end{aligned}$$

(20)

$$\begin{aligned}&k_{i^{\prime }} \left( t \right) =\left\{ {\begin{array}{ll} k_\mathrm{e} ,&{}\quad \left| {C_{i^{\prime }} } \right| >l_{i^{\prime }} \\ 0,&{}\quad \left| {C_{i^{\prime }} } \right| \le l_{i^{\prime }} \\ \end{array}} \right. \end{aligned}$$

(21)

where $k_{i^{\prime }} \left( t \right)$ is the stiffness coefficient of an arbitrary cable element $i^{\prime }$ at time $t; k_\mathrm{e}$ is the linearized tensile stiffness of cable elements.

The force-length ratio matrix $\mathbf{Q}_\mathbf{k} \left( t \right) \left( {\in {\mathbb {R}}^{m\times m}} \right)$ is

$$\begin{aligned} \mathbf{Q}_\mathbf{k} \left( t \right) ={\mathrm{diag}}(\mathbf{q}_\mathbf{k} \left( t \right) ),\hbox { }{} \mathbf{q}_\mathbf{k} \left( t \right) =\mathbf{K}\left( t \right) \circ {\varvec{\delta }}{} \mathbf{l}\left( t \right) \end{aligned}$$

(22)

As the mass of the cable net is ignored, there are no external forces applied on free nodes during the deployment. The equilibrium equations of these free nodes at time t are

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{T}_\mathrm{f}^T \mathbf{Q}_\mathbf{k} \left( t \right) {\varvec{\Delta }}{} \mathbf{x}(t)=0 \\ \mathbf{T}_\mathrm{f}^T \mathbf{Q}_\mathbf{k} \left( t \right) {\varvec{\Delta }}{} \mathbf{y}(t)=0 \\ \mathbf{T}_\mathrm{f}^T \mathbf{Q}_\mathbf{k} \left( t \right) {\varvec{\Delta }}{} \mathbf{z}(t)=0 \\ \end{array}} \right. \end{aligned}$$

(23)

where $\mathbf{T}_\mathrm{f}$ is the topological matrix of free nodes, refer to our companion paper [19].

The whole deployment process is divided into numerous time steps, and the coordinates of boundary nodes in each time step can be obtained by the geometry of the truss. In order to guarantee good surface accuracies after the antennas are latched, the coordinates of free nodes obtained by form finding are used as the initial values and the trust-region algorithm is adopted to solve nonlinear equations. The present form finding methods have a high precision itself, and the trust-region algorithm can also improve robustness when starting far from the solution. The combination of these two methods provides an effective way to find suitable initial values which are essential to ensure the computational efficiency [19]. Then, the inverse process from deployed to stowed state is analyzed and the coordinates of free nodes in each time step during this process can be solved by Eq. (23). After that, the corresponding elastic energy of the cable net is derived

$$\begin{aligned} E_\mathrm{c} \left( t \right) =\sum _{i^{\prime }=1}^m {\left\{ {\frac{1}{2}k_{i^{\prime }} \left( t \right) \left[ {\left| {C_{i^{\prime }} } \right| -l_i } \right] ^{2}} \right\} } \end{aligned}$$

(24)

The cable net is stretched gradually under the pulling of the truss, so the relationship between the elastic energy and the deployment angle can be shown by Eq. (25). The polynomial fitting method is used to get the formula of the elastic energy, and this process is introduced in detail in Sect. 4.

$$\begin{aligned} E_\mathrm{c} =f\left( \varphi \right) \end{aligned}$$

(25)

The deployed configuration of antennas is chosen as the standard configuration of the zero gravitational energy, and then the gravitational energy in the deployment process is

$$\begin{aligned} E_\mathrm{g}= & {} n\left[ {\frac{1}{2}\left( {m_\mathrm{t} +m_\mathrm{f} +m_\mathrm{d} +m_1 +m_3 } \right) +m_2 } \right] \nonumber \\&\times gR_2 \sin \left( {\frac{1}{2}\pi -\varphi } \right) \end{aligned}$$

(26)

The total potential energy is

$$\begin{aligned} E=E_\mathrm{c} +E_\mathrm{g} \end{aligned}$$

(27)

3.3 Dynamic equations

The deployment is a slow and highly controlled process, so the damping of hinges can be regarded as the viscous damping which is proportional to the angular velocity of the deployment [19]. According to the definition of the Rayleigh’s dissipation function [20], the dissipation function of the reflector antenna is derived that

$$\begin{aligned} \varPsi =\sum _{i=1}^{4n} {\xi \int _0^v {f(v)\mathrm{d}v=} } \sum _{i=1}^{4n} {\frac{1}{2}} \cdot \xi \dot{\varphi }^{2}=2n\xi \dot{\varphi }^{2} \end{aligned}$$

(28)

where $\xi$ is the damping coefficient of the hinges.

The Lagrange function L is

$$\begin{aligned} L=T-E \end{aligned}$$

(29)

Based on the Lagrange’s equations of the second kind, the kinetic energy of the truss, the elastic energy of the cable net, the gravity energy and the dissipative damping forces of hinges are considered to obtain the dynamic equation of the system, shown by Eq. (30).

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial L}{\partial \dot{\varphi }}} \right) -\frac{\partial L}{\partial \varphi }+\frac{\partial \varPsi }{\partial \dot{\varphi }}=Q_\varphi \end{aligned}$$

(30)

where $Q_\varphi$ is the generalized moment corresponds to the generalized coordinate $\varphi$.

As the reflector antennas are driven by the cable that connected with motors, the driving force along the cable can be calculated by

$$\begin{aligned} Q_l =Q_\varphi \frac{\sqrt{R_1^2 +R_2^2 -2R_1 R_2 \cos (\pi -\varphi )}}{R_1 R_2 \hbox {cos}\left( {\frac{1}{2}\pi -\varphi } \right) } \end{aligned}$$

(31)

4 Numerical simulation

By using the dynamic model and equations in Sect. 3, some numerical simulations are conducted in this section and the results are compared with experimental data in other literature.

4.1 Simulation parameters

The deployment process of a mesh reflector antenna model with 18 parallelograms is simulated and analyzed in this section. The parameters are shown in Table 1.

The topology of the cable net is shown in Fig. 5, and cable elements have been numbered according to rules introduced in our companion paper [19]. The original length of cable elements is shown in Table 2.

According to Eq. (31), the required driving force at the beginning of the deployment, when the deployment angle is equal to zero, is extremely large. To get rid of dead point, the deployment angle is designed to vary from 1$^{\circ }$ to 90$^{\circ }$, and Eq. (32) shows the predesigned deployment motion. As shown in Fig. 6, the deployment consists of three stages: uniform acceleration, uniform speed, and uniform deceleration. The antenna models are deployed smoothly in this process and the angular velocity gradually decreases to zero before the antennas are latched. This deployment motion effectively avoids impact and vibration before the latching, so it is considered as an ideal deployment motion. The kinetic and potential energy under this predesigned motion can be calculated according to equations in Sects. 3.1 and 3.2.

$$\begin{aligned} \varphi =\left\{ {\begin{array}{ll} -\varphi _0 \left( {\frac{5}{2}\frac{t^{4}}{\left( {T/5} \right) ^{3}}-3\frac{t^{5}}{\left( {T/5} \right) ^{4}}+\frac{t^{6}}{\left( {T/5} \right) ^{5}}} \right) {+}\varphi _s &{}\quad 0\le t<T/5 \\ -\varphi _0 t+T\varphi _0 \hbox {/10+}\varphi _s &{} T/5\le t<4T/5 \\ -\varphi _0 t+\varphi _0 \left( {\frac{5}{2}\frac{\left( {t-4T/5} \right) ^{4}}{\left( {T/5} \right) ^{3}}-3\frac{\left( {t-4T/5} \right) ^{5}}{\left( {T/5} \right) ^{4}}+\frac{\left( {t-4T/5} \right) ^{6}}{\left( {T/5} \right) ^{5}}} \right) {+}T\varphi _0 \hbox {/10+}\varphi _s &{}\quad 4T/5\le t\le T \\ \end{array}} \right. \end{aligned}$$

(32)

where $\varphi _0 =-\frac{5\pi }{8T}+\frac{5\varphi _s }{4T};\varphi _s =\frac{\pi }{180};T=10{,}000$.

The coordinates of free nodes during the deployment are solved by Eqs. (16–23) in Sect. 3.2, and the coordinates in the deployed configuration are used as the initial values in the numerical calculation. These coordinates are obtained by the form finding [21], and the corresponding surface accuracy is $1.112547\times 10^{-5}\hbox {m}$. Then, the elastic energy is calculated and shown in Fig. 7. This curve is fitted by a four-order polynomial, and the resulted formula is shown by Eq. (33).

$$\begin{aligned} E_\mathrm{c} =\left\{ {\begin{array}{l} 0\quad , \quad 0.0175\le \varphi \le 1.415 \\ 768{,}694.98-2,044,332.781\varphi \\ \quad +\,2,036,621.286\varphi ^{2}-900{,}821.57\varphi ^{3}\\ \quad +\,149,273.485\varphi ^{4}\hbox {, }1.415<\varphi \le 0.5\pi \\ \end{array}} \right. \end{aligned}$$

(33)

By substituting kinetic and potential energy into the dynamic equations in Sect. 3.3, the required driving force under the predesigned deployment motion is derived by Eqs. (34) and (35). A, B, C, D and E are shown by Eqs. (36-40) in the “Appendix”.

$$\begin{aligned} Q_l= & {} \left\{ {\begin{array}{l} l^{\prime }\times \left\{ {\frac{1}{2}\sum \limits _{j=2}^{11} {\left[ {\left( {m_1 +m_\mathrm{t} +m_\mathrm{f} } \right) A+\left( {2m_2 +m_3 +m_\mathrm{d} } \right) B+\left( {\frac{1}{6}m_2 R_2^2 +\frac{1}{12}m_3 } \right) C} \right] } } \right. +\left( {\frac{4}{3}m_2 +\frac{2}{3}m_3 } \right. \\ \left. {+\,2m_\mathrm{d} } \right) \times R_2^2 \ddot{\varphi } +\left( \frac{5}{6}m_2 +\frac{1}{6}m_3 +\frac{1}{2}m_\mathrm{t} +\frac{1}{2}m_\mathrm{f} +\frac{1}{8}m_\mathrm{d} \right) D-\left[ {6\left( {m_\mathrm{t} +m_\mathrm{f} +m_\mathrm{d} +m_1 +m_3 } \right) +\,12m_2} \right] \\ \times \left. {gR_2 \cos \left( {\frac{1}{2}\pi -\varphi } \right) +\,4n\xi \dot{\varphi }} \right\} ,0.0175\le \varphi \le 1.362 \\ \\ l^{\prime }\times \left\{ {\frac{1}{2}\sum \limits _{j=2}^{11} {\left[ {\left( {m_1 +m_\mathrm{t} +m_\mathrm{f} } \right) A+\left( {2m_2 +m_3 +m_\mathrm{d} } \right) B+\left( {\frac{1}{6}m_2 R_2^2 +\frac{1}{12}m_3 } \right) C} \right] } } \right. +\left( {\frac{4}{3}m_2 +\frac{2}{3}m_3 } \right. \\ \left. {+\, 2m_\mathrm{d} } \right) \times R_2^2 \ddot{\varphi } +\left( \frac{5}{6}m_2 +\frac{1}{6}m_3 +\frac{1}{2}m_\mathrm{t} +\frac{1}{2}m_\mathrm{f} +\frac{1}{8}m_\mathrm{d} \right) D-\left[ {6\left( {m_\mathrm{t} +m_\mathrm{f} +m_\mathrm{d} +m_1 +m_3 } \right) +12m_2 } \right] \\ \times \, gR_2 \cos \left( {\frac{1}{2}\pi -\varphi } \right) +E\left. {+4n\xi \dot{\varphi }} \right\} \hbox {, }1.362<\varphi \le 0.5\pi \\ \end{array}} \right. \end{aligned}$$

(34)

$$\begin{aligned} l^{\prime }= & {} \frac{\sqrt{R_1^2 +R_2^2 -2R_1 R_2 \cos (\pi -\varphi )}}{R_1 R_2 \hbox {cos}\left( {\frac{1}{2}\pi -\varphi } \right) } \end{aligned}$$

(35)

Table 1 Parameters of the antenna model with 18 parallelograms

Fig. 5

Topology of the cable net

4.2 Comparisons with the lumped mass model

The simulated driving force under the predesigned deployment motion is shown in Fig. 8. In the simulation, the antenna model is deployed within 10,000 s, and the acceleration of gravity g is set to 0. According to Ref. [12], the damping coefficient $\xi$ is set to 1 (Nm) /(deg/s) in the following simulation.

Table 2 Original length of cable elements (mm)

The antenna model is deployed slowly and smoothly, and the whole process lasts 10,000 s. As shown in Fig. 8a, the required driving force is very small at first, and then it starts to increase rapidly due to the stretching of the cable net. The trend of the curve in Fig. 8a agrees well with the experimental data (Fig.13 in Ref. [15] and Fig. 14 in Ref. [22]). This proves that the cable tensions have great influences on the driving forces of reflector antennas, so the accurate calculation of cable tensions is essential.

Then, the antenna model is deployed within 180 s, and the simulation results are shown in Figs. 10 and 11. Likewise, the acceleration of gravity g is set to 0. The deployment occurs in a shorter time and the speed is faster, so the required driving force before the stretching of the cable net increases obviously (see the comparison between Figs. 8a and 10a). Meanwhile, the kinetic energy in Fig. 10b is significantly larger than that in Fig. 9a.

Fig. 6

Predesigned deployment motion. a Deployment angle. b Angular velocity

Fig. 7

Elastic potential energy of the cable net

Fig. 8

Driving force under the predesigned deployment motion. a Overall graph. b Partial enlargement graph

Fig. 9

Variation of energies during the deployment. a Kinetic energy. b Potential energy

Fig. 10

Deployment within 3 min. a Driving force under predesigned motion. b Variation of energies during deployment

Figure 10b displays the variation of energy during the deployment, and this figure matches the result of Fig. 21 in Ref. [13]. Through the comparison of Figs. 8, 9 and 10, it can be found that the speed of deployment has influences on kinetic energy and the driving force at the initial stage. In the previous lumped mass model, the rotation of rods is mostly ignored and this makes the calculated kinetic energy inaccurate. Figure 11 shows the comparison of results by using the model in this paper (curve A) and in previous Refs. [12, 15, 16] (curve B). It shows that the driving force and kinetic energy obtained using the presented model are obviously larger, and these differences may even bigger if the deployment is faster.

Fig. 11

Comparison to previous model. a Comparison of driving force. b Comparison of kinetic energy

4.3 Influences of gravity

As the ground test is indispensable before the reflector antenna is applied in space, the simulation about the deployment under gravity is provided in this section to show the influences of gravity in ground tests. The simulation lasts for 10,000 s and the acceleration of gravity g is set to 9.8 N/kg. It can be seen from Fig. 12 that the required driving force is negative at first and then becomes positive. This is because the reduced gravitational potential is more than the increased kinetic energy, and some braking forces are required to obtain the deployment motion in Fig. 6. But as the antenna is driven by the cable, there is only tension force but not pressure force in the cable, and the negative force is unfeasible. Therefore, the antenna model cannot be deployed as the motion described in Fig. 6, and the actual deployment may be faster.

Fig. 12

Deployment under gravity. a Driving force under predesigned motion. b Variation of potential energy

Figure 12a proves that the antenna may deploy by itself under the influence of gravity. So, the driving force obtained by ground tests without gravity compensation devices cannot provide accurate references for the deployment in space. As shown in Fig. 12b, before the cable net is stretched, the potential energy mainly consists of the gravitational potential and it decreases with the increasing of the deployment angle. After the cable net is tensioned, the potential energy consists of the gravitational potential and the elastic energy, and the total potential energy increases in the deployment process. In general, the deployment is a process in which the elastic potential energy is stored.

4.4 Discussions of the “ideal deployment motion” and “feasible deployment motion”

The deployment of the antenna model with 12 parallelograms is simulated in this section. The aperture and focal length are the same as the antenna model in Sect. 4.1. Other parameters are listed in Table 3.

Table 3 Parameters of the antenna model with 12 parallelograms

Fig. 13

Topology of the cable net

The topology of the cable net is shown in Fig. 13, and the original length of cable elements is listed in Table 4. The surface accuracy obtained by the form finding is $1.85072\times 10^{-5}\hbox {m}$. The predesigned deployment motion is the same as it is in Fig. 6, and 14 shows the simulation result.

Table 4 Original length of cable elements (mm)

Fig. 14

Deployment of the antenna model with 12 parallelograms. a Driving force under the predesigned motion. b Variation of energies during deployment

Fig. 15

Modified deployment motion. a Deployment angle. b Angular velocity

As shown in Fig. 14a, the driving force is negative at the end of the deployment, but the negative force is unfeasible for cable-driven mechanisms. That’s because the angular velocity is designed to decrease at the later stage of deployment (as shown in Fig. 6), and the corresponding kinetic energy decreases as well. But meanwhile, the potential energy in Fig. 14b starts to decrease, too. The decreased potential energy is consumed by fiction, damping, as well as transferred to kinetic energy, which leads to the continuous acceleration instead of the predesigned deceleration. Therefore, even though the predesigned motion in Fig.6 is the “ideal deployment motion”, it is not the “feasible deployment motion” at this condition

In order to obtain a feasible driving force, the deployment motion is changed to the curve shown in Fig. 15, and the corresponding simulation results are shown in Fig. 16.

Fig. 16

Deployment of the antenna model with 12 parallelograms. a Driving force under the modified motion. b Variation of energies during deployment

In comparison with the driving force in Fig. 14a, there are no negative values in Fig. 16a. It means the driving force becomes more feasible by changing the deployment motion to the modified motion in Fig. 15. As shown in Fig. 16b, the potential energy decreases while the kinetic energy increases at the end of the deployment. In this condition, the increased kinetic energy can be provided by the transformation of the potential energy, and not too much driving force is required. So the driving force is approximate to zero at the end. The motion in Fig. 15 is feasible, but the angular velocity increases rapidly at the later stage of the deployment, and the antenna model obtains a very large speed before it is latched. Large impacts and vibrations become inevitable, and these will bring about the performance deterioration. Simulation results show that the deployment motion in Fig. 15 is not ideal though it is feasible.

Fig. 17

Topology of the cable net

Table 5 Original length of cable elements (mm)

Fig. 18

Deployment of the antenna model with 12 parallelograms. a Driving force under the predesigned motion. b Variation of energies during deployment.

The topology in Fig. 17 is adopted to obtain a feasible and ideal deployment motion, and the original length of cable elements is listed in Table 5. The surface accuracy of this cable net in the deployed configuration is $1.40076\times 10^{-5}\hbox {m}$. Other parameters remain unchanged, and the simulation result is shown in Fig. 18.

The antenna model is deployed according to the motion in Fig. 6. Although the topology of the cable net is changed, the surface accuracy in the deployed state remains at the same level. There are also no negative values in Fig. 18a, so the driving force is feasible in theory. As shown in Fig. 6, the velocity decreases continuously before the antenna is latched and this helps to reduce impacts and vibrations. Under this circumstance, the deployment is both feasible and ideal. The numerical examples in this section show that the topology and parameters design as well as the motion planning should be combined to obtain a smooth and feasible deployment motion.

5 Conclusion

This paper conducts the dynamic modeling and analysis of mesh reflector antennas considering the motion feasibility. Unlike previous simplified models, the truss model in this paper consists of hinges whose mass is concentrated on their centroids and rods with mass evenly distributed along their length. The rigid body motion of the truss is fully considered, the translation and rotation parameters are derived and the corresponding kinetic energy of the truss under the predesigned deployment motion is calculated. Then, the cable net is discretized into multiple cable elements that are modeled by springs. The slacked and tensioned state of cable elements during the deployment are captured by updating the stiffness matrix of cable elements real-timely. The elastic energy of the cable net can be obtained by solving the systematic equilibrium equations. Finally, the dynamic equations are formulated based on Lagrange equations, and the required driving force under predesigned deployment motion is derived.

Several numerical examples are provided and simulation results agree well with experimental data in other literature. Simulations show that the kinetic energy calculated in this paper is more accurate than results obtained by previous approaches. Meanwhile, the influence of gravity on the deployment process is also analyzed. The feasibility of the predesigned deployment motion in inverse dynamics is discussed. It is proven that the previous motion planning cannot ensure the feasibility of the deployment, and the topology and parameters design as well as the motion planning should be combined in the analysis and design to obtain smooth and feasible deployment motions. The work in this paper provides a general and effective way to analyze the deployment of mesh reflector antennas and the conclusions can be used in the design and drive control of these devices.

Appendix

$$\begin{aligned} A= & {} 2\left( {a_j ^{2}+b_j ^{2}} \right) R_2^2 d_1 +\frac{1}{2}\left[ {\left( {-1} \right) ^{j-1}-1} \right] ^{2}\nonumber \\&\times \, R_2^2 d_2 -\,\left\{ \sin \left( {\pi -2\varphi } \right) \right. \nonumber \\&\left. \times \,R_2^2 \dot{\varphi }^{2}\left\{ {\frac{1}{4}\left[ {\left( {-1} \right) ^{j-1}-1} \right] ^{2}-\left( {a_j ^{2}+b_j ^{2}} \right) } \right\} \right\} \end{aligned}$$

(36)

$$\begin{aligned} B= & {} \frac{1}{2}\left[ {\left( {a_j +a_{j+1} } \right) ^{2}+\left( {b_j +\,b_{j+1} } \right) ^{2}} \right] \nonumber \\&\times R_2^2 d_1 +\frac{1}{8}\left[ {\left( {-1} \right) ^{j-1}+\left( {-1} \right) ^{j}-2} \right] R_2^2 d_2 \nonumber \\&-\,\left\{ {\sin \left( {\pi -2\varphi } \right) R_2^2 \dot{\varphi }^{2}} \right. \times \left\{ {\frac{1}{16}\times } \right. \nonumber \\&\left. \left. \left[ {\left( {-1} \right) ^{j-1}+\left( {-1} \right) ^{j}-2} \right] ^{2}\right. \right. \nonumber \\&\left. \left. -\frac{1}{4}\left[ {\left( {a_j +\,a_{j+1} } \right) ^{2}+\left( {b_j +b_{j+1} } \right) ^{2}} \right] \right\} \right\} \end{aligned}$$

(37)

$$\begin{aligned} C= & {} 2\left[ {\left( {a_{j+1} -a_j } \right) ^{2}+\left( {b_{j+1} -b_j } \right) ^{2}} \right] d_1 \nonumber \\&+\,\frac{1}{2}\left[ {\left( {-1} \right) ^{j}-\left( {-1} \right) ^{j-1}} \right] d_2 \nonumber \\&-\,\left\{ {\sin \left( {\pi -2\varphi } \right) \dot{\varphi }^{2}} \right. \times \left\{ {\frac{1}{4}\times } \right. \left[ {\left( {-1} \right) ^{j}} \right. \nonumber \\&-\left. {\left. {\left. {\left( {-1} \right) ^{j-1}} \right] ^{2}-\left[ {\left( {a_{j+1} -a_j } \right) ^{2}+\left( {b_{j+1} -b_j } \right) ^{2}} \right] } \right\} } \right\} \end{aligned}$$

(38)

$$\begin{aligned} D= & {} 2\left\{ \left\{ {\sum _2^{12} {\cos [\left( {k-2} \right) \theta ]} } \right\} ^{2}\right. \nonumber \\&\left. +\,\left\{ {\sum _2^{12} {\sin [\left( {k-2} \right) \theta ]} } \right\} ^{2} \right\} R_2^2 d_1 +R_2^2 d_2 \nonumber \\&-R_2^2 \dot{\varphi }^{2}\left\{ {\sin \left( {\pi -2\varphi } \right) } \right. \nonumber \\&\times \left. {\left\{ {1-\left\{ {\sum _2^{12} {\cos [\left( {k-2} \right) \theta ]} } \right\} ^{2}-\left\{ {\sum _2^{12} {\sin [\left( {k-2} \right) \theta ]} } \right\} ^{2}} \right\} } \right\} \end{aligned}$$

(39)

$$\begin{aligned} E= & {} -\,2044332.781+4073242.57\varphi \nonumber \\&-2702464.71\varphi ^{2}+597093.94\varphi ^{3} \end{aligned}$$

(40)

$$\begin{aligned} d_1= & {} \sin ^{2}\left( {\frac{1}{2}\pi -\varphi } \right) \ddot{\varphi }-\sin \left( {\pi -2\varphi } \right) \dot{\varphi }^{2} \end{aligned}$$

(41)

$$\begin{aligned} d_2= & {} \cos ^{2}\left( {\frac{1}{2}\pi -\varphi } \right) \ddot{\varphi }+\sin \left( {\pi -2\varphi } \right) \dot{\varphi }^{2} \end{aligned}$$

(42)

$$\begin{aligned} a_j= & {} \sum _{k=2}^j {\cos \left[ {\left( {k-2} \right) \theta } \right] } \end{aligned}$$

(43)

$$\begin{aligned} b_j= & {} \sum _{k=2}^j {\sin \left[ {\left( {k-2} \right) \theta } \right] } \end{aligned}$$

(44)