1 Introduction

Neurons are basic units of neural systems through which information is transmitted from one neuron to other neurons in the form of action potentials (APs) via synapses. Conduction is unidirectional; thus, APs can only be transmitted from the axon of a neuron to other neuron’s dendrites or a cell body and cannot be transmitted in the opposite direction because neurotransmitters are released only in the axon terminal of a presynaptic neuron. However, anatomical experiments found that some neurons in the brain have a special structure, in which the axon ending of a neuron is not connected to dendrites of other neurons but instead to itself. Neurons with this type of structure are called autaptic neurons. Autaptic neurons are found in a variety of brain regions, for example, the rat hippocampus [1], the pyramidal cells [2], the visual cortex of cats [3, 4], the substantia nigra and white matter [5]. In the cerebral cortex, there is a class of specific inhibitory neurons called “fast-spiking cells”, which generate rich autapses. Because of the self-limitation with the body, inhibitory autapses are more common in neurons. In contrast, excitatory autapse generates positive feedback and leads to the senses being out of control and epileptic events, which is clearly not the best state of the brain [6]. The arrival of APs at synapses will cause the release of neurotransmitters through the cleft, resulting in the depolarization or hyperpolarization of the postsynaptic membrane potential. Accordingly, the autapse could be divided into two categories [7, 8]: excitatory and inhibitory.

Recently, some experiments have shown that the autaptic structure plays an important role in the regulation of brain function [9]. In a physiological experiment, Saada [10] found the positive feedback caused by excitatory autapses can stimulate the B31/B32 neurons of Aplysia to be active persistently. It is necessary for these neurons to initiate and maintain components of feeding behavior via persistent activities. Therefore, the autaptic structure contributes to control of the continuous operation of a nervous system through self-adjustment of some areas [11, 12]. In addition, there are also some studies that reveal the effects of the neuronal autaptic structure on their dynamic behaviors [13,14,15,16,17], bifurcations and enhancement of neuronal firings induced by negative feedback from an inhibitory autapse [18, 19], as well as the disturbance of ion channel noise to autaptic neurons [20]. For example, in fast-spiking interneurons, autaptic inhibition influences the threshold for APs, input-output gain, firing patterns and multi-stability regions under different parameters setting [21]. The inhibitory chemical autapse can maintain the accuracy of firing sequences of a neuron to control the synchronization of the neuron APs [22]. Self-feedback induced by autapse adjusts the synchronization transition in a Newman-Watts neuronal network with time delay [23,24,25] and mediates propagation of weak rhythmic activity across small-world neuronal networks [26, 27]. Stochastic resonance which occurs at the beat frequency in neural systems at both the single neuron and the population level, is studied here. [28]. The dynamics of multiple synchronous behaviors are controlled or adjusted based on the time delay and coupling strength in inhibitory coupled neurons [29], and the autapse also plays a regulatory role of irregular firing behaviors [30]. According to different types of autapses, irregular firings are generated based on a single neuron and the autaptic innervation can tame and modulate neural dynamics. In addition to a single neuron, information transmission and autapse-induced synchronization are studied in a coupled neuronal network [31,32,33].

In the nervous system, information processing costs an enormous amount of metabolic energy [34, 35]. More than \(70\%\) of the cortical energy costs are directly used for neural signal processing within cortical circuits in the subcellular level [36]. For example, opening or closing of ionic channels for APs, and neurotransmitters release underlying synaptic transmission [37, 38]. This huge energy consumption suggests that our brains must operate energy efficiently, i.e., the brains should process as much as possible information at the lowest energy cost and it is argued that maximizing the ratio of the coding capacity to energy cost is one of key principles chosen by the nervous system to evolve under selective pressure [39, 40]. In the past decades, many studies have revealed the strategy that the neural systems employed to operate energy efficiently, including optimizing the ion channel kinetics [41, 42] or developing a warm body temperature to minimize the energy cost of single action potentials [43, 44], optimizing the number of channels on a single neuron and the number of neurons in the neuronal network [45,46,47], low probability release of neurotransmitters at the synapse [48, 49], representing information with sparse spikes [50,51,52].

In this paper, we study the information transmission capacity and energy efficiency of a single Hodgkin–Huxley (HH) neuron with the inhibitory chemical autapse. Experimental results show that in the inhibitory chemical autapse HH model, the transmitted effective information of the system is the highest, the encoding ability of information is the highest, and the energy efficiency of the system is optimal when the delay time of the autapse is half of the input signal period at a certain autaptic coupling strength. In addition, at the same delay time, the greater the self-synaptic coupling intensity is, the more obvious the information transmission capability, and the more optimal energy efficiencies of the system are.

The paper is organized as follows: Sect. 2 describes the chemical autapse HH neuronal model. The methods for calculation of the information entropy and energy cost efficiency are also introduced in this section. In Sect. 3, we first demonstrate the firing dynamics of the HH neuron with both excitatory and inhibitory autapses, and then we focus on the information capacity and the energy cost of the HH neuron with inhibitory autapses. We demonstrated in this section how the autaptic strength and the delay time influence the information transmission and the energy efficiency of neurons. Conclusions are made in Sect. 4.

2 Model and methods

2.1 The chemical autaptic HH model

The chemical autaptic HH neuron model is as follows:

$$\begin{aligned}&C\frac{{\mathrm{d}}V}{{\mathrm{d}}t} = -\, g_{\mathrm{Na}}m^{3}h(V-E_{\mathrm{Na}})-\, g_{\mathrm{K}}n^{4}(V-E_{\mathrm{K}}) \nonumber \\&\qquad \qquad \,\,\,-g_{\mathrm{L}}(V-E_{\mathrm{L}})+I_{\mathrm{ext}}+I_{\mathrm{asy}}+\xi (t), \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mathrm{d}m}{\mathrm{d}t}=\alpha _{m}(V)(1-m)-\beta _{m}(V)m, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\mathrm{d}h}{\mathrm{d}t}=\alpha _{h}(V)(1-h)-\beta _{h}(V)h, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\mathrm{d}n}{\mathrm{d}t}=\alpha _{n}(V)(1-n)-\beta _{n}(V)n, \end{aligned}$$
(4)

where V is the membrane potential of the neuron, C is the membrane capacitance, \(I_{\mathrm{ext}}\) is the external stimulus current, and \(I_{\mathrm{asy}}\) is the autaptic current. m, h and n are the gating variables of the sodium and potassium channels. \(\alpha _{i} (V)\) and \(\beta _{i} (V)\) (\(i=m,h,n\)) are the voltage-dependent opening and closing rates, respectively, which read

$$\begin{aligned} \alpha _{m}(V)= & {} \frac{0.1(V+40)}{1-e^{-(V+40)/10}}, \end{aligned}$$
(5)
$$\begin{aligned} \beta _{m}(V)= & {} 4e^{-(V+65)/18}, \end{aligned}$$
(6)
$$\begin{aligned} \alpha _{h}(V)= & {} 0.07e^{-(V+65)/20}, \end{aligned}$$
(7)
$$\begin{aligned} \beta _{h}(V)= & {} \frac{1}{1+e^{-(V+35)/10}}, \end{aligned}$$
(8)
$$\begin{aligned} \alpha _{n}(V)= & {} \frac{(V+55)/100}{1-e^{-0.1(V+55)}}, \end{aligned}$$
(9)
$$\begin{aligned} \beta _{n}(V)= & {} 0.125e^{-(V+65)/80}. \end{aligned}$$
(10)

The explicit form of the autaptic current \(I_{\mathrm{asy}}\) is defined as follows:

$$\begin{aligned} I_{\mathrm{asy}}=-g_{\mathrm{asy}}\sum _{\mathrm{spikes}}\alpha _{\mathrm{asy}}(t-t_{\mathrm{spikes}}-\tau )(V(t)-E_{\mathrm{A}}), \end{aligned}$$
(11)

where \(g_{\mathrm{asy}}\) is the maximal conductance and \(E_{\mathrm{A}}\) is the reversal potential of the autapse. \(t_{\mathrm{spikes}}\) is the presynaptic spiking time, and \(\tau \) is the delay time caused by the propagation of AP along the axons from initiation zone to synapse [53]. The sum is extended over the train of presynaptic spikes occurring at \(t_{\mathrm{spikes}}\). The dynamic process of the postsynaptic conductance is as follows:

$$\begin{aligned} \alpha _{\mathrm{asy}}(t)=\frac{1}{\tau _{d}-\tau _{r}}\left( e^{-\frac{t}{\tau _{d}}}-e^{-\frac{t}{\tau _{r}}}\right) , \end{aligned}$$
(12)

where \(\tau _{d}\) and \(\tau _{r}\) represent the decay and rise time, respectively, of the function and determine the duration of the synaptic response.

The external stimulus current \(I_{\mathrm{ext}}\) is a train of pulse-like current stimuli with the inter-pulse interval following a Poisson distribution with mean interval of 50 ms:

$$\begin{aligned} I_{\mathrm{ext}}=\sum _{j}I^{j}(t), \end{aligned}$$
(13)

where \(I^{j}(t)\) is the single pulse current in the following form:

$$\begin{aligned} I^{j}(t) = \left\{ \begin{array}{ll} I_{0}(t-t_{s}^{j})e^{-\frac{t-t_{s}^{j}}{\sigma }},&{}\quad t_{s}^{j}\le t \le t_{c}^{j} \\ 0, &{}\quad t<t_{s}^{j} \quad or \quad t>t_{c}^{j} \end{array}, \right. \end{aligned}$$
(14)

where j represents the jth pulse, \(I_{0}\) is the intensity of pulse currents and \(I_{0}= 10~\upmu \mathrm{A}\). \(t_{s}^{j}\) is the time when the released neurotransmitter is in contact with the postsynaptic membrane (start time of a pulse), \(t_{c}^{j}\) is a pulse off time (end time of a pulse, \(t_{c}^{j}=t_{s}^{j}+\varDelta t\), \(\varDelta t=8\) ms), and the value of the time constant \(\sigma \) is 2 ms.

A Gaussian white noise \(\xi (t)\) with zero mean value is also added in Eq. (1) to mimic the background activities from other neurons,

$$\begin{aligned} {<}\xi (t){>}=0; {<}\xi (t)\xi (t^{'}){>}=2D\delta (t-t^{'}), \end{aligned}$$
(15)

where D is noise density and \(D=2\) by default.

Table 1 Parameters in the chemical autapse HH model
Full size table

The stochastic equations in the simulation were solved using the Euler-forward method with a time step of 0.01 ms. The parameters involved in the calculation are listed in Table 1.

2.2 Methods of the information entropy and energy efficiency

To quantify the information transmission ability of the HH neuronal model with autapse, we use the “direct method” proposed by Strong [54] to measure the information entropy rate of the spiking sequence generated by the neuron. First, the spiking train is packaged into time bins with length of \(\varDelta t\) and discretized to a binary string, which is composed elements of “0” (no APs) or “1” (APs). Next, the binary sequence is scanned by moving a sliding time window T and then converted to a sequence of “words” with the length of k (\(k=\frac{T}{\varDelta t}\)). Finally, after obtaining the probability \(P_{i}\) of i-th word, the total entropy rate is calculated as,

$$\begin{aligned} H_{\mathrm{total}}=-\lim _{T \rightarrow \infty }\frac{1}{T} \sum _{i}P_{i}\mathrm{log}_{2}P_{i}. \end{aligned}$$
(16)

The time-dependent word probability distribution at a particular time is estimated over all the repeated presentations of the stimulus [54]. At each time t, we calculate the time-dependent entropy of words and then take the average (over all times) of these entropies,

$$\begin{aligned} H_{\mathrm{noise}}=<-\lim _{T \rightarrow \infty }\frac{1}{T} \sum _{i}P_{i}(t)log_{2}P_{i}(t)>_{t}, \end{aligned}$$
(17)

where \(< \ldots >_{t}\) denotes the average over all times t.

The average information rate that the neurons spike trains encode regarding the stimulus is then calculated as the difference between \(H_{\mathrm{total}}\) and \(H_{\mathrm{noise}}\),

$$\begin{aligned} I=H_{\mathrm{total}}-H_{\mathrm{noise}}. \end{aligned}$$
(18)

The coding efficiency is defined as the ratio of mutual information rate I to total entropy rate \(H_{\mathrm{total}}\),

$$\begin{aligned} \eta =\frac{I}{H_{\mathrm{total}}}. \end{aligned}$$
(19)

The coding efficiency ranges between zero and one. If all of the spike train structure is utilized to encode information regarding the stimulus, then the noise entropy is zero, and the efficiency measure equals one; on the contrary, if the spike train carries no information regarding the stimulus, then the coding efficiency is zero.

The generation of APs in the neurons requires an energy supply that is realized by hydrolyzing ATP molecules to restore the ion concentration inside and outside the cell. Normally, the energy cost can be estimated by calculating the total ATP consumption by counting the number of entries of Na\(^{+}\) [55]. However, the energy cost can also be estimated through calculating the equivalent electrical circuit of the HH model, which is argued to be more accurate than the Na\(^{+}\) counting method. The energy consumption rate of the HH neuron is then calculated [56].

$$\begin{aligned} \frac{\mathrm{d}E(t)}{\mathrm{d}t}= & {} VI_{\mathrm{ext}}-g_{\mathrm{Na}}m^{3}h(V-V_{\mathrm{Na}})^{2}\nonumber \\&-\,g_{\mathrm{K}}n^{4}(V-V_{\mathrm{K}})^{2} \nonumber \\&-\,g_{\mathrm{L}}(V-V_{\mathrm{L}})^{2}. \end{aligned}$$
(20)

Because each AP will lead to one synaptic event at the autapse, we assume each synaptic event cost \(\alpha \) times of energy \(E_{\mathrm{sgl}}\) for one AP. \(E_{\mathrm{sgl}}\) is estimated by integrating Eq. (20) during the period of one AP. Thus, the energy cost per second of a spike train could be estimated in the following manner:

$$\begin{aligned} E_{\mathrm{asy}}={<}E+n \cdot \alpha \cdot E_{\mathrm{sgl}}{>}_{t}, \end{aligned}$$
(21)

where E is the E(t) integrated over entire period of the spike train, and n is the number of spikes in the spike train. \({<}...{>}_{t}\) denotes the average over entire period of the spike train.

Finally, the energy efficiency that measures how much information the system encoded in the spike train with the consumption of unit energy is defined as

$$\begin{aligned} \varepsilon _{\mathrm{asy}}=\frac{I}{E_{\mathrm{asy}}}. \end{aligned}$$
(22)

3 Results and discussion

In the following, we set the delay time \(\tau \) of the autapse between 0 and 60 ms (the mean rate of pulse inputs) and the coupling intensity \(g_{\mathrm{asy}}\) in the range of 0–\(3~\mathrm{ms/cm}^{2}\), and then we calculate the corresponding information capacity, as well as the energy cost, to investigate how the delay time and coupling strength affect the energy efficiency of autaptic neurons.

3.1 Dynamical behaviors of the chemical autapse HH model

First, we set the reversal potential of autapse to \(E_{\mathrm{A}}=0\) so that it could induce the excitatory autaptic currents. As demonstrated in Fig. 1a, b, the APs (spikes at \(t=100\) ms and \(t=500\) ms, green line in Fig. 1a) evoked by the input would generate an excitatory synaptic current at approximately \(t=400\) ms and \(t=800\) ms with the time delay of \(\tau =300\) ms (shown in Fig. 1b). This excitatory synaptic current will cause another two APs at \(t=400\) ms and \(t=800\) ms (blue line in Fig. 1a). Meanwhile, the autaptic current induced AP at \(t=400\) ms will induce another AP at \(t=700\) ms (shown in Fig. 1a). Therefore, during the above process, this positive feedback will lead to the increase in spike rate, until the refractory period of neuron stops the increase in spikes per unit time. In contrast, for the inhibitory autapse with reversal potential of \(E_{\mathrm{A}}=-80\) mV, as demonstrated in Fig. 1c, d, the APs evoked by inputs (shown in Fig. 1c) will generate inhibitory synaptic current (shown in Fig. 1d), which will hyperpolarize the membrane potential. Thus, it appears that this negative feedback cannot play a positive role in the neural information processing.

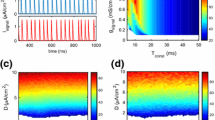
However, when the background noise is taken into consideration, the noise can induce spontaneous firings. As demonstrated in Fig. 2 for the raster plot of 200 neurons with the same inputs, the spontaneous APs occur between the input-induced APs. We then calculated the firing probability of the spontaneous APs among the mean inter-pulse interval and found that when the autaptic time delay is added (shown in Fig. 2c, d), there are less spontaneous APs because some of them are suppressed by inhibitory synaptic currents; moreover, the distribution of the spontaneous APs is narrower than that when there is no autapse (shown in Fig. 2a, b). The narrow distribution of spontaneous APs implies that there is less variability in the firing sequence of the autaptic neurons; the underlying mechanism will be elucidated in the following context.

Fig. 1
figure 1

The response of the chemical autapse HH model to square wave stimulus currents. Sub-graphs a and b show the membrane potentials and the autaptic currents, respectively, of the neuron in the excitatory autaptic mode, where the autaptic intensity is \(g_{\mathrm{asy}}=0.3~\mathrm{ms/cm}^{2}\). Sub-graphs c and d show the membrane potentials and the autaptic currents, respectively, of the neuron in the inhibitory autaptic mode, where the autaptic intensity is \(g_{\mathrm{asy}}=1~\mathrm{ms/cm}^{2}\). In the whole model, the intensity of external stimulus current is \(I_{0}=10~\upmu \)A and the autaptic delay time is \(\tau =300\) ms. (Color figure online)

Full size image
Fig. 2
figure 2

The firing raster of the inhibitory chemical autapse HH model for pulse stimulus currents and the firing probability of the spontaneous APs among the mean inter-pulse interval. a shows firings of 200 neurons, and b shows the firing probability when the autaptic coupling strength is \(g_{\mathrm{asy}}=0~\mathrm{ms/cm}^{2}\) and the delay time is \(\tau =0\) ms. c shows firings of 200 neurons, and d shows the firing probability when the autaptic coupling strength is \(g_{\mathrm{asy}}=3~\mathrm{ms/cm}^{2}\) and the delay time is \(\tau =35\) ms. In the whole model, the intensity of external stimulus current is \(I_{0}=10~\upmu \)A, and the noise density is \(D=2\)

Full size image

3.2 Information transmission

As demonstrated above, the inhibitory autaptic current induced by the spikes in response to external signal will act on the neuron itself. This negative feedback loop will finally have an impact on the firing dynamics, and thus the information transmission of the neuron.

Fig. 3
figure 3

The total entropy rate \(H_{\mathrm{total}}\) of the ICA HH model

Full size image

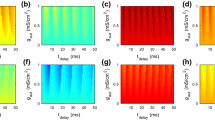
The dependence of the total information rate on the autaptic strength and the time delay is demonstrated in Fig. 3. It is seen that when the autaptic strength is zero, i.e., there is no autaptic current acting on the neuron, the total information rate is the largest. Once the inhibitory autaptic current takes effects, it will reduce the excitability of the neuron. However, even in the presence of the autaptic current, there are two cases that the inhibitory effects are canceled by the APs. One case is when the delay time is very short, such that the inhibitory current induced by an AP acts on it immediately. The other case is when the time delay \(\tau \) is approximately 35 ms, in which case there is a high probability that the inhibitory current will act on the AP induced by the next pulse input. In both cases, after the threshold-crossing of membrane potential and before the ending of refractory period, the neuron’s membrane potential will not be disturbed by the external inputs. Therefore, the total entropy rate is almost the same as that without autapse.

When autaptic strength is not zero, the total entropy rate exhibits two minima, one around the delay time of \(\tau = 18\) ms and the other around the delay time of 50 ms. The minimum becomes lower as the autaptic strength is increased, because of the higher inhibitory current generated by the autapse. The first minimum at approximately \(\tau = 18\) ms is mainly caused by the reduction in the spontaneous firings by the inhibitory autaptic current. After the end of the refractory period of an AP evoked by pulse input, the noise can evoke spontaneous firings alone. Theoretically, these spontaneous APs can fires at any time with the same probability in the intervals between two input evoked APs. Therefore, an input evoked AP would suppress the spontaneous AP that occurs soon after it via its inhibitory autaptic current, as long as the time delay is just the same as the time interval between these two APs. However, the spontaneous APs cannot be suppressed by an autapse with longer time delay because its membrane potential has already crossed the threshold. Therefore, between the time point when the refractory period of input evoked AP ends and when the autaptic current starts to take effect, there exists a time window that allows the spontaneous APs to occur. The longer the delay time, the wider this time window, and thus, the more spontaneous APs to occur. As a result, the total entropy rate increases again as the time delay increases. Further increasing the time delay will cause the total entropy to drop again approximately \(\tau = 50\) ms. This second minimum occurs mainly because the inhibitory current suppressed the following input evoked APs when their inter-pulse intervals are less than the mean value of 50 ms.

As discussed above, the inhibitory autaptic current would suppress the spontaneous firings evoked by noise in the time interval between the two inputs, thus reducing the trial-to-trial variability of the spike trains. Therefore, we expect the noise entropy to decrease in this time interval, as seen in Fig. 4. Finally, the mutual information rate (the information entropy rate I), which is the difference between the total entropy rate and the noise entropy rate, exhibits a maximum for the time delay that is half of the inter-pulse interval of the inputs (Fig. 5). Note that, compared to the case in which there is no autapse and the mutual information rate is enhanced as the inhibitory autaptic current is introduced, increasing the autaptic strength increases the information rate. As we discussed above, the mismatch between the refractory period and the time delay of the autapse will result in a narrow time window that allows the generation of noise-induced APs. Spontaneous APs generated in this narrow window are relatively reliable, leading to much less variability of the spike trains compared to the case without autapse. In other words, the inhibitory autapse enables the noise-induced APs to fire in a consistent manner, and take the noise-induced APs as the second responses to the pulse inputs. This phenomenon appears as if the excitatory autapse can induce other APs; however, the difference in our case is the second AP evoked by noise, and the autapse plays the role of regulating these spontaneous firings.

Fig. 4
figure 4

The noise entropy rate \(H_{\mathrm{noise}}\) of the ICA HH model

Full size image
Fig. 5
figure 5

The information entropy rate I of the ICA HH model

Full size image

Because the increased amount of information through regulation of the spontaneous firings with inhibitory autaptic current does not introduce additional spikes in the spike train, the autapse also increases the average information carried by each spike, which is defined as the ratio of the mutual information rate to the mean firing rate of the spike train (Fig. 6). Moreover, when the delay time is half of the inter-pulse interval, the relatively high total entropy rate and lower noise entropy rate yields a maximum of the coding efficiency (Fig. 7).

Fig. 6
figure 6

The information entropy rate \(I_{\mathrm{sgl}}\) of the ICA HH model on per spike

Full size image
Fig. 7
figure 7

The encoding efficiency \(\eta \) of the ICA HH model

Full size image

3.3 Energy consumption and energy efficiency

In this subsection, we calculated the energy cost of the HH neuron with the inhibitory autaptic synapse in the above information transmission processing, according to Eq. (21). First, we fixed the synaptic strength \(g_{\mathrm{asy}}=3\) to investigate how \(\alpha \), the ratio of the energy cost for one synaptic event to the energy cost of one AP, affects the dependence of the energy cost of the autaptic neuron on the delay time. It is seen from Fig. 8 that for different values of \(\alpha \), the dependence of the energy cost on the delay time is the same as the dependence of the total entropy rate on the delay time, i.e., one minimum at \(\tau =18\) ms and another minimum at \(\tau =45\) ms. In addition, a larger value of \(\alpha \) yields a larger contrast between the maximal and minimal values of the energy cost. Next, the dependence of the total energy cost on different delay times and autaptic strengths are plotted in Fig. 9. It is seen that the dependence of the energy cost on the autaptic strength and delay time is the same as the dependence on the total entropy rate, because a higher total entropy rate implies a higher spike rate, and thus a higher energy cost.

Note that the energy efficiency, defined as the ratio between the mutual information rate and the energy cost per second (Fig. 10), is maximized when the delay time is half of the mean inter-pulse interval. This result implies that, when the delay time is half of the input rate, the inhibitory autapse could enable the neuron to transmit information not only with maximal capacity (as discussed above), but also in an energy efficient manner, i.e., the information transmission consumes minimal metabolic energy. In addition, with this inhibitory autapse, the information and energy efficiency could be maximized simultaneously, whereas for other parameters, such as, temperature or number of ion channels, the optimal value for information and that for energy efficiency are not identical; thus, the information and energy efficiency could not be maximized simultaneously.

Fig. 8
figure 8

The energy consumption \(E_{\mathrm{alpha}}\) of the ICA HH model for different \(\alpha \)

Full size image
Fig. 9
figure 9

The energy consumption \(E_{\mathrm{asy}}\) of the ICA HH model

Full size image
Fig. 10
figure 10

The energy efficiency \(\varepsilon _{\mathrm{asy}}\) of the ICA HH model

Full size image

4 Conclusions

In this paper, we investigated the effects of inhibitory autapse on the information transmission and energy efficiency of the HH neuron in response to the pulse train inputs. We found that when the delay time is approximately half of the mean inter-pulse interval of the input pulse train, the inhibitory autaptic current acting on the neuron itself leads to more ordered firing of the spontaneous APs, resulting in spike trains that are more informational (measured with mutual information rate) than that of the neuron without autapse. Meanwhile, the energy efficiency is also maximized around this optimal autaptic time delay.

The neural information is carried by APs and then transmitted from one neuron to other neurons through synapses [57, 58]. However, in some neurons, the synapses are connected to the neurons themselves, forming positive or negative feedback loops [59,60,61]. Many works showed that this autaptic feedback may play a positive role in the regulation of the firing rhythm of the neurons or the neuronal network. Here, in this paper, we used information theory to further elucidate the constructive role of inhibitory autapse in the information transmission of the neurons. It is interesting to find that the inhibitory feedback of autapse could regulate the spontaneous firings induced by noise; thus, these spontaneous APs could also carry information about the inputs. However, it still remains unknown what characters of the inputs are encoded in these spontaneous firings and how the information carried by these spontaneous firings is utilized by the neural systems.

The processing of neural information requires a huge amount of metabolic energy, which acts as a selective pressure to influence many aspects of neural design and functions. In this work, we also investigated how the inhibitory autapse influences the energy efficiency of the neuronal information transmission. We found that there exists an optimal delay time of the autapse with which the energy efficiency could be maximized. The efficient energy usage is the result of two aspects caused by the autapse: (1) the reduced spontaneous APs that carry no information regarding the inputs but waste energy and (2) the increased information because of more regulated spontaneous firings via negative feedbacks. The results suggest that the inhibitory autaptic feedback could serve as a mechanism to transmit neural information efficiently.

In conclusion, we studied the effects of the inhibitory autaptic synapse on the information transmission and energy efficiency of neurons in a noisy environment. We found that there exists an optimal autaptic delay time (which is almost half of the mean input rate), with which the neurons could not only transmit information with maximal capacity, but also with highest energy efficiency. The underlying mechanism is the more ordered spontaneous firings induced by inhibitory synaptic currents. In other words, the negative feedback of autapse enables the spontaneous firings to carry more information of the inputs. Future work will focus on how the neuronal systems determine the information carried by these spontaneous firings. Our work elucidated the role of inhibitory autaptic current in the energy efficient information processing of neuronal systems, and may help to further understand the basic design principles [62] of neural systems.