1 Introduction

Nonlinear science has focused on complex nonlinear systems, such as biological systems, for a long time. Nonlinear dynamics plays important roles in identifying various complex firing or oscillation patterns in the nervous system [1, 2]. Firing patterns often show changes in their dynamics, called bifurcations [1, 2], because biological parameters change continuously. Bifurcations are helpful in investigating the neural coding mechanism and integrated behavior of the nervous system. For example, various bifurcations of firing patterns have been observed in experiments on an isolated neural pacemaker when the ion channel parameters were changed [3–7]. Furthermore, bifurcations have been used to identify neural information coding mechanisms in baroreceptors [8] and cold receptors [9].

In addition to ion channel parameters, synaptic parameters can influence neuronal firing patterns as well as complex spatiotemporal dynamics of a neuronal network [10–21]. Electrical and chemical synapses between different neurons play important roles in information transmission and are studied extensively. For example, electrical and chemical excitatory synapses help to achieve synchronization, and inhibitory synapses help to achieve anti-phase synchronous behaviors [10–13, 22]. Recently, inhibitory synapses with slow decay characteristics or time delays have been shown to induce synchronization of networks, which provides a novel viewpoint that differs from the common assumption that inhibitory synapses desynchronize activities of a neuronal network [10, 14, 15, 22–24].

Recently, firing activity of neurons or spatiotemporal dynamics of a neuronal network with an autapse, which is a synapse from a neuron onto itself [25], have been investigated in theoretical models [17–21, 26–30]. For example, an inhibitory autapse with a time delay can suppress chaotic behavior of a neuron [26]. The time constant or time delay of the autapse can influence the firing frequency and interspike intervals of a neuron [27, 28]. In addition, an autapse can regulate behaviors of neuronal networks [17–21]. For example, an autapse can help enhance the collective activities of a neuronal network and induce target and spiral waves when a time delay is introduced [18–20]. It has been shown experimentally that autapses exist in many regions of brain such as the cerebral cortex, neocortex, cerebellum, hippocampus, striatum, and visual cortex [25, 31–37]. Autapses play an important role in controlling firing activity of neurons. For example, positive feedback mediated by an excitatory autapse can induce persistent firing [31]. An inhibitory autapse can have significant negative feedback effects on an interneuron, which leads to repetitive firing with precise spike timing [32–34].

The present paper investigates the dynamics of a Morris–Lecar (ML) model with an inhibitory autapse. Although an inhibitory synapse can suppress firing amplitude, we found that an inhibitory synapse enhances neuronal firing activities near an inverse Hopf bifurcation point and enlarges the parameter region of neuronal firing. This provides a novel viewpoint that differs from the suppression effect of inhibitory autapses. Furthermore, enhancement of neuronal firing activities near the inverse Hopf bifurcation can be well interpreted by the dynamic responses of the resting state stimulated by an inhibitory impulse current. The nonlinear dynamics near the inverse Hopf bifurcation help elucidate the physiological phenomenon of depolarization block, a phenomenon in which a neuron enters from firing to resting state when it receives excessive excitatory or depolarizing current. Complex dynamic behaviors including coexisting behaviors and codimension-2 bifurcations induced by the inhibitory synapse are identified. The remainder of the paper is organized as follows. Section 2 presents the ML model with an autapse. Section 3 identifies the effects of an inhibitory \(\alpha \)-dynamical autapse on neuronal firing using 1-parameter and 2-parameter bifurcation analysis. Section 4 presents the conclusions.

2 The ML model with an autapse

A ML model neuron with an autapse is considered in the present paper [38], and the equations of the model are as follows:

$$\begin{aligned}&C \frac{\mathrm{d}V}{\mathrm{d}t} = -g_\mathrm{Ca}m_{\infty }(V-V_\mathrm{Ca})-g_{K}w(V-V_\mathrm{K})\nonumber \\&\phantom {C \frac{\mathrm{d}V}{\mathrm{d}t} =}-\,g_\mathrm{L}(V-V_\mathrm{L})+I_\mathrm{app}+I_\mathrm{aut}, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\mathrm{d}w}{\mathrm{d}t} = \phi \frac{w_{\infty }-w}{\tau _{w}}. \end{aligned}$$
(2)

where the first 3 terms on the right-hand side of Eq. (1) represent the voltage-gated \(\text {Ca}^{2+}\) current, the voltage-gated delayed rectifier \(\text {K}^{+}\) current, and the leak current, respectively. Parameter C is the membrane capacitance. Variables V(t) and w(t) are the membrane voltage and activation of the delayed rectifier \(\text {K}^{+}\) current, respectively. \(m_{\infty }, w_{\infty }\), and \(\tau _{w}\) are dependent on V(t) and are as follows:

$$\begin{aligned}&m_{\infty }=0.5\left[ 1+{\text{ tanh }}\left( \frac{V(t)-V_{1}}{V_{2}}\right) \right] \end{aligned}$$
(3)
$$\begin{aligned}&w_{\infty }=0.5\left[ 1+ {\text{ tanh }}\left( \frac{V(t)-V_{3}}{V_{4}}\right) \right] \end{aligned}$$
(4)
$$\begin{aligned}&\tau _{w}=\left[ {\text{ cosh }}\left( \frac{V(t)-V_{3}}{2V_{4}}\right) \right] ^{-1} \end{aligned}$$
(5)

The parameters \(g_\mathrm{Ca}, g_\mathrm{K}\), and \(g_\mathrm{L}\) are the maximal conductance of the calcium current, potassium current, and leak current, respectively. The parameters \(V_\mathrm{Ca}, V_\mathrm{K}\), and \(V_\mathrm{L}\) are the reversal potentials of the calcium current, potassium current, and leak current, respectively. \(I_\mathrm{app}\) and \(I_\mathrm{aut}\) are the applied and autaptic currents, respectively.

The parameter values of the ML model are as follows: \(C=20~\upmu \text {F/cm}^{2},\, V_\mathrm{Ca}=120\, \hbox {mV}, V_\mathrm{K}=-84\, \hbox {mV}, \,V_\mathrm{L}=-60\, \hbox {mV},\, g_\mathrm{Ca}=4~\upmu \text {S/cm}^{2}, g_\mathrm{K}=8~\upmu \text {S/cm}^{2}, \,g_\mathrm{L}=2~\upmu \text {S/cm}^{2},\, V_{1}=-1.2\,\, \hbox {mV}, V_{2}=18 \,\hbox {mV},\, V_{3}=12\, \hbox {mV}, \,V_{4}=17.4\, \hbox {mV}, \,\hbox {and} \,\,\phi =0.067\).

In the present paper, the so-called \(\alpha \)-dynamical synapse, which models a synapse that is modulated by \(\hbox {GABA}_\mathrm{A}\) and \(\hbox {GABA}_\mathrm{B}\) and is found in areas of the central nervous system such as the neocortex and hippocampus [15, 39], is used and described as the following form:

$$\begin{aligned} I_\mathrm{aut}=-g_\mathrm{aut}s(t)(V_\mathrm{pos}(t)-V_\mathrm{syn}). \end{aligned}$$
(6)

where the parameters \(g_\mathrm{aut}\) and \(V_\mathrm{syn}\) are the coupling strength and the reversal potential of the autapse, respectively. \(V_\mathrm{pos}(t)\) is the membrane potential of the postsynaptic neuron. For an autapse, \(V_\mathrm{pos}(t)=V(t)\). The variable s(t) is the gating variable of the autapse and is described by the following ordinary equation:

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}=\alpha {\varGamma }(V_\mathrm{pre}(t))(1-s)-\beta s. \end{aligned}$$
(7)

where \(\alpha \) and \(\beta \) are the parameters that modulate the rise and decay times of the synaptic current, receptively. \(\alpha =6\) in the present paper. \(V_\mathrm{pre}(t)\) is the membrane potential of the presynaptic neuron. For an autapse, \(V_\mathrm{pre}(t)=V(t). \,{\varGamma }(V_\mathrm{pre}(t))=1/(1+{\hbox {exp}}(-V_\mathrm{pre}(t)-\theta _\mathrm{syn}))=1/(1+{\hbox {exp}}(-V(t)-\theta _\mathrm{syn})). \,\theta _\mathrm{syn}\) is the synaptic threshold and was set to 0 mV to ensure that each spike or action potential could cross the threshold. \(V_\mathrm{syn}=-60\, \hbox {mV}\), which is below the minimal value of V(t) to ensure that the autapse was inhibitory.

The fast threshold modulatory (FTM) autapse [39–41] was also considered. The FTM autapse, which corresponds to a realistic autapse that is modulated by \(\text {GABA}_\mathrm{A}\) and is found in the nervous system such as the leech heart central pattern generator [39, 41], is given by

$$\begin{aligned} I_\mathrm{aut}=-g_\mathrm{aut}{\varGamma }(V_\mathrm{pre}(t))(V_\mathrm{pos}(t)-V_\mathrm{syn}). \end{aligned}$$
(8)

The parameter values were \(V_\mathrm{syn}=-60\, \hbox {mV}, \theta _\mathrm{syn}=0\).

Fig. 1
figure 1

a Bifurcations of the ML model without an autapse. The solid, dotted, and dashed lines represent the stable node, the saddle, and the unstable equilibrium, respectively. The SNIC, \(\hbox {SubH}_{1}\), and \(\hbox {LPC}_{3}\) represent a saddle-node bifurcation on an invariant circle at \(I_\mathrm{app}\approx 39.96\,\upmu \hbox {A/cm}^{2}\), a subcritical Hopf bifurcation at \(I_\mathrm{app}\approx 97.65\,\upmu \hbox {A/cm}^{2}\), and a saddle-node bifurcation of the limit cycle at \(I_\mathrm{app}\approx 115.9\,\upmu \hbox {A/cm}^{2}\), respectively. The upper and lower solid (open) circles represent the maximum and minimum amplitudes of the stable (unstable) limit cycle, respectively. b Phase portrait when \(I_\mathrm{app}=39.96\,\upmu \hbox {A/cm}^{2}\)

Full size image

The parameters \(I_\mathrm{app}, g_\mathrm{aut}\), and \(\beta \) were chosen as the bifurcation parameters. The equations were solved by the Runge–Kutta method with an integrating step of 0.01 ms. The bifurcation results were acquired using the software XPPAUT [42] and Matcont [43].

3 Results

3.1 Bifurcations of a ML model without an autapse

The bifurcations of the ML model without an autapse (\(g_\mathrm{aut}=0\)) with respect to \({I_\mathrm{app}}\) are shown in Fig. 1a. The equilibrium points correspond to the thin curves containing 3 branches when \({I_\mathrm{app}}<39.96 \,\upmu \text {A/cm}^{2}\). The solid, dotted, and dashed lines represent the stable node (lower branch), the saddle (middle branch), and the unstable equilibrium (upper branch), respectively. The appearance of a saddle-node bifurcation on an invariant circle (SNIC) must be satisfied: a standard saddle-node bifurcation of equilibrium point occurs and the equilibrium point is on an invariant circle. When \(I_\mathrm{app}\approx 39.96 \,\upmu \text {A/cm}^{2}\), the eigenvalues are 0 and \(-0.0989\), and the equilibrium point is on an invariant circle, as shown in Fig. 1b, which shows that the SNIC appears. The interaction point between the lower and middle branches is a saddle-node on an invariant circle bifurcation (SNIC) at \(I_\mathrm{app}\approx 39.96 \,\upmu \text {A/cm}^{2}\). When \(I_\mathrm{app}>39.96\,\upmu \text {A/cm}^{2}\), with increasing \(I_\mathrm{app}\), a stable limit cycle appears and its maximum and minimum amplitudes are shown by upper and lower solid circles, respectively; a subcritical Hopf bifurcation point (\(\text {SubH}_{1}\)) through which the unstable equilibrium point is changed into a stable focus appears at \(I_\mathrm{app}\approx 97.65 \,\upmu \text {A/cm}^{2}\). An unstable limit cycle is bifurcated from the \(\text {SubH}_{1}\), and its maximum and minimum amplitudes are shown by upper and lower open circles, respectively. The interaction point of the unstable and stable limit cycles is a saddle-node or fold bifurcation of a limit cycle (\(\text {LPC}_{3}\)) and appears at \(I_\mathrm{app}\approx 115.9 \,\upmu \text {A/cm}^{2}\). The membrane potential V(t) of the resting state near the SNIC is much less than 0. For example, \(V(t)=-29.39\) mV when \(I_\mathrm{app}= 39.96 \,\upmu \text {A/cm}^{2}\). The membrane potential of the resting state near the \(\text {SubH}_{1}\) is much higher than that near the SNIC. For example, \(V(t)=9.41\) mV when \(I_\mathrm{app}=117~ \,\upmu \text {A/cm}^{2}\). The firing amplitude is approximately 50–80 mV.

3.2 Different responses of the ML model with 2 forms of inhibitory autapse

Inhibitory autapses are abundant in regions of the central nervous system such as the hippocampus and visual cortex [35, 36]. In a biological experiment on a GABAergic interneuron with an inhibitory autapse in layer V of neocortical slices [32], paired depolarizing current pulses failed to elicit a second spike in the control but could evoke a spike doublet in the presence of gabazine, which blocked the inhibitory autapse. This shows that the spike of a neuron with an inhibitory autapse can have an inhibitory effect on electrical activity after the spike.

Fig. 2
figure 2

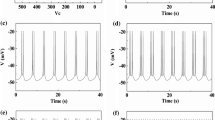
Responses of the ML model neuron (\(I_\mathrm{app}\approx 39.5\,\upmu \hbox {A/cm}^{2}\)) to paired step depolarization current. a With an \(\alpha \)-dynamical inhibitory autapse when \(\beta =0.01\) and \(g_\mathrm{aut}=1.0\,\upmu \hbox {S/cm}^{2}\); b with an \(\alpha \)-dynamical inhibitory autapse when \(\beta =1\) and \(g_\mathrm{aut}=1.0\,\upmu \hbox {S/cm}^{2}\); c with a FTM inhibitory autapse when \(g_\mathrm{aut}=1.0\,\upmu \hbox {S/cm}^{2}\); d without an autapse

Full size image

To explain the experimental observation, 2 depolarizing current pulses were applied to the ML model neuron with/without an autapse when \(I_\mathrm{app}= 39.5~\,\upmu \text {A/cm}^{2}\). The width and strength of the pulse were 10 ms and \(16\, \hbox {mA}/\text {cm}^{2}\), respectively, and the interval between the 2 pulses was 1 s. For the \(\alpha \)-dynamical inhibitory autapse, the second pulse failed to elicit a spike when \(\beta =0.01\) and \(g_\mathrm{aut}=1.0~\upmu \text {S/cm}^{2}\), as shown in Fig. 2a; however, a spike doublet was evoked when \(\beta =1\) and \(g_\mathrm{aut}=1.0~\upmu \text {S/cm}^{2}\), as illustrated in Fig. 2b. For the FTM autapse, 2 spikes corresponding to 2 pulses were evoked when \(g_\mathrm{aut}=1.0 ~\upmu \text {S/cm}^{2}\), as depicted in Fig. 2c. For a neuron without an autapse, 2 spikes were also evoked, as shown in Fig. 2d. The inhibitory current is represented by the dotted line in Fig. 2a–c. The inhibitory current shown in Fig. 2a is much slower than those depicted in Fig. 2b, c. The results show that the inhibitory autapse of the GABAergic interneuron of layer V in neocortical slices may have slow decay characteristics. The \(\alpha \)-dynamical inhibitory autapse with \(\beta =1\) was not slow enough. The results also show that the \(\alpha \)-dynamical inhibitory autapse with \(\beta =0.01\) was suitable for simulating the autapse of the GABAergic interneuron.

3.3 Changes from resting state to firing or oscillation near SubH\(_{1}\) induced by an inhibitory autapse

The ML model neuron without an autapse exhibited a resting state with \(V(t)=9.41\) mV when \(I_\mathrm{app}= 117~\upmu \text {A/cm}^{2}\), which is near the \(\hbox {SubH}_{1}\) shown in Fig. 1a. When a hyperpolarizing current impulse with strength \(-35 \,\upmu \text {A/cm}^{2}\) was introduced, a post-inhibitory spike or oscillation could be elicited, as shown in Fig. 3a, b, respectively. If the duration of the impulse was long (10 ms), spikes were evoked, as depicted in Fig. 3a. If the duration was short (5 ms), oscillations were induced, as shown in Fig. 3b.

Fig. 3
figure 3

The resting state of the ML model neuron changed to firing or oscillation when receiving hyperpolarizing or inhibitory current. a Firing induced by a hyperpolarizing step current (strength \(-35 \,\upmu \hbox {A/cm}^{2}\) and duration 10 ms) when \(I_\mathrm{app}= 117\,\upmu \hbox {A/cm}^{2}\). b Oscillations induced by a hyperpolarizing step current (strength \(-35 \,\upmu \hbox {A/cm}^{2}\) and duration 5 ms) when \(I_\mathrm{app}= 117\,\upmu \hbox {A/cm}^{2}\). c Changes from the resting state to firing when the \(\alpha \)-dynamical inhibitory autapse was introduced at time 900 ms. \(g_\mathrm{aut}=1.0\,\upmu \hbox {S/cm}^{2}, \beta =0.01\), and \(I_\mathrm{app}= 117\,\upmu \hbox {A/cm}^{2}\). d Changes from the resting state to oscillations when the \(\alpha \)-dynamical inhibitory autapse was introduced at time 900 ms. \(g_\mathrm{aut}=5.2\,\upmu \hbox {S/cm}^{2}, \beta =0.01\), and \(I_\mathrm{app}= 117\,\upmu \hbox {A/cm}^{2}\)

Full size image

If the \(\alpha \)-dynamical autapse with \(\beta =0.01\) and \(g_\mathrm{aut}=1.0~\upmu \text {S/cm}^{2}\) was introduced, the resting state of the ML model neuron when \(I_\mathrm{app}= 117~\upmu \text {A/cm}^{2}\) changed to firing, as shown by the solid line in Fig. 3c. The inhibitory autaptic current is shown by the dotted line, and the duration of each inhibitory current impulse was relatively long, as shown in Fig. 3c. Each inhibitory autaptic current impulse played a role similar to the hyperpolarizing current impulse shown in Fig. 3a. When \(\beta =0.01\) and \(g_\mathrm{aut}=5.2 ~\upmu \text {S/cm}^{2}\), the resting state of the ML model neuron when \(I_\mathrm{app}= 320~\upmu \text {A/cm}^{2}\) changed to oscillation as shown by the solid line in Fig. 3d. Compared with Fig. 3c, the duration of each inhibitory autaptic current impulse (dotted line) became short, as shown in Fig. 3d. Each inhibitory autaptic current impulse in Fig. 3d played a role similar to the hyperpolarizing current impulse shown in Fig. 3b.

3.4 Changes from resting state of the coexisting behaviors to monostable firing induced by the inhibitory autapse

Fig. 4
figure 4

Changes from the resting state of coexisting behavior of the ML model neuron without an autapse to firing when the \(\alpha \)-dynamical inhibitory autapse was introduced at time 9000 ms. \(g_\mathrm{aut}=0.08\,\upmu \hbox {S/cm}^{2}, \beta =0.01\), and \(I_\mathrm{app}= 100\,\upmu \hbox {A/cm}^{2}\). a The bold solid line, dot, and dashed curve are the firing, resting state, and unstable limit cycle of the ML model without an autapse, respectively. The thin solid (red) line represents the trajectory of the changing process from resting state to firing when an autapse was introduced. b Changes of the membrane potential (solid line) and inhibitory autaptic current (dotted line) as resting state was changed to firing induced by introducing an autapse at 9000 ms

Full size image

The ML model neuron without an autapse exhibited coexisting behaviors of resting state and firing corresponding to a stable limited cycle when \(97.65<I_\mathrm{app}<115.9~\upmu \text {A/cm}^{2}\). When \(I_\mathrm{app}=100~\upmu \text {A/cm}^{2}\), the coexisting resting state (the dot) corresponding to a stable equilibrium and firing (the bold solid line) corresponding to a stable limit cycle were separated by an unstable limit cycle (dashed line) as shown in Fig. 4a. If the \(\alpha \)-dynamical autapse was introduced, the resting state of the coexisting behaviors could be changed to monostable firing. For example, when \(\beta =0.01\) and \(g_\mathrm{aut}=0.08 ~\upmu \text {S/cm}^{2}\), the trajectory (V(t), w(t)) when the resting state changed to firing is shown by the thin solid (red) line in Fig. 4a. The trajectory could run across the threshold (unstable limit cycle) and converge to a stable limit cycle close to the original stable limit cycle (the bold solid line) of the ML model without an autapse, which also shows that the stable resting state of the ML model without an autapse lost its stability. The changes of the inhibitory autaptic current (the dotted line) and the membrane potentials (the solid line) are shown in Fig. 4b.

3.5 One-parameter bifurcations of the ML model with an \(\alpha \)-dynamical inhibitory autapse

The ML model without an autapse exhibited a SNIC bifurcation point when \(I_\mathrm{app}\) was low and a subcritical Hopf bifurcation point with a fold bifurcation of the limit cycle when \(I_\mathrm{app}\) was high, as shown in Fig. 1a. The firing activity locates between the SNIC bifurcation point and the fold bifurcation of the limit cycle.

Fig. 5
figure 5

Bifurcations of the ML model with the \(\alpha \)-dynamical autapse with respect to \(I_\mathrm{app}\) at different values of \(g_\mathrm{aut}\). a \(g_\mathrm{aut}=1.0\,\upmu \hbox {S/cm}^{2}\). b \(g_\mathrm{aut}=3.0\,\upmu \hbox {S/cm}^{2}\). c \(g_\mathrm{aut}=3.95\,\upmu \hbox {S/cm}^{2}\). d \(g_\mathrm{aut}=4.05\,\upmu \hbox {S/cm}^{2}\). e \(g_\mathrm{aut}=4.25\,\upmu \hbox {S/cm}^{2}\). f \(g_\mathrm{aut}=4.7\,\upmu \hbox {S/cm}^{2}\). g \(g_\mathrm{aut}=5.2\,\upmu \hbox {S/cm}^{2}\). h \(g_\mathrm{aut}=5.3\,\upmu \hbox {S/cm}^{2}\). i \(g_\mathrm{aut}=5.45\,\upmu \hbox {S/cm}^{2}\). j \(g_\mathrm{aut}=6.0\,\upmu \hbox {S/cm}^{2}\). The thin solid, dashed, and dotted lines correspond to stable equilibrium, unstable equilibrium, and saddle point, respectively. The upper and lower solid points (open cycles) are the maximum and minimum values of the stable (unstable) limit cycles, respectively. SNIC represents saddle-node bifurcation on an invariant circle. \(\hbox {SubH}_{2}\) is a subcritical bifurcation point. \(\hbox {SupH}_{1}, \hbox {SupH}_{2}, \hbox {LSupH}_{2}\), and \(\hbox {RSupH}_{2}\) are supercritical bifurcation points. \(\hbox {LPC}_{1}, \hbox {LPC}_{2}\), and \(\hbox {LPC}_{3}\) are saddle-node bifurcation points of the limit cycle

Full size image

The bifurcations of the ML model with the \(\alpha \)-dynamical inhibitory autapse with respect to \(I_\mathrm{app}\) at different \(g_\mathrm{aut}\) levels are shown in Fig. 5. Compared with Fig. 1a, Fig. 5 shows the following 3 characteristics: (1) The right boundary of firing expands to the right, which leads to enlargement of the parameter region of firing. (2) Some bifurcations leading to appearance of complex nonlinear phenomena, such as coexisting behaviors, appear at middle \(g_\mathrm{aut}\) levels. (3) The stable node and the SNIC show little change.

First, enlargement of the parameter range of firing was found when \(g_\mathrm{aut}= 1.0, 3.0, 3.95, 4.05, 4.25, 4.7, 5.2, 5.3, 5.45\), and \(6 \,\upmu \text {S/cm}^{2}\) as shown in Fig. 5a–j, which was induced by a right shift of the bifurcation point from firing to resting state. Driven by inhibitory current of the autapse, the resting state of the ML model without an autapse changed to firing when the autapse was introduced. Generation of firing was similar to that shown in Figs. 3a, c and 4. When \(g_\mathrm{aut} = 1.0 \,\upmu \text {S/cm}^{2}\) and \(g_\mathrm{aut}= 3.0 \,\upmu \text {S/cm}^{2}\), the \(\hbox {SubH}_{1}\) and \(\hbox {LPC}_{3}\) expanded to the right, as shown in Fig. 5a, b, respectively. When \(g_\mathrm{aut}= 3.95, 4.05, 4.25, 4.7, 5.2, 5.3, 5.45\), and \(6 \,\upmu \text {S/cm}^{2}\), the right boundary of firing became a supercritical Hopf bifurcation point at \(I_\mathrm{app}\approx 277.69 \,\upmu \text {A/cm}^{2}(\text {SupH}_{2}),\, I_\mathrm{app}\approx 281.98~\upmu \text {A/cm}^{2} (\text {SupH}_{2}),\, I_\mathrm{app}\approx 234.6\,\upmu \text {A/cm}^{2} (\text {SupH}_{2}),\, I_\mathrm{app}\approx 309.06\,\upmu \text {A/cm}^{2} (\text {RSupH}_{2}),\, I_\mathrm{app}\approx 271.3\,\upmu \text {A/cm}^{2} (\text {SupH}_{1}),\, I_\mathrm{app}\approx 276\,\upmu \text {A/cm}^{2} (\text {SupH}_{1}),\, I_\mathrm{app}\approx 283.1\,\upmu \text {A/cm}^{2} (\text {SupH}_{1}),\, \hbox {and} I_\mathrm{app}\approx 308.2\,\upmu \text {A/cm}^{2} (\text {SupH}_{1})\), respectively, as shown in Fig. 5c–j. When \(g_\mathrm{aut}=5.2~\,\upmu \text {S/cm}^{2}\), to the right of firing, there was an oscillation between left and right supercritical Hopf bifurcation points, which is labeled \(\text {LSupH}_{2} (I_\mathrm{app}\approx 306.6\,\upmu \text {A/cm}^{2})\) and \(\text {RSupH}_{2} (I_\mathrm{app}\approx 331.5\,\upmu \text {A/cm}^{2})\), respectively, as shown in Fig. 5g. The oscillation was induced by the inhibitory current of the autapse, which is similar to those shown in Fig. 3b, d. Similar results were found when \(g_\mathrm{aut}=5.3\,\upmu \text {S/cm}^{2}\) and \(g_\mathrm{aut}=5.45\,\upmu \text {S/cm}^{2}\), as shown in Fig. 5h, i. When \(g_\mathrm{aut}=6.0\,\upmu \text {S/cm}^{2}\), the oscillatory behavior disappeared.

Second, some bifurcations that lead to complex nonlinear phenomenon, such as coexisting behaviors, appeared within relatively narrow parameter regions of \(I_\mathrm{app}\) at middle \(g_\mathrm{aut}\) levels. For example, when \(g_\mathrm{aut}=4.05\,\upmu \text {S/cm}^{2}\), there were 2 subcritical Hopf bifurcation points (\(\text {LSubH}_{2}\) at \(I_\mathrm{app}\approx 216.5\,\upmu \text {A/cm}^{2}\) and \(\text {RSubH}_{2}\) at \(I_\mathrm{app}\approx 220.52\,\upmu \text {A/cm}^{2}\)), which led to the coexistence of oscillatory and firing behaviors, as shown in Fig. 5d. When \(g_\mathrm{aut}=4.25\,{\upmu }\text {S/cm}^{2}\), there were 2 supercritical Hopf bifurcation points (\(\text {SupH}_{1}\) at \(I_\mathrm{app}\approx 225.5\,{\upmu }\text {A/cm}^{2}\) and \(\text {SupH}_{2}\) at \(I_\mathrm{app}\approx 290.9\,{\upmu }\text {A/cm}^{2}\)), a fold bifurcation of the limit cycle (\(\text {LPC}_{1}\) at \(I_\mathrm{app}\approx 225.4\,{\upmu }\text {A/cm}^{2}\)), and a subcritical Hopf bifurcation point (\(\text {SubH}_{2}\) at \(I_\mathrm{app}\approx 234.0\,{\upmu }\text {A/cm}^{2}\), which resulted in the coexistence of the resting state and firing, as shown in Fig. 5e. When \(g_\mathrm{aut}=4.7\,{\upmu }\text {S/cm}^{2}\), there was coexistence of oscillation and firing between \(\text {LPC}_{1}\) (\(I_\mathrm{app}\approx 244.3\,{\upmu }\text {A/cm}^{2}\)) and \(\text {SupH}_{1} (I_\mathrm{app}\approx 247.21\,{\upmu }\text {A/cm}^{2}\)), coexistence of resting state and firing between \(\text {SupH}_{1}\) and \(\text {LSupH}_{2} (I_\mathrm{app}\approx 264.43\,{\upmu }\text {A/cm}^{2}\)), and coexistence of oscillation and firing between \(\text {LSupH}_{2}\) and \(\text {LPC}_{2}\) (\(I_\mathrm{app}\approx 266.52\,{\upmu }\text {A/cm}^{2}\)), as shown in Fig. 5f. When \(g_\mathrm{aut}=5.2\,{\upmu }\text {S/cm}^{2}\), there were towfold bifurcation points of the limit cycle (\(\text {LPC}_{4}\) at \(I_\mathrm{app}\approx 279\,{\upmu }\text {A/cm}^{2}\) and \(\text {LPC}_{1}\) at \(I_\mathrm{app}\approx 261.7\,{\upmu }\text {A/cm}^{2}\)), which led to coexistence of firing and oscillation as shown in Fig. 5g. Similar results are shown in Fig. 5h with \(g_\mathrm{aut}=5.3\,{\upmu }\text {S/cm}^{2}\).

Finally, the reason that the stable node and the SNIC changed little in the present paper can be introduced simply as follows. The V(t) value of the SNIC point is \(-29.39\, \hbox {mV}\) and \(\theta _\mathrm{syn}=0\). \({\varGamma }(-29.39)= 1/(1+{\hbox {exp}}(-(-29.39-0)))\rightarrow 0\), which leads to the equation shown as follows:

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}t}=\alpha {\varGamma }(V_\mathrm{pre})(1-s)-\beta s \rightarrow 0. \end{aligned}$$
(9)

Then \(s(t)={\hbox {e}}^{-\beta t}\rightarrow 0\) and is stable because of \(-\beta <0\), which leads to \(I_\mathrm{aut}=-g_\mathrm{aut}s(V_\mathrm{pos}-V_\mathrm{syn})\rightarrow 0\). Therefore, the inhibitory autaptic current \(I_\mathrm{aut}\) had little effect on the ML model with parameters corresponding to SNIC. As determined from the above derivation process, if the ML model without an autapse has an equilibrium \(E_{0}\) with a V(t) value much less than 0 as with the stable node, the inhibitory autapse would have little effect on the equilibrium, and the ML model with an autapse would have an equilibrium point very close to \(E_{0}\) and the stability would remain unchanged. This is the reason that the value and stability of the low branch of the equilibrium point show little change in all panels of Fig. 5. In addition, it should be noted that if \(\theta _\mathrm{syn}\) is a value much less than 0, \(I_\mathrm{aut}\) would have an inhibitory effect on the ML model and suppress firing behavior. In the present paper, we did not study behaviors near the SNIC point and the suppression effect of the inhibition. In addition, comparing Figs. 1a and 5 indicates that the firing amplitude decreased as the coupling strength of the autapse increased, which is consistent with those found in the experiment reported in Ref. [32]. In the present paper, we did not examine the inhibitory effect of the inhibitory autapse on firing amplitude.

3.6 Two-parameter bifurcations of the ML model with an \(\alpha \)-dynamical inhibitory autapse

The detailed relationships between 1-parameter bifurcations at different \(g_\mathrm{aut}\) levels shown in Fig. 5 could be found in 2-parameter bifurcations in a plane (\(I_\mathrm{app}, g_\mathrm{aut}\)), as shown in Fig. 6a (\(\beta =0.01\)). The different levels of \(g_\mathrm{aut}\) used in Fig. 5 are labeled by the 10 parallel right arrows in the left part of Fig. 6a. Figure 6b is the enlargement of a part containing several codimension-2 bifurcation points of Fig. 6a.

Fig. 6
figure 6

a Two-parameter bifurcations of the ML model neuron with an \(\alpha \)-dynamical inhibitory autapse in the plane (\(I_\mathrm{app}, g_\mathrm{aut}\)) when \(\beta \)= 0.01. b Enlargement of bifurcation diagram in (a). SNIC represents saddle-node bifurcation on invariant circle. \(\hbox {SubH}_{2}\) and \(\hbox {SubH}_{1}\) are subcritical bifurcation curves. \(\hbox {SupH}_{1}\) and \(\hbox {SupH}_{2}\) are supercritical bifurcation curves. \(\hbox {LPC}_{1}, \hbox {LPC}_{2}, \hbox {LPC}_{3}\), and \(\hbox {LPC}_{4}\) are saddle-node bifurcation of the limit cycle. \(\hbox {CPC}_{1}\) and \(\hbox {CPC}_{2}\) are cusp bifurcations of the limit cycle. \(\hbox {GH}_{1}, \hbox {GH}_{2}\), and \(\hbox {GH}_{3}\) are Bautin bifurcations

Full size image

The bold vertical dashed line to the left of \(I_\mathrm{app}= 50~\,{\upmu }\text {A/cm}^{2}\) is the SNIC curve. The solid curve located in the right part of Fig. 6 represents the inverse Hopf bifurcation curve, which is divided into 4 parts by 3 codimension-2 bifurcation points, Bautin bifurcation points \(\text {GH}_{1}\) (\(I_\mathrm{app}\approx 263.36~\,{\upmu }\text {A/cm}^{2}, \,g_\mathrm{aut}\approx 3.62~\,{\upmu }\text {A/cm}^{2}), \text {GH}_{2} (I_\mathrm{app}\approx 238.35~{\upmu }\text {A/cm}^{2},\, g_\mathrm{aut}\approx 4.31~{\upmu }\text {A/cm}^{2}\)), and \(\text {GH}_{3} (I_\mathrm{app}\approx 221.99~{\upmu }\text {A/cm}^{2},\, g_\mathrm{aut}\approx 4.18~{\upmu }\text {A/cm}^{2}\)). The Bautin bifurcation points are labeled by open circles. The 4 parts of the Hopf bifurcation curve from low to high endpoints are subcritical, supercritical, subcritical, and supercritical Hopf bifurcations and labeled as \(\text {SubH}_{1}, \,\text {SupH}_{2},\, \text {SubH}_{2}\), and \(\text {SupH}_{1}\). Both \(\text {SubH}_{2}\) and \(\text {SupH}_{2}\) contain left and right branches corresponding to the labels \(\text {LSubH}_{2}, \text {RSubH}_{1}, \text {LSupH}_{2}\), and \(\text {RSupH}_{2}\) used in Fig. 5. The labels \(\text {SubH}_{1}\) and \(\text {SupH}_{1}\) are the same as those used in Fig. 1a and Fig. 5. The dotted line labeled \(\text {LPC}_{3}\) is a fold bifurcation of the limit cycle, connected to the Bautin bifurcation point \(\text {GH}_{3}\). Two dotted curves labeled \(\text {LPC}_{1}\) and \(\text {LPC}_{2}\), which are related to Bautin bifurcation points \(\text {GH}_{1}\) and \(\text {GH}_{2}\), respectively, represent fold bifurcation of the limit circles. In addition to the curves \(\text {LPC}_{1}\) and \(\text {LPC}_{2}\), there is another curve of fold bifurcation of the limit circle labeled \(\text {LPC}_{4}\), which intersects with curves \(\text {LPC}_{1}\) and \(\text {LPC}_{1}\) at points \(\text {CPC}_{1} (I_\mathrm{app}\approx 266.61~{\upmu }\text {A/cm}^{2}, g_\mathrm{aut}\approx 5.42~{\upmu }\text {A/cm}^{2}\)) and \(\text {CPC}_{2}\) (\(I_\mathrm{app}\approx 282.52~{\upmu }\text {A/cm}^{2}, g_\mathrm{aut}\approx 4.8~{\upmu }\text {A/cm}^{2}\)), respectively. The \(\text {CPC}_{1}\) and \(\text {CPC}_{2}\) points are codimension-2 bifurcation points of the limit cycle and are also called cusp bifurcation of the limit cycle. The labels \(\text {LPC}_{1}, \text {LPC}_{2}, \text {LPC}_{3}\), and \(\text {LPC}_{4}\) correspond to those used in Figs. 1a or 5.

The plane (\(I_\mathrm{app}, g_\mathrm{aut}\)) is divided into 9 subregions (labeled with circled numbers 1–9) by the 6 curves(SNIC, \(\text {LPC}_{1},\, \text {LPC}_{2},\, \text {LPC}_{3},\, \text {LPC}_{4}\), and the Hopf bifurcation curve containing \(\text {SubH}_{1},\, \text {SubH}_{2},\, \text {SupH}_{2}\), and \(\text {SupH}_{1}\)) and 2 other important horizontal borders as shown in Fig. 6. One lies between \(\text {CPC}_{2}\) and the right branch of \(\text {SupH}_{2}\) to form the border between subregions 3 and 4. The other is the border between subregions 4 and 6, which runs across the intersection point of \(\text {LPC}_{4}\) and the left branch of \(\text {SupH}_{2}\) and lies between \(\text {SupH}_{1}\) and the left branch of \(\text {SupH}_{2}\). There is a stable equilibrium point with low and high membrane potentials in subregions 1 and 2, respectively, which are labeled by horizontal lines. The behavior is firing represented by vertical lines in subregion 3. The behavior in subregion 4 is oscillation. The coexistence of resting state and firing (both horizontal and vertical lines) exists in subregions 5 and 6. In subregions 7–9, coexistence of 2 stable limit cycles, firing and oscillation, appears. It was found that an inhibitory autapse could enhance neuronal firing activities near the inverse Hopf bifurcation point from firing to resting state with a high membrane potential.

4 Conclusion

The \(\alpha \)-dynamical autapse with a slowly decaying autaptic current was tested and exhibited dynamics similar to the inhibitory autapse of a GABAergic interneuron in rat neocortical slices [32]. In the present paper, it was found that such a slow inhibitory autapse could enhance neuronal firing. The resting state near an inverse Hopf bifurcation point could change to firing activity when an inhibitory autapse was introduced. This shows that negative feedback of the inhibitory autapse can play a positive role in enhancing neuronal firing, which differs from the traditional viewpoint that inhibitory synapses often suppress neuronal activities. Because the inhibitory autaptic current decays slowly, inhibitory autaptic current induced by a spike can have an inhibitory effect during the phase after the spike and induce post-inhibitory spikes or oscillation [2], which depend on the membrane potential of the resting state, the coupling strength of the autapse, and the duration of the inhibitory impulse current. This is the reason that neuronal firing is enhanced. Changing from the resting state to firing leads to a right shift of the Hopf bifurcation point and enlargement of the parameter region of neural firing, which can be identified using the 1- and 2-parameter bifurcations.

An inhibitory autapse can induce complex dynamical behaviors. Multiple codimension-2 bifurcation points including Bautin bifurcation of equilibrium and cusp bifurcation of the limit cycle were found, which led to coexisting behaviors. Compared with coexistence of stable equilibrium and limit cycle in the ML model without an autapse, more coexisting behaviors appeared in the model with an inhibitory autapse, such as coexistence of 2 equilibrium points, coexistence of limit cycles, and coexistence of an equilibrium point with 2 limit cycles. Coexisting behaviors or bistability and multistability have been investigated in many studies on several types of neurons, such as Purkinje cells, mitral cells, and motoneurons, and have been proposed to endow neurons with richer information processing and motor control [44–47]. For example, the Purkinje cell may play a key role in short-term processing and storage of sensory information in the cerebellar cortex, which involves bistability [46, 47].

Neuronal firing and resting state are 2 major states corresponding to equilibrium point and limit cycle in nonlinear dynamics, respectively. In general, resting state can change to firing or firing activity can be enhanced if a neuron receives excitatory or depolarizing current [48]. A special phenomenon known as depolarization block occurs if a neuron enters from firing to resting state when it receives excessive excitatory or depolarizing current [48]. In this case, the depolarizing current exceeds a certain level that corresponds to the inverse Hopf bifurcation point. The improvement of depolarization block by inhibitory autapse is due to the activity of autapse by higher resting potential (equilibrium) and inhibitory current induced neuron to firing or oscillation. Bistability has been observed during the transition process to depolarization block in many neurons [49–51]. Depolarization block has been found to be related to many functions and some diseases, such as neural coding [46, 47], schizophrenia, migraine, and seizure. Depolarization block has been suggested to explain the therapeutic effect of some antipsychotic drugs [52, 53]. The antipsychotic drugs are capable of regulating the excitability of neurons and inducing neurons changed to an inactive state corresponding to depolarization block. In the present paper, the modulation of inhibitory autapse can influence the depolarization block, which maybe a therapeutic method of schizophrenia. Spreading depression, which may occur during migraine and some seizures, is pathological discharge and is characterized by a slowly propagating depolarization wave, during which neurons go into depolarization block, and followed by a shutdown of brain activity [54, 55]. During the depolarization block, the resting membrane potential (stable equilibrium) is much higher than the threshold of firing, and action potentials (stable limit cycle) cannot be triggered [55, 56]. The improvement of depolarization block of inhibitory autapse may alleviate the symptom of migraine and some seizures effectively. The results of the present paper provide a method to relieve the depolarization block as well as shift the Hopf bifurcation by regulating the inhibitory autapse. This maybe an effective method for the treatment of schizophrenia and other diseases.