1 Introduction

Underactuated systems are mechanical control systems with greater number of degrees of freedom than the controls, and the actuated degrees of freedom and the underactuated degrees of freedom are usually nonlinear coupling. Some degrees of freedom cannot be controlled but must be self-stabilized when the controlled state variables converge to the desired value. In resent years, there has been extensive interest among the researchers in controlling underactuated systems due to their extensive applications. Many control systems including the mobile robots [1, 2], the acrobot [3], the underactuated surface vessel [4, 5] and the crane systems [6, 7] are underactuated. The study of underactuated systems is meaningful and challenging in light of these considerations.

Robust control has been widely used in nonlinear systems [8, 9], underactuated systems [11,12,13,14,15,16,17] and time-delay systems [18, 19]. So far, there is no general control method for all underactuated systems except feedback linearization methods, while work has been done on a certain class or kind of underactuated systems. Fuzzy control [10], sliding mode control [2, 11] and intelligent backstepping control [12] are proposed to control the wheeled inverted pendulum. Planning-based adaptive control [6], adaptive fuzzy sliding mode control [13], integral sliding mode control method [14] and robust control [15] are applied to the crane system. Since the sliding mode control (SMC) is robust to the model uncertainties and less sensitive to disturbances, it is widely applied to nonlinear underactuated systems.

It has been proved that the SMC algorithm can robustly stabilize a class of underactuated nonlinear system such as a mobile robot and an underactuated underwater vehicle [20]. Huang [21] proposed a velocity controller for the mobile wheeled inverted pendulum based on sliding mode. Tuan [7] proposed a control strategy which combines the SMC and the partial feedback linearization for 3D overhead cranes. Much work has been done based on benchmark cascade form for a class of underactuated system by using the SMC. Saleh [22] proposed a sliding mode controller for the control of a class of underactuated systems which are described in cascaded form with external disturbances. Mcninch [23] proposed an optimizing sliding mode cascade control structure for the underactuated unmanned surface vessel systems which look upon the physical limits of the underactuated system as input saturations.

The conventional SMC loses the property of invariance in the presence of unmatched uncertainties and disturbances. The robustness of SMC controller can be obtained by increasing the switch gain k of SMC to suppress the disturbances and model uncertainties. In some cases, it is difficult to obtain or estimate the upper bounds of the unknown disturbances, or the estimated upper bounds are too conservative. In order to stabilize the system, the parameter of sliding mode control k in the item \(k\hbox {sgn}(s)\) has to be significantly increased. Unfortunately, with the increasing k, the chattering phenomenon also becomes serious accordingly. It is well known that the “chattering” is the main drawback of the SMC. Combining the SMC with other approaches which estimate the disturbances is an attractive proposition to overcome this deficiency. The disturbance observer (DO) technology might be a candidate solution for this problem. The DO is originally proposed by Chen [24] to deal with the disturbances of nonlinear system. Recently, several results using the disturbance observer combining with the SMC approach for mismatched nonlinear system have been reported in the researches [25,26,27,28]. It turns out that the DO-based SMC strategies can enhance the control accuracies as well as reduce the “chattering” in the above researches.

It should be noted that most of the DOs are based on the assumption that the disturbance is bounded [29] and its first-order derivative dies away gradually [24, 30] or is bounded [31,32,33], or the disturbance itself is of vanishing type in the steady states [25, 26]. Whereas this assumption is too restrictive for many practical systems. For example, this assumption cannot describe the cases in which the control system is affected by external disturbance which is a time varying such as polynomials with respect to time t [34]. In these cases, the derivative of disturbance does not converge to zero in the steady states.

In this paper, we propose an extended disturbance observer (EDO) which relaxes the aforementioned assumption. To the best of our knowledge, this study might be the first attempt to discuss the high-order DO-based control design method for “general” underactuated systems. The main contribution of our work includes: (1) the extension of DO technology to enable the estimations of both the disturbance and its derivatives for a class of underactuated systems; (2) a sliding mode controller based on the extended disturbance observer (SMCDO) which can both alleviate the chattering and enhance the control accuracy for the underactuated systems; (3) the stability analysis for both the proposed EDO and SMCDO approaches.

The rest of this paper is organized as follows. The EDO for a class of underactuated system is proposed in Sect. 2. Based on the EDO, a sliding mode controller based on a cascade form of a general underactuated system is derived in Sect. 3. An example is presented to demonstrate the theoretical analysis in Sect. 4, followed by a conclusion in Sect. 5.

2 Extended disturbance observer design for underactuated systems

In this section, we propose an extended disturbance observer (EDO) for a general second-order underactuated system. The proposed EDO relaxes the conventional assumption that the first-order derivatives of disturbances go to zero or they are bounded.

2.1 Problem statement

A general second-order underactuated system is considered. The Lagrange equations of motion for the underactuated system with disturbances can be written as:

$$\begin{aligned}&{m_{11}}( q ){{\ddot{q}}_1} + {m_{12}}( q ){{\ddot{q}}_2} + {h_1}( {q,\dot{q}} ) = {d_1} \nonumber \\&{m_{21}}( q ){{\ddot{q}}_1} + {m_{22}}( q ){{\ddot{q}}_2} + {h_2}( {q,\dot{q}} ) = u + {d_2} \end{aligned}$$
(1)

where \(h_{1}\) and \(h_{2}\) contain the Coriolis, the centrifugal and the gravity terms. \(d_{1}\) and \(d_{2}\) are lumped disturbance terms containing the model uncertainties and disturbances of the system.

Consider the underactuated system described by (1) with two degrees of freedom (\(q_1, q_2\)) and symmetry property \(M(q) = M(q_2)\). Obviously, the degree of freedom \(q_2\) is actuated. First we introduce the following global transform of coordinate [35]

$$\begin{aligned} \begin{aligned} x_1&= q_1+\beta (q_2),\\ \displaystyle x_2&= m_{11} \dot{q}_1+m_{12} \dot{q}_2 = \frac{\partial L}{\partial \dot{q}_1},\\ x_3&= q_2,\\ x_4&= \dot{q}_2,\\ \end{aligned} \end{aligned}$$
(2)

where \(\beta (q_2) = \int _{0}^{q_2}m_{11}^{-1}(s)m_{12}(s)\hbox {d}s\). \(L=E_\mathrm{k}-Ep=\frac{1}{2} \dot{q}^\mathrm{T}M(q)\dot{q}-E_\mathrm{p}(q)\). \(E_\mathrm{k}\) is the kinetic energy. \(E_\mathrm{p}\) is the potential energy.

Based on the global transform of coordinate (2), the dynamic model (1) can be further transformed into a special cascade nonlinear system in feedback form:

$$\begin{aligned} \begin{aligned} \dot{x}_1&= \dot{q}_1 + m_{11}^{-1}m_{12}\dot{q}_2 = m_{11}^{-1}x_2,\\ \displaystyle \dot{x}_2&=\frac{\hbox {d}(m_{11}\dot{q}_1+m_{12} \dot{q}_2)}{\hbox {d}t} = \frac{\hbox {d}}{\hbox {d}t}\frac{\partial L}{\partial \dot{q}_1}=f_1+d_1,\\ \dot{x}_3&= \dot{q}_2,\\ \displaystyle \dot{x}_4&= f_2+bu+d_{12}, \end{aligned} \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{aligned}&mm=m_{11}m_{22}-m_{12}m_{21},\quad \displaystyle f_1 = \frac{\partial L}{\partial q_1},\\&\displaystyle f_2 = \frac{m_{21}h_1-m_{11}h_2}{mm},\\&\displaystyle b = \frac{m_{11}}{mm}, \quad \displaystyle d_{12} = \frac{-m_{21}d_1+m_{11}d_2}{mm}. \end{aligned} \end{aligned}$$

Remark 1

The dynamic model (1) is derived by Lagrangian method, where \(f_1=\partial L/ \partial q_1 \), \(L=E_\mathrm{k}-Ep=\frac{1}{2} \dot{q}^\mathrm{T}M(q)\dot{q}-E_\mathrm{p}(q)\). Since \(q_1\) is the underactuated joint, we have \(M(q)=M(q_2)\) and \(f_1=- \partial E_\mathrm{p}/ \partial q_1\), which is related to the first-order partial derivative of potential energy of the system with respect to \(q_1\). In most cases, the potential energy \(E_\mathrm{p}\) is only related to the position variables (\(q_1, q_2\)) and has nothing to do with the velocity variables (\(\dot{q}_1, \dot{q}_2\)). That is, \({\partial f_1}/{\partial x_2}\) and \({\partial f_1}/{\partial x_4} \) are usually equal to zero, and \(\partial f_1 / \partial x_3\) is invertible and bounded. In this paper, only this situation is considered.

For simplicity, we rewrite (3) as the following vector form:

$$\begin{aligned} \dot{X} = F_1(X)+G_1(X)u+G_2d, \end{aligned}$$
(4)

where

$$\begin{aligned}&X=[x_{1}\quad x_{2}\quad x_{3}\quad x_{4}]^\mathrm{T}\\&F_{1}(X) = \left[ \begin{array}{cccc} m_{11}^{-1} x_2\\ f_{1}\\ x_{4}\\ f_{2}\end{array} \right] ,\, G_{1}(X) = \left[ \begin{array}{cccc} 0\\ 0\\ 0\\ b\end{array} \right] ,\,\\&\quad G_{2} = \left[ \begin{array}{cccc} 0 &{} 0 \\ 1 &{}0 \\ 0 &{}0 \\ 0 &{} 1 \end{array} \right] ,\, d = \left[ \begin{array} {cc} d_1\\ d_{12} \end{array}\right] . \end{aligned}$$

2.2 A second-order disturbance observer

Assumption 1

The disturbance d is continuous, and its first-order derivative \(\dot{d}\) and second-order derivative \(\ddot{d}\) exist.

Assumption 2

\(\ddot{d}\) is bounded and satisfies \(||\ddot{d}||\le \mu _1\). Here \(\mu _1>0\) is a constant.

The second-order disturbance observer for the underactuated system (4) is proposed as

$$\begin{aligned} \begin{aligned}&\hat{d}=z_1+p_1(X),\\&\dot{z}_1=L_1\left( -F_1(X)-G_1(X)u-G_2\hat{d}\right) +\hat{\dot{d}},\\&\hat{\dot{d}}=z_2+p_2(X),\\&\dot{z}_2=L_2\left( -F_1(X)-G_1(X)u-G_2\hat{d}\right) , \end{aligned} \end{aligned}$$
(5)

where \(\hat{d}\) and \(\hat{\dot{d}}\) are the estimates of d and \(\dot{d}\), respectively. The disturbance observer constant gain matrix \(L_i\) is defined as

$$\begin{aligned} L_i= \partial p_i(X) / \partial X,~~i=1,2, \end{aligned}$$
(6)

where

$$\begin{aligned} L_i=\left[ \begin{array}{llll} k_{2i-1,1}&{}k_{2i-1,2}&{}k_{2i-1,3}&{}k_{2i-1,4}\\ k_{2i,1}&{}k_{2i,2}&{}k_{2i,3}&{}k_{2i,4} \end{array}\right] . \end{aligned}$$

Theorem 1

Considering the underactuated system (4), assume that the disturbance d and its first-order derivative \(\dot{d}\) exist, and its second-order derivative can be negligible (i.e., \(\ddot{d}=0)\). Choosing proper \(L_i\) satisfying that \(A_1\) is negative definite, the disturbance observer given in (5) with the auxiliary vector \({L_i}\) defined in (6) ensures that the disturbance tracking error converges exponentially to zero. If the disturbance d and its first-order derivative \(\dot{d}\) exist, and its second-order derivative \(\ddot{d}\) is bounded (i.e., \(||\ddot{d}||\le \mu _1)\), choosing proper \(L_i\) satisfying that \(A_1\) is negative definite, then the disturbance observer given in (5) with the auxiliary vector \({L_i}\) defined in (6) ensures that the disturbance tracking error is globally uniformly ultimately bounded.

Here

$$\begin{aligned} {A_1}=\left[ \begin{array}{ll} -L_1G_2 \quad \mathbf {I}\\ -L_2G_2 \quad \mathbf {0} \end{array}\right] , \end{aligned}$$

where \(\mathbf {I}\) is a 2\(\times 2\) identity matrix. \(\mathbf {0}\) is a 2\(\times 2\) zero matrix.

Proof

Let the estimation errors to be defined as

$$\begin{aligned} \begin{aligned} \tilde{d}= & {} d-\hat{d},\\ \tilde{\dot{d}}= & {} \dot{d}-\hat{\dot{d}}, \end{aligned} \end{aligned}$$
(7)

where \(\tilde{d}\) is the estimation error between d and its estimate \(\hat{d}\), and \(\tilde{\dot{d}}\) is the estimation error between \({\dot{d}}\) and its estimate \(\hat{\dot{d}}\).

Differentiating the first equation of (7), we can get:

$$\begin{aligned} \begin{aligned} \dot{\tilde{d}}&=\dot{d}-\dot{\hat{d}}\\ \quad&=\dot{d}-L_1\left( -F_1-G_1 u -G_2\hat{d}\right) -\hat{\dot{d}}-\dot{p}_1\\&= \dot{d}-L_1G_2\tilde{d}-\hat{\dot{d}}=\tilde{\dot{d}}-L_1G_2\tilde{d}. \end{aligned} \end{aligned}$$
(8)

According to the second equation of (7), we have:

$$\begin{aligned} \begin{aligned} \dot{\tilde{\dot{d}}}&=\ddot{d}-\dot{\hat{\dot{d}}}\\&=\ddot{d} -L_2\left( -F_1-G_1u-G_2\hat{d}\right) -L_2\dot{X} \\&=\ddot{d}-L_2G_2\tilde{d}. \end{aligned} \end{aligned}$$
(9)

According to (8) and (9), the error vector \(D_1 =\left[ \tilde{d} \quad \tilde{\dot{d}}\right] ^\mathrm{T}\) can be expressed as

$$\begin{aligned} \dot{{D}}_1 = A_1D_1+B_1\ddot{d}, \end{aligned}$$
(10)

where \(B_1=[{\mathbf {0_1}}\quad {\mathbf {I_1}}]^\mathrm{T}\). \({\mathbf {0_1}}\) is a \(2 \times 2 \) zero matrix. \({\mathbf {I_1}}\) is a \(2 \times 2 \) identity matrix.

Since \(A_1\) is a negative definite matrix, the eigenvalues of \(A_1\) are negative. There exists a positive defined matrix \(Q_1\) satisfying \(A_1^\mathrm{T}P_1+P_1A_1^\mathrm{T}=-Q_1\).

Choose the following Lyapunov function

$$\begin{aligned} V_1 ={D}_1^\mathrm{T}P_1{D}_1, \end{aligned}$$

where \(P_1\) is a positive defined matrix.

By differentiating \(V_1\), we have

$$\begin{aligned} \begin{aligned} \dot{V}_1&= {D}_1^\mathrm{T}(A_1^\mathrm{T}P_1+P_1A_1^\mathrm{T}){{D}_1}+2{D_1}^\mathrm{T}P_1B_1\ddot{d}\\&= -{D_1}^\mathrm{T}Q_1{D_1}+2{D_1}^\mathrm{T}P_1B_1\ddot{d}\\&\le -\lambda _{1\min }\Vert D_1 \Vert ^2+2\Vert D_1^\mathrm{T}P_1B_1\Vert \cdot \mu _1\\&\le -\Vert D_1\Vert \left( \lambda _{1\min }\Vert D_1 \Vert -2\Vert P_1B_1\Vert \cdot \mu _1\right) , \end{aligned} \end{aligned}$$

where \(\lambda _{1min}\) is the minimum eigenvalue of \(Q_1\).

$$\begin{aligned} \dot{V}_1\le - \Vert D_1\Vert (\lambda _{1\min }\Vert D_1 \Vert -2\Vert P_1B_1\Vert \cdot \mu _1). \end{aligned}$$

That is, after a sufficiently long time, the norm of the estimation error is bounded by

$$\begin{aligned} \Vert D_1\Vert \le \frac{2\Vert P_1B_1\Vert \cdot \mu _1}{\lambda _{1\min }}. \end{aligned}$$

Thus, if the disturbance d and its first-order derivative \(\dot{d}\) exist, and its second-order derivative satisfies \(\ddot{d}= 0\), the disturbance tracking error converges exponentially to zero. If the disturbance d and its first-order derivative \(\dot{d}\) exist, and its second-order derivative \(\ddot{d}\) is bounded, the tracking error is globally uniformly ultimately bounded. \(\square \)

2.3 Extension of disturbance observer to nth-order cases

Assumption 3

The disturbance d is continuous, and its nth-order derivative exists.

Assumption 4

\({d}^{(n)}\) is bounded and satisfies \(\Vert {d}^{(n)}\Vert \le \mu \). Here \(\mu >0\) is a constant.

The extended disturbance observer for the underactuated system (4) is proposed as:

$$\begin{aligned} \hat{d}= & {} z_1+p_1(X)\nonumber \\ \dot{z}_1= & {} L_1(-F_1(X)-G_1(X)u-G_2\hat{d})+\hat{\dot{d}}\nonumber \\ \vdots \nonumber \\ \hat{{d}}^{(i-1)}= & {} z_i+p_i(X)\nonumber \\ \dot{z}_i= & {} L_i(-F_1(X)-G_1(X)u-G_2\hat{d})+\hat{{d}}^{(i)}\nonumber \\ \vdots \nonumber \\ \hat{d}^{(n-1)}= & {} z_n+p_n(X)\nonumber \\ \dot{z}_n= & {} L_n(-F_1(X)-G_1(X)u-G_2\hat{d}), \end{aligned}$$
(11)

where \(\hat{d}^{(i)}\) is the estimate of \({d}^{(i)}\). The disturbance observer gain matrix \(L_i\) is defined as:

$$\begin{aligned} L_i= \partial p_i(X) / \partial X,~~i=1,2,\ldots , n. \end{aligned}$$
(12)

Theorem 2

Considering the underactuated system (4), assume that the disturbance d and its derivatives \({d}^{(i)}\) exist, and its nth derivative can be negligible (i.e., \({d}^{(n)}= 0)\). Choosing proper \(L_i\) satisfying that A is negative definite, the extended disturbance observer given in (11) with the auxiliary vector \({L_i}\) defined in (12) ensures that the disturbance tracking error converges exponentially to zero. If the disturbance d and its derivatives \({d}^{(i)}\) exist, and its n-th derivative \({d}^{(n)}\) is bounded (i.e., \(||{d}^{(n)}||\le \mu )\), choosing proper \(L_i\) satisfying that A is negative definite, the disturbance observer given in (11) with the auxiliary vector \({L_i}\) defined in (12) ensures that the disturbance tracking error is globally uniformly ultimately bounded.

Here

$$\begin{aligned} {A}=\left[ \begin{array}{ccccc} -L_1G_2 &{} \mathbf {I} &{} \mathbf {0} &{}\cdots &{}\mathbf {0}\\ -L_2G_2 &{} \mathbf {0} &{} \mathbf {I}&{} \cdots &{} \mathbf {0}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ -L_{n-1}G_2 &{} \mathbf {0}&{} \mathbf {0}&{} \cdots &{} \mathbf {I}\\ -L_{n}G_2 &{} \mathbf {0} &{} \mathbf {0}&{} \cdots &{} \mathbf {0}\\ \end{array}\right] , \end{aligned}$$

where \(i=1,2 \ldots n\). \(\mathbf {I}\) is 2\(\times 2\) identity matrix. \(\mathbf {0}\) is 2\(\times 2\) zero matrix.

Proof

Let the estimation errors to be defined as

$$\begin{aligned} \begin{aligned} \tilde{d}&=d-\hat{d}\\ \vdots \\ \tilde{{d}}^{(i)}&= d^{(i)}-\hat{{d}}^{(i)}\\ \vdots \\ \tilde{{d}}^{(n-1)}&= d^{n-1}-\hat{{d}}^{(n-1)}, \end{aligned} \end{aligned}$$
(13)

where \(i=1,2,\ldots ,n-1\). \(\tilde{d}^{(i)}\) is the estimation error between \({d}^{(i)}\) and its estimate \(\hat{d}^{(i)}\) .

Differentiate the first \(n-1\) equations of (13), and substitute (11) into them. It follows that

$$\begin{aligned} \begin{aligned} \dot{\tilde{d}}^{(i)}&={d}^{(i+1)}-\dot{\hat{d}}^{(i)}\\&={d}^{(i+1)}-L_{i+1}(-F_1-G_1 u -G_2\hat{d})-\hat{{d}}^{(i+1)}-\dot{p}_{i+1}\\&= {d}^{(i+1)}-L_{i+1}G_2\tilde{d}-\hat{{d}}^{(i+1)}=\tilde{{d}}^{(i+1)} -L_{i+1}G_2\tilde{d}, \end{aligned} \end{aligned}$$
(14)

where \(i=0,1,\ldots , n-2\).

According to the last two equations of (11), we obtain

$$\begin{aligned} \begin{aligned} \dot{\hat{ d}}^{(n-1)}&=\dot{z}_n+\dot{p}_n(X)\\&=L_n(-F_1-G_1u-G_2\hat{d})+L_n\dot{X}. \end{aligned} \end{aligned}$$
(15)

Differentiating the last equation of (13) and substituting it to (15), we have

$$\begin{aligned} \dot{\tilde{{d}}}^{(n-1)}= d^{{n}}-L_n\left( -F_1-G_1u-G_2\hat{d}\right) -L_n\dot{X}. \end{aligned}$$

That is, we have:

$$\begin{aligned} \dot{\tilde{{d}}}^{(n-1)}={d}^{(n)}-L_nG_2\tilde{d}. \end{aligned}$$
(16)

According to (14) and (16), the error vector \( D =\left[ \tilde{d} \quad \tilde{\dot{d}},\ldots , \tilde{d}^{(n-1)}\right] ^\mathrm{T}\) can be expressed as

$$\begin{aligned} \dot{{D}}=AD+B{d}^{(n)}, \end{aligned}$$
(17)

where \(B=[\mathbf {0_{(n-1)}}\quad \mathbf {I_1}]^\mathrm{T}.\) \({\mathbf {0_{(n-1)}}}\) is a \(2(n-1) \times 2 \) zero matrix. \({\mathbf {I_1}}\) is a \(2 \times 2 \) identity matrix.

Since A is a negative definite matrix, the eigenvalues of A are negative. There exists a positive defined matrix Q satisfying \(A^\mathrm{T}P+PA^\mathrm{T}=-Q\).

Choose Lyapunov function

$$\begin{aligned} V ={D}^\mathrm{T}P{D}, \end{aligned}$$

where P is a positive defined matrix.

In the light of the mathematical derivation in Sect. 2.2, it is easy to obtain

$$\begin{aligned} \dot{V}\le - \Vert D\Vert (\lambda _{\min }\Vert D \Vert -2\Vert PB\Vert \cdot \mu ), \end{aligned}$$

where \(\lambda _{min}\) is the minimum eigenvalue of Q. That is, after a sufficiently long time, the norm of the estimation error is bounded by

$$\begin{aligned} \Vert D\Vert \le \frac{2\Vert PB\Vert \cdot \mu }{\lambda _{\min }}. \end{aligned}$$

Based on the above inequality, we can easily draw the conclusion of this theorem. \(\square \)

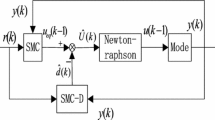
3 Sliding mode control with an extended disturbance observer

Based on the obtained EDO in Sect. 2, we propose a sliding mode controller with disturbance observer (SMCDO) for the general second-order underactuated system (3) in this section.

For simplicity, we rewrite (3) as

$$\begin{aligned} \begin{aligned} \dot{x}_1&= m_{11}^{-1}x_2,\\ \dot{x}_2&= f_1(x_1,x_2,x_3,x_4)+d_1,\\ \dot{x}_3&= x_4,\\ \dot{x}_4&= f_2(x_1,x_2,x_3,x_4)+b(x_1,x_2,x_3,x_4)u+d_{12}. \end{aligned} \end{aligned}$$
(18)

The sliding surface is chosen as:

$$\begin{aligned} s = c_1e_1+c_2e_2+c_3e_3+e_4, \end{aligned}$$
(19)

where \(e_1 = x_1-x_{1d}, e_2 = x_2-x_{2d}, e_3=f_1+d_1-f_{1d}-\hat{d}_1\), \( \displaystyle e_4 = \frac{\hbox {d} f_1}{\hbox {d} t }+{{d}}_{12}-\hat{{d}}_{12}-\dot{f}_{1d} \). Here \(x_{1d}\), \(x_{2d}\), \(f_{1d}\), \(\dot{f}_{1d}\) are the desired values.

Remark 2

Since we have \(\dot{x}_3=x_4\), and \(\dot{x}_4\) is related to input u, then \(\dot{s}\) should include \(\dot{x}_4\). To meet the requirement, if \(f_1\) is related to \(x_4\), the sliding mode surface is selected as \(s=c_1e_1+c_2e_2+e_3\). If \(f_1\) only has a relationship with \(x_3\), the sliding mode surface is then chosen as \(s=c_1e_1+c_2e_2+c_3e_3+e_4\). As analyzed in Remark 1, we have \(\partial f_1/\partial x_4=0\). Then the sliding mode surface is chosen as (19).

Differentiating the errors \(e_1, e_2, e_3\), it follows that

$$\begin{aligned} \dot{e}_1= & {} \dot{x}_1-\dot{x}_{1d}=m_{11}^{-1}x_2-m_{11}^{-1}x_{2d} =m_{11}^{-1}(x_2-x_{2d})\nonumber \\= & {} m_{11}^{-1}e_2,\nonumber \\ \dot{e}_2= & {} \dot{x}_2-\dot{x}_{2d}= f_1+d_1-(f_{1d}+\hat{d}_1)=e_3,\nonumber \\ \displaystyle {\dot{e}}_3= & {} \frac{\hbox {d} f_1}{\hbox {d} t }-\dot{f}_{1d}+\dot{d}_1{-}\dot{\hat{d}}_1=e_4-{{d}}_{12}+\hat{{d}}_{12}{+}\dot{d}_1{-}\dot{\hat{d}}_1\nonumber \\= & {} e_4-\tilde{d}_{12}+\dot{\tilde{d}}_1. \end{aligned}$$
(20)

When the system state approaches the sliding mode surface (19), it satisfies \(s=\gamma \) where \(|\gamma |\le \kappa \), i.e.,

$$\begin{aligned} e_4=- c_1e_1-c_2e_2-c_3e_3+\gamma . \end{aligned}$$
(21)

According to (20) and (21), the error \(E=[e_1\quad e_2\quad e_3]^\mathrm{T}\) can be expressed as

$$\begin{aligned} \dot{E}=ME+N D_1+\varUpsilon , \end{aligned}$$
(22)

where

$$\begin{aligned} M = \left[ \begin{array}{ccc} 0 &{} m_{11}^{-1} &{} 0\\ 0 &{} 0 &{} 1 \\ -c_1 &{} -c_2 &{}-c_3 \end{array} \right] , N=\left[ \begin{array}{cccc} 0&{} 0 &{} 0 &{} 0\\ 0&{}0&{} 0 &{} 0\\ 0&{}-1 &{}1&{}0 \end{array}\right] , \varUpsilon =\left[ \begin{array}{ccc}0\\ 0\\ \gamma \end{array}\right] . \end{aligned}$$

Proper parameters \(c_{1},c_{2},c_{3}\) can be selected satisfying the condition that the real parts of eigenvalues of M are negative.

Considering the sliding surface (19), the system dynamics on the sliding surface is asymptotically stable if \(D_1\) and \(\gamma \) vanish as time goes by. That is, the underactuated part of the system can be self-stabilized on the sliding mode surface. And the system dynamics is uniformly ultimately bounded on the sliding surface if \(D_1\) and \(\gamma \) exist all the time.

Theorem 3

Considering a general nonlinear underactuated system (18), the state trajectories will be driven to the sliding mode surface (19) and uniformly ultimately bounded when the SMCDO (23) is applied:

$$\begin{aligned} u = -\left( \frac{\partial f_1}{\partial x_3}b\right) ^{-1}\left( K+k \hbox {sgn}(s)+\lambda s\right) , \end{aligned}$$
(23)

where

$$\begin{aligned} K= & {} \displaystyle c_1 m_{11}^{-1}x_2+c_2f_1+c_3\left( \frac{\partial f_1}{\partial x_1}m_{11}^{-1}x_2 \displaystyle +\frac{\partial f_1}{\partial x_3}x_4 \right) \\&+\,\frac{\partial f_1}{\partial x_1}m_{11}^{-1}f_1 \displaystyle +\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial f_1}{\partial x_1}m_{11}^{-1}\right) x_2 +\frac{\hbox {d}}{\hbox {d}t}\frac{\partial f_1}{\partial x_3}x_4\\&+\,\frac{\partial f_1}{\partial x_3}f_2-c_1\dot{x}_{1d} \\&-\,c_2\dot{x}_{2d}-c_3\dot{f}_{1d}-\ddot{f}_{1d} +\left( c_2+\frac{\partial f_1}{\partial x_1}m_{11}^{-1}\right) \hat{d}_1\\&+\,\frac{\partial f_1}{\partial x_3}\hat{d}_{12},\, k> \left( c_2+\frac{\partial f_1}{\partial x_1 }m_{11}^{-1}\right) \tilde{d}_1 +\frac{\partial f_1}{\partial x_3}\tilde{d}_{12}\\&+\,c_3\tilde{\dot{d}}_1+\tilde{\dot{d}}_{12},\lambda >0. \end{aligned}$$

Proof

Choose the Lyapunov function as

$$\begin{aligned} V =\frac{1}{2}s^\mathrm{T}s. \end{aligned}$$

Differentiating both sides of V and substituting (23) into it, we have

$$\begin{aligned} \begin{array}{l} {{\dot{V}}} = \dot{s}s\\ = s\left( {\underbrace{{c_1}m_{11}^{ - 1}{x_2} - {c_1}{{\dot{x}}_{1d}}}_{{c_1}{{\dot{e}}_1}} + \underbrace{{c_2}{f_1} + {c_2}{d_1} - {c_2}{{\dot{x}}_{2d}}}_{{c_2}{{\dot{e}}_2}} + \underbrace{{c_3}\left( \frac{{\partial {f_1}}}{{\partial {x_1}}}m_{11}^{ - 1}{x_2} + \frac{{\partial {f_1}}}{{\partial {x_3}}}{x_4} - {{\dot{f}}_{1d}} + \tilde{\dot{d}}_1\right) }_{{c_3}{{\dot{e}}_3}} + {{\dot{e}}_4}}\right) . \end{array} \end{aligned}$$

The derivative of \(e_4\) can be calculated as follows:

$$\begin{aligned} {e_4}= & {} \frac{{\hbox {d}{f_1}}}{{\hbox {d}t}} + {d_{12}} - {\widehat{d}_{12}} - {{\dot{f}}_{1d}} \Rightarrow \\ {{\dot{e}}_4}= & {} \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\hbox {d}{f_1}}}{{\hbox {d}t}}} \right) + \tilde{\dot{d}}_{12} - {{\ddot{f}}_{1d}}. \end{aligned}$$

As analyzed in Remark 1 , we have \(\partial f_1/ \partial x_2 = 0\) . It follows that

$$\begin{aligned} \dot{e}_4= & {} \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}} {{\dot{x}}_1} + \frac{{\partial {f_1}}}{{\partial {x_3}}}{{\dot{x}}_3}} \right) + \tilde{\dot{d}}_{12} - {{\ddot{f}}_{1d}}\\= & {} \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}m_{11}^{ - 1}{x_2} + \frac{{\partial {f_1}}}{{\partial {x_3}}}{x_4}} \right) + \tilde{\dot{d}}_{12} - {{\ddot{f}}_{1d}}. \end{aligned}$$

Substituting (18) into it, we have

$$\begin{aligned} \dot{e}_4= & {} \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}} m_{11}^{ - 1}} \right) {x_2} + \frac{{\partial {f_1}}}{{\partial {x_1}}} m_{11}^{ - 1}{{\dot{x}}_2} + \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\partial {f_1}}}{{\partial {x_3}}}} \right) {x_4} \\&+\, \frac{{\partial {f_1}}}{{\partial {x_3}}} {{\dot{x}}_4} + \tilde{\dot{d}}_{12} - {{\ddot{f}}_{1d}}\\= & {} \frac{\hbox {d}}{{\hbox {d}t}}\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}} m_{11}^{ - 1}} \right) {x_2} + \frac{{\partial {f_1}}}{{\partial {x_1}}} m_{11}^{ - 1}\left( {{f_1} + {d_1}} \right) \\&+\, \frac{\hbox {d}}{{\hbox {d}t}} \left( {\frac{{\partial {f_1}}}{{\partial {x_3}}}} \right) {x_4} + \frac{{\partial {f_1}}}{{\partial {x_3}}}\left( {{f_2} {+} bu {+} {d_{12}}} \right) {+} \tilde{\dot{d}}_{12} {-} {{\ddot{f}}_{1d}}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \dot{V}= & {} s\left( \displaystyle c_1 m_{11}^{-1}x_2+c_2f_1+c_3\left( \frac{\partial f_1}{\partial x_1}m_{11}^{-1}x_2 \displaystyle +\frac{\partial f_1}{\partial x_3}x_4 \right) \displaystyle \right. \\&\left. +\frac{\partial f_1}{\partial x_1}m_{11}^{-1}f_1 +\,\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial f_1}{\partial x_1}m_{11}^{-1}\right) x_2 +\frac{\hbox {d}}{\hbox {d}t}\frac{\partial f_1}{\partial x_3}x_4\right. \\&\left. +\frac{\partial f_1}{\partial x_3}f_2-c_1 \dot{x}_{1d}-\,c_2\dot{x}_{2d}-c_3\dot{f}_{1d}-\ddot{f}_{1d}\right. \\&\left. +\left( c_2 +\frac{\partial f_1}{\partial x_1 }m_{11}^{-1}\right) {d_1} +\frac{\partial f_1}{\partial x_3}{d}_{12}\right. \\&\left. +\,c_3\tilde{\dot{d}}_1 +\tilde{\dot{d}}_{12}+\frac{\partial f_1}{\partial x_3}bu\right) \\ \displaystyle= & {} s\left( \left( c_2+\frac{\partial f_1}{\partial x_1 }m_{11}^{-1}\right) \tilde{d}_1 +\frac{\partial f_1}{\partial x_3}\tilde{d}_{12}+c_3\tilde{\dot{d}}_1 +\tilde{\dot{d}}_{12}\right) \\&-\,\lambda s^2-ks\cdot \hbox {sgn}(s)\\ \displaystyle\le & {} |s|\left( \left( c_2+\frac{\partial f_1}{\partial x_1 }m_{11}^{-1} +\frac{\partial f_1}{\partial x_3}+c_3+1\right) \Vert D_1\Vert -\lambda |s|-k\right) \\{\vspace{8pc}} \displaystyle\le & {} |s|\left( \left( c_2+\frac{\partial f_1}{\partial x_1 }m_{11}^{-1} +\frac{\partial f_1}{\partial x_3}+c_3+1\right) \right. \\&\left. \frac{2\Vert PB\Vert \cdot \mu }{\lambda _{\min }}-\lambda |s|-k\right) . \end{aligned}$$

It is easy to obtain that after a sufficiently long time, |s| is bounded by

$$\begin{aligned} \displaystyle |s| \le \frac{2\left( c_2+\frac{\partial f_1}{\partial x_1 }m_{11}^{-1} {+}\frac{\partial f_1}{\partial x_3}{+}c_3{+}1\right) \Vert PB\Vert \mu -k\lambda _{\min }}{\lambda \lambda _{\min }}. \end{aligned}$$

It is worth to notice that |s| can be lowered by increasing \(\lambda \) or k.

If the nth-order derivative of d can be negligible (i.e., \({d}^{(n)}= 0, \mu =0\)), then the Lyapunov function V is globally asymptotic convergent to 0, and the actuated states are driven to the sliding mode surface. The effect of the disturbance can also be eliminated completely.

On the other hand, \(\Vert D\Vert \) is uniformly ultimately bounded if the nth-order derivative \({d}^{(n)}\) is bounded (\(||{d}^{(n)}||\le \mu \)). In this case, the magnitude of sliding variable |s| and Lyapunov function V are uniformly ultimately bounded. The actuated states move around the sliding mode surface, and the bounds can be lowered by selecting proper control parameter \(k, \lambda \). \(\square \)

4 Simulation results

In order to test and verify the proposed EDO and SMCDO, we provide an example to illustrate the theory analysis in this section.

4.1 The model of acrobot system

The acrobot is a two-link planar robot with two joints and the elbow is the actuator, which is an inherent unstable, underactuated system, as shown in Fig. 1.

The dynamic model of acrobot is given by [36]

$$\begin{aligned} m_{11}\ddot{q}_1+m_{12}\ddot{q}_2+h_1+\phi _1= & {} d_1,\nonumber \\ m_{21}\ddot{q}_1 +m_{22} \ddot{q}_2 +h_2+\phi _2= & {} \tau +d_2, \end{aligned}$$
(24)

where

$$\begin{aligned} m_{11}= & {} a+b \cos (q_2),\quad m_{12} = c+0.5 b \cos (q_2),\\ m_{12}= & {} m_{21}, m_{22}=c\\ a= & {} m_1l_{c1}^2+m_2\left( l_1^2+l_{c2}^2\right) +I_1+I_2,\\ c= & {} m_2l_{c2}^2, b = 2m_2l_1l_{c2}\\ h_1= & {} -m_2l_1l_{c2}\sin (q_2){\dot{q}_2}^2-2m_2l_2l_{c2}\sin (q_2)\dot{q}_1\dot{q}_2,\\ h_2= & {} m_2l_1l_{c2}\sin (q_2){\dot{q}_1}^2, \\ \phi _1= & {} \left( m_1l_{c1}+m_2l_1\right) g \cos (q_1){+}m_2l_{c2}g\cos (q_1{+}q_2),\\ \phi _2= & {} m_2l_{c2}g\cos (q_1+q_2). \end{aligned}$$

\(d_1,d_2\) are the disturbances including model uncertainties and external disturbance.

Fig. 1
figure 1

The mechanical structure of acrobot

Full size image

Obviously, it satisfies that \(M(q)=M(q_2)\) and \(q_2\) is actuated. Choose new states and the global change of the coordinate

$$\begin{aligned} x_1= & {} q_1+\beta (q_2),\nonumber \\ x_2= & {} m_{11} \dot{q}_1+m_{12} \dot{q}_2 = {\partial L}/{\partial \dot{q}_1},\nonumber \\ x_3= & {} q_2,\nonumber \\ x_4= & {} \dot{q}_2, \end{aligned}$$
(25)

where \( \beta (q_2) = \frac{q_2}{2}+\frac{2c-a}{\sqrt{a^2-b^2}}\arctan (\sqrt{\frac{a-b}{a+b}} \tan (\frac{q_2}{2})).\)

The dynamic model (24) is then transformed into a cascade nonlinear system in strict feedback form:

$$\begin{aligned} \dot{x}_1= & {} m_{11}^{-1}x_2,\nonumber \\ \dot{x}_2= & {} f_1+d_1,\nonumber \\ \dot{x}_3= & {} x_4,\nonumber \\ \dot{x}_4= & {} f_2+bu+d_{12}, \end{aligned}$$
(26)

where

$$\begin{aligned} f_1&{=}&{-}\,\left( m_1l_{c1}{+}m_2l_1\right) g \cos (q_1){-}m_2l_{c2}g\cos (q_1{+}q_2)\\= & {} -\,\left( m_1l_{c1}+m_2l_1\right) g \cos (x_1-\beta )\\&-m_2l_{c2}g\cos (x_1-\beta +x_3)\\ \displaystyle f_2= & {} \frac{m_{21}(h_1+\phi _1)-m_{11}(h_2+\phi _1)}{m_{11}m_{22}-m_{12}m_{21}},\\ \displaystyle b= & {} \frac{m_{11}}{m_{11}m_{22}-m_{12}m_{21}},\\ \displaystyle d_{12}= & {} \frac{\left( -m_{12}d_1+m_{11}d_2\right) }{m_{11}m_{22}-m_{12}m_{21}}. \end{aligned}$$
Table 1 The parameters of an acrobot
Full size table

An obvious equilibrium of the acrobot system can be easily obtained

$$\begin{aligned} X =[x_1\quad x_2\quad x_3\quad x_4]^\mathrm{T}=[\pi /2 \quad 0 \quad 0 \quad 0]^\mathrm{T}. \end{aligned}$$

4.2 The simulation results of acrobot controlled by the proposed method

In the simulation, the parameters of the acrobot are given in Table 1. The initial conditions are chosen as:

$$\begin{aligned} {q_1} = \pi /2 + 0.2,\;\;{q_2} = - 0.5,\;\;{\dot{q}_1} = 0,\;\;\;{\dot{q}_2} = 0. \end{aligned}$$

The friction and model uncertainties will vanish as the system gradually approaches the equilibrium. In order to test the EDO and SMCDO, the external disturbance is also considered. Without loss of the generality, the first-order, second-order, third-order and fourth-order disturbance observers are discussed, respectively, in the following. The equilibrium control of acrobot will be discussed in the following cases.

Fig. 2
figure 2

The simulation result of sliding mode control for acrobot with \(d_1=0, d_2=0\)

Full size image
Fig. 3
figure 3

The simulation result of EDOs with \(d_1 = 0.2(q_1-\pi /2)+ 0.1q_2+0.3\dot{q}_1\) and \(d_2 = 0.2(q_1-\pi /2)+ 0.5q_2+0.3\dot{q}_1+0.5\dot{q}_2+ 0.5t+0.2t^2\)

Full size image
Fig. 4
figure 4

The errors between disturbance and its estimations with \(d_1 = 0.2(q_1-\pi /2)+ 0.1q_2+0.3\dot{q}_1, d_2 = 0.2(q_1-\pi /2)+ 0.5q_2+0.3\dot{q}_1+0.5\dot{q}_2+ 0.5t+0.2t^2\)

Full size image

Case 1

The situation that there is no disturbance is considered.

$$\begin{aligned} {d}_1 = 0, \quad {d}_2 = 0. \end{aligned}$$

The simulation of the acrobot system without disturbances controlled by sliding mode controller is shown in Fig. 2. It is shown that the sliding mode controller can drive the inherent unstable system to the sliding surface, and it takes about 25 s.

Case 2

In this case, the disturbances are assumed to be

$$\begin{aligned} d_1= & {} 0.2(q_1-\pi /2)+ 0.1q_2+0.3\dot{q}_1,\\ d_2= & {} 0.2(q_1-\pi /2)+ 0.5q_2+0.3\dot{q}_1\\&+\, 0.5\dot{q}_2+ 0.5t+0.2t^2, \end{aligned}$$

where \(d_1\) dies away as the states tend to converge to zero. \(d_2\) satisfies \({d}_2 \rightarrow \infty \), \(\dot{d}_2 \rightarrow \infty \), \(|\ddot{d}_2|\le \mu \) and \({d}^{(3)}_2={d}^{(4)}_2=0\).

The simulation results of EDOs are shown in Figs. 3 and 4. From the figures, it can be seen that the first-order disturbance observer (DO(1st)) cannot estimate the disturbance. The second-order disturbance observer (DO(2nd)) tracks the disturbance with a steady-state error. The third-order disturbance observer (DO(3rd)) and the fourth-order disturbance observer (DO(4th)) are able to track the disturbance accurately.

According to (17), for the DO(1st), the estimation error satisfies \(\dot{D}=AD+B\dot{d}\). Since we have \(\dot{d} \rightarrow \infty \), the stability of estimation error cannot be guaranteed. This is why the DO(1st) cannot estimate the disturbance. For the DO(2nd), the estimation error satisfies \(\dot{D}=AD+B\ddot{d}\). Since we have \(\Vert \dot{d} \Vert \le \mu \), the DO(2nd) estimates the disturbance with a steady error. For the DO(3rd) and DO(4th), the estimation errors satisfy \(\dot{D}=AD+Bd^{(3)}\) and \(\dot{D}=AD+Bd^{(4)}\), respectively. Since we have \(d^{(3)}=d^{(4)}=0\), these DOs can estimate the disturbance accurately, as shown in Fig. 3

The simulation results of the acrobot controlled by SMCDO (23) are shown in Fig. 5. Obviously, the sliding mode control with first-order disturbance observer (SMCDO(1st)) cannot drive the states to the equilibrium. The sliding mode control with second-order disturbance observer (SMCDO(2nd)) drives the states to the equilibrium with a steady error. The sliding mode control with third-order disturbance observer (SMCDO(3rd)) and fourth-order disturbance observer (SMCDO(4th)) drives the states to the equilibrium.

Fig. 5
figure 5

The simulation result of SMCDO for acrobot with \(d_1 = 0.2(q_1-\pi /2)+ 0.1q_2+0.3\dot{q}_1, d_2 = 0.2(q_1-\pi /2)+ 0.5q_2+0.3\dot{q}_1+0.5\dot{q}_2+ 0.5t+0.2t^2\)

Full size image
Fig. 6
figure 6

The simulation results of EDOs with \( d_1 = 0.1\sin (t+1), d_2 = \sin (0.5t)\)

Full size image

Case 3

In this case, more complex disturbance which is superimposed on types of bounded disturbance is considered to test the EDO and the SMCDOs. Choose \(d_1\) and \(d_2\) as

$$\begin{aligned} \begin{aligned} d_1&= 0.1\sin (t+1),\\ d_2&= \sin (0.5t), \end{aligned} \end{aligned}$$

where \(d_1, d_2\) include the friction, model uncertainties and external disturbance. Their nth-order derivatives exist and are bounded (\(\Vert d^{(n)}\Vert \le \mu \)).

Fig. 7
figure 7

The errors between disturbance and its estimations with \( d_1 = 0.1\sin (t+1), d_2 = \sin (0.5t)\)

Full size image
Fig. 8
figure 8

The simulation results of SMC and SMCDOs for acrobot with \( d_1 = 0.1\sin (t+1), d_2 = \sin (0.5t)\)

Full size image

The simulation results of the EDOs are shown in Figs. 6 and 7. The tracking errors between system states and the reference are globally uniformly ultimately bounded. Because of the slow change of disturbance(\(f_1=1/2\pi , f_2=1/4\pi )\), the higher order of the derivative of \(d_2\), the smaller the upper bounded of \(d^{(n)}\). As analyzed in Theorem 2, we can get smaller tracking error by using the disturbance observer of higher order.

The simulation results of the acrobot controlled by the SMC and the SMCDOs are shown in Fig. 8. Both the SMC and the SMCDOs cannot guarantee that the states converge to the desired value when \({d}^{(n)}\) does not vanish. As analyzed in Theorem 3, the effect of disturbance cannot be eliminated completely. As shown in Fig. 8, compared to the SMC, the proposed SMCDOs are more effective. Using the EDO of higher order, better control performance can be obtained.

Fig. 9
figure 9

The results of SMCDO(4th) compared with the method in Ref. [33] for acrobot with \( d_1 = 0.1\sin (t+1), d_2 = \sin (0.5t)\)

Full size image
Fig. 10
figure 10

The results of SMCDO(4th) compared with the method in Ref. [33] for acrobot with \( d_1 = 0.1\sin (t+1), d_2 = \sin (0.5t)\)

Full size image

4.3 Comparison results

In order to verify the superiority of the proposed method, a comparison study is carried out in this subsection.

The simulation results of proposed SMCDO controller are compared with those of method in Ref. [33]. In Ref. [33], a global sliding mode control is presented to improve the robustness and stability of the underactuated system with external disturbances, and the conditions of asymptotic stability are presented by linear matrix inequalities. Based on the controller, states of the system converge to the sliding mode surface exponentially.

Considering the method in Ref. [33] applied to a class of underactuated systems with bounded external disturbances, the disturbance is chosen as given in Case 3 in Sect. 4.2. In the comparison, the proposed SMC with fourth-order DO is used. The system trajectories with initial states \(q_1=\pi /2+0.2, q_2=-0.5\) are illustrated in Fig. 9. The trajectories of sliding mode motion and control signal are shown in Fig. 10. These results verify that the proposed control approach has better performance in comparison with the controller in Ref. [33].

5 Conclusion

In this paper, we proposed an extended disturbance observer which relaxes the assumption that the first-order derivatives of disturbances go to zero or they are bounded in steady states. The sliding mode surface control is also generalized for a class of underactuated systems based on the nth-order disturbance observer. It is proved that the ultimate boundedness of the sliding variable and disturbance estimation error can be guaranteed. Compared to the conventional SMC, the switching gain of proposed SMCDO is only required to be designed greater than the bound of the disturbance estimation error rather than that of the disturbance. The SMCDO has the ability to compensate the disturbances and obtain more satisfactory control performance. An example of acrobot is proposed to verify the effectiveness of proposed method in comparison with the results of the controller proposed in Ref. [33]. By using the proposed method, both the chattering and the tracking error are significantly reduced even there exist various disturbances. The proposed technology also yields better robust performance compared to the results presented in Ref. [33]. In the future, experiments will be conducted to further validate the theory analysis.