Extended state observer-based adaptive sliding mode control of differential-driving mobile robot with uncertainties

Abstract

Based on the uncertain nonlinear kinematic model of the differential-driving mobile robots, an adaptive sliding mode control method is used to design a controller for trajectory tracking of the differential-driving mobile robots with unknown parameter variations and external disturbances. The total uncertainties of the robot are estimated online by an improved linear extended state observer (ESO) with the error compensating term. The adaptive sliding mode controller with the switching gain is adjustable real-time online is developed by selecting the appropriate PID-type sliding surface. The convergence of the tracking errors for wheeled mobile robots is proved by the Lyapunov stability theory. Moreover, the simulation and real experiment results all show that the effectiveness and superiority of the proposed the adaptive sliding mode control method, in comparison with the traditional sliding model control and backstepping control method.

1 Introduction

The wheeled mobile robot (WMR) is a kind of electromechanical device, which is suited for working in the complex environment. The WMRs have highly automatic programming, organizing and adapting ability. In the past decades, the WMRs have been applied in scientific research, national defense, industrial production, logistics industry and the other areas. Furthermore, trajectory tracking control is the key to implement the autonomous movement of the WMR. However, since the WMR is the nonlinear system with multivariate, strong coupling, and time-varying parameters, it is difficult to obtain good tracking control performance [1–3].

In order to further improve the tracking control performance of the WMR, the nonlinear trajectory-tracking control methods are adopted for the kinematic control include input–output linearization [4], integrator backstepping approach [5], sliding mode control (SMC) [6, 7], and intelligent control [8–11]. Among them, the sliding mode control system is insensitive to parameter perturbation and external disturbance effects, and sliding mode controller is widely used in nonlinear robot systems with uncertainties [12]. Yang and Kim [13] proposed the controller design of the WMR based on polar coordinates. The SMC can overcome the external disturbance was proposed, but there was an assumption that the bound of the disturbance was known. The work above, however, becomes inapplicable when the parameters of the mobile robots are not available. In order to reach a fast convergence and alleviate the control chattering effect, I/O linearization and a second-order SMC technique [14] have been proposed to implement the robust output tracking control of the nonholonomic mobile robot with model uncertainties. In [15], the robust trajectory-tracking problem for a mobile robot in the presence of uncertainties has been solved by means of a SMC law based on the discrete-time WMR dynamical model. No particular assumptions are needed except for the bound of the uncertainties. In [16–18] present a time-varying global adaptive controller at the torque level that simultaneously solves both tracking and stabilization for the WMR with unknown kinematic and dynamic parameters. This controller is based on Lyapunov’s direct method and backstepping technique. However, the use of the sign function and high switch gain in the SMC lead to a high-frequency chattering which affects control performance due to the discontinuous control when the system states approach the sliding surface. The high-frequency chattering usually causes serious problems for the controller and actuator in practical engineering.

At present, adaptive control has been applied widely to solve many engineering problems [19–23]. The adaptive vehicle skid control [19] is designed for stability and tracking of a vehicle during slippage of its wheels without braking. Bobtsov et al. [20] illustrated a possibility for application of their adaptive algorithms to control libration angle of satellite. Wu et al. [21] realized an adaptive robust motion tracking control method for controlling an X–Y table driven by linear motors with a high precision. Ouyang et al. [22] proposed an adaptive control scheme for trajectory tracking of robot manipulators in an iterative operation mode. Li et al. [23–25] proposed an robust adaptive control scheme for trajectory tracking of robot manipulators in the presence of uncertainties and external disturbances. Lim and Zhang [26] designed a control scheme incorporating PID control and robust model reference adaptive control to realize the levitation control of Lorentz force-type self-bearing motors. It is well known that conventional SMC, which can provide great properties such as insensitivity to parameter variations and external disturbance rejection is a forceful control scheme for nonlinear systems. In [27], it has been shown that an adaptive controller can improve the closed-loop system’s performance as the continuous adaptation. Unfortunately, if only the adaptive control rule is designed for the WMR with parameter perturbation and external disturbance, the closed-loop system has a poor robustness. For this reason, this study combines both the adaptive control and the sliding mode control to overcome both the uncertainties and the disturbances in the whole WMR system. Since the Jing-qing [28] proposed the ESO technology, the ESO has been used to estimate unknown states and disturbance of system. The ESO has a less dependence on system model, and has a stronger robustness to the external nonlinear disturbance.

Accordingly, we propose control strategy which combines both the adaptive control and the sliding mode control to apply trajectory tracking control for the WMR with unknown parameter variations and external disturbances. More specifically, the main contribution of our work is follows. Firstly, the nonlinear kinematic model of the WMR with uncertainties is established at the kinematic level, and the certainties and the uncertainties in kinematic model are separated by the Taylor expansion. Secondly, a modified linear extended state observer with the error compensation term is presented to estimate total unknown uncertainty online. The adaptive sliding model controller with switching gain which is adjustable real-time online is developed by selecting the appropriate PID-type sliding surface. Moreover, stability and convergence are analyzed rigorously and effectively by Lyapunov stability theory. Finally, simulation and experiment results are all provided to verify the performance of the proposed adaptive trajectory-tracking controller.

The remaining part of the paper is organized as follows. The trajectory-tracking model of wheeled mobile robot will be presented in Sect. 2, followed by the design of a robust adaptive sliding mode controller with disturbance observer in Sect. 3. In Sect. 4, the proposed WMR control system stability is analyzed based on Lyapunov stability theory. In Sect. 5, the designed controller is implemented in numerical simulations and real experiments, and the performance of the designed controller in this paper is compared to that of the conventional SMC with disturbance observer and the backstepping control method. Section 6 concludes the paper.

2 Kinematic model of wheeled mobile robots

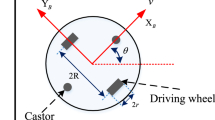
We consider the differential wheeled mobile robot with two independent driving wheels. Trajectory-tracking schematic of mobile robot is shown as Fig. 1. The two front wheels are driven independently by two direct-current servo motors respectively. The two rear wheels are omnidirectional wheels, which only play the role of supporting car body, without guiding role.

Assumption 1

The mobile robots are subject to a ‘pure rolling without slipping’.

Assumption 2

There is a superposition both center of mass and rotating geometric center of the WMR.

Fig. 1

Wheeled mobile robot trajectory-tracking scheme

As can be seen from Fig. 1, at time t, we suppose that the geometric center O of the WMR is rotating around the instantaneous center A along the dotted circle. $R_a$ is the turning radius around the instantaneous rotation center A at time t, L is the distance between two driving wheels; $v_1$ and $v_2$ are linear velocities of left and right wheels, respectively.

The velocity of the middle of the two driving wheels is given by

$$\begin{aligned} v_c =\frac{v_1 +v_2 }{2} \end{aligned}$$

(1)

If $u_1$ and $u_2$ denote direct-current servo motor armature voltage of left and right driving wheels of the mobile robot, respectively, $T_m$ is direct-current motor load time constant, $k_d$ denotes the back-EMF constant of direct-current motor, r is radius of the driving wheels, n is the transmission ratio of the reducing gear, and driving gain of the mobile robot is denoted by $k_s$, which can be obtained as [29]

$$\begin{aligned} k_s =\frac{2\pi rk_d }{60n} \end{aligned}$$

(2)

According to the characteristics of direct-current servo motor, the following transfer functions are obtained as [29]

$$\begin{aligned} \left\{ {\begin{array}{l} V_1 (s)=\frac{k_s }{1+T_m s}U_1 (s) \\ V_2 (s)=\frac{k_s }{1+T_m s}U_2 (s) \\ \end{array}} \right. \end{aligned}$$

(3)

where $V_1 (s)$, $V_2 (s)$, $U_1 (s)$ and $U_2 (s)$ denote the Laplace transform of $v_1$, $v_2$, $u_1$ and $u_2$ respectively.

When there is the deviation in tracking path of the robot, it is necessary to add or subtract a correction control voltage $\Delta u$ to the driving motors, respectively, then $u_1$ and $u_2$ can be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} u_1 =u_c +\Delta u \\ u_2 =u_c -\Delta u \\ \end{array}} \right. \end{aligned}$$

(4)

where $u_c$ is the voltage reference of direct-current motor, which can actuate robot to keep moving at the speed of $v_c$ forward. Accordingly, the linear velocities of the left and right wheels can be written as

$$\begin{aligned} \left\{ {\begin{array}{l} v_1 =v_c +\Delta v \\ v_2 =v_c -\Delta v \\ \end{array}} \right. \end{aligned}$$

(5)

where $\Delta v$ is the linear velocity variation of the driving wheels.

In Fig. 1, $\theta$ is the heading angle of the robot, the point P is the reference point, d is the central position shift (the distance from geometrical center O to the point P), $\phi$ is the tangential angle at tangential point P. In a very short time interval of $\Delta t$, $\Delta \theta$ and $\Delta d$ are variations of $\theta$ and d, respectively, from the geometric relationships in the Fig. 1, $\Delta \theta$ and $\Delta d$ are obtained as

$$\begin{aligned} \left\{ {\begin{array}{l} \Delta \theta =\frac{(v_2 -v_1 )\Delta t}{R_a } \\ \Delta d=\frac{(v_1 +v_2 )\Delta t}{2}\sin \theta \\ \end{array}} \right. \end{aligned}$$

(6)

As $\Delta t\rightarrow 0$, differential equations can be obtained as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{\theta }=\frac{v_2 -v_1 }{R_a }=-\frac{2}{R_a }\Delta v \\ \dot{d}=\frac{(v_1 +v_2 )}{2}\sin \theta =v_c \sin \theta \\ \end{array}} \right. \end{aligned}$$

(7)

where $R_a$ is the turning radius of the robot.

Remark 1

$R_a$ can be determined by the images of the navigation camera installed in the front of the robot body.

Applying Laplace transformation for Eqs. (4) and (5), the first equation is subtracted by the second equation in (3), the following equation is obtained as

$$\begin{aligned} \Delta V(s)=\frac{V_1 (s)-V_2 (s)}{2}=\frac{k_s }{1+T_m s}\Delta U(s) \end{aligned}$$

(8)

where $\Delta V(s)$ and $\Delta U(s)$ are Laplace transforms of $\Delta v$ and $\Delta u$ respectively. From (9), if Laplace inverse transformation is used, the following differential equation can be obtained as

$$\begin{aligned} \Delta \dot{v}(t)=-\frac{1}{T_m }\Delta v(t)+\frac{k_s }{T_m }\Delta u(t) \end{aligned}$$

(9)

If vectors $x=\left[ {{\begin{array}{lll} {x_1 }&{} {x_2 }&{} {x_3 } \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{lll} d&{} \theta &{} {\Delta v} \\ \end{array} }} \right] ^{\mathrm{T}}$ and $u=\left[ {\Delta u} \right]$ are defined, and the system input is selected as $y=\theta =x_2$, from Eqs. (7) and (9), the following equations can be obtained as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =v_c \sin x_2 \\ \dot{x}_2 =-\frac{2x_3 }{R_a } \\ \dot{x}_3 =-\frac{1}{T_m }x_3 +\frac{k_s }{T_m }u \\ y=x_2 \\ \end{array}} \right. \end{aligned}$$

(10)

3 Design of tracking controller

3.1 Modeling of mobile robot with uncertainty

In practical engineering, there are always some uncertainties because of the existence of reduction gear clearance, motor parameters variation caused by some conditions such as temperature, material abrasion and wheels are worn in robot system, that all will cause a direct-current servo motor transmission torque changes. Therefore, in the control system design, it is necessary to consider the harmful effect caused by driving gain of motor and transmission structure $k_s$ and time constant $T_m$ change. If $\Delta T_m$ and $\Delta k_s$ are uncertainties of $T_m$ and $k_s$, from Eq. (10), a more general state equation are obtained as following:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =v_c \sin x_2 \\ \dot{x}_2 =-\frac{2x_3 }{R_a } \\ \dot{x}_3 =-\frac{1}{T_m +\Delta T_m }x_3 +\frac{k_s +\Delta k_s }{T_m +\Delta T_m }u+w \\ y=x_2 \\ \end{array}} \right. \end{aligned}$$

(11)

where $\Delta T_m$ and $\Delta k_s$ are uncertainties of $k_s$ and $T_m$, respectively, w is unknown external disturbance of robot system.

Assumption 3

External disturbance w and parameter variations $\Delta T_m$ and $\Delta k_s$ are unknown but bounded.

Remark 2

in Assumption 3, $\Delta T_{m}$ and $\Delta k_{s}$ are uncertainties of $T_{m}$ and $k_{s}$, respectively, caused by some adverse factors such as the gear clearance of the reducer, ambient temperature, material wear, and the change of the friction coefficient. Therefore, in the design of the robotic controller, the damage caused by the uncertainties of the parameters $T_{m}$ and $k_{s}$ must be considered.

Now we consider the following function:

$$\begin{aligned} \frac{1}{x+\Delta x}=\frac{1}{x}\cdot \frac{1}{1+\Delta x/x} \end{aligned}$$

(12)

where the function $1/(1+\Delta x/x)$ can be regarded as a function of $\Delta x/x$. If a first-order Taylor expansion has been used at point of zero, the first two of the first-order Taylor expansion are selected, the following equation is obtained as

$$\begin{aligned} \frac{1}{x+\Delta x}\approx \frac{1}{x}\left( 1-\frac{\Delta x}{x}\right) \end{aligned}$$

(13)

According to Eq. (13), the state Eq. (11) can be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =v_c \sin x_2 \\ \dot{x}_2 =-\frac{2x_3 }{R_a } \\ \dot{x}_3 =-\frac{1}{T_m }x_3 +\frac{\Delta T_m }{T_m^2 }x_3 \\ \quad \quad \quad +\frac{k_s }{T_m }u+\left( \frac{\Delta k_s }{T_m +\Delta T_m }-\frac{\Delta T_m k_s }{T_m^2 }\right) u+w \\ y=x_2 \\ \end{array}} \right. \end{aligned}$$

(14)

If the total system uncertainties caused by parameter variations and external disturbances are defined as

$$\begin{aligned} D=\frac{\Delta T_m }{T_m^2 }x_3 +\left( \frac{\Delta k_s }{T_m +\Delta T_m }-\frac{\Delta T_m k_s }{T_m^2 }\right) u+w \end{aligned}$$

The Eq. (14) can be rewritten as follows

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =v_c \sin x_2 \\ \dot{x}_2 =-\frac{2x_3 }{R_a } \\ \dot{x}_3 =-\frac{1}{T_m }x_3 +\frac{k_s }{T_m }u+D \\ y=x_2 \\ \end{array}} \right. \end{aligned}$$

(15)

3.2 Design of observer

In Eq. (15), since the total uncertainties D in system (15) are unknown, it is necessary to estimate uncertainties D by using the ESO. The ESO is a novel observe algorithm, which is able to estimate the internal and external disturbance online [29].

If new state variables $x_1^*=x_2$, $x_2^*=-2x_3 /R_a$ are defined, the second equation and the third equation in (15) can be rewritten as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1^*=x_2^*\\ \dot{x}_2^*=ax_2^*+bu+D^{*} \\ y=x_1^*\\ \end{array}} \right. \end{aligned}$$

(16)

where $a=-1/T_m$, $b=-2k_s /R_a T_m$ and $D^{*}=-2D/R_a$. If the total disturbance $D^{*}$ in the system (16) is expanded into a new state $x_3^*$, then Eq. (16) can be expanded into a new linear system

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1^*=x_2^*\\ \dot{x}_2^*=ax_2^*+x_3^*+bu \\ \dot{x}_3^*=\dot{D}^{*} \\ y=x_1^*\\ \end{array}} \right. \end{aligned}$$

(17)

In order to obtain real-time estimation of disturbance $D^{*}$, based on Eq. (17), an improved three-order linear ESO with compensation term $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)$ is designed as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{\hat{{x}}}_1^*=\hat{{x}}_2^*-\beta _1 (\hat{{x}}_1^*-x_1^*) \\ \dot{\hat{{x}}}_2^*=\hat{{x}}_3^*-\beta _2 (\hat{{x}}_1^*-x_1^*)+bu+f_c (\hat{{x}}_1^*,\hat{{x}}_2^*) \\ \dot{\hat{{x}}}_3^*=-\beta _3 (\hat{{x}}_1^*-x_1^*) \\ \end{array}} \right. \end{aligned}$$

(18)

where $\hat{{x}}_1^*$ denotes the estimation of $x_1^*$, $\hat{{x}}_2^*$ is the estimation of $x_2^*$, $\hat{{x}}_3^*$ is the estimation of total disturbance $x_3^*=D^{*}$ in system (16), which is also denoted by $\hat{{D}}^{*}$; $\beta _i >0,i=1,2,3$ are the observer gain parameters which can be chosen, compensation term $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)=ax_2^*$.

Remark 3

The estimation of the total disturbance D in system (15) is obtained as $\hat{{D}}=-\hat{{D}}^{*}R_a /2$.

The following observer errors are defined as $e_{o1} =\hat{{x}}_1^*-x_1^*$, $e_2 =\hat{{x}}_{o2}^*-x_2^*$, $e_{o3} =\hat{{x}}_3^*-x_3^*=\hat{{x}}_3^*-D^*$, $e_o =\left[ {{\begin{array}{lll} {e_{o1} }&{} {e_{o2} }&{} {e_{o3} } \\ \end{array} }} \right] ^{\mathrm{T}}$. From (17) and (18), the error dynamic equations of the ESO are obtained as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{e}_{o1} =-\beta _1 e_{o1} +e_{o2} \\ \dot{e}_{o2} =-\beta _2 e_{o1} +ae_{o2} +e_{o3} \\ \dot{e}_{o3} =-\beta _3 e_{o1} -\dot{D}^{*} \\ \end{array}} \right. \end{aligned}$$

(19)

Equation (19) can be rewritten as

$$\begin{aligned} \dot{e}_o =Ae_o +\bar{{b}}\dot{D}^{*} \end{aligned}$$

(20)

where matrix $A=\left[ {{\begin{array}{lll} {-\beta _1 }&{} 1&{} 0 \\ {-\beta _2 }&{} a&{} 1 \\ {-\beta _3 }&{} 0&{} 0 \\ \end{array} }} \right]$, matrix $\bar{{b}}=\left[ {{\begin{array}{lll} 0&{} 0&{} {-1} \\ \end{array} }} \right] ^{\mathrm{T}}$. The characteristic polynomial of the matrix A is shown as

$$\begin{aligned} \lambda (s)=s^{3}+a_2 s^{2}+a_1 s+a_0 \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{array}{l} a_2 =\beta _1 -a \\ a_1 =\beta _2 -a\beta _1 \\ a_0 =\beta _3 \\ \end{array} \end{aligned}$$

It is obvious that the coefficients $a_i ,i=0,1,2$ of the characteristic polynomial satisfy the following conditions:

$$\begin{aligned} \left\{ {\begin{array}{l} a_i >0,i=0,1,2 \\ a_1 a_2 -a_0 =(\beta _1 -a)(\beta _2 -a\beta _1 )-\beta _3 >0 \\ \end{array}} \right. \end{aligned}$$

(22)

The Routh–Hurwitz stability criterion ensures that all eigenvalues of the system matrix A in Eq. (20) have negative real parts. Thus, it means the linear observer error system (20) is asymptotically stable; it is to say that the observer errors $e_o =\left[ {{\begin{array}{lll} {e_{o1} }&{} {e_{o2} }&{} {e_{o3}} \\ \end{array} }} \right] ^{\mathrm{T}}$ converge consequently to $\left[ {{\begin{array}{ccc} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}}$ as $t\rightarrow \infty$.

Remark 4

If there is no compensation term $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)=ax_2^*$ in Eq. (18), the error dynamic equation of the ESO is shown as

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{e}_{o1} =-\beta _1 e_{o1} +e_{o2} \\ \dot{e}_{o2} =-\beta _2 e_{o1} -ax_2^*+e_{o3} \\ \dot{e}_{o3} =-\beta _3 e_{o1} -\dot{D} \\ \end{array}} \right. \end{aligned}$$

(23)

From Eq. (23), we know that there is an additional term $ax_2^*$, which leads to an intrinsic estimation error caused by $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)=ax_2^*$. However, after the ESO being compensated by $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)$, the $ax_2^*$ is transformed into the eliminable error $ae_2$ in Eq. (19). Thereby, the estimation precision of the ESO can be improved markedly by employing the compensating term $f_c (\hat{{x}}_1^*,\hat{{x}}_2^*)$.

The parameters of the ESO $\beta _i ,i=1,2,3$ are determined by bandwidth technology [30]. According to reference [30], the desired characteristic polynomial of the ESO is as follow

$$\begin{aligned} \lambda _o (s)=(s+\omega _o )^{3}=s^{3}+3\omega _o s^{2}+3\omega _o^2 s+\omega _o^3 \end{aligned}$$

(24)

where $\omega _o$ is the bandwidth of the ESO.

From (21) and (24), the gain parameter of the ESO can be obtained as

$$\begin{aligned} \begin{array}{l} \beta _1 =3\omega _o +a \\ \beta _2 =3\omega _o^2 +3a\omega _o +a^{2} \\ \beta _3 =\omega _o^3 \\ \end{array} \end{aligned}$$

(25)

So the parameter tuning process of the ESO is greatly simplified.

3.3 Design of adaptive sliding mode controller

Since the SMC has some remarkable advantages such as insensitivity to parameter variations, external disturbance rejection and fast dynamic response, SMC is a forceful control scheme for nonlinear systems. Thus, it is very suitable to design the trajectory-tracking controller of mobile robot with uncertainties. Control objective of trajectory-tracking controller of the robot is not only to guarantee heading angle $\theta$ of the robot tend to the tangential angle $\phi$ of the given reference trajectory, but also to make the center position shift d tend to zero. That is to say that mobile robot is able to track a given trajectory smoothly as far as possible.

If $y_d =\theta _d$ denotes the desired value of input y, that is the tangential angle $\phi$ at the reference point P in Fig. 1, then tracking error is obtained as $e=\theta -\phi =y-y_d =x_2 -y_d$. In order to improve robustness of the control system, a time-varying PID-type switching function can be designed as [31]:

$$\begin{aligned} s=c_1 e+\dot{e}+c_2 \int _0^t {e(t) \hbox {d}t} \end{aligned}$$

(26)

where $c_1$ and $c_2$ are positive constants. $s=0$ can be obtained reasonably on switching surface. At this moment, from Eq. (26), the differential equation can be obtained as $c_1 e+\dot{e}+c_2 \int _0^t {e(t)\hbox {d}t} =0$, it is possible to guarantee $e(t)\rightarrow 0$ in a finite time by selecting the appropriate $c_1$ and $c_2$.

From Eq. (26), the following equation is obtained as

$$\begin{aligned} \dot{s}= & {} c_1 \dot{e}+\ddot{e}+c_2 e=c_1 \dot{e}+\ddot{y}-\ddot{y}_d +c_2 e \nonumber \\= & {} c_1 \dot{e}+\ddot{x}_2 -\ddot{\phi }+c_2 e \end{aligned}$$

(27)

where $\phi$ is the tangential angle of the given reference trajectory (See Fig. 1). Substituting Eq. (15) into Eq. (27) yields

$$\begin{aligned} \dot{s}=c_1 \dot{e}+\frac{2}{R_a }\left( \frac{1}{T_m }x_3 -\frac{k_s }{T_m }u-\hat{{D}}\right) -\ddot{\phi }+c_2 e \end{aligned}$$

(28)

With the reaching law method the SMC makes the trajectory outside the switching surface reach the switching surface in a limited time. Meanwhile, in order to make the SMC have low chattering in the sliding motion. A modified reaching law is chosen as [32]

$$\begin{aligned} \dot{s}=-\varepsilon \left| s \right| ^{\alpha }\hbox {sgn}(s)-k\left| s \right| ^{\beta }s \end{aligned}$$

(29)

where $k>0$, $\varepsilon >0$, $0<\alpha <1$ and $0<\beta <1$ are positive constant, $\hbox {sgn}(\cdot )$ is signum function.

Remark 5

The modified reaching law combines exponential reaching law and idempotent reaching law, which can overcome the shortcomings of the two laws and combine the advantages of them. Thus the performance of control system is improved, and chattering is reduced as possible as it could. Meanwhile, the reaching rate of exponential reaching term can be adjusted adaptively by additional term $-k\left| s \right| ^{\beta }s$. And so the reaching rate can be adjusted adaptively according to the distance between the current state and sliding surface. In order to estimate the domain of attraction of the modified reaching law (29), the following Lyapunov function is chosen as

$$\begin{aligned} V_a =\frac{1}{2}s^{2} \end{aligned}$$

(30)

Then

$$\begin{aligned} \dot{V}_a= & {} s\dot{s}=s(-\varepsilon \left| s \right| ^{\alpha }\hbox {sgn}(s)-k\left| s \right| ^{\beta }s)\nonumber \\= & {} -\varepsilon s\left| s \right| ^{\alpha }\hbox {sgn}(s)-ks^{2}\left| s \right| ^{\beta } \nonumber \\= & {} -\varepsilon \left| s \right| ^{\alpha +1}-k\left| s \right| ^{\beta +2}\le 0 \end{aligned}$$

(31)

From (31), we know $V_a$ is a function of t does not increase in $t\in [0,\infty )$, so $V_a \le V_a (0)=\frac{1}{2}s^{2}(0)$, that is $\dot{V}_a \le 0$ is ensured if only s is bounded real number. The reachability condition is satisfied in the modified reaching law (29). So domain of attraction of the modified reaching law (29)can be denoted by the following set

$$\begin{aligned} \Omega (s)=\left\{ {s\in R\left| {V_a \le \frac{1}{2}s^{2}(0)} \right. } \right\} \end{aligned}$$

(32)

where $s=c_1 e+\dot{e}+c_2 \int _0^t {e(t)\mathrm{d}t}$ is switching function, $s(0)=c_1 e(0)+\dot{e}(0)$ is the initial value of s.

From Eqs. (28) and (29), sliding mode control law is obtained as

$$\begin{aligned} u= & {} \frac{x_3 }{k_s }-\frac{T_m \hat{{D}}}{k_s }+\frac{T_m R_a }{2k_s }[c_1 \dot{e}+c_2 e+\varepsilon \left| s \right| ^{\alpha }\hbox {sgn}(s)\nonumber \\&+\,k\left| s \right| ^{\beta }s-\ddot{\phi }] \end{aligned}$$

(33)

In order to eliminate chatter caused by sign function switch frequently, signum function $\hbox {sgn}(s)$ is replaced by saturation function $\hbox {sat}(s,\delta )$, sliding mode control law (33) can be rewritten as

$$\begin{aligned} u= & {} \frac{x_3 }{k_s }-\frac{T_m \hat{{D}}}{k_s }+\frac{T_m R_a }{2k_s }[c_1 \dot{e}+c_2 e\nonumber \\&+\,\varepsilon \left| s \right| ^{\alpha }\hbox {sat}(s,\delta )+k\left| s \right| ^{\beta }s-\ddot{\phi }] \end{aligned}$$

(34)

where $\hbox {sat}(s,\delta )$ is defined as follows

$$\begin{aligned} \hbox {sat}(s,\delta )=\left\{ {\begin{array}{l} -1\hbox { }s<-\delta \\ s/\delta \hbox { }-\delta \le s<\delta \\ 1\hbox { }s\ge \delta \\ \end{array}} \right. \end{aligned}$$

where $\delta$ is a positive constant.

By adjusting parameters k and $\varepsilon$ in the reaching law (29), the excellent dynamic performance can be guaranteed in the process of sliding mode reach to the switching surface, the high-frequency chattering of the control signal can be markedly reduced also [12]. In control law (34), the cut-and-try method is often used to determine switching gain $\varepsilon$ in practical engineering. In order to avoid trouble of adjusting parameter $\varepsilon$ manually, to overcome effects of disturbances caused by the system parameters variations and to enhance robustness of the closed-loop robot system, the following adaptive update law of switching gain $\varepsilon (t)$ is designed as:

$$\begin{aligned} \dot{\hat{{\varepsilon }}}(t)= & {} \rho \cdot \hbox {sgn}(\hat{{\varepsilon }})\sqrt{c+\left| {\hat{{\varepsilon }}} \right| }[\hat{{\varepsilon }}s\left| s \right| ^{\alpha }\hbox {sat}(s,\delta )\nonumber \\&-\lambda x_1^2 -v_c x_1 \sin x_2 ] \end{aligned}$$

(35)

where $\hat{{\varepsilon }}$ is estimation of $\varepsilon$, $\rho$, $\lambda$ and c are positive constants. The sliding mode control law (34) can be rewritten as

$$\begin{aligned} u= & {} \frac{x_3 }{k_s }-\frac{T_m \hat{{D}}}{k_s }+\frac{T_m R_a }{2k_s }[c_1 \dot{e}+c_2 e\nonumber \\&+\,\hat{{\varepsilon }}\left| s \right| ^{\alpha }\hbox {sat}(s,\delta )+k\left| s \right| ^{\beta }s-\ddot{\phi }] \end{aligned}$$

(36)

From above analysis, we can conclude that adaptive sliding mode control based on the ESO of the mobile robot can be described by the following close-loop control system structure, as shown in Fig. 2.

Fig. 2

Adaptive sliding mode control principle diagram of mobile robot

4 Stability analyses of control system

Lemma 1

(Barbalat lemma [27]) If f(x) is uniformly continuous and if the limit of the integral $\mathop {\lim }\limits _{t\rightarrow \infty } \int _0^t {f(x)} dx$ exists and is finite, then $\mathop {\lim }\limits _{t\rightarrow \infty } f(t)=0$.

Theorem 1

Considering the uncertain nonlinear mobile robot system described by (15). Under sliding mode control law (36) with switching function (27)and reaching law (29), if the adaptive update law (35) is applied to the mobile robot, then the tracking errors (heading angle error e and the center position shift $x_1 =d$) converge asymptotically to zero.

Proof

The Lyapunov candidate function can be defined as

$$\begin{aligned} V=\frac{1}{2}s^{2}+\frac{2}{\rho }\sqrt{c+\left| {\hat{{\varepsilon }}} \right| }+\frac{1}{2}x_1^2 \ge 0 \end{aligned}$$

(37)

The derivative of the Lyapunov function V is given by

$$\begin{aligned} \dot{V}=s\dot{s}+\frac{\dot{\hat{{\varepsilon }}}\hbox {sgn}(\hat{{\varepsilon }})}{\rho \sqrt{c+\left| {\hat{{\varepsilon }}} \right| }}+x_1 \dot{x}_1 \end{aligned}$$

(38)

Substituting (27) into (38) yields

$$\begin{aligned} \dot{V}=s(\ddot{x}_2 -\ddot{\phi }+c_1 \dot{e}+c_2 e)+\frac{\dot{\hat{{\varepsilon }}}\hbox {sgn}(\hat{{\varepsilon }})}{\rho \sqrt{c+\left| {\hat{{\varepsilon }}} \right| }}+x_1 \dot{x}_1 \end{aligned}$$

(39)

Substituting (15), (35) and (36) into (39) yields

$$\begin{aligned} \dot{V}= & {} s[-ks\left| s \right| ^{\beta }-\hat{{\varepsilon }}\left| s \right| ^{\alpha }\hbox {sat}(s,\delta )]\nonumber \\&+\frac{\dot{\hat{{\varepsilon }}}\hbox {sgn}(\hat{{\varepsilon }})}{\rho \sqrt{c+\left| {\hat{{\varepsilon }}} \right| }}+v_c x_1 \sin x_2 =-k\left| s \right| ^{\beta +2}-\lambda x_1^2\nonumber \\ \end{aligned}$$

(40)

From Eq. (40), we can obtain as

$$\begin{aligned} \dot{V}=-k\left| s \right| ^{\beta +2}-\lambda x_1^2 \le 0 \end{aligned}$$

(41)

The adaptive update law (35) ensures V is negative semi-definite. With the adaptive law (35) and sliding mode control law (36), V is a function of t does not increase, that is

$$\begin{aligned} V(s(t),x_1 (t))\le V(s(0),x_1 (0))<\infty ,\forall t\ge 0 \end{aligned}$$

(42)

From Eqs. (37) and (41), we know that s, $x_1$ and V are bounded in $t\in [0,\infty )$, that is, $V\in L_\infty$, $x_1 \in L_\infty$, $s\in L_\infty$.

From Eq. (41), we can obtain

$$\begin{aligned} \dot{V}=-k\left| s \right| ^{\beta +2}-\lambda x_1^2 \le -k\left| s \right| ^{\beta +2} \end{aligned}$$

(43)

From Eq. (43), the following equation can be obtained as

$$\begin{aligned} \int _0^\infty {\left| s \right| ^{\beta +2}\hbox {d}t} \le -\frac{1}{k}\int _0^\infty {\dot{V}\hbox {d}t} =\frac{1}{k}(V(0)-V(\infty ))<\infty \end{aligned}$$

(44)

Similarly

$$\begin{aligned} \int _0^\infty {x_1^2 \hbox {d}t} \le -\frac{1}{\lambda }\int _0^\infty {\dot{V}\hbox {d}t} =\frac{1}{\lambda }(V(0)-V(\infty ))<\infty \end{aligned}$$

(45)

Because of s is bounded, from Eqs. (15) and (29), we know $\dot{x}_1$ and $\dot{s}$ are all bounded, thus $x_1$ and s are uniformly continuous. Barbalat’s lemma [27] shows that $x_1 \rightarrow 0$, $\left| s \right| ^{\beta +2}\rightarrow 0$ as $t\rightarrow \infty$, thus $s\rightarrow 0$ as $t\rightarrow \infty$. As $s=0$, the following differentiating equation can be obtained as

$$\begin{aligned} c_1 e+\dot{e}+c_2 \int _0^t {e(t)\hbox {d}t} =0 \end{aligned}$$

(46)

By taking the derivative of the Eq. (46), the following differential equation is obtained as

$$\begin{aligned} \ddot{e}+c_1 \dot{e}+c_2 e=0 \end{aligned}$$

(47)

If the following conditions: $c_1 >0$, $c_2 >0$, $c_1^2 >4c_2$ are satisfied, the solution of differential Eq. (47) can be given as

$$\begin{aligned} e(t)= & {} k_1 \exp \frac{-c_1 +\sqrt{c_1^2 -4c_2 }}{2}t\nonumber \\&+\,k_2 \exp \frac{-c_1 -\sqrt{c_1^2 -4c_2 }}{2}t \end{aligned}$$

(48)

where $k_1$ and $k_2$ are positive constants that are determined by initial error e(0). From Eq. (48), we know $e(t)\rightarrow 0$ as $t\rightarrow \infty$.

Given the above, tracking error $x_1 =d\rightarrow 0$, $e(t)=\theta -\phi \rightarrow 0$ as $t\rightarrow \infty$. $\square$

5 Simulations and experiment

5.1 Simulations

Computer simulation results are given to demonstrate and compare the effectiveness and superiority of the proposed adaptive sliding mode controller based on the ESO (ESO$+$ASMC), conventional sliding mode controller based on the ESO (ESO$+$SMC), and backstepping control method. ESO$+$ASMC and ESO$+$SMC are described by the Eqs. (18, 35, 36) and Eqs. (18, 33) respectively, based on Eq. (15), backstepping control law is designed according to Ref. [27].

Table 1 The physical parameters of the robot

To observe and compare the simulation results more easily, we choose two kinds of reference trajectories for the simulations: One is a straight-line trajectory, and the other is a circle one. System parameters of the WMR are shown in Table 1.

In the simulations, the design parameters are chosen as (1) parameters of the ESO: bandwidth parameter $\omega _o =60$; (2) parameters of the ASMC: $c_1 =16$, $c_2 =62$, $k=5$, $\rho =0.5$, $\alpha =0.8$, $\beta =0.085$, $c=0.1$, $\lambda =1$, $\delta =0.08$ and initial estimation of switching gain $\hat{{\varepsilon }}(0)=0$; (3) switching gain of the SMC $\varepsilon =5$.

In particular, the reasons of choosing $\delta$ of the saturation function $\hbox {sat}(s,\delta )$ in (36) are follows: the thickness of the boundary layer $\delta$ in saturation function is a very important parameter which affects the performance of the sliding mode controller. The affect results are follows: (1) If the parameter $\delta$ is increased, which will reduce the speed of the system get into a stable state along the sliding manifold. Under the same conditions, the steady-state error of the closed-loop system will be increasing; (2) If value of the parameter $\delta$ is reduced, the change of the control signal will be too frequent, that leads to inevitable chatter of the control signal. Meanwhile, the control energy consumption will be increased, and the control efficiency will be decreased. From what we have mentioned above, in order to guarantee the sliding mode control system has a satisfactory dynamic performance and steady-state performance, and to avoid the chatter of the control signal, the cut-and-try method is often used to determine the thickness of the boundary layer $\delta =0.08$.

5.1.1 The straight-line trajectory tracking

The equation of the straight-line trajectory is given as

$$\begin{aligned} \left\{ {{\begin{array}{l} {x=t} \\ {y=t} \\ \end{array} }} \right. \end{aligned}$$

where $t\ge 0$is simulation time. The initial posture of the reference trajectory is set at

$$\begin{aligned} \left[ {{\begin{array}{ccc} {x_r (0)}&{} {y_r (0)}&{} {\theta _r (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{ccc} 0&{} 0&{} {\pi /4} \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

The actual initial posture of the mobile robot is

$$\begin{aligned} \left[ {{\begin{array}{ccc} {x(0)}&{} {y(0)}&{} {\theta (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {-{\begin{array}{ccc} 2&{} {-2}&{} {\pi /4} \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

The initial state is

$$\begin{aligned} \left[ {{\begin{array}{ccc} {\Delta v(0)}&{} {d(0)}&{} {\theta (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{ccc} 0&{} 0&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

The initial value of switching gain estimation is $\hat{{\varepsilon }}(0)=0$.

(1) The straight-line trajectory tracking without parameters variations and disturbances

In this case, there are no uncertainties and disturbances. Evidently, both of the two architectures have a nice tracking ability, as shown in Fig. 3, and this also proves that no matter what architectures we use, these three controllers can trace the desired straight-line trajectory. However, at the beginning of simulation, the SMC and the backstepping controller has the bigger tracking errors than the ASMC, and the error convergence speed of the ASMC is faster than the other two controllers.

Fig. 3

The straight-line trajectory tracking without parameters variations and disturbances. a Straight-line trajectory tracking. b Tracking error $\theta -\phi$. c Central position shift d. d Switching gain $\varepsilon$ of ASMC. e Control input u

(2) The straight-line trajectory tracking with parameter variations and disturbances

In this conditions, at 25 s, the parameter variations and external disturbances D(t) are fed in

$$\begin{aligned} D(t)=\sin 2\pi t+n(t) \end{aligned}$$

where n(t) is the Gaussian white noise. Its amplitude lies in $[-1,1]$. We suppose the initial states of the disturbance observer are all zeros.

Fig. 4

The straight-line trajectory tracking with parameters variations and disturbances. a Straight-line trajectory tracking. b Tracking error $\theta -\phi$. c Central position shift d. d Switching gain $\varepsilon$ of ASMC. e Control input u

The assumption for the uncertainties in the robot’s parameters variations and external disturbances, results of trajectory tracking are revealed as Fig. 4. At the beginning of simulation, SMC and the backstepping controller has the bigger tracking errors than the ASMC. At $25\hbox {s}$, the total unknown disturbances are fed in, where a disturbance is introduced with a magnitude bounded by 2, obviously, the track errors of the SMC and backstepping controller have oscillated drastically, but the efficacy of the ASMC is still maintained.

5.1.2 The circle trajectory tracking

The equation of the circle trajectory is given as

$$\begin{aligned} \left\{ {\begin{array}{l} x=2\cos t \\ y=2\sin t \\ \end{array}} \right. \end{aligned}$$

where $t\ge 0$ is simulation time. The initial posture of the reference trajectory is set at

$$\begin{aligned} \left[ {{\begin{array}{ccc} {x_r (0)}&{} {y_r (0)}&{} {\theta _r (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{ccc} 2&{} 0&{} {\pi /2} \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

The actual initial posture of the WMR is

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {x(0)}&{} {y(0)}&{} {\theta (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{ccc} {-1}&{} 0&{} {\pi /4} \\ \end{array} }} \right] ^{{\mathrm{T}}}\\&\left[ {{\begin{array}{ccc} {\Delta v(0)}&{} {d(0)}&{} {\theta (0)} \\ \end{array} }} \right] ^{\mathrm{T}}=\left[ {{\begin{array}{ccc} 0&{} 3&{} {\pi /4} \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

The initial value of switching gain estimation is $\hat{{\varepsilon }}(0)=0$.

(1) The circle trajectory tracking without parameters variations and disturbances

In order to further verify the effectiveness and superiority of the proposed control strategy under the environment of different reference trajectory, the control system parameters of the mobile robot are all the same as in the previous simulations. In this case, there are no uncertainties and disturbances. In this situation, both of these three architectures have a similar tracking ability, but at the beginning of 7–8 s, as shown in Fig. 5, the backstepping and SMC methods have the bigger angle error and the central position shift error than the ASMC.

Fig. 5

The circle trajectory tracking without parameter variations and disturbances. a Circle trajectory tracking. b Tracking error $\theta -\phi$. c Central position shift d. d Switching gain $\varepsilon$ of ASMC. e Control input u

(2) The circle trajectory tracking with parameters variations and disturbances

The parameter variations and the external disturbances which generated at 25 s are the same as in the preceding simulation. The uncertainty influences on the backstepping control and the SMC are bigger than the ASMC. In Fig. 6b, c tracking error $\theta -\phi$ and central position shift d of the ASMC could converge to zeros more quickly than backstepping controller and SMC. In the simulation results, we illustrate that the ASMC is robust enough to resist the parameter variations and the external disturbances.

Fig. 6

The circle trajectory tracking with parameters variations and disturbances. a Circle trajectory tracking. b Tracking error $\theta -\phi$. c Central position shift d. d Switching gain $\varepsilon$ of ASMC. e Control input u

Fig. 7

Disturbances observation of the extended state observer for ASMC. a The straight-line trajectory tracking. b The circle trajectory tracking

Figure 7 show the real total disturbance and total disturbance estimations by using the ESO, respectively, in two kinds of reference trajectories in ASMC. Comparing disturbance estimation with real disturbance, it is obvious that disturbance estimation is rather accurate and smoother except for a light oscillation as total disturbances are fed in circle trajectory tracking.

(3) Control effect comparison on performance index $H_\infty$

In order to further the quantitative analysis of the control effect of the closed-loop robot system, the controller performs with a performance index such as $H_\infty$ is employed, the calculation formula is shown as follows

$$\begin{aligned} \left\| G \right\| _\infty =\sup \left\{ {\frac{\left\| z \right\| _2 }{\left\| w \right\| _2 },w\in H_2 ,\left\| w \right\| _2 \ne 0} \right\} \end{aligned}$$

where w and z are input and output signals of the controlled closed-loop system. The norm $\left\| z \right\| _2$ and $\left\| w \right\| _2$ are calculated as follows

$$\begin{aligned}&\left\| z \right\| _2^2 =\int _0^\infty {z^{{\mathrm{T}}}(t)z(t)} \hbox {d}t=\int _0^\infty {\theta ^{2}(t)} \hbox {d}t, \\&\left\| w \right\| _2^2 =\int _0^\infty {w^{{\mathrm{T}}}(t)w(t)} \hbox {d}t=\int _0^\infty {\theta _d^2 (t)} \hbox {d}t \end{aligned}$$

In following case: the circle trajectory tracking with parameters variations and disturbances. From Fig. 2, we know $\theta _d (t)$ and $\theta (t)$ are input and output signals of the controlled robotic system, the control effect comparison of three control methods (ESO+ASMC, ESO+SMC and backstepping) on performance index $H_\infty$ are shown as Table 2.

From Table 2, it is clear that the ASMC based on ESO control algorithm has the minimal value for performance index on $H_\infty$, which implies the ASMC+ESO control algorithm has a better tracking control effect than the other two control algorithms.

5.2 Real experiment

In order to demonstrate the effectiveness, superiority and applicability of the proposed method, a real-time control system is implemented for the mobile robot. In the experiment, a mobile robot with one vision navigation system fixed on the top moves along the marking line. Figure 8 shows the picture of the robot which is used in the experiment. It has the same structure as Fig. 8, with two driving wheels and two passive wheels. The diameter of the robot is 50 cm and the radius of driving wheel is 12.5 cm. The driving wheels are driven by motors with the maximum permissible speed of 3900n/min. The motor and the driving wheel are connected by a reduction gears box. For convenient for comparing, the control parameters are all same as the simulations.

The control board of the mobile robot consists of the main controller and motor controller. The main controller of the robot is dsPIC30F6014, which is running at 32 MHz. It is used to communicate with host computer and motor controller. It receives the voltage instruction from the host computer and calculates the voltage distribution on the right and left motors, respectively, and then sends the data through SPI communication to the auxiliary motor controller, dsPIC4012. The motor controller generates PWM signal with different duty cycles according to the voltage instruction.

Table 2 Control effect comparison on performance index $H_\infty$

Fig. 8

Mobile robot used in the experiment

Figure 9 shows the whole schematic diagram of the trajectory-tracking system for the mobile robot. Because of the complexity of the calculation process, the adaptive sliding mode controller is carried out in the main computer running at the frequency of 1.86 MHz. The software for implementing the algorithm is developed in Visual C++6.0. After the path has been set up, the sliding mode controller generates the real voltage instruction. The dsPIC controller can generate the PWM signal to control the velocity of the mobile robot so that the mobile robot moves according to the instruction. The vision navigation system evaluates the posture of the robot and feedback the information to the host computer until the posture error is minimized.

Fig. 9

Schematic diagram of the experiment control system

Fig. 10

Experimental results for the straight-line tracking errors with initial error (0 m, 0 rad). a Tracking error of $\theta$. b Tracking error of d

In order to validate the applicability of the proposed control scheme, the mobile robot was required to track reference trajectories. The real position of the mobile robot is feedback to the mobile robot every 0.5 s by camera navigation system.

In order to prove the superiority of the proposed adaptive sliding mode controller based on ESO (ESO$+$ASMC), the traditional sliding mode controller based on ESO (ESO$+$SMC), the backstepping control method are implemented for the desired trajectory of a straight line. The robot started tracking with initial errors $d = 0$ cm and $\theta = 0\,\hbox {rad}$. At 25 s, the following external disturbance is fed in

$$\begin{aligned} \left| {D(t-25)} \right| =\left| {\hbox {randon}(t-25)} \right| \le 2 \end{aligned}$$

where a disturbance is introduced with a magnitude bounded by 2. The experimental results are shown as Fig. 10. From Fig. 10, we can see that the tracking errors of the proposed ASMC algorithm is smaller than the traditional sliding mode controller (ESO$+$SMC) and the backstepping algorithm. The mobile robot eventually approaches the reference trajectory with asymptotic stability within 1.5 s to 0.3 % error bound by the proposed adaptive sliding mode controller. While the traditional sliding mode controller takes 9.5 s to be within 0.3 % of the desired trajectory and the backstepping controller takes 12.5 s to be within 0.3 % of the desired trajectory in the same conditions. Two factors demonstrate the superiority of the proposed adaptive sliding mode controller.

6 Conclusion

In this paper, an improved linear ESO has been adopted to estimate unknown parameter variations and external disturbances online. An adaptive sliding model controller that switching gain is adaptively adjustable is designed to use for a controller for trajectory tracking of the differential-driving mobile robots with parameter variations and external disturbances. The actual trajectory of mobile robot is able to converge asymptotically to the desired trajectory by the designed tracking controller. The convergence of the tracking errors of wheeled mobile robots is proved by the Lyapunov stability theory. Moreover, the simulation and real experiment results all show that the proposed the ASMC method greatly compensates the effects of parameter perturbation and external disturbances and improves the system tracking accuracy and robustness, in comparison with traditional sliding model control law and backstepping control law.