1 Introduction

Nonlinear systems control has received considerable attention in the control community, and phenomenal progress has been made during the last decades. Numerous novel methodologies for nonlinear feedback control have been generated to control the engineering systems [1]. One of the influential notions is the input-to-state stability (ISS) invented by Sontag [2] in the late 1980s, which has become a central concept in nonlinear systems analysis. As an integral variant of ISS, integral input-to-state stability (iISS) is another meaningful but much weaker notion. Since it is introduced in [3, 4], there has an ever increasing interest in this topic [5,6,7,8,9] recently. It is noted that in [10], supposing the dynamic uncertainty subject to the iISS property, a unifying framework is presented for global output feedback regulation control from ISS to iISS, which extends many known classes of output feedback form systems in several directions. Subsequently, some further results were obtained based on such class of nonlinear systems, see [11,12,13,14], etc.

However, all aforementioned output regulation controller does not consider the uncertain external disturbance except in [14]. It is known that the uncertainties that arise from external disturbance are essentially the major concern in the nonlinear control design. During the past two decades, many fruitful results have been proposed to reject the external disturbances [15, 16]. Recently, the extended state observer (ESO) by Han in his pioneer works [17] is regarded as the major creativity toward the active disturbance rejection control (ADRC). As written in [18], the ESO not only possesses the state observation capability but also provides real-time estimation of generalized disturbances between the plant and the model of the considered system, such as external disturbances and modeling uncertainties caused by parameter deviations. Based on the ADRC strategy together with the ESO, the robust control was addressed for several classes of nonlinear systems with disturbances and uncertainties in [19,20,21,22]. Another fruitful tool is the disturbance observer-based control (DOBC) technique proposed in [23], which provides a promising approach to handle the system disturbances and improve robustness [24,25,26,27] when the system states are available.

In this paper, we further investigate the output regulation control problem for a class of cascade nonlinear systems subject to the external disturbance. The studied system is a perturbed version of its counterpart in [10, 11]. The purpose of this paper is to construct a robust regulation controller via output feedback for a more general class of nonlinear uncertain system in the presence of external disturbance, which does not require to be square integrable or vanishing at the origin. Using the idea of ESO, we generalize the disturbance as an extended state, and then, design a novel observer whose gain is updated by a time-varying Riccati differential equation. The main contributions contained in this paper are highlighted as follows:

(1) The disturbance attenuation is addressed for a class of nonlinear systems with external disturbance in the control input channel. Different from the existing related works in [14], the external disturbance does not require to be square integrable. Consequently, the proposed control algorithm allows a larger class of disturbance signals, such as the constant signal.

(2) The system in question can accommodate some serious uncertainties such as the unknown control coefficients, which makes the state compensator design extremely difficult in the case of the unavailable system states. Technically, this hurdle is tactfully overcome by introducing a coordinate transformation and designing an ESO based a Riccati differential equation.

(3) The global set-point regulation control is solved for the fan speed control systems in the presence of external disturbances. This result improves the existing works where the external disturbance in the armature voltage is not considered.

Notations The following notations are adopted in the paper. If x is a possibly time-varying vector, then |x(t)| is the Euclidean norm of x at time t, \(\Vert x\Vert _{p}=\Big [\int _0^{\infty }|x(\tau )|^p\mathrm{d}\tau \Big ]^{\frac{1}{p}},~ p\in [1,\infty ),~\Vert x\Vert _{\infty }=\sup _{0\le {t}}|x(t)|\), and \(x\in {L_{p}}\) when \(\Vert x\Vert _{p}\) exists, \(x\in {L_{\infty }}\) when \(\Vert x\Vert _{\infty }\) exists. \(A^T\) denotes its transpose for a matrix A. For a n-dimension vector \(x=(x_1,\ldots ,x_n)\in {R^n}\), we denote \(x_{[i]}=(x_1,\ldots ,x_i)\) when \(i=2,\ldots ,n-1\). \(\pi _1(s)=O(\pi _2(s))\) as \(s\rightarrow 0^{+}\) means that \(\pi _1(s)\le {c_1}\pi _2(s)\) for some constant \(c_1>0\) and all s in a small neighborhood of zero, and \(\pi _1(s)=O(\pi _2(s))\) as \(s\rightarrow \infty \) means that \(\pi _1(s)\le {c_1}\pi _2(s)\) for some constant \(c_2>0\) and all large enough s.

2 Model description and scheme

2.1 Problem formulation

In this paper, we study the following class of cascade nonlinear systems described by

$$\begin{aligned}&\dot{\zeta }=q(\zeta ,y)\nonumber \\&\dot{x}_i=b_ix_{i+1}+\lambda _i(t)x_i+g_i(\zeta ,y), i=1,\ldots , n-1,\nonumber \\&\dot{x}_n=b_nu+\lambda _n(t)x_n+g_n(\zeta ,y)+\mathrm{d}(t)\nonumber \\&y=x_1 \end{aligned}$$
(1)

where \((\zeta ,x)\in {R^{r}\times R^{n}}\) are system states, \(u\in {R}\) is control input, and \(y=x_1\) is the observable output. \(\lambda _i(t)(i=1,\ldots ,n)\) are known time-varying functions, and \(\mathrm{d}(t)\) represents the unknown external disturbance. The signs of nonzero control coefficients \(b_1,\ldots ,b_{n-1}\) as well as the high-frequency gain \(b_n\) are not known a priori. The uncertain functions \(q(\cdot )\) and \(g_i(\cdot )(i=1,\ldots ,n)\) are supposed to be locally Lipschitz for existence and uniqueness of solutions. The state \((x_2,\ldots ,x_n)\) and the state \(\zeta \) of the \(\zeta \)-subsystem, which is referred to as the inverse system, are not assumed to be measurable.

The objective of this paper is to design a robust controller to globally asymptotically regulate system (1) to the origin using only the output signal. For future reference, we record the following definition [28].

Definition 1

  System (1) is said to be globally asymptotically regulated by the following time-varying output feedback controller

$$\begin{aligned} \dot{\hat{x}}=\nu (t,\hat{x},y),~u=\mu (t,\hat{x},y) \end{aligned}$$
(2)

in such a way that, for all initial conditions \((\zeta (0),x(0),\hat{x}(0))\), the solutions of the closed-loop system (1) and (2) are well defined and bounded on \([0,+\infty )\). In particular, \(\zeta (t)\) and x(t) converge to zero as \(t\rightarrow \infty \).

The following assumptions are needed in order to achieve the stated control objective.

Assumption 1

 The \(\zeta \) dynamics is iISS with an iISS-Lyapunov function \(U_0(\zeta )\) satisfying

$$\begin{aligned} \frac{\partial {U_0}}{\partial {\zeta }}q(\zeta ,y)\le -\alpha (|\zeta |)+\gamma (|y|), \end{aligned}$$
(3)

where \(\alpha \) is a positive definite continuous function, \(\gamma \in K_{\infty }\), and moreover

$$\begin{aligned} \gamma (s)=O(s^2)~~\text{ as }~s\rightarrow 0^+. \end{aligned}$$
(4)

Assumption 2

 For \(i=1,\ldots ,n\), there exist two unknown positive constants \(\delta _{i1}\) and \(\delta _{i2}\), and two known positive semidefinite, smooth functions \(\phi _{i1}(\cdot )\) and \(\phi _{i2}(\cdot )\), such that

$$\begin{aligned} |g_i(\zeta ,y)|\le \delta _{i1}\phi _{i1}(|\zeta |)+\delta _{i2}\phi _{i2}(|y|). \end{aligned}$$
(5)

Moveover, the following additional conditions hold:

$$\begin{aligned} \phi _{i1}^2(s)=O\big (\alpha (s)\big ) ~~\text{ as }~s\rightarrow 0^+, \end{aligned}$$
(6)

and in case \(\alpha \) is bounded,

$$\begin{aligned} \limsup _{s\rightarrow \infty }\frac{\phi _{i1}^2(s)}{\alpha (s)}<\infty , ~1\le i\le n. \end{aligned}$$
(7)

Assumption 3

 The time-varying functions \(\lambda _i(t)(i=1,\ldots ,n)\) are uniformly bounded and differentiable sufficiently many times, and further assumed to have bounded derivatives. To be precisely, for each \(i=1,\ldots ,n\), there exists a unknown positive number \(\bar{\lambda }\), such that

$$\begin{aligned} \sup _{t\ge 0}\Big \{|\lambda _i(t)|\Big \}\le \bar{\lambda }. \end{aligned}$$
(8)

Assumption 4

 The external disturbance \(\mathrm{d}(t)\) satisfies the following properties:

$$\begin{aligned} d(t)\in {L_{\infty }},~\dot{d}(t)\in {L_{\infty }},~\dot{d}(t)\in {L_{2}}. \end{aligned}$$
(9)

Remark 1

 Few remarks are made here.

(1) As stated in [12], the system (1) represents a larger class of nonlinear systems in output feedback form. From Assumption 1, the cascaded \(\zeta \)-subsystem is iISS, which is a less restrictive condition than ISS. More generally, it could allow the presence of uncertainty in the supply rates of \((\alpha ,\gamma )\) such as in [8]. As the condition C2) in [10, 11], the uncertain nonlinearities \(g_i(\eta ,y)(i=1,\ldots ,n)\) in Assumption 2 are assumed to be vanishing or unbiased. In addition, it is also not required to satisfy any kind of polynomial bounds.

(2) Assumption 4 shows that the external disturbance \(\mathrm{d}(t)\) is not required to be \(L_{2}\). This is in sharp contrast to the existing closely related results, such as [14]. Here, it does only require that \(\dot{d}(t)\in {L_2}\). This is a more relaxed version of noise signals. As a simple example, \(\mathrm{d}(t)=constant\) is not square integrable, but it is clear that \(\dot{d}(t)\in {L_2}\). It is shown that some kind of extended state observer based on a Riccati differential equation will do the job in the case of such general class of noise signals satisfying Assumption 4.

Remark 2

 Considering the inverse system state \(\zeta \) is not available for feedback, as in [10, 14], some local small-gain type conditions in (4) (6) and (7) play key roles in dealing with the unmeasured state \(\zeta \). In fact, we have the following lemma from [10].

Lemma 1

 For \(i=1,\ldots ,n\), if the local conditions (6) and (7) are available, then the following hold true

$$\begin{aligned} \int _0^t\phi _{i1}^2(|\zeta (s)|)\mathrm{d}s{\le }\bar{\psi }_{i0}(|\zeta (0)|)+\int _0^t\psi _{i1}(|y(s)|)\mathrm{d}s,\nonumber \\ \end{aligned}$$
(10)

where \(\bar{\psi }_{i0}\) is a positive definite continuous function, and \(\psi _{i1}\in K_\infty \) is quadratic near the origin.

2.2 A dynamic output feedback control scheme based on ESO

In this section, we present a step-by-step procedure to design a dynamic output feedback law to solve the global regulation problem for system (1).

To be first, we choose the new state variables \(\xi _i\)’s in the form of

$$\begin{aligned} \xi _i=\frac{x_i}{b_i{\cdots }b_n},~i=1,\ldots ,n. \end{aligned}$$
(11)

With this change of coordinates, system (1) is turned into

$$\begin{aligned}&\dot{\xi }_i=\xi _{i+1}+\lambda _i(t)\xi _i+\frac{1}{b_i{\cdots }b_n}g_i(\zeta ,y),~i=1,\ldots ,n-1,\nonumber \\&\dot{\xi }_{n}=u+\lambda _n(t)\xi _n+\frac{1}{b_n}\mathrm{d}(t)+\frac{1}{b_n}g_n(\zeta ,y). \end{aligned}$$
(12)

In the following context, the external disturbance \(\frac{1}{b_n}\mathrm{d}(t)\) is viewed as a generalized state. For notational consistence, we choose the following notation

$$\begin{aligned} \xi _{n+1}=\frac{1}{b_n}\mathrm{d}(t), \end{aligned}$$
(13)

and its derivative is defined by h(t), i.e.,

$$\begin{aligned} {\dot{\xi }}_{n+1}=\frac{1}{b_n}{\dot{\mathrm{d}}}(t)={h(t)}. \end{aligned}$$
(14)

Then, one can get the following \((n+1)\)-order augmented system

$$\begin{aligned}&\dot{\xi }_i=\xi _{i+1}+\lambda _i(t)\xi _i+\frac{1}{b_i{\cdots }b_n}g_i(\zeta ,y),~i=1,\ldots ,n-1,\nonumber \\&\dot{\xi }_{n}=u+\lambda _n(t)\xi _n+\xi _{n+1}+\frac{1}{b_n}g_n(\zeta ,y)\nonumber \\&\dot{\xi }_{n+1}=h(t). \end{aligned}$$
(15)

Remark 3

It is noted that here, if the unknown disturbance \(\mathrm{d}(t)\) is assumed to be constant, then its derivative h(t) becomes zero. This case can usually be found in the set-point regulation or in the presence of sensor disturbances. For example, in some cases, the value of the control may not be completely known due to a desired (unknown) equilibrium point, see [29]. It can be seen that according to Assumption 4, actually a broader class of external disturbance can be allowed in (1), such as \(\mathrm{d}(t)=\arctan (t)\) or constant, which shows the disturbance does not require to be vanishing. In this sense, the results reported in [10] with vanishing nonlinearities can be extended to the case of nonvanishing uncertainties.

Let \(\xi =[\xi _1,\xi _2,\cdots ,\xi _n,\xi _{n+1}]^T\), the system dynamics in (15) can be rewritten into the following compact form

$$\begin{aligned} \dot{\xi }=\Big (A+\Lambda (t)\Big )\xi +C_nu+C_{n+1}h(t)+B{\cdot }G(\zeta ,y)\nonumber \\ \end{aligned}$$
(16)

with \(A{=}\left[ \begin{array}{cc} 0 &{}\quad I_{n}\\ 0 &{}\quad 0 \end{array} \right] \), \(\Lambda (t){=}\mathrm{diag}\{\lambda _1(t),\cdots ,\lambda _n(t),0\}\), \(B=\mathrm{diag}\{\frac{1}{b_1{\cdots }b_n},\frac{1}{b_2{\cdots }b_n},\ldots , \frac{1}{b_{n}},0\}\), and

$$\begin{aligned}&G(\zeta ,y)=\left[ \begin{array}{c} g_1(\zeta ,y)\\ \vdots \\ g_n(\zeta ,y)\\ 0 \end{array} \right] ,~C=\left[ \begin{array}{c} 1\\ 0\\ \vdots \\ 0 \end{array} \right] ,\nonumber \\&C_2=\left[ \begin{array}{c} 0\\ 1\\ \vdots \\ 0 \end{array} \right] ,~\cdots \,,~C_{n}=\left[ \begin{array}{c} 0\\ \vdots \\ 1\\ 0 \end{array} \right] ,~C_{n+1}=\left[ \begin{array}{c} 0\\ \vdots \\ 0\\ 1 \end{array} \right] . \end{aligned}$$

Then, for the system (16), a modified version of dynamic observer in [11] is designed as follows

$$\begin{aligned} \dot{\widehat{\xi }}=\Big (A+\Lambda (t)\Big )\widehat{\xi }+C_{n}u-PCC^{T\,\,}\widehat{\xi }, \end{aligned}$$
(17)

where the observer gain P(t) is updated by a time-varying Riccati differential equation

$$\begin{aligned} \left\{ \begin{array}{lcl} \dot{P}{=}P\Big (A+\Lambda (t)\Big )^T+\Big (A+\Lambda (t)\Big )P-\mathrm{PCC}^TP+I\\ P(0)=P_0>0. \end{array} \right. \nonumber \\ \end{aligned}$$
(18)

Furthermore, we note that the Riccati differential equation defined in (18) is solvable. In fact, we have the following lemma which ensures that the observer (17) and (18) makes sense, and its proof can be found in [30, 31].

Lemma 2

For the matrix differential equation (18), if the functions \(\lambda _i(t)(i=1,\ldots ,n)\) are known, continuous and uniformly bounded, the unique solution \(P(t)={\big (P(t)\big )}^T\) exists and there are two strictly positive real numbers \(p_{\min }\) and \(p_{\max }\) such that \(p_{\min }I\le P(t)\le p_{\max }I,~t\ge 0\).

Define the observation error variables

$$\begin{aligned} \varepsilon _i=\xi _i-\widehat{\xi }_i,~i=1,\ldots ,n+1. \end{aligned}$$
(19)

From (12) and (17), it can be concluded that the \(\varepsilon _i\)’s satisfy the following differential equation:

$$\begin{aligned} \dot{\varepsilon }= & {} \Big (A+\Lambda (t)-PCC^T\Big )\varepsilon \nonumber \\&+\,\frac{PC}{b_1{\cdots }b_n}x_1+C_{n+1}h(t)+B{\cdot }G(\zeta ,y). \end{aligned}$$
(20)

In order to obtain the computable gain functions of \(\frac{PC}{b_1{\cdots }b_n}x_1\) and \(B{\cdot }G(\zeta ,y)\), we choose a scaled error variable \({e}=({e}_1,\ldots ,{e}_{n+1})^T\) by setting

$$\begin{aligned} e= & {} \frac{1}{\delta ^*}\varepsilon ,\nonumber \\ ~\delta ^*= & {} \max \bigg \{\frac{1}{|b_1{\cdots }b_n|},\frac{\delta _{i1}}{|b_i{\cdots }b_n|}, \frac{\delta _{i2}}{|b_i{\cdots }b_n|},\delta _{11}^2,\delta _{12}^2,1\bigg |1{\le } i{\le } n\bigg \}.\nonumber \\ \end{aligned}$$
(21)

Accordingly, (20) is turned into

$$\begin{aligned} \dot{{e}}= & {} \Big (A+\Lambda (t)-PCC^T\Big ){e}+\frac{PC}{\delta ^*{b_1{\cdots }b_n}}x_1\nonumber \\&+\frac{1}{\delta ^*}C_{n+1}h(t)+\,\frac{1}{\delta ^*}B{\cdot }G(\zeta ,y). \end{aligned}$$
(22)

Take the error e as the (unmeasured) state, and the error system (22) is iISS with inputs \((\zeta ,y)\) and h(t). In fact, we have the following proposition, and its proof is given in “Appendix.”

Proposition 1

For the e-subsystem (22), we choose the Lyapunov function

$$\begin{aligned} V_{{e}}={e}^TP^{-1}(t){e}, \end{aligned}$$
(23)

then, its derivative is such that

$$\begin{aligned} \dot{V}_{{e}}\le & {} -\frac{1}{2}{e}^TP^{-2}(t){e} +8\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |)\nonumber \\&+\,y^2+8\sum \limits _{i=1}^{n}\phi _{i2}^2(|y|)+4h^2(t). \end{aligned}$$
(24)

Now, we are ready to present the anti-disturbance regulation controller using the backstepping method in a recursive manner. For notational convenience, we denote \(b={b_1{\cdots }b_n}\) in what follows. The augmented system convenient for feedback design is in the form of

(25)

Following the conventional backstepping procedure, for the \(\widehat{\xi }_{i}\)-subsystem, we take the variable of \(\widehat{\xi }_{i+1}\) as the virtual control, \(\vartheta _i\) as the desired control law, and \({z}_i=\widehat{\xi }_{i+1}-\vartheta _i(i=1,\ldots ,n-1)\) as the error.

Step 1: Choose the first Lyapunov function candidate

$$\begin{aligned} V_1=V_{{e}}+\frac{1}{2}y^2. \end{aligned}$$
(26)

In view of (24), its time derivative satisfies

$$\begin{aligned} \dot{V}_1\le & {} -\frac{1}{2}{e}^TP^{-2}{e} +y^2+8\sum \limits _{i=1}^{n}\phi _{i2}^2(|y|)\nonumber \\&+\,y\Big (b\vartheta _1+b{z}_1+b\delta ^*{e}_2+\lambda _1(t)x_1+g_1(\zeta ,y)\Big )\nonumber \\&+\,8\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |)+4h^2(t). \end{aligned}$$
(27)

Using the completion of squares \(2 a b {\le }\frac{1}{\Delta }a^2+{\Delta }b^2,~a,b\in {R},~\Delta >0\), it holds

$$\begin{aligned}&by{z}_1 \le \frac{1}{2}y^2+\frac{1}{2}b^2{z}_1^2, \end{aligned}$$
(28)
$$\begin{aligned}&b\delta ^*{e}_2y\le \epsilon {e}^TP^{-2}{e}+{\bar{\epsilon }}\,y^2,~~\epsilon>0,\nonumber \\&\bar{\epsilon }=\frac{1}{4\epsilon } b^2{\delta ^*}^2p_{\max }^2>0, \end{aligned}$$
(29)
$$\begin{aligned}&yg_1(\zeta ,y) \le \frac{1}{2}y^2+\delta _{11}^2\phi _{11}^2(|\zeta |)+\delta _{12}^2\phi _{12}^2(|y|). \end{aligned}$$
(30)

Introduce the notation

$$\begin{aligned} \phi _1(\zeta )=8\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |) +\delta _{11}^2\phi _{11}^2(|\zeta |), \end{aligned}$$
(31)

then, substitute (28), (29), (30) and (31) into (27), one can get

$$\begin{aligned} \dot{V}_1\le & {} -\left( \frac{1}{2}-\epsilon \right) {e}^TP^{-2}{e}+b y\vartheta _1+8\sum \limits _{i=1}^{n}\phi _{i2}^2(|y|)\nonumber \\&+\,\delta _{12}^2\phi _{12}^2(|y|) +{\bar{\epsilon }}\,y^2+\lambda _1(t)y^2+2y^2\nonumber \\&+\,\frac{1}{2}b^2{z}_1^2+\phi _1(\zeta )+4h^2(t). \end{aligned}$$
(32)

As the suggestion of the work [10], we design the virtual control law

$$\begin{aligned} \vartheta _1=N(s)\beta (y)y,~\dot{s}=\kappa \beta (y)y^2 \end{aligned}$$
(33)

where the Nussbaum function \(N(\cdot )\) is taken as \(N(s)=s^2\cos (0.5\pi s)\), \(\kappa >0\) is a design constant gain, and \(\beta (\cdot )\ge 1\) is a positive smooth function satisfying

$$\begin{aligned}&\beta (y)y^2\nonumber \\&\quad \ge \max \Big \{y^2,\phi _{i2}^2(|y|),\psi _{i1}(|y|),\gamma (|y|)\big | 1\le i\le n\Big \}.\nonumber \\ \end{aligned}$$
(34)

Let \(r=8n+\delta _{12}^2+\bar{\epsilon }+\bar{\lambda }+3\), and the following holds true due to (33) and (34):

$$\begin{aligned}&8\sum \limits _{i=1}^{n}\phi _{i2}^2(|y|)+\delta _{12}^2\phi _{12}^2(|y|) +{\bar{\epsilon }}\,y^2+\lambda _1(t)y^2\nonumber \\&\quad +2y^2\le {r}\beta (y)y^2. \end{aligned}$$
(35)

A direct substitution (35) into (32), one can get

$$\begin{aligned}&\dot{V}_1 \le -(\frac{1}{2}-\epsilon ){e}^TP^{-2}{e}+b N({s})\beta (y)y^2 +{r}\beta (y)y^2\nonumber \\&\quad \qquad +\,\frac{1}{2}b^2{z}_1^2+\phi _1(\zeta )+4h^2(t). \end{aligned}$$
(36)

Remark 4

 Thanks to the local conditions in (4) (6) and (7), the smooth positive function \(\beta (\cdot )\) can be found to meet (34). For example, with the help of \(\gamma (s)=O(s^2)\), there exists a nonnegative function \(\hat{\gamma }(\cdot )\), such that \(\gamma (s)\le {\widehat{\gamma }}(s)s^2\). Consequently, it only suffices to satisfy \(\beta (s)\ge \widehat{\gamma }(s)\) in (34). Additionally, a requisite assumption on the bounding functions of \(\phi _{i2}(|y|)\) is that \(\phi _{i2}\)’s are vanishing, i.e., \(\phi _{i2}(0)=0(i=1,\ldots ,n)\).

Step 2: Considering the appearance of some unknown constant gains in the following control design, we define a new unknown constant \(\Theta \) in the form of

$$\begin{aligned} \Theta =\max \big \{\frac{|b|}{2},\frac{b^2}{4},\delta ^{*}+{\bar{\epsilon }}\big \}, \end{aligned}$$
(37)

and adopt \(\widehat{\Theta }(\cdot )\) to supply a online estimate of \(\Theta \) with the estimate error \(\widetilde{\Theta }(\cdot )=\Theta -\widehat{\Theta }(\cdot )\).

Then, we choose the Lyapunov function

$$\begin{aligned} V_2=V_1+\frac{1}{2}{z}_1^2+\frac{1}{2\Upsilon }\widetilde{\Theta }^2,~~\Upsilon >0. \end{aligned}$$
(38)

Together with (25) (36) and \(\dot{{z}}_1=\dot{\widehat{\xi }}_2-\dot{\vartheta }_1\), it can be checked that

$$\begin{aligned} \dot{V}_2\le & {} -\left( \frac{1}{2}-\epsilon \right) {e}^TP^{-2}{e}\nonumber \\&+\,{z}_1\Big (\vartheta _2+\lambda _2(t)\widehat{\xi }_2 -C_2^TPC\widehat{\xi }_1 -\frac{\partial {\vartheta _1}}{\partial {y}}\lambda _1(t)x_1 -\frac{\partial {\vartheta _1}}{\partial {{s}}}\dot{{s}}\Big )\nonumber \\&+\,bN({s})\beta (y)y^2+{r}\beta (y)y^2\nonumber \\&+\,{z}_1{z}_2-\frac{1}{\Upsilon }\widetilde{\Theta }\dot{\widehat{\Theta }} +\phi _1(\zeta )+4h^2(t)\nonumber \\&-\,{z}_1\frac{\partial {\vartheta _1}}{\partial {y}}\Big (b({z}_1+\vartheta _1) +b\delta ^{*}{e}_2+g_1(\zeta ,y)\Big ). \end{aligned}$$
(39)

By completing the squares, the following calculations hold

$$\begin{aligned}&-\,b\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1^2 \le {z}_1^2+\frac{b^2}{4}\Big (\frac{\partial {\vartheta _1}}{\partial {y}}\Big )^2{z}_1^2, ~-b\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1\vartheta _1 \le \beta (y)y^2\nonumber \\&\quad +\,\frac{b^2}{4}{z}_1^2\beta (y)\Big (\frac{\partial {\vartheta _1}}{\partial {y}}N({s})\Big )^2, \end{aligned}$$
(40)
$$\begin{aligned}&-\,\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1b{\delta ^{*}}{e}_2 \le \epsilon {e}^TP^{-2}{e}+\frac{1}{4\epsilon } b^2{\delta ^*}^2p_{\max }^2(\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1)^2, \end{aligned}$$
(41)
$$\begin{aligned}&-\,\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1g_1(\zeta ,y) \le {\delta ^*}\Big (\frac{\partial {\vartheta _1}}{\partial {y}}\Big )^2{z}_1^2+\frac{g_1^2(\zeta ,y)}{4\delta ^{*}}, ~\frac{g_1^2(\zeta ,y)}{4\delta ^{*}}\nonumber \\&\quad \le \frac{1}{2}\phi _{11}^2(|\zeta |)+\frac{1}{2}\phi _{12}^2(|y|). \end{aligned}$$
(42)

Take the notations \(\varphi _1(t,{s})=2\big (\frac{\partial {\vartheta _{1}}}{\partial {y}}\big )^2 +\beta (y)\Big (\frac{\partial {\vartheta _{1}}}{\partial {y}}N({s})\Big )^2\), and in view of \(\frac{1}{2}\phi _{12}^2(|y|)\le \frac{1}{2}\beta (y)y^2\), we have

$$\begin{aligned}&-\,b\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1({z}_1+\vartheta _1) -\frac{\partial {\vartheta _1}}{\partial {y}}{z}_1\Big (b\delta ^{*}{e}_2+g_1(\zeta ,y)\Big )\nonumber \\&\quad \le \epsilon {e}^TP^{-2}{e} +\Theta \varphi _1(y,{s}){z}_1^2\nonumber \\&\quad +\,\frac{1}{2}\phi _{11}^2(|\zeta |)+\frac{3}{2}\beta (y)y^2. \end{aligned}$$
(43)

Combining (39) and (43), we have

$$\begin{aligned} \dot{V}_2\le & {} bN({s})\beta (y)y^2 \nonumber \\&+\,{z}_1\Big (\vartheta _2+\rho _1{z}_1+\lambda _2(t)\widehat{\xi }_2 -C_2^TPC\widehat{\xi }_1\nonumber \\&-\,\frac{\partial {\vartheta _1}}{\partial {{s}}}\dot{{s}} -\frac{\partial {\vartheta _1}}{\partial {y}}\lambda _1(t)x_1 +\widehat{\Theta }\varphi _1(\cdot ){z}_1\Big )\nonumber \\&-\,\left( \frac{1}{2}-2\epsilon \right) {e}^TP^{-2}{e}-\left( \rho _1-1\right) {z}_1^2\nonumber \\&+\left( {r}+\frac{3}{2}\right) \beta (y)y^2+\,\frac{1}{\Upsilon }\widetilde{\Theta }\Big (\Upsilon \varphi _1(y,{s}){z}_1^2-\dot{\widehat{\Theta }}\Big )\nonumber \\&+\,{z}_1{z}_2+\,\phi _1(\zeta )+\frac{1}{2}\phi _{11}^2(|\zeta |)+4h^2(t). \end{aligned}$$
(44)

Denote \(\tau _1=\Upsilon \varphi _1(y,{s}){z}_1^2, \phi _2(\zeta )=\phi _1(\zeta )+\frac{1}{2}\phi _{11}^2(|\zeta |), \Omega _{N,2}(t,{e},{z}_{1})=(\frac{1}{2}-2\epsilon ){e}^TP^{-2}{e}+(\rho _1-1){z}_1^2, \Omega _{P2}(t,y,\widehat{\xi }_{[2]},{s},\widehat{\Theta })=\lambda _2(t)\widehat{\xi }_2 -C_2^TPC\widehat{\xi }_1-\frac{\partial {\vartheta _1}}{\partial {{s}}}\dot{{s}}-\frac{\partial {\vartheta _1}}{\partial {y}}\lambda _1(t)x_1 +\widehat{\Theta }\varphi _1(y,{s}){z}_1\), and we choose the virtual control

$$\begin{aligned} \vartheta _2=-\rho _1{z}_1-\Omega _{P2}(t,y,{\widehat{\xi }}_{[2]},{s},\widehat{\Theta }),~\rho _1>0, \end{aligned}$$
(45)

then, a direct substitution into (44) yields

$$\begin{aligned} \dot{V}_2\le & {} -\Omega _{N,2}(t,{e},{z}_{1}) +bN({s})\beta (y)y^2\nonumber \\&+\,\big ({r} +\frac{3}{2}\big )\beta (y)y^2+{z}_1{z}_2 +\phi _2(\zeta )\nonumber \\&+\,\frac{1}{\Upsilon }\widetilde{\Theta }\big (\tau _1-\dot{\widehat{\Theta }}\big )+4h^2(t). \end{aligned}$$
(46)

Step i \((3\le i\le n)\): Assume that, in Step \(i-1\), we have designed the virtual control \(\vartheta _j(\cdot )\) and tuning function \(\tau _{j-1}\), such that, with \({z}_{j}=\widehat{\xi }_{j+1}-\vartheta _{j}(3 \le j \le i-1)\), the time derivative of the function

$$\begin{aligned} V_{i-1}=V_{e}+\frac{1}{2}y^2+\sum \limits _{j=1}^{i-2}\frac{1}{2}{z}_{j}^2 +\frac{1}{2\Upsilon }\widetilde{\Theta }^2 \end{aligned}$$
(47)

satisfies

$$\begin{aligned} \dot{V}_{i-1}\le & {} -\Omega _{N,i-1}(t,{e},z_{[i-2]}) +bN({s})\beta (y)y^2\nonumber \\&+{r}_{i-1}\beta (y)y^2\nonumber \\&+\,\frac{1}{\Upsilon }\Big (\widetilde{\Theta }+\Upsilon \sum _{j=2}^{i-2} \frac{\partial {\vartheta _j}}{\partial {\widehat{\Theta }}}{z}_j\Big )\big (\tau _{i-2}-\dot{\widehat{\Theta }}\big )\nonumber \\&+\,{z}_{i-2}{z}_{i-1}+\phi _{i-1}(\zeta )+4h^2(t) \end{aligned}$$
(48)

with \({r}_{i}={r}+\frac{3}{2}(i-1)(i=1,\ldots ,n)\) and

$$\begin{aligned} \Omega _{Ni}(t,{e},z_{[i-1]})= & {} \left( \frac{1}{2}-i\epsilon \right) {e}^TP^{-2}{e}\nonumber \\&+\,\big (\rho _1-(i-1)\big ){z}_1^2\nonumber \\&+\,\sum _{j=2}^{i-1}\rho _j{z}_j^2, \rho _j>0, i=3,\ldots ,n.\nonumber \\ \end{aligned}$$
(49)

In the sequel, one shows that a similar property of inequality (48) holds in Step i. To this end, we consider the function

$$\begin{aligned} V_{i}=V_{i-1}+\frac{1}{2}{z}_{i-1}^2. \end{aligned}$$
(50)

Note that the variable \(V_{i}\) satisfies

$$\begin{aligned} \dot{V}_i\le & {} {z}_{i-1}\left( {z}_i+\vartheta _i+\lambda _i(t)\widehat{\xi }_i-C_i^TPCC^T\widehat{\xi }\right. \nonumber \\&\left. -\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\big (g\widehat{\xi }_2 +g\delta ^*{e}_2+\lambda _1(t)x_1+g_1(\zeta ,y)\right) \nonumber \\&-\frac{\partial {\vartheta _{i-1}}}{\partial {t}} -\frac{\partial {\vartheta _{i-1}}}{\partial {{s}}}\dot{{s}} -\frac{\partial {\vartheta _{i-1}}}{\partial {\widehat{\Theta }}}\dot{\widehat{\Theta }} -\sum _{j=1}^{i-1}\frac{\partial {\vartheta _{i-1}}}{\partial {\widehat{\xi }_j}}\dot{\widehat{\xi }}_j\Big )\nonumber \\&+\,bN({s})\beta (y)y^2+{r}_{i-1}\beta (y)y^2+\phi _{i-1}(\zeta )\nonumber \\&-\,\Omega _{N,i-1}(t,{e},z_{[i-2]})+{z}_{i-2}{z}_{i-1}\nonumber \\&+\,\frac{1}{\Upsilon }\Big (\widetilde{\Theta }+\Upsilon \sum _{j=2}^{i-2} \frac{\partial {\vartheta _j}}{\partial {\widehat{\Theta }}}{z}_j\Big )\big (\tau _{i-2}-\dot{\widehat{\Theta }}\big )+4h^2(t).\nonumber \\ \end{aligned}$$
(51)

As in Step 2, using the completion of the squares, we have

$$\begin{aligned}&-\,b\frac{\partial {\vartheta _{i-1}}}{\partial {y}}{z}_{i-1}({z}_1+\vartheta _1)\nonumber \\&\qquad \le {z}_1^2+\beta (y)y^2 +\Theta \bigg (\Big (\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\Big )^2\nonumber \\&\qquad +\,\beta (y)\Big (\frac{\partial {\vartheta _{i-1}}}{\partial {y}}N({s})\Big )^2\bigg ){z}_{i-1}^2, \end{aligned}$$
(52)
$$\begin{aligned}&-\frac{\partial {\vartheta _{i-1}}}{\partial {y}}{z}_{i-1}\Big (b\delta ^{*}{e}_2+g_1(\zeta ,y)\Big )\nonumber \\&\qquad \le \epsilon {e}^TP^{-2}{e}\nonumber \\&\quad \quad +\,\frac{1}{4\epsilon } b^2{\delta ^*}^2p_{\max }^2\Big (\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\Big )^2{z}_{i-1}^2 +{\delta ^*}\Big (\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\Big )^2{z}_{i-1}^2\nonumber \\&\qquad +\,\frac{g_1^2(\zeta ,y)}{4\delta ^{*}}, \end{aligned}$$
(53)

this together with (42) and \(\frac{1}{2}\phi _{12}^2(|y|)\le \frac{1}{2}\beta (y)y^2\), then, the following holds

$$\begin{aligned}&-\frac{\partial {\vartheta _{i-1}}}{\partial {y}}{z}_{i-1}\Big (b\delta ^{*}{e}_2+g_1(\zeta ,y)\Big ) \le \epsilon {e}^TP^{-2}{e}\nonumber \\&\qquad +\,\Theta \Big (\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\Big )^2{z}_{i-1}^2 +\frac{1}{2}\phi _{11}^2(|\zeta |)+\frac{1}{2}\beta (y)y^2.\nonumber \\ \end{aligned}$$
(54)

Let

$$\begin{aligned} \varphi _i\left( t,y,{\widehat{\xi }}_{[i]},{s},\widehat{\Theta }\right)= & {} 2\left( \frac{\partial {\vartheta _{i}}}{\partial {y}}\right) ^2 +\beta (y)\Big (\frac{\partial {\vartheta _{i}}}{\partial {y}}N({s})\Big )^2,\nonumber \\ ~i= & {} 2,\ldots ,n-1, \end{aligned}$$
(55)

and in accordance with (52–54), we further obtain

$$\begin{aligned}&-\,b\frac{\partial {\vartheta _{i-1}}}{\partial {y}}{z}_{i-1}({z}_1+\vartheta _1) -\frac{\partial {\vartheta _{i-1}}}{\partial {y}}{z}_{i-1}\Big (b\delta ^{*}{e}_2+g_1(\zeta ,y)\Big )\nonumber \\&\qquad \le \epsilon {e}^TP^{-2}{e}+{z}_1^2 +\frac{3}{2}\beta (y)y^2\nonumber \\&\quad \qquad +\,\Theta \varphi _{i-1}\left( t,y,{\widehat{\xi }}_{[i-1]},{s},\widehat{\Theta }\right) {z}_{i-1}^2 +\frac{1}{2}\phi _{11}^2(|\zeta |). \end{aligned}$$
(56)

Let

$$\begin{aligned}&\tau _{i-1}=\Upsilon \varphi _{i-1}(t,y,{\widehat{\xi }}_{[i-1]},{s},\widehat{\Theta }){z}_{i-1}^2, \end{aligned}$$
(57)
$$\begin{aligned}&\phi _{i}(\zeta )=\phi _{i-1}(\zeta ) +\frac{1}{2}\phi _{11}^2(|\zeta |), \end{aligned}$$
(58)
$$\begin{aligned}&\Omega _{Pi}\left( t,y,\widehat{\xi }_{[i]},{s},\widehat{\Theta }\right) \nonumber \\&\quad ={z}_{i-2}-C_i^TPCC^T\widehat{\xi } +\lambda _i(t)\widehat{\xi }_i-\frac{\partial {\vartheta _{i-1}}}{\partial {{s}}}\dot{{s}} \nonumber \\&\quad -\sum _{j=1}^{i-1}\frac{\partial {\vartheta _{i-1}}}{\partial {\widehat{\xi }_j}}\dot{\widehat{\xi }}_j-\frac{\partial {\vartheta _{i-1}}}{\partial {y}}\lambda _1(t)x_1 -\,\frac{\partial {\vartheta _{i-1}}}{\partial {t}}\nonumber \\&\quad +\,2\widehat{\Theta }\varphi _{i-1}(t,y,{\widehat{\xi }}_{[i-1]},{s},\widehat{\Theta }){z}_{i-1}\nonumber \\&\quad -\,\frac{\partial {\vartheta }_{i-1}}{\partial {\widehat{\Theta }}}\tau _{i-2}-\,2\Upsilon \sum _{j=2}^{i-1}\frac{\partial {\vartheta }_j}{\partial {\widehat{\Theta }}}{z}_j \varphi _{i-1}(y,{s}){z}_{i-1},\nonumber \\ \end{aligned}$$
(59)

substituting (57–59) into (51), and we obtain

$$\begin{aligned} \dot{V}_i\le & {} -\Omega _{N,i}({e},z_{[i-1]})\nonumber \\&+\,bN({s})\beta (y)y^2+{r}_{i}\beta (y)y^2\nonumber \\&+\,{z}_{i-1}\Big (\vartheta _i+\rho _{i-1}{z}_{i-1}+\Omega _{Pi}(t,y,\widehat{\xi }_{[i]},{s},\widehat{\Theta })\Big )\nonumber \\&+\,{z}_{i-1}{z}_i+\phi _{i}(\zeta ) +\frac{1}{\Upsilon }\Big (\widetilde{\Theta }+\Upsilon \sum _{j=2}^{i-1} \frac{\partial {\vartheta _j}}{\partial {\widehat{\Theta }}}{z}_j\Big )\nonumber \\&\times \big (\tau _{i-1}-\dot{\widehat{\Theta }}\big )+\,4h^2(t). \end{aligned}$$
(60)

Take the virtual control input

$$\begin{aligned} \vartheta _i=-\rho _{i-1}{z}_{i-1}-\Omega _{Pi}(t,y,\widehat{\xi }_{[i]},{s},\widehat{\Theta }), \end{aligned}$$
(61)

which makes (60) further satisfy

$$\begin{aligned}&\dot{V}_i\le -\Omega _{N,i}({e},z_{[i-1]}) +bN({s})\beta (y)y^2+{r}_i\beta (y)y^2\nonumber \\&\quad +\,\frac{1}{\Upsilon }\Big (\widetilde{\Theta }+\Upsilon \sum _{j=2}^{i-1} \frac{\partial {\vartheta _j}}{\partial {\widehat{\Theta }}}{z}_j\Big )\big (\tau _{i-1}-\dot{\widehat{\Theta }}\big )\nonumber \\&\quad +\,{z}_{i-1}{z}_i +\phi _{i}(\zeta )+4h^2(t). \end{aligned}$$
(62)

Step n: Because of the estimate \(\widehat{\xi }_{n+1}\) for the external disturbance \(\mathrm{d}(t)\), this step is crucial and slightly different from the Step n in traditional Backstepping design procedure. For notational consistence, \({z}_n\), \(\vartheta _n\) and the control u can be written in the form of \({z}_n=0,~u+\widehat{\xi }_{n+1}=\vartheta _n\), and \(z=(z_1,\ldots ,z_n)\). To obtain the real control input u, we consider the function

$$\begin{aligned} V_{n}=V_{n-1}+\frac{1}{2}{z}_{n-1}^2. \end{aligned}$$
(63)

After some similar calculations such as (52–54) and (42) with \(i=n\) in Step i, the time derivative of (63) has the following form

$$\begin{aligned}&\dot{V}_n \le -\Omega _{Nn}({e},z)\nonumber \\&\quad +\,{z}_{n-1}\Big (u+\rho _{n-1}{z}_{n-1}+\widehat{\xi }_{n+1}+\Omega _{Pn}(t,y,\widehat{\xi },{s},\widehat{\Theta })\Big ) \nonumber \\&\quad +\,bN({s})\beta (y)y^2\nonumber \\&\quad +\,{r}_n\beta (y)y^2 +\frac{1}{\Upsilon }\Big (\widetilde{\Theta }+\Upsilon \sum _{j=2}^{n-1} \frac{\partial {\vartheta _j}}{\partial {\widehat{\Theta }}}{z}_j\Big )\big (\tau _{n-1}-\dot{\widehat{\Theta }}\big ) \nonumber \\&\quad +\,\phi _{n}(\zeta )+\,4h^2(t). \end{aligned}$$
(64)

Take the real control input

$$\begin{aligned} u= & {} -\widehat{\xi }_{n+1}+\vartheta _n\nonumber \\ {}= & {} -\widehat{\xi }_{n+1}-\rho _{n-1}{z}_{n-1}-\Omega _{Pn}(t,y,\widehat{\xi },{s},\widehat{\Theta }), \end{aligned}$$
(65)

and the adaptive law

$$\begin{aligned} \dot{\widehat{\Theta }}=\tau _{n-1}=\sum _{i=1}^{n-1}\varphi _{i}(t,y,{\widehat{\xi }}_{[i]},{s},\widehat{\Theta }){z}_{i}^2, \end{aligned}$$
(66)

then, a direct substitution yields that

$$\begin{aligned}&\dot{V}_n\le -\Omega _{Nn}({e},z) +bN({s})\beta (y)y^2+{r}_{n}\beta (y)y^2\nonumber \\&\qquad +\phi _{n}(\zeta )+\,4h^2(t). \end{aligned}$$
(67)

Choose the positive constant \(\chi =\max \Big \{\frac{n-1}{2}+\delta _{11}^2,1\Big \}\), and one can get

$$\begin{aligned} \phi _{n}(\zeta )= & {} \frac{n-1}{2}\phi _{11}^2(|\zeta |)+\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |)\nonumber \\&+\,\delta _{11}^2\phi _{11}^2(|\zeta |)\le {\chi }\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |). \end{aligned}$$
(68)

As a result, it holds

$$\begin{aligned} \dot{V}_n\le & {} -\Omega _{Nn}({e},z) +bN({s})\beta (y)y^2+{r}_{n}\beta (y)y^2\nonumber \\&+\,{\chi }\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |)+4h^2(t). \end{aligned}$$
(69)

At this stage, the design procedure of the output feedback adaptive control has been completed.

2.3 Main results

Now we present the main theorem of this paper.

Theorem 1

Suppose that Assumptions 1–4 hold for the controlled system (1). Then, using the observer (17) and (18), we can find a smooth adaptive control scheme, such that the global robust regulation control problem is solvable for the cascade nonlinear system (1) subject to the external disturbance. Moreover, we have the following statements:

(a):

 the solutions of the closed-loop system are globally uniformly bounded;

(b):

 the asymptotic convergence of system state is achieved, that is,

$$\begin{aligned} \lim _{t\rightarrow \infty }\big (|\zeta (t)|+|x(t)|\big )=0; \end{aligned}$$
(70)
(c):

the control input is bounded, and moreover,

$$\begin{aligned} \lim _{t\rightarrow \infty }u(t)=0~~~\text{ if } ~~\lim _{t\rightarrow \infty }\mathrm{d}(t)=0. \end{aligned}$$
(71)

Proof

  It is easy to see that the right-hand sides of closed-loop system are locally Lipschitz in a domain of initial conditions and hence the system has a unique solution \(\big (y(t),{z}(t),\widehat{\xi }(t),{s}(t),\widehat{\Theta }(t)\big )\) on a small interval \([0,t_f)\). Assume, without loss of generality, \([0,t_f)\) be its maximal interval of the existence and uniqueness. We will show that \(t_f=\infty \). To begin with, for the term of \(\Omega _{Nn}({e},{z})\) defined in (49) with \(i=n\), choose the suitable constants satisfying

$$\begin{aligned} \epsilon <\frac{1}{2n},~\rho _1>n-1,~\rho _i>0,~i=2,\ldots ,n-1,\nonumber \\ \end{aligned}$$
(72)

which guarantees

$$\begin{aligned} \Omega _{Nn}({e},{z})= & {} \left( \frac{1}{2}-n\epsilon \right) {e}^TP^{-2}{e}+\Big (\rho _1-(n-1)\Big ){z}_1^2\nonumber \\&+\sum _{j=2}^{n-1}\rho _j{z}_j^2>0. \end{aligned}$$
(73)

Furthermore, it holds

$$\begin{aligned} \dot{V}_n\le & {} b N({s})\beta (y)y^2+{r}_{n}\beta (y)y^2+{\chi }\sum \limits _{i=1}^{n}\phi _{i1}^2(|\zeta |)\nonumber \\&+\,4h^2(t). \end{aligned}$$
(74)

Considering \(\dot{{s}}=\kappa \beta (y)y^2\) in (33), (74) turns into

$$\begin{aligned} \dot{V}_n \le \frac{1}{\kappa }\Big (bN({s})+{r}_{n}\Big )\dot{s}\,+\chi \sum _{i=1}^n\phi ^2_{i1}(|\zeta |)+\,4h^2(t). \end{aligned}$$
(75)

From (10) and (34), the following calculations hold true

$$\begin{aligned}&\int _0^t\phi _{i1}^2(|\zeta (s)|)\mathrm{d}s\ \nonumber \\&\qquad \le \ \bar{\psi }_{i0}(|\zeta (0)|) +\int _0^t\psi _{i1}(|y(s)|)\mathrm{d}s\ \nonumber \\&\qquad \le \ \bar{\psi }_{i0}(|\zeta (0)|) +n\cdot \frac{1}{\kappa }\int _0^t\dot{{s}}(\tau )\mathrm{d}\tau . \end{aligned}$$
(76)

Then, integrate both sides of (75), and one can get

$$\begin{aligned}&V_n(t)\le C_0+\frac{1}{\kappa }\int _0^{t}\big (bN({s})\nonumber \\&\quad +{r}_n+n\chi \big )\dot{{s}}(\tau )\mathrm{d}\tau +4\int _0^th^2(\tau )\mathrm{d}\tau ,~ \forall ~t>0 \end{aligned}$$
(77)

with constants \(C_0=V_n(0)+\chi \sum \limits _{i=1}^{n}\bar{\psi }_{i0}(|\zeta (0)|)\). According to Assumption 4, one can get

$$\begin{aligned} h(t)=\frac{1}{b}\, \dot{{d}}(t)\in {L_{2}}, \end{aligned}$$
(78)

and then, the term \(4\int _0^th^2(\tau )\mathrm{d}\tau \) in the right-hand side satisfies

$$\begin{aligned} 4\int _0^th^2(\tau )d\tau <+\infty ,~\forall ~t>0. \end{aligned}$$
(79)

Using the argument of contradiction, it can be concluded that s(t), \(V_n(y,\varepsilon ,{z},\widetilde{\Theta })\) and then \(\big (y(t),{e}(t),{z}(t),\widetilde{\Theta }(t)\big )\) must be bounded over \([0,t_f)\). Also, \(\widehat{\Theta }(t)\) is bounded on \([0,t_f)\). The boundedness of y(t) means that \(z_1(t)\) is bounded. This together with the boundedness of e(hence \({e}_1\)) ensures that \(\widehat{\xi }_1(t)\) is bounded. Noting the boundedness of s(t) and y(t) on \([0,t_f)\), we know that \(\vartheta _1(\cdot )\) is bounded on \([0,t_f)\). Due to \({z}_1=\widehat{\xi }_2-\vartheta _1(\cdot )\), it follows that \(\widehat{\xi }_2(t)\) is bounded. Similarly, \(\vartheta _{i-1}(\cdot )\), \(\widehat{\xi }_i(t)(3\le i\le n)\) are also bounded on \([0,t_f)\). In particular, considering \({e}_{n+1}\) is bounded with \({e}_{n+1}=\frac{1}{\delta ^{*}}\varepsilon _{n+1}=\frac{1}{\delta ^{*}}(z_{n+1}-\widehat{\xi }_{n+1})\), and \(z_{n+1}=\frac{1}{b}d(t)\) is bounded according to Assumption 4, we can conclude that \(\widehat{\xi }_{n+1}\in {L_{\infty }}\). Considering s(t) is bounded and \(\int _0^t\gamma \big (y(s)\big )ds<\int _0^t\dot{{s}}(s)ds =\big ({s}(t)-{s}(0)\big )\) for all \(t>0\), we then obtain \(\int _0^t\gamma \big (y(s)\big )ds<\infty , \forall ~t>0\). It thus follows, using Prop.6 in [3], that \(\zeta (t)\) is bounded on \([0,t_f)\). So far all the closed-loop system signals are bounded on \([0,t_f)\). This shows that the finite time escape will not happen. Therefore, it is natural that \(t_f\) can be maximized to \(+\infty \). This completes the property (a).

Since all signals in closed-loop are bounded over \([0,+\infty )\), from (69) and (77), one can obtain

$$\begin{aligned}&{e}_i\in {L_{2}}(i=1,\ldots ,n+1),\nonumber \\&{z}_i\in {L_{2}}(i=1,\ldots ,n-1). \end{aligned}$$
(80)

The property of \(\dot{{e}}_i\in {L_{\infty }}\) and \(\dot{{z}}_i\in {L_{\infty }}\) implies that both \({e}_i(t)\) and \({z}_i(t)\) are uniformly continuous. By Barbalat’s Lemma, we have

$$\begin{aligned}&\lim \limits _{t\rightarrow \infty }{e}_i(t)=0(i=1,\ldots ,n+1),\nonumber \\&\lim \limits _{t\rightarrow \infty }{z}_i(t)=0(i=1,\ldots ,n-1). \end{aligned}$$
(81)

The fact of \(y(t),\dot{y}(t)\in {L_{\infty }}\) implies that \(\kappa \beta (y)y^2\) is uniformly continuous. Furthermore, s(t) is monotonically nondecreasing over \([0,+\infty )\) because of \(\dot{{s}}(t)\ge 0\), which together with \({s}(t)\in {L_{\infty }}\) results \(\kappa \beta (y)y^2\) is integrable over \([0,+\infty )\). Considering the choice of \(\beta (\cdot )\ge 1\) and \(\kappa >0\), one can derive that \(\lim \limits _{t\rightarrow \infty }y(t)=0\). Hence, \(z_1(t)\) and \(\vartheta _1(\cdot )\) go to zero as \(t\rightarrow \infty \). In view of \({e}_1=\frac{1}{\delta ^{*}}(\xi _1-\widehat{\xi }_1)\), we have \(\lim \limits _{t\rightarrow \infty }\widehat{\xi }_1(t)=0\). In a recursive manner, \(\vartheta _i(\cdot )\) and \(\widehat{\xi }_i(t)(i=1,\ldots ,n)\) asymptotically converge to zero. Particularly, with \({e}_i=\frac{1}{\delta ^{*}}(\xi _i-\widehat{\xi }_i)\), it follows that \(\xi _i(t)\rightarrow 0\) as \(t\rightarrow \infty \), which leads to \(\lim \limits _{t\rightarrow \infty }x_i(t)=0(i=1,\ldots ,n)\). Since \(\int _0^t\gamma \big (y(s)\big )ds<\infty \), again using Prop.6 in [3], we derive that \(\lim \limits _{t\rightarrow \infty }\zeta (t)=0\). This shows the property (b).

Next, we are ready to prove the last part (c) in Theorem 1. According to the aforementioned calculations, we have established \(\widehat{\xi }_{n+1}\in {L_{\infty }}\) and \(\lim _{t\rightarrow \infty }\vartheta _n(t)=0\). Considering the control law defined by

$$\begin{aligned} u=-\widehat{\xi }_{n+1}+\vartheta _n, \end{aligned}$$
(82)

it is clear that \(u\in {L_{\infty }}\). Additionally, considering

$$\begin{aligned}&{e}_{n+1}=\xi _{n+1}-\widehat{\xi }_{n+1},\nonumber \\&\lim _{t\rightarrow \infty }{e}_{n+1}(t)=0,~z_{n+1}=\frac{1}{b}\,\mathrm{d}(t)\in {L_{\infty }}, \end{aligned}$$
(83)

one can conclude

$$\begin{aligned}&\lim _{t\rightarrow \infty }\widehat{\xi }_{n+1}(t)=0~~~\text{ if }\nonumber \\&\lim _{t\rightarrow \infty }d(t)=0, \end{aligned}$$
(84)

which in turn shows that

$$\begin{aligned} \lim _{t\rightarrow \infty }u(t)=0~~~\text{ if } ~~\lim _{t\rightarrow \infty }\mathrm{d}(t)=0. \end{aligned}$$
(85)

This ends the proof. \(\square \)

3 Numerical results and discussion

In this section, the fan speed control system subject to external disturbance is used a practical example to illustrate our output feedback design methodology. It is shown that even disturbed by some external nonvanishing disturbances in the armature voltage, to realize the asymptotic regulation control of any desired constant reference signal for the fan speed, the proposed speed controller does the job.

3.1 Model analysis

From [29], the dynamics of a fan driven by a DC motor is described by

$$\begin{aligned}&{J_1}\dot{\upsilon }={k_1}I-{\tau _L}-{\tau _D}(\upsilon )\nonumber \\&J_2\dot{I}={u_0}-{k_2}\upsilon -RI+d(t)\nonumber \\&\bar{y}=\upsilon \,, \end{aligned}$$
(86)

where \(\upsilon \) is the fan speed, I is the armature current, \(\tau _L\) is an uncertain constant load torque, \({\tau _D}(\upsilon )\) is an uncertain drag torque, \(u_0\) is the armature voltage which is considered as the input, \({J_1},{k_1},{k_2},R\) are known positive constants, and the inductance \(J_2\) may be an unknown constant. The function \(\mathrm{d}(t)\) represents the uncertain external disturbance. The control task is the set-point regulation control of the fan speed \(\upsilon \) to the constant value \(\upsilon _r(=\bar{y}_r)\), irrespective of the unknown \(\tau _L\), \({\tau _D}(\upsilon )\) and the disturbance \(\mathrm{d}(t)\).

Fig. 1
figure 1

The system states of the closed-loop system

Full size image

Assumption 5

  For the drag torque \({\tau _D}(\upsilon )\) and each \(\upsilon _r\in \mathcal {R}\), there exist an unknown constant \(\sigma >0\) and a known smooth function \(\omega (\cdot )\) such that

$$\begin{aligned} |{{\tau _D}(\upsilon )-{\tau _D}({{\upsilon _r}})}|\le \sigma \cdot {\omega }({|{\upsilon -{\upsilon _r}}|}),\forall ~\upsilon \in {R}. \end{aligned}$$
(87)

In order to realize the control objective, to be first, we introduce the change of coordinates [10]

$$\begin{aligned}&\chi _1=\upsilon ,~~\chi _2=\frac{k_1}{J_1}\,I,\nonumber \\&\bar{u}=\frac{k_1}{J_1}(u_0-k_2\upsilon -RI)+\frac{k_1}{J_1}\,\mathrm{d}(t)\,, \end{aligned}$$
(88)

and let \(\eta (\upsilon )=-\frac{1}{J_1}(\tau _L+\tau _D(\upsilon ))\), \(b=\frac{1}{{{J_2}}}\), then we have

$$\begin{aligned}&\dot{\chi }_1=\chi _2+\eta (\bar{y})\nonumber \\&\dot{\chi }_2=b\bar{u}\nonumber \\&\bar{y}=\chi _1. \end{aligned}$$
(89)

For any \(L>0\), define the auxiliary variables

$$\begin{aligned} \dot{\Pi }=-L\, \Pi -L,~\dot{\Xi }=-L\, \Xi +\bar{u}. \end{aligned}$$
(90)

Let \(\eta ^*=\eta (\bar{y}_r)\), where \(\bar{y}_r=\upsilon _r\) is some desired setting-point constant speed, and introduce the new coordinate variables \((\zeta ,x_1,x_2)\)

$$\begin{aligned}&{x_1}=\chi _1-\bar{y}_r=\upsilon -\upsilon _r,\nonumber \\&\zeta ={\chi _2}-L{x_1}-b\,\Xi -\Pi {\eta ^*},\nonumber \\&{x_2}=b\,\Xi +(\Pi +1){\eta ^*}. \end{aligned}$$
(91)

Then, in view of \(x_1=\bar{y}-\bar{y}_r\), we can newly define system output \(y=x_1\) and \(u=\frac{k_1}{J_1}(u_0-k_2\upsilon -RI)\). It can be verified that

$$\begin{aligned}&\dot{\zeta }=-L\zeta -L^2x_1-L(\eta (y+\upsilon _r)-\eta (\upsilon _r))\nonumber \\&\dot{x}_1=x_2+Lx_1+\zeta +\eta (y+\upsilon _r)-\eta (\upsilon _r)\nonumber \\&\dot{x}_2=bu-Lx_2+b\frac{k_1}{J_1}\mathrm{d}(t)\nonumber \\&y=x_1. \end{aligned}$$
(92)

Clearly, regarded \(\zeta \)-subsystem as the cascaded dynamics, the system (92) falls into the form of (1) with \(\lambda _{1}(t)=L\), \(\lambda _{2}(t)=-L\), \(g_1(\zeta ,y)=\zeta +\eta (y+\upsilon _r)-\eta (\upsilon _r)\), \(g_2(\zeta ,y)=0\), and the inductance coefficient \(J_2\) (actually \(1 / J_2 \)) serving as the unknown high-frequency gain. Moreover, like the calculations in [12], the \(\zeta \) dynamics is ISS (consequently iISS) with \(\zeta \) as the state and \(x_1\) as the input, together with an ISS-Lyapunov function \(U_0(\zeta )=\zeta ^2 / 2L \) satisfying

$$\begin{aligned} \dot{U}_0(\zeta )\le -\frac{1}{2}\zeta ^2+L^2x_1^2+\frac{{\sigma }^2}{J_1^2}{\omega }^2(|x_1|). \end{aligned}$$
(93)

This fulfills Assumption 1. From Assumption 5, the following calculations hold true

$$\begin{aligned} |g_1(\zeta ,y)|\le & {} |\zeta |+|\eta (y+\upsilon _r)-\eta (\upsilon _r)|\nonumber \\ {}\le & {} |\zeta |+\frac{\sigma }{J_1}{\omega }(|y|). \end{aligned}$$
(94)

Hence, it is evident that Assumption 2 holds with \(\delta _{11}=1\), \(\delta _{12}=\sigma / J_1 \), \(\phi _{11}(|\zeta |)=|\zeta |\) and \(\phi _{12}(|y|)={\omega }(|y|)\). In simulation, we choose

$$\begin{aligned} d(t)=\theta \cdot \arctan {t},~\dot{d}(t)=\frac{\theta }{1+t^2},~\theta \in {R}. \end{aligned}$$
(95)

This shows d(t) and \(\dot{d}(t)\) meets Assumption 4. The Assumption 3 is clear since \(\lambda _{1}(t)=L\), \(\lambda _{2}(t)=-L\) with the constant \(L>0\).

Fig. 2
figure 2

The state estimates, errors and control input of the closed-loop system

Full size image

3.2 The fan speed regulator design

Similar to the proposed control method in Sect. 3, define

$$\begin{aligned} \xi _1= & {} \frac{1}{b}x_1=J_2x_1,\nonumber \\ ~\xi _2= & {} \frac{1}{b}x_2=J_2x_2,\nonumber \\ ~\xi _3= & {} \frac{k_1}{J_1}\mathrm{d}(t),~h(t)=\frac{k_1}{J_1}\mathrm{\dot{{d}}}(t), \end{aligned}$$
(96)

and we have the following new state equations

$$\begin{aligned} \dot{\xi }_1= & {} \xi _2+L\xi _1+J_2\zeta +J_2\big (\eta (y+\upsilon _r)-\eta (\upsilon _r)\big )\nonumber \\ \dot{\xi }_2= & {} u-L\xi _2+\xi _3\nonumber \\ \dot{\xi }_3= & {} h(t)\nonumber \\ y= & {} x_1(=\upsilon -\upsilon _r). \end{aligned}$$
(97)

For simulation purposes, we set the bounding function \(\omega (s)={\varpi }s\) with \(\varpi >0\) in Assumption 5, and hence, according to (93) and (94), the gain function \(\beta (\cdot )\) can be picked as some constant \(\beta >0\). Then, using the proposed control algorithm in Sect. 3, we design the control law

$$\begin{aligned} u= & {} -\rho _1z_1+L\widehat{\xi }_2+p_{12}(t)\widehat{\xi }_1-\widehat{\xi }_3\nonumber \\&+\frac{\partial {\vartheta _1}}{\partial {y}}Lx_1 +\,\frac{\partial {\vartheta _1}}{\partial {{s}}}\dot{{s}} -\widehat{\Theta }\varphi _1(y,{s})z_1, \end{aligned}$$
(98)

and the adaption law

$$\begin{aligned} \dot{\widehat{\Theta }}=\Upsilon \varphi _1(y,{s})z_1^2 \end{aligned}$$
(99)

with \(\varphi _1(y,{s})=2\beta ^2N^2({s}) +{\beta }^3N^4({s})\), \(\vartheta _1={\beta }N({s})y,~\dot{{s}}=\kappa {\beta }y^2\).

3.3 Simulation results

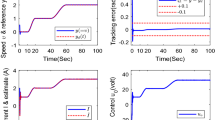
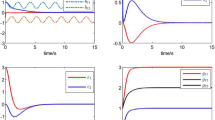
The parameter values in (86) are set to \(J_1=J_2=R=k_1=k_2=1\), \(\sigma =1\), \(L=1\), \(\rho _1=1\), \(\Upsilon =1\), \(\kappa =1\), \(\theta =1\), and the initial conditions: \(\zeta (0)=1\), \(x(0)=(0,0)\), \(s(0)=0\), \(\hat{\xi }(0)=(0,0,0.5)\), \(\widehat{\Theta }(0)=0\). The external disturbance \(\mathrm{d}(t)\) is chosen as in (95). From the simulation results shown in Figs. 1, 2 and 3, it can be seen that the good set-point regulation performance can be achieved by use of the proposed methodology in the paper. In this way, the regulation of the fan speed \(\upsilon \) to a desired value \(\upsilon _r\) by output feedback is solved, even under the external disturbance in the armature voltage.

Fig. 3
figure 3

The power consumption of the closed-loop system

Full size image

3.4 Discussion

It is noted that when the armature current I is not measured, the control signal

$$\begin{aligned} u_0=\frac{J_1}{k_1}u+k_2\upsilon +RI \end{aligned}$$
(100)

is not implemented. Here we construct a current observer for the unmeasured armature current I in the form of

$$\begin{aligned} J_2\dot{\hat{I}}={u_0}-{k_2}\upsilon -R\hat{I}. \end{aligned}$$
(101)

Let the observer error \(\tilde{I}=I-\hat{I}\), then the error dynamics is

$$\begin{aligned} J_2\dot{\tilde{I}}=-R\tilde{I}+\mathrm{d}(t). \end{aligned}$$
(102)

Form the above analysis, it can be proved that \(\mathrm{d}(t)\) tends to zero so does \(\tilde{I}\).

Remark 5

 In consideration of the armature voltage \(u_0\) and the armature current I in (86), we can calculate the power of \(P=u_0 I\) with the help of our proposed controller (98). It can be shown that the power consumption is dependent on the target speed signal to be tracked. The larger the fan speed, the more power it consumes. For example, the power consumption increases along with the set-point speed value from \(\upsilon _r=1\) to \(\upsilon _r=3\). Observe that the numerical results shown in Fig.3 are consistent with the analytical discussion. More details on this topic can be found in [32].

4 Conclusion

In this paper, the global robust regulation problem is solved for a class of disturbed nonlinear uncertain systems in cascade. Using the ideas of the Nussbaum-type gain and the disturbance as a generalized state, we design a dynamic ESO based on a Riccati differential equation to handle the unknown control coefficients and external disturbances. Moreover, in this setting, it is shown that the additive disturbance does not require to be square integrable, which broadens the family of admissible noise signals. As a continuing research of our previous results, the proposed control scheme is verified by the fan speed control system with some external disturbance in the armature voltage. It is of interest to investigate the global robust regulation control in the presence of nonvanishing nonlinear uncertainties in the future research works.