1 Introduction

In recent years, chaos and chaotic systems have been identified as very interesting nonlinear dynamical phenomena and have received a flurry of research effort. Chaotic systems have several special features such as extraordinary sensitivity on initial conditions and strange attractors. Second-order chaotic systems are a broad class of the dynamical systems. There are many examples of physical and engineering second-order nonautonomous systems that exhibit chaos. For instance, it is known that the gyroscope system is a second- order dynamical system that shows chaotic behavior [1]. The gyroscope has been found in many applications in optics, navigation, aeronautics, and space engineering fields. Another interesting second- order chaotic dynamical system is the horizontal platform system [2]. It is a mechanical device that can freely rotate around the horizontal axis and is widely used in offshore and earthquake engineering. As another example, the Van der Pol oscillator [3] is a second-order model of electrical oscillator with chaotic behaviors. In addition, many other second-order nonautonomous dynamical systems, such as MLC circuit [4], Duffing–Holmes system [5], extended Rayleigh oscillator [3], and coronary artery system [6], exhibit complex and chaotic dynamics. Due to the existence of chaos in real practical second-order systems and many useful applications in physics and engineering fields, there has been increasing interest in the subject of control and synchronization of second-order chaotic systems in the past few years [7–9].

Fractional calculus, with more than 300-years-old history, generalizes the ordinary differentiation and integration to arbitrary (noninteger) order. Although it has a long history, it has been used in physics and engineering only during the last few years. It has been known that many fractional-order differential systems, such as fractional-order Chen system [10], fractional-order Lu system [11], fractional-order Rossler system [12], fractional-order Arneodo system [13], fractional-order Lorenz system [14], fractional-order unified system [15], fractional-order Genesio-Tesi system [16], fractional-order Chua circuit [17], and fractional-order Duffing system [18], exhibit rich and chaotic dynamics.

In particular, control and synchronization of fractional-order chaotic systems have attracted the attention of many scholars and some techniques have been used to control/synchronize fractional-order chaotic systems. In [19], an adaptive controller has been designed to synchronize chaotic systems of fractional orders. Synchronization of two identical fractional-order chaotic systems using linear error feedback control has been addressed in [20]. A local stability criterion for synchronization of in-commensurate fractional-order chaotic systems has been derived in [21]. Lu [22] has proposed a nonlinear observer to synchronize a class of identical fractional-order chaotic systems. However, most of the works in the literature toward synchronization/stabilization of chaotic fractional-order systems have been performed based on the local stability of the closed-loop system.

The sliding mode control technique is one of the most attractive robust nonlinear control methods. The main feature of a sliding mode controller is to switch the control law to force the state trajectories of the system from the initial states onto some prescribed sliding surface in finite time. Once the state trajectories of the system reach the sliding surface (i.e., when the sliding motion occurs), the closed-loop system dynamics is reduced to the sliding surface dynamics which has desired properties such as good stability and tracking capability.

In [23], the authors have proposed an active sliding mode approach to synchronize chaotic fractional-order systems. They have designed a simple linear sliding surface and have derived an n-dimensional control signals for the n-dimensional synchronization error system based on the active control theory. Hosseinnia et al. [24] have reported design of a linear sliding surface with corresponding switching law for synchronization of two identical uncertain two-dimensional fractional-order chaotic systems. However, these works have not performed the stability discussion of the system on the basis of the fractional-order Lyapunov stability theory. Recently, we have used the latest version of the fractional Lyapunov stability theorem to design some suitable controllers for chaotic systems [25–27].

On the other hand, an important problem in the stabilization or synchronization of chaotic systems is how to realize the control or synchronization of chaotic systems by designing a single controller, which is particularly significant both for theoretical research and practical applications. In practical situations, the problem of multi-input control schemes is a very critical issue. Indeed, from a practical engineering standpoint, it is more valuable to stabilize or synchronize the chaotic system with a single control input. However, to our best knowledge, most of the previous works in the literatures, which have been proposed to stabilize or synchronize fractional nonautonomous chaotic systems, either have not considered the effects of unknown nonlinear terms, model uncertainties, and external disturbances or are sometimes specific and multi-input.

Motivated by the above discussions, this paper proposes a novel nonsingular terminal fractional-order sliding mode controller for robust stabilization/synchronization of second-order fractional nonautonomous chaotic systems in the presence of both model uncertainties and external disturbances. After introducing a novel terminal fractional-order sliding surface, its finite-time stability is proven. Then, on the basis of fractional-order Lyapunov stability theory, a robust sliding control law is derived to guarantee the occurrence of the sliding motion in a given finite time. The proposed control law is single and practical in real world applications. Finally, two illustrative examples are given to demonstrate the applicability and robustness of the proposed control technique and to validate the theoretical results of the paper.

The rest of this paper is organized as follows. In Sect. 2, some preliminaries of fractional calculus are restated. The system description and problem formulation are given in Sect. 3. In Sect. 4, the design procedure of the proposed terminal fractional-order sliding mode approach is included. Section 5 presents two illustrative examples. Finally, conclusions are included in Sect. 6.

2 Preliminaries of fractional calculus

The main definition of fractional integration is as follows [28].

Definition 1

The \(\alpha \)th-order fractional integration of function \(f(t)\) is given by

$$\begin{aligned} {}_{t_0}I_t^\alpha f(t)=\frac{1}{\Gamma (\alpha )}\int \limits _{t_0}^t \frac{f(\tau )}{({t-\tau })^{1-\alpha }}\mathrm{d}\tau , \end{aligned}$$
(1)

where \(\Gamma (.)\) is the Gamma function.

Two important and commonly used definitions of fractional derivatives are listed below [28].

Definition 2

Let \(m-1<\alpha \le m, m\in N\), the Riemann–Liouville fractional derivative of order \(\alpha \) of function \(f(t)\) is defined as follows:

$$\begin{aligned} {}_{t_0}^{RL} D_t^\alpha f(t)&= \frac{\mathrm{d}^{\alpha }f(t)}{\mathrm{d}t^{\alpha }}\nonumber \\&= \frac{1}{\Gamma (m-\alpha )}\frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}}\int \limits _{t_0}^t \frac{f(\tau )}{({t-\tau })^{\alpha -m+1}}\mathrm{d}\tau \end{aligned}$$
(2)

Definition 3

The Caputo fractional derivative of order \(\alpha \) of function \(f(t)\) is defined as follows:

$$\begin{aligned} {}_{t_0}^C D_t^\alpha f(t)\!=\!\left\{ {{\begin{array}{l@{\quad }l} \frac{1}{\Gamma (m\!-\!\alpha )}\int _{t_0}^t \frac{f^{(m)}(\tau )}{(t\!-\!\tau )^{\alpha -m+1}}\mathrm{d}\tau , &{} m\!-\!1\!<\!\alpha \!<\!m\\ \frac{\mathrm{d}^{m}}{\mathrm{d}t^{m}}f(t), &{} \alpha \!=\!m \\ \end{array}}} \right. \nonumber \\ \end{aligned}$$
(3)

where \(m\) is the smallest integer number, larger than \( \alpha \).

Property 1

For the Caputo derivative, we have [28]

$$\begin{aligned} {}_{t_0}^C D_t^{1-\alpha } \left( {}_{t_0}^C D_t^\alpha f(t)\right) ={}_{t_0}^C D_t^1 f(t)=\dot{f}(t) \end{aligned}$$
(4)

Property 2

For the Caputo derivative, the following equality holds [28].

$$\begin{aligned} {}_{t_0}^C D_t^\alpha \left( {{}_{t_0}^C D_t^{-\beta } f(t)}\right) ={}_{t_0}^C D_t^{\alpha -\beta } f(t), \end{aligned}$$
(5)

where \(\alpha \ge \beta \ge 0\).

Property 3

The following equality holds for the Caputo derivative [28].

$$\begin{aligned} {}_{t_0}^C D_t^\alpha \left( {{}_{t_0}^C D_t^m f(t)}\right) ={}_{t_0}^C D_t^{\alpha +m} f(t), \end{aligned}$$
(6)

where \(m=0, 1, 2, \ldots ; n-1<\alpha <n\).

In the rest of this paper, the notation \(D^{\alpha }\) indicates the Caputo fractional derivative.

The following theorem is the latest version of the fractional Lyapunov stability theorem [29].

Theorem 1

Let \(x=0\) be an equilibrium point for the Caputo fractional nonautonomous system

$$\begin{aligned} D^{\alpha }x(t)=f(x,t), \end{aligned}$$
(7)

where \(f(x,t)\) satisfies the Lipschitz condition with Lipschitz constant \(l>0\) and \(\alpha \in (0,1)\). Assume that there exists a Lyapunov function \(V(t, x(t))\) satisfying

$$\begin{aligned} \alpha _1 \Vert x\Vert ^{a}&\le V(t,x)\le \alpha _2 \Vert x\Vert \end{aligned}$$
(8)
$$\begin{aligned} \dot{V}(t, x)&\le -\alpha _3 \Vert x\Vert , \end{aligned}$$
(9)

where \(\alpha _1, \alpha _2, \alpha _3\), and \(a\) are positive constants and \(\Vert \cdot \Vert \) denotes an arbitrary norm. Then the equilibrium point of the system (7) is Mittag-Leffler stable.

Remark 1

Mittag-Leffler stability implies asymptotic stability [29].

3 System description and problem statement

Consider the following second-order uncertain nonautonomous fractional-order chaotic system.

$$\begin{aligned} \left\{ {{\begin{array}{l} {D^{\alpha }x_1 =x_2} \\ {D^{\alpha }x_2 =f({X,t})+\Delta f(X)+d^{x}(t)+u(t)} \\ \end{array}}}\right. \end{aligned}$$
(10)

where \(\alpha \in (0, 1)\) is the fractional order of the system, \(X(t)=\left[ {x_1, x_2}\right] ^\mathrm{T}\in R^{2}\) is the state vector of the system, \(f(X,t)\in R\) is a given nonlinear function of \(X\) and \(t\), \(\Delta f(X)\in R\) represents an unknown model uncertainty term, \(d^{x}(t)\in R\) is an external disturbance of the system, and \(u(t)\in R\) is the single control input to be designed later.

We define the chaos synchronization problem as follows: design an appropriate controller for the response system (10) such that its state trajectories track the state trajectories of the following drive chaotic system.

$$\begin{aligned} \left\{ {{\begin{array}{l} D^{\alpha }y_1 =y_2\\ D^{\alpha }y_2 =g\left( {Y,t}\right) +\Delta g(Y)+d^{y}(t),\\ \end{array}}}\right. \end{aligned}$$
(11)

where \(Y(t)=\left[ {y_1, y_2}\right] ^\mathrm{T}\in R^{2}\) is the state vector of the system, \(g(Y,t)\in R\) is a given nonlinear function of \(Y\) and \(t, \Delta g(Y)\in R\) is an unknown model uncertainty term, and \(d^{y}(t)\in R\) is an external disturbance.

Assumption 1

The uncertainty terms \(\Delta f({X})\) and \(\Delta g(Y)\) are assumed to be bounded by

$$\begin{aligned} \left| D^{1-\alpha }\left( {\Delta f(X)-\Delta g(Y)}\right) \right| \le \gamma _1, \end{aligned}$$
(12)

where \(\gamma _1\) is a known positive constant.

Assumption 2

The external disturbances \(d^{x}(t)\) and \(d^{y}(t)\) are assumed to be bounded by

$$\begin{aligned} \left| {D^{1-\alpha }\left( {d^{y}(t)-d^{x}(t)}\right) }\right| \le \gamma _2, \end{aligned}$$
(13)

where \(\gamma _2\) is a given positive constant.

Defining the synchronization error as \(E(t)=Y(t)-X(t)\), one can obtain

$$\begin{aligned} E(t)\!=\!Y(t)\!-\!X(t)\!&= \!\left[ y_1, y_2\right] ^\mathrm{T}\!-\!\left[ x_1, x_2,\right] ^\mathrm{T}\nonumber \\&= \left[ e_1, e_2\right] ^\mathrm{T}. \end{aligned}$$
(14)

Consequently, the synchronization error dynamics is obtained as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {D^{\alpha }e_1 =e_2} \\ D^{\alpha }e_2 =g(Y,t)+\Delta g(Y)+d^{y}(t)-f(X,t)\\ -\Delta f(X)-d^{x}(t)-u(t) \\ \end{array}}}\right. \end{aligned}$$
(15)

Definition 4

Consider the error system described by Eq. (15). If there exists a constant \(T=T(E(0))>0\), such that \(\lim _{t\rightarrow T} \Vert E(t)\Vert =0\) and \(\Vert E(t)\Vert \equiv 0\), if \(t\ge T\), then states of the error system (15) will converge to zero in the finite time \(T\).

The control goal of this paper is to design a suitable robust nonsingular terminal fractional sliding mode controller for stabilization of the resulting error system around zero in the sense of Definition 4.

Remark 2

It is obvious that if \(Y(t)=0\), then the synchronization problem is transformed to the stabilization problem of the fractional-order uncertain chaotic system (10).

4 Design of robust nonsingular terminal fractional sliding mode controller

In this section, first a novel fractional terminal sliding surface is introduced. Then, proper sliding mode control laws are proposed to ensure the existence of the sliding motion in finite time.

In general, the sliding mode control approach is composed of an equivalent control part that describes the behavior of the system when the trajectories stay over the sliding surface and a variable structure control part that enforces the trajectories to reach the sliding surface and remain on it evermore. In other words, a sliding mode controller includes two major steps. The first step is to select a suitable terminal sliding surface. In this paper, we propose a novel fractional-order terminal sliding surface as follows:

$$\begin{aligned} s(t)=e_2 +D^{\alpha -1}\left( {k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }}\right) , \end{aligned}$$
(16)

where \(e_i, i=1, 2\) are the system error states, \(\rho \in (0, 1)\) is a constant, and \(k_1\) and \(k_2\) are positive scalars.

Once the system operates in the sliding mode, it satisfies the following equation [30].

$$\begin{aligned} s(t)=0 \end{aligned}$$
(17)

Therefore, using Eqs. (16) and (17), the following sliding mode dynamics is obtained.

$$\begin{aligned} e_2 +D^{\alpha -1}\left( {k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }}\right) =0 \end{aligned}$$
(18)

Using the first equation of (15), one obtains

$$\begin{aligned}&D^{\alpha }e_1 +D^{\alpha -1}\left( {k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }}\right) =0 \end{aligned}$$
(19)
$$\begin{aligned}&D^{\alpha }e_1 =-D^{\alpha -1}\left( {k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }}\right) \end{aligned}$$
(20)

In the following theorem, we prove the finite-time stability of the sliding mode dynamics (20).

Theorem 2

The sliding mode dynamics (20) is stable and its state trajectories converge to the equilibrium \(e_1 (t)=0\) in a finite time.

Proof

Choose the following positive definite function as a Lyapunov function candidate.

$$\begin{aligned} V_1 (t)=|e_1 (t)| \end{aligned}$$
(21)

Taking the time derivative of \(V_1 (t)\), we have

$$\begin{aligned} \dot{V}_1 (t)=\mathrm{sign}(e_1)\dot{e}_i(t) \end{aligned}$$
(22)

Based on Property 1 and Eq. (4), one has

$$\begin{aligned} \dot{V}_1 (t)=\mathrm{sign}(e_1)\left( D^{1-\alpha }(D^\alpha e_1)\right) \end{aligned}$$
(23)

Substituting \(D^{\alpha }e_1\) from (20) into the above equation, one obtains

$$\begin{aligned}&\dot{V}_1 (t)=-\mathrm{sign}(e_1)\nonumber \\&\left( D^{1-\alpha }\left( D^{\alpha -1}\left( k_1 e_1+k_2\, \mathrm{sign}(e_1)|e_1|^\rho \right) \right) \right) \nonumber \\ \end{aligned}$$
(24)

Using Property 2 and Eq. (5), we have

$$\begin{aligned} \dot{V}_1 (t)=-\left( k_1|e_1|+k_2|e_1|_\rho \right) \end{aligned}$$
(25)

Defining \(k=\min \left\{ {k_1, k_2}\right\} \), one has

$$\begin{aligned} \dot{V}_1 (t)\le -k\left( |e_1|+|e_1|^{\rho }\right) \le -k|e_1| \end{aligned}$$
(26)

Therefore, based on Theorem 1, the error \(e_1\) will converge to zero asymptotically. In the following, we show the convergence to zero occurs in finite time.

From the inequality (26), one has

$$\begin{aligned} \dot{V}_1 (t)=\frac{\mathrm{d}|e_1|}{\mathrm{d}t}\le -k\left( |e_1|+|e_1|^{\rho }\right) \end{aligned}$$
(27)

After simple calculations, we have

$$\begin{aligned} \mathrm{d}t&\le -\frac{\mathrm{d}|e_1|}{k\left( {|e_1|+|e_1|_1^\rho }\right) }=-\frac{|e_1|_1^{-\rho } \mathrm{d}|e_1|}{k\left( {|e_1|_1^{1-\rho }+1}\right) }\nonumber \\&=-\frac{1}{k\left( {1-\rho }\right) }\frac{\mathrm{d}|e_1|_1^{1-\rho }}{\left( {|e_1|_1^{1-\rho } +1}\right) } \end{aligned}$$
(28)

Taking integral of both sides of (28) from \(t_r\) to \(t_s\) and knowing \(e_1 (t_s)=0\), we have

$$\begin{aligned} t_s -t_r&\le -\frac{1}{k(1-\rho )}\int \limits _{X(t_r)}^{X(t_s)} \frac{\mathrm{d}|e_1|_1^{1-\rho }}{|e_1|_1^{1-\rho } +1}\nonumber \\&=-\frac{1}{k(1-\rho )}\mathrm{ln}\left( {|e_1|_1^{1-\rho } +1}\right) \left| {\begin{array}{l} e_1 (t_s) \\ e_1 (t_r)\\ \end{array}}\right. \nonumber \\&=\frac{1}{k(1-\rho )}\mathrm{ln}\left( {|e_1|_1^{1-\rho }+1}\right) . \end{aligned}$$
(29)

Therefore, the error \(e_1\) will converge to zero in the finite time \(T_1 \le \frac{1}{k(1-\rho )}\mathrm{ln}\left( {|e_1|_1^{1-\rho }+1}\right) +t_r\). Thus, the proof is achieved completely.\(\square \)

Remark 3

In the works [31, 32] integer-order terminal sliding mode manifolds \(s=\dot{e}+\beta e^{q/p}\) and \(s=\dot{e}+\alpha e +\beta e^{q/p}\) have been designed, respectively, where \(\alpha , \beta >0, p>q>0\) are odd integers. Since the control laws in these works contain the term \(e^{(q/p)-1}\), one can see that for \(e<0\), the fractional power \((q/p)-1\) may lead to the term \(e^{(q/p)-1}\notin R\), which leads to \(\dot{e}\notin R\) and \(u(t)\notin R\). This singularity restricts the practical implementation of the controllers in [31, 32]. On the other hand, our proposed fractional nonsingular terminal sliding mode in (16) overcomes this singularity.

Having established the suitable nonsingular terminal sliding surface, the next step is to determine an input signal \(u(t)\) to guarantee that the error system trajectories reach to the sliding surface \(s(t)=0\) and stay on it forever. In general, the sliding mode control law is composed of two parts: (1) an equivalent control that expresses the behavior of the system when the state trajectories stay over the sliding manifold; and (2) a reaching control that enforces the state trajectories to attain the sliding manifold. When the closed-loop system is moving on the sliding surface, it satisfies \(\dot{s}(t)=0\) [30] and then the equivalent control law \(u_\mathrm{eq} (t)\) can be computed as follows:

$$\begin{aligned} \dot{s} (t)=0 \end{aligned}$$
(30)

Replacing \(s(t)\) from Eq. (16) into Eq. (30), it yields

$$\begin{aligned} \dot{s}(t)&= \frac{\mathrm{d}}{\mathrm{d}t}\left( e_2 +D^{\alpha -1}\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \right) \nonumber \\&= 0 \end{aligned}$$
(31)

On the basis of Property 3 and Eq. (6), we have

$$\begin{aligned} \dot{s}(t)=\dot{e}_2 +D^{\alpha }\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) =0 \end{aligned}$$
(32)

Using Property 1 and Eq. (4), one obtains

$$\begin{aligned} \dot{s}(t)&= D^{1-\alpha }\left( D^{\alpha }e_2\right) +D^{\alpha }\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \nonumber \\&= 0 \end{aligned}$$
(33)

From the error system dynamics (15), one has

$$\begin{aligned} \dot{s} (t)&= D^{1-\alpha }\left( g(Y,t)+\Delta g(Y)+d^{y}(t)-f(X,t)\right. \nonumber \\&\left. -\Delta f(X)-d^{x}(t)-u_{\mathrm{eq}} (t)\right) \nonumber \\&+D^{\alpha }\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) =0 \end{aligned}$$
(34)

Therefore, the equivalent control \(u_{\mathrm{eq}} (t)\) is obtained as follows:

$$\begin{aligned} u_{\mathrm{eq}} (t)&= g(Y,t)+\Delta g(Y)+d^{y}(t)-f(X,t)\nonumber \\&-\Delta f(X)-d^{x}(t)\nonumber \\&+D^{2\alpha -1}\left( {k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }}\right) . \end{aligned}$$
(35)

Here, the reaching law is selected as follows:

$$\begin{aligned} u_r (t)=D^{\alpha -1}\left( \zeta _1 s+\zeta _2 |s|^{\delta }\mathrm{sign}(s)\right) , \end{aligned}$$
(36)

where \(\zeta _1, \zeta _2 >0\) are the switching gains and constant scalars and \(\delta \in (0,1)\) is a constant.

Therefore, the overall control \(u(t)\) in the proposed control scheme is determined by

$$\begin{aligned} u(t)&= u_{\mathrm{eq}} (t)+u_r (t)=g(Y,t)+\Delta g(Y)+d^{y}(t)\nonumber \\&-f(X,t)-\Delta f(X)-d^{x}(t)\nonumber \\&+D^{2\alpha -1}\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \nonumber \\&+D^{\alpha -1}\left( \zeta _1 s+\zeta _2 |s|^{\delta }\mathrm{sign}(s)\right) . \end{aligned}$$
(37)

However, since in practical applications, the system uncertainty terms \(\Delta g(Y)\) and \(\Delta f(X)\) and external disturbances \(d^{y}(t)\) and \(d^{x}(t)\) are unknown, the proposed control input is modified as follows:

$$\begin{aligned} u(t)&= g(Y,t)-f(X,t)+D^{\alpha -1}\left[ \left( {\gamma _1 +\gamma _2}\right) \mathrm{sign}(s)\right] \nonumber \\&+D^{2\alpha -1}\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \nonumber \\&+D^{\alpha -1}\left( \zeta _1 s+\zeta _2 |s|^{\delta }\mathrm{sign}(s)\right) \end{aligned}$$
(38)

To guarantee the existence of the sliding motion (i.e., to ensure that the error trajectories \(e_i (t)\) converge to the sliding surface \(s(t)=0)\), the following theorem is proposed and proved.

Theorem 3

Consider the error system (15). If this system is controlled by the control signal (38), then the system trajectories will converge to the sliding surface \(s(t)=0\) in a finite time.

Proof

Selecting a Lyapunov function in the form of \(V_2 (t)=|s(t)|\) and taking its time derivative, one has

$$\begin{aligned} \dot{V}_2(t)=\mathrm{sign}(s)\dot{s} (t) \end{aligned}$$
(39)

Inserting \(\dot{s}(t)\) from (34) into (39), we have

$$\begin{aligned} \dot{V}_2(t)&= \mathrm{sign}(s)\left( D^{1-\alpha }\left( g(Y,t) +\Delta g(Y)+d^{y}(t)\right. \right. \nonumber \\&\left. \left. -f(X,t)-\Delta f(X)-d^{x}(t)-u(t)\right) \right. \nonumber \\&\left. +D^{\alpha } \left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \right) \end{aligned}$$
(40)

It is clear that

$$\begin{aligned} \dot{V}_2 (t)&\le \left| D^{1-\alpha }\left( \Delta g(Y)-\Delta f(X)\right) \right| \nonumber \\&+\left| D^{1-\alpha }\left( d^{y}(t)-d^{x}(t) \right) \right| \nonumber \\&+\, \mathrm{sign}(s)\left( D^{1-\alpha }\left( g(Y,t) -f(X,t)-u(t)\right) \right. \nonumber \\&\left. +D^{\alpha }\left( k_1 e_1 +k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \right) \end{aligned}$$
(41)

Based on Assumptions 1 and 2 and inequalities (12) and (13), one has

$$\begin{aligned} \dot{V}_2 (t)&\!\le \!&\gamma _1\! +\!\gamma _2 \!+\!\mathrm{sign}(s)\left( D^{1-\alpha }\left( g(Y,t)\right. \right. \nonumber \\&\left. \left. \!-\!f(X,t)\!-\!u(t)\right) \!+\!\!D^{\alpha } \left( k_1 e_1 \!+\!k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \right) \nonumber \\ \end{aligned}$$
(42)

Introducing the control law (38) into the right-hand side of the above inequality, one obtains

$$\begin{aligned} \dot{V}_2 (t)&\le \gamma _1 +\gamma _2 +\mathrm{sign}(s)\left( D^{1-\alpha }\left( g(Y,t)-f(X,t)\right. \right. \nonumber \\&\left. \!-\!\left( g(Y,t)\! -\!f(X,t)\!+\!D^{\alpha -1}\left[ \left( \gamma _1 +\gamma _2\right) \mathrm{sign}(s)\right] \right. \right. \nonumber \\&+D^{2\alpha -1}\left( k_1 e_1+k_2 \mathrm{sign}(e_1) |e_1|^{\rho }\right) \nonumber \\&\left. \left. +D^{\alpha -1}\left( \zeta _1 s+\zeta _2 |s|^{\delta }\mathrm{sign}(s)\right) \right) \right) \nonumber \\&\left. +D^{\alpha }\left( k_1 e_1+k_2 \mathrm{sign}(e_1)|e_1|^{\rho }\right) \right) \end{aligned}$$
(43)

After some simple manipulations and based on Properties 1 and 3 and Eqs. (4) and (6), one can obtain

$$\begin{aligned} \dot{V}_2 (t)\le -\mathrm{sign}(s)\left( \zeta _1 s+\zeta _2 |s|^{\delta }\mathrm{sign}(s)\right) \end{aligned}$$
(44)

Based on \(\mathrm{sign}(s)s=|s|\) and \(\mathrm{sign}^{2}(s)=1\), one has

$$\begin{aligned} \dot{V}_2(t)\le -\left( \zeta _1 s+\zeta _2 |s|^{\delta }\right) \le -\zeta |s|, \end{aligned}$$
(45)

where \(\zeta =\min \left\{ \zeta _i (i=1, 2)\right\} \).

Therefore, according to Theorem 1, the state trajectories of the error system (15) will converge to \(s(t)=0\) asymptotically. In order to show that the sliding motion occurs in finite time, we can obtain the reaching time as follows.

From inequality (45), we have

$$\begin{aligned} \dot{V}_2 (t)=\frac{\mathrm{d}|s|}{\mathrm{d}t}\le -\zeta \left( |s|+|s|^{\delta }\right) \end{aligned}$$
(46)

It is clear that

$$\begin{aligned} \mathrm{d}t&\le -\frac{\mathrm{d}|s|}{\zeta \left( |s|+|s|^{\delta }\right) }=-\frac{|s|^{-\delta }\mathrm{d}|s|}{\zeta \left( |s|^{1-\delta }+1\right) }\nonumber \\&=-\frac{1}{\zeta \left( 1-\delta \right) }\frac{\mathrm{d}|s|^{1-\delta }}{\left( |s|^{1-\delta }+1\right) } \end{aligned}$$
(47)

Taking integral of both sides of (47) from 0 to \(t_r\) and setting \(s(t_r)=0\), we have

$$\begin{aligned} t_r&\le -\frac{1}{\zeta (1-\delta )}\int \limits _{s(0)}^{s(t_r)} \frac{\mathrm{d}|s|^{1-\delta }}{|s|^{1-\delta }+1}\nonumber \\&=-\frac{1}{\zeta (1-\delta )}\mathrm{ln}\left( |s|^{1-\delta }+1\right) \left| {{\begin{array}{l} s(t_r)\\ s(0)\\ \end{array}}} \right. \nonumber \\&=\frac{1}{\zeta (1-\delta )}\mathrm{ln}\left( |s(0)|^{1-\delta }+1\right) \end{aligned}$$
(48)

Therefore, the state trajectories of the error system (15) will converge to \(s(t)=0\) in the finite time \(T_2 \le \frac{1}{\zeta (1-\delta )}\mathrm{ln}\left( |s(0)|^{1-\delta }+1\right) \). This completes the proof.\(\square \)

Remark 4

The proposed fractional sliding mode controller of Eqs. (16) and (38) is applicable for synchronization of two identical uncertain fractional-order chaotic systems with different initial conditions, if the systems (10) and (11) satisfy \(f(\cdot )=g(\cdot )\).

Theorem 4

Consider the fractional-order chaotic system (10). If this system is controlled by the single control signal (49), then the system trajectories will converge to the sliding surface \(s(t)=x_2+D^{\alpha -1}\left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) =0\) in a finite time.

$$\begin{aligned} u(t)&= -\left( f(X,t)+D^{\alpha -1}\left[ \left( \sigma _1+\sigma _2\right) \mathrm{sign}(s)\right] \right. \nonumber \\&+D^{2\alpha -1} \left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \nonumber \\&\left. +D^{\alpha -1} \left( \xi _1 s+\xi _2 |s|^{\mu }\mathrm{sign}(s)\right) \right) , \end{aligned}$$
(49)

where \(\left| D^{1-\alpha }\Delta f(X)\right| \le \sigma _1, \left| D^{1-\alpha }d^{x}(t)\right| \le \sigma _2, \sigma _1\) and \(\sigma _2\) are given positive constants, \(\mu \in (0, 1)\) is a constant, and \(\xi _1\) and \(\xi _2\) are two positive gains.

Proof

Choosing a Lyapunov function in the form of \(V_3 (t)=|s(t)|\) and taking its time derivative, one has

$$\begin{aligned} \dot{V}_3 (t)=\mathrm{sign}(s)\dot{s}(t) \end{aligned}$$
(50)

Knowing \(\dot{s}(t)=\dot{x}_2 +D^{\alpha }\left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \) and based on Property 3 and Eq. (6), we have

$$\begin{aligned} \dot{V}_3 (t)\!=\!\mathrm{sign}(s)\left( \dot{x}_2\! +\!D^{\alpha }\left( k_1 x_1\! +\!k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \right) \nonumber \\ \end{aligned}$$
(51)

Using Property 1 and Eq. (4), one obtains

$$\begin{aligned} \dot{V}_3(t)&= \mathrm{sign}(s)\left( D^{1-\alpha } \left( D^{\alpha }x_2\right) \right. \nonumber \\&\left. +D^{\alpha }\left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho } \right) \right) \end{aligned}$$
(52)

Using the system dynamics (10), one can obtain

$$\begin{aligned} \dot{V}_3 (t)&\!=\!&\mathrm{sign}(s)\left( D^{1-\alpha }\left( f(X,t)\! +\!\Delta f(X)\right. \right. \nonumber \\&\left. \left. \!+\!d^{x}(t)\!+\!u(t)\right) \!+\!D^{\alpha }\left( k_1 x_1\! +\!k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \right) \nonumber \\ \end{aligned}$$
(53)

It is obvious that

$$\begin{aligned} \dot{V}_3 (t)&\le \left| D^{1-\alpha }\Delta f(X)\right| +\left| D^{1-\alpha }d^{x}(t)\right| \nonumber \\&+\, \mathrm{sign}(s)\left( D^{1-\alpha } \left( f(X,t)+u(t)\right) \right. \nonumber \\&\left. +D^{\alpha }\left( k_1 x_1 +k_2 \mathrm{sign}(x_1) |x_1|^{\rho }\right) \right) \end{aligned}$$
(54)

Introducing control law (49) into the right-hand side of (54), we get

$$\begin{aligned} \dot{V}_3 (t)&\le \sigma _1 +\sigma _2 +\mathrm{sign}(s)\left( D^{1-\alpha }\left( f(X,t)\right. \right. \nonumber \\&-\left( \left( f(X,t) +D^{\alpha -1}\left[ \left( \sigma _1 +\sigma _2\right) \mathrm{sign}(s)\right] \right. \right. \nonumber \\&+D^{2\alpha -1} \left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \nonumber \\&\left. \left. \left. +D^{\alpha -1}\left( \xi _1 s+\xi _2 |s|^{\mu }\mathrm{sign}(s)\right) \right) \right) \right) \nonumber \\&\left. +D^{\alpha }\left( k_1 x_1 +k_2 \mathrm{sign}(x_1)|x_1|^{\rho }\right) \right) \end{aligned}$$
(55)

From some simple mathematical manipulations and on the basis of Properties 2 and 3 and Eqs. (5) and (6), we have

$$\begin{aligned} \dot{V}_3 (t)\le -\left( \xi _1 s+\xi _2 |s|^{\mu }\right) \le -\xi |s|, \end{aligned}$$
(56)

where \(\xi =\min \{\xi _1, \xi _2\}\).

Therefore, from Theorem 1, the state trajectories of the chaotic system (10) will converge to \(s(t)=0\) asymptotically. Moreover, based on the inequality (56) and using a similar approach in Eqs. (46)–(48), one can easily prove that the sliding motion happens in the finite time \(T_3 \le \frac{1}{\xi (1-\mu )}\mathrm{ln}\left( |s(0)|^{1-\mu }+1\right) \). Thus the proof is completed.

Remark 5

It should be noticed that as mentioned in [30], the nonsmooth Lyapunov functions such as \(V(t)=|e(t)|\) and \(V(t)=|s(t)|\) are usual to show the finite-time stability of a system.

Remark 6

It is noted that due to the existence of chaos in real world systems and many useful applications in engineering, synchronization and stabilization of chaotic fractional/integer-order systems have attracted significant interests in the recent years [33–48].

5 Numerical simulations

In this section, two illustrative examples are presented to illustrate the effectiveness and applicability of the proposed fractional sliding mode scheme and to verify the theoretical results of the paper. Numerical simulations are performed using MATLAB software. The numerical approach described in the following subsection with a step time of 0.001 is applied to solve the fractional-order equations.

5.1 Numerical method for solving fractional differential equations

Diethelm et al. [49] have proposed a reliable approximate numerical technique for numerical solving of fractional-order differential equations, which is a generalization of the Adams–Bashforth–Moulton algorithm for ordinary differential equations. This method works on the basis of a predictor–corrector scheme using the Caputo definition of the fractional-order differential equations. The main procedure of this approach is as follows.

Consider the following fractional-order differential equation.

$$\begin{aligned}&D^{\alpha }y(t)=f(y,t),\quad 0\le t\le T\nonumber \\&y^{(k)}(0)=y_0^{(k)} , k=0, 1, \ldots , m-1 (m=\lceil \alpha \rceil ) \end{aligned}$$
(57)

which is equivalent to the following Volterra integral equation.

$$\begin{aligned} y(t)\!=\!\sum _{k=0}^{m-1} y_0^{(k)} \frac{t^{k}}{k!}\!+\!\frac{1}{\Gamma (\alpha )}\int \limits _0^t (t-s)^{\alpha \!-\!1}f(y(s), s)\mathrm{d}\nonumber \\ \end{aligned}$$
(58)

Setting \(h=\frac{T}{N}, t_n =nh, n=0, 1, 2, \ldots , N\), the above equation becomes

$$\begin{aligned} y_h (t_{n+1})&= \sum _{k=0}^{m-1} c_k\frac{t_{n+1}^k}{k!}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}f(y_h^p (t_{n+1}), t_{n+1})\nonumber \\&+\frac{h^{\alpha }}{\Gamma (\alpha +2)}\mathop \sum \limits _{j=0}^n a_{j, n+1} f(y_h (t_j), t_j) \end{aligned}$$
(59)

where

$$\begin{aligned}&a_{j, n+1} \!=\!\left\{ {{\begin{array}{l@{\quad }l} n^{\alpha +1}\!-\!(n\!-\!\alpha )(n\!+\!1)^{\alpha } &{}\mathrm{if} j\!=\!0 \\ (n\!-\!j\!+\!2)^{\alpha +1}\!+\!(n\!-\!j)^{\alpha +1}\\ -2(n\!-\!j\!-\!1)^{\alpha +1} &{}\mathrm{if} 1\le j\le n\\ 1 &{}\mathrm{if} j\!=\!n\!+\!1 \\ \end{array}}} \right. \nonumber \\&y_h^p (t_{n+1})\!=\!\sum _{k=0}^{m-1} c_k \frac{t_{n+1}^k}{k!}\!+\!\frac{1}{\Gamma (\alpha )} \sum _{j=0}^n b_{j, n\!+\!1} f(y_h (t_j), t_j)\nonumber \\&b_{j,n+1}\!=\!\frac{h^{\alpha }}{\alpha }\left( (n\!+\!1\!-\!j)^{\alpha }\!-\!(n\!-\!j)^{\alpha }\right) \end{aligned}$$
(60)

The estimation error of this technique is

$$\begin{aligned} e\!=\!\max \left| y(t_j)\!-\!y_h (t_j)\right| \!=\!O(h^{p}), j\!=\!1, 2, \ldots , N,\nonumber \\ \end{aligned}$$
(61)

where \(p=\min (2, 1+\alpha )\).

5.2 Example 1: Synchronization of fractional-order Duffing–Holmes and Van der Pol systems

This example illustrates the effectiveness of the proposed fractional terminal sliding mode controller in solving the problem of chaos synchronization between two different fractional-order chaotic systems. Consider the following fractional-order uncertain Duffing–Holmes system [24] as the slave system and the fractional-order uncertain Van der Pol system [50] as the master system.

$$\begin{aligned}&\hbox {Duffing--Holmes system:} \,\left\{ {\begin{array}{l} D^{\alpha }x_1 \!=\!x_2\\ D^{\alpha }x_2 \!=\!x_1 \!-\!0.25x_2\! -\!x_1^3\\ \! +\,0.3\cos (t)\!+\!\Delta f(X)\\ \!+\,d^{x}(t)\!+\!u(t)\\ \end{array}}\right. \nonumber \\ \end{aligned}$$
(62)
$$\begin{aligned}&\hbox {Van der Pol system: }\left\{ {\begin{array}{l} D^{\alpha }y_1 \!=\!y_2\\ D^{\alpha }y_2 \!=\!-\!y_1 \!-\!\left( {1\!-\!y_1^2}\right) \\ \left( {1.2\!-\!3y_1^2}\right) y_2 \!+\!\sin (0.4t)\\ \!+\,\Delta g(Y)\!+\!d^{y}(t)\\ \end{array}}\right. \end{aligned}$$
(63)

The uncertainty terms of the drive and response systems are selected as follows:

$$\begin{aligned} \Delta f(X)+d^{x}(t)&= 0.15\cos (3t)x_2 -0.1\sin (t) \end{aligned}$$
(64)
$$\begin{aligned} \Delta g(Y)+d^{y}(t)&= 0.1\sin (2t)y_2 +0.15\cos (5t) \end{aligned}$$
(65)

Initial conditions of the slave and master systems are selected as \(x_1 (0)=0.2, x_2 (0)=-0.2\) and \(y_1 (0)=-0.1, y_2 (0)=0.3\), respectively. The control parameters for the controller (38) are chosen as \(k_1 =k_2 =1, \rho =\delta =0.9, \zeta _1 =\zeta _2 =2\), and \(\gamma _1 =\gamma _2 =0.75\). The fractional-order \(\alpha \) is also set to 0.9 to ensure the existence of chaos for the Duffing–Holmes and Van der Pol systems [24, 50].

We use Eq. (16) and design the following sliding surface.

$$\begin{aligned} s(t)=e_2 +D^{-0.1}\left( e_1 +\mathrm{sign}(e_1)|e_1|^{0.9}\right) \end{aligned}$$
(66)

Subsequently, according to Eq. (33), the proper control input is designed as follows:

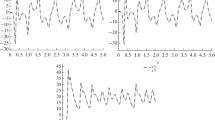
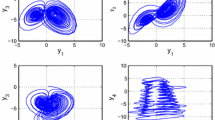
$$\begin{aligned} u(t)&= -\, y_1 -(1\!-\!y_1^2)(1.2\!-\!3y_1^2)y_2 +\sin (0.4t)-x_1\nonumber \\&+\, 0.25x_2 +x_1^3 \!-\!0.3\cos (t)+1.5D^{-0.1}\mathrm{sign}(s)\nonumber \\&+\, D^{0.8}\left( e_1 +\mathrm{sign}(e_1)|e_1|^{0.9}\right) \nonumber \\&+\, D^{-0.1}\left( 2s+2|s|^{0.9}\mathrm{sign}(s)\right) \end{aligned}$$
(67)

The synchronization errors between the fractional-order uncertain Duffing–Holmes system and Van der Pol system are shown in Fig. 1. It can be seen that the synchronization errors converge to zero, which indicates that the fractional-order Duffing–Holmes and Van der Pol systems are indeed synchronized, as illustrated in Figs. 2 and 3. The time response of the sliding surface (66) is plotted in Fig. 4. It is clear that the sliding surface converges to zero in finite time. The time history of the applied control input (67) is depicted in Fig. 5. Obviously, the control input is feasible in practical applications.

Fig. 1
figure 1

State trajectories of the synchronization error system

Full size image
Fig. 2
figure 2

State trajectories of the master and slave systems (\(x_1 -y_1)\)

Full size image
Fig. 3
figure 3

State trajectories of the master and slave systems (\(x_2 -y_2\))

Full size image
Fig. 4
figure 4

Time response of the applied sliding surface for the synchronization error system

Full size image
Fig. 5
figure 5

Time history of the applied control input for the synchronization error system

Full size image

5.3 Example 2: chaos control of fractional-order nonautonomous gyro

The usefulness and applicability of the proposed method are validated in this example via chaos control of a fractional-order gyro. The mathematical equations of an uncertain fractional-order gyro with control input are represented as follows [26]:

$$\begin{aligned} \hbox {Gyro system: }\left\{ {\begin{array}{l} {{\begin{array}{l} D^{\alpha }x_1 =x_2\\ D^{\alpha }x_2 =\frac{-100\left( {1-\cos x_1}\right) ^{2}}{\sin ^{3}x_1}\\ -0.5x_2 -0.05x_2^3 +\sin x_1\\ +35.5\sin 25t\sin x_1 \\ \end{array}}} \\ +\Delta f(X)+d^{x}(t)+u(t)\\ \end{array}}\right. \end{aligned}$$
(68)

where \(x_1 \) denotes the rotation angle, \(x_2\) represents the rotation angle velocity, and \(\Delta f(X)+d^{x}(t)=0.1\cos (2t)x_2-0.15\sin (t)\). For \(\alpha =0.97\), the maximal Lyapunov exponent of this system is equal to \(\lambda _\mathrm{max} =0.2703\), which indicates that the fractional-order gyro system possesses chaotic behavior.

In order to suppress the chaotic behavior of the fractional-order gyro (68), we apply the proposed sliding mode controller (49) with \(k_1 =k_2 =2, \xi _1 =\xi _1 =0.5, \mu =\rho =0.9, \sigma _1 =0.45\), and \(\sigma _2 =0.5\). Initial conditions of the gyro system are selected as \(x_1 (0)=1\) and \(x_2 (0)=-1\).

Based on Theorem 4, the following terminal sliding surface is applied.

$$\begin{aligned} s(t)=x_2 +D^{-0.03}\left( {2x_1 +2\mathrm{sign}(x_1)|x_1|^{0.9}}\right) \end{aligned}$$
(69)

Accordingly, using Eq. (49), the following control input is designed.

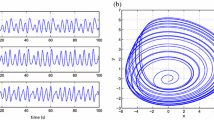
$$\begin{aligned} u(t)&= -\! \left( \frac{\!-\!100\left( {1\!-\!\cos x_1}\right) ^{2}}{\sin ^{3}x_1}\!-\!0.5x_2\! -\!0.05x_2^3 \!+\!\sin x_1\right. \nonumber \\&+\,35.5\sin 25t\sin x_1 \!+\!0.95D^{-0.03}\mathrm{sign}(s)\nonumber \\&+\,D^{0.94}\left( 2x_1 \!+\!2\mathrm{sign}(x_1)|x_1|^{0.9}\right) \nonumber \\&\left. +\,D^{-0.03}\left( 0.5s\!+\!0.5|s|^{0.9}\mathrm{sign}(s)\right) \right) \end{aligned}$$
(70)

Figure 6 shows the state trajectories of the controlled fractional-order gyro system (68). It is seen that the chaotic behavior of the system is suppressed and, therefore, there is no strange attractor anymore. The time response of the sliding surface (69) is revealed in Fig. 7. One can see that the sliding surface approaches to the origin over a finite time. Moreover, the time history of the applied control input (70) is plotted in Fig. 8. It is seen that the control input is practical.

Fig. 6
figure 6

State trajectories of the controlled fractional gyro system

Full size image
Fig. 7
figure 7

Time response of the applied sliding surface for controlling the fractional gyro system

Full size image
Fig. 8
figure 8

Time history of the applied control input for controlling the fractional gyro system

Full size image

6 Conclusions

This paper concerns the problem of stabilization/synchronization of second-order uncertain nonautonomous fractional chaotic systems. We proposed a new fractional terminal sliding surface which has the finite-time stability characteristics. Then, based on the sliding mode control theory and fractional Lyapunov stability theory, a robust switching sliding mode control law is designed to ensure the occurrence of the sliding motion in a finite time. Simulation results show that the proposed controller can effectively synchronize two different uncertain fractional second-order chaotic systems. Moreover, an illustrative example illustrates the effectiveness of the proposed scheme in chaos control of an uncertain fractional gyro system. The main advantages of the proposed fractional sliding mode are as follows: (1) It is robust against system uncertainties and external disturbances; (2) It guarantees that the closed-loop system is stable in a given finite time rather than merely asymptotic stability; and (3) It has only one control input. Therefore, it is simple and easy to implement.