1 Introduction

Autonomous unmanned aerial vehicles (AUAV) have been the focus of research due to their high flight flexibility. These vehicles have been used in various applications such as rescue missions (Bravo et al., 2019), mapping for 3D reconstruction purposes (Saska et al., 2017), civil applications (Finn & Wright, 2012) and use in wireless network (Jawhar et al., 2016), as well as traffic monitoring (Kanistras et al., 2013). In recent years, control researchers have paid more attention to the 3-degree-of-freedom (DoF) laboratory helicopter, which is considered a type of the AUAV (Castañeda et al., 2016). Despite the simple mechanical structure of the 3-DoF helicopter, it is a very complex system from the control point of view due to the nonlinearity, model uncertainties and external disturbances (Zhu & Li, 2021). The control problem of the 3-DoF helicopter has been studied through different control approaches.

In recent decades, various types of controllers are proposed and applied to a 3-DoF helicopter.

In Meza-Sánchez et al. (2015), a sliding mode controller is designed along with a velocity sliding mode observer. It should be noted that the sliding mode-based methods suffer from the chattering phenomenon. In another study, a decentralized consensus control is developed for multiple helicopters with a disturbance estimator in the presence of uncertainties (Li et al., 2015). An uncertainty estimator is designed to observe the unknown dynamics in Zhu et al. (2015). In Guzey et al. (2019), an LQR controller is combined with a sliding surface to deal with the external disturbance and model uncertainty. Note that the utilized LQR method depends on the linear dynamic model around the equilibrium point, so it will be highly affected by the model uncertainty, originating from the model linearization. In addition, the control efforts have large values and the chattering phenomenon happens as a result of the dominant effect of the model uncertainty, which is mainly due to the model linearization. In Chaoui and Yadav (2020), an adaptive control algorithm is designed to stabilize a 3-DoF helicopter subjected to structured and unstructured model uncertainty. In this study, the parameters of the system are estimated through online learning of the inverse dynamic model. In another study (Li et al., 2018), an output backstepping control along with a state observer is developed to estimate the velocity state to be used in the control scheme. It is claimed that the control approach is robust; however, the effects of the model uncertainties and the external disturbance are ignored. In Castañeda et al. (2016), a continuous differentiator along with an adaptive super twisting scheme is proposed for a 3-DoF helicopter in the presence of the model uncertainties. In this method, a continuous differentiator is used to estimate the state of the system. In this case, replacing the inverse dynamic with the adaptation law results in a higher control effort which in turn requires high-power actuators. Although there has been much research focused on the control of the 3-DoF Helicopter, there are some practical issues like actuator saturation which are less noticed in nonlinear control design. The actuator saturation is a practical problem that arises as a constraint on the control effort. This issue may diminish the performance and effectiveness of the control systems and in some cases even may lead to instability of the closed-loop systems (Lin, 1995).

The actuators saturation problem has been addressed for several nonlinear systems such as cable robots (Ameri et al. 2021a, c) and surface vessels (Zheng et al., 2017). Generally, there are two well-known methods for tackling actuator saturation: observer-based approaches (Fazeli et al., 2022) and dynamic surface control schemes (Ameri et al., 2021b, 2023). The observer-based control design is addressed in several researches to deal with the actuators saturation (Lan et al., 2017a, b; Chen et al., 2015). One of the limitations of the observer-based method for compensating for the actuator saturation is a practical limitation in terms of the real-time computation requirements. It is mainly due to the fact that the response of the observers in practice should be faster than the actual dynamic (Bu et al., 2015). This requirement obliges the designer to have a higher sampling rate for the control loop, which is costly both in terms of the instrumentation and the real-time computation. As mentioned earlier, the other method to deal with actuator saturation is the dynamic surface control approach. In Mousavi and Khayatian (2011, 2016), a backstepping-based dynamic surface control scheme is introduced, which is developed for a class of uncertain saturated systems. In Ponce et al. (2018), a robust controller based on \(H_\infty \) synthesis is designed to control a 3-DoF helicopter in the presence of dead-zone phenomenon in the actuators. This is done through the online linearization of the actual nonlinear dynamic of the system. One of the shortcomings of this method is the computation time for online linearization, leading to delays in practice. In Fischer et al. (2013), a continuous robust integral of the sign of the error control law is proposed for a class of second-order nonlinear systems with a hyperbolic tangent-based saturation approximation. In another study (Liu, 2017), an adaptive backstepping control scheme with a new saturation approximation function is developed for a class of uncertain nonlinear systems. Apart from the above, several researches have been conducted on the theory part of controlling uncertain systems under input saturation (Wen et al., 2011). However, they are limited to the specific classes of uncertain systems, and there is no general method that can include different kinds of uncertainties as a unified approach to be applicable to the 3-DoF helicopter. Moreover, the theoretical outcomes of such researches cannot be directly applied to the AUAV systems. It is mainly due to the their specific definition of the considered class of nonlinear dynamic model. On the other hand, the purely backstepping control is not robust under the model uncertainties and external disturbance. Hence, it has to be used along with another auxiliary controller to guarantee robustness under the model uncertainties and external disturbance.

In this paper, a robust constrained control approach is developed for the 3-DoF helicopter system subjected to the actuator saturation problem, model uncertainties and external disturbance. In this approach, a dynamic surface backstepping control equipped with an adaptive radial basis function (RBF) neural network (NN) is utilized to be robust under the dynamic model uncertainties and external disturbances. In addition, a prevention function is used as a smooth approximation model of the actuator saturation to avoid the undesirable effects of the non-smooth saturation function. Moreover, a Nussbaum-type function is utilized to deal with the complex problem of the inverse calculation of the first derivative of the prevention function. Besides, the weights of the utilized RBF NN are designed as an adaptive law, ensuring the network does not violate the system stability. The closed-loop stability of the overall system is analyzed through Lyapunov’s second method. Finally, a simulation study is performed in detail to evaluate the performance of the proposed approach.

The remainder of the paper is organized as follows. The preliminaries are introduced in Sect. 2. The problem statement is given in Sect. 3. The control design is developed in Sect. 4. The stability analysis is discussed in Sect. 5. In Sect. 6, the simulation study is performed on a 3-DoF helicopter, and in Sect. 7, the paper is concluded.

2 RBF Neural Network

In this section, an overview of RBF NN is presented to be used in the control approach. Radial basis function neural network is a compact network with three layers of input, hidden and output. It is designed to estimate unknown continuous nonlinear functions with the least error. In this type of network, the hidden layer neurons are utilized by an RBF function. The Gaussian function of the desired RBF network is defined as follows:

$$\begin{aligned} g(x) = \exp \left( - \frac{{{x^2}}}{{2{\sigma ^2}}}\right) , \end{aligned}$$
(1)

where \(\sigma \) is the standard deviation. To have a desirable estimation performance of the NN, its adjustable weights must be set correctly in which the estimation error converges to a small vicinity of the origin. Suppose that x, q and W are the network input, the number of hidden layer nodes and the network weights, respectively. The RBF network algorithm is defined as follows (Park & Sandberg, 1991):

$$\begin{aligned} \left\{ \begin{array}{l} {h_j} = g({{{(x - c_{j}^2)}} / {{b_j^2}}}),\\ f(x) = {W^T}h(x) + \varepsilon , \end{array} \right. \end{aligned}$$
(2)

where \(h = [h_1,..., h_q]^T\) is a vector of the Gaussian function \({h_j}\) of all of the hidden layers q, \(c_j\) is the jth neuron’s center point, and \(b_j\) is the width of the Gaussian basis function. The RBF network is used to estimate the function f(.), whose propagation error is \(\varepsilon \le \varepsilon _N\) in which \(\varepsilon _N\) is a bounded upper bound. Moreover, the estimation of f(.), which is the network output, is designed as follows:

$$\begin{aligned} {{\hat{f}}(x)} = {{{\hat{W}}}^T}h(x), \end{aligned}$$
(3)

where \({{\hat{W}}}\) is the adapted weight such that the NN estimation error tends to a small vicinity of the origin. Moreover, the adaptation law of the network weights should be designed to ensure closed-loop system stability. It is to be noted that the adaptive weights are states of the closed-loop system. Therefore, they should also be incorporated in the Lyapunov candidate function through the stability analysis procedure to ensure the overall system stability.

3 Problem Statement

The general dynamic of a 3-DoF helicopter includes three motions of elevation, travel and pitch, which are specified in the schematic plan of a 3-DoF represented in Fig. 1. As this type of helicopter possesses only two actuators, the control scheme can just force two system states to follow a desired path and the remained state follows a trajectory that depends on the motions of the other states. In this paper, the dynamics of elevation and pitch motions are considered for motion control. Hence, the dynamic equations of a 3-DoF Helicopter are represented according to Lan et al. (2017b), as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} {\ddot{\alpha }= \frac{{{k_f}{L_a}}}{{{J_\alpha }}}({u_1} + {u_2})\cos (\gamma ) - \frac{{({M_h}g{L_a})}}{{J_\alpha }}\sin ({\alpha }) + {\zeta _\alpha }},\\ {\ddot{\gamma }= \frac{{{k_f}{L_h}}}{{{J_\gamma }}}({u_1} - {u_2}) + {\zeta _\gamma }}, \end{array}} \right. \end{aligned}$$
(4)

where \(\alpha \) and \(\gamma \) are the elevation and pitch angles, respectively. Furthermore, \({k_f}\) is the propeller force-thrust constant, g is the gravity acceleration, \(L_a\) is the distance between the travel axis and the helicopter body, \(L_h\) is the distance between the pitch axis and each motor, \(M_h\) is the mass of the helicopter, and \(J_\alpha \) and \(J_\gamma \) are the moments of inertia of the elevation and pitch axes, respectively. Moreover, \({\zeta _\alpha }\), \({\zeta _\gamma }\), \(u_1\) and \(u_2\) are the external disturbances and unmodeled dynamics of the elevation and pitch channels and the control input of the front and back motors, respectively.

Fig. 1
figure 1

Schematic plan of a 3-DoF helicopter

Full size image

In order to simplify the dynamic equations, without loss of generality, the augmented motion, control input and disturbance are defined as \(\varvec{x} = {[\alpha ~\gamma ]^T}\), \(\varvec{u} = {[{u_1}~{u_2}]^T}\) and \(\varvec{\zeta }_\textrm{aug} = {[{\zeta _\alpha }~{\zeta _\gamma }]^T}\), respectively. It is worth noting that the actuator saturation constraint on the control input is considered in this work as a nonlinear prevention function \({\varvec{u}_\textrm{sat}} = \varvec{\Omega } (\varvec{u})\), which affects the actuators input \(\varvec{u}\). Thus, (4) is rewritten as:

$$\begin{aligned} \varvec{\ddot{x}} = \varvec{\phi } (\varvec{x}) + \varvec{\xi } (\varvec{x}){\varvec{u}_\textrm{sat}} + \varvec{\zeta }_\textrm{aug}. \end{aligned}$$
(5)

In (5), the nonlinear vector \(\varvec{\phi } (\varvec{x})\) and nonlinear matrix \(\varvec{\xi } (\varvec{x})\) are defined as follows:

$$\begin{aligned} \begin{array}{l} \varvec{\phi } (\varvec{x}) = \left[ {\begin{array}{*{20}{c}} { - \frac{{({M_h}g{L_a})}}{{J_\alpha }}\sin ({x_1})}\\ 0 \end{array}} \right] ,\\ \varvec{\xi } (\varvec{x}) = \left[ {\begin{array}{*{20}{c}} {{b_1}\cos ({x_2})}&{}{{b_1}\cos ({x_2})}\\ {{b_2}}&{}{ - {b_2}} \end{array}} \right] , \end{array} \end{aligned}$$
(6)

where \(b_1 = \frac{k_f L_a}{J_\alpha }\) and \(b_2 = \frac{{{k_f}{L_h}}}{{{J_\gamma }}}\).

Remark 1

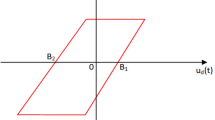
The nonlinear prevention function in this work is selected as a differentiable hyperbolic tangent function, as below:

$$\begin{aligned} \varvec{\Omega }(\varvec{u}) = {u_m}\tanh \bigg (\frac{\varvec{u}}{u_m}\bigg ), \end{aligned}$$
(7)

where \(u_m\) is the bound of the saturation constraint.

Remark 2

As the actuator saturation is treated in this research by posing a prevention function on the designed control input \(\varvec{u}\), the resultant generated \(\varvec{u}\) is passed through the prevention function before being fed to the actuator.

Assumption 1

The control input \(\varvec{u}\), in this paper, is continuous and differentiable with the first derivative being

$$\begin{aligned} \dot{\varvec{u}} = \varvec{\psi }. \end{aligned}$$
(8)

Therefore, designing \(\varvec{\psi }\) as the new controller for the system, \(\dot{\varvec{u}}\) is determined. Thereafter, \(\varvec{u}\) is derived by integrating from \(\dot{\varvec{u}}\).

4 Control Design

In the previous section, (5) represents a non-affine dynamic equation with respect to the control input \(\varvec{u}\), meaning nonlinear dependency on the control input. It is worth noting that the traditional control methods have been developed for affine system and there is no general method to generalize them to the non-affine systems. To address this problem in this section, the dynamic is changed to an affine third-order dynamic equation of motion. Consider the saturated control input \({\varvec{u}_\textrm{sat}}\) as a new system state, we have:

$$\begin{aligned} \varvec{\chi } = {\varvec{u}_\textrm{sat}}. \end{aligned}$$
(9)

Taking the first derivative of (9) and using (8) yield:

$$\begin{aligned} {{\dot{\varvec{\chi }}}} = {\frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}} \varvec{\psi } }. \end{aligned}$$
(10)

To describe the entire dynamic of the third-order system in state space form, new states can be defined as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{\varvec{z}_1} = \varvec{x}},\\ {{\varvec{z}_2} = {\varvec{\dot{x}}}},\\ {{\varvec{z}_3} = \varvec{\chi } }. \end{array}} \right. \end{aligned}$$
(11)

Differentiating (11) and using (10) and (5), the third-order dynamic equation of the 3-DoF helicopter in the presence of actuator saturation is described in the state space form as:

$$\begin{aligned} \left\{ {\begin{array}{l} {{{ {\varvec{\dot{z}}}}_1} = {{\varvec{z}}_2}},\\ {{{ {\varvec{\dot{z}}}}_2} = \varvec{\phi } ({\varvec{z}_1}) + \varvec{\xi } ({\varvec{z}_1}){\varvec{z}_3} + \varvec{\zeta }_\textrm{aug} },\\ {{{ {\varvec{\dot{z}}}}_3} = \frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}} \varvec{\psi } }. \end{array}} \right. \end{aligned}$$
(12)

Note that the above dynamic system is affine with respect to the control input \(\varvec{\psi }\). Besides, the model uncertainties are supposed to be as follows:

$$\begin{aligned} \left\{ {\begin{array}{l} \varvec{\phi } ({\varvec{z}_1}) = {\hat{\varvec{\phi }}} ({\varvec{z}_1}) + \Delta \varvec{\phi },\\ \varvec{\xi } ({\varvec{z}_1}) = {\hat{\varvec{\xi }}} ({\varvec{z}_1}) + \Delta \varvec{\xi }, \end{array}} \right. \end{aligned}$$
(13)

where \(\hat{*}\) and \(\Delta *\) represent the nominal values and the uncertainty terms, respectively. Substituting (13) into (12) results in:

$$\begin{aligned} \left\{ {\begin{array}{l} {{{ {\varvec{\dot{z}}}}_1} = {{\varvec{z}}_2}},\\ {{{ {\varvec{\dot{z}}}}_2} = {\hat{\varvec{\phi }}} ({\varvec{z}_1}) + {\hat{\varvec{\xi }}} ({\varvec{z}_1}){\varvec{z}_3} + \varvec{\zeta } },\\ {{{ {\varvec{\dot{z}}}}_3} = \frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}} \varvec{\psi } }, \end{array}} \right. \end{aligned}$$
(14)

where \(\varvec{\zeta } = \varvec{\zeta }_\textrm{aug} + {\Delta \varvec{\phi }} + {\Delta \varvec{\xi }}{\varvec{z}_3}\) includes all the disturbances and uncertainties in the system. As the control purpose is trajectory tracking, the following tracking errors are defined:

$$\begin{aligned} {\varvec{\mu } _1}= & {} {\varvec{z}_1} - \varvec{x_d}, \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{\mu } _2}= & {} {\varvec{z}_2} - {\varvec{\sigma } _1}, \end{aligned}$$
(16)
$$\begin{aligned} {\varvec{\mu } _3}= & {} {\varvec{z}_3} - {\varvec{\sigma } _2}, \end{aligned}$$
(17)

in which \(\varvec{x_d}\), \({\varvec{\sigma } _1}\) and \({\varvec{\sigma } _2}\) are the desired trajectories to be followed by the angular velocities of the helicopter, the designable desired trajectories for \({\varvec{z}_2}\) and \({\varvec{z}_3}\) which works as a virtual controller in the first and second steps in the backstepping control scheme, respectively.

According to the backstepping control nature, the following three steps are allocated to propose the control scheme for each subsystem of the third-order dynamic system of the errors (15), (16), (17).

4.1 First Step

Taking the first derivative of (15) and using (14), one can write:

$$\begin{aligned} {{{\dot{\varvec{\mu }} }_1} = {\varvec{z}_2} - {\varvec{\dot{x}}_d}}. \end{aligned}$$
(18)

From (16), we have:

$$\begin{aligned} {{\dot{\varvec{\mu }} }_1} = {\varvec{\mu } _2} + {\varvec{\sigma } _1} - {\varvec{\dot{x}}_d}, \end{aligned}$$
(19)

where \({\varvec{\sigma } _1}\) acts as a virtual controller for this dynamic subsystem. The virtual control law \({\varvec{\sigma } _1}\) is designed to stabilize this dynamic equation, as follows:

$$\begin{aligned} {{\varvec{\sigma } _1} = {\varvec{\dot{x}}_d} - {\varvec{\lambda } _1}{\varvec{\mu } _1}}, \end{aligned}$$
(20)

where \({\varvec{\lambda }_1}\) is a diagonal positive definite matrix.

The Lyapunov function \({V_1} = \frac{1}{2}(\varvec{\mu } _1^T{\varvec{\mu } _1})\) is selected to evaluate the stability of the first subsystem. Taking its first derivative and substituting (19), we have:

$$\begin{aligned} {{\dot{V}}_1} = {\varvec{\mu }_1}^T{{\dot{\varvec{\mu }} }_1} = {\varvec{\mu }_1}^T({\varvec{\mu }_2} + {\varvec{\sigma }_1} - {\varvec{\dot{x}}_d}). \end{aligned}$$
(21)

Recalling the designed virtual control (20) and simplifying yield:

$$\begin{aligned} {{\dot{V}}_1} = - {\varvec{\mu }_1}^T{\varvec{\lambda } _1}{\varvec{\mu }_1} + {\varvec{\mu }_1}^T{\varvec{\mu }_2}. \end{aligned}$$
(22)

4.2 Second Step

The dynamic equation of the second subsystem can be provided by taking the derivative of (16), which results in:

$$\begin{aligned} {{\dot{\varvec{\mu }} }_2} = {\hat{\varvec{\phi }}} ({\varvec{z}_1}) + {\hat{\varvec{\xi }}} ({\varvec{z}_1})({\varvec{\mu } _3} + {\varvec{\sigma } _2}) + \varvec{\zeta } - {{\dot{\varvec{\sigma }} }_1}. \end{aligned}$$
(23)

It is to be noted that \(\varvec{\zeta }\) is estimated in this paper using RBF NN, so it is considered as \(\varvec{\zeta } = \varvec{\omega }^T \varvec{\theta }\) where \(\varvec{\omega }\) represents the actual network weights and \(\varvec{\theta }\) stands for the basis function vector. In (23), \({\varvec{\sigma }_2}\) plays the virtual controller role for (23), so it should be designed to stabilize the dynamic subsystem (23). Hence, this virtual controller is proposed as:

$$\begin{aligned} {\varvec{\sigma } _2}= & {} {{\hat{\varvec{\xi }}} ^{ - 1}}({\varvec{z}_1})( - \varvec{\hat{\phi }} ({\varvec{z}_1}) - {{\hat{\varvec{\omega }} }^T} \varvec{\theta } ({\varvec{z}_1})\nonumber \\{} & {} + {{\dot{\varvec{\sigma }}}_1} - {\varvec{\lambda } _2}{\varvec{\mu } _2} - {\varvec{\mu } _1}), \end{aligned}$$
(24)

where \({\varvec{\lambda } _2}\) is a diagonal positive definite matrix. The stability of the second subsystem with the virtual controller, proposed in (24), is analyzed via the following candidate Lyapunov function:

$$\begin{aligned} {V_2} = \frac{1}{2}(\varvec{\mu } _2^T{\varvec{\mu } _2} + tr({\tilde{\varvec{\omega }}^T}{\varvec{\Lambda } ^{ - 1}}{\tilde{\varvec{\omega }}} )). \end{aligned}$$
(25)

In this function, \({{\tilde{\varvec{\omega }}} = {\hat{\varvec{\omega }}} - \varvec{\omega } }\) is the adaptation errors of the NN weights, \(\varvec{\hat{\omega }}\) is the estimated value for the NN weights using an adaption law and \(\varvec{\Lambda }\) is an invertible diagonal positive definite matrix. Taking the first derivative of the Lyapunov function with respect to time and substituting (23) result in:

$$\begin{aligned} {\dot{V}}_2= & {} {\varvec{\mu } _2}^T{{\dot{\varvec{\mu }} }_2} + tr({{\varvec{\tilde{\omega }}}^T}{{\varvec{\Lambda } }^{ - 1}}\varvec{\dot{{\hat{\omega }}}} )\nonumber \\= & {} {\varvec{\mu } _2}^T({\hat{\varvec{\phi }}} ({\varvec{z}_1}) + {\hat{\varvec{\xi }}} ({\varvec{z}_1})({\varvec{\mu } _3} + {\varvec{\sigma } _2})\nonumber \\{} & {} + \varvec{\zeta } - {{\dot{\varvec{\sigma }} }_1}) + tr({\varvec{\tilde{\omega }}^T}{\varvec{\Lambda } ^{ - 1}}\varvec{\dot{{\hat{\omega }}}} ). \end{aligned}$$
(26)

Substituting (24) into (26), sorting and simplifying yield:

$$\begin{aligned} {\dot{V}}_2= & {} {\varvec{\mu } _2}^T {\hat{\varvec{\xi }}} ({\varvec{z}_1}){\varvec{\mu } _3} - {\varvec{\mu } _2}^T{\varvec{\lambda } _2}{\varvec{\mu } _2} - {\varvec{\mu } _2}^T{\varvec{\mu } _1} \nonumber \\{} & {} + tr({{\tilde{\varvec{\omega }} }^T}[{\varvec{\Lambda } ^{ - 1}} \varvec{\dot{{\hat{\omega }}}} - \varvec{\theta } ({\varvec{z}_1}) {\varvec{\mu } _2}^T]). \end{aligned}$$
(27)

As mentioned earlier, an RBF NN is utilized to achieve robust performance in the presence of dynamic uncertainties and external disturbances. Hence, there is still a requirement to design an adaptation law for the NN weights to update them online. Therefore, the adaptation law is proposed as follows:

$$\begin{aligned} \varvec{\dot{{\hat{\omega }}} = \varvec{\Lambda } \varvec{\theta } {\varvec{\mu } _2}^T }. \end{aligned}$$
(28)

Substituting (28) into (27) yields:

$$\begin{aligned} {\dot{V}}_2 = {\varvec{\mu } _2}^T {\hat{\varvec{\xi }}} ({\varvec{z}_1}){\varvec{\mu } _3} - {\varvec{\mu } _2}^T {\varvec{\lambda } _2}{\varvec{\mu } _2} - {\varvec{\mu } _2}^T {\varvec{\mu } _1}. \end{aligned}$$
(29)

4.3 Third Step

The dynamic equation of \({\varvec{\mu } _3}\) is created by taking the first derivative of (17) and using (14), as:

$$\begin{aligned} {{{\dot{\varvec{\mu }} }_3} = \frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}} \varvec{\psi } \, - {{\dot{\varvec{\sigma }} }_2}}. \end{aligned}$$
(30)

Hence, (30) is controlled via proposing an adaptive NN backstepping control scheme, as follows:

$$\begin{aligned} \varvec{\psi }= & {} \varvec{F} ( \varvec{\rho } ) \varvec{{\bar{\psi }}}, \end{aligned}$$
(31)
$$\begin{aligned} \varvec{{\bar{\psi }}}= & {} {{\dot{\varvec{\sigma }} }_2} - {{\hat{\varvec{\xi }}} ^T}({\varvec{z}_1}){\varvec{\mu }_2} - {\varvec{\lambda } _3}{\varvec{\mu } _3}, \end{aligned}$$
(32)

where \({\varvec{\lambda }_3}\) is a diagonal positive definite matrix, and \({F_i}({\rho _i})\) is a Nussbaum-type function which is defined as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{F_i}({\rho _i}) = \rho _i^2\cos ({\rho _i})},\\ {{{{\dot{\rho }} }_i} = \vartheta {{{\bar{\psi }} }_i}{{\mu _3}_i},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right. \end{aligned}$$
(33)

in which \(\vartheta \) is a positive constant parameter. The following definition is given for the Nussbaum function.

Definition 1

Wen et al. (2011): If the following equations held for a function F(n), thus it is a Nussbaum function.

$$\begin{aligned} \left\{ {\begin{array}{l} {\mathop {\lim }\limits _{k \rightarrow \pm \infty } \sup \,\frac{1}{k}\int _0^k {F(n)\textrm{d}n = + \infty } },\\ {\mathop {\lim }\limits _{k \rightarrow \pm \infty } \inf \,\frac{1}{k}\int _0^k {F(n)\textrm{d}n = - \infty } }. \end{array}} \right. \end{aligned}$$
(34)

The stability of this subsection is also assessed via the Lyapunov function selected as \({V_3} = {\varvec{\mu } _3}^T {\varvec{\mu } _3}\). Taking the first derivative of this Lyapunov function with respect to time and substituting (30), one may write:

$$\begin{aligned} {\dot{V}}_3 = {\varvec{\mu } _3}^T{{\dot{\varvec{\mu }} }_3} = \varvec{\mu _3}^T\left( \frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}} \varvec{\psi } \, - {{\dot{\varvec{\sigma }} }_2}\right) . \end{aligned}$$
(35)

Substituting (31) into (35) yields:

$$\begin{aligned} {\dot{V}}_3 = {\varvec{\mu } _3}^T\left( \frac{{\partial \varvec{\Omega } }}{{\partial \varvec{u}}}\varvec{F}(\varvec{\rho }) - \,{\varvec{I}_2}\right) \varvec{{\bar{\psi }}} + {\varvec{\mu } _3}^T(\varvec{{\bar{\psi }}} - {{\dot{\varvec{\sigma }} }_2}). \end{aligned}$$
(36)

Using (33) and (32), we have:

$$\begin{aligned} {\dot{V}}_3= & {} - {\varvec{\mu } _3}^T{{\hat{\varvec{\xi }}} ^T}({\varvec{z}_1}){\varvec{\mu } _2} - {\varvec{\mu } _3}^T{\varvec{\lambda } _3}{\varvec{\mu } _3} \nonumber \\{} & {} + \frac{1}{\vartheta }\sum \limits _{i = 1}^2 {\left( {{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i}(\rho _i) - 1\right) } {{{\dot{\rho }} }_i}. \end{aligned}$$
(37)

The present section is allocated to the stability of the subsystems, while the next section presents the stability analysis of the entire system using the results achieved in the present section.

5 Stability Analysis

To analyze the stability of the overall third-order dynamic equations of the system, Theorem 1 is illustrated after Lemma 1 which is used in the proof of the theorem.

Lemma 1

Wen et al. (2011): Let \({F({\rho _i})}\) be a Nussbaum function and V(.) and \(\rho \) be smooth functions defined on \(\left[ {0,{t_f}} \right) \) with \(V(t) \ge 0\) and \(\forall t \in \left[ {0,{t_f}} \right) \), and assume that the following inequality is held:

$$\begin{aligned} V(t) \le V(0){e^{ - ct}} + \frac{{{e^{ - ct}}}}{\vartheta }\int _0^t {\sum \limits _{i = 1}^2 {\left( {{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1\right) } {{{\dot{\rho }} }_i}{e^{c\tau }}d\tau }, \nonumber \\ \end{aligned}$$
(38)

in which \(c>0\), \({{{\frac{{\partial \Omega }}{{\partial u}}}_i}} > 0\) and \(\vartheta >0\). Thus, V(.), \(\rho _i\) and \({\sum \limits _{i = 1}^2 {({{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1)} {{{\dot{\rho }} }_i}{e^{c\tau }}d\tau }\) are bounded on \(\left[ {0,{t_f}} \right) \).

Theorem 1

Consider the closed-loop system of a 3-DoF helicopter with the dynamic equations (4), input prevention function (7), dynamical control law (8) and the proposed control law (31) along with the adaptation law of the NN weights (28) and the Nussbaum function (33) is stable and all the signals of the system are proved to be bounded.

Proof

The following Lyapunov function, including the candidate functions of the three subsystems, is selected as follows:

$$\begin{aligned} V = V_1 + V_2 + V_3. \end{aligned}$$
(39)

Taking the first derivative of (39) with respect to time yields:

$$\begin{aligned} {\dot{V}} = {\dot{V}}_1 + {\dot{V}}_2 + {\dot{V}}_3. \end{aligned}$$
(40)

Substituting (22), (29) and (37) into (40), simplifying and sorting result in:

$$\begin{aligned} {\dot{V}}= & {} - {\varvec{\mu } _1}^T{\varvec{\lambda } _1}{\varvec{\mu } _1} - {\varvec{\mu } _2}^T{\varvec{\lambda } _2}{\varvec{\mu } _2} - {\varvec{\mu } _3}^T{\varvec{\lambda } _3}{\varvec{\mu } _3} \nonumber \\{} & {} + \frac{1}{\vartheta }\sum \limits _{i = 1}^2 {\left( {{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1\right) } {{{\dot{\rho }} }_i}. \end{aligned}$$
(41)

Using (39), we have:

$$\begin{aligned} {\dot{V}} \le cV + \frac{1}{\vartheta }\sum \limits _{i = 1}^2 {\left( {{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1\right) } {{\dot{\rho }}_i}. \end{aligned}$$
(42)

In (42), \(c = \min \{ 2{{\underline{\lambda }}_1},2{{\underline{\lambda }}_2},2{{\underline{\lambda }}_3}\}\), and also \({\underline{\lambda }}_1\), \({\underline{\lambda }}_2\) and \({\underline{\lambda }}_3\) are the minimum eigenvalues of \({\lambda _1}\), \({\lambda _2}\) and \({\lambda _3}\), respectively. Integration (42) yields:

$$\begin{aligned} 0 \le V(t) \le \Theta (t), \end{aligned}$$
(43)

where

$$\begin{aligned} \Theta (t) = V(0){e^{ - ct}} + \frac{{{e^{ - ct}}}}{\vartheta }\int _0^t {\sum \limits _{i = 1}^2 {\left( {{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1\right) } {{{\dot{\rho }} }_i}{e^{c\tau }}d\tau }. \nonumber \\ \end{aligned}$$
(44)

Considering (43) and using Lemma 1, it is obviously clear that \(\rho _i\), \(\int _0^t {\sum \limits _{i = 1}^2 {({{\frac{{\partial \Omega }}{{\partial u}}}_i}{F_i} - 1)} {{{\dot{\rho }} }_i}{e^{c\tau }}d\tau }\), \(\Theta (t)\) and V(t) are bounded. Hence, all the error signals of the overall system will be bounded. \(\square \)

6 Simulation Results

The effectiveness of the proposed method is evaluated through a simulation study on a 3-Dof helicopter with parameters presented in Table 1. In this study, we consider \(10\%\) uncertainties on the matrices of the model to investigate the robustness of the proposed approach under uncertain conditions. As the control aim in this study is to track the desired trajectories with suitable tracking performance, we consider two distinct simulation scenarios with different reference trajectories.

Table 1 Parameters of the helicopter model Lan et al. (2017b)
Full size table

Scenario 1. In this study, an exponential desired trajectory is considered, as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {x_d}_1 = 0.3 + 1.5{e^{ - t}} - 1.8{e^{ - t/1.2}},\\ {x_d}_2 = 0.2 + {e^{ - t}} - 1.2{e^{ - t/1.2}}. \end{array}\right. \end{aligned}$$
(45)

Moreover, the control parameters are selected as in Table 2. The performance of the control scheme in this scenario can be seen in Fig. 2, representing the angular motion tracking. As it is obvious from the figure, the actual signals are completely converged to the desired trajectories. However, to provide further details about the quality of the tracking performance, the tracking errors are illustrated in Fig. 3. As it is demonstrated, the maximum values in the elevation and pitching channels are in the order of \(10^{-4}\).

Table 2 Parameters of the proposed controller
Full size table
Fig. 2
figure 2

Desired and actual values of the angular positions for the first simulation scenario

Full size image
Fig. 3
figure 3

Tracking errors of the proposed scheme for the first simulation scenario

Full size image

In addition, the control efforts of the front and back motors are depicted in Fig. 4. In this figure, we can see the influence of the actuator saturation in the control law where the control signals are limited to 3V, the prescribed upper limit for the control input. The signals \(u_\textrm{sat}\) in this figure are fed to the motors directly. However, in the control scheme, we have an ideal control signal u, which is a dynamic signal and it has to pass through the saturation function to produce the saturated control law \(u_\textrm{sat}\). Figure 5 represents this control law u. As it is obvious, the ideal control signals have large values compared to the upper bound of the saturation function, which is affecting the actuators control efforts. Although the control law is saturated as depicted in Fig. 4, the closed-loop system can retain its suitable performance as can be seen in Fig. 3. Furthermore, the estimation errors of the adaptive RBF NN are presented in Fig. 6. Because of this suitable performance of the NN estimation, one can result in the control scheme successfully suppressing the undesirable effects of the external disturbances and the model uncertainties.

Fig. 4
figure 4

Saturated control efforts \(u_\textrm{sat}\) of the front and back motors for the first simulation scenario

Full size image
Fig. 5
figure 5

Ideal control efforts u of the front and back motors for the first simulation scenario

Full size image
Fig. 6
figure 6

Estimation errors of the adaptive RBF NN for the first simulation scenario

Full size image

Apart from the above, the external disturbance effect can be investigated by repeating the above maneuver, while the external disturbance is added to the system in \(10<t<15\) as \(\zeta _{\alpha } = 0.01*\sin (10t)\) and \(\zeta _{\alpha } = 0.01*\sin (5t)\). Imposing the external disturbance, the tracking errors are illustrated in Fig. 7. It can be seen that the effect of the external disturbance is successfully suppressed where the tracking errors in \(10<t<15\) are in the order of \(10^{-4}\) (Fig. 8).

Fig. 7
figure 7

Tracking errors of the proposed scheme for the exponential scenario in the presence of external disturbance

Full size image

Besides, the unsaturated ideal control signals \(\varvec{u}\) are illustrated in Fig. 9. In addition, the control signals for the front and back motors are demonstrated in Fig. 8. It is to be noted that these signals are passed from the prevention function that is discussed earlier. Nonetheless, achieving a suitable tracking performance according to the tracking errors in Fig. 7 shows the suitable performance of the proposed control method in the presence of the model uncertainty and external disturbance.

Fig. 8
figure 8

Saturated control efforts \(u_\textrm{sat}\) of the front and back motors for the exponential scenario in the presence of external disturbance

Full size image
Fig. 9
figure 9

Ideal control efforts u of the front and back motors for the exponential scenario in the presence of external disturbance

Full size image

Scenario 2. In this scenario, a sinusoidal trajectory is considered to be tracked by the angular positions of the 3-DoF helicopter. Due to the periodic nature of the sinusoidal signals, such a reference path illustrates the repeatability performance of the closed-loop system. However, the initial value of the actual angular position of the helicopter is selected with a distance 0.1 rad far away from the desired trajectory, revealing the potential abilities of the method to make the system rapidly converge to the reference trajectory despite the initial difference. Furthermore, to perform this simulation study, the control parameters are the same as in the first scenario in Table 2.

By implementing this scenario, the compliance of the actual and desired signals of the helicopter angles is shown in Fig. 10. In this figure, it is obvious that the actual signal suitably tracks the desired one. To have a better analysis of the precision of the motion tracking, the tracking errors are depicted in Fig. 11. In this figure, one can see that the initial value of the errors is equal to the distance between the desired path and the initial value of the helicopter, but before long, the steady-state errors are rapidly going to be in the order of \(10^{-6}\), showing the fast convergence performance. The root-mean-square (RMS) values of the tracking errors are represented in Table 3. In this table, two studies are reported. In the first study, the signals are considered at all the time, but in the second study they are just considered from second 2 to the end of the time. In the RMS values of the first study, there are bigger values than the values of the second study. However, the second study just contains information on the errors in the steady state. This difference is mainly because of the initial values, which are considered on the angular positions of the helicopter.

Fig. 10
figure 10

Desired and actual values of the angular positions for the sinusoidal trajectory

Full size image
Fig. 11
figure 11

Tracking errors of the proposed scheme for the sinusoidal trajectory

Full size image
Table 3 Root-mean-square values of the tracking errors
Full size table

Moreover, the saturated control law is depicted in Fig. 12. In this figure, the saturation influence has illustrated in the control input. However, as the control law is designed to be robust under the actuator saturation, we can see the suitable tacking performance in Figs. 10 and 11.

Fig. 12
figure 12

Saturated control efforts \(u_\textrm{sat}\) of the front and back motors for the sinusoidal trajectory

Full size image

As the control law is designed based on an adaptive NN to be robust in the presence of the model uncertainties and external disturbances, the estimation errors are represented in Fig. 13. In this figure, the order of the estimation error is \(10^{-3}\), which shows a suitable performance for the adaptive RBF NN.

Fig. 13
figure 13

Estimation errors of the adaptive RBF NN

Full size image

On top of the above, this maneuver is repeated for the same setting with different initializations as the initial elevation and pitching angular positions are considered as 0.15 and 0.05, respectively. Moreover, the external disturbance is added to the system in \(10<t<15\) as \(\zeta _{\alpha } = 0.01*\sin (10t)\) and \(\zeta _{\alpha } = 0.01*\sin (5t)\). Considering these settings, the tracking errors are demonstrated in Fig. 14. It is clear from the figure that the proposed method successfully managed to handle the initial difference between the reference signal and the initial angular position. Moreover, the effect of the external disturbance is suitably suppressed which shows the robustness of the proposed method. Additionally, the saturated control efforts for the motors are exhibited in Fig. 15. In this figure, the effect of the saturation can be seen in some points, while the method represents suitable tracking performance.

Fig. 14
figure 14

Tracking errors of the proposed scheme for the second scenario in the presence of external disturbance and different initial angular positions

Full size image
Fig. 15
figure 15

Saturated control efforts \(u_\textrm{sat}\) of the motors for the second scenario in the presence of external disturbance and different initial angular positions

Full size image

7 Conclusion

In this paper, the dynamic surface robust control of a 3-DoF helicopter was studied in the presence of the model uncertainties, external disturbances and actuators saturation. In this study, we included the actuator saturation into the dynamic model of the system which resulted in a second-order non-affine system. To deal with the non-affine model, the control input was included in the state variables and then the third-order system was considered for the control. For the control purpose, a backstepping control scheme was developed which was equipped with an adaptive RBF NN to be robust under undesirable effects of the uncertainties and disturbances. Furthermore, an adaptation law was proposed to adjust the NN weights. Moreover, the stability of the proposed methodology was ensured through the Lyapunov method. The results of the simulation showed suitable performance of the proposed method to deal with the actuator saturation, as well as the model uncertainties.