Nonlinear dynamic modeling and performance analysis of a redundantly actuated parallel manipulator with multiple actuation modes based on FMD theory

Abstract

A novel redundantly actuated parallel manipulator (PM) with multiple actuation modes was developed recently by the author. In this paper, the further research is implemented and a systematic methodology is proposed to develop the rigid–flexible coupling dynamic model (RFDM) of the novel PM based on the flexible multi-body dynamics theory. Firstly, under the floating frame of reference, an arbitrary flexible link of the novel PM is regarded as an Euler–Bernoulli beam and the finite element approach is employed to discretize the flexible beam. Then, one kind of planar beam element with lumped masses and moments of inertia at both ends is presented and a corresponding dynamic model is deduced based on the Lagrangian formulation. On this basis, the RFDM of system is formulated by virtue of the augmented Lagrangian multipliers approach. Given the stiff characteristic of system dynamic model, the hybrid TR-BDF2 numerical algorithm combined with Baumgarte stabilization approach is employed to address the nonlinear RFDM so as to balance the solution efficiency and precision. Based on the RFDM and its degradation model, i.e., the rigid dynamic model, one dynamic simulation experiment is designed to investigate the dynamic performance of the PM. Numerical results indicate that the practical motion of the PM manifests rigid–flexible coupling characteristic, and the redundant actuation modes can attenuate the effect of link flexibility and improve the trajectory tracking precision of end-effector in comparison with the non-redundant actuation modes. Finally, to validate the presented methodology, the obtained numerical results are compared with a virtual prototype model developed based on SimMechanics. The results will be helpful for structure optimization and efficient controller design of the PM with multiple actuation modes.

1 Introduction

In comparison with serial manipulators, parallel manipulators (PMs) have some advantages in terms of higher stiffness, higher loading capacity, higher precision, less error accumulation and excellent dynamic performance [1, 2]. Therefore, the application of PMs has increased in various manufacturing industries, such as motion simulator, aviation manufacturing, electronic packaging and medical surgery. Nevertheless, owing to the closed-loop constraints within the topological structure of a PM, there are some complex singular configurations (mainly Type II singularities [3, 4]) inside the workspace of a PM such that the actually available workspace is very small and only one subzone of the whole reachable workspace. Thus, the superior performance of PMs cannot be exploited adequately. With respect to this problem, the academia proposed some approaches [5,6,7,8,9,10,11,12,13,14] to conquer Type II singularities of PMs. These proposed approaches can avoid the singularities within workspace of PMs in some extent. Amongst them, the redundancy approach is demonstrated to be one much more effective strategy during the avoidance of singularities. Basically, there are two types of redundancy strategies included in this approach, i.e., kinematic redundancy [8, 9] and actuation redundancy [10,11,12,13,14]. The topological structure of the original mechanism is generally modified since some new components are integrated into a certain PM by using redundancy approach. Owing to the extra degrees of freedom (DOFs) introduced by kinematic redundancy, the complexity of control for the nonlinear dynamic system increases in some extent. In contrast, by using actuation redundancy, no extra DOFs are introduced into the PM, and the manipulability as well as dynamic performance of system can be enhanced with the elimination of Type II singularities.

Bearing in mind this issue mentioned above, the authors have performed some innovative designs with respect to the traditional planar 2-DOF 5R PM recently and proposed a novel redundantly actuated PM which can realize multiple potential actuation modes [14, 15]. This novel PM has some promising application prospects, such as 3D printing and electronic packaging.

As is well known, with the rapid development of advanced manufacturing technology, the demand for the dynamic performance of manipulators in industry field is higher and higher. Under this circumstance, the manipulators should possess the capabilities of high speed and high precision. Fortunately, with the aid of materials science, more and more novel materials are applied to design the manipulators so that the weights of manipulators can be reduced a lot and high speed as well as high ratio of payload/weight can be achieved in the meantime. However, in the case of high-speed motion, the deformations of links for a certain manipulator readily occur owing to the flexibilities of links and the effect of external actuation forces. The elastic deformations of links will certainly affect the whole rigid-body motions of manipulator and even cause the motion instability. In other words, under the circumstance of high-speed motion, the practical movement of manipulator is the outcome of rigid–flexible coupling effect when the flexibilities of links are considered. Consequently, in practical application, establishing an effective rigid–flexible coupling dynamic model (RFDM) is of great significance to investigate the dynamic performance and design effective nonlinear dynamic controllers for the manipulator.

At present, the rigid dynamics of mechanism has been developed maturely. Many basic formulations of dynamics can be employed to establish the rigid multi-body dynamic model of a manipulator, such as Newton–Euler formulation [16], Kane’s formulation [17], Lagrangian formulation [18], virtual work principle [19], Hamilton’s principle [20] and Gibbs–Appell formulation [21]. However, due to the flexible effects of links and joints, the modeling complexity of flexible manipulators is much higher than that of rigid manipulators. The main difficulties depend on whether the description of deformation field for the flexible body and the treatment to the rigid–flexible coupling relationship are reasonable or not. With regard to this issue, the academia has made much beneficial exploitation and extensive research.

A flexible manipulator is such a dynamic system that encompasses one or more flexible components, and thus can be called as flexible multi-body dynamic system [22]. The accurate and complete flexible multi-body dynamic model for a flexible manipulator should not only involve the influence of rigid-body motions on elastic deformations, but also involve the influence of elastic deformations on rigid-body motions and elastic deformations of other flexible links within the flexible manipulator. With respect to the dynamic modeling for flexible manipulators, a variety of modeling approaches have been proposed by researchers. On the whole, these approaches can be mainly classified into two categories [23]. First, an arbitrary flexible link of a manipulator is regarded as a continuous body which has infinite DOFs [24,25,26]. The equations of motion are developed in the form of nonlinear partial differential equations (PDEs). System responses are obtained by solving the system equations with numerical algorithms for simple configurations and boundary conditions. In research work using this approach, some important assumptions are frequently utilized to reduce the complexity of dynamic model. Generally, this approach is applicable for the system with uniform beams which are small in number. Consequently, this approach has some limitations in practical application. The second approach makes some discretization with respect to a flexible body and treats it as a discrete system possessing finite elastic DOFs. Subsequently, the dynamic model of system can be deduced by virtue of the fundamental principles used in the dynamic modeling for rigid bodies. The common discrete strategies mainly include lumped parameter method [27], assumed mode method (AMM) [28,29,30], finite element method (FEM) [31,32,33,34,35] and finite segment method (FSM) [36,37,38]. Amongst them, the FEM and AMM are two most commonly used ones in practice. Theoretically, the FEM can be applied for any flexible system. If the element number is reasonable, an accurate dynamic model can be developed to describe the dynamic performance of system very well by using FEM. A comparison of the FEM and the AMM used to model link flexibility is presented in detail in Ref. [39].

In the past several decades, the academia has proposed multiple coordinate frameworks to describe the rigid–flexible coupling relation of motions. In general, the widely used methods in practice mainly include kineto-elasto dynamics (KED) method [40,41,42,43], floating frame of reference formulation (FFRF) method [22, 44,45,46] and absolute nodal coordinate formulation (ANCF) method [47,48,49,50,51]. First, the KED method developed earlier and obtained extensive research in the past few decades. In the early research work using KED method, the assumption of instantaneous structure is generally employed. Only the influence of rigid-body motions (nominal motions) on the elastic deformations is considered, while the influence of elastic deformations on the rigid-body motions is neglected during the modeling process. By using the KED method, a set of ordinary differential equations (ODEs) with simple form can be obtained and solved easily. The KED method is generally applicable to the dynamic modeling for the flexible mechanisms in which the flexibilities of links are not significant and the motion speed of links is not too high. However, in the case of high-speed motions, or when the flexibilities of links are much higher, it is difficult for the KED method to describe accurately the real motion state of flexible mechanisms. Given that, some scholars abandoned the assumption of instantaneous structure to overcome the roughness of dynamic model deduced through the KED method [40]. Second, the FFRF method is such one that distinguishes between the rigid-body motion and the elastic motion of a flexible body by introducing a floating coordinate system into the modeling process. Since the rigid–flexible coupling effect is considered in the FFRF method, the derived dynamic model of system contains the nonlinear rigid–flexible coupling term. Moreover, the dynamic model of system can be further simplified easily in future by using the FFRF method. In order to deal with the large deformation problem of flexible bodies, Shabana [47] proposed the ANCF method which no longer distinguished between the rigid-body motion and the elastic motion of a flexible body but uniformly employed the absolute position coordinates of element nodes and the material derivatives to describe the motion of a flexible body. The ANCF method is very applicable to handling the geometric nonlinear problem of large deformations of flexible bodies. At present, this method has been drawn a wide attention from the academia and obtained some developments [48, 49, 51]. It is worth noting that, since the floating coordinate system is removed from the ANCF method, the obtained mass matrix is constant, while the stiffness matrix is highly nonlinear. That is to say, the coupling relationship between the rigid-body motion and the elastic motion of the flexible body is not eliminated but transferred from the mass matrix into the stiffness matrix. Because the number of generalized coordinates is extremely high and the computation of elastic forces is complex in the ANCF method, the computation efficiency for the complex system is lower than the FFRF method to some extent. Besides, it is not convenient for the ANCF method to simplify further the dynamic model of system so as to be suitable for the design of dynamic controller. Nevertheless, it cannot be denied that the ANCF method will obtain a good development in future with the progress of theoretical research.

With respect to the research about the flexible mechanisms, the academia has made great contributions. The comprehensive review of these works can be found in Refs. [52,53,54]. The research subjects mostly concentrate on the open-loop serial manipulators with one or two flexible links [25, 26, 28,29,30,31, 55,56,57,58,59,60] and some four-bar mechanisms [24, 27, 32, 40,41,42, 50, 61,62,63,64]. In contrast, the researches with respect to complex closed-loop mechanisms, such as the PMs containing one or more closed-loop constraints, are rather fewer in number. Some research contributions are summarized as follows. Gasparetto et al. [65] developed a dynamic model of a flexible planar 5R PM using FEM and carried out an experiment to verify the effectiveness of the model presented. Piras et al. [66] implemented elastic dynamic modeling with respect to a planar 3PRR PM with flexible links by virtue of KED method and obtained a set of linear ODEs of motion. Wang et al. [67] presented a FEM model of the flexible planar 3PRR PM and made a strain rate feedback control simulation based on a simplified model. Kang et al. [68] and Zhang et al. [23] applied the AMM to establish two different dynamic models of the flexible planar 3PRR PM based on two different boundary conditions, respectively. Based on AMM, Zhang et al. [69] derived a dynamic model of a planar 3PRR PM with flexible links and performed a trajectory tracking control simulation. Yu et al. [70] developed an elastic dynamic model of a planar 3RRR PM with flexible links by virtue of KED method and implemented experiments to verify the effectiveness of the model presented. Subsequently, Zhang et al. [71] employed the Hamilton’s principle and FEM to establish a dynamic model of the flexible planar 3RRR PM and solved the dynamic equations based on the assumption of KED. Liu et al. [72] employed KED method and spatial beam elements to derive a dynamic model of a flexible 3RRS PM. However, the number of elements is so small that the dynamic model of system is not precise enough. Zhao et al. [73] derived a dynamic model of a spatial 8PSS PM with flexible links using KED method and FEM. Mukherjee et al. [74] employed Newton–Euler formulation to derive a dynamic model of the Stewart platform. However, each supporting leg is merely modeled as a spring–damper system whose axial stiffness is considered merely in the dynamic model. Song et al. [75] applied KED method and spatial beam elements to establish an elastic dynamic model of a PM with two DOFs of rotation and implemented natural characteristic analysis based on the dynamic model deduced. Sun et al. [76] implemented the elastic dynamic modeling with respect to a Delta-string manipulator based on KED method.

From the relevant researches about flexible PMs, one can discover that the most of researches concentrate on the KED method which commonly ignores the nonlinear rigid–flexible coupling term such that the dynamic models deduced generally are not precise enough to some extent. Meanwhile, the number of researches about flexible PMs is far less than that of the serial manipulators. Additionally, the dynamic modeling approaches for flexible PMs are not systematic. Consequently, in order to satisfy the requirements of future engineering application and theoretical research, it is necessary to expand the research scope of flexible PMs and develop much more systematic and effective approaches to establish the dynamic models of flexible PMs.

To overcome the shortcomings of former works about flexible PMs, we will propose a systematic modeling methodology in this paper to develop the RFDM of the novel PM with multiple actuation modes based on the FMD theory. The main contributions of this paper can be drawn as follows:

• Firstly, the general dynamic model for one kind of planar beam element containing lumped masses and moments of inertia at both ends is derived, which can be conveniently assembled to formulate the RFDM of system with any number of lumped parameters. Moreover, this kind of element can be conveniently transformed into the common element only through simple parameters setting.

• Secondly, a strategy of combining the hybrid TR-BDF2 numerical algorithm with Baumgarte stabilization approach is proposed to address the nonlinear RFDM of system to balance the solution efficiency and precision.

• Thirdly, the dynamic performance of the PM with multiple actuation modes is comprehensively investigated via a numerical simulation experiment. Moreover, the validity of the RFDM is exactly verified by a FSM-based VPM which is developed for the first time by virtue of SimMechanics.

• Eventually, owing to the compact form of the RFDM developed in this study, some dynamic controllers can be efficiently designed in future based on the RFDM via some strategies, such as modal synthesis technique.

2 Topology description

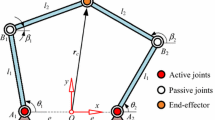
Figure 1 shows the schematic diagram of the traditional planar 5R PM [4]. The output point C where the end-effector can be mounted is connected to the base by two branches, each of which consists of three revolute joints and two links. The two branches are connected to a common point (point C) with the common revolute joint at the end of each branch. In each of the two branches, the revolute joint connected to the base is actuated by one servo motor. Thus, such a manipulator is able to position its output point in a plane. It should be noted that, in order to obtain a reachable workspace without holes, the lengths of proximal and distal links are usually identical to each other [4, 14].

Fig. 1

The traditional planar 5R PM without redundant actuations [14]

However, owing to the singular curves existing within the reachable workspace of the traditional planar 5R PM, the usable workspace is very small and only a subzone of the whole reachable workspace so that the performance of the manipulator is restricted a lot. Consequently, how to avoid singularities (especially the Type II singularities) within the workspace of a certain PM and improve the dynamic performance is a continuous hot issue in the research field of PMs. With respect to the aforementioned issue, we have implemented innovative designs based on the traditional planar 5R PM and presented some redundant actuation schemes to conquer the defects of the traditional planar 5R PM. Considering the theoretical research significance and practical engineering requirements, we have selected one of some available redundant actuation schemes as the optimum one that encompasses parallelogram structure branches (PSBs) [77] with the help of some selection criteria [14]. The corresponding mechanism is named as RAParM (derived from “Redundantly Actuated Parallel Manipulator”) which possesses two DOFs. Moreover, the optimum redundant actuation scheme determined by us includes two configurations named, respectively, as RAParM-I and RAParM-II based on the layout of the PSBs, as depicted in Fig. 2 [14].

Fig. 2

The redundantly actuated planar 2DOF PM with parallelogram structure branches [14]: a RAParM-I, b RAParM-II

Fig. 3

Virtual prototypes (RAParM) [14]: a RAParM-I, b RAParM-II

Table 1 Potential actuation modes of RAParM [14]

Based upon the two topological configurations, two preliminary virtual prototypes can be constructed by means of commercial software $\hbox {Solidworks}^{{\circledR }}$, which are shown in Fig. 3 [14], in which some attachments are not shown in detail.

Considering the similar structure characteristic between the two configurations of RAParM, in Ref. [14], we have implemented detailed analysis with respect to one of the two configurations, i.e., RAParM-I. Owing to the special structure characteristic, this novel PM can achieve 9 potential actuation modes, as illustrated in Table 1 [14]. Moreover, we have carried out kinematic analysis about RAParM-I and established the uniformly dynamic model at the level of rigid-body dynamics. Based on rigid dynamic model (RDM), the dynamic dimensional synthesis has been implemented to obtain the optimal dimensional parameters. The results indicate that the PM can realize high kinematic and rigid dynamic performance after dynamic dimensional synthesis.

3 Rigid–flexible coupling dynamic modeling

Since the flexible PM is a rigid–flexible coupling multi-body dynamic system, it is much more difficult to establish the dynamic model for the flexible dynamic system compared with the rigid dynamic system, and much more factors need to be considered in the modeling process. Especially for the PM with multiple closed-loops and multiple actuation modes, such as RAParM, establishing the rigid–flexible coupling dynamic model (RFDM) considering the flexibilities of all links and the multiple actuation modes has received less attention. Therefore, it is extremely significant and challenging to solve this problem.

Considering the modeling complexity, we first cut virtually all the joints of the mechanism and obtain each independent flexible body. In subsequence, the dynamic model for each independent flexible body is deduced. Finally, we assemble the dynamic equations of all the flexible bodies and incorporate the constraint equations by virtue of Lagrangian multipliers to achieve the nonlinear RFDM of system.

3.1 Discretization for any flexible body based on finite element approach

In general, the deformations of links for a lightweight mechanism readily arise during high-speed motion. Manifested in Fig. 4 is the possible situation of deformations for RAParM-I due to the flexibilities of links during high-speed motion.

Fig. 4

The elastic deformations of links for RAParM-I during high-speed motion

In order to conveniently simplify the dynamic model of system in future, in this paper, the floating frame of reference is employed to describe the deformation of the flexible link. Because the cross-sectional area of the flexible link for RAParM-I is small, the Euler–Bernoulli beam is adaptable to modeling the deformation of the flexible link. Without loss of generality, shown in Fig. 5 is the deformation description of a certain flexible body (denoted by j where $j=1,2,{\ldots },N$ in which N represents the total sum of flexible bodies of manipulator) during the large overall motion. In order to establish the dynamic equations for an arbitrary flexible body conveniently, some assumptions are made here [56]:

• The material of each flexible body is uniform and isotropic, and the constitutive relation satisfies Hooke’s law.

• Each flexible body satisfies the small deformation assumption, and the cross section of the beam is vertical to the central axis forever.

• The axial and transverse deformations are taken into consideration, while the shear and torsion effects are negligible.

Fig. 5

The deformation description of an arbitrary flexible body during the movement

As shown in Fig. 5, $O{-}x{-}y$ represents the global coordinate system, i.e., the inertial coordinate system. $O_j {-}\bar{{x}}{-}\bar{{y}}$ represents the relative coordinate system, which is fixed to the body and can be called body-fixed coordinate system. P is an arbitrary point located on the central axis of the body and $P^{\prime }$ represents the practical position of point P after the occurrence of deformation. ${\varvec{r}}_{O_j}$ represents the radius vector of the original point of body-fixed coordinate system, which is expressed in the global coordinate system. ${\varvec{r}}_{0,j} =[{\begin{array}{ll} {\bar{{x}}} &{} 0 \\ \end{array} }]^{\mathrm{T}}$ represents the radius vector of point P in the body-fixed coordinate system before the occurrence of deformation. $\varvec{\delta }_p$ represents the vector of deformation displacements from point P to point $P^{\prime }$ (see Fig. 5), which is expressed in the body-fixed coordinate system. ${\varvec{r}}_p$ represents the position vector of point P in the global coordinate system. Based upon the vector relationship depicted in detail in Fig. 5, one can obtain

$$\begin{aligned} {\varvec{r}}_P ={\varvec{r}}_{O_j } +{\varvec{R}}\left( {\phi _j } \right) \left( {{\varvec{r}}_{0,j} +\varvec{\delta }_p } \right) \end{aligned}$$

(1)

where ${\varvec{R}}\left( {\phi _j } \right)$ is the rotational transformation matrix between the $O_j {-}\bar{{x}}{-}\bar{{y}}$ system and the $O{-}x{-}y$ system, and

$$\begin{aligned} {\varvec{R}}\left( {\phi _j } \right) =\left[ {{\begin{array}{l@{\quad }l} {\cos \phi _j }&{} {-\sin \phi _j } \\ {\sin \phi _j }&{} {\cos \phi _j } \\ \end{array} }} \right] \end{aligned}$$

(2)

where $\phi _j$ is the angular displacement of flexible body j as shown in Fig. 5.

It should be noted that Eq. (1) represents the position vector of an arbitrary point P of the uniformly flexible beam. Herein, the finite element approach is employed to discretize the flexible beam and the type of element is determined as the planar beam element. The number of nodal coordinates of the beam element is 8, as depicted in Fig. 6. Without loss of generality, the element number is marked with i, and the flexible body number is marked with j.

Fig. 6

The discretization of an arbitrary flexible body using finite element approach

Let the array of flexible generalized coordinates of an arbitrary element $i\, (i=1,2,\cdots ,n_j )$ in flexible body j be

$$\begin{aligned} {\varvec{u}}_{f_i }^j =\left[ {{\begin{array}{llllllll} u_{1,i}^j &{} u_{2,i}^j &{} u_{3,i}^j &{} u_{4,i}^j &{} u_{1,i+1}^j &{} u_{2,i+1}^j &{} u_{3,i+1}^j &{} u_{4,i+1}^j \\ \end{array} }} \right] ^{\mathrm{T}}\nonumber \\ \end{aligned}$$

(3)

where $u_{1,i}^j$ and $u_{1,i+1}^j$ denote the axial elastic displacements of the two nodes for element i; $u_{2,i}^j$ and $u_{2,i+1}^j$ denote the transverse elastic displacements of the two nodes for element i; $u_{3,i}^j$ and $u_{3,i+1}^j$ denote the elastic angles of the two nodes for element i; $u_{4,i}^j$ and $u_{4,i+1}^j$ denote the elastic curvatures of the two nodes for element i. Based upon the above assumption, the deformation displacements of an arbitrary point $P_i^j$ of element i in flexible body j can be expressed as

$$\begin{aligned} \varvec{\delta }_{Pi}^j =\left[ {{\begin{array}{l} {v_i^j (\bar{{x}}_i ,t)} \\ {w_i^j (\bar{{x}}_i ,t)} \\ \end{array} }} \right] ={\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{u}}_{f_i }^j \end{aligned}$$

(4)

where ${\varvec{N}}_i^j (\bar{{x}}_i )$ represents the shape function matrix of element i in flexible body j, and

$$\begin{aligned} {\varvec{N}}_i^j (\bar{{x}}_i )= & {} \left[ {{\begin{array}{l} {{\varvec{N}}_{i,1}^j (\bar{{x}}_i )} \\ {{\varvec{N}}_{i,2}^j (\bar{{x}}_i )} \\ \end{array} }} \right] \nonumber \\ = & {} \left[ {{\begin{array}{l@{}l@{}l@{}l@{}l@{}l@{}l@{}l} f_{i,1}^j &{} 0&{} 0&{} 0&{} f_{i+1,1}^j &{} 0&{} 0&{} 0 \\ 0&{} f_{i,2}^j &{} f_{i,3}^j &{} f_{i,4}^j &{} 0&{} f_{i+1,2}^j &{} f_{i+1,3}^j &{} f_{i+1,4}^j \\ \end{array}}} \right] \nonumber \\ \end{aligned}$$

(5)

in which the corresponding shape functions are given by

$$\begin{aligned}&f_{i,1}^j =1-\zeta _i^j \\&f_{i,2}^j =1-10\zeta _i^{j3} +15\zeta _i^{j4} -16\zeta _i^{j5} \\&f_{i,3}^j =l_i^j \left( \zeta _i^j -6\zeta _i^{j3} +8\zeta _i^{j4} -3\zeta _i^{j5} \right) \\&f_{i,4}^j =\frac{1}{2}l_i^{j2} \left( \zeta _i^{j2} -3\zeta _i^{j3} +3\zeta _i^{j4} -\zeta _i^{j5}\right) \\&f_{i+1,1}^j =\zeta _i^j \\&f_{i+1,2}^j =10\zeta _i^{j3} -15\zeta _i^{j4} +6\zeta _i^{j5} \\&f_{i+1,3}^j =l_i^j \left( -4\zeta _i^{j3} +7\zeta _i^{j4} -3\zeta _i^{j5} \right) \\&f_{i+1,4}^j =\frac{1}{2}l_i^{j2} \left( \zeta _i^{j3} -2\zeta _i^{j4} +\zeta _i^{j5}\right) \end{aligned}$$

$\zeta _i^j =\frac{\bar{{x}}_i }{l_i^j },$ with $l_i^j$ being the length of element i in flexible body j.

Assume the array of global deformation displacements of flexible body j is

$$\begin{aligned} {\varvec{U}}_f^j= & {} \left[ u_{1,1}^j \,\, u_{2,1}^j \,\, u_{3,1}^j \,\, u_{4,1}^j \,\, \cdots \,\, u_{1,n_j +1}^j \,\, u_{2,n_j +1}^j \right. \nonumber \\&\left. u_{3,n_j +1}^j \,\, u_{4,n_j +1}^j \right] ^{\mathrm{T}} \end{aligned}$$

(6)

After the discretization using finite element approach for flexible body j, the displacement vector of arbitrary point $P_i^j$ of element i in flexible body j can be expressed as

$$\begin{aligned} {\varvec{r}}_{Pi}^j ={\varvec{r}}_{O_j } +{\varvec{R}}^{j}(\phi _j )\left( {{\varvec{r}}_{0,i}^j +{\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \end{aligned}$$

(7)

where ${\varvec{r}}_{0,i}^j =\big [ {{\begin{array}{ll} {\sum \nolimits _{k=0}^{i-1} {l_k^j +\bar{{x}}_i } }&{} 0 \\ \end{array} }} \big ]^{\mathrm{T}}\, (l_0^j =0)$ represents the coordinate array of point $P_i^j$ of element i before the deformation of flexible body j; ${\varvec{B}}_i^j \in \mathbb {R}^{8\times 4(n_j +1)}$ represents the Boolean indicated matrix which is determined by the element number as

$$\begin{aligned}&\hbox {No} \,\,\qquad 1 \qquad 2 \qquad \cdots \qquad i \quad i+1 \,\, \cdots \,\, n_j \,\, n_j +1 \nonumber \\&{\varvec{B}}_i^j =\left[ {{\begin{array}{cccccccc} {\mathbf{0}_{4\times 4} } &{} {\mathbf{0}_{4\times 4} } &{} \cdots &{} {{\varvec{I}}_{4\times 4} } &{} {\mathbf{0}_{4\times 4} } &{} \cdots &{} {\mathbf{0}_{4\times 4} } &{} {\mathbf{0}_{4\times 4} } \\ {\mathbf{0}_{4\times 4} } &{} {\mathbf{0}_{4\times 4} } &{} \cdots &{} {\mathbf{0}_{4\times 4} } &{} {{\varvec{I}}_{4\times 4} } &{} \cdots &{} {\mathbf{0}_{4\times 4} } &{} {\mathbf{0}_{4\times 4} } \\ \end{array} }} \right] \end{aligned}$$

(8)

where ${\varvec{u}}_f^j$ represents the array of independent global deformation displacements; ${\varvec{D}}^{j}$ represents the transformation matrix of global deformation generalized coordinates. For instance, with respect to a cantilever beam, based on the boundary conditions, the axial and transverse elastic displacements and elastic angle of the first node for No. 1 element are null. Meanwhile, the elastic curvature of the second node for the last element is null as well. Therefore, the corresponding transformation matrix of global deformation generalized coordinates can be written as

$$\begin{aligned} {\varvec{D}}^{j}=\left[ {{\begin{array}{l} {\mathbf{0}_{3\times 4n_j } } \\ {{\varvec{I}}_{4n_j \times 4n_j } } \\ {\mathbf{0}_{1\times 4n_j } } \\ \end{array} }} \right] \end{aligned}$$

(9)

Let ${\varvec{q}}_j =\left[ {{\begin{array}{lll} {{\varvec{r}}_{O_j }^{\mathrm{T}} }&{} {\phi _j }&{} {{\varvec{u}}_f^{j{\mathrm{T}}} } \\ \end{array} }} \right] ^{\mathrm{T}}$ be the vector of generalized coordinates of flexible body j. Differentiating Eq. (7) with respect to time yields

$$\begin{aligned} {\dot{{\varvec{r}}}}_{Pi}^j ={\bar{{\varvec{S}}}}_i^j {\dot{{\varvec{q}}}}_j \end{aligned}$$

(10)

where

$$\begin{aligned} {\bar{{\varvec{S}}}}_i^j= & {} \left[ {\varvec{I}}_{2\times 2} \,\, {\frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }\left( {{\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j +{\varvec{r}}_{0,i}^j} \right) } \right. \nonumber \\&\left. {\varvec{R}}(\phi _j ){\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j} \right] _{2\times (3+4n_j )} \end{aligned}$$

(11)

3.2 Dynamic modeling for element i in flexible body j

In this paper, the Lagrangian formulation is employed to derive the dynamic model of element i in flexible body j. Therefore, the kinetic energy and potential energy of element i in flexible body j should be first determined.

3.2.1 Kinetic energy of element i

The flexible bodies of RAParM-I contain many lumped masses and moments of inertia (see Figs. 2, 3), such as the masses and moments of inertia of joints. So a novel dynamic model of element i with lumped masses and moments of inertia at both ends will be deduced here. Thus, the kinetic energy of element i consists of two parts, i.e., the kinetic energy corresponding to the intermediate continuous section and both the translational and rotational kinetic energies corresponding to the lumped masses and moments of inertia, respectively. The associated element with lumped masses and moments of inertia is depicted in Fig. 7.

Fig. 7

The common element and the present element with lumped masses and moments of inertia

(1) Kinetic energy of intermediate continuous section

Assume the mass of intermediate continuous section of element i in flexible body j is $m_{di}^j$. Based on the aforementioned kinematic analysis, the kinetic energy of intermediate continuous section of element i can be written as

$$\begin{aligned} T_{t,i}^j= & {} \frac{1}{2}\int _{V_i^j } {\rho {\dot{{\varvec{r}}}}_{Pi}^{j{\mathrm{T}}} } {\dot{{\varvec{r}}}}_{Pi}^j \hbox {d}V_i^j \nonumber \\= & {} \frac{1}{2}\int _{V_i^j } {\rho {\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\bar{{\varvec{S}}}}_i^{j{\mathrm{T}}} {\bar{{\varvec{S}}}}_i^j {\dot{{\varvec{q}}}}_j \hbox {d}V_i^j } \nonumber \\= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_{t,i}^j {\dot{{\varvec{q}}}}_j \end{aligned}$$

(12)

where $\rho$ represents the mass density of element material, $V_i^j$ represents the volume of the intermediate continuous section of element i, and ${\varvec{M}}_{t,i}^j$ represents the mass matrix corresponding to the intermediate continuous section of element i and can be expressed as

$$\begin{aligned} {\varvec{M}}_{t,i}^j= & {} \int _{V_i^j } {\rho {\bar{{\varvec{S}}}}_i^{j{\mathrm{T}}} {\bar{{\varvec{S}}}}_i^j \hbox {d}V_i^j } \nonumber \\= & {} \left[ {{\begin{array}{lll} {{\varvec{M}}_{t,i,rr}^j }&{} {{\varvec{M}}_{t,i,r\phi }^j }&{} {{\varvec{M}}_{t,i,rf}^j } \\ {{\varvec{M}}_{t,i,\phi r}^j }&{} {M_{t,i,\phi \phi }^j }&{} {{\varvec{M}}_{t,i,\phi f}^j } \\ {{\varvec{M}}_{t,i,fr}^j }&{} {{\varvec{M}}_{t,i,f\phi }^j }&{} {{\varvec{M}}_{t,i,ff}^j } \\ \end{array} }} \right] \end{aligned}$$

(13)

Owing to the space limitation, the expression of each component for ${\varvec{M}}_{t,i}^j$ is not shown in detail here.

(2) Translational kinetic energy and rotational kinetic energy of lumped masses and moments of inertia

Assume the lumped masses located at both ends of element i are denoted by $m_{O_{1i} }^j$ and $m_{O_{2i} }^j$, respectively. The corresponding lumped moments of inertia are denoted by $J_{O_{1i} }^j$ and $J_{O_{2i} }^j$, respectively. Based upon the aforementioned kinematic analysis, after the deformation of flexible body j, the displacement vectors of both end points of element i can be expressed as

$$\begin{aligned}&{\varvec{r}}_{O_{1i} }^j ={\varvec{r}}_{O_j } +{\varvec{R}}(\phi _j) \left( {\left[ {{\begin{array}{ll} {l_{O_{1i} }^j }&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \nonumber \\\end{aligned}$$

(14)

$$\begin{aligned}&{\varvec{r}}_{O_{2i} }^j ={\varvec{r}}_{O_j } +{\varvec{R}}(\phi _j) \left( {\left[ {{\begin{array}{ll} {l_{O_{2i} }^j }&{} 0 \\ \end{array}}} \right] ^{\mathrm{T}}+{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \nonumber \\ \end{aligned}$$

(15)

where ${\varvec{R}}(\phi _j )$ is the rotational transformation matrix and $\left[ {{\begin{array}{ll} l_{O_{1i} }^j &{} 0 \\ \end{array} }} \right] ^{\mathrm{T}}$ and $\left[ {{\begin{array}{ll} l_{O_{2i} }^j &{} 0 \\ \end{array} }} \right] ^{\mathrm{T}}$ are the arrays of coordinates corresponding to the two end points $O_{1i}^j$ and $O_{2i}^j$ of element i in the undeformed state, respectively.

Differentiating Eqs. (14) and (15) with respect to time yields

$$\begin{aligned} {\dot{{\varvec{r}}}}_{O_{1i} }^j= & {} {\dot{{\varvec{r}}}}_{O_j } +\frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j} \nonumber \\&\left( {\left[ {{\begin{array}{ll} {l_{O_{1i} }^j }&{} 0 \\ \end{array}}} \right] ^{\mathrm{T}}+{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \dot{\phi }_j \nonumber \\&+\,{\varvec{R}}(\phi _j ){\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \end{aligned}$$

(16)

$$\begin{aligned} {\dot{{\varvec{r}}}}_{O_{2i} }^j= & {} {\dot{{\varvec{r}}}}_{O_j } +\frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j} \nonumber \\&\left( {\left[ {{\begin{array}{ll} {l_{O_{2i} }^j }&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \dot{\phi }_j \nonumber \\&+\,{\varvec{R}}(\phi _j ){\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \end{aligned}$$

(17)

Therefore, the translational kinetic energy of lumped masses located at both ends of element i can be obtained as

$$\begin{aligned} T_{t,c}^j= & {} \frac{1}{2}m_{O_{1i} }^j {\dot{{\varvec{r}}}}_{O_{1i} }^{j{\mathrm{T}}} {\dot{{\varvec{r}}}}_{O_{1i} }^j +\frac{1}{2}m_{O_{2i} }^j {\dot{{\varvec{r}}}}_{O_{2i}}^{j{\mathrm{T}}} {\dot{{\varvec{r}}}}_{O_{2i} }^j \nonumber \\= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_{O_{1i} }^j {\dot{{\varvec{q}}}}_j +\frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_{O_{2i} }^j {\dot{{\varvec{q}}}}_j \end{aligned}$$

(18)

where ${\varvec{M}}_{O_{1i} }^j$ and ${\varvec{M}}_{O_{2i} }^j$ represent the mass matrices corresponding to the lumped masses of element i.

Furthermore, according to kinematic analysis, the rotational angles of both end points of element i can be expressed as

$$\begin{aligned} \theta _{O_{1i} }^j= & {} \phi _j +\left. {\frac{\partial w_i^j (\bar{{x}}_i ,t)}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} \nonumber \\= & {} \phi _j +\left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i)}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j \end{aligned}$$

(19)

$$\begin{aligned} \theta _{O_{2i} }^j= & {} \phi _j +\left. {\frac{\partial w_i^j (\bar{{x}}_i ,t)}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j} \nonumber \\= & {} \phi _j +\left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j } {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j \end{aligned}$$

(20)

Differentiating Eqs. (19) and (20) with respect to time yields

$$\begin{aligned}&\quad \dot{\theta }_{O_{1i} }^j =\dot{\phi }_j +\left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} {\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \end{aligned}$$

(21)

$$\begin{aligned}&\quad \dot{\theta }_{O_{2i} }^j =\dot{\phi }_j +\left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j } {\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \end{aligned}$$

(22)

Therefore, the rotational kinetic energy of lumped moments of inertia at both ends of element i can be obtained as

$$\begin{aligned} T_{r,c}^j= & {} \frac{1}{2}J_{O_{1i} }^j \dot{\theta }_{O_{1i} }^{j2} +\frac{1}{2}J_{O_{2i} }^j \dot{\theta }_{O_{2i} }^{j2} \nonumber \\= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_{J_{O1i} }^j {\dot{{\varvec{q}}}}_j +\frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_{J_{O2i} }^j {\dot{{\varvec{q}}}}_j \end{aligned}$$

(23)

where ${\varvec{M}}_{J_{O1i} }^j$ and ${\varvec{M}}_{J_{O2i} }^j$ represent the mass matrices corresponding to the lumped moments of inertia of element i.

(3) Total kinetic energy of element i

Based upon above analysis, the total kinetic energy of element i can be expressed as

$$\begin{aligned} T_i^j= & {} T_{t,i}^j +T_{t,c}^j +T_{r,c}^j \nonumber \\= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} \left( {{\varvec{M}}_{t,i}^j +{\varvec{M}}_{O_{1i} }^j +{\varvec{M}}_{O_{2i} }^j +{\varvec{M}}_{J_{O1i} }^j +{\varvec{M}}_{J_{O2i} }^j } \right) {\dot{{\varvec{q}}}}_j \nonumber \\= & {} \frac{1}{2}{\dot{{\varvec{q}}}}_j^{\mathrm{T}} {\varvec{M}}_i^j {\dot{{\varvec{q}}}}_j \end{aligned}$$

(24)

where ${\varvec{M}}_i^j$ represents the mass matrix of element i in flexible body j, which is a symmetric positive definite matrix, and is written as

$$\begin{aligned} {\varvec{M}}_i^j =\left[ \begin{array}{l@{\quad }l@{\quad }l} {{\varvec{M}}_{i,rr}^j }&{} {{\varvec{M}}_{i,r\phi }^j }&{} {{\varvec{M}}_{i,rf}^j } \\ {{\varvec{M}}_{i,\phi r}^j }&{} {M_{i,\phi \phi }^j }&{} {{\varvec{M}}_{i,\phi f}^j } \\ {{\varvec{M}}_{i,fr}^j }&{} {{\varvec{M}}_{i,f\phi }^j }&{} {{\varvec{M}}_{i,ff}^j } \\ \end{array}\right] \end{aligned}$$

(25)

in which

$$\begin{aligned}&{\varvec{M}}_{i,rr}^j =\left( m_{di}^j +m_{O_{1i} }^j +m_{O_{2i} }^j \right) {\varvec{I}}_{2\times 2} \\&{\varvec{M}}_{i,r\phi }^j =\frac{\partial {\varvec{R}}(\phi _j)}{\partial \phi _j} \\&\quad \left( \bar{{\varvec{N}}}_{i,1}^j +\bar{{\varvec{N}}}_{i,2}^j {\varvec{u}}_f^j +m_{O_{1i}}^j \left( \left[ \begin{array}{l} l_{O_{1i} }^j \\ 0 \\ \end{array} \right] +{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j \right) \right. \\&\quad \left. +\,m_{O_{2i}}^j \left( \left[ \begin{array}{l} l_{O_{2i}}^j \\ 0 \\ \end{array} \right] +{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j \right) \right) \\&{\varvec{M}}_{i,rf}^j ={\varvec{R}}(\phi _j ) \\&\quad \left( {{\bar{{\varvec{N}}}}_{i,2}^j +m_{O_{1i} }^j {\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}+m_{O_{2i} }^j {\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}} \right) \\&{\varvec{M}}_{i,\phi r}^j ={\varvec{M}}_{i,r\phi }^{j{\mathrm{T}}} \\&M_{i,\phi \phi }^j ={\bar{{\varvec{N}}}}_{i,3}^j +2{\bar{{\varvec{N}}}}_{i,4}^j {\varvec{u}}_f^j +{\varvec{u}}_f^{j{\mathrm{T}}} {\bar{{\varvec{N}}}}_{i,5}^j {\varvec{u}}_f^j +m_{O_{1i} }^j \\&\quad \left( {\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)} \right) \\&\quad \left( {\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \\&\quad +\,m_{O_{2i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) } \right) \\&\quad \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) +J_{O_{1i} }^j +J_{O_{2i} }^j \end{aligned}$$

$$\begin{aligned}&{\varvec{M}}_{i,\phi f}^j ={\bar{{\varvec{N}}}}_{i,6}^j +{\varvec{u}}_f^{j{\mathrm{T}}} {\bar{{\varvec{N}}}}_{i,7}^j \\&\quad +\,m_{O_{1i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)} \right) \\&\quad \tilde{{\varvec{K}}}{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,m_{O_{2i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) } \right) \\&\quad \tilde{{\varvec{K}}}{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j} +J_{O_{1i} }^j \left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} {\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,J_{O_{2i} }^j \left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j } {\varvec{B}}_i^j {\varvec{D}}^{j} \\&{\varvec{M}}_{i,fr}^j ={\varvec{M}}_{i,rf}^{j{\mathrm{T}}} \\&{\varvec{M}}_{i,f\phi }^j ={\varvec{M}}_{i,\phi f}^{j{\mathrm{T}}} \\&{\varvec{M}}_{i,ff}^j ={\bar{{\varvec{N}}}}_{i,5}^j +m_{O_{1i} }^j {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0){\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,m_{O_{2i} }^j {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) {\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,J_{O_{1i} }^j {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} \left. {\frac{\partial {\varvec{N}}_{i,2}^{j{\mathrm{T}}} (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} \left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =0} {\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,J_{O_{2i} }^j {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} \left. {\frac{\partial {\varvec{N}}_{i,2}^{j{\mathrm{T}}} (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j } \left. {\frac{\partial {\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }} \right| _{\bar{{x}}_i =l_i^j } {\varvec{B}}_i^j {\varvec{D}}^{j} \end{aligned}$$

The integration constants in the mass matrix ${\varvec{M}}_i^j$ of element i are given by

$$\begin{aligned} {\bar{{\varvec{N}}}}_{i,1}^j= & {} \int _{V_i^j } \rho {\varvec{r}}_{0,i}^j \hbox {d}V_i^j \\ {\bar{{\varvec{N}}}}_{i,2}^j= & {} \int _{V_i^j } \rho {\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}V_i^j \\ \bar{{N}}_{i,3}^j= & {} \int _{V_i^j } \rho {\varvec{r}}_{0,i}^{j{\mathrm{T}}} {\varvec{r}}_{0,i}^j \hbox {d}V_i^j \\ {\bar{{\varvec{N}}}}_{i,4}^j= & {} \int _{V_i^j } \rho {\varvec{r}}_{0,i}^{j{\mathrm{T}}} {\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}V_i^j \\ {\bar{{\varvec{N}}}}_{i,5}^j= & {} \int _{V_i^j } \rho {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (\bar{{x}}_i ){\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}V_i^j \\ {\bar{{\varvec{N}}}}_{i,6}^j= & {} \int _{V_i^j } {\rho {\varvec{r}}_{0,i}^{j{\mathrm{T}}} } \tilde{{\varvec{K}}}{\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}V_i^j \\ {\bar{{\varvec{N}}}}_{i,7}^j= & {} \int _{V_i^j } \rho {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (\bar{{x}}_i )\tilde{{\varvec{K}}}{\varvec{N}}_i^j (\bar{{x}}_i ){\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}V_i^j \end{aligned}$$

where $\tilde{\varvec{K}}=\left[ {{\begin{array}{l@{\quad }l} 0&{} 1 \\ -1&{} 0 \\ \end{array} }} \right]$ is a $2\times 2$ unit skew matrix.

3.2.2 Potential energy of element i

Since the structure of the manipulator is horizontal overall layout and the working plane is $O{-}x{-}y$ plane, the gravitational potential energy of RAParM-I can be not taken into consideration [14]. Herein, the tensional strain energy and bending strain energy are taken into consideration, while the shear and torsion strain energies are negligible in this paper. Therefore, the total potential energy of element i in flexible body j can be expressed as

$$\begin{aligned} U_{p,i}^j= & {} \frac{1}{2}\int _0^{l_i^j } {\textit{EI}\left( {\frac{\partial ^{2}w_i^j (\bar{{x}}_i ,t)}{\partial \bar{{x}}_i^2 }} \right) } ^{2}\hbox {d}\bar{{x}}_i \nonumber \\&+\,\frac{1}{2}\int _0^{l_i^j } {\textit{EA}} \left( {\frac{\partial v_i^j (\bar{{x}}_i ,t)}{\partial \bar{{x}}_i }} \right) ^{2}\hbox {d}\bar{{x}}_i \nonumber \\= & {} \frac{1}{2}{\varvec{q}}_j^{\mathrm{T}} {\varvec{K}}_i^j {\varvec{q}}_j \end{aligned}$$

(26)

where E represents the Young’s modulus of beam material; I represents the area moment of inertia of beam cross section; A represents the cross-sectional area. ${\varvec{K}}_i^j$ represents the stiffness matrix of element i and can be written as

$$\begin{aligned} {\varvec{K}}_i^j =\left[ \begin{array}{l@{\quad }l@{\quad }l} \mathbf{0}_{2\times 2} &{} \mathbf{0}_{2\times 1} &{} \mathbf{0}_{2\times 4n_j} \\ \mathbf{0}_{1\times 2} &{} 0 &{} \mathbf{0}_{1\times 4n_j} \\ \mathbf{0}_{4n_j \times 2} &{} \mathbf{0}_{4n_j \times 1} &{} {\varvec{K}}_{i,ff}^j \\ \end{array} \right] \end{aligned}$$

(27)

where

$$\begin{aligned} {\varvec{K}}_{i,ff}^j= & {} \int _0^{l_i^j } {\textit{EI}{\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} \frac{\partial ^{2}{\varvec{N}}_{i,2}^{j{\mathrm{T}}} (\bar{{x}}_i )}{\partial \bar{{x}}_i^2 }} \frac{\partial ^{2}{\varvec{N}}_{i,2}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i^2 }{\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}\bar{{x}}_i \nonumber \\&+\,\int _0^{l_i^j } {\textit{EA}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} \frac{\partial {\varvec{N}}_{i,1}^{j{\mathrm{T}}} (\bar{{x}}_i )}{\partial \bar{{x}}_i }\frac{\partial {\varvec{N}}_{i,1}^j (\bar{{x}}_i )}{\partial \bar{{x}}_i }{\varvec{B}}_i^j {\varvec{D}}^{j}\hbox {d}\bar{{x}}_i\nonumber \\ \end{aligned}$$

(28)

3.2.3 Dynamic model of element i

Substituting the kinetic energy and potential energy of element i into the Lagrangian formulation yields

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial \mathscr {L}_i^j }{\partial {\dot{{\varvec{q}}}}_j }} \right) -\frac{\partial \mathscr {L}_i^j }{\partial {\varvec{q}}_j }={\varvec{F}}_{e,i}^j \end{aligned}$$

(29)

where $\mathscr {L}_i^j =T_i^j -U_{p,i}^j$ represents the Lagrangian function of element i and ${\varvec{F}}_{e,i}^j$ represents the column matrix of generalized external forces of element i.

Through a series of mathematical derivation, the dynamic model of element i in flexible body j can be expressed in a compact form as

$$\begin{aligned} {\varvec{M}}_i^j {\ddot{\varvec{q}}}_j +{\varvec{C}}_i^j {\dot{{\varvec{q}}}}_j +{\varvec{K}}_i^j {\varvec{q}}_j ={\varvec{F}}_{e,i}^j \end{aligned}$$

(30)

where ${\varvec{M}}_i^j$ and ${\varvec{K}}_i^j$ are the mass and stiffness matrices, respectively, which are displayed in the Sects. 3.2.1 and 3.2.2 of this paper. ${\varvec{C}}_i^j$ is the centrifugal and Coriolis force matrix of element i in flexible body j. In order to obtain the detailed expression of ${\varvec{C}}_i^j$, let

$$\begin{aligned} \hat{\varvec{C}}_{i1}^j= & {} \frac{\partial {\varvec{M}}_i^j }{\partial {\varvec{q}}_j^{\mathrm{T}}}\left( {{\dot{{\varvec{q}}}}_j } \otimes {\varvec{I}} \right) \end{aligned}$$

(31)

$$\begin{aligned} \hat{\varvec{C}}_{i2}^j= & {} \frac{1}{2}\left( {{\varvec{I}}\otimes {\dot{{\varvec{q}}}}_j } \right) ^{\mathrm{T}}\frac{\partial {\varvec{M}}_i^j }{\partial {\varvec{q}}_j } \end{aligned}$$

(32)

where ${\varvec{I}}$ represents a identity matrix and signal “$\otimes$” represents the Kronecker product. Through a series of derivation, one can obtain

$$\begin{aligned} \hat{\varvec{C}}_{i1}^j =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\varvec{C}}_{i1,rr}^j &{} {\varvec{C}}_{i1,r\phi }^j &{} {\varvec{C}}_{i1,rf}^j \\ {\varvec{C}}_{i1,\phi r}^j &{} C_{i1,\phi \phi }^j &{} {\varvec{C}}_{i1,\phi f}^j \\ {\varvec{C}}_{i1,fr}^j &{} {\varvec{C}}_{i1,f\phi }^j &{} {\varvec{C}}_{i1,ff}^j \\ \end{array}}} \right] \end{aligned}$$

(33)

where

$$\begin{aligned}&{\varvec{C}}_{i1,rr}^j =\mathbf{0}_{2\times 2} \\&{\varvec{C}}_{i1,r\phi }^j =\dot{\phi }_j \frac{\partial ^{2}{\varvec{R}}(\phi _j )}{\partial \phi _j^2 }{\bar{{\varvec{N}}}}_{i,1}^j +\dot{\phi }_j \frac{\partial ^{2}{\varvec{R}}(\phi _j )}{\partial \phi _j^2 }{\bar{{\varvec{N}}}}_{i,2}^j {\varvec{u}}_f^j \\&\quad +\,\frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }{\bar{{\varvec{N}}}}_{i,2}^j{\dot{{\varvec{u}}}}_f^j +m_{O_{1i} }^j \dot{\phi }_j \frac{\partial ^{2}{\varvec{R}}(\phi _j )}{\partial \phi _j^2 }\\&\quad \times \left( {\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \\&\quad +\,m_{O_{1i} }^j \frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \\&\quad +\,m_{O_{2i} }^j \dot{\phi }_j \frac{\partial ^{2}{\varvec{R}}(\phi _j )}{\partial \phi _j^2 }\left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \\&\quad +\,m_{O_{2i} }^j \frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\dot{{\varvec{u}}}}_f^j \\&{\varvec{C}}_{i1,rf}^j =\dot{\phi }_j \frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }{\bar{{\varvec{N}}}}_{i,2}^j \\&\quad +\,\frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j }\dot{\phi }_j \left( {m_{O_{1i} }^j {\varvec{N}}_i^j (0)+m_{O_{2i} }^j {\varvec{N}}_i^j \left( l_i^j\right) } \right) {\varvec{B}}_i^j {\varvec{D}}^{j} \\&{\varvec{C}}_{i1,\phi r}^j ={\varvec{C}}_{i1,r\phi }^{j{\mathrm{T}}} \\&C_{i1,\phi \phi }^j =2{\bar{{\varvec{N}}}}_{i,4}^j {\dot{{\varvec{u}}}}_f^j +2{\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\bar{{\varvec{N}}}}_{i,5}^j {\varvec{u}}_f^j \\&\quad +\,2m_{O_{1i} }^j {\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0) \\&\quad \left( \left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j \right) \\&\quad +\,2m_{O_{2i} }^j {\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \\&\quad \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j}{\varvec{u}}_f^j } \right) \\&{\varvec{C}}_{i1,\phi f}^j ={\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\bar{{\varvec{N}}}}_{i,7}^j +m_{O_{1i} }^j {\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0) \\&\quad \tilde{{\varvec{K}}}{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}^{j} \\&\quad +\,m_{O_{2i} }^j {\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} {\varvec{D}}^{j{\mathrm{T}}}{\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \tilde{{\varvec{K}}}{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}^{j} \\&{\varvec{C}}_{i1,fr}^j ={\varvec{C}}_{i1,rf}^{j{\mathrm{T}}} \\&{\varvec{C}}_{i1,f\phi }^j ={\varvec{C}}_{i1,\phi f}^{j{\mathrm{T}}} \\&{\varvec{C}}_{i1,ff}^j =\mathbf{0}_{4n_j \times 4n_j} \end{aligned}$$

$$\begin{aligned} \hat{\varvec{C}}_{i2}^j =\left[ \begin{array}{l@{\quad }l@{\quad }l} {\varvec{C}}_{i2,rr}^j&{} {\varvec{C}}_{i2,r\phi }^j &{} {\varvec{C}}_{i2,rf}^j \\ {\varvec{C}}_{i2,\phi r}^j &{} C_{i2,\phi \phi }^j &{} {\varvec{C}}_{i2,\phi f}^j \\ {\varvec{C}}_{i2,fr}^j &{} {\varvec{C}}_{i2,f\phi }^j &{} {\varvec{C}}_{i2,ff}^j \\ \end{array} \right] \end{aligned}$$

(34)

where

$$\begin{aligned}&{\varvec{C}}_{i2,rr}^j =\mathbf{0}_{2\times 2} \\&{\varvec{C}}_{i2,r\phi }^j =\mathbf{0}_{2\times 1} \\&{\varvec{C}}_{i2,rf}^j =\mathbf{0}_{2\times 4n_j } \\&{\varvec{C}}_{i2,\phi r}^j=\frac{1}{2}\dot{\phi }_j \\&\quad \left( {\begin{array}{l} {\bar{{\varvec{N}}}}_{i,1}^{j{\mathrm{T}}} +{\varvec{u}}_f^{j{\mathrm{T}}} {\bar{{\varvec{N}}}}_{i,2}^{j{\mathrm{T}}} +m_{O_{1i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{1i}}^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)} \right) \\ +m_{O_{2i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] ^{\mathrm{T}}+{\varvec{u}}_f^{j{\mathrm{T}}} {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j \right) } \right) \\ \end{array}} \right) \\&\qquad \frac{\partial ^{2}{\varvec{R}}^{\mathrm{T}}(\phi _j )}{\partial \phi _j^2 } \\&\quad +\,\frac{1}{2}{\dot{{\varvec{u}}}}_f^{j{\mathrm{T}}} \left( {{\bar{{\varvec{N}}}}_{i,2}^{j{\mathrm{T}}} +m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)+m_{O_{2i}}^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j \right) } \right) \\&\qquad \frac{\partial {\varvec{R}}^{\mathrm{T}}(\phi _j )}{\partial \phi _j } \\&C_{i2,\phi \phi }^j =\frac{1}{2}{\dot{{\varvec{r}}}}_{O_j }^{\mathrm{T}} \frac{\partial ^{2}{\varvec{R}}(\phi _j )}{\partial \phi _j^2 } \\&\quad \left( {\begin{array}{l} {\bar{{\varvec{N}}}}_{i,1}^j +{\bar{{\varvec{N}}}}_{i,2}^j {\varvec{u}}_f^j +m_{O_{1i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}_i^j {\varvec{u}}_f^j } \right) \\ +m_{O_{2i} }^j \left( {\left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array} }} \right] +{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}_i^j {\varvec{u}}_f^j } \right) \\ \end{array}} \right) \\&{\varvec{C}}_{i2,\phi f}^j =\frac{1}{2}{\dot{{\varvec{r}}}}_{O_j }^{\mathrm{T}} \frac{\partial {\varvec{R}}(\phi _j )}{\partial \phi _j } \\&\quad \left( {{\bar{{\varvec{N}}}}_{i,2}^j +m_{O_{1i} }^j {\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}_i^j +m_{O_{2i}}^j {\varvec{N}}_i \left( l_i^j \right) {\varvec{B}}_i^j {\varvec{D}}_i^j } \right) \\ \end{aligned}$$

$$\begin{aligned}&{\varvec{C}}_{i2,fr}^j =\frac{1}{2}\dot{\phi }_j \left( {\bar{{\varvec{N}}}}_{i,2}^{j{\mathrm{T}}} +m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0) \right. \\&\quad \left. +\,m_{O_{2i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \right) \frac{\partial {\varvec{R}}^{\mathrm{T}}(\phi _j )}{\partial \phi _j } \\&{\varvec{C}}_{i2,f\phi }^j =\frac{1}{2} \left( {\bar{{\varvec{N}}}}_{i,2}^{j{\mathrm{T}}} +m_{O_{1i}}^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0) \right. \\&\quad \left. +\,m_{O_{2i}}^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \right) \frac{\partial {\varvec{R}}^{\mathrm{T}}(\phi _j )}{\partial \phi _j }{\dot{{\varvec{r}}}}_{O_j} \\&\quad +\,\left( {\begin{array}{l} {\bar{{\varvec{N}}}}_{i,4}^{j{\mathrm{T}}} +{\bar{{\varvec{N}}}}_{i,5}^j {\varvec{u}}_f +m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)\left[ {{\begin{array}{l} {l_{O_{1i} }^j } \\ 0 \\ \end{array}}} \right] \\ \quad +\,m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0){\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}_i^j {\varvec{u}}_f^j \\ \quad +\,m_{O_{2i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \left[ {{\begin{array}{l} {l_{O_{2i} }^j } \\ 0 \\ \end{array}}} \right] \\ \quad +\,m_{O_{2i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) {\varvec{N}}_i \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}_i^j {\varvec{u}}_f^j \\ \end{array}} \right) \dot{\phi }_j \\&\quad +\,\frac{1}{2}\left( {\bar{{\varvec{N}}}}_{i,7}^j +m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)\tilde{{\varvec{K}}}{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}_i^j \right. \\&\quad \left. +\,m_{O_{2i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \tilde{{\varvec{K}}}{\varvec{N}}_i \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}_i^j \right) {\dot{{\varvec{u}}}}_f^j \\&{\varvec{C}}_{i2,ff}^j =\frac{1}{2}\left( {\bar{{\varvec{N}}}}_{i,7}^j +m_{O_{1i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} (0)\tilde{{\varvec{K}}}{\varvec{N}}_i^j (0){\varvec{B}}_i^j {\varvec{D}}_i^j \right. \\&\quad \left. +\,m_{O_{2i} }^j {\varvec{D}}_i^{j{\mathrm{T}}} {\varvec{B}}_i^{j{\mathrm{T}}} {\varvec{N}}_i^{j{\mathrm{T}}} \left( l_i^j\right) \tilde{{\varvec{K}}}{\varvec{N}}_i^j \left( l_i^j\right) {\varvec{B}}_i^j {\varvec{D}}_i^j \right) \dot{\phi }_j \end{aligned}$$

Therefore, the centrifugal and Coriolis force matrix of element i in flexible body j can be obtained as

$$\begin{aligned} {\varvec{C}}_i^j= & {} \frac{\partial {\varvec{M}}_i^j }{\partial {\varvec{q}}_j^{\mathrm{T}} } \left( {{\dot{{\varvec{q}}}}_j \otimes {\varvec{I}}} \right) -\frac{1}{2}\left( {{\varvec{I}}\otimes {\dot{{\varvec{q}}}}_j } \right) ^{\mathrm{T}}\frac{\partial {\varvec{M}}_i^j }{\partial {\varvec{q}}_j } \nonumber \\= & {} \hat{\varvec{C}}_{i1}^j -\hat{\varvec{C}}_{i2}^j =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\varvec{C}}_{i,rr}^j &{} {\varvec{C}}_{i,r\phi }^j &{} {\varvec{C}}_{i,rf}^j \\ {\varvec{C}}_{i,\phi r}^j &{} {\varvec{C}}_{i,\phi \phi }^j &{} {\varvec{C}}_{i,\phi f}^j \\ {\varvec{C}}_{i,fr}^j &{} {\varvec{C}}_{i,f\phi }^j &{} {\varvec{C}}_{i,ff}^j \\ \end{array}}} \right] \end{aligned}$$

(35)

where

$$\begin{aligned} {\varvec{C}}_{i,rr}^j= & {} {\varvec{C}}_{i1,rr}^j -{\varvec{C}}_{i2,rr}^j ,\,{\varvec{C}}_{i,r\phi }^j \\= & {} {\varvec{C}}_{i1,r\phi }^j -{\varvec{C}}_{i2,r\phi }^j ,\,{\varvec{C}}_{i,rf}^j ={\varvec{C}}_{i1,rf}^j -{\varvec{C}}_{i2,rf}^j \\ {\varvec{C}}_{i,\phi r}^j= & {} {\varvec{C}}_{i1,\phi r}^j -{\varvec{C}}_{i2,\phi r}^j ,\,{\varvec{C}}_{i,\phi \phi }^j \\= & {} {\varvec{C}}_{i1,\phi \phi }^j -{\varvec{C}}_{i2,\phi \phi }^j ,\,{\varvec{C}}_{i,\phi f}^j ={\varvec{C}}_{i1,\phi f}^j -{\varvec{C}}_{i2,\phi f}^j \\ {\varvec{C}}_{i,fr}^j= & {} {\varvec{C}}_{i1,fr}^j -{\varvec{C}}_{i2,fr}^j ,\,{\varvec{C}}_{i,f\phi }^j \\= & {} {\varvec{C}}_{i1,f\phi }^j -{\varvec{C}}_{i2,f\phi }^j ,\,{\varvec{C}}_{i,ff}^j ={\varvec{C}}_{i1,ff}^j -{\varvec{C}}_{i2,ff}^j. \end{aligned}$$

Remark 1

The dynamic model of an arbitrary element i with lumped masses and moments of inertia in flexible body j can be transformed conveniently into the dynamic model of common element only through modifying the parameters of lumped masses and moments of inertia of element i presented in this paper to null (see Fig. 7). Consequently, the dynamic model of element i deduced here can be conveniently assembled into the dynamic model of a certain flexible body with any number of lumped masses and moments of inertia.

3.3 Dynamic model of flexible body j

The total generalized coordinates of arbitrary flexible body j are selected as the generalized coordinates of the dynamic model of element i within flexible body j. To obtain the dynamic model of arbitrary flexible body j, we need only to add all the dynamic equations of elements within flexible body j together. Thus, assembling the dynamic model of an arbitrary element i, one can further obtain the dynamic model of flexible body j as

$$\begin{aligned} {\bar{\varvec{M}}}_j {\ddot{\varvec{q}}}_j +{\bar{\varvec{C}}}_j {\dot{{\varvec{q}}}}_j {+}{\bar{\varvec{K}}}_j {\varvec{q}}_j ={\bar{\varvec{F}}}_{e,j} \end{aligned}$$

(36)

where ${\bar{\varvec{M}}}_j =\sum \nolimits _{i=1}^{n_j } {{\varvec{M}}_i^j}$: mass matrix of flexible body j; ${\bar{\varvec{C}}}_j =\sum \nolimits _{i=1}^{n_j} {{\varvec{C}}_i^j }$: centrifugal and Coriolis force matrix of flexible body j; ${\bar{\varvec{K}}}_j =\sum \nolimits _{i=1}^{n_j } {{\varvec{K}}_i^j }$: stiffness matrix of flexible body j; ${\bar{\varvec{F}}}_{e,j} =\sum \nolimits _{i=1}^{n_j } {{\varvec{F}}_{e,i}^j }$: column matrix of generalized external forces of flexible body j; $n_j$ represents the number of elements in flexible body j.

Remark 2

It should be mentioned that the dynamic model of flexible body j derived here is generally applicable for planar PMs with flexible links. That is to say, the dynamic model of flexible body j can be assembled modularly to achieve the RFDM of a certain flexible planar PM and can be realized conveniently by programming as well. In the following section, the establishment of complete dynamic model of system will be elaborated in detail.

3.4 Dynamic model of system

3.4.1 Dynamic model of system without constraints

In our study, RAParM-I encompasses totally 8 flexible bodies. Therefore, the vector of generalized coordinates of system is denoted as ${\varvec{q}}^{(\mathrm{s})}=[{\begin{array}{lllllll} {{\varvec{r}}_{O_1}^{\mathrm{T}} }&{} {\phi _1 }&{} {{\varvec{u}}_f^{1\mathrm{T}} }&{} \cdots &{} {{\varvec{r}}_{O_1 }^{\mathrm{T}} }&{} {\phi _8 }&{} {{\varvec{u}}_f^{8\mathrm{T}} } \\ \end{array} }]^{\mathrm{T}}$. Based upon the above analysis, assembling the dynamic equations of all the flexible bodies of system, one can obtain the flexible multi-body dynamic model of system without constraint as

$$\begin{aligned} {\bar{\varvec{M}}}^{(\mathrm{s})}{\ddot{\varvec{q}}}^{(\mathrm{s})}+{\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}+{\bar{\varvec{K}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}={\bar{\varvec{F}}}_e^{(\mathrm{s})} \end{aligned}$$

(37)

where ${\bar{\varvec{M}}}^{(\mathrm{s})}$ is the mass matrix of system; ${\bar{\varvec{C}}}^{(\mathrm{s})}$ is the centrifugal and Coriolis force matrix of system; ${\bar{\varvec{K}}}^{(\mathrm{s})}$ is the stiffness matrix of system; ${\bar{\varvec{F}}}_e^{(\mathrm{s})}$ is the column matrix of generalized external forces of system. These four matrices are expressed as follows:

$$\begin{aligned} {\bar{\varvec{M}}}^{(\mathrm{s})}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\bar{\varvec{M}}}_1 }&{} &{} &{} \\ &{} {{\bar{\varvec{M}}}_2 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{\bar{\varvec{M}}}_8 } \\ \end{array} }} \right] , \nonumber \\ {\bar{\varvec{C}}}^{(\mathrm{s})}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\bar{\varvec{C}}}_1 }&{} &{} &{} \\ &{} {{\bar{\varvec{C}}}_2 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{\bar{\varvec{C}}}_8 } \\ \end{array} }} \right] , \nonumber \\ {\bar{\varvec{K}}}^{(\mathrm{s})}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\bar{\varvec{K}}}_1 }&{} &{} &{} \\ &{} {{\bar{\varvec{K}}}_2 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {{\bar{\varvec{K}}}_8 } \\ \end{array} }} \right] \nonumber \\ {\bar{\varvec{F}}}_e^{(\mathrm{s})}= & {} \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {{\bar{\varvec{F}}}_{e,1}^{\mathrm{T}} }&{} {{\bar{\varvec{F}}}_{e,2}^{\mathrm{T}} }&{} \cdots &{} {{\bar{\varvec{F}}}_{e,8}^{\mathrm{T}} } \\ \end{array} }} \right] ^{\mathrm{T}} \end{aligned}$$

(38)

3.4.2 Constraint equations of system

It should be mentioned that the dynamic model of system manifested in Eq. (37) is achieved through assembling the dynamic model of arbitrary flexible body j obtained via cutting virtually the joints of mechanism, which contains no constraints. In other words, the dynamic model shown in Eq. (37) is open-loop. Consequently, in order to establish the complete dynamic model of system, some constraint equations of system should be introduced into the open-loop dynamic model. The schematic diagram and topological graph of RAParM-I are shown in Fig. 8, from which one can discover that there are three independent closed-loop constraints, i.e., loop I, II and III, respectively. In addition, since the joint position coordinates of flexible body j are introduced in the dynamic model, some related joint constraint equations of flexible body j should be constructed to restrain the redundant degrees of freedom caused by the joint position coordinates. Therefore, 8 set of joint constraint equations need to be constructed here. The 8 joints are joints $A_{1}$, $B_{1}$, $D_{1}$, $E_{1}$, $A_{2}$, $B_{2}$, $D_{2}$ and $E_{2}$, respectively.

Fig. 8

The schematic diagram and topological graph of RAParM-I

Based upon above analysis, there are totally 22 constraint equations, which can be expressed as follows: (1) Constraint equations for joint $A_{1}$

$$\begin{aligned} {\varvec{r}}_{A_1 } =\left[ {{\begin{array}{l} -e \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(39)

(2) Constraint equations for joint $B_{1}$

$$\begin{aligned} {\varvec{r}}_{B_1 } =\left[ {{\begin{array}{c} -e \\ 0 \\ \end{array} }} \right] +{\varvec{R}}(\phi _1 )\left[ {{\begin{array}{c} l_1 +u_{1,\bar{{x}}}^{\mathrm{end}} \\ u_{1,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \end{aligned}$$

(40)

(3) Constraint equations for joint $D_{1}$

$$\begin{aligned} {\varvec{r}}_{D_1} =\left[ {{\begin{array}{c} -e \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(41)

(4) Constraint equations for joint $E_{1}$

$$\begin{aligned} {\varvec{r}}_{E_1 } =\left[ {{\begin{array}{c} -e \\ 0 \\ \end{array} }} \right] +{\varvec{R}}(\phi _2 )\left[ {{\begin{array}{c} l_a +u_{2,\bar{{x}}}^{\mathrm{end}} \\ u_{2,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \end{aligned}$$

(42)

(5) Constraint equations for joint $A_{2}$

$$\begin{aligned} {\varvec{r}}_{A_2 } =\left[ {{\begin{array}{l} e \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(43)

(6) Constraint equations for joint $B_{2}$

$$\begin{aligned} {\varvec{r}}_{B_2 } =\left[ {{\begin{array}{c} e \\ 0 \\ \end{array}}} \right] +{\varvec{R}}(\phi _5 )\left[ {{\begin{array}{c} l_1 +u_{5,\bar{{x}}}^{\mathrm{end}} \\ u_{5,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \end{aligned}$$

(44)

(7) Constraint equations for joint $D_{2}$

$$\begin{aligned} {\varvec{r}}_{D_2 } =\left[ {{\begin{array}{c} e \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(45)

(8) Constraint equations for joint $E_{2}$

$$\begin{aligned} {\varvec{r}}_{E_2 } =\left[ {{\begin{array}{c} e \\ 0 \\ \end{array}}} \right] +{\varvec{R}}(\phi _6 )\left[ {{\begin{array}{c} l_a +u_{6,\bar{{x}}}^{\mathrm{end}} \\ u_{6,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \end{aligned}$$

(46)

(9) Constraint equations for closed-loop I

$$\begin{aligned}&{\varvec{r}}_{B_1 } +{\varvec{R}}(\phi _4 )\left[ {{\begin{array}{c} l_a +u_{4,\bar{{x}}}^{\mathrm{mid}} \\ u_{4,\bar{{y}}}^{\mathrm{mid}} \\ \end{array} }} \right] ={\varvec{r}}_{E_1 } +{\varvec{R}}(\phi _3 )\left[ {{\begin{array}{c} l_1 +u_{3,\bar{{x}}}^{\mathrm{end}} \\ u_{3,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(47)

(10) Constraint equations for closed-loop II

$$\begin{aligned}&{\varvec{r}}_{B_2 } +{\varvec{R}}(\phi _8 )\left[ {{\begin{array}{c} l_a +u_{8,\bar{{x}}}^{\mathrm{mid}} \\ u_{8,\bar{{y}}}^{\mathrm{mid}} \\ \end{array} }} \right] ={\varvec{r}}_{E_2 } +{\varvec{R}}(\phi _7 )\left[ {{\begin{array}{c} l_1 +u_{7,\bar{{x}}}^{\mathrm{end}} \\ u_{7,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(48)

(11) Constraint equations for closed-loop III

$$\begin{aligned}&{\varvec{r}}_{B_1} +{\varvec{R}}(\phi _4 )\left[ {{\begin{array}{c} l_2 +u_{4,\bar{{x}}}^{\mathrm{end}} \\ u_{4,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] ={\varvec{r}}_{B_2 } +{\varvec{R}}(\phi _8 )\left[ {{\begin{array}{c} l_2 +u_{8,\bar{{x}}}^{\mathrm{end}} \\ u_{8,\bar{{y}}}^{\mathrm{end}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(49)

where ${\varvec{r}}_{\mathrm{joint}_i }$ represents the position vector of a certain joint; $u_{j,\bar{{x}}}^{\mathrm{mid}}$ and $u_{j,\bar{{y}}}^{\mathrm{mid}}$ represent, respectively, the axial and transverse elastic displacements of element node at the position of middle joint (see Fig. 8) for flexible body j ($j=4,8$); $u_{j,\bar{{x}}}^{\mathrm{end}}$ and $u_{j,\bar{{y}}}^{\mathrm{end}}$ represent, respectively, the axial and transverse elastic displacements of element node at the position of end joint for flexible body $j\, (j=1,2,\cdots ,8)$. These above constraint equations can be uniformly expressed in a compact form as

$$\begin{aligned} \varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) =\mathbf{0} \end{aligned}$$

(50)

where $\varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) \in \mathbb {R}^{22}$. Taking first-order differentiation for Eq. (50) with respect to time yields

$$\begin{aligned} \varvec{{\varPhi }}_c \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\dot{{\varvec{q}}}}^{(\mathrm{s})}+\varvec{{\varPhi }}_t =\mathbf{0} \end{aligned}$$

(51)

where $\varvec{{\varPhi }}_c \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) =\frac{\partial \varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) }{\partial {\varvec{q}}^{(\mathrm{s})\mathrm{T}}}$ represents the constraint Jacobian matrix of system, which is a sparse matrix, $\varvec{{\varPhi }}_t =\frac{\partial \varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) }{\partial t}$ and ${\dot{{\varvec{q}}}}^{(\mathrm{s})}=[{\begin{array}{lllllll} {\dot{{\varvec{r}}}}_{O_1 }^{\mathrm{T}} &{} \dot{\phi }_1&{} {\dot{{\varvec{u}}}}_f^{1\mathrm{T}} &{} \cdots &{} {\dot{{\varvec{r}}}}_{O_8 }^{\mathrm{T}} &{} \dot{\phi }_8 &{} {\dot{{\varvec{u}}}}_f^{8\mathrm{T}} \\ \end{array}}\!]^{\mathrm{T}}$. Furthermore, taking second-order differentiation for Eq. (50) with respect to time yields

$$\begin{aligned} \varvec{{\varPhi }}_c \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\ddot{\varvec{q}}}^{(\mathrm{s})}={\varvec{\gamma }} \end{aligned}$$

(52)

where ${\ddot{\varvec{q}}}^{(\mathrm{s})}=[{\begin{array}{lllllll} {\ddot{\varvec{r}}_{O_1 }^{\mathrm{T}} }&{} {\ddot{\phi }_1 }&{} {\ddot{\varvec{u}}_f^{1\mathrm{T}} }&{} \cdots &{} {\ddot{\varvec{r}}_{O_1 }^{\mathrm{T}} }&{} {\ddot{\phi }_8 }&{} {\ddot{\varvec{u}}_f^{8\mathrm{T}}} \\ \end{array}}]^{\mathrm{T}}$, and ${\varvec{\gamma }}\in \mathbb {R}^{22\times 1}$ represents the right-hand side of acceleration constraint equations and is given by

$$\begin{aligned} {\varvec{\gamma }}= & {} -\frac{\partial }{\partial {\varvec{q}}^{(\mathrm{s})\mathrm{T}}}\left( {\frac{\partial \varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) }{\partial {\varvec{q}}^{(\mathrm{s})\mathrm{T}}}{\dot{{\varvec{q}}}}^{(\mathrm{s})}} \right) {\dot{{\varvec{q}}}}^{(\mathrm{s})} \nonumber \\&-2\frac{\partial }{\partial t}\left( {\frac{\partial \varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) }{\partial {\varvec{q}}^{(\mathrm{s})\mathrm{T}}}} \right) {\dot{{\varvec{q}}}}^{(\mathrm{s})}-\frac{\partial ^{2}\varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) }{\partial t^{2}} \end{aligned}$$

(53)

3.4.3 Complete dynamic model of system

By assembling the open-loop dynamic model of system shown in Eq. (37) and the constraint equations of system shown in Eq. (50), and incorporating the Lagrangian multipliers, one can obtain the complete dynamic model of system as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\bar{\varvec{M}}}^{(\mathrm{s})}{\ddot{\varvec{q}}}^{(\mathrm{s})}+{\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}{+}{\bar{\varvec{K}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}+\varvec{{\varPhi }}_c^{\mathrm{T}} \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\varvec{\lambda }}={\bar{\varvec{F}}}_e^{(\mathrm{s})} } \\ {\varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) =\mathbf{0}_{22\times 1} } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(54)

where ${\varvec{\lambda }}\in \mathbb {R}^{22}$ is the vector of Lagrangian multipliers which denotes the magnitude of the generalized constraint reactions; ${\bar{\varvec{F}}}_e^{(\mathrm{s})}$ is the column matrix of generalized external forces of system, which can be expressed as

$$\begin{aligned}&{\bar{\varvec{F}}}_e^{(\mathrm{s})} =\left[ \begin{array}{llll} \underbrace{{\begin{array}{lll} {\mathbf{0}_{1\times 2} }&{} {\tau _1 }&{} {\mathbf{0}_{1\times 4n_1 } } \\ \end{array} }}_{ \hbox {body-}1} &{} \underbrace{{\begin{array}{lll} {\mathbf{0}_{1\times 2} }&{} {\tau _2 }&{} {\mathbf{0}_{1\times 4n_2 } } \\ \end{array} }}_{\hbox {body-2}} &{} \underbrace{\mathbf{0}_{1\times (4n_3 +3)}}_{\hbox {body-3}}&{} \underbrace{\mathbf{0}_{1\times (4n_4 +3)} }_{\hbox {body-4}} \\ \end{array} \right. \nonumber \\&\quad \left. {{\begin{array}{llll} {\underbrace{{\begin{array}{lll} {\mathbf{0}_{1\times 2} }&{} {\tau _5 }&{} {\mathbf{0}_{1\times 4n_5 } } \\ \end{array} }}_{\hbox {body-5}}}&{} {\underbrace{{\begin{array}{lll} {\mathbf{0}_{1\times 2} }&{} {\tau _6 }&{} {\mathbf{0}_{1\times 4n_6 } } \\ \end{array}}}_{\hbox {body-6}}} &{} {\underbrace{\mathbf{0}_{1\times (4n_7 +3)} }_{\hbox {body-7}}}&{} {\underbrace{\mathbf{0}_{1\times (4n_8 +3)} }_{\hbox {body-8}}} \\ \end{array}}} \right] ^{\mathrm{T}}\nonumber \\ \end{aligned}$$

(55)

where $\tau _1$, $\tau _2$, $\tau _5$ and $\tau _6$ represent, respectively, the driving torques offered by the servo motors mounted at the base of RAParM-I (see Fig. 3). It is worth noting that different actuation modes can be achieved here via selecting different driving torques as the practical driving ones, for instance,

• when $\tau _1 \ne 0$, $\tau _2 \equiv 0$, $\tau _5 \ne 0$, $\tau _6 \equiv 0$, the actuation mode is “$\oplus \ominus \oplus \ominus$”;

• when $\tau _1 \ne 0$, $\tau _2 \ne 0$, $\tau _5 \ne 0$, $\tau _6 \equiv 0$, the actuation mode is “$\oplus \oplus \oplus \ominus$”;

• when $\tau _1 \ne 0$, $\tau _2 \ne 0$, $\tau _5 \ne 0$, $\tau _6 \ne 0$, the actuation mode is “$\oplus \oplus \oplus \oplus$.”

Likewise, the other actuation modes can also be obtained easily by using analogous method, and the relevant actuation modes are illustrated in Ref. [14].

Equation (55) is also called index-3 dynamic model, which is a group of differential and algebraic equations (DAEs).

This type of dynamic equations can be solved by virtue of the direct integration methods, such as Newmark-$\beta$ method [78], Wilson-$\theta$ method [79], HHT method [80] and generalize $\alpha$ method [81].

Furthermore, combined with Eqs. (52), (54) can be transformed into

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\bar{\varvec{M}}}^{(\mathrm{s})}{\ddot{\varvec{q}}}^{(\mathrm{s})}+{\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}+{\bar{\varvec{K}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}+\varvec{{\varPhi }}_c^{\mathrm{T}} \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\varvec{\lambda }}={\bar{\varvec{F}}}_e^{(\mathrm{s})} } \\ {\varvec{{\varPhi }}_c \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\ddot{\varvec{q}}}^{(\mathrm{s})}={\varvec{\gamma }}_{22\times 1} } \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(56)

Equation (56) is also called index-1 dynamic model, whose constraint equations are described at the level of acceleration.

Remark 3

If the flexibilities of links are not considered, namely the values of flexible generalized coordinates are null, the rigid–flexible coupling dynamic model (RFDM) of system shown in Eqs. (54) or (56) will degrade into the rigid dynamic model (RDM) of system (refer to Ref. [14]).

4 Solution strategy for the RFDM of system

Since the constraint equations of system are expressed at the level of acceleration, and there are many dependent generalized coordinates in the index-1 dynamic model of system, the violations of position and velocity constraint equations may occur during the integration with respect to the index-1 dynamic model of system. Under this circumstance, based on the method of Baumgarte stabilization [82] and the idea of feedback control, the right-hand side of acceleration constraint equations can be modified as

$$\begin{aligned} {\bar{\varvec{\gamma }}}= & {} {\varvec{\gamma }}-2\alpha \left( {\varvec{{\varPhi }}_c \left( {{\varvec{q}}^{(\mathrm{s})},t} \right) {\dot{{\varvec{q}}}}^{(\mathrm{s})}+\varvec{{\varPhi }}_t } \right) -\beta ^{2}\varvec{{\varPhi }}\left( {{\varvec{q}}^{(\mathrm{s})},t} \right) \nonumber \\ \end{aligned}$$

(57)

where $\alpha$ and $\beta$ are the stability coefficients, whose value range generally holds $0\le \alpha ,\beta \le 50$. Therefore, the dynamic model shown in Eq. (56) can be transformed as

$$\begin{aligned} \left[ {{\begin{array}{ll} {\bar{\varvec{M}}}^{(\mathrm{s})}&{} \varvec{{\varPhi }}_c^{\mathrm{T}} \\ {\varvec{{\varPhi }}_c }&{} \mathbf{0} \\ \end{array}}}\right] \left[ {{\begin{array}{lll} {{\ddot{\varvec{q}}}^{(\mathrm{s})}} \\ {\varvec{\lambda }} \\ \end{array}}} \right] =\left[ {{\begin{array}{l} {{\bar{\varvec{F}}}_e^{(\mathrm{s})} -{\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}-{\bar{\varvec{K}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}} \\ {{\bar{\varvec{\gamma }}}_{22\times 1} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(58)

Thus, one can further utilize the elimination method to remove the Lagrangian multipliers, and change the dynamic model of system from the DAEs to the ODEs.

From Eq. (58), one can obtain the expression of Lagrangian multipliers as

$$\begin{aligned} {\varvec{\lambda }}= & {} \left( {\varvec{{\varPhi }}_c \left( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \right) ^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}}} \right) ^{-1} \nonumber \\&\left( {\varvec{{\varPhi }}_c \left( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \right) ^{-1}\left( {{\bar{\varvec{F}}}_e^{(\mathrm{s})} -{\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}-{\bar{\varvec{K}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}} \right) -{\bar{\varvec{\gamma }}}} \right) \nonumber \\ \end{aligned}$$

(59)

Since $\big ( {\varvec{{\varPhi }}_c \big ( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \big )^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \big )^{-1}$ may be ill-conditioned during computation by programming, the pseudoinverse of$\big ( {\varvec{{\varPhi }}_c \big ( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \big )^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \big )$, i.e., $\big ( {\varvec{{\varPhi }}_c \big ( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \big )^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \big )^{+}$, can take place of $\big ( {\varvec{{\varPhi }}_c \big ( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \big )^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \big )^{-1}$ during computation. Substituting Eq. (59) into Eq. (58) results in the simplified dynamic model of system as

$$\begin{aligned} {\tilde{\bar{\varvec{M}}}}^{\mathrm{(s)}}{\ddot{\varvec{q}}}^{(\mathrm{s})}+{\tilde{\bar{\varvec{H}}}}^{(\mathrm{s})}+{\tilde{\bar{\varvec{K}}}}^{(\mathrm{s})}{\varvec{q}}^{(\mathrm{s})}={\tilde{\bar{\varvec{F}}}}_e^{(\mathrm{s})} \end{aligned}$$

(60)

where ${\tilde{\bar{\varvec{M}}}}^{\mathrm{(s)}}$ represents the equivalent mass matrix of system; ${\tilde{\bar{\varvec{H}}}}^{(\mathrm{s})}$ represents the quadratic velocity forces of system; ${\tilde{\bar{\varvec{K}}}}^{(\mathrm{s})}$ represents the equivalent stiffness matrix of system; ${\tilde{\bar{\varvec{F}}}}_e^{(\mathrm{s})}$ represents the equivalent column matrix of generalized forces of system; and they are given by

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\tilde{\bar{\varvec{M}}}}^{{\varvec{(s)}}}={\bar{\varvec{M}}}^{(\mathrm{s})}} \\ {{\tilde{\bar{\varvec{H}}}}^{(\mathrm{s})}={\tilde{\varvec{\varPhi }}}_c {\bar{\varvec{C}}}^{(\mathrm{s})}{\dot{{\varvec{q}}}}^{(\mathrm{s})}-\varvec{{\varPhi }}_c^{\mathrm{T}} \left( {\varvec{{\varPhi }}_c \left( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \right) ^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \right) ^{-1}{\bar{\varvec{\gamma }}}} \\ {{\tilde{\bar{\varvec{K}}}}^{(\mathrm{s})}={\tilde{\varvec{\varPhi }}}_c {\bar{\varvec{K}}}^{(\mathrm{s})}} \\ {{\tilde{\bar{\varvec{F}}}}_e^{(\mathrm{s})} ={\tilde{\varvec{\varPhi }}}_c {\bar{\varvec{F}}}_e^{(\mathrm{s})} } \\ {{\tilde{\varvec{\varPhi }}}_c ={\varvec{I}}-\varvec{{\varPhi }}_c^{\mathrm{T}} \left( {\varvec{{\varPhi }}_c \left( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \right) ^{-1}\varvec{{\varPhi }}_c^{\mathrm{T}} } \right) ^{-1}\varvec{{\varPhi }}_c \left( {{\bar{\varvec{M}}}^{(\mathrm{s})}} \right) ^{-1}} \\ \end{array} }} \right. \end{aligned}$$

(61)

The dynamic model shown in Eq. (60) is a group of rigid–flexible coupling and nonlinear time-varying ODEs, which can be solved by virtue of the numerical algorithms. There are many numerical algorithms to deal with this issue, mainly including two types, i.e., direct integration algorithms and reduced-order algorithms. The reduced-order algorithms commonly used include the classical four/five order Runge–Kutta algorithm, trapezoidal algorithm, Adams algorithm, BDFs algorithm (Gear algorithm) [83], NDFs algorithm [84] and hybrid TR-BDF2 algorithm [85]. The adaptively variable step size can be applied in these algorithms to balance the precision and efficiency in the meantime. In general, these reduced-order methods can guarantee good precision and stability during computation.

The RFDM of system contains slow-varying components of rigid displacements and fast-varying components of elastic displacements simultaneously. Consequently, the dynamic equations of system display strongly the “stiff” characteristic. In this case, the classical Runge–Kutta algorithm is not adaptable to solve this type of equations, and the solution efficiency is also slow. Within the reduced-order algorithms mentioned above, Gear algorithm, NDFs algorithm and hybrid TR-BDF2 algorithm are relatively adaptable to solve the “stiff” differential equations. To balance efficiency and precision, in this paper, the hybrid TR-BDF2 algorithm, which is L-stable [85], is employed to solve the rigid–flexible coupling dynamic equations of system; namely, the trapezoidal algorithm and the BDFs algorithm are utilized, respectively, in the first and second stages within the implicit Runge–Kutta formulation [85].

5 Dynamic simulation experiment

In order to investigate the dynamic performance under different actuation modes of RAParM-I where the flexibilities of all the links are considered during high-speed motion, this section will employ numerical algorithm to implement dynamic simulation analysis based on the RFDM established in this paper.

5.1 Degrees of freedom of the RFDM of system

The dynamic model of arbitrary flexible body j deduced in above sections encompasses $n_j$ elements and is a general model. Theoretically, the more the number of elements is, the higher the accuracy is. However, during the practical computation, the complexity of system dynamic model should be taken into consideration. Thus, the number of elements for each flexible body of system should be set reasonably to guarantee the solution efficiency and precision simultaneously. In this paper, RAParM-I encompasses totally 8 flexible bodies. Herein, the total number of elements is set as 20, and the detailed discretization using finite element approach is depicted in Fig. 9.

Fig. 9

The detailed discretization of RAParM-I using finite element approach. Notice that j-Ei represent element i in flexible body j

After discretization using finite element approach, the number of flexible generalized coordinates is 80, the number of rigid generalized coordinates is 24 (including 8 rotational angle coordinates of body-fixed coordinate systems and 16 position coordinates of original points of body-fixed coordinate systems), and the total number of generalized coordinates of system is 104. The associated physical parameters of RAParM-I are listed in Table 2.

Table 2 The associated physical parameters of RAParM-I

5.2 Design of simulation flow

As is mentioned in Remark 3, once the flexibilities of links are not considered, the RFDM derived in this paper will degrade into the rigid dynamic model (RDM), which can be referred to in Ref. [14]. Therefore, the mechanism will move rigorously according to the desired trajectory when the driving torques obtained through inverse solutions of RDM are utilized to actuate the “rigid” mechanism (the flexibilities of links are not considered). However, once the flexibilities of links are considered, the elastic deformations of links of mechanism may arise under the actuations of driving torques during high-speed motion. As a consequence of the rigid–flexible coupling effect, the practical trajectory of mechanism may deviate from the desired trajectory so that the tracking precision of trajectory may be affected in some extent. In the following content, we will investigate the rigid–flexible coupling dynamic performance of RAParM-I and elaborate the tracking precisions of trajectory for the manipulator under different actuation modes through numerical simulation so as to lay a good foundation for the design of nonlinear controller based on the RFDM in future.

On the basis of above statements, the simulation flow chart is designed and shown in Fig. 10. There are mainly three modules in the simulation flow chart. Firstly, according to the trajectory planning for the end-effector, the desired motion rules of all the joints of mechanism are obtained through inverse kinematics [14] of RAParM-I. Secondly, the driving torques associated with the “rigid” mechanism are obtained through the inverse solutions of RDM and taken as the feed-forward input of the third module. It should be noted that the driving torques under redundant actuation modes are obtained through the method of minimizing the Euclidian 2-norm [14], such that the practical control can be realized conveniently by using this method. Finally, the dynamic responses of system are obtained through solving forwardly the RFDM by virtue of the aforementioned hybrid TR-BDF2 algorithm.

Fig. 10

The simulation flow chart

5.3 Numerical simulation example

In Ref. [14], we have demonstrated that there are many complex singularities within the workspace of RAParM-I when non-redundant actuation modes are considered. In this paper, in order to make a comparative analysis conveniently about the trajectory tracking precisions of end-effector under different actuation modes (including non-redundant actuation modes), the desired trajectory of end-effector is planned without crossing the singular zones (corresponding to the non-redundant actuation modes) inside the task workspace of RAParM-I.

5.3.1 Trajectory planning

In this simulation example, the desired trajectory of end-effector of RAParM-I is planned as a complex square trajectory that is marked with blue color, as shown in Fig. 11. The position coordinates of four end points of the square trajectory within the task workspace are set as: A (50, 314) mm, B (−50, 314) mm, C (−50, 214) mm, D (50, 214) mm. The center of task workspace for RAParM-I is denoted by Q (0, 264) mm. The motion direction of the desired trajectory is $A\rightarrow B\rightarrow C\rightarrow D\rightarrow A$, as depicted in Fig. 11.

Fig. 11

The desired trajectory of end-effector planned within task workspace of RAParM-I

Fig. 12

The driving torques of RAParM-I under different actuation modes: a non-redundant actuation modes; b redundant actuation modes

In order to avoid the impact caused by sudden change of acceleration for end-effector when RAParM-I is started or stopped, a kind of trapezoidal modified velocity planning strategy is employed within each section of the desired square trajectory. Taking the first section of trajectory as an example, the corresponding motion rules of acceleration and velocity of end-effector are described as follows:

$$\begin{aligned}&\left\{ {{\begin{array}{l@{\quad }l} a_c =a_{\max } \sin \left( {\frac{2{\uppi }}{T}t} \right) , &{} t_0 \le t<t_1 \\ a_c =0, &{} t_1 \le t<t_2 \\ a_c =-a_{\max } \sin \left( {\frac{2{\uppi }}{T}t} \right) , &{} t_2 \le t\le t_3 \\ \end{array}}} \right. \end{aligned}$$

(62)

$$\begin{aligned}&\left\{ {{\begin{array}{l@{\quad }l} v_c =-a_{\max } \frac{T}{2{\uppi }}\cos \left( {\frac{2{\uppi }}{T}t} \right) +a_{\max } \frac{T}{2{\uppi }}, &{} t_0 \le t<t_1 \\ v_c =a_{\max } \frac{T}{{\uppi }}, &{} t_1 \le t<t_2 \\ v_c =a_{\max } \frac{T}{2{\uppi }}\cos \left( {\frac{2{\uppi }}{T}t} \right) +a_{\max } \frac{T}{2{\uppi }}, &{} t_2 \le t\le t_3 \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$

(63)

where $T=\sqrt{\frac{{\uppi }s}{a_{\max } }}$, s represents the length of each section of the desired square trajectory; $a_{\max }$ represents the maximum acceleration of end-effector; $t_0 =0$, $t_1 =T/2$, $t_2 =T$ and $t_3 =3T/2$. In this simulation case, the maximum acceleration of end-effector is set as $a_{\max } =40$ m/s$^{2}$. The total simulation time is 0.7 s, in which the practical motion time of square trajectory is $6\sqrt{\frac{{\uppi }s}{a_{\max } }}\approx 0.532\,\hbox {s}$ and the dwelling time is $\left( {0.7-6\sqrt{\frac{{\uppi }s}{a_{\max } }}} \right) \approx 0.168\,\hbox {s}$.

By taking into account multiple actuation modes depicted in Ref. [14], one can obtain the dynamic responses of RAParM-I under different actuation modes. As a matter of fact, since some actuation modes are symmetric, we can merely analyze 6 actuation modes (see Table 1), which are “$\oplus \ominus \oplus \ominus$,” “$\ominus \oplus \ominus \oplus$,” “$\oplus \ominus \ominus \oplus$,” “$\oplus \oplus \oplus \ominus$,” “$\oplus \oplus \ominus \oplus$” and “$\oplus \oplus \oplus \oplus$,” respectively. Amongst the 6 actuation modes mentioned above, the first three ones are non-redundant actuation ones and the latter three ones are redundant actuation ones.

Fig. 13

The axial (1) and transverse (2) elastic displacements, and elastic angles (3) of end points for links 1 and 4: a link 1, b link 4

5.4 Simulation experiment results and discussions

The numerical simulation experiment is implemented in the environment of the commercial software MATLAB$^{{\circledR }}$ because various application scenarios [86,87,88,89,90] have been successfully simulated by using this software. Thus, according to the simulation flow chart shown in Fig. 10, the numerical simulations are performed in $\hbox {MATLAB}^{{\circledR }}$ 2013b on the computer with Intel (R) Pentium (R) G2020 processor (2.90 GHz), 6.00 G system memory and Windows 7 operating system.

First, the driving torques of RAParM-I under different actuation modes are obtained based on the RDM resulting from the degradation of RFDM, as shown in Fig. 12. From Fig. 12, one can discover that the driving torques show significant differences amongst different actuation modes. Since the method of minimizing the Euclidian 2-norm is applied to obtain the optimal driving torques, the peak values of driving torques for the redundant actuation modes are much smaller in comparison with the non-redundant actuation modes. Moreover, the peak value of driving torques for “$\oplus \oplus \oplus \oplus$” mode is the smallest, and about 7 Nm, and the distributions of driving torques under this actuation mode are balanced as well. That is to say, this actuation mode may be helpful to prolong the lifetime of servo motor and may further improve the performance of manipulator.

Based upon the third module of simulation flow chart, we solve forwardly the RFDM of system and can obtain the dynamic responses of RAParM-I under different actuation modes. Figure 13 illustrates the time-varying curves of axial and transverse elastic displacements, and the elastic angles of end points for links 1 and 4 under the “$\oplus \oplus \oplus \oplus$” actuation mode. Owing to the space limitation, the simulation results under the other actuation modes are not manifested in detail here. The relevant simulation results can be obtained through implementing similar procedure based on the simulation flow chart shown in Fig. 10. From Fig. 13, one can discover that the links of the RAParM-I display obvious deformations because of the flexibilities of links during the high-speed motions. Moreover, the values of transverse elastic displacements of links are much bigger than those of axial elastic displacements, and the ratio of magnitude order between them is up to $10^{3}$. This result coincides with the structural characteristic of link, i.e., the axial tensional stiffness are much bigger than the transverse bending stiffness. Consequently, in future research of simplifying the dynamic model of system, only the transverse elastic deformation of flexible link can be considered, whereas the effect of axial elastic deformation can be ignored. In addition, since the effects of external and structural damping are not considered, when the tracking to the desired square trajectory is completed and from the beginning of 0.532 s, the links display residual vibrations with approximately equal amplitudes and the residual vibrations will hold all the time, as shown in Fig. 13.

Figure 14 manifests the motion curves of angular displacements, velocities and accelerations of all the links for RAParM-I under the “$\oplus \oplus \oplus \oplus$” actuation mode. Herein, the blue lines represent the practical motion rules of all the flexible links, and the red lines represent the desired motion rules of the “rigid” links whose flexibilities are not considered.

Fig. 14

The motion rules of angular displacements, velocities and accelerations of all the links for RAParM-I under the “$\oplus \oplus \oplus \oplus$” actuation mode: a link 1; b link 2; c link 3; d link 4; e link 5; f link 6; g link 7; h link 8

It can be observed from Fig. 14 that the rigid-body motions of all the links are affected strongly by the flexible effects of links, and the practical motions of links display rigid–flexible coupling characteristics, which are different from the results obtained by the method of KED because the nominal motions (rigid-body motions) are not affected by the elastic deformations in the assumption of KED method. From the simulation results, one can further discover that, with respect to each flexible link, there exists deviation between the practical angular displacement and the desired angular displacement. Moreover, the motion rules of velocity and acceleration of each flexible link display high-frequency oscillations relative to the desired motion rules, especially for the motion rule of acceleration. In addition, it is worth mentioning that, after the completion of tracking to the desired square trajectory and from the beginning of 0.532 s, the motion rule of angular displacement of each link displays small oscillation with approximately equal magnitude. This phenomenon can be explained as follows. Since the effects of external and structural damping are not considered in this study, when the driving torques are removed ($t\ge 0.532\,\hbox {s}$), the inertia effect and the residual vibrations of flexible links will excite the oscillations of rigid-body motion rules.

Fig. 15

The trajectory of the end-effector of RAParM-I under the “$\oplus \oplus \oplus \oplus$” actuation mode

Fig. 16

The motion curves of displacements, velocities and accelerations of end-effector: a x direction, b y direction

Based on the analysis with respect to the simulation results shown in Figs. 13 and 14, it is concluded that the elastic deformations and the rigid-body motions of links are coupled mutually, and the coupling effect between them will result in the practical trajectory of end-effector for RAParM-I. Owing to the space limitation, we display only the practical trajectory of end-effector for RAParM-I under the “$\oplus \oplus \oplus \oplus$” actuation mode, as depicted in Fig. 15, in which the blue line represents the practical trajectory and the red line represents the desired trajectory. Correspondingly, the motion curves of displacements, velocities and accelerations in the directions of x and y are illustrated in Fig. 16, in which the blue lines represent the practical motion rules and the red lines represent the desired motion rules. From the results shown in Figs. 15 and 16, one can discover that the practical trajectory of end-effector deviates from the desired trajectory in some extent. Moreover, the motion curves of velocities and accelerations in the directions of x and y manifest high-frequency oscillations relative to the desired motion rules, especially for the motion rules of accelerations in the two directions. In addition to these, it is manifested that the motion rules of displacements in the directions of x and y display small residual oscillations relative to the static values after the tracking to the desired square trajectory is completed ($t\ge 0.532\,\hbox {s}$). It is not difficult to infer this phenomenon based on the simulation results illustrated in Figs. 13 and 14 as well.

Fig. 17

The Poincare phase diagrams of motions of end-effector for RAParM-I under the “$\oplus \oplus \oplus \oplus$” actuation mode. a The phase diagrams of displacement/velocity: 1 x direction; 2 y direction. b The phase diagrams of velocity/acceleration: 1 x direction; 2 y direction

Furthermore, one can obtain the Poincare phase diagrams of motion rules (the displacement/velocity phase diagram and the velocity/acceleration phase diagram) in the directions of x and y for end-effector, which are shown in Fig. 17, in which the blue lines represent the Poincare phase diagrams of practical motions and the red lines represent the ones of desired motions. From the Poincare phase diagrams shown in Fig. 17, one can easily discover that, as a result of the rigid–flexible coupling effect, the practical motion rules deviate from the desired motion rules in some extent, especially for the motion rules of velocities and accelerations in the directions of x and y. The results manifested in Fig. 17 coincide well with the results shown in Fig. 16.

Fig. 18

The trajectory tracking errors of end-effector for RAParM-I under different actuation modes. a “$\oplus \ominus \oplus \ominus$” mode. b “$\ominus \oplus \ominus \oplus$” mode. c “$\oplus \ominus \ominus \oplus$” mode. d “$\oplus \oplus \oplus \ominus$” mode. e “$\oplus \oplus \ominus \oplus$” mode. f “$\oplus \oplus \oplus \oplus$” mode

In order to make comparative analysis about the dynamic performance of RAParM-I under different actuation modes, the trajectory tracking errors of end-effector under different actuation modes are manifested in Fig. 18, in which the blue lines represent trajectory tracking errors in the direction of x and the red lines represent the ones in the direction of y. It is observed that the trajectory tracking precisions of end-effector under redundant actuation modes are superior to the ones under non-redundant actuation modes. That is to say, the redundant actuation modes can restrain the flexible effects of links in some extent. Meanwhile, the redundant actuation modes are not affected by the Type II singularities within the workspace of RAParM-I, and the motion stabilities of manipulator are also very well so that the trajectory tracking precision of end-effector can be improved. From the results shown in Fig. 18a, one can further discover that, from the beginning of about 0.25 s, the trajectory tracking error in the direction of y increases rapidly. This phenomenon can be explained as follows. From the beginning of about 0.25 s, the end-effector approaches gradually the singular curve (but not crosses it) inside the workspace of RAParM-I under the traditional non-redundant actuation mode “$\oplus \ominus \oplus \ominus$” such that the stiffness performance of the manipulator will be decreased. Therefore, the dynamic performance of system will be further degraded under “$\oplus \ominus \oplus \ominus$” actuation mode such that the trajectory tracking errors of end-effector will increase, and even the desired trajectory of end-effector cannot be tracked under this circumstance. In addition, one can also discover that, under the two redundant actuation modes of “$\oplus \oplus \oplus \ominus$” and “$\oplus \oplus \oplus \oplus$,” the end-effector of RAParM-I can obtain relatively higher trajectory tracking precisions.

Considering that the trajectory tracking errors vary with time, to evaluate quantitatively the trajectory tracking precisions of end-effector for RAParM-I under different actuation modes, the mean-square deviation error $(\bar{{\varDelta }}_{\mathrm{error}})$ is employed as the performance index, which is defined as follows:

$$\begin{aligned} \bar{{\varDelta }}_{\mathrm{error}} =\sqrt{\frac{1}{n_{\mathrm{sample}} }\sum _{i=1}^{n_{\mathrm{sample}}} {\left( {\left( {x_i -x_i^\mathrm{d}} \right) ^{2}+\left( {y_i -y_i^\mathrm{d} } \right) ^{2}} \right) } }\nonumber \\ \end{aligned}$$

(64)

where $n_{\mathrm{sample}}$ represents the number of sample points on the trajectory; $x_i^\mathrm{d} ,y_i^\mathrm{d}$ represent the position coordinates of the $i{\mathrm{th}}$ sample point on the desired trajectory; $x_i ,y_i$ represent the position coordinates of the $i{\mathrm{th}}$ sample point on the practical trajectory. Table 3 manifests $\bar{{\varDelta }}_{\mathrm{error}}$ of RAParM-I under different actuation modes.

Table 3 $\bar{{\varDelta }}_{\mathrm{error}}$ under different actuation modes for RAParM-I

From the data manifested in Table 3, one can discover that the trajectory tracking precisions of end-effector under redundant actuation modes are much higher than those under non-redundant actuation modes. This coincides with the simulation results shown in Fig. 18. With respect to the tracking effect for the square trajectory planned in this experiment, the difference of trajectory tracking precisions amongst the three redundant actuation modes (“$\oplus \oplus \oplus \ominus$,” “$\oplus \oplus \ominus \oplus$,” “$\oplus \oplus \oplus \oplus$”) is not significant. Taking into account both the kinematic and rigid dynamic performance, the redundant actuation mode “$\oplus \oplus \oplus \oplus$” has significant advantage over the other redundant actuation modes in practical application. That is, under this redundant actuation mode, not only nice kinematic performance of the manipulator can be guaranteed, but also nice dynamic performance can be realized. In addition, we also have implemented simulation experiments of trajectory tracking with respect to some other trajectories, including linear path and circular path. The corresponding simulation results indicate that the redundant actuation modes can improve obviously the trajectory tracking precision of end-effector for RAParM-I. Moreover, the redundant actuation mode “$\oplus \oplus \oplus \oplus$” can always ensure good tracking effect in all kinds of simulation experiments of trajectory tracking. Consequently, from the two levels of rigid multi-body dynamics and flexible multi-body dynamics, the redundant actuation mode “$\oplus \oplus \oplus \oplus$” is a superior actuation mode and will be further researched in future.

Fig. 19

The flexible link modeled with multiple successive equal rigid-body segments and massless torsional springs (with spring constants $k_{\mathrm{t}}$). Notice that $\theta _1$, $\theta _2$, ..., $\theta _n$ represent the absolute rotational angles of rigid-body segments and $\varphi _2$, $\varphi _2$, ..., $\varphi _n$ represent the relative rotational angles

Fig. 20

The virtual prototype model (VPM) of RAParM-I established in SimMechanics

Fig. 21

The configuration of VPM at some point during the dynamic simulation

Fig. 22

The angle and angular curves of all flexible links calculated by the RFDM and the VPM under the “$\oplus \oplus \oplus \oplus$” actuation mode: a link 1; b link 2; c link 3; d link 4; e link 5; f link 6; g link 7; h link 8

6 Model verification

In order to validate the RFDM presented in this paper, a virtual prototype model (VPM) of RAParM-I will be established by virtue of $\hbox {SimMechanis}^{{\circledR }}$. In the VPM, the same trajectory for the end-effector is planned. Meanwhile, a similar simulation flow (designed in Sect. 5.2) is applied in the VPM.

6.1 Virtual prototype model (VPM) in SimMechanics

Reference [38] proposed a FSM-based approach to model link flexibility, i.e., a certain flexible link is discretized into multiple successive equal rigid-body segments which are connected to one another by massless torsional springs. Without loss of generality, Fig. 19 illustrates the discretization of a certain flexible link using the aforementioned method. For the model shown in Fig. 19, each one of the rigid-body segments (1, 2, ..., n) has the same mass m, moment of inertia of beam cross section I and length l. The total length of the flexible link is $L=nl$ when it is in the undeformed state. The spring constants are denoted by $k_{\mathrm{t}}$, which can be computed by $k_{\mathrm{t}} = \textit{nEI}/ L$, where E is Young’s modulus of flexible link. Thus, one can utilize some modeling methods, such as Lagrangian formulation or Newton–Euler formulation, to establish the equivalent dynamic model of system.

Since the aforementioned method can be realized through rigid-body dynamic analysis, some multi-body simulation software, such as $\hbox {SimMechanics}^{{\circledR }}$, can be employed to establish an equivalent dynamic model of system without deducing the dynamic equations. Herein, we will employ this method to develop a VPM for RAParM-I in $\hbox {SimMechanics}^{{\circledR }}$ for the first time. In accordance with the aforementioned idea, a VPM can be constructed by virtue of some modules within $\hbox {SimMechanics}^{{\circledR }}$, as shown in Fig. 20. It should be emphasized that each flexible link of RAParM-I is modeled with multiple rigid-body segments. These segments are connected with each other by the massless spring–damper modules in SimMechanics$^{{\circledR }}$, and the flexible links are connected by the revolute joint modules (see Fig. 20). Meanwhile, the lumped masses and moments of inertia are also considered in the VPM, which are fixed at the associated positions of links via some welding joint modules in SimMechanics$^{{\circledR }}$. The driving torques obtained through the inverse solutions of RDM (see Fig. 12) are taken as the feed-forward control input which is emphasized with a green rectangle, as shown in Fig. 20.

6.2 Comparison of results

The same trajectory planning strategy (used in the above numerical example) is applied in the VPM. Thus, the simulation time is 0.7 s. The gravity field is set to null in the VPM. Figure 21 displays the configuration of VPM at some point. In the VPM, the manipulator is totally discretized into 56 rigid-body segments. Amongst them, links 1, 3, 4, 5, 7 and 8 are, respectively, discretized into 8 rigid-body segments, while links 2 and 6 are, respectively, discretized into 4 rigid-body segments.

Without loss of generality, let us take the “$\oplus \oplus \oplus \oplus$” actuation mode as an example. The angle and angular velocity curves of all flexible links calculated by the RFDM and the VPM are illustrated in Fig. 22. Comparisons manifest that the results calculated from the two approaches are consistent. Especially for the angle curves, the two approaches match very well. With respect to the angular velocity curves, there exists small difference between the two approaches. The reason can be explained as follows. On the one hand, the discretization methodologies used in the two approaches are different. The FSM is utilized in the VPM, while the FEM is utilized in the presented RFDM. On the other hand, the numbers of generalized coordinates of elements in the two approaches are also different. Within the VPM, for an arbitrary element, only one generalized coordinate, i.e., the rotational angle of the rigid-body segment, is encompassed. However, within the RFDM, the nodal coordinates of an arbitrary element contain multiple flexible generalized coordinates, such as axial elastic displacement, transverse elastic displacement, elastic angle and curvature. Consequently, the small difference of the results derived from the two approaches may exist.

The trajectories of end-effector calculated by the RFDM and the VPM are illustrated in Fig. 23. By comparison, one can discover that the trajectory tracking effects of end-effector achieved through the two approaches are consistent.

Fig. 23

The practical trajectories for end-effector achieved through the RFDM and the VPM under the “$\oplus \oplus \oplus \oplus$” actuation mode

The above comparative results indicate that the RFDM of RAParM-I with multiple actuation modes presented in this paper is valid. In future research work, combining with the analyzed results of this paper, we will further simplify the dynamic model of system by using some methods, such as modal truncation method. On this basis, the nonlinear dynamic control strategy will be further developed to restrain elastic vibrations and improve the trajectory tracking precision of end-effector for RAParM-I.

7 Conclusions

In this paper, we have established the rigid–flexible coupling dynamic model (RFDM) and implemented performance analysis with respect to a novel PM, i.e., RAParM-I, with multiple actuation modes.

Firstly, the flexibilities of all the links of RAParM-I are considered, and the finite element approach is employed to discretize the flexible link. Since RAParM-I contains many lumped masses and moments of inertia, one kind of element is presented in this paper to accommodate the dynamic modeling. On this basis, the RFDM of arbitrary element i within flexible body j is deduced by virtue of Lagrangian formulation. This kind of dynamic model of element can be transformed into the dynamic model of common element only through some simple changes. In other words, this kind of dynamic model of element can be suitable very well for the establishment of dynamic model for a certain flexible beam with any number of lumped parameters. Because the total generalized coordinates of arbitrary flexible body j are selected as the generalized coordinates of the dynamic model of element i within flexible body j, the dynamic model of arbitrary flexible body j can be easily obtained merely through summing all the dynamic equations of elements within flexible body j together. In subsequence, the open-loop dynamic model of system can be achieved conveniently by assembling all the dynamic equations of flexible bodies. By virtue of the augmented Lagrangian multipliers method, the completely RFDM of system is established.

Secondly, the dynamic model of system is expressed in the form of index-1. Based upon the Baumgarte stabilization approach, and drawing on the elimination method, the Lagrangian multipliers are removed and the simplified dynamic model of system is developed, which is a group of rigid–flexible coupling and nonlinear time-varying ODEs. Owing to the “stiff” characteristic of dynamic equations of system, a hybrid TR-BDF2 algorithm is employed to solve the “stiff” differential equations so as to balance the solution efficiency and precision well.

Finally, based on the RFDM of system and the degraded rigid dynamic model (RDM) of system, a simulation experiment of trajectory tracking is implemented with respect to RAParM-I when the flexibilities of links are considered during high-speed motion. Numerical results indicate that the practical motion of RAParM-I displays a rigid–flexible coupling characteristic. Through comparative analysis, the redundant actuation modes can realize significantly higher trajectory tracking precisions in comparison with the non-redundant actuation modes. A virtual prototype model (VPM) is further established in SimMechanics$^{{\circledR }}$ to verify the presented RFDM. The conformities of results show exact evidences to support the validity of the RFDM. The simulation experiment provides a scientific basis for the selection of redundant actuation modes in practical application.

It is worth mentioning that, in the simulation experiment, the input of RFDM is the torques obtained through the inverse solutions of RDM, whereas the feedback is not included. Consequently, in future work, we will further simplify the RFDM of system via modal synthesis approach and develop efficient dynamic controllers to restrain the elastic vibrations and improve the trajectory tracking precision with the help of superior redundant actuation mode, such as “$\oplus \oplus \oplus \oplus$” actuation mode. In addition, it is noted that the damping effects of joints are not considered in this study. These factors can be regarded as the uncertainties of model and can be identified and compensated via artificial neural network or fuzzy algorithm in the adaptive controller. Last but not least, the systematic modeling methodology developed in this paper can provide some beneficial reference for the analysis of other flexible planar PMs, especially the emerging ones with multiple actuation modes.