1 Introduction

With the increasing demand for orientation capacity in the machining of aerospace components with large size, thin wall and complex surface, 5 degree-of-freedom (DoF) hybrid mechanisms consisting of 3-DoF parallel mechanism and 2-DoF pose-adjusting mechanism have been accepted as an effective substitution of the traditional serial NC machines [1], in terms of higher dynamic performance, better accuracy and larger load-weight ratio. The famous Tricept mechanism [2–6] is a successful example of 5-DoF hybrid mechanism who wisely combines the advantages of parallel and serial mechanisms. However, it should be pointed out that the 2-DoF pose-adjusting module attached to Tricept mechanism is open-loop serial structure, and it would be designed inevitably towards large scale and huge weight in order to meet the requirements of high stiffness of the whole mechanism, which makes it a major obstacle to application. With the merit of good rigidity and compact structure, 2-DoF rotational parallel mechanism (RPM) is superior to the serial counterpart as an integration of 5-DoF hybrid mechanism.

As far as 2-DoF RPM is concerned, extensive researches [7–15] have been carried out over the decades. Spherical 5R mechanism is the earliest and simplest parallel mechanism to achieve the two rotational DoFs, whose kinematics was thoroughly discussed by Kong and Liu [7–9]. Herein, R denotes the revolute joint. By introducing parallelogram linkage to the mechanism, Baumann [10] proposed a 2-DoF RPM named PantoScope and applied it to the micro-invasive surgery. In order to deal with large orientation workspace problem of the laser detection in aerospace, Ross–Hime Designs [12] developed the famous Omni-Wrist III, whose kinematics is investigated by Sofka [13] while the rigid dynamics is analyzed by Chen [14]. It is believed that Omni-Wrist III has the advantage of good rotational capacities without singularity. In addition, several decoupled 2-DoF RPM are proposed by Liu [15].

It is found out that kinematic capacities are the main concern of the above-mentioned 2-DoF RPMs. However, it comes to the application for pose-adjusting module of 5-DoF machine center, stiffness and elastic dynamic performance need to be taken into account, which might be the shortcomings of some 2-DoF RPMs above.

Driven by the demands for pose-adjusting module with high stiffness and good dynamic performance in machining aerospace components, a novel 2-DoF RPM [16] with an articulated travelling platform is proposed and its elasto-dynamic analysis is investigated in this paper. The proposed 2-DoF RPM is believed to be without parasitic motion, good rotational capability and can be designed potentially as a compact module with large ratio of stiffness to weight. The organization of the paper is as follows: after introducing the underlying architecture of the proposed 2-DoF RPM in Sects. 2, 3 carries out the inverse kinematics by closed-loop vector method. In Sect. 4, the elasto-dynamic modeling of components is formulated and that of the whole mechanism is achieved. The natural frequencies of the 2-DoF RPM are then analyzed through an example and verified by the finite element software in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Underlying architecture

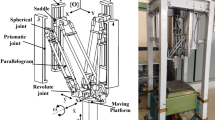
As shown in Fig. 1, the novel 2-DoF RPM is composed of a fixed base, an articulated travelling platform and two parallelogram-based limbs. The articulated travelling platform includes sub-plate I and sub-plate II, which are articulated to each other by one R joint, in which sub-plate I is regarded as the output link that connects rigidly to the end-effector. Each parallelogram-based limb contains one actuated component (represented by A or B) and two identical driven components. The actuated component A or B is adjacent to the fixed base by R joint. And the driven component connects to the actuated component and sub-plate by R joint and S joint, respectively. Herein, S represents spherical joint.

Fig. 1
figure 1

Conceptual design of the novel 2-DoF RPM with an articulated travelling platform

Full size image

As is shown Fig. 2, A i and B i (i = 1–4) denote the centers of the ith S joint and the ith R joint in the actuated components. O denotes the intersection point of B 1 B 3 and B 2 B 4, P represents the center of the articulated R joint, and C j (j = 1, 2) is the center of the R joint in actuated component A or B. The axes of the R joints at C 1, B 1, and B 3 are parallel to each other, and parallel axes also exist in R joints at C 2, B 2 and B 4. The axes of R joints in actuated component A and those in actuated component B are perpendicular. It is noticed that the axis of articulated R joint is normal to the plane of sub-plate I. Moreover, the lengths of the driven components are all equal to l ab.

Fig. 2
figure 2

Schematic diagram of the novel parallel mechanism

Full size image

In what follows, the two rotations produced by the novel parallel mechanism will be described. As shown in Fig. 2, A 1 A 3 B 3 B 1 and A 2 A 4 B 4 B 2 are two parallelograms, and the point P is a fixed point on the z axis due to the constraint of the revolute joints at B i . As a result, the pose of B 1 B 3 can be determined by actuating the revolute joint at C 1 with θ 1, and then A 1 A 3 can rotate about the x axis with θ 1. Similarly, the pose of B 2 B 4 can be determined by actuating the revolute joint at C 2 with θ 2, which leads that A 2 A 4 can rotate about the y axis with θ 2, and then A 1 A 3 can rotate about the v axis. Therefore, the novel parallel mechanism has two DoFs actuated by the revolute joints at C 1 and C 2.

For the sake of describing the motion of the proposed 2-DoF RPM, several coordinate systems are established as follows. As shown in Fig. 2, a fixed coordinate system designated as \( O - xyz \) is fixed at point O with the x and y axis pointing to point C 1 and C 2, respectively. A moving coordinate system \( P - uvw \) is assigned to point P with the v axis pointing to point A 3 and the w axis perpendicular to the sub-plate I. Then the orientation matrix R of the frame \( P - uvw \) with respect to the frame \( O - xyz \) can be expressed as

$$ \begin{aligned} \varvec{R} = \varvec{R}_{\alpha } \varvec{R}_{\beta } & = & \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {{\text{c}}\alpha } & { - {\text{s}}\alpha } \\ 0 & {{\text{s}}\alpha } & {\text{c}\alpha } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{c}}\beta } & 0 & {{\text{s}}\beta } \\ 0 & 1 & 0 \\ { - {\text{s}}\beta } & 0 & {{\text{c}}\beta } \\ \end{array} } \right] \\ & = & \left[ {\begin{array}{*{20}c} {{\text{c}}\beta } & 0 & {{\text{s}}\beta } \\ {{\text{s}}\alpha {\text{s}}\beta } & {{\text{c}}\alpha } & { - {\text{s}}\alpha {\text{c}}\beta } \\ { - {\text{c}}\alpha {\text{s}}\beta } & {{\text{s}}\alpha } & {{\text{c}}\alpha {\text{c}}\beta } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \varvec{u} & \varvec{v} & \varvec{w} \\ \end{array} } \right] \\ \end{aligned} $$
(1)

where c and s denote cosine and sine, respectively; α and β represent the angles about the x and the v axis, respectively; u, v, w denote the unit vectors of the u, v, w axes in the coordinate system \( O - xyz \), respectively.

3 Kinematic analysis

After the architecture of the novel 2-DoF RPM is outlined in Sect. 2, it is necessary to carry out the kinematic analysis including inverse position, velocity and acceleration before formulating elastic-dynamic model of mechanism.

3.1 Constraint equations

As shown in Fig. 2, the closed-loop vector equation of the novel 2-DoF RPM can be expressed as

$$ \varvec{r} = \varvec{b}_{i} + l_{\text{ab}} \varvec{w}_{i} - \varvec{Ra}_{0i} $$
(2)

where \( \varvec{r} = \left[ {\begin{array}{*{20}c} {x_{\text{p}} } & {y_{\text{p}} } & {z_{\text{p}} } \\ \end{array} } \right]^{\text{T}} \) and b i denote the position vectors of point P and B i in the coordinate system \( O - xyz \), respectively. a 0i represents the position vector of point A i in the coordinate system \( P - uvw \). w i represents the unit vector of A i B i (i = 1–4), and \( \varvec{a}_{01} = - \varvec{a}_{03} = r_{1} \left[ {\begin{array}{*{20}c} 0 & { - 1} & 0 \\ \end{array} } \right]^{\text{T}} \). In addition

$$ \begin{aligned} \varvec{b}_{1} &= - \varvec{b}_{3} = r_{1} \left[ {\begin{array}{*{20}c} 0 & { - {\text{c}}\theta_{1} } & { - {\text{s}}\theta_{1} } \\ \end{array} } \right]^{\text{T}} \hfill \\ \varvec{b}_{2}& = - \varvec{b}_{4} = r_{2} \left[ {\begin{array}{*{20}c} { - {\text{c}}\theta_{2} } & 0 & {{\text{s}}\theta_{2} } \\ \end{array} } \right]^{\text{T}} \hfill \\ \end{aligned} $$

Herein, r 1 and r 2 denote the lengths of PA 1 and PA 2, respectively.

The driven components A 2 B 2 and A 4 B 4 are constrained by the R joints of the same parallelogram-based link to move within the plane y = 0. By taking dot product with \( \varvec{e}_{\text{y}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]^{\text{T}} \) on both sides of Eq. (2) when i = 2, 4, the constraint equation is yielded as follows

$$ y_{\text{p}} = 0 $$
(3)

Similarly, the driven components A 1 B 1 and A 3 B 3 are constrained by the R joints of the same parallelogram-based link to move within the plane x = 0, which yields

$$ x_{\text{p}} = 0 $$
(4)

Furthermore, w i (i = 1–4) is parallel to r. Hence, \( \varvec{w}_{i} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{\text{T}} \) and

$$ z_{\text{p}} = l_{\text{ab}} $$
(5)

3.2 Inverse position analysis

The input parameters are represented by θ 1 and θ 2, which are the rotational angles about x and y-axis. Substitute Eq. (3)–(5) into Eq. (2) when i = 1 and i = 2, respectively, yields Ra 02 = b 2, and

$$ \theta_{1} = \alpha $$
(6)
$$ \begin{aligned} \varvec{w} & = & \frac{{\varvec{Ra}_{02} \times \varvec{v}}}{{\left\| {\varvec{Ra}_{02} \times \varvec{v}} \right\|}} \\ & = & \frac{1}{{\sqrt {1 - {\text{s}}^{2} \theta_{1} {\text{s}}^{2} \theta_{2} } }}\left[ {\begin{array}{*{20}c} {{\text{c}}\theta_{1} {\text{s}}\theta_{2} } & { - {\text{s}}\theta_{1} {\text{c}}\theta_{2} } & {{\text{c}}\theta_{1} {\text{c}}\theta_{2} } \\ \end{array} } \right]^{\text{T}} \\ \end{aligned} $$
(7)

Noticing that \( \varvec{w} = \left[ {\begin{array}{*{20}c} {{\text{s}}\beta } & { - {\text{s}}\alpha {\text{c}}\beta } & {{\text{c}}\alpha {\text{c}}\beta } \\ \end{array} } \right]^{\text{T}} \), θ 2 can be calculated as

$$ \theta_{2} = \arctan \left( {\frac{\tan \beta }{\cos \alpha }} \right) $$
(8)

3.3 Velocity analysis

Taking the derivatives of Eq. (2) with respect to time yields

$$ \dot{\theta }_{1} e_{\text{x}} \times \varvec{b}_{1} -\varvec{\omega}\times \varvec{Ra}_{01} = 0 $$
(9)
$$ \dot{\theta }_{2} \varvec{e}_{\text{y}} \times \varvec{b}_{2} - (\varvec{\omega}- \dot{\theta }\varvec{w}) \times \varvec{Ra}_{02} = 0 $$
(10)

where ω represents the angular velocity of the sub-plate I, \( \dot{\theta } \) denotes the angular velocity of the sub-plate II with respect to the sub-plate I, and \( \dot{\theta }_{1} \), \( \dot{\theta }_{2} \) are the angular velocities of the actuated component A and B.

Taking dot product with e y and w on both sides of Eq. (9) and Eq. (10), yields

$$ \dot{\theta }_{1} = \varvec{e}_{\text{x}}^{\text{T}} {\varvec{\upomega}} $$
(11)
$$ \dot{\theta }_{2} = \frac{{\left( {\varvec{Ra}_{02} \times \varvec{w}} \right)^{\text{T}} }}{{\varvec{e}_{\text{y}}^{\text{T}} (\varvec{b}_{2} \times \varvec{w})}}\varvec{\omega} $$
(12)

Rewriting Eq. (11) and (12) in matrix form as

$$ \left[ {\begin{array}{*{20}c} {\dot{\theta }_{1} } \\ {\dot{\theta }_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {e_{\text{x}}^{\text{T}} } \\ {\frac{{\left( {\varvec{Ra}_{02} \times \varvec{w}} \right)^{\text{T}} }}{{\varvec{e}_{\text{y}}^{\text{T}} (\varvec{b}_{2} \times \varvec{w})}}} \\ \end{array} } \right]\varvec{\omega}= \varvec{J\omega } $$
(13)

where J is the Jocobian matrix that represents the mapping relationships between the joint velocity and the operated velocity.

3.4 Acceleration analysis

Taking the derivatives of Eq. (9) and Eq. (10) with respect to time yields

$$ \ddot{\theta }_{1} = \varvec{e}_{\text{x}}^{\text{T}}\varvec{\varepsilon} $$
(14)
$$ \ddot{\theta }_{2} = \frac{{\left( {\varvec{Ra}_{02} \times \varvec{w}} \right)^{\text{T}} }}{{\varvec{e}_{\text{y}}^{\text{T}} (\varvec{b}_{2} \times \varvec{w})}}\varvec{\varepsilon}+ \varvec{f\omega } $$
(15)

where ε presents the angular acceleration of the sub-plate I, \( \ddot{\theta }_{1} \), \( \ddot{\theta }_{2} \) denotes the angular acceleration of the actuated component A and B, respectively. And

$$ \varvec{f} = \left[ {\begin{array}{*{20}l} {\dot{\theta }_{1} \frac{{{\text{s}}\theta_{2} {\text{c}}\theta_{2} }}{{{\text{c}}^{2} \theta_{1} }} + \dot{\theta }_{2} \left( {{\text{c}}^{2} \theta_{2} - {\text{s}}^{2} \theta_{2} } \right)\tan \theta_{1} } \\ 0 \\ {\dot{\theta }_{1} \frac{{{\text{c}}^{2} \theta_{2} }}{{{\text{c}}^{2} \theta_{1} }} - 2\dot{\theta }_{2} \tan \theta_{1} {\text{c}}\theta_{2} {\text{s}}\theta_{2} } \\ \end{array} } \right]^{\text{T}} $$

4 Elasto-dynamic modeling

In the light of kineto-elasto dynamic (KED) method, the elasto-dynamic modeling of the novel 2-DoF RPM is established on the basis of inverse kinematic analysis. The elastic-dynamic model of components (actuated component, driven component and articulated travelling platform) need to be firstly considered before formulating the elastic-dynamic equation of the whole mechanism by deformation compatibility condition.

Considering the geometry of the mechanism and the requirements of KED method, several assumptions are made as follows:

  1. (1)

    Fixed base and articulated travelling platform are regarded as rigid bodies due to their relatively high rigidity, while the other components are treated as the Euler–Bernoulli spatial beams. Frictions among contact surface are negligible.

  2. (2)

    Deformations of components satisfy linear superposition principle. The transverse displacements of the spatial beam follow the cubic polynomial distribution and the longitudinal ones follow the linear distribution.

  3. (3)

    Orientation matrixes remain constant during the coordinate transformations according to the instantaneous structure hypothesis.

Some basic theory of KED method [17] is set forth as follow. In order to deal with component elastic-dynamic problem, element coordinate system \( E_{i} - \bar{x}\bar{y}\bar{z} \) is established as shown in Fig. 3. Elastic deformation δ j of any point on spatial beam element can be described as

$$ \varvec{\delta}_{j} = \varvec{Nu},\;\dot{\varvec{\delta }}_{j} = \varvec{N\dot{u}} $$

where u denotes the generalized coordinate vector of the element in the coordinate system \( E_{i} - \bar{x}\bar{y}\bar{z} \) and \( \varvec{u} = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & \ldots & {u_{12} } \\ \end{array} } \right]^{\text{T}} \), N represents the type-function matrix [18].

Fig. 3
figure 3

The spatial beam element

Full size image

Therefore, the kinetic energy equation of the spatial beam element are formulated as

$$ T = \frac{1}{2}\int_{0}^{l} {\rho A_{c} \dot{\varvec{u}}^{\text{T}} \dot{\varvec{u}}{\text{d}}\bar{x}} $$
(16)

where ρ, A c, l represent the density, cross section area and the length of the element.

Then the potential energy equation of the spatial beam element can be formulated

$$ \begin{aligned} U = & \frac{1}{2}\int_{0}^{l} {\left[ {EA_{\text{c}} \left( {U^{\prime}} \right)^{2} + EI_{{{\bar{\text{z}}}}} \left( {V^{\prime\prime}} \right)^{2} + EI_{{{\bar{\text{y}}}}} \left( {W^{\prime\prime}} \right)^{2} + GJ\left( {\theta^{\prime}} \right)^{2} } \right]{\text{d}}\bar{x}} \\ & \quad - \int_{0}^{l} {\rho A_{c} \varvec{g}^{\text{T}} \varvec{r}_{\text{Q}} {\text{d}}\bar{x}} \\ \end{aligned} $$
(17)

where E, I y, I z represent the Young’s modulus, flexural section modulus of the element. U ′, θ ′ denote the first derivation of the longitudinal displacements of any point Q in the element with axis \( \bar{x} \). V ′′, W ′′ denote the second derivation of the transverse displacements of point Q with axes \( \bar{y} \) and \( \bar{z} \), respectively. g is the acceleration vector of gravity. r Q denotes the position vector of Q in the coordinate system \( E_{i} - \bar{x}\bar{y}\bar{z} \).

The motion differential equation of the spatial beam element can be formulated based on the Lagrange equation.

$$ {\varvec{m}}{\ddot{\varvec{u}}} + \varvec{ku} = \varvec{f} + \varvec{q} $$
(18)

where m, k, f and q represent mass matrix, stiffness matrix, interactive force vector and external force vector in the coordinate system \( E_{i} - \bar{x}\bar{y}\bar{z} \).

When calculated in the fixed coordinate system \( O - xyz \), Eq. (18) can be rewritten as

$$ {\varvec{M}}{\ddot{\varvec{U}}} + \varvec{KU} = \varvec{F} + \varvec{Q} $$
(19)

where M = T T mT, K = T T kT, F = T T f, Q = T T q, \( \varvec{T} = {\text{diag}}\left( {\begin{array}{*{20}c} {\varvec{R}_{\text{e}}^{\text{T}} } & {\varvec{R}_{\text{e}}^{\text{T}} } & {\varvec{R}_{\text{e}}^{\text{T}} } & {\varvec{R}_{\text{e}}^{\text{T}} } \\ \end{array} } \right) \), R e is the transformation matrix of the coordinate system \( E_{i} - \bar{x}\bar{y}\bar{z} \) with respect to the frame \( O - xyz \).

4.1 Elasto-dynamic modeling of components

4.1.1 The actuated component A

Considering the geometry of the actuated component A, 7 elastic-elements connected by 8 nodes are applied to describe the elastic-dynamic model as shown in Fig. 4. The corresponding coordinate system of each element is then established.

Fig. 4
figure 4

The model of actuated component A. a The virtual prototype. b The finite element model

Full size image

The boundary condition of actuated component A is analyzed. Node 11 of actuated component A coincides with point C 1 of the fixed base, resulting in the elastic deformations of Node 11 becoming 0 according to the instantaneous structure hypothesis. Affected by R joint, elastic angle about \( \bar{y}_{{{\text{A}}4}} \)-axis of Node 15 is released and the other deformations are 0. Hence the generalized coordinate vector U 1 of component A can be written as \( \varvec{U}_{1} = \left[ {\begin{array}{*{20}c} {U_{{{\text{A}}1}} } & {U_{{{\text{A}}2}} } & \ldots & {U_{{{\text{A}}37}} } \\ \end{array} } \right]^{\text{T}} \) in the fixed coordinate system \( O - xyz \). Herein, \( U_{{{\text{A}}1}} \sim U_{{{\text{A}}18}} \), \( U_{{{\text{A}}20}} \sim U_{{{\text{A}}37}} \) represent the elastic deformations of Node 12–14, Node 16–18 in sequence, and \( U_{{{\text{A}}19}} \) denotes the elastic angle of Node 15. Then the differential motion equation of the actuated component A can be formulated as follows.

$$ \varvec{M}_{1} {\ddot{\varvec{U}}}_{1} + \varvec{K}_{1} \varvec{U}_{1} = \varvec{F}_{1} + \varvec{Q}_{1} $$
(20)

where M 1, K 1, F 1, Q 1 represent the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the actuated component A in the coordinate system \( O - xyz \). Herein,

$$ \begin{aligned} \varvec{M}_{1} &= \sum\limits_{i = 1}^{7} {\varvec{J}_{{{\text{A}}i}}^{\text{T}} \varvec{M}_{{{\text{A}}i}} \varvec{J}_{{{\text{A}}i}} } ,\;\varvec{K}_{1} = \sum\limits_{i = 1}^{7} {\varvec{J}_{{{\text{A}}i}}^{\text{T}} \varvec{K}_{{{\text{A}}i}} \varvec{J}_{{{\text{A}}i}} } \hfill \\ \varvec{F}_{1} &= \sum\limits_{i = 1}^{7} {\varvec{J}_{{{\text{A}}i}}^{\text{T}} \varvec{F}_{{{\text{A}}i}} } ,\;\varvec{Q}_{1} = \sum\limits_{i = 1}^{7} {\varvec{J}_{{{\text{A}}i}}^{\text{T}} \varvec{Q}_{{{\text{A}}i}} } \hfill \\ \end{aligned} $$

where M Ai , K Ai , F Ai , Q Ai denote the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the element in the coordinate system \( O - xyz \). J Ai is the mapping matrix between the generalized coordinate vector of the element i and U 1.

4.1.2 The actuated component B

As shown in Fig. 5, the actuated component B can be divided into eight elastic-elements with eight nodes. And the coordinate system of each element is established.

Fig. 5
figure 5

The model of actuated component B. a The virtual prototype. b The finite element model

Full size image

Similar to component A, boundary conditions of actuated component B need to be considered. Node 21 is in correspondence with point C 2 of the fixed base, and Node 25 is influenced by R joint. The generalized coordinate vector U 2 of component B can be written as \( \varvec{U}_{2} = \left[ {\begin{array}{*{20}c} {U_{{{\text{B}}1}} } & {U_{{{\text{B}}2}} } & \ldots & {U_{{{\text{B}}37}} } \\ \end{array} } \right]^{\text{T}} \) in the fixed coordinate system \( O - xyz \). Herein, \( U_{{{\text{B}}1}} \sim U_{{{\text{B}}18}} \), \( U_{{{\text{B}}20}} \sim U_{{{\text{B}}37}} \) represent the elastic deformations of Node 22–24, Node 26–28 in sequence, and \( U_{{{\text{B}}19}} \) denotes the elastic angle of Node 25. Then the differential motion equation of the actuated component B can be derived as follows.

$$ \varvec{M}_{2} {\ddot{\varvec{U}}}_{2} + \varvec{K}_{2} \varvec{U}_{2} = \varvec{F}_{2} + \varvec{Q}_{2} $$
(21)

where M 2, K 2, F 2, Q 2 represent the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the actuated component B in the frame \( O - xyz \). Herein,

$$ \begin{aligned} \varvec{M}_{2} &= \sum\limits_{i = 1}^{8} {\varvec{J}_{{{\text{B}}i}}^{\text{T}} \varvec{M}_{{{\text{B}}i}} \varvec{J}_{{{\text{B}}i}} } ,\;\varvec{K}_{2} = \sum\limits_{i = 1}^{8} {\varvec{J}_{{{\text{B}}i}}^{\text{T}} \varvec{K}_{{{\text{B}}i}} \varvec{J}_{{{\text{B}}i}} } \hfill \\ \varvec{F}_{2} &= \sum\limits_{i = 1}^{8} {\varvec{J}_{{{\text{B}}i}}^{\text{T}} \varvec{F}_{{{\text{B}}i}} } ,\;\varvec{Q}_{2} = \sum\limits_{i = 1}^{8} {\varvec{J}_{{{\text{B}}i}}^{\text{T}} \varvec{Q}_{{{\text{B}}i}} } \hfill \\ \end{aligned} $$

where M Bi , K Bi , F Bi , Q Bi represent the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the element in the coordinate system \( O - xyz \). J Bi is the mapping matrix between the generalized coordinate vector of the element i and U 2.

4.1.3 The driven component

The driven component is with simple structure, thus can be divided into two elastic-elements with three nodes as shown in Fig. 6. And the coordinate systems of the two elements are parallel to each other.

Fig. 6
figure 6

The model of the driven component. a The virtual prototype. b The finite model

Full size image

The generalized coordinate vector U 2+i of the ith (i = 1–4) driven component in the fixed coordinate system \( O - xyz \) can be written as \( \varvec{U}_{2 + i} = \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}i1}} } & {U_{{{\text{C}}i2}} } & \ldots & {U_{{{\text{C}}i18}} } \\ \end{array} } \right]^{\text{T}} \). Herein, \( U_{{{\text{C}}i1}} \sim U_{{{\text{C}}i18}} \) represent the elastic deformations of Node i1–i3 in sequence. Thus the differential motion equation of the driven component can be written as follows.

$$ \varvec{M}_{2 + i} {\ddot{\varvec{U}}}_{2 + i} + \varvec{K}_{2 + i} \varvec{U}_{2 + i} = \varvec{F}_{2 + i} + \varvec{Q}_{2 + i} ,\quad \left( {i = 1\sim 4} \right) $$
(22)

where M 2+i , K 2+i , F 2+i , Q 2+i denote the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the ith driven component in the coordinate system \( O - xyz \). Herein,

$$ \begin{gathered} \varvec{M}_{2 + i} = \sum\limits_{j = 1}^{3} {\varvec{J}_{{{\text{C}}ij}}^{\text{T}} \varvec{M}_{{{\text{C}}ij}} \varvec{J}_{{{\text{C}}ij}} } ,\quad K_{2 + i} = \sum\limits_{j = 1}^{3} {\varvec{J}_{{{\text{C}}ij}}^{\text{T}} \varvec{K}_{{{\text{C}}ij}} \varvec{J}_{{{\text{C}}ij}} } \hfill \\ \varvec{F}_{2 + i} = \sum\limits_{j = 1}^{3} {\varvec{J}_{{{\text{C}}ij}}^{\text{T}} \varvec{F}_{{{\text{C}}ij}} } ,\quad \varvec{Q}_{2 + i} = \sum\limits_{j = 1}^{3} {\varvec{J}_{{{\text{C}}ij}}^{\text{T}} \varvec{Q}_{{{\text{C}}ij}} } \hfill \\ \end{gathered} $$

where M Cij , K Cij , F Cij , Q Cij represent the mass matrix, the stiffness matrix, the interactive force vector and the external force vector of the element in the coordinate system \( O - xyz \). J Cij is the mapping matrix between the generalized coordinate vector of the element j and U 2+i .

4.1.4 The articulated travelling platform

Although the articulated travelling platform is assumed to be rigid component, its displacement would be affected by the deformation of the elastic components. Therefore, the dynamic equations of the articulated travelling platform are formulated in the fixed coordinate system \( O - xyz \) as

$$ \varvec{M}_{{{\text{P}}i}} {\ddot{\varvec{U}}}_{{{\text{P}}i}} = \varvec{F}_{{{\text{P}}i}} + \varvec{Q}_{{{\text{P}}i}} ,\quad i = 1, 2 $$
(23)

where M Pi , F Pi , Q Pi and U Pi represent the mass matrix, the interactive force vector, the external force vector and the elastic deformation vector of the sub-plate I in the coordinate system \( O - xyz \) for i = 1 and those of the sub-plate II for i = 2. It should be pointed out that the elastic angles about w axis of the two sub-plates are different. In consequence, elastic deformations of point P are defined as \( \varvec{u}_{{{\text{P}}i}} = \left[ {\begin{array}{*{20}c} {\Delta x} & {\Delta y} & {\Delta z} & {\Delta \alpha } & {\Delta \beta } & {\Delta \phi_{i} } \\ \end{array} } \right]^{\text{T}} \), where the elastic displacements are measured in the fixed coordinate system \( O - xyz \) while the elastic angles are measured in the coordinate system \( P - uvw \). Then Eq. (23) can be rewritten as follows.

$$ \varvec{M}_{{{\text{P}}i}}^{e} {\ddot{\varvec{u}}}_{{{\text{P}}i}} = \varvec{F}_{{{\text{P}}i}} + \varvec{Q}_{{{\text{P}}i}} ,\quad \left( {i = 1,2} \right) $$
(24)

where \( \varvec{M}_{{{\text{P}}i}}^{e} = \varvec{M}_{{{\text{P}}i}} \left[ {\begin{array}{*{20}c} {\varvec{E}_{3 \times 3} } & {0_{3 \times 3} } \\ {0_{3 \times 3} } & \varvec{R} \\ \end{array} } \right] \).

The dynamic equation of the articulated travelling platform can be formulated as follows.

$$ \varvec{M}_{7} {\ddot{\varvec{U}}}_{7} = \varvec{F}_{7} + \varvec{Q}_{7} $$
(25)

where \( \varvec{U}_{7} = \left[ {\begin{array}{*{20}c} {\Delta x} & {\Delta y} & {\Delta z} & {\Delta \alpha } & {\Delta \beta } & {\Delta \phi_{1} } & {\Delta \phi_{2} } \\ \end{array} } \right]^{\text{T}} \), M 7, F 7, Q 7 represent the mass matrix, the interactive force vector and the external force vector of the articulated travelling platform. Herein,

$$ \varvec{M}_{7} = \sum\limits_{i = 1}^{2} {\varvec{J}_{{{\text{P}}i}}^{\text{T}} \varvec{M}_{{{\text{P}}i}}^{e} \varvec{J}_{{{\text{P}}i}} } ,\;\varvec{F}_{7} = \sum\limits_{i = 1}^{2} {\varvec{J}_{{{\text{P}}i}}^{\text{T}} \varvec{F}_{{{\text{P}}i}} } ,\;\varvec{Q}_{7} = \sum\limits_{i = 1}^{2} {\varvec{J}_{{{\text{P}}i}}^{\text{T}} \varvec{Q}_{{{\text{P}}i}} } $$

where J Pi is the mapping matrix between the generalized coordinate vector of the plate and U 7.

4.2 Deformation compatibility condition

The deformation compatibility condition is to set up the relations of generalized coordinates between different components. Considering the connection of adjacent components, deformation compatibility condition between the driven component and the articulated travelling platform can be formulated as follows.

$$ \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}i13}} } \\ {U_{{{\text{C}}i14}} } \\ {U_{{{\text{C}}i15}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{E}_{3 \times 3} } & { - \varvec{S}\left( {\varvec{a}_{i} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{E}_{3 \times 3} } & {0_{3 \times 3} } \\ {0_{3 \times 3} } & \varvec{R} \\ \end{array} } \right]\varvec{u}_{{{\text{P}}1}} ,\quad \left( {i = 1,3} \right) $$
(26)
$$ \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}i13}} } \\ {U_{{{\text{C}}i14}} } \\ {U_{{{\text{C}}i15}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{E}_{3 \times 3} } & { - \varvec{S}\left( {\varvec{a}_{i} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{E}_{3 \times 3} } & {0_{3 \times 3} } \\ {0_{3 \times 3} } & \varvec{R} \\ \end{array} } \right]\varvec{u}_{{{\text{P}}2}} ,\quad \left( {i = 2,4} \right) $$
(27)

where \( \varvec{a}_{i} = \varvec{Ra}_{0i} \), \( \varvec{S}\left( {\varvec{a}_{i} } \right) = \left[ {\begin{array}{*{20}c} 0 & { - a_{{i{\text{z}}}} } & {a_{{i{\text{y}}}} } \\ {a_{{i{\text{z}}}} } & 0 & { - a_{{i{\text{x}}}} } \\ { - a_{{i{\text{y}}}} } & {a_{{i{\text{x}}}} } & 0 \\ \end{array} } \right] \).

Similarly, deformation compatibility condition between the driven component and the actuated component is expressed as follows.

$$ \left[ {\begin{array}{*{20}c} {U_{{{\text{A}}26}} } \\ {U_{{{\text{A}}27}} } \\ {U_{{{\text{A}}28}} } \\ {U_{{{\text{A}}30}} } \\ {U_{{{\text{A}}31}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}11}} } \\ {U_{{{\text{C}}12}} } \\ {U_{{{\text{C}}13}} } \\ {U_{{{\text{C}}15}} } \\ {U_{{{\text{C}}16}} } \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}c} {U_{{{\text{A}}32}} } \\ {U_{{{\text{A}}33}} } \\ {U_{{{\text{A}}34}} } \\ {U_{{{\text{A}}36}} } \\ {U_{{{\text{A}}37}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}31}} } \\ {U_{{{\text{C}}32}} } \\ {U_{{{\text{C}}33}} } \\ {U_{{{\text{C}}35}} } \\ {U_{{{\text{C}}36}} } \\ \end{array} } \right] $$
(28)
$$ \left[ {\begin{array}{*{20}c} {U_{{{\text{B}}7}} } \\ {U_{{{\text{B}}8}} } \\ {U_{{{\text{B}}9}} } \\ {U_{{{\text{B}}10}} } \\ {U_{{{\text{B}}12}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}21}} } \\ {U_{{{\text{C}}22}} } \\ {U_{{{\text{C}}23}} } \\ {U_{{{\text{C}}24}} } \\ {U_{{{\text{C}}26}} } \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}c} {U_{{{\text{B}}26}} } \\ {U_{{{\text{B}}27}} } \\ {U_{{{\text{B}}28}} } \\ {U_{{{\text{B}}29}} } \\ {U_{{{\text{B}}31}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {U_{{{\text{C}}41}} } \\ {U_{{{\text{C}}42}} } \\ {U_{{{\text{C}}43}} } \\ {U_{{{\text{C}}44}} } \\ {U_{{{\text{C}}46}} } \\ \end{array} } \right] $$
(29)

4.3 Elasto-dynamic equations

The elasto-dynamic equation of the novel 2-DoF RPM can be calculated by elasto-dynamic models of components with the deformation compatibility conditions as

$$ \varvec{M}_{\text{s}} {\ddot{\varvec{u}}} + \varvec{K}_{\text{s}} \varvec{U} = \varvec{F}_{\text{s}} $$
(30)

where U denotes the generalized coordinate vector of the 2-DoF RPM which contains 121 elements. Generalized coordinate vector of the whole mechanism and individual components has the following relation,

$$ \varvec{U}_{j} = \varvec{B}_{j} \varvec{U }(j = 1\sim 7) $$

where B j denotes the coordinate harmonized matrix of the components in the fixed coordinate system. M s, K s represent the mass matrix and the stiffness matrix of the novel 2-DoF RPM. F s denotes the generalized external force. Herein,

$$ \begin{gathered} \varvec{M}_{\text{s}} = \sum {\varvec{B}_{j}^{\text{T}} \varvec{M}_{j} \varvec{B}_{j} } ,\;\varvec{K}_{\text{s}} = \sum {\varvec{B}_{j}^{\text{T}} \varvec{K}_{j} \varvec{B}_{j} } \hfill \\ \varvec{F}_{\text{s}} = \sum {\varvec{B}_{j}^{\text{T}} \varvec{F}_{j} \varvec{B}_{j} } \hfill \\ \end{gathered} $$

The undamped free vibration equation of the novel 2-DoF RPM can be derived from Eq. (30) as

$$ \varvec{M}_{\text{s}} {\ddot{\varvec{u}}} + \varvec{K}_{\text{s}} \varvec{U} = 0 $$
(31)

Then the natural frequencies are calculated through

$$ \det \left( {\varvec{K}_{\text{s}} - \omega^{2} \varvec{M}_{\text{s}} } \right) = 0 $$
(32)

5 Example and discussion

Under the guidance of the analysis flow in Sect. 4, an example is given to illustrate the natural frequencies of the novel 2-DoF RPM with the parameters shown in Table 1. As shown in Fig. 7, to verified the theoretical method, simulation conducted by Ansys Workbench software [19] is applied when α = 0, β = 0. The comparisons between the two approaches are illustrated in Table 2 and Fig. 8. It is obvious that the natural frequencies obtained by KED method are similar to those by finite element software, which may be resulted from the difference of finite element models and the real components with irregular shape and dimension. And the errors are within 5 %, indicating good consistency of the two methods and validating the effectiveness of KED method.

Table 1 The parameters of the virtual prototype
Full size table
Fig. 7
figure 7

The modal shapes of FEM when α = 0 and β = 0. a The 1st order modal shape. b The 2nd order modal shape. c The 3rd order modal shape. d The 4th order modal shape

Full size image
Table 2 The results of natural frequencies
Full size table
Fig. 8
figure 8

The results comparison between KED and FEM when α = 0

Full size image

After verified the theoretical method, distributions of natural frequencies in the prescribed workspace are demonstrated analytically in Fig. 9. w x and w y are used to represent the projection of the unit vector w on the x axis and that on the y axis. As shown in Fig. 9, 1st, 2nd, 3rd, 4th natural frequencies are all plane symmetrical about w y = 0 and approximately symmetrical about plane w x = 0. For the 1st and 3rd natural frequencies, they decrease as the w y goes up while they remain constant as the change of w x. The variations of 2nd and 4th natural frequencies are opposite to each other. 2nd natural frequency gradually goes up with the increase of w y but drops when w x becomes bigger. On the contrary, 4th natural frequency slowly decreases as the increment of w y while it dramatically rises as w x climbs up.

Fig. 9
figure 9

The distributions of frequencies. a The 1st order natural frequency. b The 2nd order natural frequency. c The 3rd order natural frequency. d The 4th order natural frequency

Full size image

6 Conclusions

Concerning the application for pose-adjusting module of 5-DoF hybrid machining centre, this paper proposed a novel 2-DoF RPM and carried out its elastic-dynamic analysis. The following conclusions can be drawn:

  1. (1)

    By introducing an articulated travelling platform, high rotational capability without parasitic motion is achieved by the novel 2-DoF RPM which possess advantages in terms of high rigidity, compact structure and good dynamic performance.

  2. (2)

    By utilizing the KED method, the elasto-dynamic model of the novel 2-DoF RPM can be assembled by those of components in the light of deformation compatibility condition.

  3. (3)

    The natural frequencies of the novel 2-DoF RPM are calculated and verified by finite element software. The result shows that the novel 2-DoF parallel mechanism is of good elasto-dynamic performance.