1 Introduction

Chua et al. predicted the existence of memristor theoretically in 1998 [1] and Hewlett-Packard (HP) laboratory fabricated the first solid-state memristor in 2008 [2]. The current flowing through the memristor can change its resistance, and its resistance can be permanently maintained when the power is cut off, so that the memristor is a natural non-volatile memory device. Due to its unique properties, memristor has been adopted in many scenarios, such as acting as synapses in artificial neural networks [3,4,5], increasing more possibilities in the field of communications [6, 7], enhancing chaotic image encryption effect [8]. In recent years, memristor-based chaotic circuits have become a hot topic in nonlinear dynamics [9, 10].

Generally speaking, there are two types chaotic attractor: self-excited attractor and hidden attractor.

A system with self-excited attractor has at least one basin of attraction that is intersected with unstable equilibrium, whereas a system with hidden attractor whose basins of attraction do not overlap any small neighborhood of unstable equilibrium points. The previous researches mainly focused on self-excited chaotic systems [11,12,13], but in the recent years, people have paid more attention to the hidden attractors. For example, Y Dong et al. proposed a hidden chaotic circuit based on a nonvolatile locally active memristor, and verified its non-volatility and local activity [14]. S Vaidyanathan et al. presented an electronic circuit emulating the memristor-based hyperchaotic system with hidden attractor [15], and Yu Feng et al. showed a new hidden hyperchaotic memristive oscillator with a line of equilibria [16]. Is it possible to propose a system in which the hidden and self-excited attractors coexist? This topic will be explored and analyzed in this paper.

Nonlinear systems are often accompanied by many interesting dynamic phenomena, such as multistability, and antimonotonicity. Multistability means that a system can produce the coexistence of multiple attractors by changing its initial conditions under the other parameters remain unchanged, and it is used in many physics and engineering applications, such as impulse oscillators [17, 18], the proposal of extreme multistability [19, 20] has attracted a lot of attention, and B.C. Bao et al. developed the multistable systems with memory elements [21]. Antimonotonicity is a relatively common dynamic phenomenon, and it expresses the process of beginning to form the Feigenbaum remerging trees by period-doubling bifurcation scenario and finally annihilating by inverse period-doubling scenario. Atiyeh Bayani et al. proposed a 4-D hidden chaotic system in 2018 and found the Feigenbaum remerging trees [22], and not long, Signing VR Folifack et al. also discovered this interesting phenomenon in a 4-D system [23]. This paper will study multistability and antimonotonicity from the perspective of the hidden and self-excited attractors.

Enlightened by the above considerations, a memristor-based Jerk system with hidden attractors and self-excited attractors is proposed. Some novel features and special properties of this system are as follows:

  1. (1)

    The system can change the attractor types by adjusting k, the hidden attractor with k \(>\) 0 and the self-excited attractor with k \(\le\) 0.

  2. (2)

    Multistability and antimonotonicity can be observed in both the hidden and self-excited attractor regions under the influence parameters.

  3. (3)

    The internal variable x(0) of the memristor is very sensitive to the system, and the switching of three states can be observed.

The rest parts are organized as follows. The new system and its equilibrium point are introduced in Sect. 2. Including multistability, antimonotonicity and state-switching are analyzed in Sect. 3. The analog circuit design based on Multisim is presented in Sect. 4. The last section is a summary of the full text.

2 System model and its stability

In [24], we developed a simple flux-controlled memristor and its memductance function is expressed as

$$W(\phi ) = \alpha - \beta \phi$$
(1)

where α and β are memristor’s parameters with positive values, ϕ is the flux having passed across the device, which corresponds to the integration of terminal voltage v with respect to time t. According to Ohm's law, the v-i relationship of the memristor can described as

$$i = W(\phi )v$$
(2)

Consequently, the emulator mathematically described by (2) can exhibit the pinched hysteresis loops when driven by a periodic sinusoidal signal. As shown in Fig. 1, when the excited amplitude is fixed with 4 V at different frequency, all pinched hysteresis loops pass through the origin (0, 0) and shrink as the excited frequency is increased. By introducing the memristor defined by (1) into the Jerk-like system, presented in [25], a memristor-based Jerk system is given by

$$\left. {\begin{array}{*{20}c} {\dot{x} = y} \\ {\dot{y} = z} \\ {\dot{z} = az + bxz - eW\left( x \right)y + cx^{2} + k} \\ \end{array} } \right\}$$
(3)

where x, y, and z are state variables, a, b and c are positive parameters, e is memristor’s coupled parameter, and k is a tunable parameter. In order to analyze the stability of system (3), the system parameters are fixed as \(a=5.2\), \(b=1\), c = 1, e = 1, \(\alpha = 7\), \(\beta = 1\), and k is considered as a controlled parameter with variation in the range [-15 15].

Fig. 1
figure 1

The pinched hysteresis loops of the proposed memristor

Full size image

Letting \(\dot{x}=\dot{y}=\dot{z}=0,\) the equilibrium points can be obtained as \(E({x}^{*},0, 0)\), where x* is dependent on the controlled parameter k. Due to k being a tunable parameter, system (3), thus, can be divided into the following three cases. The first case (S1) for \(k>0\), there is no equilibrium point in system (3). Then, in this case, the proposed system shows hidden attractors. The second case (S2) with \(k=0\), the system (3) has the only equilibrium point \({E}_{0}(0, 0, 0)\). The third case (S3) for \(k<0\), two equilibrium points \({E}_{\mathrm{1,2}}(\pm \sqrt{-k},0, 0)\) exist in system (3).

For S2 and S3, the equilibrium points \({E}_{0}(0, 0, 0)\) and \({E}_{\mathrm{1,2}}(\pm \sqrt{-k},0, 0)\) have the same Jacobian matrix and characteristic equation, given by

$$J = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ {2x^{*} } & { - 7 + x^{*} } & {5.2 + x^{*} } \\ \end{array} } \right]$$
(4)

and

$$\lambda^{3} + A_{1} \lambda^{2} + A_{2} \lambda + A_{3} = 0$$
(5)

where

$$\begin{gathered} A_{1} = - x^{*} - 5.2 \hfill \\ A_{2} = 7 - x^{*} \hfill \\ A_{3} = - 2x^{*} \hfill \\ \end{gathered}$$
(6)

According to Routh–Hurwitz criterion, the stability of equilibrium points \({E}_{0}(0, 0, 0)\) and \({E}_{\mathrm{1,2}}(\pm \sqrt{-k},0, 0)\) is depended on the following conditions

$$\begin{gathered} \Delta_{1} = A_{1} > 0 \hfill \\ \Delta_{2} = A_{1} A_{2} - A_{3} > 0 \hfill \\ \Delta_{3} = A_{3} (A_{1} A_{2} - A_{3} ) > 0 \hfill \\ \end{gathered}$$
(7)

Substituting \({x}^{*}=0\) into (6), it is easy to find that \({\Delta }_{1}<0\), \({\Delta }_{2}<0\), and \({\Delta }_{3}=0\), which are in contradiction with (7), the equilibrium points \({E}_{0}(0, 0, 0)\), thus, is an unstable equilibrium point. When \({x}^{*}=\sqrt{-k}\), we can conclude \({\Delta }_{1}<0\) and \({\Delta }_{2}<0\), indicating the equilibrium point \({E}_{1}(\sqrt{-k}, 0, 0)\) is unstable. Similarly, letting \({x}^{*}=-\sqrt{-k}\), we can obtain \({\Delta }_{2}=0.2\sqrt{-k }-k-36.4\). In the given parameter range of \(-15\le k\le 15\), \({\Delta }_{2}<0\), manifesting the equilibrium point \({E}_{2}(-\sqrt{-k}, 0, 0)\) is also an unstable equilibrium point. According to the above analysis, we can draw a conclusion that the equilibrium points \({E}_{0}(0, 0, 0)\) and \({E}_{\mathrm{1,2}}(\pm \sqrt{-k},0, 0)\) are all unstable and thus the system (3) in S2 and S3 shows self-excited attractors.

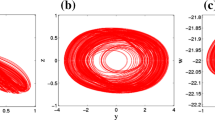
To sum up, the system (3) is a special chaotic system, which can generate not only self-excited attractors but also hidden attractors by adjusting one system parameter. To the best of our knowledge, this kind of chaotic systems has been rarely reported. The corresponding self-excited attractor and hidden attractor are shown in Figs. 2 and 3 obtained with k =  2 and k =  −2, respectively. Comparing Fig. 2 with Fig. 3, we find that the self-excited attractor and the hidden attractor have similar topological structure in the phase space. However, their formation mechanisms are quite different, one is induced by unstable equilibrium points and the other has nothing to do with any equilibrium point.

Fig. 2
figure 2

The self-excited chaotic attractor in different planes: (a) x–y plane, (b) y–z plane, (c) x–z plane with \(k=-2\)

Full size image
Fig. 3
figure 3

The hidden chaotic attractor in different planes: (a) x–y plane, (b) y–z plane, (c) x–z plane with \(k=2\)

Full size image

3 Dynamic properties of the new system

3.1 Dynamic evolution depending on parameter k

From the above analysis, we know the parameter k plays an important role in deciding the attractors generated in system (3) are self-excited or hidden. In order to explore the effect of the parameter k on dynamics, the system parameters are fixed as the above values and k varies in the range of \(-15\le k\le 15\), the bifurcation of state x is depicted in Fig. 4(a), which is obtained by plotting the local maxima of x with the initial values [− 1, 1,  7]. Based on Wolf’s method, the corresponding Lyapunov exponents are illustrated in Fig. 4(b), which shows a good coincidence with the bifurcation diagram.

Fig. 4
figure 4

Dynamics depending on parameter k: (a) Bifurcation diagram and (b) The Lyapunov exponents

Full size image

It is remarkable that attractors generated in system (3) with the range of [− 15 0] are self-excited, labeled with red color, and those in the range of (0 15] are hidden which are marked with blue color in Fig. 4(a). From Fig. 4(a) and (b), one can find whether in self-excited oscillations or hidden oscillations, the proposed system exhibits abundant and complex dynamical behaviors. Some typical phase diagrams including periodic oscillations and chaotic motions are illustrated in Fig. 5. Furthermore, period-doubling bifurcation route to chaos in self-excited regime and inverse period-doubling bifurcation scenario in hidden regime are observed. In particular, it is worth mentioning there exists a smooth transition from a self-excited attractor to a hidden chaotic attractor when k crosses zero.

Fig. 5
figure 5

The phase diagram in the x –y plane. Self-excited attractors (red): (a) Period-1 with k =  − 15, (b) Period-2 with k =  − 10, (c) Period-4 with k =  − 7 and (d) Chaos with k =  − 5. Hidden attractors (blue): (e) Chaos with k = 1, (f) Period-3 with k = 7, (g) Period-2 with k = 9 and (h) period-1 with k = 12

Full size image

3.2 Multistability of the system

Multistability is a complex dynamical phenomenon in nonlinear systems, referring to the coexistence of multiple stable attractors for the given system parameters and the different initial conditions. Due to the fact the system (3) can produce not only self-excited attractors but also hidden attractors, which is dependent on the decisive parameter k, so, in the following, we focus on self-excited and hidden multistability behavior generated from the system (3).

Letting the parameters a = 5.2, b = 1, c = 1, k =  − 0.1, α = 7 and \(\beta =1\), respectively, where k < 0 means the system is in the self-excited region, and varying parameter e in the range [1.1 1.6], the corresponding coexistence bifurcation diagrams of state x are shown in Fig. 6, where the initial conditions (-7, 1, -7) are marked with the blue color and the other initial conditions ( 1, 1,  7) with the red color. It is obvious from Fig. 6 that there are various different types of coexisting self-excited attractors, such as coexisting period-4 and chaotic attractors, coexisting period-2 and period-2 attractors, coexisting period-1 and period-2 attractors and coexisting period-1 and period-4 attractors. The corresponding phase diagrams are illustrated in Fig. 7. In order to further explore the influence of the initial values x(0) and z(0) for categories of the attractor, the basins of attraction are shown in Fig. 8, and it once again verifies the four situations in Fig. 7. It is easy to observe that multiple attractors can be generated in different regions.

Fig. 6
figure 6

Coexisting bifurcation diagrams in self-excited region: the blue points correspond to the initial conditions (− 7, 1, − 7) and the red points are related to the initial conditions (− 1, 1, − 7)

Full size image
Fig. 7
figure 7

Self-excited coexisting attractors: (a) coexisting period-4 and chaotic attractor with e = 1.15, (b) coexisting period-2 and period-2 attractor with e = 1.22, (c) coexisting period-1 and period-2 attractor with e = 1.42 and (d) coexisting period-1 and period-4 attractor e = 1.441

Full size image
Fig. 8
figure 8

Basins of self-excited attraction: fixing the parameters a = 5.2, b = 1, c = 1, k =  − 0.1, α = 7, \(\beta =1\) and y(0) = 1 (a) e = 1.15, the red stands for period-4 oscillation and the green for chaotic attractor and the blue for unbound behavior. (b) e = 1.22, the red and the green stand for period-2 oscillation and the blue for unbound behavior. (c) e = 1.42, the red stands for period-1 oscillation and the green for period-2 oscillation and the blue for unbound behavior. (d) e = 1.441, the red stands for period-1 oscillation and the green for period-4 oscillation and blue for unbound behavior

Full size image

In addition to the above coexisting self-excited attractors, the proposed system can exhibit coexisting hidden attractors. In order to make the system (3) generate hidden oscillations, let the parameter k = 0.6 and the other parameters are chosen as a = 4.2, b = 1.2, e = 1, α = 7, β = 1. By varying parameter c in the range of \(0.8\le c\le 1.5\), the coexisting bifurcation diagrams are obtained and shown in Fig. 9, where the red points correspond to the initial conditions ( 2,  3,  1) and the blue points are related to the initial conditions ( 2, 3,  1). From Fig. 8, we can see the coexistence of multiple attractors, such as coexisting period-4 and period-2 attractors, coexisting period-8 and period-2 attractors and coexisting chaotic and period-2 attractors. Some typical phase diagrams of the coexisting attractors are shown in Fig. 10 by setting different the values of the parameter c. Fixing initial value z(0) =  1, the basins of attraction relating to x(0) and y(0) are shown in Fig. 11, and it once again verifies the coexistence of attractors in Fig. 10.

Fig. 9
figure 9

Coexisting bifurcation diagrams in hidden region: the initial conditions (− 2, − 3, − 1) marked with the red color and the initial conditions (− 2, 3, − 1) marked with the blue color

Full size image
Fig. 10
figure 10

Hidden coexisting attractors: (a) coexisting period-4 and period-2 attractor with c = 0.92, (b) coexisting period-8 and period-2 attractor with c = 0.95 and (c) coexisting chaotic and period-2 attractor with c = 1.1

Full size image
Fig. 11
figure 11

Basins of hidden attraction: fixing the parameters a = 4.2, b = 1.2, e = 1, k = 0.6, α = 7, β = 1 and z(0) =  1 (a) c = 0.92, the red stands for period-4 attractor, the green for period-2 attractor and the blue for unbound behavior. (b) c = 0.95, the red stands for period-8 attractor, the green for period-2 attractor and the blue for unbound behavior. (c) c = 1.1, the red stands for chaotic attractor, the green for period-2 attractor and the blue for unbound behavior

Full size image

3.3 Three state switching based on the memristor’s internal initial state x(0)

Letting parameters (a, b, c, e, k,\(\alpha , \beta\)) = (4.2, 1.5, 1.014, 1, 0.6, 7, 1), initial conditions y(0) = z(0) = 0, and considering initial state x(0) as the controlled parameter varied in the interval of \(-2.4\le x(0)\le -1.2\), the bifurcation diagram of the variable y is shown in Fig. 12(a). It is obvious from Fig. 12(a) that the system repeatedly switches among three states: period-3 attractor, period-6 attractor, and chaotic attractor when the initial state x(0) changes. It’s worth noting that period-6 attractor is observed only in a narrow parameter interval. The corresponding Lyapunov exponents are described in Fig. 12(b). It can be seen intuitively that in the interval \(-2.4\le x(0)\le -2.19\) and \(-1.49\le x(0)\le -1.2\), the corresponding Lyapunov exponents are LE1 = 0, LE2 < 0 and LE3 < 0, meaning the system (3) is in a periodic state. And in the interval \(-2.19<x(0)<-1.49\), LE1 > 0, LE2 < 0 and LE3 < 0, resulting in that the system (3) is in a chaotic state. Obviously, there are some narrow windows interspersed in the interval \(-2.19<x(0)<-1.49\) with LE1  = 0, LE2 < 0 and LE3 < 0, showing that the system (3) is in a periodic state. The corresponding attractors are illustrated in Fig. 12(c), where period-3 attractor is obtained with x(0) =  − 1.4(green), chaotic attractor with x(0) =  − 1.8(red), and period-6 attractor with x(0) =  − 1.835(blue). Furthermore, the corresponding basin of attraction is shown in Fig. 12(d), in which the green stands for period-3 attractor, the orange for chaotic attractor, the yellow for period-6 attractor and blue for unbound behavior. In \(-2.4\le x(0)\le -1.2\), it is obvious that following the dotted line from left to right, the system first enter  the orange-yellow area from the green area and then back to the green area. This is the same as described in Fig. 12(a) and (b). The reason why this phenomenon is called state switching is that by adjusting the initial value, boundary crisis is ignited and thus leads to a qualitative change in the states of the system. This state switching phenomenon proves that the system (3) is very sensitive to the internal initial variable of the memristor, and it also reveals the generation mechanism of coexistence attractors.

Fig. 12
figure 12

State-switching phenomenon depending on x(0) with parameters (a, b, c, e, k,\(\alpha , \beta\)) = (4.2, 1.5, 1.014, 1, 0.6, 7, 1): (a) the bifurcation diagram, (b) the Lyapunov exponents, (c) phase portrait, showing that the initial condition corresponding to period-3 attractor (green) with x(0) =  − 1.4, chaotic attractor(red) with x(0) =  − 1.8, and period-6 attractor(blue) x(0) =  − 1.835, and (d) the basin of attraction with y(0) = 0

Full size image

3.4 Antimonotonicity of the system

Antimonotonicity is a dynamic behavior that periodic orbits can be born and then destroyed through anti-period bifurcation. Interestingly, this system can be observed two complete Feigenbaum remerging trees in the hidden and self-excited attractor regions. Letting the parameters b = 2, e = 1, k =  −0.1, \(\alpha =7,\mathrm{ and }\beta =1\), respectively, in which k < 0 means in self-excited region, initial conditions x(0) =  −1, y(0) = z(0) = 1, parameter a varies in the range of \(2\le a\le 9\), and the bifurcation diagram of state x is described in Fig. 13 with adjusting the parameter c. From Fig. 13 can be seen that the period-2 bubble is created with c = 2.1, then period-4 bubbles is developed with c = 1.9, and with the decrease of parameter c (c = 1.8 and c = 1.72), those bubbles gradually growing into a complete Feigenbaum remerging tree.

Fig. 13
figure 13

Bifurcation diagrams of self-exited antimonotonicity: (a) period-2 bubble with c = 2.1, (b) period-4 bubble with c = 1.9, (c) and (d) the complete Feigenbaum remerging tree with c = 1.8, c = 1.72, respectively

Full size image

Besides the above self-excited Feigenbaum remerging tree, the proposed system can be observed hidden Feigenbaum remerging tree. Letting the parameters b = 2, e = 1, k = 0.1,\(\alpha =7\mathrm{ and }\beta =1\), respectively, where k > 0, and initial conditions x(0) =  1, y(0) = z(0) = 1. Parameter c varies in the range of \(1.1\le c\le 1.7\), the bifurcation diagram of state x with respect to the parameter a is shown in Fig. 14. In light of Fig. 14, for a = 3.6, the period-2 bubble is obtained, and then period-4 bubble is observed at a = 4. With the parameter a gradually increasing, bubbles gradually develop until chaos appears (the complete Feigenbaum remerging trees appear in a = 4.12 and a = 4.2).

Fig. 14
figure 14

Bifurcation diagrams of hidden Antimonotonicity: (a) period-2 bubble with a = 3.6, (b) period-4 bubble with a = 4, (c) and (d) complete Feigenbaum remerging trees with a = 4.12 and a = 4.2, respectively

Full size image

4 Circuit simulation

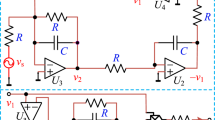
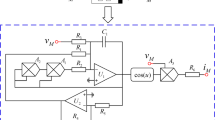
In order to verify the above two types of attractors and their coexisting attractors, a simulation circuit based on Multisim is designed in this section and shown in Fig. 15. The multipliers are selected as AD633 and operational amplifiers are TL082CD with supply voltages ± 15 V. It is worth noting that the memristor module is displayed in the red dashed box in Fig. 15. The dynamic range of the state variables x, y and z is beyond the saturation voltage 13.5 V of operational amplifiers TL082, appropriate scaling is required with x = 5x, y = 5y and z = 10z. In addition, the time constant is set to 100.

Fig. 15
figure 15

Multisim simulation circuit of the memristor-based system

Full size image

Applying Kirchhoff's law, the circuit equations are obtained:

$$\begin{gathered} \frac{{dv_{x} }}{dt} = \frac{1}{{R_{3} C_{1} }}v_{y} \hfill \\ \frac{{dv_{y} }}{dt} = \frac{1}{{R_{8} C_{2} }}v_{z} \hfill \\ \end{gathered}$$
(8)
$$\frac{d{v}_{z}}{dt}= \frac{1}{{R}_{9}{C}_{3}}{v}_{z}+ \frac{1}{10{R}_{10}{C}_{3}}{v}_{x}{v}_{z}-\left(\frac{1}{{R}_{11}{C}_{3}}- \frac{1}{10{R}_{12}{C}_{3}}{v}_{x}\right){v}_{y}+ \frac{1}{10{R}_{13}{C}_{3}}{v}_{x}{v}_{x}+ \frac{1}{{R}_{14}{C}_{3}}{E}_{v}$$

where\({v}_{x}\) \({v}_{y}\) and \({v}_{z}\) are the output voltages of the operational amplifiers, and \({E}_{v}\) is an adjustable DC voltage source. In order to capture the two types of attractors, comparing (8) with (3) and according to the system parameters (\(a, b, c ,e,\mathrm{ \alpha },\upbeta\)) = (5.2, 1, 1, 1, 7, 1), it is easy to calculate the corresponding circuit parameters, as shown in Table 1. Letting the parameter \({E}_{v}=-1v\) and adjusting the resistance of\({R}_{14}\), the self-excited attractors can be captured, as shown in Fig. 16(a)–(d). For \({E}_{v}\) = 1v, we continue to adjust the value of\({R}_{14}\), the hidden attractors are obtained as shown in Fig. 16(e)–h.

Table 1 Circuit parameters of system for verify the existence of two types of attractors
Full size table
Fig. 16
figure 16

The screenshots of the Multisim in the x–y plane for verifying two types of attractors: The self-excited attractors with \({E}_{v}=-1v\): (a) Period-1 for \({R}_{14}=666.67\mathrm{k}{\varvec{\Omega}}\), (b) Period-2 for \({R}_{1}=1000\mathrm{k}{\varvec{\Omega}}\), (c) Period-4 with \({R}_{14}=1428.57\mathrm{k}{\varvec{\Omega}}\), (d) Chaotic with \({R}_{14}=2000\mathrm{k}{\varvec{\Omega}}\). The hidden attractors with \({E}_{v}=1v\): (e) Chaotic attractor with \({R}_{14}=10000\mathrm{k}{\varvec{\Omega}}\), (f) Period-3 with \({R}_{14}=1428.57\mathrm{k}{\varvec{\Omega}}\), (g) Period-2 with \({R}_{14}=1111.11\mathrm{k}{\varvec{\Omega}}\), (h) Period-1 with \({R}_{14}=833.33\mathrm{k}{\varvec{\Omega}}\)

Full size image

In addition, we have also successfully verified the coexisting attractors in the self-excited and hidden regions, respectively. Letting the parameter \({E}_{v}=-1v\), and comparing (8) with (3), the corresponding circuit parameters are calculated by the system parameters (\(a, b, c,k,\mathrm{\alpha },\upbeta\)) = (5.2, 1, 1,  0.1, 7, 1), as shown in Table 2. Setting appropriate resistance values for \({R}_{11}\) and \({R}_{12}\), different self-excited attractors can be captured under the two cases of initial conditions (\({C}_{1}, {C}_{2}, {C}_{3}\)) = (\(-7v,1v, -7v\)) labeled with blue and (\({C}_{1}, {C}_{2}, {C}_{3}\)) = (\(-1v,1v, -7v\)) with red, as displayed in Fig. 17. Similarly, for \({E}_{v}=1v\), according to the system parameter (a, b, e, k,\(\alpha , \beta\)) = (4.2, 1.2, 1, 0.6, 7, 1), the corresponding circuit parameters for generating the coexisting hidden attractors are calculated and listed in Table 3. In Fig. 18, two different types of hidden attractors are captured by setting the appropriate resistance value of \({R}_{13}\), in which the blue corresponds to the initial conditions \(({C}_{1}, {C}_{2}, {C}_{3})\)= (\(-2v,3v, -1v\)) and red is related to the initial conditions (\({C}_{1}, {C}_{2}, {C}_{3}\)) = (\(-2v,-3v, -1v\)). These simulation results agree well with the digital simulation results of Sects. 3.1 and 3.2.

Table 2 Circuit parameters of system for verify the coexistence of multiple self-excited attractors
Full size table
Fig. 17
figure 17

The screenshots of the Multisim in the x–y plane for verifying Coexistent self-excited attractors: The blue and red graphics represent the initial values (\({C}_{1}, {C}_{2}, {C}_{3}\)) = (\(-7v,1v, -7v\)) and (\(-1v,1v, -7v\)), respectively, (a) coexisting period-4 and chaotic attractor with \({R}_{11}=248.45\mathrm{k}{\varvec{\Omega}}\) and \({R}_{12}=34.78\mathrm{k}{\varvec{\Omega}}\), (b) coexisting period-2 and period-2 attractor with \({R}_{11}=234.19\mathrm{k}{\varvec{\Omega}}\) and \({R}_{12}=32.79\mathrm{k}{\varvec{\Omega}}\), (c) coexisting period-1 and period-2 attractor with \({R}_{11}=201.2\mathrm{k}{\varvec{\Omega}}\) and \({R}_{12}=28.17\mathrm{k}{\varvec{\Omega}}\) and (d) coexisting period-1 and period-4 attractor \({R}_{11}=198.27\mathrm{k}{\varvec{\Omega}}\) and \({R}_{12}=27.76\mathrm{k}{\varvec{\Omega}}\)

Full size image
Table 3 Circuit parameters of system for verify the coexistence of multiple hidden attractors
Full size table
Fig. 18
figure 18

The screenshots of the Multisim in the x–y plane for verifying Coexistent hidden attractors: The blue and red graphics represent the initial values (\({C}_{1}, {C}_{2}, {C}_{3}\)) = (\(-2v,3v, -1v\)) and (\(-2v,-3v, -1v\)), respectively, (a) coexisting period-4 and period-2 attractor with \({R}_{13}=43.48\mathrm{k}{\varvec{\Omega}}\), (b) coexisting period-8 and period-2 attractor with \({R}_{13}=42.11\mathrm{k}{\varvec{\Omega}}\) and (c) coexisting chaotic and period-2 attractor with \({R}_{13}=36.36\mathrm{k}{\varvec{\Omega}}\)

Full size image

5 Conclusions

This paper proposes a memristor-based new Jerk system. Interestingly, the system can switch attractor types by adjusting the parameter k, for k > 0 it shows hidden attractor and for k \(\le\) 0 it shows self-excited attractors. We analyzed the rich dynamic behavior of the system through Lyapunov exponent diagrams, phase diagrams, bifurcation diagrams, and basins of attraction. By setting different initial conditions, the system can exhibit the coexistence of attractors in the hidden region and self-excited region. Moreover, the result of three state-switching verifies that the memristor’s internal initial x(0) is very sensitive. Of most interest is that the full Feigenbaum remerging trees can be developed in the hidden region and self-excited region. Finally, we implemented an analog circuit based on Multisim, two types of attractors and multistability are verified successfully.