1 Introduction

The quadrotor aircraft is a kind of small-scale unmanned aerial vehicles, which can performs different tasks in a dangerous or unaccessible environment, e.g., surveillance, investigation, film making, and search-and-rescue missions. The quadrotor aircraft can be widely used in various fields due to it has many special superiorities, such as structure simple, low cost, small size, hovering capability, vertical take-off and landing [1, 2]. Over the past few years, with the rapid development of microprocessor, microelectromechanical system, new material, power battery, sensing technique, and communication technology, the performance of quadrotor aircraft has been greatly improved from many aspects [3, 4]. From the control viewpoint, many efforts have been made to design and improve the control performance for quadrotor aircraft system. The main objective of this paper is to employ the finite-time control method (a kind of nonlinear control methods) to improve the aircraft’s control performance.

The control problem of quadrotor aircraft has been investigated by many researchers and many different nonlinear control tools have been employed. Usually, the control problem of quadrotor aircraft can be divided into two parts, one is the position control and the other one is the attitude control. With the developments and applications of nonlinear control methods [5,6,7,8,9], many kinds of nonlinear controllers have been designed to improve the control performance of quadrotor aircraft. By using sliding mode control technique, the work [10] proposed a sliding mode controller for the quadrotor aircraft. Based on the adaptive control method and nonlinear feed-forward compensations control method, the work [11] designed a new trajectory tracking controller for the quadrotor aircraft. To achieve trajectory tracking for quadrotors in the presence of uncertainties, the work [12] designed a robust decentralized and linear time-invariant controller to improve the closed-loop systems robustness. Usually, the attitude control for quadrotor aircraft is more complicated than the position control. To this end, many different attitude controllers have been proposed only for the attitude loop of quadrotors in the literature. In [13], the quaternion-based feedback controller was designed to achieve attitude stabilization and the experiment results were presented. In [14], the attitude stabilization controller was designed based on the quaternion feedback for the quadrotor aircraft. Considering the parameters uncertainties and the external disturbance (e.g., gravity and other environmental factors), in [15], an adaptive control law was proposed to address parameters uncertainties.

It is noted that the most of proposed control algorithms for quadrotor aircraft only guarantee that the closed-loop systems are asymptotically stable, that is to say that the quadrotors’ position/attitude asymptotically converge to the desired signals. To further improve the convergence rate for the closed-loop systems, this paper will employ a recent developed nonlinear control method (called finite-time control method [16]) to design control algorithms for quadrotors. Besides of the convergent performance, the quadrotor aircraft is easily influenced by various external disturbances (e.g., wind force) in the actual flight. So it is important to have better disturbance rejection performance for the aircraft control system. Actually, some theoretical and experimental results [17,18,19,20,21,22,23,24,25] have been shown that the finite-time control method has better disturbance rejection properties.

Because of the above advantages about finite-time control algorithm, this paper will use it to design control scheme for the quadrotor aircraft. Although the works [26,27,28] employed the finite-time control technique to design control algorithms for aircraft. However, different from the above papers, the quadrotor model considered in this paper is more complex, especially for the attitude control part, which is based on quaternion model. Specifically, the design procedure of finite-time controller in this paper is divided into three steps. At the first step, for the position subsystem, a saturated finite-time position controller is designed to ensure quadrotor aircraft can reach any desired position in a finite time. Then, for the attitude control subsystem, based on the model characteristic of the aircraft attitude system described by quaternion, a new fast finite-time attitude tracking control algorithm is designed. By skillfully constructing Lyapunov function, and based on finite-time stability theory, it can be proven that the aircraft attitude will converges to the desired attitude in a finite time. Finally, the controller for the motor’s speed is given. The numerical simulation results are given to demonstrate the efficiency of the proposed method.

The remainder of this paper is organized as follows: Sect. 2 introduces the operating principle of quadrotor aircraft and its mathematical model. Some useful definitions and lemmas are also given. In Sect. 3, the main results about the design of finite-time controllers are presented. Section 4 provides the numerical simulation results. Finally, the conclusion is provided in the last section.

2 Preliminaries and problem formulation

2.1 Control principle for quadrotor aircraft

The quadrotor aircraft usually consists of a rigid cross frame equipped with four rotors. By regulating the speed of four rotors, the quadrotor aircraft can complete position motion in space [29].

Fig. 1
figure 1

The structure diagram for quadrotor aircraft

Full size image

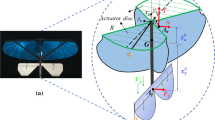
Let \(n=\{n_x,n_y,n_z\}\) be a right-hand inertial frame, where \(n_z\) denotes the vertical direction downwards into the earth. Let \(b=\{b_x,b_y,b_z\}\) be a right-hand body fixed frame for the airframe as shown in Fig. 1. The positive direction of quadrotor aircraft is same with the \(b_x\) axis in the body coordinate frame, where the angles rotated around \(b_x,b_y,b_z\) axis are, respectively, denoted by the roll angle \(~\phi \), pitch angle \(~\theta \), and yaw angle \(~\psi \). In addition, the rotation direction is based on the right-hand rule. The \(f_i=b\omega _i^2\) and \(Q_i=\kappa \omega _i^2\) presents the lift and the reactive torque generated by rotor i in free air, respectively, where \(\kappa \) and b both are positive real coefficient denoted by blades, \(i\in \{1,2,3,4\}\).

Usually, the description of a rigid body requires six degree-of-freedom information. For the quadrotor aircraft, the coordinates are given by

$$\begin{aligned} (x,y,z,\phi ,\theta ,\psi )^\mathrm{T}\in R^{6}, \end{aligned}$$
(1)

where \(p=(x,y,z)^\mathrm{T}\in R^{3}\) denotes the position of the center of mass of the quadrotor aircraft with respect to an inertial coordinate frame, and \(\eta =(\phi ,\theta ,\psi )^\mathrm{T}\in R^{3}\) denotes the three Euler angles for the description of aircraft attitude with respect to the inertial coordinate frame.

Although the quadrotor aircraft has six degree-of-freedom, there are only four inputs, that is the speed of four motors:

$$\begin{aligned} (\omega _{1},\omega _{2},\omega _{3},\omega _{4})^\mathrm{T}\in R^{4}. \end{aligned}$$
(2)

Therefore, the quadrotor aircraft is a typical under-actuated system.

2.2 System model for quadrotor aircraft

The mathematical model for the quadrotor aircraft is mainly composed of two parts. One part is position dynamical equation describing the translational characteristics of quadrotor aircraft, and the other part is attitude dynamical equation describing the rotational characteristic of quadrotor aircraft. The attitude dynamical equation is relatively independent, and the position dynamical equation is coupled with the attitude information. According to the above characteristics, the position subsystem is often defined as outer-loop, and attitude subsystem is defined as inner-loop.

2.2.1 Position dynamical equation

As that in [12], the dynamical equation for the quadrotor aircraft’s position is given as follows:

$$\begin{aligned} \ddot{x}&=\frac{-T}{m}(\cos {\phi }\sin {\theta }\cos {\psi }+\sin {\phi }\sin {\psi }),\nonumber \\ \ddot{y}&=\frac{-T}{m}(\cos {\phi }\sin {\theta }\sin {\psi }-\sin {\phi }\cos {\psi }),\nonumber \\ \ddot{z}&=\frac{-T}{m}\cos {\phi }\cos {\theta }+g, \end{aligned}$$
(3)

where m is the mass of the aircraft, g is the gravitational acceleration, T is the total thrust generated by the four rotors.

2.2.2 Attitude dynamical equation

In the literature, there are many ways to describe the dynamical equation for the quadrotor aircraft’s attitude. In order to avoid the singularity by using Euler angle, the quaternion is used to describe the aircraft’s attitude globally as that in [30, 31]. The quaternion \(q\in R^{4}\) is a four dimensional vector defined as:

$$\begin{aligned} q=[q_{0},q_{1},q_{2},q_{3}]^\mathrm{T}=[q_{0},q_{v}^\mathrm{T}]^\mathrm{T}, \end{aligned}$$
(4)

where \(q_{0}\) is the scalar part, \(q_v=[q_{1},q_{2},q_{3}]^\mathrm{T}\) is the vector part. The quaternion satisfies the constraint equation \(\Vert q\Vert =q^\mathrm{T}q=1\). The transformation relationship between the quaternion and the Euler angles is given as follows:

$$\begin{aligned} q_{0}=&\cos (\psi /2)\cos (\phi /2)\cos (\theta /2)\nonumber \\&+\,\sin (\psi /2)\sin (\phi /2)\sin (\theta /2),\nonumber \\ q_{1}=&\sin (\psi /2)\cos (\phi /2)\cos (\theta /2)\nonumber \\&-\,\cos (\psi /2)\sin (\phi /2)\sin (\theta /2),\nonumber \\ q_{2}=&\cos (\psi /2)\sin (\phi /2)\cos (\theta /2)\nonumber \\&+\,\sin (\psi /2)\cos (\phi /2)\sin (\theta /2),\nonumber \\ q_{3}=&\cos (\psi /2)\cos (\phi /2)\sin (\theta /2)\nonumber \\&-\,\sin (\psi /2)\sin (\phi /2)\cos (\theta /2), \end{aligned}$$
(5)

and

$$\begin{aligned} \phi&=\arctan \left( \frac{2(q_{0}q_{1}+q_{2}q_{3})}{1-2(q_{1}^2+q_{2}^2)}\right) ,\nonumber \\ \theta&=\arcsin \left( 2(q_{0}q_{2}-q_{1}q_{3})\right) ,\nonumber \\ \psi&=\arctan \left( \frac{2(q_{0}q_{3}+q_{1}q_{2})}{1-2(q_{2}^2+q_{3}^2)}\right) . \end{aligned}$$
(6)

As that in [32], based on quaternion, the dynamical equation for quadrotor aircraft’s attitude is described as follows:

$$\begin{aligned} J\dot{\varOmega }&=-\varOmega ^{\times }J\varOmega +\tau , \nonumber \\ \dot{q}&=\frac{1}{2}E(q)\varOmega , \end{aligned}$$
(7)

where \(J\in R^{3\,\times \,3}\) denotes a symmetric positive-definite constant inertia matrix, \(\varOmega \in R^{3}\) denotes the angular velocity of the aircraft in three directions express in the body coordinate frame, \(\tau \in R^3\) denotes the torque generated by the motor rotation. The matrix E(q) is defined as follows:

$$\begin{aligned} \begin{array} {l}E(q)=\left( \begin{array}{cc}-q_{v}^\mathrm{T}\\ q_{v}^{\times }+q_{0}I_{3}\end{array}\right) \end{array}, \end{aligned}$$
(8)

where \(I_3\) denotes the \(3\times 3\) identity matrix. For any vector \(v=[v_1,v_2,v_3]^\mathrm{T}\in R^3\), the symbol \((\cdot )^\times \) represents a \(3\times 3\) skew-symmetric matrix, which is defined as follows:

$$\begin{aligned} \begin{array} {l}v^\times =\left( \begin{array}{ccc} 0 &{} -v_3 &{} v_2 \\ v_3 &{} 0 &{} -v_1 \\ -v_2 &{} v_1 &{} 0 \\ \end{array}\right) \end{array}. \end{aligned}$$
(9)

2.2.3 Motor’s speed equation

From the previous Sects. 2.2.1 and 2.2.2, the control inputs for quadrotor aircraft are the total thrust \(T\in R\) and the torques \(\tau =(\tau _{1},\tau _{2},\tau _{3})\in R^{3}\). However, for the quadrotor aircraft, the direct control inputs are four motors’ speed \((\omega _{1},\omega _{2},\omega _{3},\omega _{4})^\mathrm{T}\). The transform relationship between motor speed and motor torque is given in the following form as that in [29]:

$$\begin{aligned} \left( \begin{array}{c} T\\ \tau _{1} \\ \tau _{2} \\ \tau _{3} \end{array}\right) = \left( \begin{array}{cccc} b &{} b &{} b &{} b \\ 0 &{} db &{} 0 &{} -db \\ db &{} 0 &{} -db &{} 0 \\ \kappa &{} -\kappa &{} \kappa &{} -\kappa \end{array}\right) \left( \begin{array}{c} \omega _{1}^2 \\ \omega _{2}^2 \\ \omega _{3}^2 \\ \omega _{4}^2 \end{array}\right) , \end{aligned}$$
(10)

where d is the distance from the rotors to the center of the mass of the quadrotor aircraft, \(\kappa \) and b are motor torque-speed coefficient and motor lift-speed coefficient, respectively, which both are positive real parameters.

2.3 Some assumptions

As that in [11, 12, 33, 34], some assumptions are given in this section.

Assumption 1

The pitch , roll, and yaw angles satisfy that \(|\phi |<\pi /2,|\theta |<\pi /2\),\(|\psi |<\pi /2\).

Assumption 2

The exact dynamic models of quadrotor are known.

2.4 Some useful definitions and lemmas

Definition 1

Denote function

$$\begin{aligned} \mathrm{sig}^{\alpha }(x)=\mathrm{sign}(x)|x|^{\alpha }, \end{aligned}$$
(11)

where \(\alpha \ge 0, x\in R, \mathrm{sign}(\cdot )\) is a standard sign function. If \(x=[x_1, x_2,\ldots , x_n]^\mathrm{T} \in R^n\) is a vector, then \(\mathrm{sig}^{\alpha }(x)=[\mathrm{sig}^{\alpha }(x_1), \mathrm{sig}^{\alpha }(x_2),\ldots , \mathrm{sig}^{\alpha }(x_n)]^\mathrm{T}\). Clearly, if \(\alpha \) is a ratio of two positive odd integers, then \(\mathrm{sig}^{\alpha }(x)=x^\alpha \).

Definition 2

Define a class of saturation functions

$$\begin{aligned} \mathrm{sat}_\alpha (x)=\left\{ {\begin{array}{*{20}c} { \mathrm{sign}(x),~~~~~\mathrm{for}~|x|>1}, \\ { \mathrm{sig}^{\alpha }(x), ~~~~~\mathrm{for}~|x|\le 1}. \\ \end{array}} \right. \end{aligned}$$
(12)

where \(0\le \alpha \le 1, x \in R\). If \(x=[x_1, x_2,\ldots , x_n]^\mathrm{T} \in R^n\) is a vector, then

$$\begin{aligned} \mathrm{sat}_{\alpha }(x)=[\mathrm{sat}_{\alpha }(x_1), \mathrm{sat}_{\alpha }(x_2),\ldots , \mathrm{sat}_{\alpha }(x_n)]^\mathrm{T}. \end{aligned}$$

Lemma 1

[16] The second-order system

$$\begin{aligned} \ddot{x}=u, \end{aligned}$$
(13)

can be globally stabilized in a finite time under the feedback control law

$$\begin{aligned} u=-k_1\mathrm{sig}^{\alpha _1}(x)-k_2\mathrm{sig}^{\alpha _2}(\dot{x}), \end{aligned}$$
(14)

with \(k_1, k_2>0, \alpha _1\in (0,1), \alpha _2=2\alpha _1/(1+\alpha _1)\).

Lemma 2

[20] Consider the following nonlinear system \(\dot{x}=f(x),\quad f(0)=0,\quad x\in R^n, \) where \(f(\cdot ):{R}^n\rightarrow {R}^n\) is a continuous function. Suppose that there exists a positive-definite continuous function V(x) such that \(\dot{V}(x)+c(V(x))^\alpha \le 0, \) where \(c>0\) and \(\alpha \in (0,1)\). Then V(x) approaches 0 in a finite time. In addition, the finite convergence time T satisfies that \(T\le \frac{V(x(0))^{1-\alpha }}{c(1-\alpha )}\).

Lemma 3

[35] If \(0<p\le 1\) and is a ratio of two odd integers, then \(|x^p-y^p| \le 2^{1-p}|x-y|^p.\)

Lemma 4

[35] Let \(c,d>0\). For any \(\gamma >0\), the following inequality holds for \(\forall x, y\in {R}: |x|^{c}|y|^{d}\le {c}/{(c+d)}\gamma |x|^{c+d}+{d}/{(c+d)}\gamma ^{-c/d}|y|^{c+d}.\)

Lemma 5

[36] For \(\forall x_i\in R,i=1,\ldots ,n,\) and a real number \(p\in (0,1]\), \((|x_1|+\cdots +|x_n|)^{p} \le |x_1|^{p}+\cdots +|x_n|^{p}.\)

3 Controller design for quadrotor aircraft

In this section, the main objective is to design a finite-time controller for the hovering control of the quadrotor aircraft, which can control the movement of quadrotor aircraft to any desired position in a finite time. From the mathematical viewpoint that is, for a given desired position \((x_{d},y_{d},z_{d})\), the control objective is to design a control law for motor speed \((\omega _{1},\omega _{2},\omega _{3},\omega _{4})\), such that the quadrotor aircraft’s position (x, y, z) can reach the desired position \((x_{d},y_{d},z_{d})\) in a finite time. Specifically, the design of controller is divided into three steps.

Step 1 :

For the position subsystem (3), based on finite-time control theory, a saturated finite-time position controller is designed to ensure the quadrotor aircraft can reach any fixed-point in a finite time.

Step 2 :

For the attitude subsystem (7), based on the finite-time control theory, an attitude controller is designed for the attitude torque \(\tau \), which can guarantee that the desired attitude can be tracked in a finite time.

Step 3 :

By using the motor’s speed equation (10), the controller for motor’s speed \((\omega _{1},\omega _{2},\omega _{3},\omega _{4})^{T}\) is obtained.

Figure 2 shows the control block diagram for quadrotor aircraft.

Fig. 2
figure 2

The control block diagram for quadrotor aircraft

Full size image

Remark 1

Note that in [8, 37], based on the terminal sliding mode control method, some finite-time control algorithms for quadrotor aircraft were also proposed. Actually, in the literature, there are usually three kinds of design methods for finite-time controller [38], i.e., the homogeneous theory-based method, adding a power integrator-based method, terminal sliding mode-based method. Here, in this paper, in order to design finite-time controllers for quadrotor, the design procedure is mainly divided into two steps, i.e., the first step is about the position-loop control, and the second step is about the attitude-loop control. For the position-loop control system, its dynamics is relatively simple (second-order system), so we employ the homogenous theory-based method to design a simple second-order finite-time controller. For the attitude-loop control system, its dynamics is relatively complex, so we employ the adding a power integrator-based method to design a finite-time attitude controller. Here, we do not employ the method of terminal sliding mode control, the main reason is that there are usually singularity and discontinuous control in the terminal sliding mode controller. Although the nonsingular terminal sliding mode control can be used to avoid singularity, it will lead to certain complexity.

3.1 Design of a saturated finite-time position controller

For the position subsystem (3) of the quadrotor aircraft, define the following virtual variables

$$\begin{aligned} \ddot{x}&=-\frac{T}{m}(\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi ):=\mu _{x},\nonumber \\ \ddot{y}&=-\frac{T}{m}(\cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi ):=\mu _{y},\nonumber \\ \ddot{z}&=-\frac{T}{m}\cos \phi \cos \theta +g:=\mu _{z}, \end{aligned}$$
(15)

where \(\mu _{x}, \mu _{y}, \mu _{z}\) are the virtual control inputs in three channels.

Assume that the desired position for the quadrotor aircraft \((x_{d},y_{d},z_{d})^\mathrm{T}\) is a constant.

Theorem 1

For the position motion model (15) for quadrotor aircraft, if the position controller is designed as follows:

$$\begin{aligned} \mu _x&=K_{px}\mathrm{sat}_{\alpha _1}(x_d-x)+K_{dx}\mathrm{sat}_{\alpha _2}(-\dot{x}),\nonumber \\ \mu _y&=K_{py}\mathrm{sat}_{\alpha _1}(y_d-y)+K_{dy}\mathrm{sat}_{\alpha _2}(-\dot{y}),\nonumber \\ \mu _z&=K_{pz}\mathrm{sat}_{\alpha _1}(z_d-z)+K_{dz}\mathrm{sat}_{\alpha _2}(-\dot{z}), \end{aligned}$$
(16)

then the quadrotor aircraft can reach desired position in a finite time, i.e., \((x,y,z)\rightarrow (x_d,y_d,z_d)\) in a finite time, where \(0<\alpha _1<1, \alpha _2=2\alpha _1/(1+\alpha _1)\), \(K_{px}>0,K_{py}>0,K_{pz}>0,K_{dx}>0,K_{dy}>0,K_{dz}>0\).

Proof

Without loss of generality, we only provide the proof for the position system along x-axis. Let \(e_x=x_d-x\). It follows from (15) and (16) that

$$\begin{aligned} \ddot{e}_x&=-K_{px}\mathrm{sat}_{\alpha _1}(e_x)-K_{dx}\mathrm{sat}_{\alpha _2}(\dot{e}_x). \end{aligned}$$
(17)

The proof is divided into two steps, i.e., globally asymptotically stable and locally finite-time stable.

Step 1 Proof of global asymptotical stability

A candidate Lyapunov function for system (17) is chosen as follows:

$$\begin{aligned} V=K_{px}\int _0^{e_x}\mathrm{sat}_{\alpha _1}(\rho )\mathrm{d}\rho +\frac{1}{2}\dot{e}_x^2. \end{aligned}$$
(18)

Since \(\frac{\mathrm{d}\int _0^{e_x}\mathrm{sat}_{\alpha _1}(\rho )\mathrm{d}\rho }{\mathrm{d}t}=\mathrm{sat}_{\alpha _1}(e_x)\dot{e}_x\), then

$$\begin{aligned} \dot{V}|_{(17)}&=K_{px}\mathrm{sat}_{\alpha _1}(e_x)\dot{e}_x+\dot{e}_x \ddot{e}_x \end{aligned}$$
(19)

Substitute (17) into (19) leads to

$$\begin{aligned} \dot{V}|_{(17)} =&-K_{dx}\mathrm{sat}_{\alpha _2}(\dot{e}_x)\dot{e}_x, \end{aligned}$$
(20)

Due to

$$\begin{aligned} \dot{e}_x \mathrm{sat}_{\alpha _2}(\dot{e}_x)=\left\{ {\begin{array}{*{20}c} { |\dot{e}_x|,~~\ \ \ \ \ \ \mathrm{for}~~|\dot{e}_x|>1}; \\ {{|\dot{e}_x|}^{1+\alpha _2}, ~~\mathrm{for}~~|\dot{e}_x|\le 1}, \\ \end{array}} \right. \end{aligned}$$
(21)

then one concludes that

$$\begin{aligned} \dot{V}\le 0. \end{aligned}$$
(22)

Define set \(\varPsi =\{(e_x,\dot{e}_x)|\dot{V}\equiv 0\}\). It follows from (20) that \(\dot{V}\equiv 0\) means \(\dot{e}_x\equiv 0\), and \(\ddot{e}_x\equiv 0\). By (17) one obtains that

$$\begin{aligned} -K_{px}\mathrm{sat}_{\alpha _1}(e_x)\equiv 0. \end{aligned}$$
(23)

Note that, \(K_{px}>0\), then \( e_x\equiv 0\). Based on LaSalle’s invariant principle [9], it can be concluded that \((e_x,\dot{e}_x)\rightarrow 0\) as \(t\rightarrow \infty \). That is to say that the system (15) is globally asymptotically stable under the controller (16).

Step 2 Proof of local finite-time stability

Since system (15) is globally asymptotically stable, then the system state \((e_x,\dot{e}_x)\) will converge to the region \(|e_x|\le 1,|\dot{e}_x|\le 1\) in a finite time and stay there for ever. After then, the system (17) can be rewritten as:

$$\begin{aligned} \ddot{e}_x&=-K_{px}\mathrm{sig}^{\alpha _1}(e_x)-K_{dx}\mathrm{sig}^{\alpha _2}(\dot{e}_x). \end{aligned}$$
(24)

Basing on Lemma 1, it can be concluded that system (24) is finite-time stable, i.e., system (17) is locally finite-time stable.

Therefore, it can be concluded from [39, 40] that the system (15) under the controller (16) is globally finite-time stable since it is globally asymptotically stable and locally finite-time stable. The proof is completed. \(\square \)

Remark 2

Note that in the proposed virtual control input (16), the saturation constraint is taken into account. The main aim is to guarantee that \(g-\mu _z\) is always positive (by choosing \( K_{pz}+K_{dz}<g\)) such that there is no indetermination/discontinuity when we calculate \(\theta _d\) from (26) in the next section.

3.2 Design of a finite-time attitude controller

As that in [12], the desired attitude is generated by the position dynamical equation (3), i.e.,

$$\begin{aligned} \mu _{x}&=-\frac{T_d}{m}(\cos {\phi _d}\sin {\theta _d}\cos {\psi _d}+\sin {\phi _d}\sin {\psi _d}),\nonumber \\ \mu _{y}&=-\frac{T_d}{m}(\cos {\phi _d}\sin {\theta _d}\sin {\psi _d}-\sin {\phi _d}\cos {\psi _d}),\nonumber \\ \mu _{z}&=-\frac{T_d}{m}\cos {\phi _d}\cos {\theta _d}+g, \end{aligned}$$
(25)

which results in

$$\begin{aligned} T_d&=m\sqrt{\mu _{x}^2+\mu _{y}^2+(g-\mu _{z})^2},\nonumber \\ \phi _d&=\arcsin \Big (-m\frac{\mu _{x}\sin {\psi _d}-\mu _{y}\cos {\psi _d}}{T_d}\Big ),\nonumber \\ \theta _d&=\arctan \Big (-\frac{\mu _{x}\cos {\psi _d}+\mu _{y}\sin {\psi _d}}{g-\mu _{z}}\Big ). \end{aligned}$$
(26)

From (26), it can be found that the variable \(\psi _d\) is a free variable. For the convenience of analysis during the hovering control, the desired yaw angle is chosen as \(\psi _d=0\).

Based on the transformation equation (5), the desired attitude quaternion for the quadrotor aircraft can be obtained, which is denoted by

$$\begin{aligned} q_{d}=[q_{d0},q_{d1},q_{d2},q_{d3}]^\mathrm{T}=[q_{d0},q_{dv}^\mathrm{T}]^\mathrm{T}\in R^{4}. \end{aligned}$$
(27)

The desired attitude quaternion and desired angular velocity \(\varOmega _d\in R^3\) satisfies the following relation.

$$\begin{aligned} \dot{q}_{d}=\frac{1}{2}E(q_{d})\varOmega _{d}. \end{aligned}$$
(28)

In order to achieve the attitude tracking, as that in [30], the error between the desired attitude \(q_{d}\) and the attitude q is defined \(e=[e_{0},e_{v}^\mathrm{T}]^\mathrm{T}\in R^{4}\), which is called the quaternion error:

$$\begin{aligned} e_{0}&=q_{d0}q_{0}+q_{dv}^\mathrm{T}q_{v},\nonumber \\ e_{v}&=q_{d0}q_{v}-q_{dv}^{\times }q_{v}-q_{0}q_{dv}. \end{aligned}$$
(29)

Based on quaternion error, the dynamical equation for quadrotor aircraft’s attitude is given as follows:

$$\begin{aligned}&J\dot{\varOmega }_{e}\,=\,-\varOmega ^{\times }J\varOmega +J(\varOmega _{e}^{\times }C\varOmega _{d}-C\dot{\varOmega }_{d})+\tau ,\nonumber \\&\dot{e}=\frac{1}{2}E(e)\varOmega _{e}, \end{aligned}$$
(30)

where \(\varOmega _{e}=\varOmega -C\varOmega _{d}\) denotes angular velocity error, \(C=(1-2e_{v}^\mathrm{T}e_{v})I_{3}+2e_{v}e_{v}^\mathrm{T}-2e_{0}e_{v}^{\times }\). The matrix E(e) satisfies:

$$\begin{aligned} \begin{array}{l}E(e)=\left( \begin{array}{cc}-e_{v}^\mathrm{T}\\ e_{v}^{\times }+e_{0}I_{3}\end{array}\right) . \end{array} \end{aligned}$$
(31)

Based on the informations of relative quaternion error e and angular velocity error \(\varOmega _e\), next we will design a finite-time attitude controller to achieve finite-time attitude tracking.

Theorem 2

For the error system (30), if the control torque \(\tau \) is designed as:

$$\begin{aligned} \tau =&-\,\beta _{2}J(\varOmega _{e}^{1/r_2}+\beta _{1}^{1/r_2}e_{v})^{r_3}\nonumber \\&+\,\varOmega ^{\times }J\varOmega -J(\varOmega _{e}^{\times }C\varOmega _{d}-C\dot{\varOmega }_{d}), \end{aligned}$$
(32)

then the attitude error will converge to zero in a finite time, i.e., \((q_0,q_1,q_2,q_3)\rightarrow (q_{d0},q_{d1},q_{d2},q_{d3})\) in a finite time, where \(\beta _{1}, \beta _{2}\) are proper position gains, and \(r_{2}=1+r, r_{3}=1+2r\), \(r\in (-\frac{1}{2}, 0)\) is the ratio for a positive even integer and a positive odd integer.

Proof

For the convenience of writing, denote

$$\begin{aligned} f&=\varOmega _{e},\nonumber \\ {\bar{\tau }}&=J^{-1}\Big [\tau -\varOmega ^{\times }J\varOmega +J(\varOmega _{e}^{\times }C\varOmega _{d}-C\dot{\varOmega }_{d})\Big ]. \end{aligned}$$
(33)

Step 1 Construct a candidate Lyapunov function as:

$$\begin{aligned} V_1=(e_{0}-1)^2+e_{v}^\mathrm{T}e_{v}=2-2e_{0}, \end{aligned}$$
(34)

whose derivative along system (30) is

$$\begin{aligned} \dot{V}_1|_{(30)}=e_{v}^\mathrm{T}f_{}=e_{v}^\mathrm{T}f_{}^*+e_{v}^\mathrm{T}(f{}-f^*). \end{aligned}$$
(35)

By backstepping design, design a virtual control \(f^*\in R^3\) as:

$$\begin{aligned} f^*=-\beta _1 e_{v}^{r_2}, \end{aligned}$$
(36)

where \(r_{2}=1+r\), \(r\in (-\frac{1}{2}, 0)\) is the ratio for a positive even integer and a positive odd integer, and a constant gain \(\beta _1>0\). Under this virtual control law, it follows from (35) that

$$\begin{aligned} \dot{V}_1|_{(30)} \le&-\beta _1(e_{1}^{1+r_2}+e_{2}^{1+r_2}+e_{3}^{1+r_2})+e_{v}^\mathrm{T}(f_{}-f^*). \end{aligned}$$
(37)

Step 2 Take the error between the real state \(f_{}^*\) and the virtual \(f_{}\) as a new state. Define

$$\begin{aligned} \xi =f^{1/{r_2}}-f^{*1/{r_2}}\in R^3.\end{aligned}$$
(38)

Choose the Lyapunov function

$$\begin{aligned} V_2=V_{1}+\sum _{j=1}^3 \int _{ f_{j}^*}^{ f_{j}}(s^{1/r_2}-{f_{j}}^{*1/r_2})^{{2-r_2}}\mathrm{d}s. \end{aligned}$$
(39)

With (37) in mind, the derivative of \(V_2\) along system (30) is

$$\begin{aligned} \dot{V}_2|_{(30)} \le&-\beta _1(e_{1}^{1+r_2}+e_{2}^{1+r_2}+e_{3}^{1+r_2})+e_{v}^\mathrm{T}(f_{}-f^*). \nonumber \\&+\sum _{j=1}^3\xi _{j}^{{2-r_{2}}}{\bar{\tau }}_{j}\nonumber \\&+\sum _{j=1}^3\frac{\mathrm{d}[-{ f_{j}}^{*1/r_2}]}{\mathrm{d}t}\int _{ f_{j}^*}^{{f_{j}}}(s^{1/r_2}-{f_{j}} ^{*1/r_2})^{{1-r_2}}\mathrm{d}s. \end{aligned}$$
(40)

First, it follows from Lemma 3 and 4 that

$$\begin{aligned} e_{v}^\mathrm{T}(f_{}-f^*)&=\sum _{j=1}^3e_{j}(f_{j}-f_{j}^*)\nonumber \\&\le \sum _{j=1}^3 |e_{j}|\cdot \left| (f_{j}^{1/{r_2}})^{r_2}-(f_{j}^{*1/{r_2}})^{r_2}\right| \nonumber \\&\le 2^{1-r_2}\sum _{j=1}^3 |e_{j}|\cdot |\xi _{j}|^{r_2}\nonumber \\&\le \sum _{j=1}^3\Big ( \frac{1}{2}|e_{j}|^{1+r_2}+c_1 |\xi _{j}|^{1+r_2}\Big ). \end{aligned}$$
(41)

for a positive constant \(c_1\).

Second, it follows (36) and (30) that

$$\begin{aligned} \Big |\frac{\mathrm{d}[-{f_{j}}^{*1/r_2}]}{\mathrm{d}t}\Big |&= \beta _{1}^{1/r_2}|{\dot{e}_{j}}{}|\nonumber \\&\le \frac{\beta _{1}^{1/r_2}}{2} \sum _{j=1}^3 |f_{j}|\nonumber \\&= \frac{\beta _{1}^{1/r_2}}{2}\sum _{j=1}^3 \Big |\xi _{j}+{f_{j}}^{*1/{r_2}}\Big |^{r_2}. \end{aligned}$$
(42)

By Lemma 3, we further obtain

$$\begin{aligned} \Big |\frac{\mathrm{d}[-{f_{j}}^{*1/r_2}]}{\mathrm{d}t}\Big |&\le \frac{\beta _{1}^{1/r_2}}{2}\sum _{j=1}^3 \Big ( |\xi _{j}|^{r_2}+|{ f_{j}}^{*}|\Big ) \nonumber \\&= \frac{\beta _{1}^{1/r_2}}{2}\sum _{j=1}^3\Big ( |\xi _{j}|^{r_2}+\beta _1 |e_{j}|^{r_2}\Big ). \end{aligned}$$
(43)

Meanwhile, by Lemma 3, we obtain

$$\begin{aligned} \Big |\int _{f_{j}^*}^{{f_{j}}}(s^{1/r_2}-{f_{j}} ^{*1/r_2})^{1-r_2}\mathrm{d}s\Big |&\le |\xi _{j}|^{1-r_2}|f_{j}-f_{j}^*| \nonumber \\&\le 2^{1-r_2}|\xi _{j}|. \end{aligned}$$
(44)

As a matter of fact, it follows from (43) and (44), and Lemma 4 that

$$\begin{aligned}&\sum _{j=1}^3\frac{d[-{f_{j}}^{*1/r_2}]}{dt}\int _{f_{j}^*}^{{f_{j}}}(s^{1/r_2}-{f_{j}} ^{*1/r_2})^{{1-r_2}}\mathrm{d}s \nonumber \\&\quad \le \sum _{j=1}^3 \Big ( \frac{1}{2}|{e_{j}}|^{1+r_2}+ c_2 |\xi _{j}|^{1+r_2}\Big ). \end{aligned}$$
(45)

for a positive constant \(c_2\).

Finally, it follows from (40), (41), and (45) that

$$\begin{aligned} \dot{V}_2|_{(30)} \le&-(\beta _1-1)\sum _{j=1}^3e_{j}^{1+r_2}+\sum _{j=1}^3(c_1+c_2) |\xi _{j}|^{1+r_2} \nonumber \\&+\sum _{j=1}^3\xi _{j}^{{2-r_{2}}}{\bar{\tau }}_{j}. \end{aligned}$$
(46)

Thus, under the proposed controller (32), we obtain

$$\begin{aligned} {\bar{\tau }}_{j}^*&=-\beta _2 \xi _{j}^{r_3} ~~\mathrm{with~ a~ constant~}\beta _{2}\ge 1+c_1+c_2, \end{aligned}$$
(47)

where \(r_{3}=1+2r\). Under this controller, it can be concluded from (46) that

$$\begin{aligned} \dot{V}_2|_{(30)} \le&-\sum _{j=1}^3e_{j}^{1+r_2}-\sum _{j=1}^3\xi _{j}^{1+r_2}. \end{aligned}$$
(48)

Hence, the states \((e_{v},\xi )\rightarrow 0\) asymptotically as \(t\rightarrow \infty \). Note that \(e_{v}\rightarrow 0\) means that \(e_{0}\rightarrow \pm 1\) and the equilibrium \((-1,0,0,0)^\mathrm{T}\) is unstable whose proof/explanation can be found in [41, 42]. So there is a finite-time instant \(t^*\) such that \(e_{0}(t)\ge 0\) for all \(t\ge t^*.\) By the definition of \(V_1\), we conclude that

$$\begin{aligned} V_1&=(1-e_{0})^2+e_{v}^\mathrm{T}e_{v}\nonumber \\&\le (1-e_{0})(1+e_{0})+e_{v}^\mathrm{T}e_{v}\nonumber \\&=2e_{v}^\mathrm{T}e_{v}=2\sum _{j=1}^3e_{j}^{2}. \end{aligned}$$
(49)

In addition, it follows from Lemma 3 that

$$\begin{aligned} \sum _{j=1}^3\int _{f_{j}^*}^{f_{j}}(s^{1/r_{2}}-{f_{j}}^{*1/r_2})^{{2-r_2}}\mathrm{d}s&\le \sum _{j=1}^3|\xi _{j}|^{2-r_{2}}|f_{j}-f_{j}^*|\nonumber \\&\le \sum _{j=1}^3 2^{1-r_{2}}\xi _{j}^2. \end{aligned}$$
(50)

which means that

$$\begin{aligned} V_{2}&\le \rho \Big (\sum _{j=1}^3e_{j}^{2}+\sum _{j=1}^3 \xi _{j}^2\Big ). \end{aligned}$$
(51)

where \(\rho =\max \{2,2^{1-r_2}\}\). Noticing that \(1+r_2=2+\tau \), and using Lemma 5, it follows from (48) and (51) that

$$\begin{aligned} \dot{V}_{2}+\rho ^{-\frac{2+\tau }{2}}V_{2}^{\frac{2+\tau }{2}} \le 0. \end{aligned}$$
(52)

By Lemma 2, it can be concluded from (52) that \(V_{2}\) will converge to zero in a finite time. The proof is completed.

As for the controller of the motor’s speed, it can be easily obtained based on the Eq. (10) with \(T=T_d\). Note that in certain cases, some elements \(\omega _i, i=1,2,3,4\) of resulting from (10) might be negative. As pointed out that in [29], this case will lead to a reversal of the rotors direction.

Remark 3

For the proposed finite-time position controller (16) and the finite-time attitude controller (32), if the fractional powers are chosen as \(\alpha _1=\alpha _2=1, r_2=r_3=1\), the controllers are reduced to the classical PD controllers. Compared with the PD controller, the finite-time controller in this paper will show faster convergence rate and stronger disturbance rejection performance, which is demonstrated in the simulation part.

4 Numerical examples and simulations

Consider the hovering control problem for the quadrotor aircraft described by system (3) and (7). The reference position is given as follow:

$$\begin{aligned} {(x_d,y_d,z_d)}=\left\{ {\begin{array}{ll} {(2,2,-3)},&{}\quad 0\le t\le 20~\mathrm{s},\\ {(3,1,1)}, &{}\quad 20~\mathrm{s}<t.\\ \end{array}} \right. \end{aligned}$$
(53)

For the model of quadrotor aircraft, the system parameters and the initial values are, respectively, set as that in [29]: \(m=0.468\) kg; \(g=9.81\,\mathrm{m/s^2}\); \((x,y,z)^\mathrm{T}=[0,0,0]^\mathrm{T}\); \((q_0,q_1,q_2,q_3)^\mathrm{T}=[0.8832,0.3,-0.2,-0.3]^\mathrm{T}\); \(b=2.9 \times 10^{-5}\,\mathrm{N/(rad^2\, s^{-2})};\kappa =1.1\times 10^{-6}\,\mathrm{N\,m/(rad^2\,s^{-2})};\) \(d=0.225\,\mathrm{m}\).

The inertia matrix of aircraft is given as:

$$\begin{aligned} \begin{array}{l}J=\left[ \begin{array}{ccc}0.0049&{}0&{}0\\ 0&{}0.0049&{}0\\ 0&{}0&{}0.0088\end{array}\right] \end{array}\mathrm{kg\,m^2}. \end{aligned}$$

For the finite-time controller (FC) proposed in this paper, the finite-time position controller (16) is set as: \(\alpha _1=3/4,{\alpha _2=6/7},K_{px}=4.2,K_{py}=K_{pz}=4.5,K_{dx}=K_{dy}=K_{dz}=3.8\), and the finite-time attitude controller (32) is set as:\(\beta _1=6, \beta _2=5, r=-2/7\).

To have a comparison, two kinds of control algorithms are employed, i.e., one is the proposed finite-time control algorithm, the other one is the PD control algorithm, which is described in Remark R3.

Table 1 The comparison of the convergence performance
Full size table
Fig. 3
figure 3

Response curves of the quadrotor aircraft’s position under two kinds of controllers in the presence of disturbance

Full size image
Fig. 4
figure 4

Response curves of the quadrotor aircraft’s attitude under two kinds of controllers in the presence of disturbance

Full size image
Fig. 5
figure 5

Response curves of the quadrotor aircraft’s control torque under two kinds of controllers in the presence of disturbance

Full size image

4.1 The case in the absence of disturbance

The convergence time for the quadrotor aircraft under the finite-time controller and PD controller in the absence of disturbance are shown in Table 1. It is clear that the finite-time controller (16) can provide a faster convergence performance.

4.2 The case in the presence of disturbance

When there is an external disturbance, such as wind disturbance, the disturbance signal is directly act on the aircraft’s attitude control torque channel, i.e., \(J\dot{\varOmega }=-\varOmega ^{\times }J\varOmega +\tau +d(t)\). Assume that there is the following disturbances: \(d(t)=[d_{1}(t),d_{2}(t),d_{3}(t)]^\mathrm{T}\in R^3\), \(d_{1}(t)=0.8\mathrm{sin}(1.5t)\), \(d_{2}(t)=0.5\mathrm{sin}(2t), d_{3}(t)=0.2\mathrm{sin}(2t)\).

The response curves of the quadrotor aircraft in the presence of disturbance are shown in Figs. 3, 4 and 5. The results show that the finite-time controller (32) proposed in this paper offers a better convergence rate and a stronger disturbance rejection performance than the PD control.

5 Conclusion

The hovering control problem for quadrotor aircraft based on finite-time algorithm has been investigated in this paper. By finite-time control theory, the controllers have been designed for position subsystem and attitude subsystem, respectively. Compared to the classical PD control, it has been shown that the finite-time control can improve the closed-loop system’s dynamical performances.