1 Introduction

Dielectric elastomers (DE) are generally regarded to have superior material properties due to their extreme flexibility, excessive deformation, light weight, low cost, as well as chemical and biological compatibilities. The excellent properties make them prosperous materials and excellent candidates in practical designs [1]. Because of its high efficiency in transforming electrical energy to mechanical work, dielectric elastomers have received increasing research interest both in theory and engineering applications [2,3,4,5,6]. When subjected to a voltage, the thickness of a dielectric elastomer membrane reduces while its area expands, possibly straining over 100% [1]. In the past, the quasi-static deformation behavior was extensively studied [2] before the dynamic response [3, 4, 6,7,8,9,10,11,12,13] and the hyperelastic or viscoelastic dielectric characteristics of the elastomers [14,15,16,17,18,19] were investigated.

A thermodynamic model with analysis for deformed dielectric elastomers of different shapes has been developed [1, 20,21,22,23,24,25]. The elastomer material deformation is governed by a nonlinear differential equation involving stretching that evolves with time. Zhu et al. [21] investigated the inflation of dielectric elastomer balloon under pressure and applied voltage as a second-order differential equation following the thermodynamics of dielectric elastomers. For a constant pressure and voltage, the membrane may attain equilibrium while sinusoidal voltage may excite sub-harmonic, harmonic and super-harmonic resonance to the membrane. Besides, the nonlinear oscillation resonant behavior [22] and instabilities [25, 26] of dielectric elastomer membranes have also been studied.

The previous research in this area mostly focused on the dynamic characteristics of dielectric elastomers by numerical methods, while general and specific analytical solutions for various engineering conditions with interest are still not known today. In this paper, the analytical periodic solutions and periods of the nonlinear free vibration system are investigated by using a coupled approach that uses the Newton’s method and the harmonic balance method, namely the Newton–harmonic balance (NHB) method [27].

In this paper, an excellent NHB analytical method that is able to yield very accurate approximate analytical solutions for the nonlinear free vibration of a dielectric elastomer spherical membrane is applied. Different to the classical harmonic balance method, Wu et al. [27] proposed this method by firstly linearizing governing equations by Newton’s method prior to harmonic balancing. Depending on the level of accuracy necessary, this NHB method is able to yield explicit higher-order analytical approximations. Besides, this method is also algebraically much simpler and it avoids solving a set of complex nonlinear algebraic equations. In the previous studies, the NHB method was applied to solve various engineering problems, including analogy to double sine-Gordon equation [28], large post-buckling deformation of elastic rings [29], large amplitude vibration of spring-hinged beam [30], hydrothermal buckling deformation of beams [31], large amplitude vibration of simply supported laminated plates [32], and oscillation of current-carrying wires [33].

Nonlinear free vibration of a hyperelastic dielectric elastomer spherical balloon that is subjected to static pressure and constant voltage is investigated here. It is modeled as an autonomous second-order differential equation with general nonlinearity (\(\lambda \), \(\lambda ^{2}\), and \(\lambda ^{3})\) and negatively powered term (\(\lambda ^{-5})\). Although the NHB method has been successful in some cases above, it is still a great challenge to extend and generalize this method to this dielectric elastomer balloon vibration system. As it will become clearer below, this is because the governing equation does not only have concurrent presence of odd and non-odd nonlinear terms, but also contains highly negative-powered restoring terms. The coexistence of these terms makes the system extremely nonlinear, and hence, higher-order approximation and assurance of numerical accuracy will become a challenge. Based on the nonlinear problem with odd and even nonlinearities, two new nonlinear equations with odd nonlinearity are proposed. The accurate analytical approximations of the original nonlinear problem are mathematically formulated by combining piecewise approximate solutions from such two new nonlinear systems [34]. The details of modeling and approximations are presented below. In the illustrative examples specified by certain material parameters and initial conditions, the approximate analytical solutions are derived and subsequently verified by separately comparing to numerical integration solutions.

2 Problem definition, formulation and methodology

2.1 Problem definition and formulation

The dynamic inflation of dielectric elastomers, based on the neo-Hookean model, with different shapes has been extensively studied. The model of a dielectric elastomer balloon [21] under static pressure and voltage is adopted in this paper.

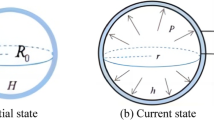
Figure 1 shows a spherical balloon of radius R and thickness H in the reference state. The balloon membrane is made of dielectric elastomer with density \(\rho \) and it is assumed incompressible. Both sides of the membrane are coated with compliant electrode materials. In the presence of an applied voltage, the electrostatic force causes the membrane to compress in thickness while the balloon expands in volume and surface area.

Fig. 1
figure 1

Deformation of a dielectric elastomer balloon under static pressure and voltage [21]: a reference state and b current state

Full size image

In the presence of an applied pressure P and an electric potential difference \(\Phi \) with electrode charges \(+\) Q and −Q as shown in Fig. 1, the balloon deforms from an initial radius R to a final radius r. Isothermal condition is assumed here and hence no temperature change will be considered explicitly. Further let H be the initial reference thickness, the balloon then represents a thermodynamic system of two variables \(\lambda \) and D [1, 21,22,23, 25], in which

$$\begin{aligned} \lambda =\frac{r}{R} \end{aligned}$$
(1)

is the membrane stretching parameter, and

$$\begin{aligned} D=\frac{Q}{4\pi r^{2}} \end{aligned}$$
(2)

is the membrane electric displacement. Hence, this thermodynamic system that is characterized by the Helmholtz free energy density \(W(\lambda ,D)\) is a function of these dependent variables. Because this ideal model of dielectric elastomers has been used almost exclusively to analyze many devices, it is adopted here. The ideal dielectric elastomer material properties are also considered. The free energy function of the dielectric elastomer can be expressed as a sum of two parts

$$\begin{aligned} W\left( {\lambda ,D} \right) =\frac{\mu }{2}\left( {2\lambda ^{2}+\lambda ^{-4}-3} \right) +\frac{D^{2}}{2\varepsilon } \end{aligned}$$
(3)

where the first part represents the elastic energy with shear modulus \(\mu \) and the second part is the dielectric energy with permittivity \(\varepsilon \). For an ideal dielectric elastomer assumed here, the permittivity is a constant independent of deformation.

According to Zhu et al. [21], the nonlinear governing equation of the system is

$$\begin{aligned} \frac{d^{2}\lambda }{dT^{2}}+g\left( {\lambda ,p,\Phi } \right) =0 \end{aligned}$$
(4)

where

$$\begin{aligned} g(\lambda ,p,\Phi )=2\lambda -2\lambda ^{-5}-\frac{pR}{\mu H}\lambda ^{2}-2\frac{\varepsilon \Phi ^{2}}{\mu H^{2}}\lambda ^{3} \end{aligned}$$
(5)

with dimensionless parameters for time \(T=t/{\left( {R\sqrt{\rho /\mu }} \right) }\), pressure \({pR}/{\mu H}\) and electric potential difference \({\left( {\sqrt{\varepsilon /\mu }\Phi } \right) }/H\). Equations (4) and (5) are the governing differential equation for this model with evolving stretch as a function of dimensionless timeT. In this paper, the approximate analytical solution to the nonlinear free vibration of this dielectric elastomer balloon under static pressure and potential difference is studied.

For static dimensionless pressure and electrical potential difference, i.e., \(\frac{pR}{\mu H}\) and \(\frac{\varepsilon \Phi ^{2}}{\mu H^{2}}\) in the governing equations (4) and (5) are constants, which make \(g(\lambda ,p,\Phi )\) only a function of one variable \(\lambda \). With reference to Eq. (4), a general nonlinear vibration system can thus be expressed as follows [35]

$$\begin{aligned} \frac{d^{2}\lambda }{dT^{2}}+g\left( \lambda \right) =0 \end{aligned}$$
(6)

and initial conditions

$$\begin{aligned} \lambda \left( \hbox {0} \right) =A,\quad \frac{d\lambda }{dT}\left( \hbox {0} \right) =0 \end{aligned}$$
(7)

The potential energy is given by \(V(\lambda )=\int {g\left( \lambda \right) d\lambda } \) and the vibration system reaches its minimum energy at \(\lambda =\lambda _0 \). For a specific and known A, the corresponding potential energy function is

$$\begin{aligned} V\left( \lambda \right) =\frac{1}{2\lambda ^{4}}+\lambda ^{2}-\frac{pR}{3\mu H}\lambda ^{3}-\frac{\varepsilon \Phi ^{2}}{2\mu H^{2}}\lambda ^{4} \end{aligned}$$
(8)

2.2 Approximate analytical solution for odd nonlinear system

If the restoring force \(-g\left( \lambda \right) \) in Eq. (6) is only an odd function of \(\lambda \) (i.e., \(-g\left( \lambda \right) =g\left( {-\lambda } \right) )\), the system oscillates between symmetric bounds \(\left[ {-A,A} \right] \). The period and periodic solution depend on the initial amplitude A. The solution procedure in brief is described here. Following the NHB method [27], the first-order and second-order periodic solutions \(\lambda _1 \left( T \right) \) and \(\lambda _2 \left( T \right) \) can be derived as

$$\begin{aligned} \lambda _1 \left( T \right) =A\cos \tau ,\;\;\tau =\sqrt{\Omega _1 }T \end{aligned}$$
(9)

and

$$\begin{aligned}&\lambda _2 \left( T \right) =\left( {A+c_1 \left( A \right) } \right) \cos \tau -c_1 \left( A \right) \cos 3\tau ,\nonumber \\&\tau =\sqrt{\Omega _2 }T \end{aligned}$$
(10)

where

$$\begin{aligned}&\Omega _1 =\frac{a_1 }{A} \end{aligned}$$
(11)
$$\begin{aligned}&\Omega _2 =\Omega _1 +\Delta \Omega _1 \end{aligned}$$
(12)
$$\begin{aligned}&c_1 \left( A \right) =\frac{2a_3 A}{\left( {b_2 +b_4 -b_0 -b_6 } \right) A+18a_1 } \end{aligned}$$
(13)

and

$$\begin{aligned} \Delta \Omega _1 =-\frac{a_3 \left[ {\left( {b_0 -b_4 } \right) A-2a_1 } \right] }{A\left[ {\left( {b_2 +b_4 -b_0 -b_6 } \right) A+18a_1 } \right] } \end{aligned}$$
(14)

The Fourier coefficients \(a_{2i-1} \) and \(b_{2\left( {i-1} \right) } \quad ( i=1,2,3,\ldots )\) above can be derived from

$$\begin{aligned}&a_{2i-1} =\frac{4}{\pi }\int _0^{\pi /2} {g\left( {A\cos \tau } \right) \cos \left[ {\left( {2i-1} \right) \tau } \right] d\tau } ,\nonumber \\&\qquad i=1,2,3,\ldots \end{aligned}$$
(15)
$$\begin{aligned}&b_{2\left( {i-1} \right) } =\frac{4}{\pi }\int _0^{\pi /2} {g_\lambda \left( {A\cos \tau } \right) \cos \left[ {2\left( {i-1} \right) \tau } \right] d\tau } ,\nonumber \\&\qquad i=1,2,3,\ldots \end{aligned}$$
(16)

In Eq. (16), the subscript \(\lambda \) denotes the derivative of \(g\left( \lambda \right) \) with respect to \(\lambda \).

2.3 Approximate analytical solution for general nonlinear system

For a system governed by Eq. (6) that has a restoring force \(-g(\lambda )\) with non-classical non-odd nonlinearities (i.e., \(-g\left( \lambda \right) \ne g\left( {-\lambda } \right) )\), the system oscillates between asymmetric limits \(\left[ {B,A} \right] \) where both \(B\left( {B<0} \right) \) and A have the same energy level, i.e.,

$$\begin{aligned} V\left( A \right) =V\left( B \right) \end{aligned}$$
(17)

where \(V(\lambda )=\int {g\left( \lambda \right) d\lambda } \) is the potential energy of the system, and \(B<0\) can be expressed as a function of A.

To solve a nonlinear system that includes odd and even nonlinearities, the system is separated into two new systems with odd nonlinearity only, as presented in Eqs. (18) and (19) below. Both Eqs. (18) and (19) can be solved independently by the NHB method described in Sect. 2.2. By combinatory piecing of the two approximate analytical solutions corresponding to, respectively, the two new systems introduced, we can construct approximate analytical solutions to the original system, as illustrated below.

These two new odd nonlinear systems introduced are [32,33,34,35]

$$\begin{aligned} \frac{d^{2}\lambda }{dT^{2}}+f\left( \lambda \right) =0,\quad \lambda \left( 0 \right) =A,\quad \frac{d\lambda }{dT}\left( 0 \right) =0 \end{aligned}$$
(18)

and

$$\begin{aligned} \frac{d^{2}\lambda }{dT^{2}}+h\left( \lambda \right) =0,\lambda \left( 0 \right) =-B\left( {B<0} \right) , \frac{d\lambda }{dT}\left( 0 \right) =0 \end{aligned}$$
(19)

where

$$\begin{aligned} f\left( \lambda \right) =\left\{ {{\begin{array}{l} {g\left( \lambda \right) ,\quad \lambda \ge 0} \\ {-g\left( {-\lambda } \right) ,\quad \lambda <0} \\ \end{array} }} \right. \end{aligned}$$
(20)

and

$$\begin{aligned} h\left( \lambda \right) =\left\{ {{\begin{array}{l} {-g\left( {-\lambda } \right) ,\quad \lambda >0} \\ {g\left( \lambda \right) ,\quad \lambda \le 0} \\ \end{array} }} \right. \end{aligned}$$
(21)

In Eqs. (18) and (19), the restoring functions \(-f\left( \lambda \right) \)and \(-h\left( \lambda \right) \) are both odd functions of \(\lambda \).

The first-order analytical period \(T_1 \left( A \right) \) and the corresponding periodic solution \(\lambda _1 \left( T \right) \) to Eq. (6) are

$$\begin{aligned} T_1 \left( A \right) =\frac{T_{1f} \left( A \right) }{2}+\frac{T_{1h} \left( B \right) }{2} \end{aligned}$$
(22)

and

$$\begin{aligned} \lambda _1 \left( T \right) =\left\{ {{\begin{array}{l} {\lambda _{1f} \left( T \right) ,\quad 0\le T \le \frac{T_{1f} \left( A \right) }{4}} \\ {\lambda _{1h} \left( {T-\frac{T_{1f} \left( A \right) }{4} +\frac{T_{1h} \left( B \right) }{4}} \right) ,\quad \frac{T_{1f} \left( A \right) }{4}\le T\le \frac{T_{1f} \left( A \right) }{4}+\frac{T_{1h} \left( B \right) }{2}\;} \\ {\lambda _{1f} \left( {T+\frac{T_{1f} \left( A \right) }{2} -\frac{T_{1h} \left( B \right) }{2}} \right) ,\quad \frac{T_{1f} \left( A \right) }{4}+\frac{T_{1h} \left( B \right) }{2}\;\le T\le \frac{T_{1f} \left( A \right) }{2}+\frac{T_{1h} \left( B \right) }{2}\;} \\ \end{array} }} \right. \end{aligned}$$
(23)

where subscripts “1f” and “1h” of T and \(\lambda \) denote the period and periodic response of the first-order approximation solution for the systems (18) and (19), respectively.

The second-order analytical period \(T_2 \left( A \right) \) and the corresponding solution \(\lambda _2 \left( T \right) \) to Eq. (6) are

$$\begin{aligned} T_2 \left( A \right) =\frac{T_{2f} \left( A \right) }{2}+\frac{T_{2h} \left( B \right) }{2} \end{aligned}$$
(24)

and

$$\begin{aligned} \lambda _2 \left( T \right) =\left\{ {{\begin{array}{l} {\lambda _{2f} \left( T \right) ,\quad 0\le T \le \frac{T_{2f} \left( A \right) }{4}} \\ {\lambda _{2h} \left( {T-\frac{T_{2f} \left( A \right) }{4} +\frac{T_{2h} \left( B \right) }{4}} \right) ,\quad \frac{T_{2f} \left( A \right) }{4}\le T\le \frac{T_{2f} \left( A \right) }{4} +\frac{T_{2h} \left( B \right) }{2}\;} \\ {\lambda _{2f} \left( {T+\frac{T_{2f} \left( A \right) }{2} -\frac{T_{2h} \left( B \right) }{2}} \right) ,\quad \frac{T_{2f} \left( A \right) }{4}+\frac{T_{2h} \left( B \right) }{2}\;\le T \le \frac{T_{2f} \left( A \right) }{2}+\frac{T_{2h} \left( B \right) }{2}\;} \\ \end{array} }} \right. \end{aligned}$$
(25)

where subscripts “2f” and “2h” of T and \(\lambda \) denote the period and periodic response of the second-order approximation solution for the systems (18) and (19), respectively.

2.4 Approximate analytical solution for dielectric elastomer balloon

For convenience and brevity, the restoring force function in Eq. (6) is expressed as

$$\begin{aligned} -g\left( \lambda \right) =-\left( {\alpha \lambda ^{-5}+\beta \lambda +\gamma \lambda ^{2}+\rho \lambda ^{3}} \right) \end{aligned}$$
(26)

where \(\alpha =-2\), \(\beta =2\), \(\gamma =-\frac{pR}{\mu H}\) and \(\rho =-2\frac{\varepsilon \Phi ^{2}}{\mu H^{2}}\) are the parameters related to material, geometry and loading properties. By setting the restoring function be zero, the equilibrium position \(\lambda _0 \hbox {=}0\) may not exist. When \(\lambda _0 \ne 0\) the analytical approximation should be constructed as follows

$$\begin{aligned} \lambda =x+\lambda _0 \end{aligned}$$
(27)

Here \(\lambda _0 \) is the equilibrium point. Through the translation in Eq. (27), the equilibrium point for x is \(x_0 =0\). The analytical approximation for the dielectric elastomer stretch \(\lambda \) can thus be substituted by the approximation for the newly introduced variable x. Substituting Eq. (27) to Eqs. (6) and (26) yields

$$\begin{aligned} \frac{d^{2}x}{dT^{2}}+g\left( x \right) =0 \end{aligned}$$
(28)

in which

$$\begin{aligned} g\left( x \right)= & {} \alpha \left( {x+\lambda _0 } \right) ^{-5} +\beta \left( {x+\lambda _0 } \right) +\gamma \left( {x+\lambda _0 } \right) ^{2}\nonumber \\&+\rho \left( {x+\lambda _0 } \right) ^{3} \nonumber \\= & {} \frac{\alpha +\beta \left( {x+\lambda _0 } \right) ^{6} \!+\!\gamma \left( {x+\lambda _0 } \right) ^{7}+\rho \left( {x \!+\!\lambda _0 } \right) ^{8}}{\left( {x+\lambda _0 } \right) ^{5}}\nonumber \\ \end{aligned}$$
(29)

with the following initial conditions

$$\begin{aligned} x\left( 0 \right) ={A}'=\lambda \left( 0 \right) -\lambda _0 =A-\lambda _0 ,\; \frac{dx\left( 0 \right) }{dT}=0 \end{aligned}$$
(30)

where \({A}'\) here is used to distinguish from the original initial amplitude A.

The potential energy of Eq. (28) can be expressed as

$$\begin{aligned}&V\left( x \right) =\int g\left( x \right) dx\nonumber \\&\quad =\frac{-3\alpha +6\beta \left( {x+\lambda _0 } \right) ^{6}+4\gamma \left( {x+\lambda _0 } \right) ^{7}+3\rho \left( {x+\lambda _0 } \right) ^{8}}{12\left( {x+\lambda _0 } \right) ^{4}}\nonumber \\ \end{aligned}$$
(31)

By the same principle as mentioned in Sect. 2.3, the two odd nonlinear systems introduced are

$$\begin{aligned}&\frac{d^{2}x}{dT^{2}}+f\left( x \right) =0, x\left( \hbox {0} \right) ={A}',\frac{dx}{dT}\left( \hbox {0} \right) =0 \end{aligned}$$
(32)
$$\begin{aligned}&f\left( x \right) =\left\{ {{\begin{array}{l} {g\left( x \right) ,\hbox { if }x\ge 0} \\ {-g\left( {-x} \right) \hbox {, if }x<0} \\ \end{array} }} \right. \end{aligned}$$
(33)

and

$$\begin{aligned}&\frac{d^{2}x}{dT^{2}}+h\left( x \right) =0,x\left( 0 \right) =-{B}'\left( {{B}'<0} \right) ,\nonumber \\&\frac{dx}{dT}\left( 0 \right) =0 \end{aligned}$$
(34)
$$\begin{aligned}&h\left( x \right) =\left\{ {{\begin{array}{l} {-g\left( {-x} \right) ,\hbox { if }x>0} \\ {g\left( x \right) \hbox {, if }x\le 0} \\ \end{array} }} \right. \end{aligned}$$
(35)

Following Eqs. (9)–(25), the approximate solution of Eq. (28) for \(x\left( T \right) \) can be derived. Then, the approximate solution for \(\lambda \left( T \right) \) in Eq. (4) can be obtained in accordance with Eq. (27). It is noted that the value of \({B}'\) can be expressed in terms of \({A}'\) by solving \(V\left( {{A}'} \right) =V\left( {{B}'} \right) \). The Fourier coefficients of the restoring force functions in Eqs. (32) and (34) can be readily derived by using symbolic manipulation softwares, e.g., Mathematica.

3 Results and discussion

In this paper, the following dimensionless parameters for pressure and potential difference,\(\frac{pR}{\mu H}=0.1\) and \(\frac{\varepsilon \Phi ^{2}}{\mu H^{2}}=0.1\), are considered [21], which means \(\gamma =-0.1\) and \(\rho =-0.2\) in Eq. (26). The restoring force function thus becomes

$$\begin{aligned} -g\left( \lambda \right) =2\lambda ^{-5}-2\lambda +0.1\lambda ^{2}+0.2\lambda ^{3} \end{aligned}$$
(36)

The analytical approximation for the nonlinear dynamical system represented by Eq. (6) is then sought by referring to the aforementioned method. By solving \(g\left( \lambda \right) =0\) in Eq. (36), the only stable equilibrium state is \(\lambda _\mathrm{eq} =1.029\), while the other roots are either negative or complex which do not have physical grounds. In stability analysis, the eigenvalues of the Jacobian matrix of the nonlinear system (i.e., Eqs. (6, 36)) at \(\lambda _\mathrm{eq} =1.029\) are \(\pm 3.09559i\). One other real root of \(g\left( \lambda \right) =0\) is \(\lambda _\mathrm{eq} =2.920\) with eigenvalues \(\pm 1.9193\) in qualitative analysis, yielding unstable solution. This stable equilibrium state at \(\lambda _\mathrm{eq} =1.029\) is also consistent with the conclusions of Zhu et al. [21].

Fig. 2
figure 2

a Time history and b phase diagram for \(\lambda \left( 0 \right) =1.1\)

Full size image

Numerical solutions obtained through the NHB method for several examples with \(\lambda \left( 0 \right) =1.1\), \(\lambda \left( 0 \right) =1.2\), \(\lambda \left( 0 \right) =1.5\), \(\lambda \left( 0 \right) =2.5\) and \(\lambda \left( 0 \right) =2.8\) are separately solved to illustrate the accuracy of NHB and its applicability to autonomous dynamic models. The time history for the periodic response and the phase diagram are presented in Figs. 2, 3, 4, 5, and 6, respectively. The time–history responses shown in Figs. 2a, 3a, 4a, 5a, and 6a are the periodic solutions obtained by the first-order and second-order approximations. These approximate solutions are compared with the Runge–Kutta numerical integration solutions because there is no exact solution available. The corresponding phase diagrams are also shown in Figs. 2b, 3b, 4b, 5b, and 6b. The system oscillation for this DE balloon is not symmetric about its equilibrium position, but it oscillates between asymmetric limits with the same energy level according to the principle of energy conservation.

Fig. 3
figure 3

a Time history and b phase diagram for \(\lambda \left( 0 \right) =1.2\)

Full size image
Fig. 4
figure 4

a Time history and b phase diagram for \(\lambda \left( 0 \right) =1.5\)

Full size image

In Fig. 2, the analytical approximation and numerical integration solutions are highly consistent due to a small \(\lambda (0)\). In Fig. 3a, the time history for the periodic response is highly consistent, with only a very little deviation to the Runge–Kutta solution in the phase diagram in Fig. 3b. For \(\lambda \) between 1 and 1.05, there are two distortions in the vertical axis, \(\dot{\lambda }\approx 0.4\) and \(\dot{\lambda }\approx -0.4\) (\(\dot{\lambda }=d\lambda /dT)\). Similar patterns can be observed in Fig. 4 for \(\lambda (0)=1.5\). In Fig. 4b, for \(\lambda \) between 0.95 and 1.1, there are two distortions in the vertical axis, \(\dot{\lambda }\approx 1.0\) and \(\dot{\lambda }\approx -1.0\). This is possibly due to the analytical solutions that are obtained by combining the approximations of two new nonlinear systems about its equilibrium position.

Fig. 5
figure 5

a Time history and b phase diagram for \(\lambda \left( 0 \right) =2.5\)

Full size image
Fig. 6
figure 6

a Time history and b phase diagram for \(\lambda \left( 0 \right) =2.8\)

Full size image

For \(\lambda (0)=2.5\) in Fig. 5a, the first-order approximation is different from the Runge–Kutta solution, while the second-order approximation is excellent comparing with the Runge–Kutta solution. The difference in the phase space curves in Fig. 5b is relatively larger. In Fig. 6a, both the first-order and second approximations deviate from the Runge–Kutta solution, and the deviation is more significant in Fig. 6b. To derive more accurate approximate solutions, a higher-order approximation following the aforementioned procedure in Sect. 2 should be constructed.

From Figs. 2, 3, 4, and 5, it is observed that when the initial amplitude is less than 2.5, the NHB periodic solutions agree excellently with the numerical integration solution obtained by using the Runge–Kutta method. In Fig. 6, it is also obvious that the second-order approximation is far more accurate than the first-order approximation for an initial condition larger than 2.5. The phase diagrams clearly show the difference between the two approximations. When \(\lambda (0)=2.5\), it means that the balloon has inflated to 2.5 times to the original state, which is quite a large deformation comparing with \(100\% \) [1].

Fig. 7
figure 7

Time history obtained by Runge–Kutta numerical solution for \(\lambda \left( 0 \right) =2.920\)

Full size image

For an initial amplitude approximately 2.9, it is possible to obtain the first-order approximate solution but the second-order periodic solution fails to converge. It is most probably due to numerical instability. For initial amplitudes at 2.920 or larger, neither NHB analytical solutions nor Runge–Kutta numerical solutions exist. As observed in Fig. 7, with increasing T, the deformation goes unbounded quickly. It is because the system loses its stability when the initial conditions approach the unstable equilibrium at \(\lambda _\mathrm{eq} =2.920\). It is concluded that this NHB method can derive highly accurate response for this hyperelastic DE balloon when the initial amplitude is large and before the system loses its stability.

In general, the NHB method is not only applicable for dealing with nonlinear ordinary differential equations, it is also capable of solving electromechanical systems governed by an integral-differential form [36]. It is highly possible to explore the application of the present method for the electromechanical coupled system of beams or plates with piezoelectric vibration absorbers [37,38,39]. These systems can be attempted by first linearizing the governing equations and then obtaining the transformed models by modal truncation techniques with the Galerkin method. The method proposed in this paper may be possibly applied to solve the transformed models of the electromechanical systems.

4 Conclusions

In this paper, based on the neo-Hookean model to account for hyperelastic characteristics, the large amplitude nonlinear free vibration of a DE balloon under static pressure and voltage has been investigated analytically and numerically. It specifically focuses on the development of a Newton–harmonic balance analytical approximation approach to derive very accurate periods and periodic solutions including time history and phase space solutions for different material and initial parameters. For static pressure and potential difference, the balloon is modeled as a general non-odd nonlinear differential model including a rather high negative-powered restoring term that has rarely been found in many physical nonlinear systems. The system is thus very nonlinear, and many previous analytical approaches such as the classical harmonic balance method or the common perturbation method are unable to yield accurate solutions. This paper explores this subject and develops accurate analytical approximate solutions for the nonlinear engineering system based on the NHB method. Making use of this method, only linear algebraic equations, replacing complex nonlinear equations, are involved and hence accurate approximate analytical solutions can be derived. The numerical solutions obviously show very accurate second-order analytical approximations for an initial amplitude at 2.5 or lower while higher-order analytical approximations can be constructed for higher initial amplitude conditions. The analytical approximate time history and phase space response in various examples for this dielectric elastomer balloon provide a much better understanding on the physics of the nonlinear dynamic inflation response for which numerical solutions can hardly reveal. Through the time history and phase diagrams, it is shown that the free vibration for this hyperelastic DE balloon is periodic and depends on the initial stretch ratio. Further works will be conducted to investigate a non-autonomous differential model for forced nonlinear vibration systems that include harmonic pressure and/or applied voltage.