1 Introduction

Dielectric elastomers (DEs) are a type of soft polymer materials, which exhibit significant deformation behaviors under the electric fields, and thus the DE structures are widely used in mechanical engineering and biomedical fields [1,2,3,4], such as transducer structures and biomimetic actuators. For the aspect of motion forms, the flexible tidal power generation devices, the flexible electric pumps and the bionic jellyfish robots can often be described by the spherical shells geometrically. The shells frequently undergo complex deformations influenced by various external factors, which may result in structural instability and failure. Therefore, it is essential to investigate the nonlinear dynamical responses of the DE spherical shells.

In early researches of the DE materials, Pelrine et al. [5,6,7] discussed dynamical properties of the electroconstriction of electroactive polymers and potential applications in the micro robots, acoustic devices and displays. Zhao and Suo [8,9,10,11] proposed the electromechanical stability analysis theory and method, which serve as the foundational theoretical work for DEs. Based on these theories, subsequent researchers adopted various approximate analytical methods, such as the Newton-harmonic balance method [12], incremental harmonic balance method [13] and multiple scales method [14], to investigate the vibrations of the DE balloon. By the coupled dielectric theory, Ni et al. [15] investigated the nonlinear dynamics of functionally graded graphene nanoplatelet reinforced composite dielectric and porous membrane. These efforts have not only advanced the application and theoretical exploration of the DE materials, but also offered the crucial guidance for technological advancements and innovations in related fields.

The DE materials possess many advantages, such as fast response, light weight, large deformation and high energy density. Thus, the vibration responses of the DE structures have attracted considerable attention. Under the combined pressure and voltage, Zhu et al. [16] and Chen et al. [17] investigated the dynamical behaviors of the DE spherical membrane, respectively. Additionally, Chen and Wang [18] found that when the DC and AC voltages reach a certain critical value, the dynamic electromechanical instability occurs. Kumar and Sarangi [19] proposed a new energy density function to describe the electrostriction phenomenon for a class of incompressible isotropic DE materials. These researches are significant for comprehending and exploring the dynamical behaviors of the DE structures without the damping, contributing to the advancement of their applications in fields of mechanics, electronics and medicine. In these works, the influence of structural damping on nonlinear dynamical behaviors is ignored. However, considering the structural damping provides a more accurate prediction of the dynamical response under the external excitation.

Taking the damping effect into account, Jin et al. [20] presented the random response of the DE spherical membranes subjected to combined excitations of the random pressure and harmonic voltage. The results indicated that the intensity of the random pressure, as well as the frequency and amplitude of the harmonic voltage, are important for the stochastic jump bifurcation. Lv et al. [21] analyzed the dynamical behaviors of the DE balloon incorporating stiffening and damping effects. Tian et al. [22] investigated the reliability evaluation of the ideal DE balloon subjected to the harmonic voltage and random pressure simultaneously. Yong et al. [23] presented the nonlinear vibrations of a thick-walled spherical shell, moreover, the authors gave the critical voltage under various loading conditions. He et al. [24] employed both the neo-Hookean model and the Arruda-Boyce model to analyze the electromechanical instability of the thick-walled DE shell, and discussed the instability of the spherical shell under different thicknesses and boundary conditions. Zhao et al. [25, 26] investigated the dynamical behavior of the hyperelastic spherical shell. In summary, these studies provided a significant theoretical guidance for the DE structures in investigating the influence of material parameters, understanding their nonlinear dynamical response characteristics and analyzing the stability and reliability.

The chaotic motion has consistently been a prominent topic in the field of nonlinear dynamics, particularly in the theoretical investigation of cylindrical and spherical structures [27]. Regarding the DE structures, Alibakhshi and Heidari [28, 29] investigated the nonlinear vibrations of the DE balloon composed of the Gent-Gent material, and showed that the second invariant of the material model suppresses the chaotic motion of the system. Zou et al. [30] found that the damping can suppress the chaotic vibrations of the circular DE membrane. Xie et al. [31] examined the evolution of bifurcation in the pressurized DE balloon subjected to an additional electric actuation. Silva et al. [32, 33] examined the complex nonlinear dynamical behaviors of the membrane and shell. Gu et al. [34] summarized the challenges and opportunities for the further studies in terms of mechanism design, dynamics modeling and autonomous control. Interestingly, a comprehensive understanding of chaotic vibrations is likely to contribute significantly to enhancing the stability and reliability of electroactive structures. Additionally, it can play a crucial role in promoting the development and application of related technologies.

In the present studies, the strain energy density functions of the DE materials are mainly characterized by the neo-Hookean model and the Gent model [35,36,37]. However, the neo-Hookean model fails to accurately describe the stress–strain behavior of the DE materials under large strains, whereas the Gent model is inadequate for small and moderate deformations. In comparison to these two models, the Ogden model demonstrates superior applicability in characterizing material properties and mechanical behaviors [38]. In engineering applications, the dielectric elastomer, as an electromechanical transducer, can convert mechanical energy and electrical energy into each other. Chaotic phenomena can enhance the performance of the energy harvester by the nonlinear resonance effects. Meanwhile, through studying the non-chaotic regions, the design parameters can be provided to make the structure produce stable periodic response, which can ensure the service performance of the equipment.

In this work, the chaotic vibrations of the DE spherical shell characterized by the third-order Ogden model are investigated. The effects of various parameters on the chaotic responses of the shell are studied. In Sect. 2, the mathematical model of the shell is established, and the governing equation is derived by the Euler–Lagrange equation. In Sect. 3, the effects of the pressure and voltage on the potential wells, as well as the natural frequencies, are analyzed. In Sect. 4, the effects of the structural damping, pressure, DC voltage and AC voltage on the chaotic vibrations are discussed. In Sect. 5, the conclusions are presented.

2 Mathematical model

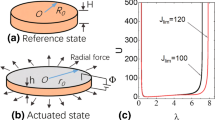
This work considers an incompressible DE spherical shell subjected to the voltage, where the inner and outer surfaces are coated with the positive and negative electrodes, respectively. In the initial state, the radius and thickness of the shell are denoted by \(R_{0}\) and \(H\), respectively. In the current state, due to the electromechanical coupling effects, the radius and thickness are presented by \(r\) and \(h\), respectively. Additionally, the pressure on the inner surface is denoted by \(P\), as shown in Fig. 1.

Fig. 1
figure 1

Configurations of DE spherical shell

Full size image

The initial and current configurations of the shell are denoted as \((R,\Theta ,\Psi )\) and \((r,\theta ,\psi )\), respectively. Under the assumption of the radially symmetric motion, the relation between the initial and current configurations in the spherical coordinate system is represented as follows

$$ {\text{D}}_{{0}} { = }\left\{ {(r,\theta ,\psi )|r = r(R,t),\theta = \Theta ,\psi = \Psi } \right\},\;r(R,t) > 0 $$
(1)

where \(r = r(R,t)\) is the radial deformation function related to the time \(t\).

The deformation gradient tensor is used to characterize the relations between the two configurations, with the following form

$$ {\mathbf{F}} = {\text{diag}}\left( {\frac{\partial r}{{\partial R}},\frac{r}{R},\frac{r}{R}} \right) = {\text{diag}} \left( {\lambda_{1} ,\lambda_{2} ,\lambda_{3} } \right) $$
(2)

where \(\lambda_{1} = \frac{\partial r}{{\partial R}}\) and \(\lambda_{2} = \lambda_{3} = \frac{r}{R}\) are the radial and circumferential stretches, respectively.

Due to the incompressibility constraint \(\lambda_{1} \lambda_{2} \lambda_{3} = 1\), it yields that

$$ \frac{\partial r}{{\partial R}} = \frac{{R^{2} }}{{r^{2} }} $$
(3)

Let

$$ \lambda_{2} = \lambda_{3} = \lambda ,\;\lambda_{1} = \lambda^{ - 2} $$
(4)

where \(\lambda = \lambda (t)\) is used to describe the stretch ratio related to the time \(t\).

Based on the thermodynamic theory [39], the Helmholtz free energy function is composed of the elastic strain energy and the electrostatic energy [11], that is,

$$ \tilde{W}(\lambda ,D) = W(\lambda ) + \frac{{D^{2} }}{2\varepsilon } $$
(5)

where \(\varepsilon\) is the dielectric constant of elastomer, and \(D\) is the electric displacement associated with the electric field \(E\). The corresponding relation is presented as follows

$$ D = \varepsilon E $$
(6)
$$ E = \lambda^{2} V/H $$
(7)

where \(V\) is the voltage applied at the shell.

For the incompressible third-order Ogden model, the corresponding strain energy function is given by

$$ W(\lambda_{1} ,\lambda_{2} ) = \sum\limits_{i = 1}^{3} {\frac{{\mu_{i} }}{{\alpha_{i} }}\left[ {(\lambda_{1}^{ - 1} \lambda_{2}^{ - 1} )^{{\alpha_{i} }} + \lambda_{1}^{{\alpha_{i} }} + \lambda_{2}^{{\alpha_{i} }} - 3} \right]} $$
(8)

where \(\mu_{i} (i = 1,2,3)\) and \(\alpha_{i} (i = 1,2,3)\) are the material constants satisfying \(\mu_{i} \alpha_{i} > 0\,(i = 1,2,3)\). The corresponding parameters are taken as \(\mu_{1} = 0.5\), \(\mu_{2} = 9\), \(\mu_{3} = - 0.00425\), \(\alpha_{1} = 0.05004\), \(\alpha_{2} = 0.0872858\) and \(\alpha_{3} = - 3\) [40].

In terms of Eqs. (5), (7) and (8), the Helmholtz free energy function is denoted as follows

$$ \tilde{W}(\lambda ,D) = \sum\limits_{i = 1}^{3} {\frac{{\mu_{i} }}{{\alpha_{i} }}\left( {\lambda^{{ - 2\alpha_{i} }} + 2\lambda^{{\alpha_{i} }} - 3} \right) + } \frac{\varepsilon }{2}\left( \frac{V}{H} \right)^{2} \lambda^{4} $$
(9)

For the thin-walled shell, the volume \(\Omega_{0}\) is expressed as follows

$$ \Omega_{0} = 4\pi R^{2} H $$
(10)

The potential energy and the kinetic energy of the shell are respectively given by

$$ U_{s} = \int\limits_{\Omega } {\tilde{W}(\lambda ,D){\text{d}}\Omega } = 4\pi R^{2} H\left[ {\frac{\varepsilon }{2}\left( \frac{V}{H} \right)^{2} \lambda^{4} + \sum\limits_{i = 1}^{3} {\frac{{\mu_{i} }}{{\alpha_{i} }}\left( {\lambda^{{ - 2\alpha_{i} }} + 2\lambda^{{\alpha_{i} }} - 3} \right)} } \right] $$
(11)

and

$$ U_{k} = \frac{1}{2}\int\limits_{\Omega } {\rho v^{2} } {\text{d}}\Omega = 2\pi \rho HR^{4} \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}t}}} \right)^{2} $$
(12)

where \(\rho\) is the density, \(\Omega\) represents the initial volume.

The works done by the static pressure \(P\) and the voltage \(V\) are denoted by

$$ W_{p} = 4\pi P\int_{R}^{r} {r^{2} {\text{d}}r} = \frac{4\pi P}{3}(r^{3} - R^{3} ) = \frac{{4\pi PR^{3} }}{3}(\lambda^{3} - 1) $$
(13)

and

$$ W_{V} = 4\pi R^{2} H\varepsilon \left( \frac{V}{H} \right)^{2} \lambda^{4} $$
(14)

Rayleigh’s dissipation function is introduced to describe the damping force, as follows,

$$ W_{R} = \frac{1}{2}\left( {c_{1} \dot{r}^{2} + c_{2} \dot{\theta }^{2} + c_{3} \dot{\phi }^{2} } \right) $$
(15)

where \(c_{1}\) is the damping ratio in the radial direction, \(c_{2}\) and \(c_{3}\) are the damping ratios in the longitude and latitude direction, respectively. Since the motion of the shell is radially symmetric, it leads to \(c_{2} = c_{3} = 0\).

Substituting Eqs. (2) and (4) into Eq. (15) yields

$$ W_{R} = \frac{1}{2}c_{1} R^{2} \dot{\lambda }^{2} $$
(16)

The generalized force is

$$ Q = - \frac{{{\text{d}}W_{R} }}{{{\text{d}}\dot{\lambda }}}{ + }\frac{{{\text{d}}W_{P} }}{{{\text{d}}\lambda }}{ + }\frac{{{\text{d}}W_{V} }}{{{\text{d}}\lambda }} $$
(17)

In order to obtain the governing equation of the shell, the Euler–Lagrange equation is introduced as follows

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial (U_{k} - U_{s} )}}{{\partial \dot{\lambda }}}} \right) - \frac{{\partial (U_{k} - U_{s} )}}{\partial \lambda } = Q $$
(18)

Further, substituting Eqs. (11)–(17) into Eq. (18) yields

$$ \rho R^{2} \ddot{\lambda } + \frac{{c_{1} }}{4\pi H}\dot{\lambda } + \sum\limits_{i = 1}^{3} {\mu_{i} \left( {2\lambda^{{\alpha_{i} - 1}} - 2\lambda^{{ - 2\alpha_{i} - 1}} } \right)} - \frac{PR}{H}\lambda^{2} - 2\varepsilon \left( \frac{V}{H} \right)^{2} \lambda^{3} = 0 $$
(19)

In this work, the shell is subjected to the combined voltages, the action form is taken as

$$ V = \varphi_{dc} + \varphi_{ac} \sin (\omega t) $$
(20)

where \(\varphi_{dc}\) is the DC voltage, \(\varphi_{ac}\) denotes the amplitude of the AC voltage, and \(\omega\) is the corresponding frequency of the AC voltage.

To obtain qualitative and quantitative properties of the governing equation, it is necessary to introduce the following dimensionless notations

$$ \begin{gathered} \mu_{2} = k_{2} \mu_{1} ,\;\mu_{3} = k_{3} \mu_{1} ,\;\tau = t/\left( {R\sqrt {\rho /\mu_{1} } } \right),\;P_{e} = \frac{PR}{{\mu_{1} H}},\;\overline{\omega } = \omega R\sqrt {(\rho /\mu_{1} )} , \hfill \\ \varphi = \frac{{\varepsilon \varphi_{dc}^{2} }}{{\mu_{1} H^{2} }},\;A = \frac{{\varphi_{ac} }}{{\varphi_{dc} }},\;c = \frac{{c_{1} }}{{4\pi HR\sqrt {(\rho \mu_{1} )} }} \hfill \\ \end{gathered} $$
(21)

With the help of Eq. (21), the governing Eq. (19) can be transformed into the following form

$$ \ddot{\lambda } + c\dot{\lambda } + g(\lambda ,P_{e} ,\varphi ) = 0 $$
(22)

where

$$ g(\lambda ,P_{e} ,\varphi ) = \sum\limits_{i = 1}^{3} {k_{i} \left( {2\lambda^{{\alpha_{i} - 1}} - 2\lambda^{{ - 2\alpha_{i} - 1}} } \right)} - P_{e} \lambda^{2} - 2\varphi \left( {1 + A\sin (\overline{\omega }\,\tau )} \right)^{2} \lambda^{3} $$
(23)

Omitting the nonlinear terms of Eq. (22), the natural frequency \(\omega_{0}\) of the shell is given by

$$ \omega_{0}^{2} = \partial g(\lambda_{eq} ,P_{e} ,\varphi )/\partial \lambda $$
(24)

where \(\lambda_{eq}\) is the stretch ratio of the shell under the equilibrium state.

When the shell is subjected to the constant load, integrating Eq. (22) with respect to \(\lambda\) gives the first integral, as follows,

$$ H_{0} = \dot{\lambda }^{2} /2 + E{(}\lambda {)} $$
(25)

where

$$ E{(}\lambda {)} = - \left[ {P_{e} \lambda^{3} /3 + \varphi \lambda^{4} /2 - \left( {2\lambda^{{\alpha_{1} }} + \lambda^{{ - 2\alpha_{1} }} } \right)/\alpha_{1} - \sum\limits_{i = 2}^{3} {k_{i} \left( {2\lambda^{{\alpha_{i} }} + \lambda^{{ - 2\alpha_{i} }} } \right)/\alpha_{i} } } \right] $$
(26)

is the potential energy function and \(H_{0}\) is the energy constant determined by the initial conditions.

3 Numerical analyses

In order to investigate the response of the system, it is essential to analyze the type of equilibrium points and the frequency components of the periodic vibrations. In this section, equilibrium point curves, dual potential well curves and the natural frequency characteristics are discussed.

In terms of Eq. (23), the equilibrium point curves for different DC voltages are shown in Fig. 2. It can be seen that the equilibrium point curves have two monotonically increasing intervals and one monotonically decreasing interval, which correspond to the two stable states and to the unstable state, respectively. It can be shown that the two stable equilibrium points corresponds to the center points, while the unstable equilibrium point corresponds to the saddle point.

As mentioned in Ref. [39], if the voltage increases from zero to the peak point \(\varphi_{M}\), the stretch caused by the voltage gradually increases. Under the action of voltage, the thickness of the system decreases, resulting in higher electric field and electrostatic force. The increased force further squeezes the system, creating a positive feedback effect. When the system is squeezed, the elastic resistance also increases. The peak point is the critical condition where the positive feedback competes with the increase in the elastic resistance. After the peak, positive feedback is dominant and the electromechanical instability occurs. When the system is only subjected to voltage, there is a maximum critical voltage (\(\varphi_{M} = 0.4489\)).

Fig. 2
figure 2

Equilibrium point curves for different DC voltages \(\varphi\)

Full size image

When \(\lambda_{\min } = 1.4489 < \lambda < 2.6834 = \lambda_{\max }\), the deformation curve is monotonically decreasing for \(\varphi = 0\). With the increasing DC voltage, \(\lambda_{{{\text{min}}}}\) reaches to 1, and \(\lambda_{\max }\) gradually increases, as shown in Fig. 2. Since this work mainly discusses the motion near the saddle point, the initial condition of the system is taken as \(\lambda (0) = 1.8\). In terms of the above analyses, \(\lambda = 1.8\) must lie within the decreasing interval, which indicates that it is near the saddle point. When the system is subjected to the AC voltage, it may result in a transverse intersection of stable and unstable manifolds, consequently leading to chaotic phenomena.

To further interpret the reasons behind the dynamical behaviors with different pressures and DC voltages, the potential energy curves of the system are presented in Figs. 3 and 4. In Eq. (26), when \(\varphi < 0.13\), it has only one extreme value, which indicates that the system has only one potential well. However, the increases of the pressure and DC voltage enhance the depth of the second potential well.

Fig. 3
figure 3

Dual parameter potential energy curves for different DC voltages

Full size image
Fig. 4
figure 4

Dual parameter potential energy curves for different pressures \(P_{e}\)

Full size image

As the depth of the second potential well increases, the system is more prone to perform a periodic vibration in the well. Generally, electroactive polymers require a high voltage to be excited, and the results in this work show that the high voltage can deepen the second well. Therefore, the above results can offer guidance on the parameter design for a stabler response, thus ensuring that the equipment can operate in a safer environment.

The variation of the natural frequency of the system with the pre-stretch is shown in Fig. 5, noting that the points of intersection with the x-axis at \(\omega_{0}^{2} = 0\) are \(\lambda_{l}\) and \(\lambda_{r} (\lambda_{l} < \lambda_{r} )\), respectively. The natural frequency decreases with the increasing structural deformation when \(\lambda < \lambda_{l}\). On contrary, the natural frequency increases with the increasing structural deformation when \(\lambda > \lambda_{r}\). Furthermore, the voltage also exerts a significant effect on the natural frequency, however, distinct behaviors are observed in the two intervals. As the voltage increases, the natural frequency decreases at a slower rate for \(\lambda < \lambda_{l}\).

Fig. 5
figure 5

Relations of natural frequency \(\omega_{0}\) versus pre-stretch \(\lambda\) for different voltages \(\varphi\)

Full size image

Using the fourth-order Runge–Kutta method, the phase portraits and time histories of Eq. (22) can be obtained. The Poincaré map of the system is obtained via the stroboscopic method [41]. To further investigate the chaotic motion of the system, the bifurcation diagrams and the maximum Lyapunov exponents (MLEs) are plotted based on the Poincaré map and the wolf algorithm [42,43,44], respectively.

4 Influences of pressure and voltage

In general, the nonlinear system exhibits a complex dynamical competition between periodic and chaotic solutions. This section employs the bifurcation diagram, maximum Lyapunov exponent [45], time history curve, phase portrait and Poincaré map to analyze the effects of different parameters (including the pressure, DC voltage and amplitude) on the periodic and chaotic vibrations of the system.

For the governing parameters, i.e., damping, frequency and pressure, the maximum Lyapunov exponents with dual parameters are shown in Figs. 6, 7 and 8, where the negative exponents correspond to periodic behaviors (black), the null exponents correspond to quasi-periodic behaviors (red), and the positives are chaotic behaviors (blue).

Fig. 6
figure 6

Maximum Lyapunov exponents versus damping \(c\) and frequency \(\overline{\omega }\) for \(P_{e} = 0.5\), \(\varphi = 0.25\) and \(A = 0.5\)

Full size image
Fig. 7
figure 7

Maximum Lyapunov exponents versus pressure \(P_{e}\) and frequency \(\overline{\omega }\) for \(c = 1.5\), \(\varphi = 0.25\) and \(A = 0.5\)

Full size image
Fig. 8
figure 8

Maximum Lyapunov exponents versus pressure \(P_{e}\) and DC voltage \(\varphi\) for \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\)

Full size image

Figure 6 shows the maximum Lyapunov exponents versus the damping \(c\) and the frequency \(\overline{\omega }\). Particularly, for the given parameters, \(P_{e} = 0.5\), \(\varphi = 0.25\) and \(A = 0.5\), the natural frequency obtained by Eq. (24) is 2.7166, which is far away from \(\overline{\omega } = 1\). That is to say, the primary resonant responses are not excited in this situation, which indicates that the system presents the periodic vibrations when \(\overline{\omega } < 1\) and \(c = 0\). For \(\overline{\omega } > 1\), the system requires suitable parameters to avoid chaotic motions. For \(2 < \overline{\omega } < 4\), the maximum Lyapunov exponents alternate between positive and negative values, which means the motion becomes more complex.

Figure 7 gives the maximum Lyapunov exponents versus the pressure \(P_{e}\) and the frequency \(\overline{\omega }\). For the given parameters, \(c = 1.5\), \(\varphi = 0.25\) and \(A = 0.5\), it can be seen that with the increase of the amplitude, the chaotic region in the frequency domain direction becomes smaller. Meanwhile, under the high-frequency AC voltage, the chaotic response region of the system becomes larger, which indicates that the system response is more sensitive to the frequency parameters of the pressure.

Figure 8 gives the maximum Lyapunov exponents versus the pressure \(P_{e}\) and DC voltage \(\varphi\). For the given parameters, \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\), there is a decreasing trend in the chaotic region of the system as the pressure and DC voltage increase. Remarkably, when the pressure exceeds 1, the positive maximum Lyapunov exponents are seldom observed. This suggests that the pressure mitigates the emergence of chaotic response to a certain extent. For specific details, please refer to Figs. 9, 10 and 11.

Fig. 9
figure 9

Bifurcation and maximum Lyapunov exponent diagrams under different DC voltages \(\varphi\) for \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\)

Full size image
Fig. 10
figure 10

Time history curves for different pressures \(P_{e}\) with \(c = 1.5\), \(A = 0.5\) and \(\varphi = 0.3\)

Full size image
Fig. 11
figure 11

Phase portraits and Poincaré maps for different pressures \(P_{e}\) with \(c = 1.5\), \(A = 0.5\) and \(\varphi = 0.3\)

Full size image

Figure 9 shows the bifurcation diagrams and the maximum Lyapunov exponents for different DC voltages. For the given parameters, \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\), the system appears periodic and quasi-periodic vibrations with the increase of the pressure. Particularly, the curve in the periodic vibration windows is connected to the dark line in the chaotic vibration windows. Under a certain DC voltage, the increasing pressure may maintain the stability of the system when the larger deformation occurs.

For \(\varphi = 0.3\) and \(\varphi = 0.4\), Figs. 9b and c present the corresponding bifurcation diagrams and maximum Lyapunov exponents. With the increase of the DC voltages, the chaotic vibration regions increase gradually. Meanwhile, the period-1, period-2, period-4 and quasi-period vibrations appear. For \(P_{e} > 0.7\), the system shows the periodic vibration, which corresponds to the negative maximum Lyapunov exponents.

Figure 10 gives the time history curves of the system for \(P_{e} = 0.12\), \(0.2\), \(0.4\) and \(0.65\), respectively. For the given parameters, \(c = 1.5\), \(A = 0.5\) and \(\varphi = 0.3\), the increasing pressure makes the vibration of the system evolve from the small deformation to the large deformation. Moreover, if the system overcomes the energy barrier, its vibration may be more complicated and move between the two potential wells.

Figure 11 presents the phase portraits and Poincaré maps of the system for different pressures. For the given parameters, \(c = 1.5\), \(A = 0.5\), \(\varphi = 0.3\) and \(P_{e} = 0.12\), the system performs the quasi-period vibrations, as shown in Figs. 11a and e. For \(P_{e} = 0.2\) and \(0.65\), the period-2 vibrations occur, as shown in Figs. 11b and c. The strange attractors appear in Figs. 11d and f, which further demonstrate the existence of the chaotic vibrations.

Figure 12 gives the maximum Lyapunov exponents versus the damping \(c\) and the DC voltage \(\varphi\). For the given parameters, \(P_{e} = 0.5\), \(\overline{\omega } = 2\) and \(A = 0.5\), it can be seen that with the increase of the damping, the region of the positive maximum Lyapunov exponents gradually decreases, which emphasizes the importance of considering damping when designing the DE shell. If the damping is appropriate, the system can maintain the stable periodic motion under a high DC voltage. For specific details, please refer to Figs. 13, 14 and 15.

Fig. 12
figure 12

Maximum Lyapunov exponents versus damping \(c\) and DC voltage \(\varphi\) for \(P_{e} = 0.5\), \(\overline{\omega } = 2\) and \(A = 0.5\)

Full size image
Fig. 13
figure 13

Bifurcation and maximum Lyapunov exponent diagrams for \(c = 1.5\), \(\overline{\omega } = 2\), \(A = 0.5\) and \(P_{e} = 0.5\)

Full size image
Fig. 14
figure 14

Time history curves for different DC voltages \(\varphi\) with \(c = 1.5\), \(\overline{\omega } = 2\), \(A = 0.5\) and \(P_{e} = 0.5\)

Full size image
Fig. 15
figure 15

Phase portraits and Poincaré maps for different DC voltages \(\varphi\) with \(c = 1.5\), \(\overline{\omega } = 2\), \(A = 0.5\) and \(P_{e} = 0.5\)

Full size image

Figure 13 gives the bifurcation and the maximum Lyapunov exponents of the system for \(c = 1.5\), \(\overline{\omega } = 2\), \(A = 0.5\) and \(P_{e} = 0.5\). It indicates that the orbit of the period-doubling bifurcation can enter chaos, and the periodic and chaotic vibrations alternate with the increasing DC voltages. Moreover, the bifurcation diagram of the DC voltage has self-similarity, as shown in Fig. 13b.

Figure 16 presents the maximum Lyapunov exponents versus the damping \(c\) and amplitude of the AC voltage \(A\). For the given parameters, \(P_{e} = 0.5\), \(\overline{\omega } = 2\) and \(\varphi = 0.25\), it can be seen that with the increase of the damping, the positive maximum Lyapunov exponents do not decrease significantly. However, in the region of large AC voltage amplitudes, a distinct region of the periodic motion emerges. While the damping changes, the region remains essentially unchanged. Moreover, the periodic vibration regions increase gradually with the increasing damping, which further enhances the robustness of the system.

Fig. 16
figure 16

Maximum Lyapunov exponents versus the damping \(c\) and amplitude of AC voltage \(A\) for \(P_{e} = 0.5\), \(\overline{\omega } = 2\) and \(\varphi = 0.25\)

Full size image

Figure 17 presents the maximum Lyapunov exponents versus the pressure \(P_{e}\) and amplitude of AC voltage \(A\). For the given parameters, \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\), it is not difficult to find that the influence of the AC voltage amplitude is more complex compared to the other parameters. As the amplitude increases, the chaotic region exhibits a trend of initially increasing and subsequently decreasing. Additionally, within the chaotic region, there exist some regions of periodic response parameters. The parameter combinations in these stable regions can provide a reference for maintaining the periodic response behavior of practical structures under a high voltage. For specific details, please refer to Figs. 18, 19 and 20.

Fig. 17
figure 17

Maximum Lyapunov exponents versus pressure \(P_{e}\) and AC voltage amplitude \(A\) for \(c = 1.5\), \(\overline{\omega } = 2\) and \(A = 0.5\)

Full size image
Fig. 18
figure 18

Bifurcation and maximum Lyapunov exponent diagrams for \(\overline{\omega } = 2\) and \(\varphi = 0.25\)

Full size image
Fig. 19
figure 19

Time history curves for different amplitudes of AC voltage \(A\) with \(c = 1\), \(\overline{\omega } = 2\), \(\varphi = 0.25\) and \(P_{e} = 0.7\)

Full size image
Fig. 20
figure 20

Phase portraits and Poincaré maps for different amplitudes of AC voltages \(A\) with \(c = 1\), \(\overline{\omega } = 2\), \(\varphi = 0.25\) and \(P_{e} = 0.7\)

Full size image

For the given parameters, \(c = 1.5\), \(P_{e} = 0.5\) and \(c = 1\), \(P_{e} = 0.7\), Figs. 18a and b present the bifurcation diagrams and the maximum Lyapunov exponents, respectively. For \(A < 0.4\), the system performs period-1 motion. With the increase of the amplitude, the periodic and chaotic vibrations alternate. Moreover, it shows a pronounced period-doubling and inverse period-doubling bifurcation in the second periodic window in Fig. 18b.

For the given parameters, \(c = 1\), \(\overline{\omega } = 2\), \(\varphi = 0.25\) and \(P_{e} = 0.7\), Figs. 19 and 20 present the time history curves, phase portraits and Poincaré maps of the system under different amplitudes of AC voltage \(A\). With the increase of the amplitude, the vibration behaviors of the system become more complicated, as shown in Fig. 19. Moreover, it shows that there exist the period-1, period-2, period-4, quasi-period and chaotic vibrations in the system, as shown in Fig. 20. Particularly, the typical strange attractors further indicate the chaotic vibrations of the system, as shown in Figs. 20e and f.

In this section, the structural response characteristics under various combinations of parameters are analyzed in detail. The parameter domain range of the chaotic response is identified. With the changes of the pressure and voltage, the system may undergo a series of bifurcations and chaotic transitions. Under the influences of the pressure and voltage, the system may re-enter a stable and predictable state. This phenomenon often occurs within specific parameter regions, which may be associated with the nonlinear characteristics. According to these analysis results, the motion behaviors of the DE shells can be designed. For the energy harvesting system, the parameters can be set in the chaotic region to improve the energy harvesting efficiency of the equipment.

5 Conclusions

Under the combined actions of the pressure and voltage, the periodic and chaotic vibrations of the DE spherical shell described by the third-order incompressible Ogden model are investigated. The governing equation of the shell is obtained by the Euler–Lagrange equation. The effects of different parameters on the dynamical behaviors are analyzed, including the structural damping, voltage and pressure. The main conclusions are given as follows.

  1. 1.

    In terms of the influences of the pressure and DC voltage on the depth of the potential energy well, it is observed that the increasing parameters may have significant influence on the second potential well, namely, deepen its depth, while have little influence on the first potential well. In other words, the increasing depth of the second potential well can make the periodic response of the system stabler, which may provide a theoretical reference for the design of the DE structures requiring stable periodic responses.

  2. 2.

    Based on the qualitative and quantitative analyses, it is observed that (i) for the given damping and AC voltage parameters, the critical value of the system holding periodic vibration is found by the dual-parameter Lyapunov exponents of the pressure and DC voltage. (ii) Some interesting phenomena, such as the period-doubling bifurcation, inverse period-doubling bifurcation, alternation of period-chaos-period, abundant variation of chaotic interval, line-type attractor with a slender local structure, etc., are found.