Performance characteristics of a real-power viscoelastic isolation system under delayed PPF control and base excitation

Abstract

The paper mainly presents the dynamical characteristics of a base-excited viscoelastic isolation system with real-power geometric nonlinearities under a delayed PPF controller. This controller is coupled to the main system with 1:1 internal resonance. Firstly, the perturbation method of multiple scales is adopted to explicitly find the coupled relationship of the frequency response equations. The results demonstrate that under over-linear restoring force, the amplitude–frequency responses of the viscoelastic isolation system are of the hardening type, which only appears on the right branch of the double-peak response. In this respect, increasing the detuning parameter of the controller results in the appearance of frequency island phenomenon on the right branch of the double-peak response, while the amplitude of the controller degenerates into the traditional single-peak response along with the frequency island. Then, it is worth noting that the vibration can be suppressed effectively by the viscoelastic damping parameters. Furthermore, eight types of interesting dynamical response phenomena are found with the change in time delays under different excitation amplitudes. To this end, the stability analysis, showing the performance of the controller strategy, is carried out by combining the response characteristics. Finally, from the perspective of suppressing the peak amplitude and maintaining the resonance stability, the suitable feedback gains and time delays are determined by means of frequency responses as well as stability conditions.

1 Introduction

Viscoelastic materials are extensively applied in numerous engineering structures such as viscoelastic rectangular plates [1], viscoelastic sandwich beams [2], sandwich viscoelastic cylindrical shells [3]. Specifically, since viscoelastic materials are easier to mold in any shape and to tailor it to meet almost any specifications, these characteristics make them excellent candidates for applications in vibration isolators or absorbers. Actually, in recent years, viscoelastic isolators or absorbers have received increasing attention [4, 5]. For examples, in order to control vibration induced by the imbalance motion, and meanwhile to decrease the additional stress of the hull structure, generally, the viscoelastic isolation structure is widely applied in the automobiles and commercial airplanes [6]. In Ref. [5], it is found that a hysteretic material model can be described by the viscoelastic materials model with four fractional parameters, in which the generalized quantities of the pendulum type absorbers have been discussed.

Naturally, the performance of the vibration isolation structure is essentially to be considered, which is usually evaluated by the following several indexes: force or displacement transmissibility, energy cost, implementation convenience, and loading capacity [7,8,9]. With the development of the vibration isolation technologies, how to improve these indexes is the problem which has to be solved, thus the effective control strategy is essentially implemented. In fact, it has been many years since the researchers began to concentrate on the vibration control of isolation systems.

Numerous control strategies have been used in the dynamical systems, such as adaptive control [10], fuzzy control [11], backstepping feedback control [12], and impulsive control [13]. Particularly, the position feedback control as a second-order filter, which was originally suggested by Goh and Caughey [14], has been utilized to the stabilization of high frequency gain by improving the frequency roll-off of the system. Then, the technique of the positive position feedback (PPF) control has been used to control vibration of the large-scale structure in Ref. [15]. Subsequently, the PPF controller has been developed and utilized to the experimental single-link flexible manipulator for controlling the multi-mode vibrations in Ref. [16]. Since the realization of the PPF controller is simple and the displacement signal is used to accomplish the vibration suppression, various control strategies have been developed for improving the performance of the control. For instance, an adaptive modal PPF method, which was used to control the vibration and shape of flexible structure, has been developed in Ref. [17]. After that, for controlling the multimodal vibration of the frequency varying structures, an adaptive PPF controller has been proposed in Ref. [18], in which the estimated nature frequency was adjusted in every step. Further, the amplifications of the optimal output feedback controller have been considered in Ref. [19], which was presented through casting a PPF controller in the state space. Recently, based on the PPF control strategy, the active absorber for suppressing the high amplitude response of a flexible beam has been put forward in Ref. [20].

Additionally, the PPF control has also been combined with the delayed feedback control to design a more robust controller [21, 22]. In fact, the inherent and compounding time delays, which are caused by transport delay, online computation and system states’ test [23,24,25], might unintentionally transfer energy into or out of the system at erroneous time. They might induce the instability and have a negative influence on the control performance. The comprehensive investigation of the absorber with time delay on effectively suppressing the vibration has been explored by El-Gohary and El-Ganaini [26, 27]. More specifically, the delayed PPF (DPPF) controller has been proposed by El-Ganaini et al. [28]. The DPPF controller, which couples with the main system by 1:1 internal resonance, has been applied to reduce the horizontal vibration of a magnetically levitated body under multi-force excitations in Ref. [28]. However, for the vibration isolation systems, limited analytical results on the dynamics of the controlled vibration isolation systems have been reported to date. Thus, it is a fabulous choice for the applications of the DPPF controller in the vibration isolation systems.

In the present study, complex dynamical properties of a viscoelastic isolation system with a real-power restoring force under DPPF control are investigated. The amplitude–frequency response function is a significant aspect in the evaluation of the response of the vibration isolation system; thus, based on the method of multiple scales, firstly the frequency responses of the main system as well as the controller are derived. Then, in order to understand the performance of the controlled viscoelastic isolation system in detail, the effects of the relative parameters on the control output are considered. Lastly, with the purpose of obtaining the stable response, the appropriate choice of the feedback parameters is considered by combining the stability conditions.

2 Nonlinear system model and perturbation analysis

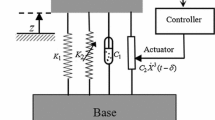
Without loss of generality, the main system investigated in this paper is presented in Fig. 1. It comprises an isolated mass and a base which vibrates harmonically; the motion of the base is given by $Z_0 \cos (\Omega _e \tilde{t})$. The mass is isolated with the base by an isolator modeled as a viscoelastic damper and a nonlinear spring. The viscoelastic isolation system coupled with the DPPF controller is described by following nonlinear differential equations,

$$\begin{aligned} \left\{ {{\begin{array}{l} M\ddot{X}(\tilde{t})+K_1 X(\tilde{t})+Ksgn(X)\left| X \right| ^{\alpha }+B_1 R[X(\tilde{t})]\\ \quad =FZ_0 \cos (\Omega _e \tilde{t})+Q_1 Y(\tilde{t}-\tilde{\tau }_1 ), \\ {m\ddot{Y}(\tilde{t})+\xi _0 \dot{Y}(\tilde{t})+K_Y Y(\tilde{t})=Q_2 X(\tilde{t}-\tilde{\tau }_2 ).} \\ \end{array} }} \right. \end{aligned}$$

(1)

where dots present the derivatives with respect to time $\tilde{t}$, X is the relative displacement $X=u-v$, K is the nonlinear stiffness coefficient, $B_1$ is the viscoelastic damping coefficient, Y is the variable of the DPPF controller, and $\xi _0$ and $K_Y$ are the damping ratio and the linear stiffness of the controller, respectively. The control law for DPPF control is $Q_1 y(\tilde{t}-\tilde{\tau }_1 )$, where $Q_1 >0$. $Q_2$ presents the controller gain. $\tilde{\tau }_1$ and $\tilde{\tau }_2$ are the corresponding time delays.

Fig. 1

Schematic diagram of viscoelastic isolation system under the DPPF control

Specifically, $R[X(\tilde{t})]$ is the relaxation operator and can be expressed as [4]

$$\begin{aligned} R[X(\tilde{t})]={\int }_0^{\omega _0 \tilde{t}} {H(\omega _0 (\tilde{t}-\tilde{{t}^{\prime }}))\dot{X}(\tilde{{t}^{\prime }})} d\tilde{{t}^{\prime }}, \end{aligned}$$

(2)

where H(t) is the relaxation function.

Introducing the following dimensionless parameters

$$\begin{aligned} x= & {} \frac{X}{Z_0 }, \quad t=\omega _0 \tilde{t}, \quad \Omega =\frac{\Omega _e }{\omega _0 }, \omega ^{2}=\frac{K_1 }{M\omega _0^2 }, \hat{{k}}=\frac{KZ_0^{\alpha -1} }{M\omega _0^2 }, \\ \hat{{\zeta }}= & {} \frac{B_1 }{2M\omega _0^2 }, \hat{{f}}=\frac{F}{M\omega _0^2 }, \tau _1 =\omega _0 \tilde{\tau }_1, \tau _2 =\omega _0 \tilde{\tau }_2, \quad y=Y,\\ \hat{{\xi }}= & {} \frac{\xi _0 }{2m\omega _0 }, \quad \omega _y^2 =\frac{K_Y }{m\omega _0^2 }, \quad \hat{{C}}_1 =\frac{Q_1 }{M\omega _0^2 Z_0 }, \quad \hat{{C}}_2 =\frac{Q_2 Z_0 }{m\omega _0^2 }. \end{aligned}$$

Substituting the above transform into Eq. (1), then the following dimensionless system can be derived

$$\begin{aligned} \left\{ {{\begin{array}{l} \ddot{x}(t)+\omega ^{2}x(t)+\hat{{k}}\hbox {sgn}(x)\left| x \right| ^{\alpha }+2\hat{{\zeta }}R[x(t)]\\ \quad =\hat{{f}}\cos (\Omega t)+\hat{{C}}_1 y(t-\tau _1 ), \\ {\ddot{y}(t)+2\hat{{\xi }}\dot{y}(t)+\omega _y^2 y(t)=\hat{{C}}_2 x(t-\tau _2 ).} \\ \end{array} }} \right. \end{aligned}$$

(3)

According to Eq. (2), the corresponding relaxation operator should be

$$\begin{aligned} {R}\left[ {x(t)} \right] ={\int }_0^t {H(t-{t}^{\prime })} \dot{x}({t}^{\prime })\mathrm{d}{t}^{\prime }. \end{aligned}$$

(4)

herein, H(t) can be taken from the generalized Maxwell model [29],

$$\begin{aligned} H(t)=\sum _j \alpha _j \exp \left( -\frac{t}{\lambda _j }\right) , \end{aligned}$$

(5)

where $\alpha _j \ge 0$ and $\lambda _j >0$ are the viscoelastic damping parameters.

By introducing the small parameters $\hat{{k}}=\varepsilon k$, $\hat{{\zeta }}=\varepsilon \zeta$, $\hat{{f}}=\varepsilon f$, $\hat{{C}}_1 =\varepsilon C_1$, $\hat{{\xi }}=\varepsilon \xi$, $\hat{{C}}_2 =\varepsilon C_2$, where $\varepsilon$ is a small parameter. Then, system (3) can be rewritten as

$$\begin{aligned} \left\{ {{\begin{array}{l} \ddot{x}(t)+\omega ^{2}x(t)+\varepsilon ksgn(x)\left| x \right| ^{\alpha }\\ \quad + \,2\varepsilon \zeta {\int }_0^t {H(t-{t}^{\prime })\dot{x}({t}^{\prime })\mathrm{d}{t}^{\prime }} \\ \quad =\varepsilon f\cos (\Omega t)+\varepsilon C_1 y(t-\tau _1 ), \\ {\ddot{y}(t)+2\varepsilon \xi \dot{y}(t)+\omega _y^2 y(t)=\varepsilon C_2 x(t-\tau _2 ).} \\ \end{array} }} \right. \end{aligned}$$

(6)

To analyze the primary resonance of the controlled system by using the method of multiple scales, herein, the first-order approximation solution is introduced

$$\begin{aligned}&x(t,\varepsilon )=x_0 (T_0, T_1 )+\varepsilon x_1 (T_0, T_1 )+\cdots , \nonumber \\&y(t,\varepsilon )=y_0 (T_0, T_1 )+\varepsilon y_1 (T_0, T_1 )+\cdots , \nonumber \\&x(t-\tau _1, \varepsilon )=x_0 (T_0 -\tau _1, T_1 )+\varepsilon x_1 (T_0 -\tau _1, T_1 )+\cdots , \nonumber \\&y(t-\tau _1, \varepsilon )=y_0 (T_0 -\tau _1, T_1 )+\varepsilon y_1 (T_0 -\tau _1, T_1 )+\cdots ,\nonumber \\ \end{aligned}$$

(7)

where $T_0 =\tau$ is a fast time scale, $T_1 =\varepsilon \tau$ is a slow time scale.

Denoting the differential operators $D_0 =\partial /{\partial T_0 }$, $D_1 =\partial /{\partial T_1 }$, and $D_2 =\partial /{\partial T_2 }$, and using the following differential operators,

$$\begin{aligned} \frac{\partial }{\partial t}= & {} D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 +\cdots , \frac{\partial ^{2}}{\partial t^{2}}\nonumber \\= & {} D_0^2 +2\varepsilon D_0 D_1 +\varepsilon ^{2}(D_1^2 +2D_0 D_1)+\cdots . \end{aligned}$$

(8)

Substituting them into Eq. (6) and equating the same orders of $\varepsilon$,

$$\begin{aligned}&\varepsilon ^{0}:D_0^2 x_0 (T_0, T_1 )+\omega ^{2}x_0 (T_0, T_1 )=0, \end{aligned}$$

(9a)

$$\begin{aligned}&D_0^2 y_0 (T_0, T_1 )+\omega _y^2 y_0 (T_0, T_1 )=0, \end{aligned}$$

(9b)

$$\begin{aligned}&\varepsilon ^{1}:D_0^2 x_1 (T_0, T_1 )+\omega ^{2}x_1 (T_0, T_1 )\nonumber \\&\quad =-2D_0 D_1 x_0 (T_0, T_1 )-ksgn(x_0 )\left| {x_0 (T_0, T_1 )} \right| ^{\alpha } \nonumber \\&\qquad -\,2\zeta {\int }_0^{T_0 } {\sum _j {\alpha _j \exp (-{(T_0 -{t}^{\prime })}/{\lambda _j })D_0 x_0 ({t}^{\prime },T_1 )} } \mathrm{d}{t}^{\prime }\nonumber \\&\qquad +\,C_1 y_0 (T_0 -\tau _1, T_1 )+f\cos (\Omega T_0 ), \end{aligned}$$

(10a)

$$\begin{aligned}&D_0^2 y_1 (T_0, T_1 )+\omega _y^2 y_1 (T_0, T_1 )=-2D_0 D_1 y_0 (T_0, T_1 )\nonumber \\&\qquad -\,2\xi D_0 y_0 (T_0, T_1 )+C_2 x_0 (T_0 -\tau _2, T_1 ). \end{aligned}$$

(10b)

The solutions of Eq. (9) are

$$\begin{aligned} x_0 (T_0, T_1 )= & {} A(T_1 )\cos (\omega T_0 +\varphi (T_1 )), \nonumber \\ y_0 (T_0, T_1 )= & {} B(T_1 )\cos (\omega _y T_0 +\psi (T_1 )). \end{aligned}$$

(11)

In order to simplify Eq. (10a), by applying the Fourier series theory, $\hbox {sgn}(\cos \theta )\left| {\cos \theta } \right| ^{\alpha }$ can be expanded into [30]

$$\begin{aligned} \hbox {sgn}(\cos \theta )\left| {\cos \theta } \right| ^{\alpha } =\sum _{n=1}^\infty {a_{(2n-1)\alpha } } \cos \left[ {(2n-1)\theta } \right] ,\nonumber \\ \end{aligned}$$

(12)

where $a_{1\alpha } =\frac{2\Gamma (1+\alpha /2)}{\sqrt{\pi }\Gamma (({3+\alpha )}/2)}$, $a_{(2n-1)\alpha }$ $=\frac{(\alpha -1)(\alpha -3)\cdots (\alpha -(2n-3))}{(\alpha +3)(\alpha +5)\cdots (\alpha +(2n-1))}$ $a_{1\alpha }$, and $\Gamma$ is the Euler Gamma function. Therefore,

$$\begin{aligned}&\hbox {sgn}(x_0 )\left| {x_0 } \right| ^{\alpha }\nonumber \\&\quad =\hbox {sgn}(A\cos (\omega T_0 +\varphi ))\left| {A\cos (\omega T_0 +\varphi )} \right| ^{\alpha } \nonumber \\&\quad =\left| A \right| ^{\alpha }\sum _{n=1}^\infty {a_{(2n-1)\alpha } \cos \left[ {(2n-1)(\omega T_0 +\varphi )} \right] }.\nonumber \\ \end{aligned}$$

(13)

Then, the term $2\zeta {\int }_0^{T_0 } \sum _j \alpha _j$ $\exp (-{(T_0 -{t}^{\prime })}/{\lambda _j })D_0 x_0$ $({t}^{\prime },T_1 ) \mathrm{d}{t}^{\prime }$ can be integrated and rewritten as

$$\begin{aligned}&2\zeta {\int }_0^{T_0 } {\sum _j {\alpha _j \exp (-{(T_0 -{t}^{\prime })}/{\lambda _j })D_0 x_0 ({t}^{\prime },T_1 )} } \mathrm{d}{t}^{\prime } \nonumber \\&\quad =2\zeta \sum _j \frac{\alpha _j \lambda _j A\omega }{\left( {\omega \lambda _j } \right) ^{2}+1}\left[ \omega \lambda _j \cos (\omega T_0 +\varphi )\right. \nonumber \\&\left. \qquad -\sin (\omega T_0 +\varphi )+\exp ({-T_0 }/{\lambda _j })(\sin \varphi -\omega \lambda _j \cos \varphi ) \right] .\nonumber \\ \end{aligned}$$

(14)

Neglecting the transient parts, the contribution of viscoelastic damping can be divided into two parts: One is the viscously damping part, and the other is the stiffness part.

Denoting the excitation frequency as $\Omega =\omega +\varepsilon \sigma$, $\omega _y =\omega +\varepsilon \sigma _1$ ($\sigma$ and $\sigma _1$ are the detuning parameters) and introducing the new variables $\Phi (T_1 )=\sigma T_1 -\varphi (T_1 )$ and$\theta (T_1 )=\sigma _1 T_1 +\psi -\varphi (T_1 )$, we have

$$\begin{aligned}&D_0^2 x_1 (T_0, T_1 )+\omega ^{2}x_1 (T_0, T_1 )=2{A}^{\prime }(T_1 )\omega \sin (\omega T_0 +\varphi )\nonumber \\&\qquad +\,2\omega \sigma A(T_1 )\cos (\omega T_0 +\varphi )-2\omega A{\Phi }^{\prime }\cos (\omega T_0 +\varphi ) \nonumber \\&\qquad +\,\sum _j {\frac{2\zeta \alpha _j \lambda _j A\omega }{\left( {\omega \lambda _j } \right) ^{2}+1}} \sin (\omega T_0 +\varphi )\nonumber \\&\qquad -\,\sum _j {\frac{2\zeta \alpha _j \lambda _j^2 A\omega ^{2}}{\left( {\omega \lambda _j } \right) ^{2}+1}} \cos (\omega T_0 +\varphi ) \nonumber \\&\qquad -\,kb_{1\alpha } A^{\alpha }(T_1 )\cos (\omega T_0 +\varphi )\nonumber \\&\qquad -\,kb_{3\alpha } A^{\alpha }(T_1 )\cos (3\omega T_0 +3\varphi ) \nonumber \\&\qquad +\,f\cos \Phi \cos (\omega T_0 +\varphi )-f\sin \Phi \sin (\omega T_0 +\varphi ) \nonumber \\&\qquad +\,C_1 B\left[ \cos (\theta -\omega _y \tau _1 )\cos (\omega T_0 +\varphi )\right. \nonumber \\&\left. \qquad -\,\sin (\theta -\omega _y \tau _1 )\sin (\omega T_0 +\varphi ) \right] . \end{aligned}$$

(15)

$$\begin{aligned}&D_0^2 y_1 (T_0, T_1 )+\omega _y^2 y_1 (T_0, T_1 ) =2{B}^{\prime }(T_1 )\omega _y \sin (\omega _y T_0 +\psi )\nonumber \\&\qquad +\,2\omega _y B{\psi }^{\prime }(T_1 )\cos (\omega _y T_0 +\psi ) \nonumber \\&\qquad +\,2\xi \omega _y B\sin (\omega _y T_0 +\psi )\nonumber \\&\qquad +\,C_2 A\left[ \cos (\theta +\omega \tau _2 )\cos (\omega _y T_0 +\psi )\right. \nonumber \\&\left. \qquad +\,\sin (\theta +\omega \tau _2 )\sin (\omega _y T_0 +\psi ) \right] . \end{aligned}$$

(16)

Eliminating the secular terms in Eqs. (15) and (16), it can be derived

$$\begin{aligned} {A}^{\prime }(T_1 )= & {} -\sum _j {\frac{\zeta \alpha _j \lambda _j A}{(\omega \lambda _j )^{2}+1}} \\&+\,\frac{f}{2\omega }\sin \Phi +\frac{C_1 B}{2\omega }\sin (\theta -\omega _y \tau _1 ) \end{aligned}$$

$$\begin{aligned} A{\Phi }^{\prime }(T_1 )= & {} \sigma A-\sum _j {\frac{\zeta \alpha _j \lambda _j^2 A\omega }{(\omega \lambda _j )^{2}+1}} -\frac{k}{2\omega }b_{1\alpha } A^{\alpha }\nonumber \\&+\,\frac{f}{2\omega }\cos \Phi +\frac{C_1 B}{2\omega }\cos (\theta -\omega _y \tau _1 ), \end{aligned}$$

(17)

$$\begin{aligned} {B}^{\prime }(T_1 )= & {} -\xi B-\frac{C_2 A}{2\omega _y }\sin (\theta +\omega \tau _2 ) \end{aligned}$$

$$\begin{aligned} B{\theta }^{\prime }(T_1 )= & {} \sigma _1 B-\sum _j {\frac{\zeta \alpha _j \lambda _j^2 \omega B}{(\omega \lambda _j )^{2}+1}} -\frac{k}{2\omega }b_{1\alpha } A^{\alpha -1}B\nonumber \\&+\,\frac{fB}{2\omega A}\cos \Phi +\frac{C_1 B^{2}}{2\omega A}\cos (\theta -\omega _y \tau _1 ) \nonumber \\&-\,\frac{C_2 A}{2\omega _y }\cos (\theta +\omega \tau _2 ). \end{aligned}$$

(18)

The performance and effectiveness of the control law can be evaluated by the equilibrium solutions of Eqs. (17) and (18), thus considering the steady-state solutions of system (3) and denoting as $A_0$, $\Phi _0$, $B_0$ and $\theta _0$ with conditions ${A}^{\prime }=0$, ${B}^{\prime }=0$, ${\Phi }^{\prime }=0$ and ${\theta }^{\prime }=0$ satisfied, thus the following results yield

$$\begin{aligned} A_0^2 =\frac{4\omega _y^2 }{C_2^2 }\left[ \xi ^{2}B_0^2 +(\sigma -\sigma _1 )^{2}B_0^2 \right] , \end{aligned}$$

(19)

$$\begin{aligned} \frac{f^{2}A_0^2}{4\omega ^{2}}= & {} \left[ \sum _j \frac{\zeta \alpha _j \lambda _j A_0^2 }{(\omega \lambda _j )^{2}+1} +\frac{\xi \omega _y C_1 B_0^2 }{C_2 \omega }\cos (\omega \tau _2 +\omega _y \tau _1 )\right. \nonumber \\&\left. -\,\frac{\omega _y C_1 B_0^2 }{C_2 \omega }(\sigma -\sigma _1)\sin (\omega \tau _2 +\omega _y \tau _1 )\right] ^{2}\nonumber \\&+\,\left[ -\sigma A_0^2 +\sum _j {\frac{\zeta \alpha _j \lambda _j^2 \omega A_0^2 }{(\omega \lambda _j )^{2}+1}} +\frac{k}{2\omega }a_{1\alpha } A_0^{\alpha +1}\right. \nonumber \\&\left. +\,\frac{\xi \omega _y C_1 B_0^2 }{C_2 \omega }\sin (\omega \tau _2 +\omega _y \tau _1 )\right. \nonumber \\&\left. +\,\frac{\omega _y C_1 B_0^2 }{C_2 \omega }(\sigma -\sigma _1 )\cos (\omega \tau _2 +\omega _y \tau _1 )\right] ^{2}. \end{aligned}$$

(20)

3 Stability analysis

The stability of a particular equilibrium solution is determined by examining the eigenvalues of the Jacobian matrix of Eqs. (17)–(18). In this regard, the control law could be evaluated. To derive the stability criteria, the behavior of small deviations from the steady-state solutions is examined

$$\begin{aligned} A=A_0 +A_1, B=B_0 +B_1, \Phi =\Phi _0 +\Phi _1, \theta =\theta _0 +\theta _1. \end{aligned}$$

(21)

Substituting Eq. (21) into Eqs. (17) and (18) and neglecting the nonlinear terms, the following linearization equations of Eqs. (17) and (18) at $A_0$, $\Phi _0$, $B_0$ and $\theta _0$ can be obtained

$$\begin{aligned} {A}^{\prime }_1= & {} C_{11} A_1 +C_{12} \Phi _1 +C_{13} B_1 +C_{14} \theta _1, \nonumber \\ {\Phi }^{\prime }_1= & {} C_{21} A_1 +C_{22} \Phi _1 +C_{23} B_1 +C_{24} \theta _1, \nonumber \\ {B}^{\prime }_1= & {} C_{31} A_1 +C_{32} \Phi _1 +C_{33} B_1 +C_{34} \theta _1, \nonumber \\ \theta _1^{\prime }= & {} C_{41} A_1 +C_{42} \Phi _1 +C_{43} B_1 +C_{44} \theta _1, \end{aligned}$$

(22)

where

$$\begin{aligned} C_{11}= & {} -\sum _j {\frac{\zeta \alpha _j \lambda _j }{(\omega \lambda _j )^{2}+1}}, C_{12} =\frac{f}{2\omega }\cos \Phi _0, \\ C_{13}= & {} \frac{C_1 }{2\omega }\sin (\theta _0 -\omega _y \tau _1 ), C_{14} =\frac{C_1 B_0 }{2\omega }\cos (\theta _0 -\omega _y \tau _1 ),\\ C_{21}= & {} \frac{\sigma }{A_0 }-\sum _j {\frac{\zeta \alpha _j \lambda _j^2 \omega }{(\omega \lambda _j )^{2}+1}\frac{1}{A_0 }} -\frac{k}{2\omega }a_{1\alpha } \alpha A_0^{\alpha -2}, \\ C_{22}= & {} -\frac{f}{2\omega A_0 }\sin \Phi _0, C_{23} =\frac{C_1 }{2\omega A_0 }\cos (\theta _0 -\omega _y \tau _1 ),\\ C_{24}= & {} -\frac{C_1 B_0 }{2\omega A_0 }\sin (\theta _0 -\omega _y \tau _1 ),\\ C_{31}= & {} -\frac{C_2 }{2\omega _y }\sin (\theta _0 +\omega \tau _2 ),\\ C_{32}= & {} 0, C_{33} =-\xi , \\ C_{34}= & {} -\frac{C_2 A_0 }{2\omega _y }\cos (\theta _0 +\omega \tau _2 ),\\ C_{41}= & {} -\frac{k}{2\omega }a_{1\alpha } (\alpha -1)A_0^{\alpha -2}\\&-\,\frac{f}{2\omega A_0^2 }\cos \Phi _0 -\frac{C_1 B_0 }{2\omega A_0^2 }\cos (\theta _0 -\omega _y \tau _1 )\\&-\,\frac{C_2 }{2\omega _y B_0 }\cos (\theta _0 +\omega \tau _2 ),\\ C_{42}= & {} -\frac{f}{2\omega A_0 }\sin \Phi _0, \\ C_{43}= & {} +\,\frac{C_1 }{2\omega A_0 }\cos (\theta _0 -\omega _y \tau _1)\\&+\,\frac{C_2 A_0 }{2\omega _y B_0^2 }\cos (\theta _0 +\omega \tau _2 ),\\ C_{44}= & {} -\frac{C_1 B_0 }{2\omega A_0 }\sin (\theta _0 -\omega _y \tau _1 )+\,\frac{C_2 A_0 }{2\omega _y B_0 }\sin (\theta _0 +\omega \tau _2 ). \end{aligned}$$

The characteristic equation of the coefficient matrix of Eq. (22) is

$$\begin{aligned} \lambda ^{4}+S\lambda ^{3}+R\lambda ^{2}+P\lambda +Q=0, \end{aligned}$$

(23)

where $\lambda$ denotes the eigenvalues of the coefficient matrix and

$$\begin{aligned} S= & {} -(C_{11} +C_{22} +C_{33} +C_{44} ), \\ R= & {} C_{11} C_{22} +C_{11} C_{33} +C_{11} C_{44} +C_{22} C_{33}\\&+\,C_{22} C_{44} +C_{33} C_{44} -C_{12} C_{21} -C_{13} C_{31} \\&-\,C_{14} C_{41}, \\ P= & {} -\,C_{11} C_{22} C_{33} -C_{11} C_{33} C_{44} -C_{11} C_{22} C_{44} \\&-\,C_{22} C_{33} C_{44} -C_{12} C_{24} C_{41} -C_{12} C_{23} C_{31} \\&+\,C_{12} C_{21} C_{33} +C_{12} C_{21} C_{44} +C_{13} C_{31} C_{22} \\&+\,C_{13} C_{31} C_{44}-C_{13} C_{34} C_{41} +C_{14} C_{41} C_{22}\\&+\,C_{14} C_{41} C_{33} -C_{14} C_{43} C_{31}, \\ Q= & {} C_{11} C_{22} C_{33} C_{44} -C_{12} C_{21} C_{33} C_{44} \\&-\,C_{12} C_{23} C_{34} C_{41} -C_{12} C_{24} C_{43} C_{31} \\&+\,C_{12} C_{21} C_{34} C_{43} +C_{12} C_{24} C_{41} C_{33} \\&+\,C_{12} C_{23} C_{31} C_{44} -C_{13} C_{34} C_{42} C_{21}\\&+\,C_{13} C_{31} C_{42} C_{24} +C_{13} C_{34} C_{41} C_{22} \\&-\,C_{13} C_{31} C_{22} C_{44} -C_{14} C_{41} C_{22} C_{33} \\&-\,C_{14} C_{42} C_{23} C_{31} +C_{14} C_{43} C_{31} C_{22}. \end{aligned}$$

According to the Routh–Hurwitz criterion [31], the steady-state solutions of Eqs. (19) and (20) are asymptotically stable if the following inequalities hold simultaneously

$$\begin{aligned} S>0, \quad { SR}-P>0, \quad { SRP}-P^{2}-S^{2}Q>0, \quad Q>0. \end{aligned}$$

(24)

4 Results and comparison

In this section, to assess the validity and accuracy of the method presented previously in terms of amplitude–frequency response, stability and their characteristics of the primary resonance response, the obtained equation of the amplitude–frequency response is used to graphically show the effects of different system variables. In this regard, the solutions are verified by the numerical results which are calculated by using the fourth Runge–Kutta method. It needs to point out that according to the Leibniz calculus theory, the derivative of Eq. (4) can be derived as

$$\begin{aligned} \dot{R}[x(t)]=\sum _j {(\alpha _j \dot{x}(t)-\frac{1}{\lambda _j }R[x(t)])}, \end{aligned}$$

(25)

for simplicity, only $j=1$ is considered.

Through this paper, the main parameters of the viscoelastic isolation system are shown in Tables 1 and 2, unless otherwise specified.

4.1 Effects of the real-power exponents and viscoelastic damping on the response properties

Since the real-power exponent of the restoring force plays an important role in the viscoelastic isolation system, the performance of the system under different real-power exponent $\alpha$ is firstly investigated.

As the real-power exponent $\alpha$ is smaller than unity, which corresponds to the under-linear restoring force, the curves of the amplitude–frequency responses shown in Fig. 2a, b indicate the softening stiffness property. It can be seen that the response is of the traditional single-peak response when $\alpha =1/3$ (Fig. 2a); however, with the increase of $\alpha$, another smaller peak can be observed near the point $\sigma =0.0$, such as the case $\alpha =1/2$ depicted in Fig. 2b. Then, the responses keep the double-peak characteristic. Particularly, it is noted that in the case of $\alpha =1$ for the linear stiffness, the right branch is single-valued which is stable everywhere, as indicated in Fig. 2c.

When the real-power exponent satisfies $\alpha >1$, which corresponds to the over-linear restoring force, on the one hand, with the increase of $\alpha$, the peak of the left branch becomes larger, on the other hand, the hardening stiffness property induced due to only presents on the right branch of the response curve, which is an interesting phenomenon. And this phenomenon is also verified by the stability analysis, that is the saddle points which lie in the shaded region only exist on the right branch. The numerical results which depicted by the solid circles also verify the stability analysis and the response properties.

Table 1 Values of the parameters of the main system

Table 2 Values of the parameters of the DPPF controller

Fig. 2

Amplitude–frequency response of the viscoelastic isolation system without time delay at $\sigma _1 =0$, a $\alpha =1/3$, b $\alpha =1/2$, c $\alpha =1$, d $\alpha =3/2$, e $\alpha =5/2$, f $\alpha =9/2$, solid lines theoretical results, circles numerical results

Fig. 3

Response of the viscoelastic isolation system with the change in the viscoelastic damping for $\alpha =5/2$, a, b the main system amplitude, c, d the DPPF controller amplitude

Next, the effects of the viscoelastic damping on the system response and the DPPF controller are studied. The solution for the DPPF controller is extracted from the general form of the solution presented in Eqs. (19) and (20). Herein, the case of $\alpha =5/2$ is taken as an example, as shown in Fig. 3, with the increase in the viscoelastic damping coefficient $\zeta$ or parameter $\alpha _1$, both the amplitude $A_0$ of the main system and the amplitude $B_0$ of the controller can be suppressed effectively in the resonant region. When $\zeta$ or $\alpha _1$ is smaller, the right branch bends to right dramatically in Fig. 3. However, increasing $\zeta$ or $\alpha _1$ reduces the bend degree gradually; hence, the response will become single-valued lastly (such as the case of $\zeta =0.9$ in Fig. 3c or $\alpha _1 =0.8$ in Fig. 3d). Furthermore, Fig. 4 depicts the three-dimensional vibration amplitude of the DPPF controller for changing the viscoelastic damping $\alpha _1$ and detuning parameter $\sigma$ in the cases of $f=0.1$ and $f=0.3$, respectively, which are consistent with the results in Fig. 3.

In addition, the results show that the resonant amplitude at $\sigma =0$ almost keeps identically although different values of viscoelastic damping coefficient or parameter are considered.

Fig. 4

3D surface plots for the amplitude of the DPPF controller with the change in the viscoelastic damping $\alpha _1$ and detuning parameter $\sigma$ in the case of $\alpha =5/2$ a $f=0.1$, b $f=0.3$

4.2 Effect of the delayed signals on the responses

4.2.1 Detuning parameter vs. response amplitude

For the existence of time delays, $\omega _y \tau _1 +\omega \tau _2$ will be $\tau _1 +\tau _2$ under the case of $\omega _y =1.0$ and $\omega =1.0$, in order to better analyze the effect of time delay on the performance of the system, therefore, the amplitude $A_0$ is exhibited in Fig. 5 with the change in the detuning parameter $\sigma _1$ in the case of $\tau _1 +\tau _2 =2.0$.

Fig. 5

Vibration amplitude versus the detuning parameter of the viscoelastic isolation system for $\tau _1 +\tau _2 =2.0$

Obviously, the variation of the detuning parameter $\sigma _1$ results in the valley of the response shifting to the left side when $\sigma _1 <0$ (such as the case of $\sigma =-0.1$ in Fig. 5a) and to the right side when $\sigma _1 >0$ (such as the case of $\sigma =0.1$ in Fig. 5c and the case of $\sigma =0.2$ in Fig. 5d). Additionally, increasing $\sigma _1$ leads to the peak amplitude on the left side become larger, which can be seen apparently from the vertical coordinates of points $\mathbf{P}_{1}(-0.1950,0.1684)$, $\mathbf{P}_{2}(-0.1038, 0.2327)$, $\mathbf{P}_{3}(-0.1050,0.3395)$, and $\mathbf{P}_{4}(0.0625,0.4895)$, and what is most interesting is that the response branch on the right side will be separated into two parts along with the appearance of the frequency island phenomenon, such as the results shown in Fig. 5c, d.

Naturally, Fig. 6 depicts the effect of detuning parameter $\sigma _1$ on the amplitude $B_0$ of the controller. With the increase of $\sigma _1$, due to the strong hardening stiffness property, the double-peak response degenerates to be the phenomenon of frequency island; however, it is also different from the phenomenon discussed in Fig. 5.

Fig. 6

Controller amplitude vs the detuning parameter $\sigma$ for $\tau _1 +\tau _2 =2.0$

4.2.2 Feedback gain vs. response amplitude

The important structural parameter in the design of the DPPF controller is the feedback gain; thus, it is commonly considered the effects of the feedback gain on the amplitude of the main system as well as the controller amplitude.

As shown in Fig. 7a, for fixed system gain $C_1$, the motion can be suppressed very effectively via decreasing the controller gain $C_2$, while the properties of the response keep unchanged. Obviously, for larger $C_2$, the right peak is higher than the left one, but it reduces greatly with the decrease of $C_2$, eventually, the right peak is lower than the left one, such as the case of $C_2 =0.1$ pictured in Fig. 7a.

In Fig. 7b, the response of the main system is studied as increasing the input gain $C_1$ for given value $C_2$. On the one hand, the increase in input gain $C_1$ improves the input energy; thus, the amplitude of the maximum peak becomes larger at the right side of the $\sigma$ axis. On the other hand, the suppression performance can be observed at the exact value of the resonant frequency $(\sigma =0.0)$.

Fig. 7

Effect of the feedback gain $C_1$ and $C_2$ on the controller amplitude $B_0$ and the main system amplitude $A_0$ for $f=0.3, \alpha =3/2$ and $\tau _1 +\tau _2 =2.0$

4.2.3 Sensitivity analysis of the response to time delay

According to the above analysis, the effects of time delay on the amplitude–frequency relations of the vibration isolation system are what we are most concerned about, in what follows, for certain detuning parameters $\sigma$ and $\sigma _1$, the change in amplitude $A_0$ with the increase in time delay $\tau _1$ under different amplitude f of base excitation will be discussed in detail.

Here, the controlled viscoelastic isolation system with $C_1 =0.2$, $C_2 =0.3$, $\sigma =0.5$, $\sigma _1 =0.0$, and $\tau _2 =0.0$ is considered, two examples are indicated in Fig. 8a, b for depicting the response characteristic under different excitation amplitude f in the cases of $\alpha =5/2$ and $\alpha =3/2$, respectively. In order to clarify the complicated response characteristics, four examples ($\alpha =3$, $\alpha =5/2$, $\alpha =3/2$ and $\alpha =1/2)$ are also illustrated in Table 3.

As shown in Fig. 8, for smaller value of f (such as $f=0.02$ for $\alpha =5/2$ and $f=0.05$ for $\alpha =3/2)$, the response curve in every period is composed by three parts: two closed loops in the region of the high amplitude and one continuous curve in region of the lower amplitude. Actually, according to the simulation results, it is found that this type of response phenomenon exists in a smaller interval $f\in [0.003,0.021]$ for $\alpha =5/2$ and $f\in [0.003,0.0549]$ for $\alpha =3/2$ as presented in Table 3. Nevertheless, the two closed loops in the region of high amplitude will be attached with each other as increasing f, the thresholds for appearing this kind of phenomenon are $f\approx 0.022$ and $f\approx 0.055$ in these two cases, respectively. Naturally, continuing to increase f leads to two small attached closed loops combine into one larger loop, such as the case of $f=0.1$ shown in Fig. 8, that is the response characteristic III shown in Table 3. Then, the size of the closed loop will become bigger and bigger with the increase of f, as the comparison examples are plotted in Fig. 8b for the cases of $f=0.1$ and $f=0.3$, separately. And finally these loops will be attached with the loops in the adjacent period, which stands for the response characteristic IV presented in Table 3, the thresholds f for appearing the response characteristic IV are $f\approx 0.1963$ for $\alpha =5/2$ and $f\approx 0.4855$ for $\alpha =3/2$.

Furthermore, the attached loops become two separated curves which exist in the interval $f\in \left[ 0.1964,0.5223 \right]$ for $\alpha =5/2$ and $f\in \left[ {0.4856,0.5492} \right]$ for $\alpha =3/2$, such as the example shown in Fig. 8 for the case of $f=0.5$. Then, it is observed that under larger f the lower branch moves to the high amplitude, while the middle branch moves toward the lower amplitude. Hence, these two curves will be closer to each other gradually; in this regard, it is found that the critical values are $f\approx 0.5224$ for $\alpha =5/2$ and $f\approx 0.5493$ for $\alpha =3/2$ for these two branches attached, which is the response characteristic VI shown in Table 3.

Finally, they degenerate into closed loops in the region of the lower amplitude in every period, such as the case of $f=0.6$ in Fig. 8a and the case of $f=0.7$ in Fig. 8b. Moreover, the loops become smaller and smaller (the cases for $f=0.64$ in Fig. 8a and $f=0.79$ in Fig. 8b) and at last it disappears, that is only the curve in the region of the higher amplitude remains, such as the cases of $f=0.7$ in Fig. 8a and $f=0.9$ in Fig. 8b, respectively.

More specifically, Fig. 9 shows the three-dimensional vibration amplitude versus the changes in excitation frequency and time delay for $\alpha =5/2$. The response properties described in Table 3 can be seen more visually from the perspective of three-dimension.

Fig. 8

Response amplitude of the main system under the system parameters $C_1 =0.2$, $C_2 =0.3$, $\sigma =0.5$, $\sigma _1 =0.0$, $\tau _2 =0.0$ with the change in time delay $\tau _1$ a $\alpha =5/2$, b $\alpha =3/2$

As a conclusion, the complicated dynamical behaviors can be observed in the controlled viscoelastic isolation system; therefore, it is concluded that the stability boundaries in the primary resonance are more sensitive to the time delay. For this purpose, the analysis of the response stability induced by the time delay is presented in Fig. 10. Except for the critical cases, only five cases are considered in Fig. 10. For the response characteristics I and III ($f=0.02$ and $f=0.1)$, the lower branch of the loops lies in the unstable region I, which is the region of the saddle points. For $f=0.02$, the upper branch lies in the unstable region II; thus, only the solutions in the lower branch (approaching zero) and outside the shaded regions are stable. The difference for $f=0.1$ is that there are some parts of the loops lie outside the shaded regions which are stable.

The middle branch of the response characteristic V which includes three separated curves, such as the example $f=0.2$, lies in the unstable region I. And the solutions in both the upper and lower branches outside the shaded regions are stable. Then, for the response characteristic VII which is composed by the upper branch and the closed loops in the lower amplitude, almost upper half of the loops lies in the unstable region I; thus, only the solutions which are in the upper branch and lower half of the loops as well as outside the unstable region II are attainable. Anyway, for the simple case, that is the response characteristic VIII which is composed by one continuous curve, only some parts of the curve lie in the unstable region II.

Note that due to $B_0^2 =\frac{C_2^2 A_0^2 }{4\omega _y^2 \left[ {\xi ^{2}+(\sigma -\sigma _1 )^{2}} \right] }$, under identical values for $C_2$, $\omega _y$, $\xi$, $\sigma _1$, and $\sigma$, the properties of amplitude $B_0$ will be the same with the amplitude $A_0$ of the main system; therefore, it is not necessary to discuss the properties of amplitude $B_0$ in this section.

5 Suppression of the maximum amplitude

For a vibration isolation system, the key issue is to control the maximum amplitude of the system under a specific level. Since the maximum amplitude depends on both the system parameters and the feedback parameters, how to choose the feedback parameters under given system parameters to suppress the maximum amplitude is explained by the following examples.

Obtaining the value of $A_{\max } =2.0$ as an example, the parameters of the system are the same as in section 4.2 for $f=0.3$. It is noticed that in Fig. 11 the maximum amplitude is smaller than 2.0 when time delays $\tau _1$ and $\tau _2$ are defined in even regions shown in Fig. 11, such as region II and region IV, etc. whereas outside these regions the amplitude of the response will be larger than 2.0, that is in region I, region III, and region V, etc. The critical boundaries are depicted by the solid lines in Fig. 11. Additionally, the response becomes unstable when the parameter pairs are obtained in the cyan regions, otherwise, in the yellow regions these points are unstable.

Table 3 Response properties with the change in time delay under different base excitations

Furthermore, the case of $A_{\max } =2.0$ is under consideration; Fig. 12a illustrates the relation of time delay $\tau _1$ with feedback gain $C_1$. The critical parameter pairs are closed loops in every period, as the examples $f=0.1$ and $f=0.3$. And outside these loops, respectively, where the regions of the optional parameters corresponding to the maximum amplitude are smaller than 2. However, for larger f, the relation of the critical parameter pairs degenerate into one continue curve, such as the case of $f=0.5$. Above this curve, the maximum amplitude is smaller than 2. Nevertheless, not all parameter pairs located in the upper part or outside the loop can satisfy the stability conditions, the dot line and dash–dot line present the critical boundaries, and absolutely the response of the system becomes unstable when the parameter pairs locate in the unstable regions.

Fig. 9

3D surface plot of the amplitude $A_0$ for the change in excitation amplitude f and time delay $\tau _1$

Fig. 10

Analysis of the stability of the responses shown in Fig. 8

Likewise, as shown in Fig. 12b for the case of the maximum amplitude $A_{\max } =1.0$, comparing with Fig. 12a, the size and shape of the unstable regions are disparate, and the properties of the division line for $f=0.5$ are identical for $f=0.1$ and $f=0.3$. The parameters which locate outside the shaded regions as well as outside the closed loop will be available.

The aforementioned analysis in this section indicates the appropriate range of the feedback parameters which are advantages to vibration control and corresponding stable motion; therefore, such feedback control can play the role of damping force.

6 Conclusions

Fig. 11

Suppression of the maximum amplitude by selecting the suitable parameters of time delay

Nonlinear dynamical properties of a viscoelastic isolation system with the real-power restoring force under a delayed PPF controller were studied in this paper. The method of multiple scales was applied to determine the frequency response equation, and then, the stability analysis was performed based on both the perturbation method and the Routh–Hurwitz criterion. Specifically, the parametric sensitivity analysis was carried out, it was found that as the real-power exponent is enough smaller, the response only indicates the softening stiffness property; however, the double-peak response is induced when the real-power exponent is greater than 1, and the interesting finding is that the hardening stiffness property only appears on the right branch.

Fig. 12

Design control parameter pairs (time delay and feedback gain of the main system) for suppressing the maximum amplitude

With the existence of time delay, the detuning parameter of the controller can accurately predict the frequency shift of the lower valley; on the other hand, the phenomenon of frequency island was induced on the right branch. Additionally, the parameters of viscoelastic damping can suppress vibration effectively. Eight types (including the critical cases) of response characteristics were found with the change in time delay. In this regard, the stability analysis was performed in order to obtain the stable and unstable regions of typical response characteristics. Finally, in order to select appropriate parameters to suppress the maximum amplitude, the feedback parameter pairs were derived.