1 Introduction

The present paper investigates the dynamics of a 1D continuum which is intended as the homogenized limit of a discrete mechanical system consisting of masses connected by nonlinear springs and a pantographic microstructure. The study of different kinds of microstructures, which are today much easier to obtain thanks to the possibility of driving the manufacturing process by means of computers [1], has led to the development of new models in continuum mechanics (apart from classical works such as [2, 3], the reader can find interesting results in [4,5,6,7,8,9,10,11]). The pantographic microstructure (for a detailed description see [12, 13]) is particularly interesting because it is at the same time very simple in principle but still leads to homogenized continua that are beyond the scope of classical continuum models (see [14, 15] for convergence theorems involving structures of this type). Moreover, it displays behaviors that are very promising from a purely mechanical point of view, among which a high toughness, an advantageous strength-to-weight ratio and a very good predictability of the fracture zones (see [16,17,18,19,20]).

The material nonlinearity of the springs obviously entails that the motion of the system is described by nonlinear equations. The universe on nonlinear PDEs escapes from almost any possible generalization. Very seldom one can provide closed-form solutions, and in general even qualitative analysis of the behavior of the solutions and of the structure of their set is far from trivial. An exception, however, has to be made for those PDEs having soliton solutions: this is indeed one of the cases in which a very regular (and thus very peculiar) behavior can be shown for PDEs otherwise showing a much more complex time evolution. Recent literature also investigates, in suitable cases, solutions representing (in various senses) an approximation of a genuine soliton (see for instance [21]). This is indeed the approach we chose for the present work. Of note, soliton solutions have a significant application potential in mechanics (for a general perspective including connections with mechanical and biological phenomena, see [22]), in particular in damage detecting techniques [23].

The paper is organized as follows: in Sect. 2 a one-dimensional continuum is conjectured as the homogenized limit starting from a nonlinear discrete microstructure. In Sect. 3 a solution in form of a traveling wave is obtained; manipulating this solution we explore the possibility to have a quasi-soliton solution after having shown that exact soliton solutions are not possible. Finally, in Sect. 4 we numerically compare the quasi-soliton solution with a generic perturbation and observe markedly lesser dispersion effects in the former case.

2 Non-local 1D discrete systems

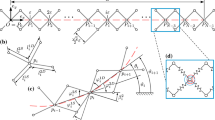
Let us consider a system consisting of an infinite number of material points \(P_i\) having equal mass \({\mathfrak {m}}\), arranged in a straight chain and connected by springs. The kinematic descriptor of each \(P_i\) is the displacement \(u_{i}\), which is assumed to be directed along the reference direction of the chain. We add to this system a set of flexible and inextensible beams connected by ideal hinges to form a pantographic microstructure [24, 25]. We thus consider two elastic interaction potentials between the masses:

  1. 1.

    An interaction due to the pantographic microstructure (see [12, 13])Footnote 1;

    $$\begin{aligned} \varPhi _{\mathrm{pan},i} = \frac{1}{2} {\mathbb {K}} \left[ u_{i-1}(t) - 2 u_i(t) + u_{i+1}(t)\right] ^2 \end{aligned}$$
    (1)
  2. 2.

    A nonlinear interaction between each pair of adjacent masses due to the introduced nonlinear springs

    $$\begin{aligned} \varPhi _{\mathrm{NL},i}= & {} \frac{1}{{2}} \kappa _1 \left[ u_{i+1}(t) - u_i(t) \right] ^2 \nonumber \\&+ \frac{1}{4} \kappa _3 \left[ u_{i+1}(t) - u_i(t) \right] ^4 \end{aligned}$$
    (2)

This kind of interaction potentials (together with a standard form for the kinetic energy) leads to an infinite set of equations by means of a standard application of the Hamilton principle:

$$\begin{aligned}&{\mathfrak {m}} {\ddot{u}}_i(t) + \kappa _1 [u_i(t)-u_{i-1}(t)] - \kappa _1 [u_{i+1}(t)-u_i(t)] \nonumber \\&\quad +\,\kappa _3 [u_i(t)-u_{i-1}(t)]^3 - \kappa _3 [u_{i+1}(t)-u_i(t)]^3 \nonumber \\&\quad -\,2 {\mathbb {K}} [u_{i-1}(t) - 2 u_i(t) + u_{i+1}(t)]\nonumber \\&\quad +\,{\mathbb {K}} [u_{i-2}(t) - 2 u_{i-1}(t) + u_{i}(t)]\nonumber \\&\quad +\,{\mathbb {K}} [u_{i}(t) - 2 u_{i+1}(t) + u_{i+2}(t)]=0 \end{aligned}$$
(3)

In this paper we only consider the longitudinal motion of the system. For what concerns the motion in the orthogonal direction, we just want to add a few very simple considerations. Within linear regime, the axial elongation of the homogenized system due to transverse displacement can of course be neglected; therefore, the material nonlinearity due to the springs plays no role. As for the pantographic microstructure, in the linear regime the energies associated to transverse and longitudinal displacements are uncoupled and have the same form (see [12, 13]). Of course, if one wants to extend the study to finite deformations, the equation for transverse and longitudinal displacement would become coupled and the whole problem harder to address (Fig. 1).

Fig. 1
figure 1

Scheme of the discrete microstructure, made by a chain of masses connected by nonlinear springs and a set of beams constrained by ideal hinges. The hinges at the nodes (i, \(i+1\), etc.) do not interrupt the continuity of the beams, but just prescribe equal displacements for two material points belonging to them

Full size image

If the distance \(\ell \) between two adjacent masses tends to zero, it is possible to identify the differences involved in the above potentials as finite difference approximations of suitable derivatives. Therefore, we can conjecture that the homogenized version of the considered discrete system is the one given by the continuous potentials specified below:

  1. 1.

    By considering the energies of pantographic substructures we obtain:

    $$\begin{aligned}&\sum \frac{1}{2} {\mathbb {K}}\ell ^4 \left[ \frac{u_{i-1}(t) - 2 u_i(t) + u_{i+1}(t)}{\ell ^2}\right] ^2 \nonumber \\&\quad \xrightarrow [\ell \rightarrow 0]{} \int \frac{1}{2} k_2 \left[ \frac{\partial ^2{u(X,t)}}{\partial X^2}\right] ^2 \text {d}X \end{aligned}$$
    (4)

    where X is the referential abscissa, \(k_2 \approx {\mathbb {K}}\ell ^3\); therefore, the homogenized continuous elastic potential in the range of small deformation can be defined as

    $$\begin{aligned} \phi _{\mathrm{pan}} = \frac{1}{2} k_2 \left[ \frac{\partial ^2{u(X,t)}}{\partial X^2}\right] ^2 \end{aligned}$$
    (5)
  2. 2.

    By considering the energies of the nonlinear springs we obtain:

    $$\begin{aligned}&\sum \left\{ \frac{1}{2} \kappa _1 \left[ u_{i+1}(t) - u_i(t) \right] ^2 + \frac{1}{4} \kappa _3 \left[ u_{i+1}(t) - u_i(t) \right] ^4\right\} \nonumber \\&\quad \xrightarrow [\ell \rightarrow 0]{}\int \left\{ \frac{1}{2} k_{1} \left[ \frac{\partial {u(X,t)}}{\partial X}\right] ^2 + \frac{1}{4} k_{3} \left[ \frac{\partial {u(X,t)}}{\partial X}\right] ^4 \right\} \text {d} X\nonumber \\ \end{aligned}$$
    (6)

    in which \(k_{1} \approx \kappa _1\ell \) and \(k_{3} \approx \kappa _3\ell ^3\); hence, the homogenized continuous elastic nonlinear potential can be assumed as:

    $$\begin{aligned} \phi _{\mathrm{NL}} = \frac{1}{2} k_{1} \left[ \frac{\partial {u(X,t)}}{\partial X} \right] ^2 + \frac{1}{4} k_{3} \left[ \frac{\partial {u(X,t)}}{\partial X} \right] ^4 \end{aligned}$$
    (7)

By using these elastic potentials and the kinetic energy:

$$\begin{aligned} E_{\text {k}} = \frac{1}{2} \varrho \left[ \frac{\partial {u(X,t)}}{\partial t} \right] ^2 \end{aligned}$$
(8)

again employing the Hamilton principle, the homogenized version of Eq. (3) becomesFootnote 2:

$$\begin{aligned} \boxed { \varrho \, u_{tt} - k_1 u_{_{XX}} \left[ 1 + 3 \beta (u_{_{X}})^2\right] + k_2 u_{_{_{XXXX}}} = 0} \end{aligned}$$
(9)

with \(\beta :=k_3/k_1\). As far as the authors know the nonlinear fourth-order PDE Eq. (9) is not found in the literature. For the sake of generality, we will also consider the same equation with the second term of the nonlinear potential (7) written in the abstract form \(\varPhi (u_{_X})\):

$$\begin{aligned} \varrho \, u_{tt} - u_{_{XX}} \left[ k_1 + \frac{\partial ^2 \varPhi }{\partial (u_{_X})^2}\right] + k_2 u_{_{_{XXXX}}} = 0 \end{aligned}$$
(10)

The system here studied can be considered a generalized model for the beam in which non-locality and material nonlinearities have been taken into account. This line of investigation can be framed in the rich literature existing on generalized beam theories [26,27,28,29,30], which includes also numerical tools that can be useful for the investigation of our system [31]. Isogeometric analysis is particularly suitable for the numerical study of this kind of systems and for its higher dimension generalizations, for its capability to comfortably include non-local effects ([32,33,34,35,36,37,38,39,40]). We finally remark that only small deformations of the pantographic microstructure have been considered to get Eqs. (9) and (10). The investigation of large deformations of the same microstructure would be of course of interest for real-world applications, but it is clearly harder due to the possible onset of instabilities of different kinds. In order to pursue this research direction, the tools developed in [41,42,43,44,45,46,47] for studying static instabilities and in [48, 49] for dynamic ones can be usefully employed.

2.1 The linear case

In Eq. (9) if \(\beta =0\), we have a linear medium whose governing equation is:

$$\begin{aligned} \varrho \, u_{tt} - k_1 u_{_{XX}} + k_2 u_{_{_{XXXX}}} = 0 \end{aligned}$$
(11)

which corresponds to the discrete set of Eq. (3) with \(\kappa _3=0\). In the discrete model we have two sources of dispersive effects, i.e., the term due to the non-local potential (1) and the discretization itself. Since Eq. (11) is linear we can seek solution in the form \(u(X,t)= A e^{-j(k X- \omega t)}\), being j the imaginary unit, k the wave number and \(\omega \) the angular frequency; thus, the dispersion relation is:

$$\begin{aligned} k^4 k_2+k^2 k_1-\varrho \omega ^2 = 0 \end{aligned}$$
(12)

that explicitly becomes:

$$\begin{aligned} \omega = \frac{k \sqrt{k^2 k_2+k_1}}{\sqrt{\rho }} \end{aligned}$$
(13)

and therefore the velocity of propagation as function of \(\omega \) can be expressed in the following way:

$$\begin{aligned} c = \frac{\omega }{k} = \frac{\sqrt{2 k_2}\, \omega }{\sqrt{\sqrt{k_1^2+4 k_2\, \rho \omega ^2}-k_1}} \end{aligned}$$
(14)

Similarly, we can proceed for the discrete system, imposing to the displacements the following time dependence: \(u_{i+N}=A e^{-j(k\ell N - \omega t)}\), \(N\in {\mathbb {Z}}\), where \(N\ell \) is the oriented distance between the N-th and the i-th masses. This leads to the dispersion relation:

$$\begin{aligned} 2 (\kappa _1+{\mathbb {K}}) - {\mathfrak {m}}\omega ^2 - 2 \kappa _1 \cos (k \ell ) - 2 {\mathbb {K}} \cos (2 k \ell ) = 0\nonumber \\ \end{aligned}$$
(15)

which gives

$$\begin{aligned} k \ell = \left[ \arctan \left( \frac{\sqrt{-2 \kappa _1^2+2 \kappa _1 \left( \sqrt{(\kappa _1+4 {\mathbb {K}})^2-4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}-4 {\mathbb {K}}\right) +4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}}{-\sqrt{\kappa _1^2+4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}+\kappa _1+4 {\mathbb {K}}}\right) +2 \pi c_1\right] \end{aligned}$$
(16)

and the wave speed:

$$\begin{aligned} c = \frac{\omega }{k} = \omega \ell \left[ \arctan \left( \frac{\sqrt{-2 \kappa _1^2+2 \kappa _1 \left( \sqrt{(\kappa _1+4 {\mathbb {K}})^2-4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}-4 {\mathbb {K}}\right) +4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}}{-\sqrt{\kappa _1^2+4 {\mathbb {K}} {\mathfrak {m}} \omega ^2}+\kappa _1+4 {\mathbb {K}}}\right) \right] \end{aligned}$$
(17)

With the micro–macro identification \(k_2 \approx {\mathbb {K}}\ell ^3\), \(k_{1} \approx \kappa _1\ell \) and \({\mathfrak {m}} \approx \varrho \ell \), we can compare the two systems as shown in Fig. 2. We note that as \(\ell \) decreases, the interval of \(\omega \) in which the continuous system well approximates the discrete one becomes larger. By Eq. (17), the continuous system is a good approximation of the discrete one as long as the wave length is larger than \(4 \ell \). Finally, we remark that the linear case is significant not only when the stiffness \(k_3\) vanishes, but also when \(\vert u_{_X} \vert \) is small.

Fig. 2
figure 2

Frequency–velocity plot for the linear version of the discrete system with different values of the scale length (dashed lines) and for the homogenized linear continuum (continuous line)

Full size image

3 Wave propagation

We search for solutions of Eq. (9) in the form of traveling waves: \(u(X,t)=f(X - c\, t) = f(\eta )\), with propagation speed c. By substituting in Eq. (10) we obtain the fourth-order ODE:

$$\begin{aligned} f^{IV}(\eta ) + f''(\eta ) \left[ A - B \frac{\partial ^2 \varPhi }{\partial (f')^2} \right] = 0 \end{aligned}$$
(18)

where \(A=\frac{\varrho \, c^2 - k_1}{k_2}\) and \(B=\frac{1}{k_2}\). Setting \(f'(\eta )=g(\eta )\) and integrating we get

$$\begin{aligned} g''(\eta ) + A g(\eta ) - {B} \frac{\partial \varPhi }{\partial g} = C_1 \end{aligned}$$
(19)

whence multiplying by \(g'(\eta )\) and integrating again

$$\begin{aligned} g'(\eta ) = \pm \sqrt{ 2{B}\varPhi [g(\eta )] - A [g(\eta )]^2 + 2 C_1 g(\eta ) + 2 C_2}\nonumber \\ \end{aligned}$$
(20)

which in case \(\varPhi \) is the second term of the nonlinear potential (7) becomes

$$\begin{aligned} g'(\eta ) = \pm \sqrt{ \frac{B}{2}[k_3\, g(\eta )]^4 - A [g(\eta )]^2 + 2 C_1 g(\eta ) + 2 C_2}\nonumber \\ \end{aligned}$$
(21)

Equation (18) is therefore solved (up to a constant) by the primitive of an elliptic function:

$$\begin{aligned}&f(X)= \int \zeta ^{-1}(g(\xi )) \text {d} \xi \quad \text { with } \nonumber \\&\zeta (g)=\pm \int \frac{\text {d}g}{\sqrt{ \frac{B}{2} k_3\, g^4 - A g^2 + 2 C_1 g + 2 C_2}} \end{aligned}$$
(22)

We remark that the signs here are not intended as mutually exclusive over the whole domain, because a solution can of course assume different signs on different intervals provided its global regularity. We will use a solution of this form in the following section.

Fig. 3
figure 3

Numerical solutions of the ODE (18) showing unbounded growth of f. In the zoom the rapidly oscillating behavior of the derivatives is visible

Full size image

When dealing with nonlinear PDEs such as (9) an interesting (and by now standard) question is whether it can admit soliton solutions [50]. In the literature the definition itself of soliton is not completely consistent among different fields of investigation. In the present work, we choose to search for solutions with the following (minimal) properties: (i) they preserve their shape; (ii) they vanish together with all their derivatives as \(\eta \) goes to infinity; (iii) they emerge unchanged after an interaction between themselves.

Point (i) is automatically satisfied by a solution verifying Eq. (18); as for point (ii), we start remarking that a very natural assumption on \(\varPhi \) is that it goes to zero when so does \(u_{_X}\). We have therefore that \(g \rightarrow 0\) implies \(g' \rightarrow 0\) if and only if \(C_2=0\), which is thus a necessary condition for the existence of soliton solutions. From Eq. (19) we obtain that \(g'' \rightarrow 0\) if

$$\begin{aligned} \frac{\partial \varPhi }{\partial g}(g(\eta )) \xrightarrow [\eta \rightarrow \infty ]{} - \frac{C_1}{B} \end{aligned}$$
(23)

Clearly, the case \(\varPhi = \frac{1}{4} k_{3} \left[ \frac{\partial {u(X,t)}}{\partial X} \right] ^4\) considered above excludes (23) if g (and therefore \(u_{_X}\)) goes to zero. This means that in our case there cannot be the typical compensation between dispersive and nonlinear effects producing soliton solutions. This result is consistent with the numerical simulations shown in Fig. 3, where some numerical solutions of the ODE (18) (with different values of initial conditions) are plotted and a zoom is shown on bottom left. The value of the function f appears to be unbounded for \(\eta \rightarrow \infty \), while the derivatives are oscillating. One can notice that, for some initial data, the growth is very slow. This, combined with the fact that the derivatives are not unbounded (even if they do not converge asymptotically to zero) makes ineteresting the search for solutions that almost preserve shape, i.e., quasi-solitons (see the following section).

Fig. 4
figure 4

Evolution of a perturbation \(\sigma (\eta )\) (applied in \(X=0\)) obtained gluing smoothly the function \(f(\eta )\) given in formula (22) on an interval \({\mathcal {I}}\) and the null function outside \({\mathcal {I}}\). The shape is almost preserved

Full size image
Fig. 5
figure 5

Evolution of a perturbation \(\alpha \,{\text {sech}}(6t)\) applied in \(X=0\), with \(\alpha =20\) selected to have the same amplitude of the previous case. It is clearly visible that the shape is not preserved

Full size image
Fig. 6
figure 6

Time history of the peak amplitude of the evolution originated by the perturbations \(\sigma \) and \(\text {sech}(6t)\)

Full size image
Fig. 7
figure 7

Time-space 3D plotting of the collision between two identical initial perturbations \(\sigma \) traveling in opposite direction. The corresponding traveling wave solutions emerge practically unchanged after the interaction, almost maintaining shape and velocity

Full size image
Fig. 8
figure 8

Same simulation shown in the previous figure but with a generic initial perturbation (\({\text {sech}}(\alpha t)\) with \(\alpha =6\)). The corresponding solutions lose amplitude and show dispersion

Full size image

Soliton solutions are found in nonlinear PDEs formally quite similar to Eq. (9) as for instance the well-known Boussinesq equation

$$\begin{aligned} u_{tt} = u_{_{XX}} (1+\beta u) + u_{_{X}}^2-u_{_{XXXX}} \end{aligned}$$
(24)

describing surface water waves in the hypotheses of weak nonlinearity and weak dispersion. The Boussinesq equation, however, displays the compensation above mentioned, which is formally described by the fact that there exist two differential operators L and M depending on a function u(X, t) such that \({\dot{L}} = [M,L]\) (where [M, L] is the commutator: \(M \circ L - L \circ M\)) holds if and only if u is a solution of Eq. (24)Footnote 3 [51]. It is interesting to observe that Eq. (10) cannot be reduced to the Boussinesq equation for any behavior of nonlinear spring described by the potential \(\varPhi \). Indeed, to get Eq. (24) from Eq. (10) it should be \(\frac{\partial ^2 \phi }{\partial (u_{_X})^2}=\frac{u_{_{X}}^2}{u_{_{XX}}} + \beta u\), which is not possible in the hypothesis that \(\varPhi \) is only depending on \(u_{_{X}}\).

4 Quasi-soliton solutions

While we have already seen that exact soliton solutions of Eq. (9) are not possible, we want to numerically investigate whether the equation, similarly to what has been observed in other cases can have quasi-soliton solutions (see [21]), i.e., localized traveling wave solutions which approximately preserve their shape and emerge unchanged after interaction among themselves.

We constructed a candidate quasi-soliton solution \(\sigma (\eta )\) by gluing smoothly the function \(f(\eta )\) given in formula (22) over an interval \({\mathcal {I}}:=(\eta _0,\eta _1)\), at the extrema of which it vanishes with its first derivative, and the null function \(f_0 \equiv 0\) over \(\mathbb {R} \setminus {\mathcal {I}}\).

Imposing \(u(0,t)=\sigma (\eta )\) as a boundary condition for Eq. (9), we obtain the result shown in Fig. 4. To allow a direct comparison, we also imposed as a boundary condition a generic function of the form \({\text {sech}}(\alpha t)\) with \(\alpha =6\); the result is shown in Fig. 5. It is directly observable that the traveling solution originated by \(\sigma \) preserves much better its shape than the generic solution originated by the hyperbolic secant. To quantitatively assess this, we plotted the time history of the peak amplitude in the two cases in Fig. 6. In is clear that the traveling solution originated by \(\sigma \) preserves almost perfectly its amplitude, while the generic solution with similar initial amplitude and speed does not. This justifies calling the former a quasi-soliton solution [21] (Figs. 7, 8).

5 Conclusions

In the present paper the dynamics of a 1D system with a pantographic microstructure and a nonlinear set of springs has been studied. A novel nonlinear PDE describing the motion of the system in small deformation regime has been investigated. Traveling wave solutions has been searched and a general form for the nonlinear potential of the spring has been considered to show that the equation cannot reduce to a Boussinesq-type, a well-known equation having soliton solutions. Gluing smoothly a suitable restriction of the traveling wave solution with a null function, quasi-soliton solutions have been numerically identified and compared with generic solutions. Further development of the mathematical study of Eq. (9) will be interesting and, as for most of nonlinear problems, far from trivial. From a mechanical point of view, future studies of this type of systems should try to weaken the simplifying assumption here introduced, for instance considering, as already mentioned, large deformations of the microstructure, and also studying its possible damage and fracture concerning both the nodes and the beams themselves. In this connection the tools developed in [52,53,54,55,56,57,58] can be useful.