Pantographic beam: a complete second gradient 1D-continuum in plane

Abstract

There is a class of planar 1D-continua which can be described exclusively by their placement functions which in turn are curves in a two-dimensional space. In contrast to the Elastica for which the deformation energy depends on the projection of the second gradient to the normal vector of the placement function, i.e. the material curvature, the proposed continuum does also depend on the projection onto the tangent vector, introduced as the stretch gradient. Thus, the deformation energy takes into account the complete second gradient of the placement function. In such a model, non-standard boundary conditions and more generalized forces such as double forces do appear. The deformation energy of the continuum is obtained by applying a heuristic homogenization procedure to a family of slender discrete pantographic structures constituted by extensional and rotational springs. Within the homogenization process, the overall length of the system is kept fixed, the number of the periodically appearing sub-systems, called cells, is increased, and the stiffnesses are appropriately scaled. For two examples, we numerically compare the family of discrete systems with the continuum. The analysis shows that the continuum represents the behaviour of the discrete system already for a relatively moderate number of cells. In particular, the behaviour of the deformation energy error between the discrete and the continuum models when the number of cells tends to infinity is determined by the homogenization process.

1 Introduction

The static behaviour of discrete systems consisting of springs connected with each other can easily get very complex. For the analysis of such systems, a discrete model is not always the first choice. Particularly, if the system is composed of similar sub-systems which appear periodically, spatially continuous formulations are also able to capture the behaviour of the system at large [1,2,3,4,5]. A particular class of such systems is so-called pantographic structures [6,7,8], i.e. pantographic mechanisms which are well known from everyday life such as pantographic mirrors, expanding fences or scissor lifts. Discrete models of such structures are obtained, if the links in these systems are modelled by extensional and rotational springs being hinge-joined together [9,10,11]. Thus, the links themselves are allowed to deform. These systems exhibit a peculiar null-energy deformation mode apart from the rigid body mode. A deformation mode is sometimes also referred to as extensional floppy mode [12], and which is characterized by its accordion-like (homogeneous) extension or compression forming a rhomboidal pattern. These pantographic structures [13,14,15] have shown to be the simplest example of structures whose continuum descriptions result in a wealth of non-standard problems in the theory of higher-gradient and micromorphic continua [9, 16,17,18] and to their related mathematical challenges [19]. Insofar, pantographic structures have proven to be an archetype in the mechanics of generalized media. This means that the overall behaviour of the system can be described synthetically at a larger length scale, i.e. at a macro-level, as a continuum model [20,21,22]. If we are instead interested in the behaviour at the smaller length scale of the periodically appearing sub-systems, i.e. at a micro-level, then the more refined discrete model is required. Accordingly, when we henceforth refer to the discrete and the continuum models, we will synonymously make use of the prefixes micro and macro, respectively. To pass from a discrete model into a continuum model, homogenization techniques can be used [17, 23,24,25,26]. These techniques require the establishment of precise micro–macro correspondences. Consequently, such techniques allow to give a precise meaning to many features of the macro-model in terms of those of the micro-model.

The last few decades have witnessed a high acceleration in the development of additive and subtractive techniques such as 3D-printing [27], non-ablative femtosecond laser exposure [28], dry etching [29], wet chemical etching [30], or micro-moulding [31]. These manufacturing processes allow for the design of materials possessing a highly controlled structure at length scales which are much smaller than those involved in many engineering systems. This partly justifies the renewed research interest in homogenization and the systematic search [32,33,34] for new micro-structures whose homogenized limits exhibit (desired) elastic extremal behaviour, e.g. auxetic, negative stiffness, highly compliant, strongly nonlinear, multistable, etc. This is the motif of the emerging field of (mechanical) metamaterials [35, 36].

Recently, Barchiesi et al. [37] presented preliminary results of the derivation and computation of a one-dimensional continuum model being capable of describing the finite planar deformation of a discrete slender pantographic structure, referred to as pantographic beam. The continuum model was deduced from a discrete model applying a variational asymptotic procedure [12, 17, 34, 38]. The proposed model generalizes the models derived in [12, 38], in which also $\Gamma$-convergence results are available for the case of free-boundary conditions (cf. also [39]). The achieved continuum model in [37] shows quite exotic features. It was shown that the deformation energy density of such a 1D-continuum does not only depend on the material curvature but also on the stretch gradient. Moreover, the derived continuum can exhibit phase transition [40] and negative stiffness as well.

Besides the derivation of the continuum model, which is more pedagogical than the one presented in [37], the aim of this paper is to numerically evaluate the differences between the micro- and the macro-model. We try to elucidate to what extent the continuum retains the relevant phenomenology of the discrete system, notwithstanding the unavoidable loss of information that a homogenization process entails. In order to pursue this aim, it is crucial to gain a better understanding of the involved asymptotic process, i.e. how the change in the micro-length scale affects the discrete model. Furthermore, special attention is given to the difference between the deformation energy of the micro- and the macro-model when the micro-length scale tends to zero, i.e. the discrete–continuum error. This deviation gives a quantitative value to assess the quality of the approximation of the continuum by its discrete counterpart and vice versa. In particular, we want to show that the behaviour of the energy error is determined by the homogenization process.

2 Heuristic homogenization

The continuum is deduced by applying Piola’s micro–macro identification procedure [17, 41], which can be considered as a heuristic variational asymptotic procedure. The general idea how this procedure is applied in the present case for a one-dimensional continuum is as follows:

• (i) A family of discrete spring systems embedded in the two-dimensional Euclidean vector space ${\mathbb {E}}^2$, i.e. the micro-model with micro-length scale $\varepsilon >0$ is introduced—generalized coordinates and energy contributions ${\mathcal {E}}_\varepsilon$ are defined

• (ii) The kinematic descriptors of the continuum, i.e. the macro-model, are introduced as continuous functions with a closed subset of the real numbers as their common domain—these functions must be chosen such that their evaluation at particular points can be related to the generalized coordinates of the micro-model

• (iii) Formulation of the deformation energy of the micro-model ${\mathcal {E}}_\varepsilon$ using the evaluation of the continuum descriptors at particular points followed by a Taylor expansion of the energy with respect to the micro-length scale $\varepsilon$

• (iv) Specification of scaling laws for the constitutive parameters in the micro-model followed by a limit process in which the energy of the continuum ${\mathcal {E}}$ is related to the micro-model by ${{\mathcal {E}}} = \lim \nolimits _{\varepsilon \rightarrow 0} {\mathcal {E}}_\varepsilon$

2.1 Discrete model

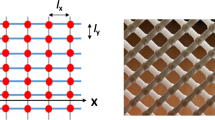
The assembly and kinematics of the system are sketched in Fig. 1. In the undeformed configuration, see Fig. 1a, N cells are arranged upon a straight line in direction of the unit basis vector $e_x\in {\mathbb {E}}^2$. The total length $L \in {\mathbb {R}}$ of the undeformed pantographic beam accounts for $N-1$ cells, as depicted in Fig. 1a. The cells are centred at the positions $P_{i} = i\varepsilon e_x$ for $i\in \left\{ 0,1,\dots ,N-1\right\}$ with $\varepsilon = L/(N-1)$. The basic ith unit cell is formed by four extensional springs hinge-joined together at $P_{i}$. Rotational springs, which are coloured in blue and red in Fig. 1d, are placed between opposite collinear springs belonging to the same cell. Note that the extensional springs are rigid with respect to bending such that they can transmit torques. White-filled circles in Fig. 1 represent hinge constraints, requiring the end points of the corresponding springs to have the same position in space.

Fig. 1

a Undeformed configuration, b generalized coordinates of ith cell, c deformed configuration with redundant kinematic quantities, and d force elements of a single cell

When not otherwise mentioned, the indices $i,\mu$, and $\nu$ belong henceforth to the following index sets: $i\in \{0,1,\dots ,N-1\}$, $\mu \in \{1,2\}$ and $\nu \in \{D,S\}$.¹ The kinematics of the spring system is locally described by finitely many generalized coordinates. The coordinates are the positions $p_{i} \in {\mathbb {E}}^2$ of the points at position $P_{i}$ in the reference configuration and the lengths of the oblique deformed springs $l_{i}^{\mu \nu } \in {\mathbb {R}}$. Nevertheless, we introduce various other kinematical quantities to formulate the total potential energy in a most compact form. Applying the law of cosines, the angles $\varphi _{i}^{\mu \nu }$ depicted in Fig. 1c are determined by the relations

$$\begin{aligned} \begin{aligned}&\varphi _{i}^{1D}&=\cos ^{-1}\left[ \frac{\Vert p_{i+1}-p_{i}\Vert ^{2}+\big (l_{i}^{1D}\big )^{2}-\big (l_{i+1}^{2S}\big )^{2}}{2l_{i}^{1D}\Vert p_{i+1}-p_{i}\Vert }\right] , \\&\varphi _{i}^{2D}&=\cos ^{-1}\left[ \frac{\Vert p_{i+1}-p_{i}\Vert ^{2}+\big (l_{i}^{2D}\big )^{2}-\big (l_{i+1}^{1S}\big )^{2}}{2l_{i}^{2D}\Vert p_{i+1}-p_{i}\Vert }\right] , \\&\varphi _{i}^{1S}&=\cos ^{-1}\left[ \frac{\Vert p_{i}-p_{i-1}\Vert ^{2}+\big (l_{i}^{1S}\big )^{2}-\big (l_{i-1}^{2D}\big )^{2}}{2l_{i}^{1S}\Vert p_{i}-p_{i-1}\Vert }\right] , \\&\varphi _{i}^{2S}&=\cos ^{-1}\left[ \frac{\Vert p_{i}-p_{i-1}\Vert ^{2}+\big (l_{i}^{2S}\big )^{2}-\big (l_{i-1}^{1D}\big )^{2}}{2l_{i}^{2S}\Vert p_{i}-p_{i-1}\Vert }\right] . \end{aligned} \end{aligned}$$

(1)

For $a\in {\mathbb {E}}^2$, $\Vert a \Vert = \sqrt{a \cdot a}$ corresponds to the norm induced by the inner product denoted by the dot. Note that $\varphi _0^{\mu S}$ and $\varphi _{N-1}^{\mu D}$ cannot be determined by the relations (1) and belong strictly speaking also to the set of generalized coordinates. However, for the sake of brevity, we will often omit them. Another restriction is that the choice of generalized coordinates holds only locally, as long as the angles $\varphi _{i}^{1D}$ and $\varphi _{i}^{2D}$ do not change sign. Throughout the derivation of the macro-model, we will assume that the angles $\varphi _{i}^{1D}$ and $\varphi _{i}^{2D}$ remain in the range $(0,\pi )$. For the reduced index set $i = \{1,2,\dots ,N-2\}$, the angle between the two vectors $p_{i}-p_{i-1}$ and $e_x$ is denoted by $\vartheta _i$. Then, the angle $\theta _{i}$ between the vectors $p_{i}-p_{i-1}$ and $p_{i+1}-p_{i}$ can easily be determined by

$$\begin{aligned} \theta _{i} = \vartheta _{i+1} - \vartheta _i = \tan ^{-1}\left[ \frac{(p_{i+1}-p_{i}) \cdot e_y }{(p_{i+1}-p_{i})\cdot e_x}\right] - \tan ^{-1}\left[ \frac{(p_{i}-p_{i-1}) \cdot e_y }{(p_{i}-p_{i-1})\cdot e_x}\right] . \end{aligned}$$

(2)

We set $\theta _0 = \theta _1$ and $\theta _{N-1}= \theta _{N-2}$ such that the deviation angles of two adjacent oblique springs from being collinear are given for the entire index set of i by

$$\begin{aligned} \beta _{i}^{1}=\theta _{i}+\varphi _{i}^{1D}-\varphi _{i}^{1S} , \quad \beta _{i}^{2}=\theta _{i}+\varphi _{i}^{2S}-\varphi _{i}^{2D} . \end{aligned}$$

(3)

For the undeformed configuration, see Fig. 1a, we have

$$\begin{aligned} l_{i}^{\mu \nu }=\frac{\sqrt{2}}{2}\varepsilon , \quad \beta _{i}^{1}=\beta _{i}^{2}=0 , \quad \Vert p_{i}-p_{i-1}\Vert =\varepsilon . \end{aligned}$$

(4)

Letting the summations for $i, \mu$, and $\nu$ range over the above introduced sets $\{0,\dots ,N-1\}$, $\{1,2\}$ and $\{D,S\}$, respectively, the micro-model deformation energy is defined as

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_{\varepsilon }&=\frac{k_{E}}{2} \sum _{i}\sum _{\mu ,\nu }\left( l_{i}^{\mu \nu }-\frac{\sqrt{2}}{2} \varepsilon \right) ^{2}+\frac{k_{F}}{2}\sum _{i}\sum _{\mu } \left( \beta _{i}^{\mu }\right) ^{2} \\&{\mathop {=}\limits ^{(3)}}\frac{k_{E}}{2}\sum _{i}\sum _{\mu ,\nu } \left( l_{i}^{\mu \nu }-\frac{\sqrt{2}}{2}\varepsilon \right) ^{2} +\frac{k_{F}}{2}\sum _{i}\sum _{\mu }\left[ \theta _{i}+\left( -1\right) ^{\mu } \left( \varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}\right) \right] ^{2}, \end{aligned} \end{aligned}$$

(5)

with $k_{E},k_{F}>0$ being the stiffnesses of the extensional and rotational springs, respectively. Boundedness of the deformation energy both for the micro-model and for the macro-model is considered throughout this paper. It is worth remarking that besides the rigid body modes, also the set of admissible configurations defined by

$$\begin{aligned} l_{i}^{\mu \nu }=\frac{\sqrt{2}}{2}\varepsilon , \quad p_{i}=p_{i-1}+K e_{x} , \quad p_{0}=P_{0} ,\qquad \mathrm {for} \; K\in \big (0,\sqrt{2}\varepsilon \big ) , \end{aligned}$$

(6)

entails null deformation energy and is referred to as extensional floppy mode [12].

For the lengths $l_{i}^{\mu \nu }$ of the oblique springs, we assume the asymptotic expansion

$$\begin{aligned} l_{i}^{\mu \nu }=\frac{\sqrt{2}}{2}\varepsilon +\varepsilon ^{2} {\tilde{l}}_{i}^{\mu \nu }+o(\varepsilon ^{2}) , \end{aligned}$$

(7)

where ${\tilde{l}}_{i}^{\mu \nu } \in {\mathbb {R}}$. Inserting assumption (7) into the energy (5) leads to

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_{\varepsilon } =\frac{k_{E}}{2}\sum _{i}\sum _{\mu ,\nu }\left[ \varepsilon ^2 {{\tilde{l}}}_{i}^{\mu \nu } + o(\varepsilon ^2)\right] ^{2}+\frac{k_{F}}{2}\sum _{i}\sum _{\mu } \left[ \theta _{i}+\left( -1\right) ^{\mu }\big (\varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}\big )\right] ^{2}. \end{aligned} \end{aligned}$$

(8)

2.2 Micro–macro identification

The slenderness of the discrete system makes it reasonable to aim for a one-dimensional continuum [42] in the limit of vanishing $\varepsilon$. The continuum is then parametrised by the arc length $s \in [0,L]$ of the straight segment of length L connecting all points $P_i$. We assume the independent kinematic Lagrangian descriptors of the macro-model to be the functions

$$\begin{aligned} \chi {:}\ \left[ 0,L\right] \rightarrow {\mathbb {E}}^2 , \quad {\tilde{l}}^{\mu \nu }{:}\ \left[ 0,L\right] \rightarrow {\mathbb {R}} . \end{aligned}$$

(9)

The placement function $\chi$ places the 1D-continuum into ${\mathbb {E}}^2$ and is best suited to describe the points $p_i \in {\mathbb {E}}^2$ of the discrete system on a macro-level. To take into account also the effect of changing spring lengths ${{\tilde{l}}}_i^{\mu \nu }$ introduced in (7), the placement function is augmented by the four micro-strain functions ${\tilde{l}}^{\mu \nu }$. We thus suggest the identification of the discrete system with a one-dimensional continuum which can be classified as a micromorphic continuum, cf. [43,44,45,46]. It is also convenient to introduce the functions $\rho {:}\,[0,L] \rightarrow {\mathbb {R}}^+$ and $\vartheta {:}\,[0,L] \rightarrow [0,2\pi )$ in order to rewrite the tangent vector field $\chi '$ as

$$\begin{aligned} \chi '(s) = \rho (s)\left[ \cos {\vartheta (s)}e_x+\sin {\vartheta (s)}e_y\right] , \end{aligned}$$

(10)

where prime denotes differentiation with respect to the reference arc length s. Thus, $\rho$ corresponds to the norm of the tangent vector $\Vert \chi ' \Vert$ and is referred to as stretch. We explicitly remark that the current curve $\chi ([0,L])$ can in general have a length $\int \limits _{0}^{L}\rho \ \mathrm {d}s$ different from L, as s is not an arc-length parametrization for $\chi$ but for the reference placement $\chi _0(s) = s e_x$. Introducing moreover the normal vector field $\chi _\bot '(s) = \rho (s)\left[ -\sin {\vartheta (s)}e_x + \cos {\vartheta (s)} e_y \right]$, being rotated against $\chi '(s)$ about $90^\circ$ in anti-clockwise direction, it can be seen by straightforward computation that

$$\begin{aligned} \rho '(s) = \frac{\chi '(s) \cdot \chi ''(s)}{\Vert \chi '(s) \Vert } , \quad \vartheta '(s) = \frac{\chi ''(s) \cdot \chi '_\bot (s)}{\Vert \chi '(s) \Vert ^2} . \end{aligned}$$

(11)

In the following, $\rho '$ and $\vartheta '$ are called stretch gradient and material curvature, respectively.

For Piola’s micro–macro identification, we relate the generalized coordinates of the discrete system with the functions (9) evaluated at $s_i = i \varepsilon$ such that

$$\begin{aligned} \chi (s_{i})=p_{i} ,\quad {\tilde{l}}^{\mu \nu }(s_{i})={\tilde{l}}_{i}^{\mu \nu } . \end{aligned}$$

(12)

For the asymptotic identification, we need to expand the energy (8) in $\varepsilon$. To approach this, the expansion of $\chi$ is given by

$$\begin{aligned} \chi (s_{i\pm 1}) =\chi (s_{i})\pm \varepsilon \chi ^{\prime }(s_{i})+\frac{\varepsilon ^{2}}{2} \chi ^{\prime \prime }(s_{i})+o(\varepsilon ^{2}) . \end{aligned}$$

(13)

Combining the asymptotic expansion (7) with (12)${}_2$, we have

$$\begin{aligned} l_{i\pm 1}^{\mu \nu } = \frac{\sqrt{2}}{2}\varepsilon + {\tilde{l}}^{\mu \nu }(s_{i\pm 1})\varepsilon ^2 + o(\varepsilon ^2) . \end{aligned}$$

(14)

Substituting ${\tilde{l}}^{\mu \nu }(s_{i\pm 1}) = {\tilde{l}}^{\mu \nu }(s_i)+o(\varepsilon ^0)$ in (14), we obtain

$$\begin{aligned} l_{i\pm 1}^{\mu \nu } = \frac{\sqrt{2}}{2}\varepsilon + {\tilde{l}}^{\mu \nu }(s_{i})\varepsilon ^2 + o(\varepsilon ^2) . \end{aligned}$$

(15)

In order to further expand (8), we subsequently need to expand the terms $\theta _i$ and $\varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}$ up to first order. The detailed expansion is given in “Appendix A”. For $\theta _i$, we have according to (56)

$$\begin{aligned} \theta _i = \vartheta '(s_i) \varepsilon + o(\varepsilon ) . \end{aligned}$$

(16)

The differences $\varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}$ are given by (63) and (64) as

$$\begin{aligned} \varphi _i^{\mu S}-\varphi _i^{\mu D} = \left. \frac{ \sqrt{2}(\rho ^2)'+4\big [({\tilde{l}}^{(3-\mu )D}-{\tilde{l}}^{(3-\mu )S})+ (\rho ^2-1)({\tilde{l}}^{\mu S}-{\tilde{l}}^{ \mu D})\big ]}{2 \sqrt{2}\rho \sqrt{2-\rho ^2}}\right| _{s=s_i} \varepsilon + o(\varepsilon ) . \end{aligned}$$

(17)

Substituting (16) and (17) into (5) together with $\rho (s_i) = \Vert \chi '(s_i) \Vert$, we compute the desired expansion of the micro-model energy ${\mathcal {E}}_{\varepsilon }$ as a function of the kinematic descriptors $\chi$ and ${\tilde{l}}^{\mu \nu }$ as

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_{\varepsilon }&=\frac{k_{E}\varepsilon ^{4}}{2} \sum _{i}\left[ \big ({\tilde{l}}^{1S}\big )^{2} +\big ({\tilde{l}}^{1D}\big )^{2} +\big ({\tilde{l}}^{2S}\big )^{2} +\big ({\tilde{l}}^{2D}\big )^{2} + o(\varepsilon ^0)\right] _{s=s_i} \\&\quad +\frac{k_{F}\varepsilon ^{2}}{2}\sum _{i}\left[ \vartheta ^{\prime }+ \frac{-\sqrt{2}(\rho ^{2})' -4\big [({\tilde{l}}^{2D}-{\tilde{l}}^{2S}) -(\rho ^{2}-1)({\tilde{l}}^{1D}-{\tilde{l}}^{1S})\big ]}{2\sqrt{2}\rho \sqrt{2-\rho ^{2}}} + o(\varepsilon ^0)\right] _{s=s_i}^{2}\\&\quad + \frac{k_{F}\varepsilon ^{2}}{2}\sum _{i}\left[ \vartheta ^{\prime }+ \frac{\sqrt{2}(\rho ^{2})'+4\big [({\tilde{l}}^{1D}-{\tilde{l}}^{1S})+(\rho ^{2}-1)({\tilde{l}}^{2S}-{\tilde{l}}^{2D})\big ]}{2\sqrt{2}\rho \sqrt{2-\rho ^{2}}} + o(\varepsilon ^0)\right] _{s=s_i}^{2} . \end{aligned} \end{aligned}$$

(18)

Let the parameters $K_{E},K_{F}>0$ be constants, which do not depend on $\varepsilon$. Then, these constants are related to the stiffnesses of each discrete system with micro-length scale $\varepsilon$ by a scaling law

$$\begin{aligned} k_{E}=K_{E}\varepsilon ^{-\kappa }\ ,\quad k_{F}=K_{F}\varepsilon ^{-\eta }\ , \end{aligned}$$

(19)

with the scaling parameters $\kappa$ and $\eta$. By choosing $\kappa =3$ and $\eta =1$ in (19), observing that $\sum _i o(\varepsilon ^n)= o(\varepsilon ^{n-1})$, the global remainder in the energy (18) becomes $o(\varepsilon ^0)$. This remainder specifies the deformation energy error between the discrete and the continuum model, called discrete–continuum energy error.

2.3 Macro-model

The continuum limit is now obtained by letting $\varepsilon \rightarrow 0$ and considering the sum to turn into an integral according to $\sum _{i}f(s_{i})\varepsilon \overset{\varepsilon \rightarrow 0}{\longrightarrow } \int \limits _{0}^{L}f\ \text{ d }s$, where f is a real- valued function defined on [0, L]. Using (18) together with the scaling law (19) for $\kappa = 3$ and $\eta = 1$, the deformation energy for the homogenized macro-model becomes

$$\begin{aligned} \begin{aligned} {\mathcal {E}}&=\int \limits _{0}^{L}\frac{K_{E}}{2} \left[ \big ({\tilde{l}}^{1S}\big )^{2} +\big ({\tilde{l}}^{1D}\big )^{2} +\big ({\tilde{l}}^{2S}\big )^{2} +\big ({\tilde{l}}^{2D}\big )^{2}\right] \mathrm {d}s \\&\quad +\int \limits _{0}^{L}\frac{K_{F}}{2}\left[ \vartheta ^{\prime }+ \frac{-\sqrt{2}(\rho ^{2})' -4\big [({\tilde{l}}^{2D}-{\tilde{l}}^{2S}) -(\rho ^{2}-1)({\tilde{l}}^{1D}-{\tilde{l}}^{1S})\big ]}{2\sqrt{2}\rho \sqrt{2-\rho {}^{2}}}\right] ^2\mathrm {d}s\\&\quad + \int \limits _{0}^{L}\frac{K_{F}}{2}\left[ \vartheta ^{\prime }+ \frac{\sqrt{2}(\rho ^{2})'+4\big [({\tilde{l}}^{1D}-{\tilde{l}}^{1S}) +(\rho ^{2}-1)({\tilde{l}}^{2S}-{\tilde{l}}^{2D})\big ]}{2\sqrt{2} \rho \sqrt{2-\rho ^{2}}}\right] ^2 \mathrm {d}s . \end{aligned} \end{aligned}$$

(20)

The basic properties of the energy are preserved during the asymptotic process. The energy of both the micro- and the macro-models (5) and (20), respectively, is invariant under superimposed rigid body motions. Also, the extensional floppy mode of the discrete model, see (6), transfers to the continuum. Namely, if $\rho '=\vartheta '={{\tilde{l}}}^{\mu \nu }=0$, a constant stretch $\rho (s)=K \in (0,\sqrt{2})$ can still be present without causing any change in the deformation energy.

The above choice of the scaling parameters is such that $k_{F}/k_{E}\thickapprox \varepsilon ^{2}$ asymptotically, as $\varepsilon \rightarrow 0$. This means that the extensional springs stiffen much faster than the rotational ones as $\varepsilon \rightarrow 0$.

Let us define the deformation energy density $\psi$ as the integrand of (20). For the energy to be stationary, the necessary conditions are obtained by the variation of the deformation energy functional (20). To begin with, we can also carry out only the variation with respect to $\tilde{l}^{\mu \nu }$. This results in a linear system of four equations given by $\partial \psi / \partial {{\tilde{l}}}^{\mu \nu }=0$ in which $\tilde{l}^{\mu \nu }$ are the unknowns. Introducing the abbreviations

$$\begin{aligned} C_{1}=\frac{2K_F}{4K_{F}(\rho ^{2} -2)- K_{E}\rho ^{2}} ,\quad C_{2}=\frac{2\sqrt{2-\rho ^{2}}K_F}{K_{E}\left( \rho ^{2}-2\right) -4K_{F}\rho ^{2}} , \end{aligned}$$

(21)

some necessary conditions for equilibrium are that

$$\begin{aligned} {\tilde{l}}^{\mu D}=\frac{\sqrt{2}}{2}\rho \left[ \rho 'C_1+(-1)^{\mu -1} \vartheta ^{\prime }C_{2}\right] ,\quad {\tilde{l}}^{\mu S}=\frac{\sqrt{2}}{2}\rho \left[ -\rho 'C_{1}+(-1)^{\mu } \vartheta ^{\prime }C_{2}\right] . \end{aligned}$$

(22)

To solve for ${{\tilde{l}}}^{\mu \nu }$, we made use of a computer algebra program. Note that ${\tilde{l}}^{1D}=-{\tilde{l}}^{1S}$ and ${\tilde{l}}^{2D}=-{\tilde{l}}^{2S}$. Moreover, if $\chi ^{\prime }=\rho e_x$ with $\rho = K \in (0,\sqrt{2})$, it follows from (22) that ${\tilde{l}}^{\mu \nu }=0$. Hence, the independent conditions for the extensional floppy mode are that $\rho '=\vartheta '=0$. We further remark that, if $\vartheta '=0$, then, from (22), we have that $l^{1D}=l^{2D}$ and $l^{1S}=l^{2S}$.

Expanding the brackets in (20), it can readily be seen that the energy contains linear and quadratic terms in $\tilde{l}^{\mu \nu }$. Asking the coefficient of $({{\tilde{l}}}^{\mu \nu })^2$ to be strictly positive, the total deformation energy functional (20) is strictly convex in $l^{\mu \nu }$. Thus, convexity is equivalent to the condition that

$$\begin{aligned} { \frac{K_{E}}{K_{F}}>2\left( 1+\frac{1}{\rho ^{2}-2}-\frac{1}{\rho ^{2}}\right) . } \end{aligned}$$

(23)

Since the right-hand side of the inequality (23) is strictly negative for $\rho \in (0,\sqrt{2})$, the inequality is always satisfied. Accordingly, the set of micro-strains (22) minimizes the deformation energy (20).

By substituting the results (22) into (20), we perform a kinematic reduction resulting in the deformation energy functional of the pantographic beam

$$\begin{aligned} {\mathcal {E}}=\int \limits _{0}^{L}K_{E}K_{F}\left[ \frac{\rho ^{2}-2}{\rho ^{2}\left( K_{E}-4K_{F}\right) -2K_{E}}{\vartheta ^{\prime }}^2+ \frac{\rho ^{2}}{\left( 2-\rho ^{2}\right) \left[ \rho ^{2}\left( K_{E}-4K_{F}\right) +8K_{F}\right] }{\rho ^{\prime }}^2\right] \mathrm {d}s , \end{aligned}$$

(24)

which merely depends on the placement function $\chi$. Notice that the complete second gradient $\chi ^{\prime \prime }$ contributes to the deformation energy. Indeed, besides the term $\bigl (\chi _{\perp }^{\prime }\cdot \chi ^{\prime \prime }\bigr )$ being related to the material curvature $\vartheta '$ by means of (11)${}_1$, also the term $\bigl (\chi ^{\prime } \cdot \chi ^{\prime \prime }\bigr )$ appears which in turn is related to the stretch gradient $\rho '$ given by the relation (24)${}_2$. We further remark that the bending stiffness in (24), i.e. the coefficient of $\vartheta '^2$, does not only depend on the scaled stiffnesses of the elements of the microstructure, but also on $\rho$. An analogous observation can be done for the coefficient of $\rho '^{2}$. Besides, we notice that the deformation energy (24) is strictly positive for $0<\rho <\sqrt{2}$ and $\vartheta ',\rho ^\prime$ different from zero, as so are the coefficients of $\vartheta '$ and $\rho ^\prime$ in (24).

In the limit $\rho \rightarrow \sqrt{2}$, the energy (24) reveals a phase transition of the model. While the bending stiffness, i.e. the coefficient of $\vartheta '^2$, tends to zero, the coefficient of $\rho '^2$ tends to infinity. As we assumed boundedness of the energy, the stretch gradient $\rho '$ must therefore tend to zero. Accordingly, the pantographic beam locally degenerates into a model of a uniformly extensible cable.

The pantographic beam problem can also be formulated by an augmented energy functional

$$\begin{aligned} \tilde{{\mathcal {E}}}={\mathcal {E}}+\int \limits _{0}^{L}\Lambda \cdot \left[ \chi ^{\prime }-\rho (\cos \vartheta e_x+\sin \vartheta e_y)\right] \mathrm {d}s . \end{aligned}$$

(25)

in which the fields $\chi$, $\rho$, and $\vartheta$ are regarded as independent kinematic descriptors. We define ${\tilde{\Psi }}$ as the sum of $\Psi$ and the integrand in Eq. (25). The Lagrange multiplier field $\Lambda$ enforces weakly the relations (10). The procedure for obtaining the corresponding Euler–Lagrange equations, not needed for our purposes and thus also not reported here, leads to the following boundary conditions in strong non-dual form

$$\begin{aligned} \begin{aligned}&\mathrm {(n)}\ \ \rho ^{\prime }(0) =0 \vee \mathrm {(e)}\ \ \rho (0)=\rho _{0}\ , \qquad \ \ \mathrm {(n)}\ \ \rho ^{\prime }(L)=0 \vee \mathrm {(e)}\ \ \rho (L)=\rho _{L} \\&\mathrm {(n)}\ \ \vartheta ^{\prime }(0)=0\vee \mathrm {(e)}\ \ \vartheta (0)=\vartheta _{0\ }, \qquad \ \mathrm {(n)}\ \ \vartheta ^{\prime }(L)=0\vee \mathrm {(e)}\ \ \vartheta (L)=\vartheta _{L} . \end{aligned} \end{aligned}$$

(26)

By (n) and (e), we denote natural and essential boundary conditions, respectively. The conditions for the Lagrange multiplier field are given in strong dual form

$$\begin{aligned} \Lambda (0)\cdot \delta \chi (0)=0\ ,\qquad \Lambda (L)\cdot \delta \chi (L)=0\ , \end{aligned}$$

(27)

which must hold for any kinematically admissible variation $\delta \chi$ of $\chi$. Let us now make explicit the sets of boundary conditions entailing $\vartheta '=0$ everywhere. To this aim, let us consider the following sets of kinematic quantities evaluated at the boundary: (1) $\{\left. \chi \right| _{0\wedge L}\cdot e_x,\mathrm {with}\ \Vert \chi _0-\chi _L\Vert <\sqrt{2}L\}$, (2) $\{\left. \chi \right| _{0\veebar L}\cdot e_x,\left. \rho \right| _{0\veebar L}<\sqrt{2}\}$, and (3) $\{\left. \chi \right| _{0\vee L}\cdot e_x,\left. \rho \right| _{0\vee L}<\sqrt{2}\}$, with $\veebar$ denoting the logical disjunction. If sets 1, 2, or 3 above are fixed as essential boundary conditions, we get $\vartheta '=0$, with $\vartheta$ being undetermined, unless the condition $\left. \vartheta \right| _{0\vee L}=\vartheta _0$ is enforced. In particular, fixing sets 1 or 2 above results in the extensional floppy mode.

2.4 Simplifications of the energy

The choice $\kappa<3\vee \eta < 1$ in Eq. (19), including $\kappa<3\veebar \eta < 1$ or even $\kappa<3 \wedge \eta <1$, results in energy functionals which are rather uninteresting from the macroscopic point of view, and we do not intend to pay them further attention. The choice $\kappa =3$ and $\eta =1$ in (19) is such that the energies deriving from all other possible choices can be obtained from the energies (20) and (24) found by means of it.

Case ${\varvec{\kappa }}{\varvec{<3}}{\varvec{\vee }}{\varvec{\eta }} \mathbf{< 1}$. The cases where $\kappa<3\veebar \eta < 1$ or even $\kappa<3 \wedge \eta <1$ are obtained by computing the limits of (24) for $K_E \rightarrow 0\veebar K_F \rightarrow 0$ or $K_E \rightarrow 0 \wedge K_F \rightarrow 0$, respectively. All cases result in a trivial null-energy functional which is rather uninteresting for further analysis. The same trivial cases are achieved when choosing vanishing stiffnesses $k_E,k_F$ already in the micro-model.

Case ${\varvec{\kappa }} {\varvec{> 3\wedge }}{\varvec{\eta }} \mathbf{= 1}$. This scaling is obtained by computing the limit of (24) by letting $K_{E}\rightarrow \infty$. Using l’Hospital’s rule, this results in

$$\begin{aligned} K_{F}\int \limits _{0}^{L}\left( R(\rho ){\vartheta '}^{2}+\frac{{\rho '}^2}{2 -\rho ^{2}}\right) \text{ d }s . \end{aligned}$$

(28)

with

$$\begin{aligned} R(\rho )={\left\{ \begin{array}{ll} 0 &{} \text {if }\rho =\sqrt{2}\\ 1 &{} \text {else} \end{array}\right. } . \end{aligned}$$

(29)

Moreover, this limit process leads to vanishing $C_1$ and $C_2$ in (21) and according to (22) even to vanishing ${\tilde{l}}^{\mu \nu }=0$. Hence, the very same energy can also be computed by just setting ${\tilde{l}}^{\mu \nu }=0$ in (20). The deformation energy (28) is given by two additive contributions, the first being the deformation energy of the Elastica [47]. Following the arguments from above, if $\rho \rightarrow \sqrt{2}$, then the continuum behaves locally like a uniformly extensible Elastica.

Note that this scaling captures the case in which the extensional springs become asymptotically so stiff to behave like rigid links in the limit. In this way, it is also possible to recover the homogenized energy for the pantographic slender system in Fig. 1 with rigid links in place of extensional springs. For a detailed computation, we refer to [37]. This suggests that interchanging $\varepsilon \rightarrow 0$ and $K_{E}\rightarrow \infty$ to $k_{E}\rightarrow \infty$ and $\varepsilon \rightarrow 0$ leads to the same deformation energy. Also for rigid links, the heuristic homogenization still gives a $o(\varepsilon ^0)$ discrete–continuum energy error.

Case ${\varvec{\kappa }} \mathbf{= 3}{\varvec{\wedge }}{\varvec{\eta }} {\varvec{> 1}}$. Carrying out the limit of (24) for $K_{F}\rightarrow \infty$, again by applying l’Hospital’s rule, we get

$$\begin{aligned} \frac{K_{E}}{4}\int \limits _{0}^{L}\left[ \frac{2-\rho ^2}{\rho ^2}{\vartheta '}^2 +\frac{\rho ^2}{(2-\rho ^{2})^2}{\rho '}^2\right] \text{ d }s . \end{aligned}$$

(30)

The values of ${{\tilde{l}}}^{\mu \nu }$ expressed in terms of $\rho$ and $\vartheta$ which are computed the same way are

$$\begin{aligned} {{\tilde{l}}}^{\mu D} = -{{\tilde{l}}}^{\mu S} = \frac{\sqrt{2}}{2}\rho \left[ \frac{\rho '}{2(\rho ^2-2)} + (-1)^{\mu } \frac{\sqrt{2-\rho ^2}}{2 \rho ^2}\vartheta ' \right] . \end{aligned}$$

(31)

In a straightforward although a bit cumbersome computation, it can readily be seen that the micro-strains of (31) satisfy the two equalities

$$\begin{aligned} 2\vartheta ^{\prime }\rho \sqrt{2}\sqrt{2-\rho ^{2}} =(-1)^\mu \left( \sqrt{2}(\rho ^2)'+4 \Big [ ({\tilde{l}}^{\mu D}-{\tilde{l}}^{\mu S})+(\rho ^{2}-1)\Big ({\tilde{l}}^{(3-\mu )S}-{\tilde{l}}^{(3-\mu )D}\Big )\Big ]\right) . \end{aligned}$$

(32)

Similar to the previous case, the energy (30) can also be obtained by inserting the results (31) directly into (20). Due to (32), the two last terms of (20) with the factor $K_F$ do vanish. In fact, it is the homogenized energy of the pantographic slender system in Fig. 1 in which two opposite oblique springs are enforced to remain collinear.

Case ${\varvec{\kappa }} {\varvec{> 3}} {\varvec{\wedge \eta > 1}}$. If both $K_{E},K_{F}\rightarrow \infty$, the micro-strains must vanish but also satisfy (31). Consequently, also $\rho ^{\prime }=\vartheta ^{\prime }=0$ allowing the continuum only to deform in the extensional floppy mode which is characterized by a placement function such that $\chi ^{\prime }=\rho e_x$ with $\rho = K \in (0,\sqrt{2})$ together with a null-energy functional.

Linearization. Let the vector valued displacement field u be defined by $u(s)=\chi (s)-se_{x}$. From Taylor expansions, it follows that $\vartheta = \tan ^{-1}(u'\cdot e_y/(1+u'\cdot e_x)) = u^\prime \cdot e_y+o(\Vert u'\Vert ) = o(\Vert u'\Vert ^0)$, $\vartheta ^{\prime }=u^{\prime \prime }\cdot e_y+o(\Vert u'\Vert ^0)$, $\rho =[(1+u'\cdot e_x)^2 + (u'\cdot e_y)^2]^{\frac{1}{2}} = 1+u^\prime \cdot e_x+o(\Vert u'\Vert ) = 1 + o(\Vert u'\Vert ^0)$, and $\rho ^{\prime }=u^{\prime \prime }\cdot e_x+o(\Vert u'\Vert ^0)$. Hence, the energy of (24) is

$$\begin{aligned} \int \limits _{0}^{L}\left[ \frac{K_{E}K_{F}}{K_{E}+4K_{F}}\Vert u''\Vert ^{2} + o(\Vert u'\Vert ^0)\right] \mathrm {d}s . \end{aligned}$$

(33)

For small-strain hypothesis, the remainder $o(\Vert u'\Vert ^0)$ in Eq. (33) can be neglected. In the limit of $K_E\rightarrow \infty$, (33) leads to

$$\begin{aligned} K_{F}\int \limits _{0}^{L}\Vert u^{\prime \prime }\Vert ^{2}\mathrm {d}s . \end{aligned}$$

(34)

This energy corresponds to the deformation energy in (5) with $K^+=K^-$ of [12], in which opposite links and the rotational spring in between have been considered as a whole by linear and inextensible Euler–Bernoulli beams.

3 Computational aspects

In this section, the solution methods employed for the macro- and micro-model are briefly recalled.

3.1 Finite element formulation of the macro-model

From the stationarity condition of the energy, (25) follows the weak form equation

$$\begin{aligned} \int \limits _{0}^{L}\left( \frac{\partial {\tilde{\Psi }}}{\partial \rho } \delta \rho +\frac{\partial {\tilde{\Psi }}}{\partial \rho '} \delta \rho '+\frac{\partial {\tilde{\Psi }}}{\partial \vartheta '} \delta \vartheta '+\frac{\partial {\tilde{\Psi }}}{\partial \Lambda }\cdot \delta \Lambda +\frac{\partial {\tilde{\Psi }}}{\partial \chi '}\cdot \delta \chi '\right) \mathrm {d}s=0\ , \end{aligned}$$

(35)

with $\delta (\cdot )$ being kinematically admissible $(\cdot )$, which can then be solved numerically by a finite element method. The weak form package of the software $\mathrm {COMSOL \ Multiphysics}$, which implements standard finite element techniques (cf. [48, 49]), was used for the discretization and the subsequent solution procedure. Default settings were set. Essential boundary conditions, see (26) and (27), were not fulfilled by the basis functions but enforced by additional Lagrange multipliers. Quadratic Lagrangian polynomials were used as basis functions for the fields $\rho$, $\vartheta$, and $\chi$. For the field $\Lambda$ linear Lagrangian polynomials were applied. The mesh size was taken uniformly equal to L / 100. Energy convergence of solutions was successfully checked for the mesh size tending to 0.

3.2 Micro-model revisited

For solving the discrete micro-model directly and without making any of the hypotheses assumed for the derivation of the continuum model, except for the scaling law (19), it is much more convenient to introduce an alternative global, minimal set of generalized coordinates than the one used for the homogenization. The kinematics of the discrete system is entirely described by the nodal points $p_i$ and $p_i^{\mu \nu }$ depicted in Fig. 2 as white-filled circles. The Cartesian coordinates of the nodes are introduced as $2 \times 1$ matrices, i.e. as “row vectors”, in accordance with $x_i = (p_i \cdot e_x,p_i \cdot e_y)$ and $x^{\mu S}_i = (p^{\mu S}_i \cdot e_x,p^{\mu S}_i \cdot e_y)$. Hence, the $f=2(3N+2)$ generalized coordinates are

$$\begin{aligned} q = (x_0, \; \cdots , \; x_{N-1}, \; x_0^{1S}, \; \cdots , \; x_N^{1S}, \; x_0^{2S}, \; \cdots , \; x_N^{2S})^{\mathsf {T}} \in {\mathbb {R}}^{f} . \end{aligned}$$

(36)

Moreover, we introduce the Boolean connectivity matrices $C^{\mu S}_i, C^{\mu D}_i \in {\mathbb {R}}^{4 \times f}$ defined by the relations

$$\begin{aligned} q_i^{\mu S} = (x_i, \; x_i^{\mu S})^{\mathsf {T}} = C_i^{\mu S} q \quad q_i^{\mu D} = (x_i, \; x_{i+1}^{\mu S})^{\mathsf {T}} = C_i^{\mu D} q . \end{aligned}$$

(37)

These are the coordinates required to formulate the energy of the extensional springs. In the energies of the rotational springs, three points are involved. Accordingly, these coordinates are extracted by the connectivity matrices $C^{\mu }_i \in {\mathbb {R}}^{6 \times f}$ defined by

$$\begin{aligned} q_i^{1} = (x_i^{1S}, \; x_i, \; x_{i+1}^{2 S})^{\mathsf {T}} = C_i^{1} q \quad q_i^{2} = (x_i^{2S}, \; x_i, \; x_{i+1}^{1 S})^{\mathsf {T}} = C_i^{2} q . \end{aligned}$$

(38)

Fig. 2

Nodal points of the micro-model

Let $q^\text {e}= (x_1,y_1,x_2,y_2)^{\mathsf {T}} \in {\mathbb {R}}^4$ be the coordinates of two points interconnected by an extensional spring . Introducing the abbreviations $\Delta x = x_2 - x_1$ and $\Delta y = y_2 - y_1$, the distance between the two points is

$$\begin{aligned} l(q^\mathrm {e}) = \sqrt{\Delta x^2 + \Delta y^2} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} . \end{aligned}$$

(39)

The derivative with respect to $q^\mathrm {e}$ is the row vector

$$\begin{aligned} \frac{\partial l}{\partial q^\mathrm {e}}(q^\mathrm {e}) = \frac{1}{l(q^\mathrm {e})}(-\Delta x,-\Delta y,\Delta x,\Delta y) . \end{aligned}$$

(40)

For the energy contributions of the rotational springs, we introduce a standard element with three points with coordinates $q^\text {r}=(x_1,y_1,x_2,y_2,x_3,y_3) \in {\mathbb {R}}^6$ . With the abbreviations $\Delta x_1 = x_2-x_1$, $\Delta x_2 = x_3-x_2$, $\Delta y_1 = y_2-y_1$ and $\Delta y_2 = y_3-y_2$, the distances between the respective points are

$$\begin{aligned} l_1(q^\text {r}) = \sqrt{\Delta x_1^2 + \Delta y_1^2} , \quad l_2(q^\text {r}) = \sqrt{\Delta x_2^2 + \Delta y_2^2} , \end{aligned}$$

(41)

with the corresponding derivatives

$$\begin{aligned} \begin{aligned} \frac{\partial l_1}{\partial q^\mathrm {r}}(q^\mathrm {r})&= \frac{1}{l_1(q^\mathrm {r})} (-\Delta x_1, -\Delta y_1, \Delta x_1, \Delta y_1, 0, 0) , \\ \frac{\partial l_2}{\partial q^\mathrm {r}}(q^\mathrm {r})&= \frac{1}{l_2(q^\mathrm {r})} (0,0,-\Delta x_2, -\Delta y_2, \Delta x_2, \Delta y_2) . \end{aligned} \end{aligned}$$

(42)

The angles between the $e_x$-axis and the vectors $\Delta x_1 e_x + \Delta y_1 e_y$ and $\Delta x_2 e_x + \Delta y_2 e_y$, respectively, are introduced by the relations

$$\begin{aligned} \phi _1(q^\text {r}) = \tan ^{-1}\left( \frac{\Delta y_1}{\Delta x_1}\right) , \quad \phi _2(q^\text {r}) = \tan ^{-1}\left( \frac{\Delta y_2}{\Delta x_2}\right) \end{aligned}$$

(43)

with the corresponding derivatives

$$\begin{aligned} \begin{aligned} \frac{\partial \phi _1}{\partial q^\mathrm {r}}(q^\mathrm {r})&= \frac{1}{l_1(q^\mathrm {r})^2} (\Delta y_1, -\Delta x_1, -\Delta y_1, \Delta x_1, 0, 0) , \\ \frac{\partial \phi _2}{\partial q^\mathrm {r}}(q^\mathrm {r})&= \frac{1}{l_2(q^\mathrm {r})^2} (0,0,\Delta y_2, -\Delta x_2, -\Delta y_2, \Delta x_2) . \end{aligned} \end{aligned}$$

(44)

The deformation energy of the micro-model, see (5), is

$$\begin{aligned} \begin{aligned} {\mathcal {E}}_\varepsilon (q) = \sum _i\sum _{\mu ,\nu } \left( \frac{k_E}{2} \left[ l\big (C_i^{\mu \nu } q \big ) - \frac{\sqrt{2}}{2} \varepsilon \right] ^2 + \frac{k_F}{2}\left[ \phi _2\big (C_i^\mu q\big ) - \phi _1\big (C_i^\mu q\big )\right] ^2 \right) . \end{aligned} \end{aligned}$$

(45)

The variation of the deformation energy $\delta {\mathcal {E}}_\varepsilon = (\partial {\mathcal {E}}_\varepsilon /\partial q) \delta q$ determines the internal generalized forces of the micro-model as

$$\begin{aligned} \begin{aligned} \left[ f^\mathrm {int}_\varepsilon (q)\right] ^{\mathsf {T}} = \frac{\partial {\mathcal {E}}_\varepsilon }{\partial q} =&\sum _i\sum _{\mu ,\nu } \left( k_E \left[ l\big (C_i^{\mu \nu } q \big ) - \frac{\sqrt{2}}{2} \varepsilon \right] \frac{\partial l}{\partial q^e}\left( C_i^{\mu \nu } q\right) C_i^{\mu \nu } \right. \\&\left. +\, k_F \left[ \phi _2\big (C_i^\mu q\big ) - \phi _1\big (C_i^\mu q\big )\right] \left[ \frac{\partial \phi _2}{\partial q^\mathrm {r}}\big (C_i^\mu q\big ) - \frac{\partial \phi _1}{\partial q^\mathrm {r}}\big (C_i^\mu q\big )\right] C_i^\mu \right) . \end{aligned} \end{aligned}$$

(46)

Kinematic boundary conditions can be imposed by perfect bilateral constraints $0 = g(q) \in {\mathbb {R}}^m$ with the virtual work contribution $\delta W^\mathrm {c} = \delta g^{\mathsf {T}} \lambda = \delta q^{\mathsf {T}} W(q) \lambda$, where $W(q)^{\mathsf {T}}=\frac{\partial g}{\partial q}(q) \in {\mathbb {R}}^{m \times f}$ is the matrix of generalized force directions and $\lambda \in {\mathbb {R}}^m$ the vector of constraint forces. Together with the generalized internal forces (46), the constrained system is thus determined by the set of nonlinear equations

$$\begin{aligned} \begin{bmatrix} f^\mathrm {int}_\varepsilon (q) + W(q)\lambda \\ g(q) \end{bmatrix} = 0 \end{aligned}$$

(47)

which can be solved, at least locally, by a Newton–Raphson iteration scheme.

To compare the numerical results of the micro- and macro-model, beyond the micro–macro identification (12), the following micro–macro correspondences were taken into account

$$\begin{aligned} \rho \left( \frac{s_i+s_{i-1}}{2}\right) \leftrightarrow \frac{\Vert p_i-p_{i-1}\Vert }{\varepsilon }, \quad \vartheta \left( \frac{s_i+s_{i-1}}{2}\right) \leftrightarrow \vartheta _i = \tan ^{-1}\left[ \frac{(p_i-p_{i-1})\cdot e_y}{(p_i-p_{i-1})\cdot e_x}\right] , \end{aligned}$$

(48)

where $i=\{1,\dots ,N-1\}$. Accepting the stretch $\rho$ and the inclination angle $\vartheta$ to be the same for $s=0$ and $s=\frac{\varepsilon }{2}$ as well as for $s=L$ and $s=L-\frac{\varepsilon }{2}$, respectively, the micro–macro relations for the boundary conditions are given by

$$\begin{aligned} \rho (0)\leftrightarrow \frac{\Vert p_{1}-p_{0}\Vert }{\varepsilon } , \quad \rho (L)\leftrightarrow \frac{\Vert p_{N-1}-p_{N-2}\Vert }{\varepsilon } ,\quad \vartheta (0)\leftrightarrow \vartheta _1 , \quad \vartheta (L)\leftrightarrow \vartheta _{N-1} . \end{aligned}$$

(49)

While the micro-strains ${{\tilde{l}}}^{\mu \nu }$ are related by

$$\begin{aligned} {\tilde{l}}^{\mu \nu }(s_i)\leftrightarrow \frac{1}{\varepsilon ^2}\left( l\big (C_i^{\mu \nu } q \big )-\frac{\sqrt{2}}{2}\varepsilon \right) , \end{aligned}$$

(50)

the deformation energy density $\psi (s)$, which is the integrand of (24), is compared by the following relation

$$\begin{aligned} \psi (s_i) \leftrightarrow \sum _{\mu ,\nu } \frac{1}{\varepsilon } \left( \frac{k_E}{2} \left[ l\big (C_i^{\mu \nu } q \big ) - \frac{\sqrt{2}}{2} \varepsilon \right] ^2 + \frac{k_F}{2}\left[ \phi _2\big (C_i^\mu q\big ) - \phi _1\big (C_i^\mu q\big )\right] ^2 \right) . \end{aligned}$$

(51)

4 Numerical investigations

In this section, we analyse the numerical solutions of two particular examples, the semicircle test and the three-point test, see Fig. 3. The focus of interest is mainly to investigate how much the solutions of discrete models deviate from the solutions of the continuum. Mostly, the solutions of the continuum model are compared with the solutions of two discrete systems made out of 41 and 101 cells, respectively. If not otherwise stated, the values $K_E={10}\hbox { J\,m}$ and $K_F={1\times 10^{-4}}\hbox { J\,m}$ were applied. For the stiffnesses of the discrete system, the scaling laws (19) were applied for $\kappa = 3$ and $\eta = 1$, i.e. $k_E = K_E \varepsilon ^{-3}$ and $k_F = K_F\varepsilon ^{-1}$.

Fig. 3

Boundary conditions, reference configuration (gray), and deformed configuration (black) for a semicircle test, $\rho _0 = 1.405$, and b three-point test, ${\bar{u}} = {0.4}\hbox { m}$

4.1 Semicircle test

A cartoon of the semicircle test is given in Fig. 3a in which the reference and deformed configurations of the discrete system are depicted. The applied boundary conditions for both the micro- and the macro-models are specified in Table 1. For a beam of undeformed length $L = \pi \hbox { m}$, the positions of both ends are fixed at the distance of $2 \hbox { m}$ from each other. Additionally, the inclination angles $\vartheta (0)=-\vartheta (\pi ) = -\pi /2$ are prescribed such that the beam is forced to a curved configuration. Since the beam is a complete second gradient continuum, also the stretch $\rho$ can be prescribed. The stretch at both ends is given by $\rho (0)=\rho (L)=\rho _0$.

Table 1 Boundary conditions and constitutive parameters for micro- and macro-model

The deformed configurations of the beam for three different values of $\rho _0$ are shown in Fig. 4. For the sake of clarity, only the micro-model’s centre points, i.e. $x_i$ for $i=\{0,\dots ,N-1\}$, are plotted. Figure 4b shows the case $\rho _0 = 1$, for which the deformed shape of the continuum is a semicircle with radius $R = {1}\hbox { m}$. Due to the vanishing stretch gradient along the beam, i.e. $\rho '=0$ as it can be seen in Fig. 5b, the total length of the beam remains equal to $\pi$ m. Moreover, the material curvature takes uniformly the value $\vartheta ' = 1/R = 1 \hbox { m}^{-1}$. This corresponds with the solution of the Elastica for the same boundary conditions. Note that the inextensibility condition inherently contained in the formulation of the Elastica does not allow to prescribe another value of the stretch than $\rho = 1$. The slight deviations of the discrete systems from the circle are mainly due to the discrete “approximation” of the boundary conditions.

In Fig. 4a, c, the influence of the prescribed stretch becomes apparent. While for $\rho _0<1$, the beam is shortened, for $\rho _0>1$, the beam is elongated. Besides the fact that it would have been a rather difficult task to find a deformation energy (24) without homogenization, another convenient feature comes along with that procedure. It allows to develop a more intuitive understanding of boundary conditions which appear in higher-gradient continua. According to Table. 1, the boundary condition of the micro-model which corresponds to the prescription of the stretch is realized by fixing the distance between two adjacent centre points. If the distance between two adjacent points is increased with respect to the reference configuration, as shown in Fig. 3a, an accordion-like (homogeneous) extension is observed in the micro-model. Moreover, the boundary conditions of both stretch $\rho$ and inclination angle $\vartheta$ effect over a much larger distance than placement boundary conditions. This is precisely the characteristics contained in higher-gradient continua.

Fig. 4

Semicircle test. Deformed configurations of micro- and macro-model for a $\rho _0=0.5$, b $\rho _0=1$, and c $\rho _0=1.405$

In Fig. 5, the micro-stretch ${\tilde{l}}^{1D}$, the stretch $\rho$, and the deformation energy density $\psi$ are plotted for different values of $\rho _0$. The symmetry in the boundary conditions is reflected in the obtained curves parametrised by $s\in [0,\pi ]$. We have the symmetry $\rho (s)=\rho (\pi -s)$ and $\vartheta (s)=-\vartheta (\pi -s)$ (not plotted). Consequently, the stretch gradient and the material curvature are odd and even functions shifted by $\pi$, respectively, i.e. $\rho '(s)=-\rho '(\pi -s)$ and $\vartheta '(s)=\vartheta '(\pi -s)$. Since all these kinematical quantities appear quadratically in (24), also the deformation energy density $\psi$ is an even function shifted by $\pi$. Furthermore, (22) implies that ${\tilde{l}}^{1\nu }(s)=-{\tilde{l}}^{2\nu }(\pi -s)$. Accordingly, only the micro-stretch ${\tilde{l}}^{1D}$ is plotted in Fig. 5.

As discussed before, for $\rho _0 = 1$, the stretch $\rho$ and the material curvature $\vartheta '$ are uniformly equal to 1. It follows then immediately from (22) to (24) that the micro-stretch and the deformation energy density take the values

$$\begin{aligned} {\tilde{l}}^{1D}= -\frac{\sqrt{2}K_F}{K_E+4K_F} = -1.41\times 10^{-5}\hbox { m}^{-1} , \quad \psi = \frac{K_E K_F}{K_E+4K_F}= 1 \times 10^{-4} \hbox { J\,m} ^{-1} , \end{aligned}$$

(52)

which is indeed the case when considering Fig. 5.

Fig. 5

Semicircle test. Stretch $\rho$, micro-strain ${\tilde{l}}^{1D}$ and deformation energy density $\psi$ of micro- and macro-model for a $\rho _0=0.5$, b $\rho _0=1$, and c $\rho _0=1.405$

In Fig. 6a, the deformation energies are given as $\rho _0$ increases. While for the continuum model, the deformation energy attains a minimum at $\rho _0=1$, this does not hold true for the micro-model, whose deformation energies attain a minimum at $\rho _0>1$. The simulation was performed to come as close to the limit case $\sqrt{2} = 1.41$ as possible. The Lagrange multipliers satisfying the boundary conditions for $\rho$ can be considered as double forces acting at the ends of the beam. Their resultant value can be obtained by Castigliano’s theorem by taking the derivative of the deformation energy with respect to $\rho$, i.e. considering the inclination angles of the curves in Fig. 6a. The closer we come to $\sqrt{2}$, the steeper the curve gets, and the double forces tend to infinity. In this extreme, regions numerical analysis gets difficult.

Fig. 6

Semicircle test. a Deformation energy of the micro-model (5), ${\mathcal {E}}_\varepsilon$, and the macro-model (24), ${\mathcal {E}}$, and b discrete–continuum energy error on a log–log scale for different boundary conditions

After a qualitative comparison between macro- and micro-model, we quantify the error by the absolute value of the difference between the deformation energy of the macro-model ${\mathcal {E}}$ and the micro-model ${\mathcal {E}}_\varepsilon$. Within the micro–macro identification procedure, we accepted a discrete–continuum energy error $o(\varepsilon ^0)$, i.e. of order 1 in $\varepsilon$. Therefore, for a meaningful analysis, the energy error in the finite element solution of the macro-model (and/or that possibly done when considering the small-strain assumption) should be $o(\varepsilon )$, so as to be negligible with respect to the discrete–continuum energy error. In Fig. 6b, the discrete–continuum energy error is plotted against $1/\varepsilon$ for the boundary stretches $\rho _0=0.75$ and $\rho _0=1.25$. An error $o(\varepsilon ^0)$ which is in particular polynomial in $\varepsilon$ behaves asymptotically like $C\varepsilon$. Thereby C depends, among others, on the considered boundary conditions, the load and constitutive parameters. Considering its logarithm, we have $\log (C\varepsilon )=\log (C)-\log (1/\varepsilon )$. In other words, if the order of convergence in $\varepsilon$ is equal to 1, the log–log energy error plot should result in a line with slope $-1$ as $\varepsilon$ tends to 0. Figure 6b shows exactly this behaviour. It is therefore clear that, for the values of $\varepsilon$ considered in our micro-to-macro convergence analysis, the mesh size chosen in solving the continuum model (constant with $\varepsilon$) is fine enough.

4.2 Three-point test

The discrete system’s reference and deformed configuration of the three-point test are depicted in Fig. 3b. The applied boundary conditions for both the micro- and the macro-models are specified in Table. 1. For a beam of undeformed length $L = 1$ m at both ends, the positions and the inclination angles are fixed. In the centre of the beam, the vertical displacement ${\bar{u}}$ is prescribed. We remark that the small-strain approximation is for each point (to different extents) as less valid as $\bar{u}$ increases and, in what follows, we have been using the deformation energy (24).

Fig. 7

Three-point test. Micro- and macro-model for $\bar{u}=0.2 \hbox { m}$ a deformed configuration, b stretch $\rho$, c inclination angle $\vartheta$, and d deformation energy density $\psi$

In Fig. 7, the deformed configuration, the stretch $\rho$, the inclination angle $\vartheta$, and the deformation energy density $\psi$ are plotted for $\bar{u}= 0.2 \hbox { m}$. Also here, the symmetry in the boundary conditions is reflected in the obtained curves parametrised by $s\in [0,1]$. We have the symmetries $\rho (s)=\rho (1-s)$ and $\vartheta (s)=-\vartheta (1-s)$. According to the same arguments given in the semicircle test, the deformation energy density (24) must be an even function shifted by 0.5. Figure 7d shows that this property is fulfilled by both the micro- and the macro-models. Due to the symmetries appearing also in the micro-stretches, in Fig. 8, only the micro-stretch ${\tilde{l}}^{1D}$ is plotted for different values of $\bar{u}$.

Fig. 8

Three-point test. Micro-stretch ${\tilde{l}}^{1D}$ of the micro- and macro-model for a ${\bar{u}}=0.1$, b $\bar{u}=0.25 \hbox { m}$, and c $\bar{u}=0.4 \hbox { m}$

In Fig. 9, the stretches $\rho$ and the deformed configurations of the continuum are plotted for different values of $\bar{u}$. The remarkable phenomena appearing in this test are that for $\bar{u}=0.4408$, one has $\rho \thickapprox \sqrt{2}$ and $\rho '\thickapprox 0$ everywhere. Hence, if $\bar{u}$ is tending to some value slightly greater than 0.4408 m, then $\rho$ tends to $\sqrt{2}$. This is the value, where the model undergoes a phase transition from a pantographic beam to a uniformly extensible cable. Even though this phase transition can be interpreted from the deformation energy (24), it is not directly captured by the continuum model due to the restrictions made in the choice of minimal coordinates. The discrete model could overcome this problem. However, as we will see below, stability problems become an issue for which reason the numerical solution procedure needs to be extended.

Fig. 9

Three-point test. a Stretch $\rho$ and b deformed configuration of macro-model

In Fig. 10, the deformation energy $\bar{u}=0.2 \hbox { m}$ as $K_E$ and $K_F$ increase. The red lines indicate the total deformation energy as the kinematic constraints corresponding to $K_E\rightarrow \infty$ and to $K_F\rightarrow \infty$ are enforced. These values are asymptotes for the black curves, indicating that the energy of the macro-model in (24), as $K_E\rightarrow \infty$, converges to that in (28) and the energy of the micro-model (5) converges to that of the same system with extensional springs replaced by rigid links. Let us consider Fig. 10a. For $\varepsilon \rightarrow 0$, the asymptotes (red lines) related to the micro-model converge to that of the macro-model, as well as the black curves do. Therefore, in agreement to what has been suggested by heuristic analytical derivations, Fig. 10a indicates that interchanging $\varepsilon \rightarrow 0$ and $K_{E}\rightarrow \infty$ to $k_{E}\rightarrow \infty$ and $\varepsilon \rightarrow 0$ leads to the same deformation energy. Similar conclusions can be drawn for $K_F\rightarrow \infty$ and $k_F \rightarrow \infty$, referring to Fig. 10b.

Fig. 10

Three-point test. Deformation energy of the micro-model (5), ${\mathcal {E}}_\varepsilon$, and the macro-model (24), ${\mathcal {E}}$, for $\bar{u}={0.2}\hbox { m}$. The red lines indicate the deformation energies for cases in which the kinematic constraints corresponding to a $k_E \rightarrow \infty , K_E\rightarrow \infty$ or b $k_F\rightarrow \infty , K_F\rightarrow \infty$ are enforced (color figure online)

In Fig. 11a, the deformation energy is plotted as the prescribed displacement $\bar{u}$ increases. According to Castigliano’s theorem, the required pulling force in the centre of the beam corresponds with the slope of the deformation energy graph $\partial {\mathcal {E}}/\partial \bar{u}$, and in turn to the Lagrange multiplier employed to enforce the corresponding kinematic constraint. The required change in force to pull the beam further (proportional—with positive ratio—to the stiffness) is positive and decreasing, tending to zero for $\bar{u}$ approaching $0.405 \hbox { m}$ (see Fig. 12). Therefore, the Newton–Raphson scheme does not converge and the simulation cannot go further. Arc-length methods such as the Riks’ arc-length method [50] have to be implemented in order to overcome this problem which is beyond the scope of this article. The continuum model could be instead solved for values of $\bar{u}$ greater than ${0.405}\hbox { m}$, showing negative and decreasing stiffness blowing up to $-\infty$ for $\bar{u}$ approaching ${0.4408}\hbox { m}$. Figure 11b shows on a log–log scale the energy error between micro- and macro-model for decreasing length scale $\varepsilon$. Also for this test, the predicted discrete–continuum energy error is $o(\varepsilon ^0)$.

Fig. 11

Three-point test. a Deformation energy of the micro-model (5), ${\mathcal {E}}_\varepsilon$, and the macro-model (24), ${\mathcal {E}}$ and b discrete–continuum energy error on a log–log scale for different boundary conditions

Fig. 12

Three-point test. Plot of the Lagrange multiplier $\lambda$ employed to enforce the constraint $\chi (1/2)\cdot e_{y}=p_{N/2}\cdot e_{y}=\bar{u}$ (reaction force, rate of deformation energy with respect to $\bar{u}$ according to Castigliano’s theorem) versus $\bar{u}$ for the continuum model (continuous line) and the discrete one (dotted line: 41 cells; dashed line: 101 cells). Newton–Raphson scheme has been employed for solving the micro-model

5 Conclusions

With (24), the deformation energy of a complete second gradient 1D-continuum in plane was derived by applying Piola’s micro–macro identification procedure. The underlying family of discrete systems does not only lead to the deformation energy but also allows for an intuitive interpretation of non-standard boundary conditions which appear in this formulation.

The results of the kinematical quantities imply a qualitatively good agreement between the discrete and the continuum models, already for a moderate number of cells. A quantification of the discrepancy between the micro- and the macro-model is given by the energy error whose behaviour is determined within the homogenization procedure by the remainder in the energy (18). For the chosen scaling law, the remainder is of order 1 in $\varepsilon$. The same order was observed in the numerical evaluation of two particular examples. This analysis of the quality of a continuum model in approximating the behaviour of a discrete system is an important passage in establishing whether such a synthetic continuum description is satisfactory. It becomes of particular interest if such a system is used as a building block of a more complex structure. Indeed, like any beam element, it can be used for the analysis of assemblies of pantographic beams involving « generalized »constraints, distributed/lumped rotational/extensional springs, etc. We can conclude the following. Any discrete pantographic beam with given micro-stiffnesses, given micro-length scale $\varepsilon$, and given total length can be regarded as embedded within a family of discrete systems of variable micro-length scale together with the proposed scaling law. The corresponding macro-stiffnesses are immediately obtained by the scaling law. We then know that the quality in terms of energy of the continuum to represent the discrete system behaves linearly in the micro-length scale $\varepsilon$. Finally, the methodology and results of the present paper should serve as prototypes for the asymptotic analysis of more complex systems, especially for a class of bi-dimensional structures which generalizes pantographic fabrics (cf. [38]).

Appendix A

The terms $\theta _i$ and $\varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}$ are expanded up to first order by using definitions (1) and (2) together with expansions (13) and (14). According to (12) and (13), the vectors between two adjacent points are

$$\begin{aligned} p_{i+1}-p_i = \varepsilon \left[ \chi '(s_i) + \frac{\varepsilon }{2} \chi ''(s_i) + o(\varepsilon )\right] , \quad p_{i}-p_{i-1} = \varepsilon \left[ \chi '(s_i) - \frac{\varepsilon }{2} \chi ''(s_i) + o(\varepsilon )\right] . \end{aligned}$$

(53)

The arguments of the $\tan ^{-1}$ in (2) can be written as functions of $\varepsilon$

$$\begin{aligned} \begin{aligned} h_{i+1}(\varepsilon )&= \frac{(p_{i+1}-p_i)\cdot e_y}{(p_{i+1}-p_i)\cdot e_x} {\mathop {=}\limits ^{(53)_1}} \frac{\chi '(s_i)\cdot e_y + \frac{\varepsilon }{2} \chi ''(s_i)\cdot e_y + o(\varepsilon )}{\chi '(s_i)\cdot e_x + \frac{\varepsilon }{2} \chi ''(s_i)\cdot e_x + o(\varepsilon )} ,\\ h_{i}(\varepsilon )&= \frac{(p_{i}-p_{i-1})\cdot e_y}{(p_{i}-p_{i-1})\cdot e_x} {\mathop {=}\limits ^{(53)_2}} \frac{\chi '(s_i)\cdot e_y - \frac{\varepsilon }{2} \chi ''(s_i)\cdot e_y + o(\varepsilon )}{\chi '(s_i)\cdot e_x - \frac{\varepsilon }{2} \chi ''(s_i)\cdot e_x + o(\varepsilon )} . \end{aligned} \end{aligned}$$

(54)

It can readily be seen that $h_i(0) = h_{i+1}(0) = \left[ \chi '(s_i)\cdot e_y\right] /\left[ \chi '(s_i)\cdot e_x\right]$. Moreover,

$$\begin{aligned} \begin{aligned} h_{i+1}'(0) = -h'_{i}(0)&= \left. \frac{1}{2 [\chi ' \cdot e_x]^2}\left[ (\chi ''\cdot e_y)(\chi '\cdot e_x)- (\chi ''\cdot e_x)(\chi '\cdot e_y)\right] \right| _{s=s_i} \\&= \left. \frac{1}{2 [\chi ' \cdot e_x]^2} \chi ''\cdot (e_y \otimes e_x - e_x \otimes e_y) \cdot \chi ' \, \right| _{s=s_i} = \frac{\chi ''(s_i) \cdot \chi '_\bot (s_i)}{2 \left[ \chi '(s_i) \cdot e_x\right] ^2} . \end{aligned} \end{aligned}$$

(55)

For a real-valued function $h(\varepsilon )$, we can expand $\tan ^{-1}(h(\varepsilon )) = \tan ^{-1}(h(0)) + \frac{h'(0)}{1+h(0)^2} \varepsilon + o(\varepsilon )$. Since $h_i(0) = h_{i+1}(0)$, the first terms in the Taylor series of both $\tan ^{-1}$ expressions in (2) coincide and we obtain

$$\begin{aligned} \theta _i&{=}&\left[ \frac{1}{1+h_{i+1}(0)^2}h_{i+1}'(0) - \frac{1}{1+h_{i}(0)^2}h_{i}'(0)\right] \varepsilon + o(\varepsilon ) \nonumber \\&{\mathop {=}\limits ^{(55)}}&\frac{1}{1+\left[ \frac{\chi '(s_i) \cdot e_y}{\chi '(s_i) \cdot e_x}\right] ^2} \frac{\chi ''(s_i) \cdot \chi '_\bot (s_i)}{\left[ \chi '(s_i) \cdot e_x\right] ^2} \varepsilon + o(\varepsilon ) \\= & {} \frac{\chi ''(s_i) \cdot \chi '_\bot (s_i)}{\Vert \chi '(s_i) \Vert ^2} \varepsilon + o(\varepsilon ) {\mathop {=}\limits ^{(11)}} \vartheta '(s_i) \varepsilon + o(\varepsilon ).\nonumber \end{aligned}$$

(56)

For the expansion (1), we first require the expansion of the norm of a vector valued function $a(\varepsilon )$, i.e. $\Vert a(\varepsilon )\Vert = \Vert a(0) \Vert + \frac{a(0) \cdot a'(0)}{\Vert a(0) \Vert } \varepsilon + o(\varepsilon )$. Taking $a(\varepsilon )$ to be the expansions appearing in the squared brackets of (53) and considering that $\rho (s) = \Vert \chi '(s) \Vert$, we can write

$$\begin{aligned} \Vert p_{i\pm 1} - p_i \Vert = \varepsilon \left[ \Vert \chi '(s_i)\Vert \pm \frac{\chi '(s_i) \cdot \chi ''(s_i)}{\Vert \chi '(s_i) \Vert } \frac{\varepsilon }{2} + o(\varepsilon )\right] = \varepsilon \left[ \rho (s_i) \pm \rho '(s_i)\frac{\varepsilon }{2} + o(\varepsilon )\right] . \end{aligned}$$

(57)

Consequently, the expansion of the squared expression of (57) is

$$\begin{aligned} \Vert p_{i\pm 1} - p_i \Vert ^2 = \varepsilon ^2 \left[ \Vert \chi '\Vert ^2 \pm (\chi ' \cdot \chi '') \varepsilon + o(\varepsilon )\right] _{s=s_i} = \varepsilon ^2 \left[ \rho ^2 \pm \rho \rho ' \varepsilon + o(\varepsilon )\right] _{s=s_i} . \end{aligned}$$

(58)

Using (15), (57), and (58) in the argument of $\cos ^{-1}$ of (1)$_{2}$, we can compute

$$\begin{aligned} \begin{aligned} h^{1S}(\varepsilon )&= \frac{\Vert p_i - p_{i-1}\Vert ^2 + (l_i^{1S})^2 - (l_{i-1}^{2D})^2}{2 l_i^{1S} \Vert p_i - p_{i-1}\Vert } \\&= \left. \frac{\varepsilon ^2 \left[ \rho ^2-\rho \rho ' \varepsilon + \sqrt{2}\varepsilon ({\tilde{l}}^{1S}-{\tilde{l}}^{2D}) + o(\varepsilon )\right] }{\varepsilon ^2 2 \left[ \frac{\sqrt{2}}{2} + {\tilde{l}}^{1S} \varepsilon + o(\varepsilon )\right] \Big [\rho - \rho ' \frac{\varepsilon }{2} + o(\varepsilon )\Big ]}\right| _{s=s_i} \\&= \left. \frac{\rho ^2+ \varepsilon \left[ \sqrt{2}({\tilde{l}}^{1S}-{\tilde{l}}^{2D}) - \rho \rho '\right] + o(\varepsilon )}{\sqrt{2}\rho + \varepsilon \big (2 {\tilde{l}}^{1S} \rho - \frac{\sqrt{2}}{2} \rho '\big )+ o(\varepsilon )}\right| _{s=s_i} . \end{aligned} \end{aligned}$$

(59)

Similarly, the expansions of the arguments of $\cos ^{-1}$ appearing in (1)$_{1,3,4}$ are

$$\begin{aligned}&h^{1D}(\varepsilon ) = \left. \frac{\rho ^2+ \varepsilon \left[ \sqrt{2}({\tilde{l}}^{1D}-{\tilde{l}}^{2S}) + \rho \rho '\right] + o(\varepsilon )}{\sqrt{2}\rho + \varepsilon \big (2 {\tilde{l}}^{1D} \rho + \frac{\sqrt{2}}{2} \rho '\big )+ o(\varepsilon )}\right| _{s=s_i} \end{aligned}$$

(60)

$$\begin{aligned}&h^{2S(D)}(\varepsilon ) = \left. \frac{\rho ^2+ \varepsilon \left[ \sqrt{2}({\tilde{l}}^{2S(D)}-{\tilde{l}}^{1D(S)}) - \rho \rho '\right] + o(\varepsilon )}{\sqrt{2}\rho + \varepsilon \big (2 {\tilde{l}}^{2S(D)} \rho - \frac{\sqrt{2}}{2} \rho '\big )+ o(\varepsilon )}\right| _{s=s_i} \end{aligned}$$

(61)

All functions are of the form $h^{\mu \nu }(\varepsilon )=\left[ a+\varepsilon b^{\mu \nu } + o(\varepsilon )\right] /\left[ c+\varepsilon d^{\mu \nu } + o(\varepsilon )\right]$ with $h^{\mu \nu }(0)=a/c$ and $(h^{\mu \nu })'(0)=(b^{\mu \nu }c-d^{\mu \nu }a)/c^2$. The angles $\varphi _i^{\mu \nu }$ can thus be expanded as

$$\begin{aligned} \varphi _i^{\mu \nu } = \cos ^{-1}\left[ h^{\mu \nu }(0)\right] - \frac{\varepsilon }{\sqrt{1-h^{\mu \nu }(0)^2}}(h^{\mu \nu })'(0) + o(\varepsilon )\,. \end{aligned}$$

(62)

Expanding $\varphi _{i}^{\mu S}-\varphi _{i}^{\mu D}$ with the help of (62), the first term thereof cancels. Inserting the derivative with respect to $\varepsilon$ evaluated at $\varepsilon =0$ of (59) and (60)${}_1$, we obtain

$$\begin{aligned} \varphi _i^{1S}-\varphi _i^{1D}&= \left. \frac{ \sqrt{2}\rho \left[ 2\rho \rho '+\sqrt{2}({\tilde{l}}^{1D}-{\tilde{l}}^{2S} +{\tilde{l}}^{2D}-{\tilde{l}}^{1S})\right] + \rho ^2\left[ 2\rho ({\tilde{l}}^{1S}-{\tilde{l}}^{1D})-\sqrt{2}\rho '\right] }{2\rho ^2\sqrt{1-\frac{\rho ^2}{2}}}\right| _{s=s_i}\varepsilon + o(\varepsilon ) \nonumber \\&= \left. \frac{ \frac{\sqrt{2}}{2}\rho \rho '+({\tilde{l}}^{2D}-{\tilde{l}}^{2S})+ (\rho ^2-1)({\tilde{l}}^{1S}-{\tilde{l}}^{1D})}{\rho \sqrt{1-\frac{\rho ^2}{2}}} \right| _{s=s_i}\varepsilon + o(\varepsilon ) \,. \end{aligned}$$

(63)

In the same manner, we obtain the expansion for the difference in angles of the oblique springs indexed by $\mu = 2$. Moreover, we manipulate the expression slightly to get rid of the fractions within the nominator and denominator which results in

$$\begin{aligned} \varphi _i^{2S}-\varphi _i^{2D} = \left. \frac{ \sqrt{2}(\rho ^2)'+4\big [({\tilde{l}}^{1D}-{\tilde{l}}^{1S})+ (\rho ^2-1)({\tilde{l}}^{2S}-{\tilde{l}}^{2D})\big ]}{2 \sqrt{2}\rho \sqrt{2-\rho ^2}}\right| _{s=s_i} \varepsilon + o(\varepsilon ) . \end{aligned}$$

(64)