1 Introduction

Nonlinearity is a fascinating feature of nature whose importance has been thought of for many years when considering large-amplitude wave motions observed in various fields ranging from fluids and plasmas to solid-state, biological and chemical systems. In that respect, solitons represent one of the most striking aspects of nonlinear phenomena [1].

The concept of soliton was introduced to science, in the first time, by John Scoot Russell in 1834. After its discovery, soliton has become an important item of research in diverse fields of Physics and Engineering. In fact, Solitons are a special class of pulse-shaped waves that propagate without changing their shape in nonlinear dispersive media. They retain their form after mutual interactions [2,3,4,5]. Thus, solitons are investigated in various nonlinear evolutions equations such as the generalized Zakharov–Kuznetsov equation [6], the coupled Korteweg-de-Vries equations [7], the coupled discrete nonlinear Schrödinger equations [8], the Fornberg–Whitham equation [9], just to cite a few. These nonlinear evolution equations described several nonlinear phenomena, among these nonlinear phenomena, the nonlinear electrical transmission lines is the specifically one which attracts our attention.

Moreover, many scientists around the world have been studied the nonlinear electrical lattice. For example, Hirota and Suzuki were the first who built the first nonlinear and dispersive line [10]. Further, Nagashima and Amagishi were the first to simulate the propagation of solitons in this medium [11]. Many studies have been undertaken in nonlinear electrical transmission lines [12,13,14,15,16,17,18]. Furthermore, Patrick [19] studied observation of nonlinear localized modes in electrical lattice. Recently, Togueu et al. [2, 4] studied a supratransmission phenomenon in a discrete electrical lattice with nonlinear dispersion and shown that in upper and lower forbidden band gab, the nonlinear Salerno equation can be derived and solutions were found under some conditions.

Therefore, in order to obtain solitons in the nonlinear lattice with nonlinear dispersion, many direct and effective methods were presented such as the auxiliary equations methods [20], The sine–cosine Method [21, 22], the extended tanh method [23], the (G/G)-expansion method [24,25,26,27], the homogeneous balance method [28, 29], and many other methods are used for constructing solitons solutions [30,31,32]. Thus, further research has been carried out by a considerable number of researchers by means of the generalized Riccati equation mapping method [33,34,35,36]. For example, Boudoue et al. in [35] investigated traveling wave and solitons solutions in nonlinear electrical transmission lines. To pursue the same idea but with different model, we also investigate solitons in the forbidden band gab of a nonlinear discrete electrical lattice by means of the generalized Riccati equation mapping method. To reach such a goal, we present the paper as follows: In Sect. 2, we will give description of the generalized Riccati equation mapping method. In Sect. 3, we describe the model and the circuit equation. In Sect. 4, we apply the generalized Riccati equation mapping method to the equation found in Sect. 3 and the last section is devoted to concluding remarks.

2 Description of the generalized Riccati equation mapping method

We consider a given nonlinear partial differential equation for u(x, t) to be in the form

$$\begin{aligned} K(u, u_t, u_x, u_{xt}, u_{xx}, u_{tt})=0. \end{aligned}$$
(1)

Step 1 By means of traveling wave transformations \(u(x,t)=U(\xi ), \quad \xi =kx-ct\), Eq. (1) is transformed to the following ordinary differential equation:

$$\begin{aligned} G(U, U', U'', \ldots )=0, \end{aligned}$$
(2)

where primes denote the derivative with respect to \(\xi \).

Step 2 We seek the solution \(U(\xi )\) of Eq. (2) in the finite series form

$$\begin{aligned} U(\xi )=\sum ^m_{i=0}{a_i\psi ^i(\xi )}, \end{aligned}$$
(3)

where the parameter m is determined by balancing the linear derivative term(s) of highest order with the highest order nonlinear term(s) in Eq. (2) and \(a_i\), \(a_m\ne 0\) are real constants to be determined. The function \(\psi (\xi )\) expresses the solution of the following generalized Riccati equation:

$$\begin{aligned} \frac{\hbox {d}\psi (\xi )}{\hbox {d}\xi }=r+p\psi (\xi )+q\psi ^2(\xi ). \end{aligned}$$
(4)

Step 3 Substituting Eq. (3) together with Eq. (4) into Eq. (2) yields an algebraic equation involving powers of \(\psi (\xi )\) and equating the coefficients of each power of \(\psi (\xi )\) to zero gives a system of algebraic equations for \(a_i\) , r , p, and q.

Step 4 Solving the resulting system of algebraic equations with the aid of a computer algebra system, such as Mathematica or Maple, to determine these constants, we can get exact solutions depending on the sign of the discriminant \(\Delta =p^2 - 4qr\).

3 Model description and circuit equation

We consider the discrete electrical lattice as illustrated in Fig. 1. For \(n\ge 1\), the line can be considered as a set of elementary cells where each cell contains a series linear inductance \(L_1\) and a linear inductance \(L_2\) in parallel with the nonlinear capacitor \(C(V_n)\). Previous works have been done in the above electrical lattice in which the capacitance of the nonlinear capacitor is assuming to be a logarithmic nonlinearity for capacitance \( C(V_n)\) as [2]

$$\begin{aligned} C(V_n)=\hbox {AC}_0\frac{\hbox {ln}(1+\frac{V_n}{A})}{V_n}, \end{aligned}$$
(5)

where A and \(C_0\) take constant values.

Fig. 1
figure 1

Schematic representations of the electrical lattice

Full size image

Applying Kirchhoff’s laws leads to the system of nonlinear equations

$$\begin{aligned} A\frac{\partial ^2}{\partial t^2}\hbox {ln}(1+\frac{V_n}{A})=u_0^2(V_{n+1}+V_{n-1}-2V_n)-\omega _0^2V_n, \end{aligned}$$
(6)

with \(u_0^2= \frac{1}{L_{1}C_{0}}\) and \(\omega _0^2=\frac{1}{L_{2}C_{0}}\).

Linearizing Eq. (6) with respect to \(V_n\) and assuming that a sinusoidal wave of \(V_n\) is proportional to \(\exp [i(kn-wt)]\) where k and w are respectively the angular frequency and wave number, the following linear dispersion law is derived [2]

$$\begin{aligned} \omega ^2=\omega _0^2+4u_0^2\;\hbox {sin}^2\left( \frac{k}{2}\right) . \end{aligned}$$
(7)

The above relation admits the lower cutoff mode frequency when \(k=0\) and upper cutoff frequency when \(k=\pi \). Graphical representation of the forbidden band gabs is shown in Fig. 2. Now, we restrict our analysis to slow temporal variations of the envelope and look for a solution of Eq. (6) in the form

$$\begin{aligned} V_n(t)=\psi _n e^{i(wt-kn)}+\hbox {c.c.} \end{aligned}$$
(8)

where c.c. stand for complex conjugate.

Fig. 2
figure 2

The linear relation of two forbidden band gabs corresponding to the shaded areas for \(u_0=1.768\times 10^6\) rad/s and \(w_0=2.127\times 10^6\) rad/s

Full size image

Consider the above relations, the nonlinear Salerno equation is derived [2]

$$\begin{aligned}&i\frac{d\phi _n}{d\tau }+(1+\mu \mid \phi _n\mid ^2)\nonumber \\&\quad \times (\phi _{n+1}e^{ik}+\phi _{n-1}e^{-ik}))-\nu \mid \phi _n\mid ^2\phi _n=0, \end{aligned}$$
(9)

with \( \psi _{n}= \phi _{n}\exp [i\tau (\omega ^2 - \omega _{0}^2 - 2u_{0}^2)/u_{0}^2]\), \(\tau = u_{0}^2 t/2\omega \), \(\mu = 1/A^2\), \(\nu =\frac{2\omega ^2 + \omega _{0}^2 + 2u_{0}^2}{u_{0}^2A^2}\), and \(n\ge 1\). \(\nu \) and \(\mu \) are respectively the nonlinear cubic and nonlinear dispersion coefficients. From this equation, in the upper forbidden band gab, we insert the following ansatz of stationary solutions in the form \(\phi _n=\chi _n e^{-i\nu \tau }\) and the following set of nonlinear coupled algebraic equations is obtained [2]

$$\begin{aligned} u_{n+1}+u_{n-1}=-\frac{\nu _1}{\mu }u_n+(\nu +\frac{\nu _1}{\mu })\frac{u_n}{1+u_n^2}, \end{aligned}$$
(10)

with \(\nu _1=\frac{2\omega ^2_{\mathrm{max}} + \omega _{0}^2 + 2u_{0}^2}{u_{0}^2A^2}\). Applying the continuum approximation by assuming that \(u_n\) varies slowly from the unit section to another and replace the discrete index n by a continuous variable x and use the Taylor expansion for the \(u_{n+1}\) under conditions \(u_n\ll 1\), it leads to [2]

$$\begin{aligned} \frac{d^2u}{dx^2}-(\nu -2)u-(\nu +\frac{\nu _1}{\mu })(-u^3+u^5)=0. \end{aligned}$$
(11)

4 Application of the generalized Riccati equation mapping method to the electrical lattice

To obtain more exact solutions by using the generalized Riccati equation mapping method presented in [3], we use the traveling wave transformations

$$\begin{aligned}&\xi =\sqrt{k}(x-ct), \quad u(x,t)=U(\xi ), \nonumber \\&U(\xi )=\pm W^{1/2}(\xi ), \end{aligned}$$
(12)

and Eq. (11) becomes

$$\begin{aligned}&-\frac{k}{4W}(\frac{\hbox {d}W}{\hbox {d}\xi })^2+\frac{k}{2}\frac{\hbox {d}^2W}{\hbox {d}\xi ^2}\nonumber \\&-(\nu -2)W-(\nu +\frac{\nu _1}{\mu })(-W^2+W^3)=0. \end{aligned}$$
(13)

We determine the parameter m by balancing the highest derivative term and the highest nonlinear term in Eq. (13), it leads to \(m=1\). Substituting Eqs. (3) and (4) into Eq. (13) and equating all the coefficients of power of \(\psi (\xi )\) to be zero, we obtain the algebraic system

$$\begin{aligned}&\psi ^0: -\frac{k}{4}a_1^2r^2+\frac{k}{2}a_0a_1pr-(\nu -2)a_0^2\nonumber \\&\quad -(\nu +\frac{\nu _1}{\mu })(-a_0^2+a_0^4)=0, \end{aligned}$$
(14)
$$\begin{aligned}&\psi ^1: -2(\nu -2)a_0a_1+\frac{k}{2}a_0a_1p^2\nonumber \\&\quad +\frac{1}{2}(2ka_0a_1q+ka_1^2p)r-\frac{k}{2}a_1^2rp\nonumber \\&\quad -(\nu +\frac{\nu _1}{\mu })(-3a_0^2a_1+4a_0^3a_1)=0, \end{aligned}$$
(15)
$$\begin{aligned}&\psi ^2: -(\nu -2)a_1^2+\frac{k}{2}a_0a_1pq \nonumber \\&\quad +\frac{1}{2}(2ka_0a_1q+ka_1^2p)p+ka_1^2qr\nonumber \\&\quad -(\nu +\frac{\nu _1}{\mu })(-3a_0a_1^2+6a_0a_1^2)\nonumber \\&\quad -\frac{k}{4}a_1^2(2rq+p^2)=0, \end{aligned}$$
(16)
$$\begin{aligned}&\psi ^3: \frac{1}{2}(2ka_0a_1q+ka_1^2p)+\frac{1}{2}ka_1^2pq\nonumber \\&\quad -(\nu +\frac{\nu _1}{\mu })(-a_1^3+4a_0a_1^3)=0, \end{aligned}$$
(17)
$$\begin{aligned}&\psi ^4:\frac{3}{4}ka_1^2q^2-(\nu +\frac{\nu _1}{\mu })a_1^4=0, \end{aligned}$$
(18)

where \(a_0, a_1, k\) are unknown parameters.

Solving the system of algebraic Eqs. (14–18) and using the computer programs such as Maple or MATLAB under condition \(\nu +\frac{\nu _1}{\mu }=\frac{16}{3}(\nu -2)\), we obtain the following constraint relations:

$$\begin{aligned} a_0= & {} \frac{3}{8}+\frac{3}{8}\sqrt{\frac{p^2}{p^2-4qr}}, \quad a_1=\frac{3}{4}\sqrt{\frac{q^2}{p^2-4qr}},\nonumber \\ k= & {} \frac{4(\nu -2)}{p^2-4qr}. \end{aligned}$$
(19)

Based on this case and on solutions given in [12], one can easily obtain new type of solutions shown as follows:

Type 1 When \(p^2-4pr>0\) and \(pq\ne 0\) (or \(qr\ne 0\)), the solutions of Eq. (11) are

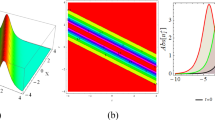
$$\begin{aligned} u_1(x,t)= & {} \pm \left\{ a_0-\frac{a_1}{2q} \left[ p+\sqrt{p^2-4qr} \tanh \right. \right. \nonumber \\&\left. \left. \times \left( \frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\right) \right] \right\} ^{\frac{1}{2}}, \end{aligned}$$
(20)

Graphical representation of Eq. (21) is given in Fig. 3. We obtain kink solutions for different values of constants.

$$\begin{aligned} u_2(x,t)= & {} \pm \left\{ a_0-\frac{a_1}{2q} \left[ p+\sqrt{p^2-4qr}\right. \right. \nonumber \\&\left. \left. \times \coth \left( \frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x{-}ct)\right) \right] \right\} ^{\frac{1}{2}},\end{aligned}$$
(21)
$$\begin{aligned} u_3(x,t)= & {} \pm \left\{ a_0-\frac{a_1}{4q} \left[ 2p+\sqrt{p^2-4qr}\right. \right. \nonumber \\&\left. \left. \times \left( \tanh \bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x-ct)\bigg ) \right. \right. \right. \nonumber \\&\left. \left. \left. \pm \cosh \bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x{-}ct)\bigg )\right) \right] \right\} ^{\frac{1}{2}}, \nonumber \\ \end{aligned}$$
(22)
$$\begin{aligned} u_4(x,t)= & {} \pm \left\{ a_0+\frac{a_1}{2q} \left[ -p+ \frac{\sqrt{(B^2-A^2)(p^2-4qr)}{+} A\sqrt{p^2-4qr}\cosh \bigg (\sqrt{p^2-4qr}\sqrt{k}(x{-}ct)\bigg )}{A\sinh \bigg (\sqrt{p^2-4qr}\sqrt{k}(x-ct)\bigg )+B}\right] \right\} ^{\frac{1}{2}},\quad \nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned} u_5(x,t)= & {} \pm \left[ a_0+\frac{2ra_1\cosh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )}{\sqrt{p^2-4qr}\sinh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )-p\cosh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )}\right] ^{\frac{1}{2}}, \end{aligned}$$
(24)

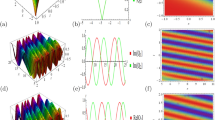
Graphical representation of the corresponding solutions is given in Fig. 4a, b for precise values of parameters. The obtained solutions are breathers.

$$\begin{aligned}&u_6(x,t)=\pm \left[ a_0-\frac{2ra_1\sinh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )}{p\sinh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )- \sqrt{p^2-4qr}\cosh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )}\right] ^{\frac{1}{2}},\quad \end{aligned}$$
(25)
$$\begin{aligned}&u_7(x,t)\nonumber \\&=\pm \left[ a_0{+}\frac{2ra_1\cosh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x{-}ct)\bigg )}{\sqrt{p^2-4qr}\sinh \bigg (\sqrt{p^2-4qr }\sqrt{k}(x-ct)\bigg ){-}p\cosh \bigg (\sqrt{p^2-4qr }\sqrt{k}(x-ct)\bigg )\pm i\sqrt{p^2-4qr}}\right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}&u_8(x,t)\nonumber \\&=\pm \left[ a_0{+}\frac{2ra_1\sinh \bigg (\frac{\sqrt{p^2-4qr}}{2}\sqrt{k}(x-ct)\bigg )}{{-}p \sinh \bigg (\sqrt{p^2-4qr}\sqrt{k}(x{-}ct)\bigg ){+}\sqrt{p^2-4qr}\cosh \bigg (\sqrt{p^2-4qr}\sqrt{k}(x{-}ct)\bigg )\pm \sqrt{p^2-4qr}}\right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(27)
Fig. 3
figure 3

Kink solutions of Eq. (21) for \(p=3\), \(q=2\), \(r=1\), \(\nu =3\) , a Kink-like solution for \(c=1\), b Antikink solution for \(c=1\) for the negative form, c Kink for \(c=0.1\), d Antikink for \(c=0.1\) with negative value

Full size image
Fig. 4
figure 4

Breathers solutions of Eq. (24) for \(p=2\), \(q=0.5\), \(r=1.5\), \(\nu =3.5\), \(B=2\), \(A=1\), a Breather for \(c=1\), b Antibreather for c=1 for negative form one, c Breather for \(c=0.1\), d Antibreather for c=0.1 in the negative form

Full size image

Graphical representation of the corresponding solutions is given in Fig. 5a–d. The obtained solutions are dark and bright.

$$\begin{aligned} u_{9}(x,t)=\pm \left[ a_0+\frac{4ra_1\sinh \bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x-ct)\bigg )\cosh \bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x -ct)\bigg )}{-2p\Gamma +2\sqrt{p^2-4qr}\cosh ^2\bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x - ct)\bigg )-\sqrt{p^2-4qr}}\right] ^{\frac{1}{2}}, \end{aligned}$$
(28)

where \(\Gamma =\sinh \bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x-ct)\bigg )\cosh \) \(\bigg (\frac{\sqrt{p^2-4qr}}{4}\sqrt{k}(x-ct)\bigg )\). A and B are two nonzero real constants with \(B^2-A^2>0\).

Fig. 5
figure 5

Dark and bright solutions of Eq. (27) for \(p=3\), \(q=0.2\), \(r=1.2\), \(\nu =3.5\), a Dark for \(c=1\), b Dark for \(c=1\), c Other form of Dark for \(c=0.1\), d Bright for \(c=0.1\)

Full size image

Type 2 When \(p^2-4pr<0\) and \(pq\ne 0\) (or \(qr\ne 0\)), the solutions of Eq. (11) are given by:

$$\begin{aligned} u_{10}(x,t)= & {} \pm \left[ a_0+\frac{a_1}{2q} \left( -p+\sqrt{4qr-p^2} \tan \right. \right. \nonumber \\&\left. \left. \times \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )\right) \right] ^{\frac{1}{2}}, \end{aligned}$$
(29)
$$\begin{aligned} u_{11}(x,t)= & {} \pm \left[ a_0-\frac{a_1}{2q} \left( p+\sqrt{4qr-p^2}\cot \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )\right) \right] ^{\frac{1}{2}}, \end{aligned}$$
(30)
$$\begin{aligned} u_{12}(x,t)= & {} \pm \left\{ a_0+\frac{a_1}{4q} \left[ -2p+\sqrt{4qr-p^2}\left( tan\bigg (\frac{\sqrt{4qr-p^2}}{4}\sqrt{k}(x-ct)\bigg ) -\coth \bigg (\frac{\sqrt{4qr-p^2}}{4}\sqrt{k}(x-ct)\bigg )\right) \right] \right\} ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} u_{13}(x,t)= & {} \pm \left\{ a_0+\frac{a_1}{2q} \left[ -p-\frac{\pm \sqrt{(A^2-B^2)(4qr-p^2)}- A\sqrt{4qr-p^2}\cos \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )}{A\sin \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )+B}\right] \right\} ^{\frac{1}{2}}, \end{aligned}$$
(32)
$$\begin{aligned} u_{14}(x,t)= & {} \pm \left[ a_0-\frac{2ra_1\cos \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}{\sqrt{4qr-p^2}\sin \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )+p\cos \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}\right] ^{\frac{1}{2}}, \end{aligned}$$
(33)
$$\begin{aligned} u_{15}(x,t)= & {} \pm \left[ a_0-\frac{2ra_1\sin \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}{p\sin \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )-\sqrt{4qr-p^2}\cos \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}\right] ^{\frac{1}{2}}, \end{aligned}$$
(34)
$$\begin{aligned} u_{16}(x,t)= & {} \pm \left[ a_0-\frac{2ra_1\cos \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}{\sqrt{4qr-p^2}\sin \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )+p\cos \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )\pm \sqrt{4qr-p^2}}\right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(35)
$$\begin{aligned} u_{17}(x,t)= & {} \pm \left[ a_0+\frac{2ra_1\sin \bigg (\frac{\sqrt{4qr-p^2}}{2}\sqrt{k}(x-ct)\bigg )}{-p \sin \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )+\sqrt{4qr-p^2}\cos \bigg (\sqrt{4qr-p^2}\sqrt{k}(x-ct)\bigg )\pm \sqrt{4qr-p^2}}\right] ^{\frac{1}{2}},\nonumber \\ \end{aligned}$$
(36)
$$\begin{aligned} u_{18}(x,t)= & {} \pm \left[ a_0+\frac{4ra_1\sin \bigg (\frac{\sqrt{4qr-p^2}}{4}\sqrt{k}(x-ct)\bigg )\cos \bigg (\frac{\sqrt{4qr-p^2}}{4}\sqrt{k}(x-ct)\bigg )}{-2p\Upsilon +2\sqrt{4qr-p^2}\cos ^2\bigg (\frac{\sqrt{4qr-p^2}}{4}\sqrt{k}(x-ct)\bigg )-\sqrt{4qr-p^2}}\right] ^{\frac{1}{2}}, \end{aligned}$$
(37)

where \(\Upsilon =\sin \bigg (\frac{\sqrt{4qr{-}p^2}}{4}\sqrt{k}(x{-}ct)\bigg )\cos \bigg (\frac{\sqrt{4qr{-}p^2}}{4}\sqrt{k}(x-ct)\bigg )\) and A and B are two nonzero real constants and satisfying \(B^2-A^2<0\).

Type 3 When \(r=0\) and \(pq\ne 0\), the solutions of Eq. (11) are

$$\begin{aligned} u_{19}(x,t)= & {} \pm \left[ a_0-\frac{a_1pd}{q\bigg (d+\cosh \big (p\sqrt{k}(x-ct)\big )-\sinh \big (p\sqrt{k}(x-ct)\big )\bigg )}\right] ^{\frac{1}{2}}, \end{aligned}$$
(38)
$$\begin{aligned} u_{20}(x,t)= & {} \pm \left[ a_0+\frac{a_1p\bigg (\cosh \big (p\sqrt{k}(x-ct)\big )+\sinh \big (p\sqrt{k}(x-ct)\big )\bigg )}{q\bigg (d+\cosh \big (p\sqrt{k}(x-ct)\big )+\sinh \big (p\sqrt{k}(x-ct)\big )\bigg )}\right] ^{\frac{1}{2}}, \end{aligned}$$
(39)

where d is an arbitrary constant.

5 Conclusion

Through this paper, using the generalized Riccati equation mapping method, various solutions are obtained for the nonlinear Salerno equation describing the nonlinear discrete electrical lattice in the forbidden band gabs. Some of these solutions are hyperbolic function solutions, other are trigonometric function solutions. Particularly, for some values of parameters, the obtained solutions are kink, anti-kink, dark, bright and breather solutions. These solutions are used for the information transmission through the electrical lattice. In the future work, we intend to apply another interesting method which can give more and new solutions.