1 Introduction

In 2015, Ionescu–Kruse derived a new two-component (N2C) system, modeling shallow-water waves by a variational approach in the Lagrangian formalism [6],

$$\begin{aligned} \left\{ \begin{array}{lc} u_{t}+3uu_{x}+v v_{x}=\left[ v^2\left( u u_{xx}+u_{xt}-\frac{1}{2}u_{x}^{2}\right) \right] _{x}, \\ v_{t} +(u v)_{x}=0, \end{array} \right. \nonumber \\ \end{aligned}$$
(1)

where \(x\in R\), \(t\in R\), u(x, t) represents the depth-averaged horizontal velocity, and v(x, t) is the free upper surface. Ionescu-Kruse [6] also showed that system (1) has a non-canonical Hamiltonian formulation and found its exact solitary wave solution. Recently, Dutykh [4] showed the existence of solitary and cnoidal-type solutions of system (1) through the method of the so-called phase-plane analysis. However, Ionescu-Kruse and Dutykh just focused on the existence of some classical solitary solutions of system  (1) [4] and obtained only one expression of the solitary-type solutions of system (1) [6] under specific initial condition and parameters condition. One may consider whether there are other expressions and other types of traveling wave solutions. Moreover, how about the dynamical behavior of these traveling wave solutions under general initial conditions and arbitrary parameters conditions? Driven by this motivation, in this paper, we study the traveling wave solutions of system (1) from the perspective of the theory of dynamical systems [2, 3, 5, 7–11, 13–24]. By presenting all possible bifurcations of phase portraits under different parameters conditions corresponding to system (1), we not only show the existence of traveling wave solutions including solitary waves, periodic waves and periodic blow-up waves, under corresponding parameters conditions, but also obtain their exact expressions.

2 Bifurcations of phase portraits

In this section, we present the bifurcations of phase portraits corresponding to system (1).

For given constant wave speed \(c>0\), substituting \(u(x,t)=\varphi (\xi ), v(x,t)=\psi (\xi )\) with \(\xi =x-ct\) into system (1), it follows,

$$\begin{aligned} \left\{ \begin{array}{lc} -c\varphi '+3\varphi \varphi '+\psi \psi '=\left[ \psi ^2\left( (\varphi -c) \varphi ''-\frac{1}{2}(\varphi ')^{2}\right) \right] ', \\ -c\psi ' +(\psi \varphi )'=0, \end{array} \right. \nonumber \\ \end{aligned}$$
(2)

where the prime stands for the derivative with respect to \(\xi \).

Integrating (2) once leads to

$$\begin{aligned} \left\{ \begin{array}{lc} G-c\varphi +\frac{3}{2}\varphi ^{2}+\frac{1}{2}\psi ^{2}=\psi ^2\left( (\varphi -c) \varphi ''-\frac{1}{2}(\varphi ')^{2}\right) , \\ -c\psi +\psi \varphi =g, \end{array} \right. \nonumber \\ \end{aligned}$$
(3)

where both g and G are integral constants, respectively.

From the second equation of system (3), we obtain

$$\begin{aligned} \psi =\frac{g}{\varphi -c}. \end{aligned}$$
(4)

Substituting (4) into the first equation of system (3), it leads to

$$\begin{aligned} 2g^{2}(\varphi -c)\varphi ''= & {} g^{2}(\varphi ')^{2} +(\varphi -c)^{2}\nonumber \\&\left( 3\varphi ^{2}-2c\varphi +2G\right) +g^{2}. \end{aligned}$$
(5)

Letting \(y=\varphi '\), we obtain a planar system

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\mathrm{d}\varphi }{\mathrm{d}\xi }=y,\\ \frac{\mathrm{d}y}{\mathrm{d}\xi }=\frac{g^{2}y^{2}\,+\,(\varphi -c)^{2}\left( 3\varphi ^{2}-2c\varphi +2G\right) +g^{2}}{2g^{2}(\varphi -c)}, \end{array} \right. \end{aligned}$$
(6)

with first integral

$$\begin{aligned} H(\varphi ,y)=\frac{g^{2}}{\varphi -c}y^{2}-\varphi ^{3}+c\varphi ^{2}-2G\varphi +\frac{g^{2}}{\varphi -c}.\nonumber \\ \end{aligned}$$
(7)

Transformed by \(\mathrm{d}\xi =2g^{2}(\varphi -c)\mathrm{d}\tau \), system (6) becomes a Hamiltonian system

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{\mathrm{d}\varphi }{\mathrm{d}\tau }=2g^{2}(\varphi -c)\ y,\\ \frac{\mathrm{d}y}{\mathrm{d}\tau }=g^{2}y^{2}+(\varphi -c)^{2}\left( 3\varphi ^{2}-2c\varphi +2G\right) +g^{2}. \end{array} \right. \nonumber \\ \end{aligned}$$
(8)

Since the first integral of system (6) is the same as that of the Hamiltonian system (8), system (6) should have the same topological phase portraits as system (8) except the straight line \(l, \varphi =c\). Therefore, we should be able to obtain the topological phase portraits of system (6) from those of system (8).

To study the singular points and their properties of system (8), let

$$\begin{aligned} f(\varphi )=(\varphi -c)^{2}\left( 3\varphi ^{2}-2c\varphi +2G\right) +g^{2}, \end{aligned}$$
(9)

then we have

$$\begin{aligned} f'(\varphi )=2(\varphi -c)\left( 6\varphi ^{2}-6c\varphi +c^{2}+2G\right) , \end{aligned}$$
(10)

and

$$\begin{aligned} f''(\varphi )=2\left( 18\varphi ^{2}-24c\varphi +7c^{2}+2G\right) . \end{aligned}$$
(11)

Obviously, \(f'(\varphi )\) has three zero points as follows,

$$\begin{aligned} {\hat{\varphi }}_{0}=c, \quad {\hat{\varphi }}_{\pm }=\frac{1}{6}\left( 3c\pm \sqrt{3{\varDelta }}\right) , \end{aligned}$$
(12)

where \({\varDelta }=c^{2}-4G>0\). Additionally, we easily get \(f(c)=g^{2}\), \(f'(c)=0\) and \(f''(c)=2\left( c^{2}+2G\right) \).

On the \(\varphi -\)axis, system (8) has at most four singular points denoted by \(S_{i}(\varphi _{i},0), \ i=1,2,3,4\). There exists no singular point of system (8) on the line \(l, \varphi =c\).

To state conveniently, denote

$$\begin{aligned} {\theta }_{+}\triangleq f({\hat{\varphi }}_{+})-g^{2}= & {} \frac{c^{4}-8c^{2}G+4G^{2}}{12}\nonumber \\&-\frac{c (c^{2}-4 G) \sqrt{c^{2}-4 G}}{3 \sqrt{3}}, \end{aligned}$$
(13)
$$\begin{aligned} {\theta }_{-}\triangleq f({\hat{\varphi }}_{-})-g^{2}= & {} \frac{c^{4}-8c^{2}G+4G^{2}}{12}\nonumber \\&+\frac{c (c^{2}-4 G) \sqrt{c^{2}-4 G}}{3 \sqrt{3}}. \end{aligned}$$
(14)

We give the number and relative positions of singular points of system (8) in the following lemma.

Lemma 1

  1. 1.

    If \(G<-\frac{c^{2}}{2}\), then we have \({\varDelta }>0\) and \(f''(c)<0\), which implies \({\hat{\varphi }}_{-}<c<{\hat{\varphi }}_{+}\).

    1. (a)

      If \(f({\hat{\varphi }}_{-})<0, f({\hat{\varphi }}_{+})<0\), i.e., \(g^{2}<-{\theta }_{+}\), system (8) has four singular points \(S_{i}(\varphi _{i},0), i=1,2,3,4\), satisfying \(\varphi _{1}<{\hat{\varphi }}_{-}<\varphi _{2}<c<\varphi _{3}<{\hat{\varphi }}_{+}<\varphi _{4}\).

    2. (b)

      If \(f({\hat{\varphi }}_{-})<0, f({\hat{\varphi }}_{+})>0\), i.e., \(-{\theta }_{+}<g^{2}<-{\theta }_{-}\), system (8) has two singular points \(S_{i}(\varphi _{i},0), i=1,2\), satisfying \(\varphi _{1}<{\hat{\varphi }}_{-}<\varphi _{2}<c<{\hat{\varphi }}_{+}\).

  2. 2.

    If \(G=-\frac{c^{2}}{2}\), then we have \({\varDelta }=0\) and \(0={\hat{\varphi }}_{-}<c={\hat{\varphi }}_{+}\). If \(f({\hat{\varphi }}_{-})<0\), i.e., \(g^{2}<-{\theta }_{-}\), system (8) has two singular points \(S_{i}(\varphi _{i},0), i=1,2\), satisfying \(\varphi _{1}<{\hat{\varphi }}_{-}=0<\varphi _{2}<c={\hat{\varphi }}_{+}\).

  3. 3.

    If \(-\frac{c^{2}}{2}<G<\frac{c^{2}}{4}\), then we have \({\varDelta }>0\) and \(f''(c)>0\), which implies \({\hat{\varphi }}_{-}<{\hat{\varphi }}_{+}<c\). If \(f({\hat{\varphi }}_{-})<0\), i.e., \(g^{2}<-{\theta }_{-}\), system (8) has two singular points \(S_{i}(\varphi _{i},0), i=1,2\), satisfying \(\varphi _{1}<{\hat{\varphi }}_{-}<\varphi _{2}<{\hat{\varphi }}_{+}<c\).

Proof

Lemma 1 follows from the analysis of signs of \({\varDelta }\) and \(f''(c)\). \(\square \)

Remark 1

Note that \(f({\hat{\varphi }}_{+})\,-\,f({\hat{\varphi }}_{-})=\frac{c (c^{2}-4 G) \sqrt{c^{2}-4 G}}{3 \sqrt{3}}\), hence the case that \(f({\hat{\varphi }}_{-})>0, f({\hat{\varphi }}_{+})<0\), will never happen, as long as \(G<\frac{c^{2}}{4}\).

Let \(\lambda (\varphi ,y)\) be the characteristic value of the linearized system of system (8) at the singular point \((\varphi ,y)\). Then we have

$$\begin{aligned} \lambda ^{2}(\varphi _{i},0) = 2g^{2}(\varphi _{i}-c)f'(\varphi _{i}). \end{aligned}$$
(15)

From (15), we see that the sign of \(f'(\varphi _{i})\) and the relative position of the singular point \(S_{i}(\varphi _{i},0), i=1,2,3,4\) with respect to the singular line \(l, \varphi =c\) can be used to determine the dynamical properties (saddle points, centers and degenerate saddle points) of the singular points according to the theory of planar dynamical systems.

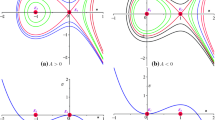
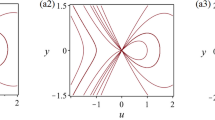
Therefore, based on the above analysis, we obtain all possible bifurcations of phase portraits of system (6) in Fig. 1.

Fig. 1
figure 1

Phase portraits of system (6). a \(G<-\frac{c^{2}}{2}\) and \(g^{2}<-{\theta }_{+}\). b \(G<-\frac{c^{2}}{2}\) and \(-{\theta }_{+}<g^{2}<-{\theta }_{-}\), or \(-\frac{c^{2}}{2}\le G<\frac{c^{2}}{4}\) and \(g^{2}<-{\theta }_{-}\)

Full size image

3 Main results and the theoretic derivations of main results

To state conveniently, let \(\mathrm{sn}(\cdot ,\cdot )\) be the Jacobian elliptic function [1], and \(h_{i}=H(\varphi _{i},0), i=1,2,3,4\), where \(H(\varphi ,y)\) is given in (7). Additionally, from (7), for a fixed integral constant h, we have

$$\begin{aligned} y^{2}= & {} \frac{1}{g^{2}}\left( \varphi ^{4}-2c\varphi ^{3}+(c^{2}+2G)\varphi ^{2}\right. \nonumber \\&\left. +(h-2cG)\varphi -(ch+g^{2})\right) \triangleq \frac{{\varOmega }(\varphi )}{g^{2}} \end{aligned}$$
(16)

Our main results will be stated in the following theorems with the proofs following.

For ease of exposition, we have omitted the expressions of v(x, t) with \(v(x,t)=\frac{g}{u(x,t)-c}\) in the rest of article.

Theorem 1

  1. (1)

    Corresponding to the homoclinic orbit, which passes the saddle points \(S_{1}(\varphi _{1},0)\) in Fig. 1a, b, there exists solitary wave solution for system (1), which possesses the explicit expression,

    $$\begin{aligned}&u(x,t)=\varphi _{1}\nonumber \\&\quad +\frac{2(\varphi _{11}-\varphi _{1})(\varphi _{12}-\varphi _{1})}{(\varphi _{12}-\varphi _{11})\cosh (\theta _{1}(x-c t))+(\varphi _{11}+\varphi _{12}-2\varphi _{1})},\nonumber \\ \end{aligned}$$
    (17)

    where \(\theta _{1}=\frac{1}{|g|}\sqrt{(\varphi _{11}-\varphi _{1})(\varphi _{12}-\varphi _{1})}\), and \(\varphi _{1i}, i=1,2\) will be given later.

  2. (2)

    Corresponding to the homoclinic orbit, which passes the saddle points \(S_{4}(\varphi _{4},0)\) in Fig. 1a, there exists solitary wave solution for system (1), which possesses the explicit expression,

    $$\begin{aligned}&u(x,t)=\varphi _{4}\nonumber \\&\quad -\frac{2(\varphi _{4}-\varphi _{42})(\varphi _{4}-\varphi _{41})}{(\varphi _{42}-\varphi _{41})\cosh (\theta _{4}(x-c t))+(2\varphi _{4}-\varphi _{41}-\varphi _{42})},\nonumber \\ \end{aligned}$$
    (18)

    where \(\theta _{4}=\frac{1}{|g|}\sqrt{(\varphi _{4}-\varphi _{42})(\varphi _{4}-\varphi _{41})}\), and \(\varphi _{4i}, i=1,2\) will be given later.

Proof

  1. (1)

    The homoclinic orbit, which passes the saddle points \(S_{1}(\varphi _{1},0)\) in Fig. 1a, b, can be expressed as,

    $$\begin{aligned}&y=\pm \frac{1}{|g|}(\varphi -\varphi _{1})\sqrt{(\varphi _{12}-\varphi )(\varphi _{11}-\varphi )},\nonumber \\&\quad \varphi _{1}<\varphi< \varphi _{11}<c<\varphi _{12}, \end{aligned}$$
    (19)

    where \(\varphi _{1i}, i=1,2\) can be obtained by letting \(h=h_{1}\) and \({\varOmega }(\varphi )=(\varphi _{12}-\varphi )(\varphi _{11}-\varphi )(\varphi -\varphi _{1})^{2}\). Substituting (19) into the first equation of system (6), and integrating along the homoclinic orbit, it follows that

    $$\begin{aligned} \int _{\varphi }^{\varphi _{11}}\frac{ \mathrm{d}s}{(s-\varphi _{1})\sqrt{(\varphi _{12}-s)(\varphi _{11}-s)}} =\frac{|\xi |}{|g|}. \end{aligned}$$
    (20)

    From (20), we obtain the solitary wave solution (17).

  2. (2)

    The homoclinic orbit, which passes the saddle points \(S_{4}(\varphi _{4},0)\) in Fig. 1a, can be expressed as,

    $$\begin{aligned}&y=\pm \frac{1}{|g|}(\varphi _{4}-\varphi )\sqrt{(\varphi -\varphi _{41})(\varphi -\varphi _{42})},\nonumber \\&\quad \varphi _{41}<c<\varphi _{42}< \varphi <\varphi _{4}, \end{aligned}$$
    (21)

    where \(\varphi _{4i}, i=1,2\) can be obtained by letting \(h=h_{4}\) and \({\varOmega }(\varphi )=(\varphi -\varphi _{41})(\varphi -\varphi _{42})(\varphi _{4}-\varphi )^{2}\). Substituting (21) into the first equation of system (6), and integrating along the homoclinic orbit, it follows that

    $$\begin{aligned} \int _{\varphi _{42}}^{\varphi }\frac{ \mathrm{d}s}{(\varphi _{4}-s)\sqrt{(s-\varphi _{41})(s-\varphi _{42})}} =\frac{|\xi |}{|g|}. \end{aligned}$$
    (22)

    From (22), we obtain the solitary wave solution (18). The proof is completed.

\(\square \)

Theorem 2

  1. (1)

    Corresponding to the periodic orbit, which surrounds the center point \(S_{2}(\varphi _{2},0)\), in Fig. 1a, b, system (1) has a periodic wave solution, which can be expressed as,

    $$\begin{aligned} u(x,t)=\frac{\bar{\varphi }_{4}(\bar{\varphi }_{3}-\bar{\varphi }_{2})\mathrm{sn}^{2}\left( \frac{x-c t}{g_{1}|g|},k_{2}\right) -\bar{\varphi }_{3}(\bar{\varphi }_{4}-\bar{\varphi }_{2})}{(\bar{\varphi }_{3}-\bar{\varphi }_{2})\mathrm{sn}^{2}\left( \frac{x-c t}{g_{1}|g|},k_{2}\right) -(\bar{\varphi }_{4}-\bar{\varphi }_{2})}\nonumber \\ \end{aligned}$$
    (23)

    where \(g_{1}=\frac{2}{\sqrt{(\bar{\varphi }_{4}-\bar{\varphi }_{2})(\bar{\varphi }_{3}-\bar{\varphi }_{1})}}\), \(k_{2}^{2}=\frac{(\bar{\varphi }_{3}-\bar{\varphi }_{2})(\bar{\varphi }_{4}-\bar{\varphi }_{1})}{(\bar{\varphi }_{4}-\bar{\varphi }_{2})(\bar{\varphi }_{3}-\bar{\varphi }_{1})}\), and \(\bar{\varphi }_{i}, i=1,2,3,4\) will be given later. Moreover, the periodic wave solution (23) tends to the solitary wave solution (17) when \(\bar{\varphi }_{2}\rightarrow \varphi _{1}\).

  2. (2)

    Corresponding to the periodic orbit, which surrounds the center point \(S_{3}(\varphi _{3},0)\), in Fig. 1b, system (1) has a periodic wave solution, which can be expressed as,

    $$\begin{aligned} u(x,t)=\frac{\tilde{\varphi }_{1}(\tilde{\varphi }_{3}-\tilde{\varphi }_{2})\mathrm{sn}^{2}\left( \frac{x-c t}{g_{2}|g|},k_{3}\right) -\tilde{\varphi }_{2}(\tilde{\varphi }_{3}-\tilde{\varphi }_{1})}{(\tilde{\varphi }_{3}-\tilde{\varphi }_{2})\mathrm{sn}^{2}\left( \frac{x-c t}{g_{2}|g|},k_{3}\right) -(\tilde{\varphi }_{3}-\tilde{\varphi }_{1})}\nonumber \\ \end{aligned}$$
    (24)

    where \(g_{2}=\frac{2}{\sqrt{(\tilde{\varphi }_{4}-\tilde{\varphi }_{2})(\tilde{\varphi }_{3}-\tilde{\varphi }_{1})}}\), \(k_{3}^{2}=\frac{(\tilde{\varphi }_{3}-\tilde{\varphi }_{2})(\tilde{\varphi }_{4}-\tilde{\varphi }_{1})}{(\tilde{\varphi }_{4}-\tilde{\varphi }_{2})(\tilde{\varphi }_{3}-\tilde{\varphi }_{1})}\), and \(\tilde{\varphi }_{i}, i = 1,2,3,4\) will be given later. Moreover, the periodic wave solution (24) tends to the solitary wave solution (18) when \(\tilde{\varphi }_{3}\rightarrow \varphi _{4}\).

Proof

  1. (1)

    The periodic orbit, surrounding the center point \(S_{2}(\varphi _{2},0)\), in Fig. 1a, b, can be expressed as,

    $$\begin{aligned} y= & {} \pm \frac{1}{|g|}\sqrt{(\bar{\varphi }_{4}-\varphi )(\bar{\varphi }_{3}-\varphi )(\varphi -\bar{\varphi }_{2})(\varphi -\bar{\varphi }_{1})},\nonumber \\&\quad \bar{\varphi }_{1}<\bar{\varphi }_{2}<\varphi<\bar{\varphi }_{3}<c<\bar{\varphi }_{4}, \end{aligned}$$
    (25)

    where \(\bar{\varphi }_{i}, i=1,2,3,4\) can be obtained by letting \(h=h_{1}\) and \({\varOmega }(\varphi )=(\bar{\varphi }_{4}-\varphi )(\bar{\varphi }_{3}-\varphi )(\varphi -\bar{\varphi }_{2})(\varphi -\bar{\varphi }_{1})\). Substituting (25) into the first equation of system (6), and integrating along the periodic orbit, it follows that

    $$\begin{aligned} \int _{\varphi }^{\bar{\varphi }_{3}}\frac{ \mathrm{d}s}{\sqrt{(\bar{\varphi }_{4}-s)(\bar{\varphi }_{3}-s)(s-\bar{\varphi }_{2})(s-\bar{\varphi }_{1})}} =\frac{|\xi |}{|g|}.\nonumber \\ \end{aligned}$$
    (26)

    From (26), we obtain the periodic waves (23). Moreover, when \(\bar{\varphi }_{2}\rightarrow \varphi _{1}\), we immediately have \(\bar{\varphi }_{1}\rightarrow \varphi _{1}\), \(\bar{\varphi }_{3}\rightarrow \varphi _{11}\), and \(\bar{\varphi }_{4}\rightarrow \varphi _{12}\), from which \(k_{2}\rightarrow 1\) and \(g_{1}\rightarrow \frac{2}{\sqrt{(\varphi _{11}-\varphi _{1})(\varphi _{12}-\varphi _{1})}}\) follow. Therefore, the periodic wave solution (23) becomes

    $$\begin{aligned}&u(x,t)\nonumber \\&\quad =\frac{\varphi _{12}(\varphi _{11}-\varphi _{1})\tanh ^{2}(\frac{\theta _{1}}{2}(x-c t))-\varphi _{11}(\varphi _{12}-\varphi _{1})}{(\varphi _{11}-\varphi _{1})\tanh ^{2}(\frac{\theta _{1}}{2}(x-c t))-(\varphi _{12}-\varphi _{1})},\nonumber \\ \end{aligned}$$
    (27)

    which is exactly the solitary wave solution (17) through simple calculation.

  2. (2)

    The periodic orbit, surrounding the center point \(S_{3}(\varphi _{3},0)\), in Fig. 1b, can be expressed as,

    $$\begin{aligned} y= & {} \pm \frac{1}{|g|}\sqrt{(\tilde{\varphi }_{4}-\varphi )(\tilde{\varphi }_{3}-\varphi )(\varphi -\tilde{\varphi }_{2})(\varphi -\tilde{\varphi }_{1})},\nonumber \\ \tilde{\varphi }_{1}<&c<\tilde{\varphi }_{2}<\varphi<\tilde{\varphi }_{3}<\tilde{\varphi }_{4}, \end{aligned}$$
    (28)

    where \(\tilde{\varphi }_{i}, i=1,2,3,4\) can be obtained by letting \(h=h_{1}\) and \({\varOmega }(\varphi )=(\tilde{\varphi }_{4}-\varphi )(\tilde{\varphi }_{3}-\varphi )(\varphi -\tilde{\varphi }_{2})(\varphi -\tilde{\varphi }_{1})\). Substituting (28) into the first equation of system  (6), and integrating along the periodic orbit, it follows that

    $$\begin{aligned} \int _{\tilde{\varphi }_{2}}^{\varphi }\frac{ \mathrm{d}s}{\sqrt{(\tilde{\varphi }_{4}-s)(\tilde{\varphi }_{3}-s)(s-\tilde{\varphi }_{2})(s-\tilde{\varphi }_{1})}} =\frac{|\xi |}{|g|}.\nonumber \\ \end{aligned}$$
    (29)

    From (29), we obtain the periodic waves (24). Moreover, when \(\tilde{\varphi }_{3}\rightarrow \varphi _{4}\), we immediately have \(\tilde{\varphi }_{1}\rightarrow \varphi _{41}\), \(\tilde{\varphi }_{2}\rightarrow \varphi _{42}\), and \(\tilde{\varphi }_{4}\rightarrow \varphi _{4}\), from which \(k_{3}\rightarrow 1\) and \(g_{2}\rightarrow \frac{2}{\sqrt{(\varphi _{4}-\varphi _{42})(\varphi _{4}-\varphi _{41})}}\) follow. Therefore, the periodic wave solution (24) becomes

    $$\begin{aligned}&u(x,t)\nonumber \\&\quad =\frac{\varphi _{41}(\varphi _{4}-\varphi _{42})\tanh ^{2}(\frac{\theta _{4}}{2}(x-c t))-\varphi _{42}(\varphi _{4}-\varphi _{42})}{(\varphi _{4}-\varphi _{42})\tanh ^{2}(\frac{\theta _{4}}{2}(x-c t))-(\varphi _{4}-\varphi _{41})},\nonumber \\ \end{aligned}$$
    (30)

    which is exactly the solitary wave solution (18) through simple calculation. Thus, the proof is completed. \(\square \)

Theorem 3

  1. (1)

    Corresponding to the two orbits, which have the same Hamiltonian with that of the center point \(S_{2}(\varphi _{2},0)\), in Fig. 1a, b, system (1) has two periodic blow-up wave solutions, which can be expressed as,

    $$\begin{aligned}&u(x,t)=\varphi _{2}\nonumber \\&\quad +\frac{2(\varphi _{22}-\varphi _{2})(\varphi _{2}-\varphi _{21})}{(2\varphi _{2}-\varphi _{21}-\varphi _{22})-(\varphi _{22}-\varphi _{21})\sin (\vartheta _{2}-\theta _{2}(x-c t))},\nonumber \\ \end{aligned}$$
    (31)

    where \(\vartheta _{2}=\arcsin \left( \frac{2\varphi _{2}-\varphi _{21}-\varphi _{22}}{\varphi _{22}-\varphi _{21}}\right) \), \(\theta _{2}=\frac{1}{|g|}\sqrt{(\varphi _{22}-\varphi _{2})(\varphi _{2}-\varphi _{21})}\), and \(\varphi _{2i}, i=1,2\) will be given later.

  2. (2)

    Corresponding to the two orbits, which have the same Hamiltonian with that of the center point \(S_{3}(\varphi _{3},0)\), in Fig. 1a, system (1) has two periodic blow-up wave solutions, which can be expressed as,

    $$\begin{aligned}&u(x,t)=\varphi _{3}\nonumber \\&\quad +\frac{2(\varphi _{32}-\varphi _{3})(\varphi _{3}-\varphi _{31})}{(2\varphi _{3}-\varphi _{31}-\varphi _{32})-(\varphi _{32}-\varphi _{31})\sin (\vartheta _{3}-\theta _{3}(x-c t))},\nonumber \\ \end{aligned}$$
    (32)

    where \(\vartheta _{3}=\arcsin \left( \frac{2\varphi _{3}-\varphi _{31}-\varphi _{32}}{\varphi _{32}-\varphi _{31}}\right) \), \(\theta _{3}=\frac{1}{|g|}\sqrt{(\varphi _{32}-\varphi _{3})(\varphi _{3}-\varphi _{31})}\), and \(\varphi _{3i}, i=1,2\) will be given later.

Proof

  1. (1)

    The two orbits, which have the same Hamiltonian with that of the center point \(S_{2}(\varphi _{2},0)\), in Fig. 1a, b, can be expressed as,

    $$\begin{aligned} y= & {} \pm \frac{1}{|g|}(\varphi -\varphi _{2})\sqrt{(\varphi -\varphi _{22})(\varphi -\varphi _{21})},\nonumber \\&\quad \varphi _{21}<\varphi _{2}<c<\varphi _{22}< \varphi , \end{aligned}$$
    (33)

    where \(\varphi _{2i}, i=1,2\) can be obtained by letting \(h=h_{2}\) and \({\varOmega }(\varphi )=(\varphi -\varphi _{22})(\varphi -\varphi _{21})(\varphi -\varphi _{2})^{2}\). Substituting (33) into the first equation of system  (6), and integrating along the two orbits, it follows that

    $$\begin{aligned} \int _{\varphi }^{+\infty }\frac{ \mathrm{d}s}{(s-\varphi _{2})\sqrt{(s-\varphi _{22})(s-\varphi _{21})}} =\frac{|\xi |}{|g|}. \end{aligned}$$
    (34)

    From (34), we obtain the periodic blow-up wave solutions (31).

  2. (2)

    The two orbits, which have the same Hamiltonian with that of the center point \(S_{3}(\varphi _{3},0)\), in Fig. 1a, can be expressed as,

    $$\begin{aligned} y= & {} \pm \frac{1}{|g|}(\varphi -\varphi _{3})\sqrt{(\varphi -\varphi _{32})(\varphi -\varphi _{31})},\nonumber \\&\quad \varphi _{31}<c<\varphi _{3}<\varphi _{32}< \varphi , \end{aligned}$$
    (35)

    where \(\varphi _{3i}, i=1,2\) can be obtained by letting \(h=h_{3}\) and \({\varOmega }(\varphi )=(\varphi -\varphi _{32})(\varphi -\varphi _{31})(\varphi -\varphi _{3})^{2}\). Substituting (35) into the first equation of system (6), and integrating along the two orbits, it follows that

    $$\begin{aligned} \int _{\varphi }^{+\infty }\frac{ \mathrm{d}s}{(s-\varphi _{3})\sqrt{(s-\varphi _{32})(s-\varphi _{31})}} =\frac{|\xi |}{|g|}.\nonumber \\ \end{aligned}$$
    (36)

    From (36), we obtain the periodic blow-up wave solutions (32). \(\square \)

4 Conclusions

In this paper, through all possible bifurcations for the system under different parameters constraint conditions, we not only show the existence of several types of traveling wave solutions including solitary waves, periodic waves and periodic blow-up waves, under corresponding parameters conditions, but also obtain their exact explicit expressions. Compared to the results in [4, 6], our work extends the results in the following aspects. First, we show the existence of different types of traveling wave solutions and give their exact explicit expressions, compared to the only one expression of the solitary and cnoidal-type solutions [4, 6]. Moreover, the solutions in [4, 6] were obtained under specific initial condition and parameter condition, while we consider the dynamical behaviors of the traveling wave solutions under general initial conditions and arbitrary parameters conditions. Additionally, the motivation and extension in this article drive us to study other mathematical physics equations [12, 25–27].