Soliton and Riemann theta function quasi-periodic wave solutions for a $(2+1)$-dimensional generalized shallow water wave equation

Abstract

In this paper, a $(2 + 1)$-dimensional generalized shallow water wave equation is investigated through bilinear Hirota method. Interestingly, the breather-type and lump-type soliton solutions are obtained. Furthermore, dynamic properties of the soliton waves are revealed by means of the asymptotic analysis. Based on Hirota bilinear method and Riemann theta function, we succeed in constructing quasi-periodic wave solutions with a generalized form. We also display the asymptotic properties of these quasi-periodic wave solutions and point out the relation between the quasi-periodic wave solutions and the soliton solutions.

1 Introduction

A lot of phenomena in physics and engineering can be described by nonlinear partial differential equations. When we try to study the physical mechanism of phenomena in nature which is described by nonlinear partial differential equations, exact solutions often are investigated. Many mathematicians and physicists are interested in looking for solitary wave solutions to these equations. In physics and other fields, these solutions may well describe miscellaneous phenomena, such as solitons and propagation with a finite speed. Thus, they may give a good insight into the physical aspects of the problems. The shallow water equations have been widely applied in hydraulic engineering, ocean and atmospheric modeling. A generalized shallow water wave (GSWW) equation is given by

$$\begin{aligned} u_{t}-u_{xxt}-\alpha u u_t-\beta u_x \int ^{x} u_{t}\hbox {d}x+u_x =0. \end{aligned}$$

(1)

This equation can be derived from the classical shallow water theory in the so-called Boussinesq approximation [1]. The Hirota bilinear form [2] and a series of exact solutions for Eq. (1) were investigated in [3–9].

The study of soliton for nonlinear equations is of great interest not only in $(1+1)$-dimensional systems, but also in higher-dimensional systems. Other exact solutions also have been investigated by many researchers, and some of powerful methods have been presented, such as the extended Jacobi elliptic function expansion method [10–13], inverse scattering transformation method [14, 15], multiple exp-function method [16, 17], extended F-expansion method [18], the Hirota method [19–25], $\frac{G'}{G}$-expansion method [26, 27], the Weierstrass elliptic function method [28–30] and so on. Nakamura [31, 32] proposed a convenient way to construct a kind of quasi-periodic solutions of nonlinear equations in his two serial papers. Recently, Fan and his collaborators [33] have extended this method to investigate the discrete Toda lattice. This approach possesses powerful features that make it practical for the determination of quasi-periodic solutions [34–38].

Many authors had studied the $(2 + 1)$-dimensional generalized shallow water wave equation

$$\begin{aligned} v_{t}+v_{xxx}-3(v r)_{x}=0, \qquad v_{x}=r_{y}, \end{aligned}$$

(2)

which can be reduced to the famous KdV equation if $y=x$. In [39], an inverse scattering scheme was developed to solve the Cauchy problem for Eq. (2). A set of solitary-like solutions for Eq. (2) were acquired by means of a symbolic-computation-based method [40, 41]. In [42], the generalized dromion solutions for Eq. (2) were obtained. In [43], the author pointed out that the symmetries of integrable model for Eq. (2) can be obtained from the conformal invariance of its Schwartz form. Lou et al. [44–46] exposed that Eq. (2) is an asymmetric part of the NNV equation and revealed its abundant dromion structures. A series of soliton-like solutions and double-like periodic solutions for Eq. (2) were constructed by the generalized algebraic method in [47]. A series of exact solutions for Eq. (2) were obtained by using a linear variable separation approach and a projective equation in [48]. In [49, 50], the authors acquired multi-periodic (quasi-periodic) wave solutions for Eq. (2) by employing Hirota bilinear method and Riemann theta function. In [51], based on the binary Bell polynomials and the bilinear form for Eq. (2), some exact solutions were presented with an arbitrary function in y. In [52], the multi-soliton solutions for Eq. (2) were obtained by means of the multiple exp-function method.

In this work, we investigate the soliton solutions and quasi-periodic wave solutions with an arbitrary function in y for Eq. (2), which have not been reported before. Furthermore, their dynamic properties, interaction mechanisms and limit behavior are analyzed. This paper is organized as the following. In Sect. 2, we present one-soliton solutions via the simplified bilinear method and acquire the rational function solution in virtue of the limit method. By means of the asymptotic analysis and graphical simulations, we reveal the dynamic properties of the solitons and investigate the breather-type and lump-type solitons. In Sect. 3, besides the multiple-soliton solutions are acquired by means of the simplified bilinear method, we also investigate their dynamic properties and interaction mechanisms. Furthermore, the breather-type and lump-type multiple solitons are analyzed. In Sect. 4, we construct Riemann theta function one-periodic wave solutions with a generalized form and establish the relation between the one-periodic solutions and one-soliton solutions. In Sect. 5, we investigate the two-periodic wave solutions similar to one-periodic wave solutions. A short conclusion is given in Sect. 6.

2 One-soliton solution

To obtain the soliton solution directly, we use the simplified version of Hirota bilinear method [23] to study Eq. (2). Letting

$$\begin{aligned} v=u_y, \qquad r=u_x, \end{aligned}$$

(3)

then Eq. (2) becomes

$$\begin{aligned} u_{yt}+u_{xxxy}-3 u_{xx}u_{y}-3 u_{x}u_{xy}=0. \end{aligned}$$

(4)

Based on the special structure of Eq. (4), we look for the solutions of Eq. (4) with the form

$$\begin{aligned} u(x,y,t)=\varphi (\xi ),\qquad \xi =k x+q \phi (y)-\gamma t+p, \end{aligned}$$

(5)

where $k, q, \gamma$ and p are arbitrary constants and $\phi (y)$ is an arbitrary function of y. Since $\varphi (\xi )$ contains an arbitrary function $\phi (y)$, it is different from the previous form. Substituting

$$\begin{aligned} u(x,y,t)=e ^{\omega _{1}},\qquad \omega _{1}=k_{1}x+q_{1}\phi (y)-\gamma _{1}t+p_{1}, \end{aligned}$$

(6)

into the linear terms of Eq. (4), and solving the equation for $\gamma _{1}$, we get $\gamma _{1}=k_{1}^{3}$. Consequently, the dispersion variable $\omega _{1}$ becomes

$$\begin{aligned} \omega _{1}=k_{1}x+q_{1}\phi (y)-k_{1}^{3}t+p_{1}. \end{aligned}$$

(7)

Now, we use the transformation

$$\begin{aligned} u(x,y,t)=R\frac{f_{x}(x,y,t)}{f(x,y,t)}, \end{aligned}$$

(8)

to determine R, where

$$\begin{aligned} f(x,y,t)=1+e ^{\omega _{1}}. \end{aligned}$$

(9)

Substituting (8) into (4), it follows that $R=-2$. Therefore, a solution for Eq. (4) is given by

$$\begin{aligned} u(x,y,t)=-k_{1}-k_{1} \tanh \left( \frac{\omega _{1}}{2}\right) . \end{aligned}$$

(10)

From (3) and (10), we obtain one-soliton solution for Eq. (2) in the form

$$\begin{aligned} v(x,y,t)= & {} -\frac{k_{1}q_{1}}{2} \phi '(y) \text {sech}^{2}\left( \frac{\omega _{1}}{2}\right) , \end{aligned}$$

(11)

$$\begin{aligned} r(x,y,t)= & {} -\frac{k_{1}^{2}}{2} \text {sech}^{2}\left( \frac{\omega _{1}}{2}\right) . \end{aligned}$$

(12)

The dynamic properties for the solitary waves are revealed by mean of the asymptotic analysis and graphical simulations as follows. From (11), we see that the characteristic plane of the wave is defined by (7).

Thus, the following two interesting solitons are acquired by selecting the special $\phi (y)$.

Case 1:

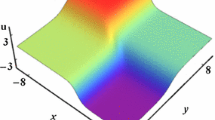
Breather-type soliton Through choosing $\phi (y)$ as periodic function, the breather-type soliton is shown in Fig. 1, where $\phi (y)=\text {sn}(y,0.3)$ in Fig. 1a and $\phi (y)=\text {cn}(y,0.9)$ in Fig. 1b.

Case 2:

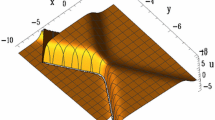
Lump-type soliton Through choosing some appropriate function $\phi (y)$, the lump-type soliton is shown in Fig. 2, where (a) $\phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}}$ in Fig. 2 and $\phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}[\sin (\ln (y^{2}+0.001))]}$ in Fig. 2b.

Similarly, applying the Hirota bilinear method to Eq. (2), we get its single singular-soliton solution

$$\begin{aligned} v(x,y,t)= & {} \frac{k_{1}q_{1}}{2} \phi '(y) \text {csch}^{2}\left( \frac{\omega _{1}}{2}\right) , \end{aligned}$$

(13)

$$\begin{aligned} r(x,y,t)= & {} \frac{k_{1}^{2}}{2} \text {csch}^{2}\left( \frac{\omega _{1}}{2}\right) . \end{aligned}$$

(14)

Let $q_{1}=k_{1}, p_{1}=0$ and $k_{1}\rightarrow 0$, and we obtain the rational function solution for Eq. (2) in the form

$$\begin{aligned} v(x,y,t)= & {} \frac{2\phi '(y)}{\left[ x+\phi (y)\right] ^{2}}, \end{aligned}$$

(15)

$$\begin{aligned} r(x,y,t)= & {} \frac{2}{\left[ x+\phi (y)\right] ^{2}}. \end{aligned}$$

(16)

Fig. 1

Steady propagation of v(x, y, t) given by (11) at $t=0$, where $k_{1}=2, q_{1}=1, p_{1}=0$ and a $\phi (y)=\text {sn}(y,0.3)$; b $\phi (y)=\text {cn}(y,0.9)$

Fig. 2

Steady propagation of v(x, y, t) given by (11) at $t=0$, where $k_{1}=2, q_{1}=1, p_{1}=0$ and a $\phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}}$; b $\phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}[\sin (\ln (y^{2}+0.001))]}$

3 Multiple-soliton solution

To get two-soliton solutions, let

$$\begin{aligned} u(x,y,t)=-2[\ln f(x,y,t)]_{x}, \end{aligned}$$

(17)

where $\omega _{1}$ is given in (7) and

$$\begin{aligned}&\omega _{2}=k_{2}x+q_{2}\phi (y)-k_{2}^{3}t+p_{2}, \end{aligned}$$

(18)

$$\begin{aligned}&f(x,y,t)=1+e ^{\omega _{1}}+e ^{\omega _{2}}+a_{12}e ^{\omega _{1}+\omega _{2}}. \end{aligned}$$

(19)

Substituting (17) into (4), the phase shift $a_{12}$ is obtained as

$$\begin{aligned} a_{12}=\frac{(k_{1}-k_{2})(q_{1}-q_{2})}{(k_{1}+k_{2})(q_{1}+q_{2})}. \end{aligned}$$

(20)

These imply that Eq. (2) has two-soliton solution

$$\begin{aligned} v(x,y,t)= & {} \chi _y, \end{aligned}$$

(21)

$$\begin{aligned} r(x,y,t)= & {} \chi _x, \end{aligned}$$

(22)

where

$$\begin{aligned} \chi =\frac{-2\left[ k_{1}e ^{\omega _{1}}+k_{2}e ^{\omega _{2}}+a_{12}(k_{1}+k_{2})e ^{\omega _{1}+\omega _{2}}\right] }{1+e ^{\omega _{1}}+e ^{\omega _{2}}+a_{12}e ^{\omega _{1}+\omega _{2}}}. \end{aligned}$$

(23)

Now, we consider the asymptotic property of $v_{4}(x,y,t)$. First, assume that $a_{12}>0, k_{1}>k_{2}>0$. From (7) and (18), we get the relation between $\omega _{1}$ and $\omega _{2}$ as

$$\begin{aligned} \omega _{2}= & {} k_{2}\left( k_{1}^{2}-k_{2}^{2}\right) t + \frac{k_{2}}{k_{1}}\omega _{1} + \left( q_{2}-\frac{k_{2}}{k_{1}}q_{1}\right) \phi (y) \nonumber \\&+ \left( p_{2}-\frac{k_{2}}{k_{1}}p_{1}\right) . \end{aligned}$$

(24)

If let $\omega _{1}=$ constant, then we get

$$\begin{aligned} v\rightarrow \left\{ \begin{aligned}&-\frac{k_{1}q_{1}}{2} \phi '(y) \text {sech}^{2}\left( \frac{m_1}{2}\right) , \qquad t\rightarrow +\infty , \\&-\frac{k_{1}q_{1}}{2} \phi '(y) \text {sech}^{2}\left( \frac{\omega _{1}}{2}\right) , \qquad t\rightarrow -\infty , \end{aligned}\right. \end{aligned}$$

(25)

where

$$\begin{aligned} m_1=\omega _{1}+\ln (a_{12}). \end{aligned}$$

(26)

Similarly, if we let $\omega _{2}=$ constant, then

$$\begin{aligned} v\rightarrow \left\{ \begin{aligned}&-\frac{k_{2}q_{2}}{2} \phi '(y) \text {sech}^{2}\left( \frac{\omega _{2}}{2}\right) , \qquad t\rightarrow +\infty , \\&-\frac{k_{2}q_{2}}{2} \phi '(y) \text {sech}^{2}\left( \frac{m_2}{2}\right) , \qquad t\rightarrow -\infty , \end{aligned}\right. \end{aligned}$$

(27)

where

$$\begin{aligned} m_2=\omega _{2}+\ln (a_{12}). \end{aligned}$$

(28)

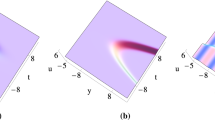
In order to understand above asymptotic property intuitively, we give four examples in Fig. 3. Also, we draw the following conclusions: (1) If $q_{1}, q_{2}>0$, then the two-soliton consists of two dark solitons, as shown in Fig. 3a. (2) If $q_{1}<0, q_{2}>0$ or $q_{1}>0, q_{2}<0$, then the two-soliton consists of a bright soliton and a dark soliton, as shown in Fig. 3b, c. (3) If $q_{1}, q_{2}<0$, then the two-soliton consists of two bright solitons, as shown in Fig. 3d. From above figures, phase shifts are evidently shown.

Fig. 3

Surface of the two-soliton via (21) on the $y-t$ plane, where $k_{1}=1, k_{2}=2, p_{1}=p_{2}=0, x=0, \phi (y)=y$ and a $q_{1}=1, q_{2}=2$; b $q_{1}=-1, q_{2}=2$; c $q_{1}=1, q_{2}=-2$; d $q_{1}=-1, q_{2}=-2$

Next, we show that the breather-type two-soliton is composed of two breather-type solitons in Fig. 4. Also, the lump-type two-soliton composed by two lump-type solitons is given in Fig. 5.

Fig. 4

Steady propagation of the two-soliton via (21) at $t=0$, where $k_{1}=2, k_{2}=3, q_{1}=1, q_{2}=2, \phi (y)=\text {sn}(y,0.3)$ and a $p_{1}=p_{2}=0$; b $p_{1}=6, p_{2}=0$

Fig. 5

Steady propagation of the two-soliton via (21) at $t=0$, where $k_{1}=2, k_{2}=3, q_{1}=1, q_{2}=2, \phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}}$ and a $p_{1}=p_{2}=0$; b $p_{1}=3, p_{2}=0$

Similarly, in order to obtain the three-soliton solution, we substitute

$$\begin{aligned} v(x,y,t)= & {} -2\left[ \ln f(x,y,t)\right] _{xy}, \nonumber \\ r(x,y,t)= & {} -2\left[ \ln f(x,y,t)\right] _{xx}, \end{aligned}$$

(29)

$$\begin{aligned} f(x,y,t)= & {} 1+e ^{\omega _{1}} + e ^{\omega _{2}} + e ^{\omega _{3}} \nonumber \\&+\,a_{12}e ^{\omega _{1}+\omega _{2}} + a_{23}e ^{\omega _{2}+\omega _{3}} \nonumber \\&+\,a_{13}e ^{\omega _{1}+\omega _{3}} +b_{123}e ^{\omega _{1}+\omega _{2}+\omega _{3}}, \end{aligned}$$

(30)

$$\begin{aligned} a_{ij} = \frac{(k_{i}-k_{j})(q_{i}-q_{j})}{(k_{i}+k_{j})(q_{i}+q_{j})}, \end{aligned}$$

(31)

into (2), we get

$$\begin{aligned} b_{123}=a_{12} a_{13} a_{23}. \end{aligned}$$

(32)

To determine the three-soliton solution explicitly, we substitute the last result for f(x, y, t) in the formula (29).

Similar to the two-soliton, the breather-type three-soliton is composed of three breather-type solitons. The lump-type three-soliton is composed of three lump-type solitons. These phenomena are revealed in Figs. 6 and 7.

Fig. 6

Steady propagation of the three-soliton via (29) at $t=0$, where $k_{1}=2, k_{2}=3, k_{3}=5, q_{1}=1, q_{2}=2, q_{3}=3, \phi (y)=\text {sn}(y,0.3) \ \text {cn}(y,0.6)$ and a $p_{1}=p_{2}=p_{3}=0$; b $p_{1}=6, p_{2}=3$, $p_{3}=-6$

Fig. 7

Steady propagation of the three-soliton via (29) at $t=0$, where $k_{1}=2, k_{2}=3, k_{3}=5, q_{1}=1, q_{2}=2, q_{3}=3, \phi (y)=\frac{\text {sn}(y,0.6)}{1+y^{2}}$ and a $p_{1}=p_{2}=p_{3}=0$; b $p_{1}=6, p_{2}=6, p_{3}=-6$

4 One-periodic waves and asymptotic properties

In order to obtain our results, we introduce the Riemann theta function

$$\begin{aligned} \vartheta (\xi ,\tau )=\sum _{n\in {{Z}^{N}}}e ^{-\pi <\tau n,n>+2\pi i<\xi ,n>}, \end{aligned}$$

(33)

here the integer value vector $n=(n_{1},\ldots ,n_{N})^\mathrm{T}$, and complex phase variables $\xi =(\xi _{1},\ldots ,\xi _{N})^\mathrm{T} \in {C}^{N}$. For two vectors $f=(f_{1},\ldots ,f_{N})$ and $g=(g_{1},\ldots ,g_{N})$, their inner product is defined by

$$\begin{aligned} \langle f,g \rangle =f_{1}g_{1}+f_{2}g_{2}+\cdots +f_{N}g_{N}. \end{aligned}$$

(34)

$\tau =(\tau _{ij})$ is a positive definite and real-valued symmetric $N\times N$ matrix, which is called the period matrix of the theta function. The entries $\tau _{ij}$ of the period matrix $\tau$ can be considered as free parameters of the theta function.

For the sake of quasi-periodic waves, we look for solution of Eq. (2) in the form

$$\begin{aligned} {\left\{ \begin{array}{ll} v=\mu _0\phi '(y)-2\partial _{xy}^2 \ln \vartheta (\xi ),\\ r=-2\partial _{xx}^2 \ln \vartheta (\xi ), \end{array}\right. } \end{aligned}$$

(35)

where $\mu _{0}$ is a free constant and $\xi _{j}=\alpha _j x+\beta _j \phi (y)+\theta _j t+\sigma _j$, $j=1,2,\ldots ,N$.

Substituting (35) into (2) and integrating with respect to x, we obtain the following bilinear form

$$\begin{aligned}&G(D_x,D_y,D_t)\vartheta (\xi )\vartheta (\xi ) \nonumber \\&\quad = \left( D_tD_y+D_x^3D_y-3\mu _0\phi '(y)D_x^2+c \right) \vartheta (\xi )\vartheta (\xi ) \nonumber \\&\quad = 0, \end{aligned}$$

(36)

where $c=c(y,t)$.

In the following, we consider one-periodic wave solutions of Eq. (2). Firstly, we take $N=1$, and then Riemann theta function reduces to the following Fourier series in n

$$\begin{aligned} \vartheta (\xi ,\tau )=\sum _{n=-\infty }^{+\infty } e ^{-\pi n^{2}\tau +2\pi i n \xi }, \end{aligned}$$

(37)

where the phase variable $\xi =\alpha x+\beta \phi (y)+\theta t+\sigma$ and the parameter $\tau >0$. The special case $\phi (y)=y$ has been considered in [50].

In order to make the theta function (37) satisfies the bilinear Eq. (36), we substitute function (37) into the left of Eq. (36), and it follows that

$$\begin{aligned}&G(D_{x},D_{y},D_{t})\vartheta (\xi )\vartheta (\xi ) \nonumber \\&\quad = \sum _{m=-\infty }^{+\infty }\sum _{n=-\infty }^{+\infty } G(D_{x},D_{y},D_{t}) \nonumber \\&\quad \quad \times \,e ^{-\pi m^{2}\tau +2\pi i m \xi }e ^{-\pi n^{2}\tau +2\pi i n \xi } \nonumber \\&\quad = \sum _{m=-\infty }^{+\infty }\sum _{n=-\infty }^{+\infty }G[2\pi i(n-m)\alpha ,2\pi i(n-m) \nonumber \\&\quad \quad \times \,\beta \phi '(y),2\pi i(n-m)\theta ] \nonumber \\&\quad \quad \times \,e ^{-\pi m^{2}\tau +2\pi i m \xi }e ^{-\pi n^{2}\tau +2\pi i n \xi } \nonumber \\&\quad = \sum _{m'=-\infty }^{+\infty } \left\{ \sum _{n=-\infty }^{+\infty }G[2\pi i(2n-m')\alpha ,2\pi i(2n-m') \right. \nonumber \\&\quad \quad \times \,\beta \phi '(y),2\pi i(2n-m')\theta ] \left. \times e ^{-\pi [n^{2}+(n-m')^{2}]\tau } \right\} \nonumber \\&\quad \quad \times \,e ^{2 \pi i m' \xi } \\&\quad \triangleq \sum _{m'=-\infty }^{+\infty } \overline{G}(m') e ^{2\pi i m' \xi }, \qquad m'=m+n. \nonumber \end{aligned}$$

(38)

In the following, we compute each series $\overline{G}(m')$ for $m'\in {Z}$. By shifting summation index by $n=n'+1$, we have the following fact

$$\begin{aligned} \overline{G}(m')= & {} \overline{G}(m'-2)e ^{-2\pi (m'-1)\tau } \nonumber \\= & {} \cdots = {\left\{ \begin{array}{ll} \overline{G}(0)e ^{-\pi m'^{2} \frac{\tau }{2}}, &{} m' \hbox { is even}, \\ \overline{G}(1)e ^{-\pi (m'^{2}-1)\frac{\tau }{2}}, &{} m' \hbox { is odd}, \end{array}\right. } \end{aligned}$$

(39)

which implies that $\overline{G}(m'), m'\in {Z}$ are completely dominated by two function $\overline{G}(0)$ and $\overline{G}(1)$. If $\overline{G}(0)=\overline{G}(1)=0$, then it follows that $\overline{G}(m')=0, m'\in {Z}$, and thus the theta function (37) is an exact solution to Eq. (36), namely $G(D_{x},D_{y},D_{t})\vartheta (\xi )\vartheta (\xi )=0$. And we have

$$\begin{aligned} \overline{G}(0)= & {} \sum _{n=-\infty }^{+\infty }[-16 \pi ^{2} n^{2}\beta \theta \phi '(y)+256\pi ^{4} n^{4}\beta \alpha ^{3}\phi '(y) \nonumber \\&+\, 48\mu _{0}\pi ^{2} n^{2}\alpha ^{2} \phi '(y)+c]e ^{-2 \pi n^{2} \tau }=0, \nonumber \\ \overline{G}(1)= & {} \sum _{n=-\infty }^{+\infty }[-4 \pi ^{2} (2n-1)^{2}\beta \theta \phi '(y) \nonumber \\&+\,16\pi ^{4} (2n-1)^{4}\beta \alpha ^{3}\phi '(y) \nonumber \\&+\,12\mu _{0}\pi ^{2} (2n-1)^{2}\alpha ^{2}\phi '(y)+c] \nonumber \\&\times \,e ^{-\pi (2n^{2}-2n+1) \tau }=0. \end{aligned}$$

(40)

By introducing the notations as

$$\begin{aligned} a_{11}= & {} \sum _{n=-\infty }^{+\infty }(-16 \pi ^{2} n^{2}\beta )\phi '(y)\wp ^{2n^{2}}, \nonumber \\ a_{12}= & {} \sum _{n=-\infty }^{+\infty }\wp ^{2n^{2}}, \nonumber \\ a_{21}= & {} \sum _{n=-\infty }^{+\infty }[-4 \pi ^{2} (2n-1)^{2}\beta ]\phi '(y)\wp ^{2 n^{2}-2 n+1}, \nonumber \\ a_{22}= & {} \wp ^{2 n^{2}-2 n+1}, \nonumber \\ b_{1}= & {} -\sum _{n=-\infty }^{+\infty }(256\pi ^{4} n^{4}\beta \alpha ^{3}+48\mu _{0}\pi ^{2} n^{2}\alpha ^{2})\nonumber \\&\times \,\phi '(y)\wp ^{2n^{2}}, \nonumber \\ b_{2}= & {} -\sum _{n=-\infty }^{+\infty }[16\pi ^{4} (2n-1)^{4}\beta \alpha ^{3} \nonumber \\&+\,12\mu _{0}\pi ^{2} (2n-1)^{2}\alpha ^{2}]\phi '(y)\wp ^{2 n^{2}-2 n+1}, \nonumber \\ \wp= & {} e ^{-\pi \tau }, \end{aligned}$$

(41)

we simply change Eqs. (40) into a linear system about the frequency $\theta$ and c, namely

$$\begin{aligned} \left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array}\right) \left( \begin{array}{cc} \theta \\ c \end{array}\right) =\left( \begin{array}{cc} b_{1} \\ b_{2} \end{array}\right) . \end{aligned}$$

(42)

Then, we get a one-periodic wave solution of Eq. (2)

$$\begin{aligned} v=\mu _0\phi '(y)-2\partial _{xy}^2 \ln \vartheta (\xi ), \qquad r=-2\partial _{xx}^2 \ln \vartheta (\xi ), \end{aligned}$$

(43)

which provided the vector $(\theta ,c)^{\mathrm {T}}$ solves Eq. (42) with the theta function $\vartheta (\xi )$ given by Eq. (37) and parameters $\theta , c$ by (42). The other parameters $\alpha , \beta , \tau , \sigma$ and $\mu _{0}$ are free. Figs. 8, 9 and 10 show one-periodic waves for some choice of the parameters and special $\phi (y)$.

Fig. 8

An one-periodic wave for the GSWW equation, where $\mu _0=\sigma =0, \alpha =0.1, \beta =0.2, \tau =0.2$, and $\phi (y)=\sin (y)$. a Perspective view of the wave and b overhead view of the wave

Fig. 9

An one-periodic wave for the GSWW equation with a interesting phenomenon, where $\mu _0=\sigma =0, \alpha =0.1$, $\beta =0.2, \tau =0.2$, and $\phi (y)=\sin (y)$. a Perspective view of the wave and b overhead view of the wave

Fig. 10

An one-periodic wave for the GSWW equation with a interesting phenomenon, where $\mu _0=\sigma =0, \alpha =0.1, \beta =0.2, \tau =0.2$, and $\phi (y)=\frac{1}{1+y^2}$. a Perspective view of the wave and b overhead view of the wave

Interestingly, we further consider asymptotic properties of the one-periodic wave solution, and the relation between the one-periodic solution (43) and the one-soliton solution (11, 12) can be established as follows. In order to obtain our conclusion clearly, we rewrite the one-soliton solution as following form

$$\begin{aligned} v=-2\left[ \ln \left( 1+e ^{\omega }\right) \right] _{xy}, \qquad r=-2\left[ \ln \left( 1+ e ^{\omega }\right) \right] _{xx}, \end{aligned}$$

(44)

where $\omega =k x+q \phi (y)-k^{3}t+p$.

Firstly, we let $\mu _{0}=0$ and write functions $a_{ij}, b_i, i, j=1, 2$ as the series about $\wp$. We write the coefficient matrix and the right-side vector of system (42) into power series of $\wp$ as

$$\begin{aligned} \left( \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array}\right)= & {} \left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array}\right) +\left( \begin{array}{cc} 0 &{} 0 \\ -8\pi ^{2}\beta \phi '(y) &{} 2 \end{array}\right) \wp \\&+\left( \begin{array}{cc} -32\pi ^{2}\beta \phi '(y) &{} 2\\ 0 &{} 0 \end{array}\right) \wp ^{2}+o(\wp ^{2}), \nonumber \end{aligned}$$

(45)

$$\begin{aligned} \left( \begin{array}{cc} b_{1} \\ b_{2} \end{array}\right)= & {} \left( \begin{array}{cc} 0 \\ -32\pi ^{4}\alpha ^{3}\beta \phi '(y) \end{array}\right) \wp \\&+\left( \begin{array}{cc} -512\pi ^{4}\alpha ^{3}\beta \phi '(y) \\ 0 \end{array}\right) \wp ^{2}+o(\wp ^{2}). \nonumber \end{aligned}$$

(46)

Substituting (45) and (46) into (42) and comparing the same order of $\wp$, we obtain

$$\begin{aligned} \theta= & {} 4\pi ^{2}\alpha ^{3}+o(\wp )\rightarrow 4\pi ^{2}\alpha ^{3}, \end{aligned}$$

(47)

$$\begin{aligned} c= & {} o(\wp )\rightarrow 0, \quad \hbox {as} \quad \wp \rightarrow 0, \end{aligned}$$

(48)

which implies that

$$\begin{aligned} 2\pi i \theta \rightarrow 8\pi ^{3} i \alpha ^{3}=-k^{3}, \quad c\rightarrow 0, \quad \hbox {as} \ \wp \rightarrow 0. \end{aligned}$$

(49)

To show the one-periodic wave (43) degenerates to the one-soliton solution (44) under the limit $\wp \rightarrow 0$, we first expand the periodic function $\vartheta (\xi )$ in the form

$$\begin{aligned} \vartheta (\xi ,\tau )= & {} 1+(e ^{2 \pi i \xi }+e ^{-2 \pi i \xi })\wp \,+\,(e ^{4 \pi i \xi }\nonumber \\&+\,e ^{-4 \pi i \xi })\wp ^{4}+\cdots \end{aligned}$$

(50)

By using the following transformation

$$\begin{aligned} \mu _{0}=0, \quad \alpha =\frac{k}{2\pi i}, \quad \beta =\frac{q}{2\pi i}, \quad \sigma =\frac{p+\pi \tau }{2 \pi i}, \end{aligned}$$

(51)

we have

$$\begin{aligned} \vartheta (\xi ,\tau )= & {} 1+e ^{\widetilde{\xi }} + (e ^{-\widetilde{\xi }} + e ^{2\widetilde{\xi }})\wp ^{2} + (e ^{-2\widetilde{\xi }} + e ^{3\widetilde{\xi }})\wp ^{6}\nonumber \\&+ \cdots \rightarrow 1+e ^{\widetilde{\xi }}, \hbox {as} \ \wp \rightarrow 0, \end{aligned}$$

(52)

where

$$\begin{aligned} \widetilde{\xi }=2\pi i \xi -\pi \tau . \end{aligned}$$

(53)

Combining (49) and (53) deduces that

$$\begin{aligned}&\widetilde{\xi }\rightarrow \omega , \quad \hbox {as} \quad \wp \rightarrow 0, \end{aligned}$$

(54)

$$\begin{aligned}&\xi \rightarrow \frac{\omega +\pi \tau }{2\pi i}, \quad \hbox {as} \quad \wp \rightarrow 0. \end{aligned}$$

(55)

So we can acquire

$$\begin{aligned} \vartheta (\xi ,\tau )\rightarrow 1+e ^{\omega }, \quad \hbox {as} \quad \wp \rightarrow 0. \end{aligned}$$

(56)

From above, we conclude that the one-periodic solution (43) just goes to the one-soliton solution (44) as the amplitude $\wp \rightarrow 0$.

5 Two-periodic waves and asymptotic properties

In this section, we consider two-periodic wave solutions of Eq. (2) and their asymptotic property. In order to obtain two-periodic solution, we consider the case of $N=2$ and the Riemann theta function (37) takes the form

$$\begin{aligned} \vartheta (\xi ,r)=\vartheta (\xi _{1},\xi _{2},r)=\sum _{n\in Z^{2}} e ^{-\pi \langle \tau n,n\rangle +2\pi i \langle \xi ,n\rangle }, \end{aligned}$$

(57)

where $n=(n_{1},n_{2})^\mathrm{T}\in Z^{2}, \xi =(\xi _{1},\xi _{2})^\mathrm{T}\in C^{2}$, $\xi _{j}=\alpha _{j}x+\beta _{j}\phi (y)+\theta _{j}t+\sigma _{j}$, $j=1,2$. Here, $\tau$ is a positive definite and real-valued symmetric $2\times 2$ matrix, which can be taken of the form

$$\begin{aligned} \tau =\left( \begin{array}{cc} \tau _{11} &{} \tau _{12} \\ \tau _{12} &{} \tau _{22} \end{array}\right) , \quad \tau _{11}>0, \quad \tau _{22}>0, \quad \tau _{11}\tau _{22}-\tau _{12}^{2}>0. \end{aligned}$$

(58)

To make the theta function (57) satisfies the bilinear Eq. (36), we substitute function (57) into the left of Eq. (36) and obtain that

$$\begin{aligned}&G(D_{x},D_{y},D_{t})\vartheta (\xi _1,\xi _2,\tau ) \vartheta (\xi _1,\xi _2,\tau ) \nonumber \\&\quad = \sum _{m,n\in Z^{2}}G[2\pi i\langle n-m,\alpha \rangle ,2\pi i \langle n-m,\beta \rangle \phi '(y), \nonumber \\&\quad \quad \times \,2\pi i \langle n-m,\theta \rangle ] \nonumber \\&\quad \quad \times \,e ^{-\pi (\langle \tau m,m\rangle +\langle \tau n,n\rangle )+2\pi i \langle \xi ,n+m\rangle } \nonumber \\&\quad = \sum _{m'\in Z^{2}} \left\{ \sum _{n\in Z^{2}}G[2\pi i\langle 2n-m',\alpha \rangle , \right. \nonumber \\&\quad \quad \times \,2\pi i\langle 2n-m',\beta \rangle \phi '(y),2\pi i\langle 2n-m',\theta \rangle ] \nonumber \\&\quad \quad \left. \times \, e ^{-\pi [\langle \tau n,n\rangle +\langle \tau (n-m'),(n-m')\rangle ]} \right\} \times e ^{2\pi i \langle \xi ,m'\rangle } \nonumber \\&\quad \triangleq \sum _{m'\in Z^{2}} \overline{G}(m'_1,m'_2) e ^{2\pi i \langle \xi ,m'\rangle }, \quad m'=m+n.\quad \quad \end{aligned}$$

(59)

In the following, we compute each series $\overline{G}(m'_1,m'_2)$ for $m'_1,m'_2\in Z^{2}$. By shifting summation index by $n=n'+\delta _{jk},k=1,2$, we obtain that

$$\begin{aligned} \overline{G}(m'_1,m'_2)= & {} \sum _{n\in Z^{2}}G[2\pi i\langle 2n-m',\alpha \rangle , \nonumber \\&\times \,2\pi i \langle 2n-m',\beta \rangle \phi '(y),\nonumber \\&\times \,2\pi i \langle 2n-m',\theta \rangle ] \nonumber \\&\times \,e ^{-\pi [\langle \tau n,n\rangle +\langle \tau (n-m'),(n-m')\rangle ]} \nonumber \\= & {} \sum _{n\in Z^{2}}G \left[ 2\pi i\sum _{j=1}^{2}(2n'_j-(m'_j-2\delta _{jk}))\alpha _j, \right. \nonumber \\&\times \,2\pi i\sum _{j=1}^{2}(2n'_j-(m'_j-2\delta _{jk}))\beta _j \phi '(y),\nonumber \\&\left. \times \,2\pi i\sum _{j=1}^{2}(2n'_j-(m'_j-2\delta _{jk}))\theta _j \right] \nonumber \\&\times \,e ^{-\pi \sum _{j,l=1}^{2}[(n'_j+\delta _{jk})(n'_l+\delta _{lk})+(m'_j-n'_j-\delta _{jk})(m'_l-n'_l-\delta _{lk})]\tau _{jl}} \nonumber \\= & {} {\left\{ \begin{array}{ll} \overline{G}(m'_1-2,m'_2)e ^{2\pi (1-m'_1)\tau _{11}-2\pi m'_2 \tau _{12}},\quad &{} k=1 , \\ \overline{G}(m'_1,m'_2-2)e ^{2\pi (1-m'_2)\tau _{22}-2\pi m'_1 \tau _{12}},\quad &{} k=2 , \end{array}\right. } \end{aligned}$$

(60)

where $\delta _{ij}$ representing Kronecker’s delta. If

$$\begin{aligned} \overline{G}(0,0)= & {} 0, \quad \overline{G}(1,0)=0, \quad \overline{G}(0,1)=0, \nonumber \\ \overline{G}(1,1)= & {} 0, \end{aligned}$$

(61)

then it follows that $\overline{G}(m',m'')=0, m',m''\in Z$, and thus the theta function (57) is an exact solution to Eq. (36), namely $G(D_{x},D_{y},D_{t})\vartheta (\xi _1,\xi _2)\vartheta (\xi _1,\xi _2)=0$. So we get

$$\begin{aligned}&\sum _{n\in Z^{2}} G(2\pi i\langle 2n-\varrho _1,\alpha \rangle , 2\pi i\langle 2n-\varrho _1,\beta \rangle \phi '(y), \nonumber \\&\quad \times \, 2\pi i\langle 2n-\varrho _1,\theta \rangle ) \nonumber \\&\quad \times \,e ^{- \pi [\langle \tau (n-\varrho _1),n-\varrho _1\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$

(62)

$$\begin{aligned}&\sum _{n\in Z^{2}} G(2\pi i\langle 2n-\varrho _2,\alpha \rangle , 2\pi i\langle 2n-\varrho _2,\beta \rangle \phi '(y), \nonumber \\&\quad \times \,2\pi i\langle 2n-\varrho _2,\theta \rangle ) \nonumber \\&\quad \times \,e ^{- \pi [\langle \tau (n-\varrho _2),n-\varrho _2\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$

(63)

$$\begin{aligned}&\sum _{n\in Z^{2}} G(2\pi i\langle 2n-\varrho _3,\alpha \rangle , 2\pi i\langle 2n-\varrho _3,\beta \rangle \phi '(y), \nonumber \\&\quad \times \,2\pi i\langle 2n-\varrho _3,\theta \rangle ) \nonumber \\&\quad \times \,e ^{- \pi [\langle \tau (n-\varrho _3),n-\varrho _3\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$

(64)

$$\begin{aligned}&\sum _{n\in Z^{2}} G(2\pi i\langle 2n-\varrho _4,\alpha \rangle , 2\pi i\langle 2n-\varrho _4,\beta \rangle \phi '(y), \nonumber \\&\quad \times \,2\pi i\langle 2n-\varrho _4,\theta \rangle ) \nonumber \\&\quad \times \,e ^{- \pi [\langle \tau (n-\varrho _4),n-\varrho _4\rangle +\langle \tau n,n\rangle ]}=0, \end{aligned}$$

(65)

where $\varrho _j=(\varrho _j^{1},\varrho _j^{2})^\mathrm{T}, \ \varrho _1=(0,0)^\mathrm{T}, \ \varrho _2=(1,0)^\mathrm{T}, \ \varrho _3=(0,1)^\mathrm{T}, \ \varrho _4=(1,1)^\mathrm{T}, \ j=1, \ 2, \ 3, \ 4,$ By introducing the notations as

$$\begin{aligned} H=(h_{jk})_{4\times 4}, \qquad b=(b_1, b_2, b_3, b_4)^\mathrm{T}, \end{aligned}$$

$$\begin{aligned} h_{j1}= & {} -4\pi ^{2}\sum _{(n_1,n_2)\in Z^{2}}\langle 2n-\delta ^{j},\beta \rangle (2n_1-\delta _1^j)\\&\times \,\phi '(y)\lambda _j(n), \\ h_{j2}= & {} -4\pi ^{2}\sum _{(n_1,n_2)\in Z^{2}}\langle 2n-\delta ^{j},\beta \rangle (2n_1-\delta _2^j)\\&\times \,\phi '(y)\lambda _j(n), \\ h_{j3}= & {} 12\pi ^{2}\sum _{(n_1,n_2)\in Z^{2}}\langle 2n-\delta ^{j},\alpha \rangle ^{2}\\&\times \,\phi '(y)\lambda _j(n), \\ h_{j4}= & {} \sum _{(n_1,n_2)\in Z^{2}}\lambda _j(n), \end{aligned}$$

$$\begin{aligned} b_{j}= & {} -16\pi ^{4}\sum _{(n_1,n_2)\in Z^{2}}\langle 2n-\delta ^{j},\alpha \rangle ^{3}\langle 2n-\delta ^{j},\beta \rangle \\&\times \,\phi '(y)\lambda _j(n), \end{aligned}$$

$$\begin{aligned} \lambda _j(n)\!=\! & {} \wp _1^{n_1^{2}+(n_1-\delta _1^j)^2} \wp _2^{n_2^{2} + (n_2-\delta _2^j)^2}\wp _3^{n_1n_{2}+(n_1-\delta _1^j)(n_2-\delta _2^j)}, \end{aligned}$$

$$\begin{aligned} \wp _{1}= & {} e ^{-\pi \tau _{11}}, \qquad \wp _{2}=e ^{-\pi \tau _{22}}, \qquad \wp _{3}=e ^{-2\pi \tau _{12}}, \nonumber \\&\hbox {where} \ j=1,2,3,4.\qquad \end{aligned}$$

(66)

Eqs. (62–65) can be written as a linear system

$$\begin{aligned} H(\theta _1,\theta _2,\mu _0,c)^\mathrm{T}=b. \end{aligned}$$

(67)

Then, we get a two-periodic wave solution of Eq. (2)

$$\begin{aligned} {\left\{ \begin{array}{ll} v=\mu _0\phi '(y)-2\partial _{xy}^2 \ln \vartheta (\xi _1,\xi _2), \\ r=-2\partial _{xx}^2 \ln \vartheta (\xi _1,\xi _2), \end{array}\right. } \end{aligned}$$

(68)

where $\vartheta (\xi _1,\xi _2,\tau )$ and parameters $\theta _1$, $\theta _2, \mu _0, c$ are given by Eqs. (57) and (67), respectively. The other parameters $\alpha _1$, $\alpha _2, \beta _1, \beta _2, \sigma _1, \sigma _2$, $\tau _{11}, \tau _{12}$ and $\tau _{22}$ are free. Figs. 11, 12, 13 and 14 show the two-periodic waves for different choice of the parameters and special $\phi (y)$.

Fig. 11

A degenerate two-periodic wave for the GSWW equation, where $\frac{\alpha _1}{\alpha _2}=\frac{\beta _1}{\beta _2}$ and $\mu _0=\sigma =0, \alpha _1=0.3, \alpha _2=0.03, \beta _1=2, \beta _2=0.2, \tau _{11}=2, \tau _{12}=0.2, \tau _{22}=2, \phi (y)=y$. This figure shows that the degenerate two-periodic wave is almost one dimensional. a Perspective view of the wave and b overhead view of the wave

Fig. 12

An asymmetric two-periodic wave for the GSWW equation, where $\mu _0=\sigma =0, \alpha _1=0.3, \alpha _2=0.2$, $\beta _1=0.2, \beta _2=-0.3, \tau _{11}=2, \tau _{12}=0.2$, $\tau _{22}=2$ and $\phi (y)=y$. This figure shows that every asymmetric two-periodic wave is spatially periodic in two directions, but it need not be periodic in either the x- or y-direction. a Perspective view of the wave and b overhead view of the wave

Fig. 13

An symmetric two-periodic wave for the GSWW equation, where $\mu _0=\sigma =0, \alpha _1=0.13, \alpha _2=0.13, \beta _1=0.13, \beta _2=-0.13, \tau _{11}=2, \tau _{12}=0.2, \tau _{22}=2$ and $\phi (y)=y$. This figure shows that the symmetric two-periodic wave is periodic both in x- or y-direction. a Perspective view of the wave and b overhead view of the wave

Fig. 14

An symmetric two-periodic wave for the GSWW equation with a interesting phenomenon, where $\mu _0=\sigma =0$, $\alpha _1=0.13, \alpha _2=0.13, \beta _1=0.13, \beta _2=-0.13$, $\tau _{11}=2, \tau _{12}=0.2, \tau _{22}=2$ and $\phi (y)=\frac{1}{1+y^2}$. a Perspective view of the wave and b overhead view of the wave

Finally, we further consider asymptotic properties of the two-periodic wave solution. In a similar way to one-periodic solution, we rewrite the two-soliton solution as the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} v=-2\left[ \ln \left( 1+e ^{\omega _{1}}+e ^{\omega _{2}}+e ^{\omega _{1}+\omega _{2}+A_{12}}\right) \right] _{xy},\\ r=-2\left[ \ln \left( 1+e ^{\omega _{1}}+e ^{\omega _{2}}+e ^{\omega _{1}+\omega _{2}+A_{12}}\right) \right] _{xx}, \end{array}\right. } \end{aligned}$$

(69)

where $A_{12}=\ln (a_{12})$ and $\omega _1, \omega _2, a_{12}$ are given in (7, 18) and (20).

Furthermore, we establish the relation between two-periodic solution (68) and the two-soliton solution (69) as follows.

Firstly, we expand the periodic function $\vartheta (\xi _1,\xi _2)$ in the following form

$$\begin{aligned} \vartheta (\xi _1,\xi _2,\tau )= & {} 1+\left( e ^{2 \pi i \xi _1}+e ^{-2 \pi i \xi _1}\right) e ^{-\pi \tau _{11}} \nonumber \\&+\left( e ^{2 \pi i \xi _2}+e ^{-2 \pi i \xi _2}\right) e ^{-\pi \tau _{22}} \\&+ \left( e ^{2 \pi i (\xi _1+\xi _2)}+e ^{-2 \pi i (\xi _1+\xi _2)}\right) \nonumber \\&\times \,e ^{- \pi (\tau _{11}+2\tau _{12}+\tau _{22})}. \nonumber \end{aligned}$$

(70)

By using the following transformation

$$\begin{aligned}&\mu _0=0, \quad \alpha _j=\frac{k_j}{2\pi i}, \quad \beta _j=\frac{q_j}{2\pi i}, \nonumber \\&\sigma _j=\frac{p_j+\pi \tau _{jj}}{2\pi i}, \quad \tau _{12}=\frac{A_{12}}{2\pi i}, \quad j=1,2, \end{aligned}$$

(71)

we get

$$\begin{aligned} \vartheta (\xi _1,\xi _2,\tau )= & {} 1+e ^{\widetilde{\xi }_1} + e ^{\widetilde{\xi }_2} + e ^{\widetilde{\xi }_1 + \widetilde{\xi }_2-2\pi \tau _{12}}+\wp _1^2e ^{-\widetilde{\xi }_1} \nonumber \\&+\,\wp _2^2e ^{-\widetilde{\xi }_2} + \wp _1^2\wp _2^2e ^{-\widetilde{\xi }_1 - \widetilde{\xi }_2-2\pi \tau _{12}} \nonumber \\&+\cdots \rightarrow 1+e ^{\widetilde{\xi }_1} + e ^{\widetilde{\xi }_2} + e ^{\widetilde{\xi }_1+\widetilde{\xi }_2+a_{12}}, \nonumber \\&\quad \hbox {as} \ \wp _1, \ \wp _2\rightarrow 0, \end{aligned}$$

(72)

where

$$\begin{aligned}&\widetilde{\xi }_j=2\pi i \xi _j\!-\!\pi \tau _{jj}\!=\!k_j x+q_j \phi (y)+\widetilde{\theta _j}t+p_j, \end{aligned}$$

(73)

$$\begin{aligned}&\widetilde{\theta _j}=2\pi i \theta _j,\quad j=1,2. \end{aligned}$$

(74)

From above, we can expand each function in $a_{jk}, b_k$, $k=1,2,3,4$ into a series with $\wp _1, \wp _2$. Actually, we only need to make the first-order expansions of matrix M and vector b with $\wp _1, \wp _2$ to show the asymptotic relations. Here, we consider their second-order expansions to see relations among parameters for the two-periodic solution and the two-soliton solution (69). The expansions for the matrix M and the vector b are given by

$$\begin{aligned} H= & {} \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) +\left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ -8\pi ^2 \beta _1\phi '(y) &{} 0 &{} 24\pi ^2 \alpha _1^2\phi '(y) &{} 2 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \wp _1 \nonumber \\&+ \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -8\pi ^2 \beta _2\phi '(y) &{} 24\pi ^2 \alpha _2^2\phi '(y) &{} 2 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \wp _2 \nonumber \\&+ \left( \begin{array}{cccc} -32\pi ^2 \beta _1\phi '(y) &{} 0 &{} 96\pi ^2 \alpha _1^2\phi '(y) &{} 2 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \wp _1^2 \nonumber \\&+ \left( \begin{array}{cccc} 0 &{} -32\pi ^2 \beta _2\phi '(y) &{} 96\pi ^2 \alpha _2^2\phi '(y) &{} 2 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) \wp _2^2 \nonumber \\&+ \left( \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ -8\pi ^2(\beta _1-\beta _2)\phi '(y) &{}\quad \varDelta _1\phi '(y) &{}\quad 24\pi ^2(\alpha _1-\alpha _2)^2\phi '(y) &{}\quad 2 \\ \end{array} \right) \nonumber \\&\times \,\wp _1\wp _2+o(\wp _1^i \wp _2^j), \end{aligned}$$

(75)

where $\varDelta _1=8 \pi ^2(\beta _1-\beta _2)-8\pi ^2(\beta _1+\beta _2)\lambda _3, \ i+j\ge 2$.

$$\begin{aligned} b= & {} \left( \begin{array}{cccc} 0 \\ -32\pi ^{4}\alpha _1^3 \beta _1\phi '(y) \\ 0 \\ 0 \\ \end{array} \right) \wp _1 +\left( \begin{array}{cccc} 0 \\ 0 \\ -32\pi ^{4}\alpha _2^3 \beta _2\phi '(y) \\ 0 \\ \end{array} \right) \wp _2 \nonumber \\&+ \left( \begin{array}{cccc} -512\pi ^{4}\alpha _1^3 \beta _1\phi '(y) \\ 0 \\ 0 \\ 0 \\ \end{array} \right) \wp _1^2+\left( \begin{array}{cccc} 0 \\ -512\pi ^{4}\alpha _2^3 \beta _2\phi '(y) \\ 0 \\ 0 \\ \end{array} \right) \wp _2^2 \nonumber \\&+ \left( \begin{array}{cccc} 0 \\ 0 \\ 0 \\ \varDelta _2\phi '(y) \\ \end{array} \right) \wp _1\wp _2 +o(\wp _1^i \wp _2^j), \end{aligned}$$

(76)

where $\varDelta _2=-32 \pi ^4(\alpha _1+\alpha _2)^3(\beta _1+\beta _2)\lambda _3-32\pi ^4(\alpha _1-\alpha _2)^3(\beta _1-\beta _2),\ i+j\ge 2$. We also assume the solution of system (67) in the following form

$$\begin{aligned} \left( \begin{array}{cccc} \theta _1 \\ \theta _2 \\ \mu _0 \\ c \\ \end{array} \right)= & {} \left( \begin{array}{cccc} \theta _1^{(0)} \\ \theta _2^{(0)} \\ 0 \\ c^{(0)} \\ \end{array} \right) +\left( \begin{array}{cccc} \theta _1^{(1)} \\ \theta _2^{(1)} \\ 0 \\ c^{(1)} \\ \end{array} \right) \wp _1 +\left( \begin{array}{cccc} \theta _1^{(2)} \\ \theta _2^{(2)} \\ 0 \\ c^{(2)} \\ \end{array} \right) \wp _2 \nonumber \\&+ \left( \begin{array}{cccc} \theta _1^{(11)} \\ \theta _2^{(11)} \\ 0 \\ c^{(11)} \\ \end{array} \right) \wp _1^2 + \left( \begin{array}{cccc} \theta _1^{(22)} \\ \theta _2^{(22)} \\ 0 \\ c^{(22)} \\ \end{array} \right) \wp _2^2 +\left( \begin{array}{cccc} \theta _1^{(12)} \\ \theta _2^{(12)} \\ 0 \\ c^{(12)} \\ \end{array} \right) \nonumber \\&\times \,\wp _1\wp _2 +o(\wp _1^i \wp _2^j), \quad i+j\ge 2. \end{aligned}$$

(77)

Substituting (75–77) into (67) and comparing the same order of $\wp$, we obtain

$$\begin{aligned}&c^{(0)}=c^{(1)}=c^{(2)}=c^{(12)}=0, \nonumber \\&\beta _1\theta _1^{(0)}=4\pi ^2\alpha _1^3\beta _1, \quad \beta _2\theta _3^{(0)}=4\pi ^2\alpha _2^3\beta _2, \nonumber \\&\beta _1\theta _1^{(1)}=0, \quad \beta _2\theta _2^{(1)}=0, \nonumber \\&c^{(11)}-32\pi ^2\beta _1\theta _1^{(0)}=-512\pi ^4\alpha _1^3\beta _1, \nonumber \\&c^{(22)}-32\pi ^2\beta _2\theta _2^{(0)}=-512\pi ^4\alpha _2^3\beta _2, \nonumber \\&\cdots \end{aligned}$$

(78)

so we can obtain

$$\begin{aligned} c= & {} o(\wp _1,\wp _2) \rightarrow 0, \nonumber \\ \theta _1= & {} 4\pi ^2\alpha _1^3+o(\wp _1,\wp _2)\rightarrow 4\pi ^2\alpha _1^3, \nonumber \\ \theta _2= & {} 4\pi ^2\alpha _2^3+o(\wp _1,\wp _2)\rightarrow 4\pi ^2\alpha _2^3, \nonumber \\&\hbox {as} \ \wp _1,\wp _2\rightarrow 0. \end{aligned}$$

(79)

From above, we conclude that the two-periodic solution (68) tends to the two-soliton solution (69) as $\wp _1,\wp _2\rightarrow 0$.

6 Conclusion

In this work, we conduct an analysis on a $(2 + 1)$-dimensional shallow water wave equation. In the light of the construction of the Eq. (4), the new special multiple-soliton solutions and the singular-soliton solutions are acquired by means of the Hirota method. Also, the rational function solution is obtained through the limit method. By means of the graphic analysis and asymptotic analysis, dynamic properties and interaction mechanisms for the solitons are revealed. Furthermore, the breather-type and lump-type solitons are obtained for the certain $\phi (y)$. The higher level soliton solutions, for $n\ge 4$ can be obtained in a parallel manner. And their dynamic properties and asymptotic analysis can be discussed similarly.

Using the Hirota method and Riemann theta function, we construct quasi-periodic wave solutions with a generalized form. Besides, the asymptotic analysis of the quasi-periodic(multi-periodic) wave solution is presented and the relation between the quasi-periodic solutions and soliton solutions acquired in this paper are rigorously established. Furthermore, all the solutions we obtained above can be verified by Maple. Also, the results perhaps can be extended to the case when $N>2$, but there are still certain numerical difficulties in the calculation. We will consider it in our future work.