1 Introduction

An actual physical system always works in a certain environment, such as ambient temperature, humidity, electromagnetic field, etc., leading to random disturbance to the system. In addition, due to the medium discontinuity, the values of system components will vary randomly, resulting in variable system parameters. According to the relationship between noise, system state variables and drive signals, noise may be divided into several types, i.e., additive noise, multiplicative noise and signal-modulated noise. The noise with intensity independent of the system states is called additive noise, the noise with strength related to the system state variable is called multiplicative noise and the noise with intensity modulated by an excitation signal is termed as signal-modulated noise [1,2,3,4,5,6,7,8]. Signal-modulated noise is widely applied in various scientific fields. For example, in optical or radio astronomy, the output signal of the amplifier is noise-modulated by periodic signals, which has an important impact on the system performance [3,4,5,6]. In optical communication process, when the signal modulates the laser carrier, the signal is inevitably modulated by the noise in the laser [7, 8].

Generally speaking, the addition of noise to a system will reduce the output performance of the system. However, under certain circumstances, with the cooperation between the noise, the system and the input signal, an appropriate amount of noise can greatly improve the output signal of the system. This nonlinear phenomenon is called stochastic resonance (SR). The phenomenon of SR with multiplicative noise has been widely studied by scholars [9,10,11,12,13,14,15,16]. Single-peak [9, 10] or multipeak [11] has been observed in the output of a bistable [9, 11] or a monostable system [10] with the multiplicative noise. Meanwhile, SRs for tristable system [12] and for fractional oscillators [13, 14] subject to multiplicative noise have also been studied. The stochastic multiresonance in an insect outbreak model [15] and the stability for a metapopulation system [16] with multiplicative noise are also analysed. SR for systems subject to signal-modulated noise was also studied [17,18,19,20]. It is found that signal-modulated noise will cause dynamic SR in a bistable system [17] and cause resonant behaviour in fractional oscillators [18,19,20].

Due to the effects of amplifier noise [21,22,23,24] and nonlinear Kerr electro-optic [25,26,27,28,29], the phase of an electric system output signal will change randomly. SR subject to random-phase sinusoidal signal-modulated noise [17] has been studied. On the other hand, square-wave signals are widely used in various physical systems. For example, in digital communication systems, square-waves are common carriers and clock signals. Square-wave voltage is adopted as droplet direction actuation to achieve asymmetric electrodes [30]. In addition, square-wave is used to drive ionic polymer metal composite (IPMC) in air operating [31] and to drive bistable system for energy harvesting [32]. SR has been found in many square-wave-driven systems, including sinusoidal potential system [33], time-delayed bistable system [34, 35], underdamped bistable system [36], overdamped monostable system [37, 38], stochastic overdamped bistable system [39] and energy harvesting bistable system [40]. It was shown that the system output signal exhibits SR phenomenon for different amplitudes of the square-wave signal for time-delayed overdamped bistable system [35] and underdamped bistable system [36] subject to dichotomous and multiplicative noises.

Yet, to the best of our knowledge, little attention has been paid on the nonlinear effect of a random-phase square-wave signal-modulated noise on a bistable system. In particular, we note that in certain physical systems, square-wave signals can exhibit asymmetry, as seen in digital systems powered by a single positive supply, where the input and output digital signals are asymmetric square-waves with two discrete voltage levels, i.e., one zero volt and one voltage same as the power supply. Single-peak phenomenon has been observed for time-delayed overdamped bistable system [35] and underdamped bistable system [36] with symmetric square-wave signals. Yet, the effect of the asymmetry of the square-wave signal is not studied. Based on this, this paper intends to investigate the SR phenomenon in a bistable system subject to random-phase asymmetric-square-wave signal-modulated noise. It is found that the asymmetry of the square-wave can induce stochastic double resonance, which means that by choosing two different amplitudes of the square-wave signal, the system output can be maximised. This new result is different from those obtained in refs [35, 36]. Thus, for stochastic systems where it is difficult to regulate the noise, it offers a more convenient approach to achieve optimal output performance.

This paper is organised as follows. In §2, the bistable system with random-phase asymmetric square-wave signal-modulated noise is introduced, the transition rates from the stable states and the system output signal-to-noise ratio (SNR) are obtained. In §3, the non-monotonous dependence of the system output on the noises and on the system parameters are discussed. Finally, some conclusions are drawn in §4.

2 The bistable system with random-phase square-wave signal-modulated noise and multiplicative noise

Consider a Brownian particle moving in a bistable potential with noise environment described by the following equation:

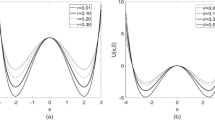
$$\begin{aligned} \dot{x} = - \frac{{\textrm{d}U(x)}}{{\textrm{d}x}} + x\varsigma (t) + \psi (t) + \eta (t) + s(t), \end{aligned}$$
(1)

where \(x = x(t)\) is the displacement of the particle at time t and \(\dot{x} = \textrm{d}x/\textrm{d}t\) is the velocity of the moving particle. The potential function of the system has the form \( U(x) = - ax^2 / 2 + bx^4/ 4\) with two stable states \( x_ \pm = \pm \sqrt{a/b} \) and one unstable state \( x_0 = 0 \). s(t) is a periodic square-wave with period T and asymmetric amplitude

$$\begin{aligned} s(t) = \left\{ {\begin{array}{*{20}c} {\kappa B,\begin{array}{*{20}c} {} &{} {} \\ \end{array}0< t \le T/2,} \\ { - B,\begin{array}{*{20}c} {} &{} {} \\ \end{array}T/2 < t \le T,} \\ \end{array}} \right. \end{aligned}$$
(2)

where \( \kappa > 0 \), \( B > 0 \). \( \kappa \) denotes the asymmetry of the square-wave signal. For symmetric square-wave signal \( \kappa = 1\). s(t) can be rewritten as

$$\begin{aligned} s(t) = Ag(t) + m, \end{aligned}$$
(3)

where

$$\begin{aligned} A = \frac{{\kappa + 1}}{2}B, \quad m = \frac{{\kappa - 1}}{2}B, \end{aligned}$$
(4)

g(t) is a symmetric square-wave signal with unit amplitude and period T

$$\begin{aligned} g(t) = \left\{ {\begin{array}{*{20}c} {1,\begin{array}{*{20}c} {} &{} {} \\ \end{array}0< t \le T/2,} \\ { - 1,\begin{array}{*{20}c} {} &{} {} \\ \end{array}T/2 \le t < T.} \\ \end{array}} \right. \end{aligned}$$
(5)

\( \psi (t) \) is a signal-modulated noise given as

$$\begin{aligned} \psi (t) = s_n (t)\xi (t), \end{aligned}$$
(6)

where \( s_n (t) \) is a random-phase signal with the same amplitude and period as signal s(t) , whose phase uniform distributed within the range \( (0,2\pi ) \). The three noise terms \( \varsigma (t) \), \( \xi (t) \) and \( \eta (t) \) are white ones with zero means and correlations

$$\begin{aligned} \begin{array}{l} \left\langle {\varsigma (t_1 )\varsigma (t_2 )} \right\rangle = 2D\delta (t_1 - t_2 ),\\ \left\langle {\xi (t_1 )\xi (t_2 )} \right\rangle = 2P\delta (t_1 - t_2 ), \\ \left\langle {\eta (t_1 )\eta (t_2 )} \right\rangle = 2Q\delta (t_1 - t_2 ). \\ \end{array} \end{aligned}$$
(7)

From eqs (6) and (7), one can see that \( \psi (t)\) is a random-phase signal-modulated noise with zero mean and correlation

$$\begin{aligned} \left\langle \psi (t_1 )\psi (t_2 ) \right\rangle = 2P(A^2 / 2 + m^2 )\delta (t_1 - t_2 ). \end{aligned}$$
(8)

It is worth to point out that the model studied in this paper is different from those in refs [17, 33, 34, 37]. In ref. [17], only additive noises are considered, i.e., the researchers consider additive signal-modulated noise and additive white noise, while in this paper we also consider multiplicative noise. Another difference is that the driven signal in this paper is of a square-wave form. In refs [33, 34, 37], the square-wave signals are symmetric ones, while in this paper they are assumed as asymmetric ones.

Applying the statistical characteristics of the noises, the Fokker–Planck equation for the probability density function \(\rho (x,t)\) corresponding to eq. (1) can be derived as

$$\begin{aligned} \frac{\partial }{{\partial t}}\rho (x,t) = - \frac{\partial }{{\partial x}}[F(x)\rho (x,t)] + \frac{{\partial ^2 }}{{\partial x^2 }}[G(x)\rho (x,t)],\nonumber \\ \end{aligned}$$
(9)

where

$$\begin{aligned}{} & {} \!\!\! F(x) = ax + Dx - bx^3 + s(t) \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \!\!\! G(x) = Dx^2 + \dfrac{{A^2 }}{2}P + m^2 P + Q = Dx^2 + M \nonumber \\{} & {} \!\!\! M = \dfrac{{A^2 }}{2}P + m^2 P + Q. \end{aligned}$$
(11)

Let the frequency \(\Omega = 2\pi /T\) of the square-wave signal is slow enough so that the system has plenty of time to reach the equilibrium during period T, i.e., the system meets adiabatic proximation condition [41]. The quasistationary probability density can be given by

$$\begin{aligned} \rho _{st}= & {} \dfrac{N}{{\sqrt{G(x)} }}\exp \left[ {\int _{}^x {\textrm{d}x'\dfrac{{F(x')}}{{G(x')}}} } \right] \nonumber \\= & {} \dfrac{N}{{\sqrt{G(x)} }}\exp \left[ { - \Phi (x)} \right] , \end{aligned}$$
(12)

where

$$\begin{aligned} \Phi (x)= & {} - \int _{}^x {\dfrac{{F(x')}}{{G(x')}}} \textrm{d}x' \nonumber \\= & {} \dfrac{b}{{2D}}x^2 - \dfrac{{a + D + b/D}}{{2D}}\ln (Dx^2 + M) \nonumber \\{} & {} + \dfrac{{s(t)}}{{\sqrt{DM} }}\arctan \left( {x\sqrt{\dfrac{D}{M}} } \right) . \end{aligned}$$
(13)

By virtue of the two-state theory [41], the transition rates out of \(x_ \pm \) can be written as

$$\begin{aligned} W_ \pm (t)= & {} \dfrac{{\sqrt{\left| {U''(x_ \pm )U''(x_0 )} \right| } }}{{2\pi }}\exp \left[ {\Phi (x_ \pm ) - \Phi (x_0 )} \right] \nonumber \\= & {} W_0 \exp [ \mp \gamma s(t)] \end{aligned}$$
(14)

with

$$\begin{aligned} \begin{aligned}&U''(x) = \frac{{\textrm{d}^2 U(x)}}{{\textrm{d}x^2 }}, \\&\gamma = \frac{1}{{\sqrt{DM} }}\arctan \left( {\sqrt{\frac{{aD}}{{bM}}} } \right) . \end{aligned} \end{aligned}$$
(15)

Here, \( W_0 \) is the characteristic transition rate for the bistable system when it is only subjected to the noises, which can be expressed as

$$\begin{aligned} W_0= & {} \frac{a}{{\sqrt{2} \pi }}\exp \Bigg [ \frac{a}{{2D}} - \Bigg ( \frac{a}{{2D}} + \frac{1}{2}+ \frac{b}{{2D^2 }} \Bigg ) \nonumber \\{} & {} \times \ln \Bigg ( {\frac{{aD}}{{bM}} + 1} \Bigg ) \Bigg ]. \end{aligned}$$
(16)

Assuming that the system output switches between a dichotomous variable d(t), then the correlation function, averaged by d(t), can be deduced as [17]

$$\begin{aligned}{} & {} \!\!\! H(t_1,t_2 ) = \left\langle {x(t_1 )x(t_2 )} \right\rangle _d \nonumber \\{} & {} \qquad \qquad \,= \omega (t_1 )\omega (t_2 ) {+} \dfrac{{8W_ {+} (t_1 )W_ {-} (t_1 )}}{{[W_ {+} (t_1 ) {+} W_ {-} (t_1 )]^3 }}\delta (t_1 {-} t_2 ) \nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \!\!\! \left\langle {x(t)} \right\rangle _d = \omega (t) = \sqrt{\frac{a}{b}} \frac{{W_ + (t_1 ) - W_ - (t_1 )}}{{W_ + (t_1 ) + W_ - (t_1 )}}. \end{aligned}$$
(18)

The autocorrelation function, averaged by d(t) and by phase of periodic force s(t), for the system output signal can be given by [36, 42]

$$\begin{aligned} K(t_0 )= & {} K(t_1 - t_2 ) \nonumber \\= & {} \left\langle {H(t_1,t_2 )} \right\rangle _{d,s}- \left\langle {x(t_1 )} \right\rangle _{d,s} \left\langle {x(t_2 )} \right\rangle _{d,s} \nonumber \\= & {} \left\langle {\omega (t_1 )\omega (t_2 )} \right\rangle _{d,s} - \left\langle {\omega (t_1 )} \right\rangle _{d,s} \left\langle {\omega (t_2 )} \right\rangle _{d,s} \nonumber \\{} & {} + 8\left\langle {\dfrac{{W_ + (t_1 )W_ - (t_1 )}}{{[W_ + (t_1 ) + W_ - (t_1 )]^3 }}} \right\rangle _{d,s} \delta (t_1 - t_2 ) \nonumber \\= & {} B(m,A)\varphi (t_0 ) + C(m,A)\delta (t_0 ) \end{aligned}$$
(19)

where

$$\begin{aligned}{} & {} \!\!\! \varphi (t_0 ) = \dfrac{4}{{\pi ^2 }}\sum \limits _{j = 0}^\infty {(2j + 1)^{ - 2} \exp [ - i(2j + 1)\Omega t_0 ]}, \nonumber \\{} & {} \!\!\! B = \frac{1}{4}[\omega (m + A) - \omega (m - A)]^2, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \!\!\! C = \frac{1}{2}[C_0 (m + A) + C_0 (m - A)], \nonumber \\{} & {} \!\!\! C_0 (\mu ) = \frac{{8W_0^2 }}{{[W_ - (\mu ) + W_ + (\mu )]^3 }}. \end{aligned}$$
(21)

Performing Fourier transform on both sides of eq. (19), the system output power spectrum can be obtained, i.e.,

$$\begin{aligned} S(\omega ) = S_1 (0) + S_2 (\omega ), \end{aligned}$$
(22)

where

$$\begin{aligned} S_1 (0)= & {} C(m,A) \nonumber \\ S_2 (\omega )= & {} B_2 (m,A)\varphi (\omega ) \nonumber \\ \varphi (\omega )= & {} \dfrac{8}{\pi }\sum \limits _{j = 0}^\infty {(2j + 1)^{ - 2} \delta [\omega - (2j + 1)\Omega ]}. \end{aligned}$$
(23)

Here \(S_1 (0)\) denotes the power density at zero frequency associated with the noise background and \(S_2 (\omega )\) is the power spectrum of the output signal. The output SNR, defined as the ratio between the power density of the signal and that of the noise at the signal frequency, can be deduced as

$$\begin{aligned} \textrm{SNR} = \frac{8}{\pi }\frac{{B(m,A)}}{{C(m,A)}}. \end{aligned}$$
(24)

3 Discussion

In this paper, a random-phase signal-modulated noise is introduced to a bistable system. Based on the statistical characteristics of the noises, stationary probability is obtained. Finally, by virtue of the two-state theory, the transition rates out of the two stable states and the system output SNR are obtained. Now let us discuss the non-monotonous dependence of the SNR on the parameters of the noises, on the parameters of the driven force and on those of the system.

Fig. 1
figure 1

The SNR vs. asymmetry \(\kappa \) of the square-wave signal for \(a = 1\), \(b = 0.4\), \(B = 0.7\), \(D = 0.25\) and \(Q = 0.2\) for different values of P of the random-phase signal-modulated noise.

Full size image
Fig. 2
figure 2

The SNR vs. asymmetry \(\kappa \) of the square-wave signal for \(a = 1\), \(b = 0.4\), \( B = 0.7\), \(Q = 0.2\) and \(P = 0.6\) for different values of D.

Full size image

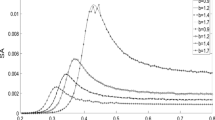
One can analyse the influence of the asymmetry of the square-wave signal on SNR from figures 1 and 2. From these two figures, one can easily find that the SNR can obtain two maximum values with the increase of asymmetry \(\kappa \) of the square-wave signal, i.e., stochastic double-resonance phenomenon appears. It is worth to mention that this double-peak phenomenon is a new result not studied in refs [17, 33, 34, 37]. This phenomenon suggests that the asymmetry of the square-wave signal can induce resonance peak at certain values of asymmetry. Thus, by tuning the asymmetry of the square-wave, the system output can be optimised. Particularly, as the asymmetry parameter varies, the output SNR ratio can exhibit two resonance peaks. This phenomenon suggests the existence of two separate asymmetry parameter values \(\kappa \) that can be chosen to optimise the system’s output performance. Given that the excitation signal is more controllable than the noise, this provides a more convenient and accessible means in engineering applications to enhance the quality of the system’s output. The double maximum phenomenon can be explained by virtue of the power spectrum for the output signal B and that for the output noise background C for the range \(1< \kappa < 10\), as shown in figure 3. From this figure we can see that, at \(\kappa \approx 1.4\), the noise spectrum C reaches a minimum while the signal spectrum B decreases gradually, leading to the first peak in the output SNR ratio. When \(\kappa \) exceeds 2, although both the signal spectrum and the noise spectrum decrease monotonically with the increase of \(\kappa \), their decline rates are different. Specifically, the decline rate of the decrease in the noise spectrum is notably faster than that of the signal spectrum, thereby enhancing the output SNR as \(\kappa \) increases. However, when \(\kappa > 6\), the rate of decline in noise spectrum starts to slow down, becoming less than that of the signal spectrum, resulting in a second maximum for the SNR. It is worth to note that the SNR for \(\kappa \ne 1\) (corresponding to an asymmetric signal) can be larger than that for \(\kappa = 1\) (corresponding to a symmetric signal), which means that the asymmetry of the square-wave can improve the system output SNR. In addition, the multiplicative noise intensity D affects the SNR non-monotonously. As seen from figure 2, for relatively smaller values of \(\kappa \) (\(\kappa < 2.2\)), the SNR increases with the increase of D, while for relatively larger values of \(\kappa \) (\(\kappa > 2.5\)), the SNR decreases with the increase of D.

Fig. 3
figure 3

The power spectrum B and C vs. asymmetry \(\kappa \) of the square-wave signal for \(a = 1\), \(b = 0.4\), \( B = 0.7\), \(Q = 0.2\), \(P = 0.6\) and \(D = 0.2\).

Full size image
Fig. 4
figure 4

The SNR vs. amplitude B of the square-wave signal for \(a = 1\), \(b = 1\), \(D = 0.3\), \(P = 0.9\) and \(\kappa = 4\) for different values of Q.

Full size image

The non-monotonous dependence of the SNR on the amplitude B of the square-wave signal can be analysed from figures 4 and 5. With the increase in B, the SNR increases firstly. After it reaches a maximum value, it decreases monotonously. Single resonance means that by adjusting the amplitude of the square-wave signal, the system output can also be maximised. We note that this single-peak phenomenon is neither investigated in an asymmetric bistable system (ref. [34]) nor studied in bias monostable system (ref. [37]). This phenomenon is different from the phenomenon occurred in underdamped bistable system (ref. [36]). In ref. [36] the SNR can obtain one maximum and one minimum value with the increase in amplitude of the square-wave signal. In addition, the additive noise intensity Q influences the SNR non-monotonously, as shown in figure 4. For small values of B (\(B<0.22\)), the SNR increases with the increase in Q, while the SNR decreases with increasing additive noise intensity Q for relatively larger values of B (\(B>0.45\)). Thus, relatively more amount of additive noise can improve the SNR when the amplitude B is relatively smaller, and relatively less amount of additive noise can enhance the system output performance when the amplitude B is relatively larger. Moreover, the asymmetry \(\kappa \) impacts the system SNR non-monotonously, which is consistent with the phenomenon presented in figures 1 and 2. As shown in figure 5, for small values of B (\(B<0.4\)), the SNR increases with the increase in \(\kappa \), while for large values of B (\(B<0.4\)), the SNR decreases with the increase in \(\kappa \).

Fig. 5
figure 5

The SNR vs. amplitude B of the square-wave signal for \(a = 1\), \(b = 1\), \( D = 0.7\), \(P = 0.9\) and \(Q = 0.05\) for different values of \(\kappa \) of the square-wave signal.

Full size image
Fig. 6
figure 6

The SNR vs. intensity P of the random-phase signal-modulated noise for \(a = 1\), \(b = 2\), \(D = 0.25\), \(B = 0.8\) and \(Q = 0.6\) for different values of \(\kappa \) of the square-wave signal.

Full size image
Fig. 7
figure 7

The SNR vs. multiplicative intensity D for \(a = 1\), \(b = 1\), \(B = 0.7\), \(P = 0.3\) and \(Q = 0.2\) for different values of \(\kappa \) of the square-wave signal.

Full size image
Fig. 8
figure 8

The SNR vs. additive noise intensity Q for \(b = 1\), \(D = 0.25\), \(B = 0.5\), \(P = 0.9\) and \(\kappa = 1.5\) for different values of a.

Full size image

The non-monotonous dependence of the SNR on the intensity of the random-phase signal-modulated noise, on the strengths of the multiplicative noise and the additive noise can be investigated from figures 6–8, respectively. From these three figures, one can find that the SNR can obtain one resonance peak with the increment of the three noise strengths, i.e., traditional SR phenomenon takes place. Therefore, one can add appropriate amount of these noises to enhance the system output signal. This phenomenon can be explained as the synergistic effect between the system nonlinearity and the noises. When the particle moves in the noise-free bistable system, the potential barrier is too high for the particle to cross over, which results in a low system output signal. In the presence of certain amount of noises, the noises may help the particle to jump over the potential barrier and move between the two potential wells, thus the system output can be enhanced. It is worth to mention that the resonance behaviour of the system output vs. the multiplicative noise intensity is not considered in ref. [17]. The single-peak phenomenon of the system output vs. the signal-modulated noise is neither studied in sinusoidal potential systems (ref. [33]), nor studied in bistable systems (refs [34, 36]) nor investigated in monostable system (ref. [37]). The SR behaviour of the SNR vs. the multiplicative and additive noise strengths is similar to those presented in refs [34, 36]. From figures 6 and 7, one can conclude that the asymmetry \(\kappa \) of the square-wave signal affects the SNR non-monotonously, which agrees with the behaviour shown in figures 1 and 2. Furthermore, system parameter a influences the SNR non-monotonously, too. It can be seen from figure 8 that for very weak additive noise intensity Q (\(Q<0.05\)), the SNR becomes smaller as parameter a increases, while for relatively strong additive noise (\(Q>0.2\)), the SNR becomes greater as a increases. This phenomenon indicates that a relatively larger value a can enhance the system SNR for relatively stronger additive noise level.

4 Conclusions

In this work, a bistable system driven by random-phase asymmetric square-wave signal-modulated noise and multiplicative noise was considered. Based on the statistical characteristics of the noises, the Fokker–Planck equation for the probability density function was deduced. Under adiabatic proximation condition and two-state theory, the stationary probability and transition rates out of the two stable states were obtained. Finally, by applying Fourier transform on the correlation function of the system output signal, the SNR was derived. Analysis results show that the asymmetry of the square-wave signal can induce double SR phenomenon, while the amplitude of the square-wave signal can lead to single-peak phenomenon on the SNR curves. Traditional SR behaviour occurs when the SNR varies with the intensity of the random-phase signal-modulated noise, with the intensity of the multiplicative and additive noise. At the same time, the system parameter affects the SNR non-monotonically. As asymmetric square-wave signal and signal-modulated noise widely exist in various scientific fields, it is believed that the results obtained in this paper has certain theoretical significance for studying the SR behaviour in nonlinear systems.