Dynamics in a diffusive modified Leslie–Gower predator–prey model with time delay and prey harvesting

Abstract

The dynamics of a diffusive predator–prey model with time delay and Michaelis–Menten-type harvesting subject to Neumann boundary condition is considered. Turing instability and Hopf bifurcation at positive equilibrium for the system without delay are investigated. Time delay-induced instability and Hopf bifurcation are also discussed. By the theory of normal form and center manifold, conditions for determining the bifurcation direction and the stability of bifurcating periodic solution are derived. Some numerical simulations are carried out for illustrating the theoretical results.

1 Introduction

Dynamics of predator–prey model is one of important subjects in ecology and mathematical ecology, and many researchers have studied it and derive some important results [1–9]. Leslie–Gower model [10, 11] is one of the classical predator–prey models. Chen et al. [12] discussed the stability/instability of the coexistence equilibrium and associated Hopf bifurcation in a diffusive Leslie–Gower predator–prey model. Aziz-Alaoui and Okiye [13] studied the boundedness and global stability in a modified Leslie–Gower predator–prey model with Holling type II functional response:

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=x\left( r_1-b_1x\right) -\frac{a_1x y}{k_1+x},\\ \dot{y}(t)&=y\left( r_2-\frac{a_2 y}{k_2+x}\right) , \end{aligned} \end{aligned}$$

(1.1)

where x and y represent the population densities of prey and predator, respectively. All parameters are positive parameters. $r_1$ and $r_2$ are the growth rate of prey and predator. $b_1$ represents the competition among individuals of prey. $a_1$ and $a_2$ are the maximum value which per capita reduction rate of prey and predator can attain. $k_1$ is the average saturation rate. In this model, in the case of prey severe scarcity, predator can switch to other foods denoted as $k_2$.

Considering time delay in the negative feedback of the predator’s density, Nindjina et al. [14] investigated the following model:

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=x\left( r_1-b_1x\right) -\frac{a_1x y}{k_1+x},\\ \dot{y}(t)&=y\left( r_2-\frac{a_2 y(t-\tau )}{k_2+x(t-\tau )}\right) , \end{aligned} \end{aligned}$$

(1.2)

In [14], Nindjina et al. discussed the global stability of the positive equilibrium by constructing a Lyapunov function. In [15], Yafia et al. investigated the Hopf bifurcations at the positive equilibrium.

For economic reasons, human needs to exploit biological resources and harvest some biological species, such as in fishery, forestry and wildlife management. Therefore, it is necessary to study the suitable population model with harvesting. Many researchers have studied system (1.2) with different types of harvesting, constant harvesting [16], linear harvesting[17], non-selective harvesting [18] and so on. Among these types of harvesting, Yuan et al. [19] suggest that Michaelis–Menten-type prey harvesting is more realistic than other types of harvesting from biological and economic points of view. They studied the following model:

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=x\left( r_1-b_1x\right) -\frac{a_1x y}{k_1+x}-\frac{q E x}{m_1E+m_2 x},\\ \dot{y}(t)&=y\left( r_2-\frac{a_2 y(t-\tau )}{k_2+x(t-\tau )}\right) . \end{aligned} \end{aligned}$$

(1.3)

All parameters are positive. q represents the catch ability, E is the effort applied to harvest prey, and $m_1$ and $m_2$ are suitable constants. In [19], Yuan et al. assume that the environment provides the same protection to both the predator and prey ($k_1=k_2$), and discuss the stability of the equilibria and obtained the critical conditions for the saddle-node-Hopf bifurcation.

In the real world, predators and their preys distribute inhomogeneous in different spatial location at time t. And they will move or diffuse to areas with smaller population concentration or more food to get a good living environment. Hence, taking into account diffusion appears to be more reasonable. In mathematics, predator–prey with diffusion will exhibit complex dynamical properties. Many researchers have shown that the diffusion coefficients may induce Turing instability and spatially non-homogeneous bifurcating periodic solution [20–23]. Hence, taking into account diffusion appears to be more reasonable and interesting. In this manuscript, we suppose the region prey and predator lived is closed and no species (prey or predator) entering and leaving region at the boundary. Therefor, we choose Neumann boundary condition. On the other hand, time delay plays an important role in many biological dynamical systems, being particularly relevant into predator–prey models [24–27]. In predator–prey models, time delay exists in maturation time, capturing time, gestation time or others. Many scholars have devote to investigating delayed predator–prey models and suggest that time delay contributes critically to the stable or unstable outcome of prey and predator’s densities. Time delay may induce bifurcating periodic solution, and prey and predator’s densities exhibit oscillatory behavior. Different from works in [19], we introduce time delay in the resource limitation of the prey which is one of important aspects [25–27]. Based on these reasons, we investigate the following system:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \frac{\partial {u(x,t)}}{\partial {t}}=D_1 \Delta u +u\left( r_1-b_1u(t-\tau )\right) -\frac{a_1u v}{k+u}-\frac{q E u}{m_1E+m_2 u}, &{} \\ \frac{\partial {v(x,t)}}{\partial {t}}=D_2\Delta v +v\left( r_2-\frac{a_2 v}{k+u}\right) , &{} x\in \Omega ,~t>0\\ u_x(x,t)=v_x(x,t)=0, &{} x\in \partial {\Omega },~t>0\\ u(x,\theta )=u_0(x,\theta )\ge 0,~~~~v(x,\theta )=v_0(x,\theta )\ge 0, &{} x\in \Omega , \theta \in [-\tau ,0]. \end{array} \right. \end{aligned} \end{aligned}$$

(1.4)

For simplicity, we also assume $k_1=k_2=k$. After the following nondimensionalization: $u=\frac{r_1}{b_1}\widetilde{u}, v= \frac{r_1}{a_1b_1}\widetilde{v}, t= \frac{\widetilde{t}}{r_1}, d_1=\frac{D_1}{r_1}, d_2=\frac{D_2}{r_1}, \alpha = \frac{1}{r_1}, \beta = \frac{a_2}{r_2a_1}, m= \frac{kb_1}{r_1}, s= \frac{r_2}{r_1}, h = \frac{qEb_1}{r_1^2m_2}, c= \frac{m_1Eb_1}{m_2r_1}$ and drop the tilde, system (1.1) can be changed to

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial {u(x,t)}}{\partial {t}}=d_1 \Delta u +u\left( 1-u(t-\tau )-\frac{\alpha v}{m+u}-\frac{h}{c+u}\right) ,\\ \displaystyle \frac{\partial {v(x,t)}}{\partial {t}}=d_2\Delta v +s v \left( 1-\frac{\beta v}{m+u}\right) , &{} x\in \Omega ,~t>0\\ u_x(x,t)=v_x(x,t)=0, &{} x\in \partial {\Omega },~t>0\\ u(x,\theta )=u_0(x,\theta )\ge 0,~~~~v(x,\theta )=v_0(x,\theta )\ge 0, &{} x\in \Omega , \theta \in [-\tau ,0]. \end{array} \right. \end{aligned}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(1.5)

In this paper, we assume $\Omega =(0,l\pi ), l> 0$.

The organization of this paper is as follows. In Sect. 2, we study the dynamics of non-delay system, including stability, Turing instability and existence of Hopf bifurcation at positive equilibrium. In Sect. 3, we study the effect of delay on the model including stability and Hopf bifurcation at positive equilibrium. In Sect. 4, we give some numerical simulations. Finally, we end the paper with a brief conclusion in Sect. 5.

2 The effect of diffusion on the non-delay model

Without delay, system (1.5) becomes

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\partial {u}}{\partial {t}}&=d_1 \Delta u +u\left( 1-u-\frac{\alpha v}{m+u}-\frac{h}{c+u}\right) \\ \displaystyle \frac{\partial {v}}{\partial {t}}&=d_2 \Delta v +s v \left( 1-\frac{\beta v}{m+u}\right) . \end{aligned} \end{aligned}$$

(2.1)

In [19], Yuan et al. have discussed the existence of trivial and positive equilibria. For convenience, in this paper we assume system (2.1) has a positive equilibrium and denote as $E_*(u_*,v_*)$.

2.1 Local stability analysis of the model without diffusion

For system (2.1) without diffusion, the Jacobian matrix at $E_*(u_*,v_*)$ is

$$\begin{aligned} J = \left( \begin{array}{ccc} a_1 &{} a_2\\ s/\beta &{} -s \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} a_1= & {} u_* \left( \frac{h}{\left( c+u_*\right) {}^2}+\frac{\alpha v_*}{\left( m+u_*\right) {}^2}-1\right) ,\nonumber \\ a_2= & {} -\frac{\alpha u_*}{m+u_*}. \end{aligned}$$

(2.2)

Obviously, $a_2<0$. The characteristic equation corresponding to $E_*(u_*,v_*)$ is

$$\begin{aligned} \lambda ^2-\lambda (a_1 -s)-s(a_1 +a_2/\beta )=0. \end{aligned}$$

(2.3)

Makeing the following hypotheses:

$$\begin{aligned} \mathbf{{(H_1)}}~~~~~~~~~~a_1 +a_2/\beta <0.~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

Theorem 2.1

Suppose $\mathbf {(H_1)}$ holds. Then for system (2.1) without diffusion, the following statements are true.

• (i) If $a_1\le 0$, for $s>0$ the equilibrium $E_*(u_*,v_*)$ is local asymptotically stable;

• (ii) If $a_1>0$, for $s>a_1$ the equilibrium $E_*(u_*,v_*)$ is local asymptotically stable;

• (iii) If $a_1>0$, the system undergoes Hopf bifurcation at $E_*(u_*,v_*)$ when $s=a_1$.

Proof

Obviously, the roots of Eq. (2.3) are given by

$$\begin{aligned} \lambda _{1,2}=\frac{1}{2}\left[ (a_1 -s)\pm \sqrt{(a_1 -s)^2+4s(a_1 +a_2/\beta )}\right] . \end{aligned}$$

Under condition (i) (or (ii)), $a_1-s<0$ holds; then, the roots of Eq. (2.3) have negative real parts. Therefore, the equilibrium $E_*(u_*,v_*)$ is local asymptotically stable.

When $s=a_1$, Eq. (2.3) has a pair of pure imaginary roots $\pm \sqrt{-4s(a_1 +a_2/\beta )}$. Meanwhile, when s near $a_1$, Eq. (2.3) has a pair of complex eigenvalues $\alpha (s)\pm i\omega (s)$, where

$$\begin{aligned}&\alpha (s)=\frac{1}{2}(a_1 -s),\nonumber \\&\omega (s)=\frac{1}{2}\sqrt{-4s(a_1 +a_2/\beta )-(a_1 -s)^2}. \end{aligned}$$

And hence, we have

$$\begin{aligned} \alpha (a_1)=0,~~\alpha '(s)|_{s=a_1}=-1/2,~~\omega (a_1)>0. \end{aligned}$$

Therefore, the system undergoes Hopf bifurcation at $E_*(u_*,v_*)$ when $s=a_1$.

2.2 Turing instability and Hopf bifurcation

For system (2.1), the characteristic equation at $E_*(u_*,v_*)$ is

$$\begin{aligned} \lambda ^2-\lambda T_n(s)+D_n(s)=0,~~n\in \mathbb {N}_0, \end{aligned}$$

(2.4)

where

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} T_n(s)=-\left( d_1+d_2\right) \frac{n^2}{l^2}+a_1 -s,\\ D_n(s)=d_1d_2\frac{n^4}{l^4}-\left( d_2a_1-sd_1\right) \frac{n^2}{l^2}-s(a_1 +a_2/\beta ), \end{array} \right. \end{aligned} \end{aligned}$$

(2.5)

and the eigenvalues are given by

$$\begin{aligned} \lambda _{1,2}^{(n)}(s)=\frac{T_n(s)\pm \sqrt{T^2_n(s)-4D_n(s)}}{2},~~~~n\in \mathbb {N}_0. \end{aligned}$$

(2.6)

Obviously, if $a_1-s<0$, then $T_n(s)\le T_0(s)<0$ for $n\in \mathbb {N}_0$. Suppose $\mathbf{(H_1)}$ holds; then, $D_0(s)=-s(a_1 +a_2/\beta )>0$, and if $s\ge \frac{ d_2a_1}{d_1}$ also holds, then $D_n(s)\ge D_0(s)>0$.

Denote

$$\begin{aligned} s_{\mp }= & {} \frac{d_2}{ d_1}\left[ -\left( 2a_2/\beta +a_1\right) \mp 2\sqrt{a_2/\beta \left( a_2/\beta +a_1\right) }\right] \nonumber \\\end{aligned}$$

(2.7)

$$\begin{aligned} z_{\mp }= & {} \frac{1}{2d_1d_2}\left[ d_2a_1-sd_1\right. \nonumber \\&\left. \mp \sqrt{(d_2a_1-sd_1)^2+4d_1d_2s(a_1 +a_2/\beta )}\right] ,\nonumber \\ \end{aligned}$$

(2.8)

and

$$\begin{aligned} \sigma =\frac{1}{a_1}\left[ -2 a_2/\beta -a_1-2 \sqrt{a_2/\beta \left( a_2/\beta +a_1\right) }\right] . \end{aligned}$$

(2.9)

Remark 2.1

Under the hypotheses $\mathbf{(H_1)}$, we can obtain the following relationship about $a_1, \frac{ d_2a_1}{d_1}$ and $s_{\pm }$:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \mathrm{if}~~\frac{d_1}{d_2}<\sigma , &{}\mathrm{then}~~0<a_1<s_-<\frac{ d_2a_1}{d_1}<s_+,\\ \mathrm{if}~~\frac{d_1}{d_2}>\sigma , &{}\mathrm{then}~~0<s_-<a_1<\frac{ d_2a_1}{d_1}<s_+. \end{array} \right. \end{aligned} \end{aligned}$$

Lemma 2.1

Suppose $\mathbf{(H_1)}$ holds; then, the following statements are true.

• (i) If for $s\in (0,s_-)\cup (s_+,\infty )$, there exists a $k \in \mathbb {N}$ such that $\frac{k^2}{l^2}\in (z_-, z_+)$, then $D_k(s)<0$;

• (ii) If one of followings holds:

  $$\begin{aligned} (1)~~s\in (s_-, s_+), \end{aligned}$$
  $$\begin{aligned}&(2)~~s\,{\in }\, (0,s_-)\cup (s_+,\infty ), \text {but there are no } k \in \mathbb {N}\\&\quad ~~ \text{ such } \text{ that }~~\frac{k^2}{l^2}\in (z_-, z_+), \end{aligned}$$

  then $D_k(s)>0$ for $n\in \mathbb {N}_0,$.

Proof

Define

$$\begin{aligned} h(z)=z^2d_1d_2-z(d_2a_1-sd_1)-s(a_1 +a_2/\beta ).\qquad \end{aligned}$$

(2.10)

If $(d_2a_1-sd_1)^2+4d_1d_2s(a_1 +a_2/\beta )>0$ that is $s\in (0,s_-)\cup (s_+,\infty )$, then $h(z)=0$ has two roots $z_{\mp }$. And if there exists a $k\in \mathbb {N}$ such that $\frac{k^2}{l^2}\in (z_-, z_+)$, then $D_k(c)=h\left( \frac{k^2}{l^2}\right) <0$. This completes the proof of (i).

From the discussion above, we know that $D_n(s)>0$ for $n=0,1,2,\ldots ,$ under the conditions of (ii). Hence, the conclusion of (ii) follows.

Theorem 2.2

Suppose $\mathbf{(H_1)}$ holds, and $\sigma$ and $s_-$ are defined by (2.9) and (2.7), respectively. Then for system (2.1), the following statements are true.

• (i) If $s>a_1$ and $s\ge \frac{ d_2a_1}{d_1}$, then the equilibrium $E_*(u_*,v_*)$ is asymptotically stable;

• (ii) If $a_1< s <\frac{ d_2a_1}{d_1}$ and $\frac{d_1}{d_2}>\sigma$, then the equilibrium $E_*(u_*,v_*)$ is asymptotically stable;

• (iii) If $a_1< s <\frac{ d_2a_1}{d_1}$ and $\frac{d_1}{d_2}<\sigma$, then the equilibrium $E_*(u_*,v_*)$ is asymptotically stable when one of the followings holds: (1) $s \in (s_-,\frac{ d_2a_1}{d_1})$; (2) $s\in (a_1,s_-)$, but there does not exist a $k\in \mathbb {N}$ such that $\frac{k^2}{l^2}\in (z_-, z_+)$;

• (iv) If $a_1<s<s_-$ and $\frac{d_1}{d_2}<\sigma$, and there exists a $k\in \mathbb {N}$ such that $\frac{k^2}{l^2}\in (z_-, z_+)$, then the equilibrium $E_*(u_*,v_*)$ is Turing unstable;

• (v) If $a_1>0$, the system (2.1) undergoes a Hopf bifurcation at $E_*(u_*,v_*)$ when $s=s_n$, for $0\le n \le n^*-1$, where $s_n$ and $n^*$ are defined in the following proof. Moreover, the bifurcating periodic solution is spatially homogeneous when $s=s_0$ and spatially non-homogeneous when $s=s_n$ for $1\le n \le n^*-1$.

Proof

Obviously, under conditions (i), (ii) or (iii), $T_n(s)<0$ and $D_n(s)>0$ for $n\in \mathbb {N}_0$. Then, all roots of Eq. (2.4) have negative real parts. Therefore, the equilibrium $E_*(u_*,v_*)$ is asymptotically stable. Under condition (iv), by Lemma (2.1, there exists a $k\in \mathbb {N}$ such that $D_k(s)<0$. Then, Eq. (2.4) has a root $\lambda ^{(k)}(s)$ with positive real parts. Therefore, the equilibrium $E_*(u_*,v_*)$ is Turing unstable.

Suppose $\mathbf{(H_1)}$ holds, and $a_1>0$, from (2.6), we know that (2.4) has purely imaginary roots if and only if

$$\begin{aligned} s=s_n:=a_1-\frac{n^2}{l^2}(d_1+d_2),~~n\in \mathbb {N}_0 \end{aligned}$$

(2.11)

and $D_n(s_n)>0$. From (2.11), we know that there exists a integer $n_1^*\ge 1$ such that $s_n>0$ for $n=0,1,2,\ldots ,n_1^*-1$, and $s_n \le 0$ for $n=n_1^*,n_1^*+1,\ldots$. Substituting $s_n$ into $D_n(s)$ (see (2.5)) yields

$$\begin{aligned} D_n(s_n)= & {} -d_1^2\frac{n^4}{l^4}+\left( 2 a_1 d_1+a_2/\beta \left( d_1+d_2\right) \right) \\&\times \frac{n^2}{l^2}-a_1\left( a_2/\beta +a_1\right) . \end{aligned}$$

By $D_0(s_0)=-a_1\left( a_2/\beta +a_1\right) >0$, we know that there exists an integer $n_2^*\ge 1$ such that $D_n(s_n)>0$ when $n=0,1,\ldots , n_2^*-1$, and $D_n(s_n)\le 0$ when $n\ge n_2^*$. Let $n^*=\min \{ n_1^*, n_2^*\}$ and

$$\begin{aligned} \lambda _n(s)=\alpha _n(s)\pm i\omega _n(s),~~n=0,1, \ldots , n^*-1 \end{aligned}$$

be the roots of Eq. (2.4) satisfying

$$\begin{aligned} \alpha _n(s_n)=0,~~\omega _n(s_n)=\sqrt{D_n(s_n)}. \end{aligned}$$

Then, when s is near $s_n$

$$\begin{aligned} \alpha _n(s)=\frac{T_n(s)}{2},~~\omega _n(s)=\sqrt{D_n(s)-\alpha _n^2(s)}, \end{aligned}$$

and from the definition of $T_n$ in (2.5), it follows that

$$\begin{aligned} \alpha '_n(s_n)=-\frac{1}{2}<0. \end{aligned}$$

(2.12)

This implies that the transversal condition is satisfied at each $s_n, n=0,1,2, \ldots , n^*-1$. Therefore, the system (2.1) undergoes a Hopf bifurcation at $E_*(u_*,v_*)$ when $s=s_n$, for $0\le n \le n^*-1$.

3 The effect of delay on the system

3.1 Stability analysis and existence of Hopf bifurcation

In the following, by analyzing the associated characteristic equation at $E_*(u_*,v_*)$, we investigate stability of $E_*(u_*,v_*)$ and existence of Hopf bifurcation for system (1.5). We always suppose $\mathbf{(H_1)}$ and one of conditions (i-iii) in Theorem (2.2) hold.

Denote

Linearizing system (1.5) at $E_*(u_*,v_*)$, we have

$$\begin{aligned} \dot{U}=D\Delta U(t)+L(U_t), \end{aligned}$$

(3.1)

where

and $L:\mathscr {C}_{\tau } \mapsto X$ is defined by

$$\begin{aligned} \begin{aligned} L(\phi _t)=L_1 \phi (0)+ L_2 \phi (-\tau ), \end{aligned} \end{aligned}$$

for $\phi =(\phi _1, \phi _2)^T \in \mathscr {C}_{\tau }$ with

$$\begin{aligned}&L_1=\left( \begin{array}{ccc} a_1+u_* &{} a_2\\ s/\beta &{} -s \end{array} \right) ,\quad L_2=\left( \begin{array}{ccc} -u_* &{}\quad 0\\ 0 &{}\quad 0 \end{array} \right) ,\nonumber \\&\phi (t)=(\phi _1(t),\phi _2(t))^T,\nonumber \\&\phi _t(\cdot )=(\phi _1(t+\cdot ),\phi _2(t+\cdot ))^T. \end{aligned}$$

From Wu [28], we obtain that the characteristic equation for linear system (3.1) is

$$\begin{aligned} \lambda y -\mathrm{d}\Delta y -L(e^{\lambda } y)=0,~~y \in \text{ dom }(\mathrm{d}\Delta ),~~y\ne 0.\qquad \end{aligned}$$

(3.2)

It is well known that the eigenvalue problem

$$\begin{aligned} -\varphi ''=\mu \varphi , ~~x\in (0,l\pi ); ~~\varphi '(0)=\varphi '(l\pi )=0 \end{aligned}$$

has eigenvalues $\mu _n=n^2/l^2~(n=0,1,\cdots )$ with corresponding eigenfunctions

$$\begin{aligned} \varphi _n(x)=\cos \frac{n\pi }{l},~~n\in \mathbb {N}_0. \end{aligned}$$

Substituting

$$\begin{aligned} y=\sum _{n=0}^{\infty } \left( \begin{array}{ccc} y_{1n}\\ y_{2n} \end{array} \right) \cos \frac{n\pi }{l} \end{aligned}$$

into the characteristic Eq. (3.2), it follows that

$$\begin{aligned}&\left( \begin{array}{cc} a_1+u_*-u_*e^{- \lambda \tau }-d_1 \frac{n^2}{l^2} &{} a_2 \\ s/\beta &{} -s-d_2 \frac{n^2}{l^2} \end{array} \right) \left( \begin{array}{ccc} y_{1n}\\ y_{2n} \end{array} \right) \\&\quad =\lambda \left( \begin{array}{ccc} y_{1n}\\ y_{2n} \end{array} \right) ,~n=0,1,\cdots . \end{aligned}$$

Therefore, the characteristic Eq. (3.2) is equivalent to

$$\begin{aligned} \Delta _n (\lambda ,\tau )=\lambda ^2+ \lambda A_n +B_n +u_*(\lambda +C_n)e^{-\lambda \tau } =0\quad \end{aligned}$$

(3.3)

where

$$\begin{aligned} A_n= & {} \left( d_1+d_2\right) \frac{n^2}{l^2}-a_1+s-u_*,\\ B_n= & {} d_1d_2\frac{n^4 }{l^4}-\left( d_2 \left( a_1+u_*\right) -s d_1\right) \frac{n^2}{l^2}\nonumber \\&-s \left( a_2/\beta +a_1+u_*\right) ,\\ C_n= & {} d_2 \frac{n^2}{l^2}+ s. \end{aligned}$$

When $\tau =0$, system (1.5) becomes (2.1); if one of conditions (i–iii) in Theorem (2.2) holds, then all the roots of Eq. (3.3) with $\tau =0$ have negative real parts for $n \in \mathbb {N}_0$ and $\Delta _n(0,\tau )>0$.

We shall seek critical values of $\tau$ such that there exists a pair of simple purely imaginary eigenvalues. $i\omega$ ($\omega >0$) is a root of Eq. (3.3) if and only if $\omega$ satisfies

$$\begin{aligned}&- \omega ^2+i \omega A_n+B_n+u_*(i \omega +C_n)(cos \omega \tau -i sin \omega \tau )\\&\quad =0. \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} -\omega ^2+B_n+\omega u_*\text {sin} \omega \tau +C_n u_*\text {cos} \omega \tau =0,\\ \omega A_n+\omega u_*\text {cos} \omega \tau -C_n u_*\text {sin} \omega \tau =0. \end{array} \right. \end{aligned} \end{aligned}$$

which lead to

$$\begin{aligned} \omega ^4 +\omega ^2(A^2_n- 2B_n-u_*^2)+ B^2_n -C^2_n u_*^2=0. \end{aligned}$$

(3.4)

Let $z = \omega ^2$, then (3.4) can be rewritten into the following form

$$\begin{aligned} z^2 -z(2B_n+u_*^2-A^2_n)+ B^2_n -C^2_n u_*^2=0. \end{aligned}$$

(3.5)

Denote

$$\begin{aligned} P= & {} 2B_n+u_*^2-A^2_n, \nonumber \\ R= & {} (2B_n+u_*^2-A^2_n)^2-4(B^2_n -C^2_n u_*^2),\nonumber \\&\text{ and }~~ Q=B^2_n -C^2_n u_*^2. \end{aligned}$$

Then, the roots of (3.5) are given by $z_{\pm }=\frac{P \pm \sqrt{R}}{2}.$ We discuss the existence of positive roots for Eq. (3.5) under these three cases:

• Case 1. (i) $R<0$; (ii) $R>0, Q>0, P<0$; (ii) $R=0, P\le 0$.

• Case 2. (i) $Q<0$; (ii) $R=0, P>0$.

• Case 3. (i) $P>0, Q>0, R>0$.

Obviously, in Case 1, Eq. (3.5) has no positive root; then, Eq. (3.3) has no root with purely imaginary. In Case 2, Eq. (3.5) has one positive root; then, Eq. (3.3) has a pair of purely imaginary roots $\pm i\omega ^+_n$ at $\tau ^{j,+}_n,~j=0,1,2,\ldots$. In Case 3, Eq. (3.5) has two positive roots; then, Eq. (3.3) has two pair of purely imaginary roots $\pm i\omega ^\pm _n$ at $\tau ^{j,\pm }_n,~j\in \mathbb {N}_0$ where

$$\begin{aligned} \begin{aligned}&\omega ^\pm _n=\sqrt{z_{\pm }},~~~\tau ^{j,\pm }_n=\tau ^{0,\pm }_n+ \frac{2j\pi }{\omega ^\pm _n},~(j=0,1,2,\ldots ),\\&\tau ^{0,\pm }_n=\frac{1}{\omega ^\pm _n} \arccos \frac{(\omega ^\pm _n)^2 \left( C_n-A_n\right) -B_n C_n}{\left( (\omega ^\pm _n)^2+C_n^2\right) u_*}. \end{aligned} \end{aligned}$$

(3.6)

Fix parameters $\alpha ,~h,~m,~c,~\beta ,~s,~d_1,~d_2,~l$, define

$$\begin{aligned} \mathcal {D}=\{k\in \mathbb {N}_0 \mid \text {Eq.}\, (3.5)\, \text{ has } \, \text {positive}\, \text {roots}\, \text {with}\, n = k.\} \nonumber \\ \end{aligned}$$

(3.7)

Lemma 3.1

Suppose one of conditions $(i-iii)$ in Theorem (2.2) and $\mathbf{{(H_1)}}$ hold.

• (i) If $R=0$, then $\text {Re}\left( \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right) |_{\tau =\tau ^{j,\pm }_n}=0$;

• (ii) If $R>0$, then $\text {Re}\left( \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right) |_{\tau =\tau ^{j,+}_n}>0, \text {Re} ( \frac{\mathrm{d} \lambda }{\mathrm{d} \tau })|_{\tau =\tau ^{j,-}_n}<0$ for $\tau \in \mathcal {D}$ and $j \in \mathbb {N}_0$.

Proof

Differentiating two sides of (3.3) with respect $\tau$, we have

$$\begin{aligned} \left( \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right) ^{-1}= \frac{2 \lambda +A_n + u_* e^{-\lambda \tau }}{\lambda u_* (\lambda +C_n) e^{-\lambda \tau }}- \frac{\tau }{\lambda }. \end{aligned}$$

Then

$$\begin{aligned}&\left[ \text {Re}\left( \frac{\mathrm{d} \lambda }{\mathrm{d} \tau }\right) ^{-1}\right] ^{-1}_{\tau =\tau ^{j,\pm }_n}=\left[ \frac{2 \lambda +A_n + u_* e^{-\lambda \tau }}{\lambda u_* (\lambda +C_n) e^{-\lambda \tau }}- \frac{\tau }{\lambda }\right] _{\tau =\tau ^{j,\pm }_n}\\&=\left[ \frac{u_* +A_n \cos \omega \tau -2\omega \sin \omega \tau +i(2\omega \cos \omega \tau )+A_n \sin \omega \tau }{-u_* \omega ^2 +iC_n u_* \omega }- \frac{\tau }{i \omega }\right] _{\tau =\tau ^{j,\pm }_n}\\&=\pm \frac{1}{\Lambda } (\omega ^{j,\pm }_n)^2 (2(\omega ^{j,\pm }_n)^2-2B_n+A^2_n-u_*^2)\\&=\pm \frac{1}{\Lambda } (\omega ^{j,\pm }_n)^2 \sqrt{(A^2_n-2B_n-u_*^2)^2 -4(B^2_n- u_* C^2_n)}\\&=\pm \frac{1}{\Lambda } (\omega ^{j,\pm }_n)^2 \sqrt{R}, \end{aligned}$$

where $\Lambda =(\omega ^{j,\pm }_n)^4 u_*^2 +C^2_n u_*^2 (\omega ^{j,\pm }_n)^2>0$. Therefore, $\alpha '_n(\tau ^{j,n}_n)>0(<0)$.

From (3.6), we have $\tau ^{0,\pm }_n<\tau ^{j,\pm }_n$ $(j\in \mathbb {N})$. For $k\in \mathcal {D}$, define the smallest $\tau$ so that the stability will change, $\tau _*=\text{ min }\{\tau ^{0,\pm }_k ~\text{ or }~ \tau ^{0,+}_k \mid k \in \mathcal {D} \}$. According to the above analysis, we have the following theorem.

Theorem 3.1

Suppose $\mathbf{(H_1)}$ and one of conditions (i–iii) in Theorem (2.2) hold; for system (1.5), the following statements are true.

• (i) In Case 1, the equilibrium $E_*(u_*,v_*)$ is local asymptotically stable for all $\tau \ge 0$;

• (ii) In Case 2 or Case 3, the equilibrium $E_*(u_*,v_*)$ is local asymptotically stable for $\tau \in [0,\tau _*)$ and unstable for $\tau \in [\tau _*,\tau _*+\epsilon )$ with some $\epsilon$;

• (iii) In Case 2 or Case 3, system (1.5) undergoes a Hopf bifurcation at the equilibrium $E_*(u_*,v_*)$ when $\tau =\tau ^{j,+}_n$ $(\tau =\tau ^{j,-}_n), j\in \mathbb {N}_0, n \in \mathcal {D}$.

3.2 Stability and direction of Hopf bifurcation

In this section, we shall study the direction of Hopf bifurcation and stability of the bifurcating periodic solution by applying center manifold theorem and normal form theorem of partial functional differential equations [28, 29]. Let $\tilde{u}(x,t)=u(x,\tau t)-u_*$ and $\tilde{v}(x,t)=v(x,\tau t)-v_*$. For convenience, we drop the tilde. Then, the system (1.5) can be transformed into

$$\begin{aligned}&\displaystyle \frac{\partial {u}}{\partial {t}}=\tau \left[ d_1 \Delta u +\left( u+u_*\right) \right. \nonumber \\&\quad \times \left. \left( 1-u(t-\tau )-u_*-\frac{\alpha \left( v+v_*\right) }{m+u+u_*}-\frac{h}{c+u+u_*}\right) \right] ,\nonumber \\&\quad \displaystyle \frac{\partial {v}}{\partial {t}}=\tau \left[ d_2 \Delta v +s \left( v+v_*\right) \left( 1-\frac{\beta \left( v+v_*\right) }{m+u+u_*}\right) \right] .\nonumber \\ \end{aligned}$$

(3.8)

for $x \in (0, l\pi )$, and $t>0$. Let

$$\begin{aligned} \tau= & {} \tilde{\tau }+\mu ,~~u_1(t)=u(\cdot ,t),~~u_2(t)=v(\cdot ,t)~~\text{ and }\\ U= & {} (u_1,u_2)^T. \end{aligned}$$

When $\mu = 0$, system (1.5) undergoes a Hopf bifurcation at the equilibrium (0, 0). Then, (3.8) can be rewritten in an abstract form in the phase space $\mathscr {C}_1:=C([-1,0],X)$

$$\begin{aligned} \frac{\mathrm{d}U(t)}{\mathrm{d}t}=\tilde{\tau }D\Delta U(t)+L_{\tilde{\tau }}(U_t)+F(U_t,\mu ), \end{aligned}$$

(3.9)

where $L_{\mu }(\phi )$ and $F(\phi ,\mu )$ are defined by

$$\begin{aligned}&\begin{aligned} L_{\mu }(\phi )=\mu \left( \begin{array}{ccc} (a_1+u_*) \phi _1(0)-u_* \phi _1(-1)+a_2 \phi _2(0)\\ s/\beta \phi _1(0)-s\phi _2(0) \end{array} \right) \end{aligned} \nonumber \\\end{aligned}$$

(3.10)

$$\begin{aligned}&F(\phi ,\mu )=\mu D\Delta \phi +L_{\mu }(\phi )+f(\phi ,\mu ), \end{aligned}$$

(3.11)

with

$$\begin{aligned} \begin{aligned}&f(\phi ,\mu )=(\tilde{\tau }+\mu )(F_1(\phi ,\mu ),F_2(\phi ,\mu ))^T,\\&F_1(\phi ,\mu )=\left( \phi _1(0)+u_*\right) \\&\times \left( 1-\phi _1(-1)-u_*-\frac{\alpha \left( \phi _2(0)+v_*\right) }{m+\phi _1(0)+u_*}-\frac{h}{c+\phi _1(0)+u_*}\right) \\&-(a_1+u_*) \phi _1(0)+u_* \phi _1(-1)-a_2 \phi _2(0),\\&F_2(\phi ,\mu )=s \left( \phi _2(0)+v_*\right) \left( 1-\frac{\beta \left( \phi _2(0)+v_*\right) }{m+\phi _1(0)+u_*}\right) \\&-\frac{s}{\beta } \phi _1(0)+s \phi _2(0). \end{aligned} \end{aligned}$$

respectively, for $\phi =(\phi _1, \phi _2)^T \in \mathscr {C}_1$.

Consider the linear equation

$$\begin{aligned} \frac{\mathrm{d}U(t)}{\mathrm{d}t}=\tilde{\tau } D \Delta U(t)+L_{\tilde{\tau }}(U_t). \end{aligned}$$

(3.12)

According to the results in Sect. 2, we know that $\Lambda _n:=\{i \omega _n \tilde{\tau },-i \omega _n \tilde{\tau }\}$ are characteristic values of system (3.12) and the linear functional differential equation

$$\begin{aligned} \frac{\mathrm{d}z(t)}{\mathrm{d}t}=-\tilde{\tau } D\frac{n^2}{l^2} z(t)+L_{\tilde{\tau }}(z_t). \end{aligned}$$

(3.13)

By Riesz representation theorem, there exists $2\times 2$ matrix function $\eta ^n(\sigma , \tilde{\tau })-1\le \sigma \le 0$, whose elements are of bounded variation functions such that

$$\begin{aligned} -\tilde{\tau } D\frac{n^2}{l^2} \phi (0)+L_{\tilde{\tau }}(\phi )= \int _{-1}^{0}\mathrm{d} \eta ^n(\sigma , \tau ) \phi (\sigma ) \end{aligned}$$

for .

In fact, we can choose

$$\begin{aligned} \begin{aligned} \eta ^n(\sigma , \tau )=\left\{ \begin{array}{l@{\quad }l} \tau E &{} \sigma =0,\\ 0 &{} \sigma \in (-1,0),\\ - \tau F &{} \sigma =-1, \end{array} \right. \end{aligned} \end{aligned}$$

(3.14)

where

$$\begin{aligned} E= & {} \left( \begin{array}{l@{\quad }l} a_1+u_*-d_1\frac{n^2}{l^2} &{} a_2\\ s/\beta &{} -s-d_2\frac{n^2}{l^2} \end{array} \right) ,\nonumber \\ F= & {} \left( \begin{array}{l@{\quad }l} -u_* &{} 0\\ 0 &{} 0 \end{array} \right) . \end{aligned}$$

(3.15)

Let $A(\tilde{\tau })$ denote the infinitesimal generators of semigroup included by the solutions of Eq. (3.13) and $A^*$ be the formal adjoint of $A(\tilde{\tau })$ under the bilinear paring

$$\begin{aligned} \begin{aligned} (\psi ,\phi )&=\psi (0) \phi (0)-\int _{-1}^{0} \int _{\xi =0}^{\sigma } \psi (\xi -\sigma ) \mathrm{d}\eta ^n(\sigma , \tilde{\tau }) \phi (\xi ) \mathrm{d} \xi \\&=\psi (0) \phi (0)+ \tilde{\tau } \int _{-1}^{0} \psi (\xi +1) F \phi (\xi ) \mathrm{d} \xi . \end{aligned} \end{aligned}$$

(3.16)

for has a pair of simple purely imaginary eigenvalues $\pm i \omega _n \tilde{\tau }$, and they are also eigenvalues of $A^*$. Let P and $P^*$ be the center subspace, that is, the generalized eigenspace of $A(\tilde{\tau })$ and $A^*$ associated with $\Lambda _n$, respectively. Then, $P^*$ is the adjoint space of P and $\text{ dim }P=\text{ dim }P^*=2$.

It can be verified that $p_1(\theta )=(1,\xi )^Te^{i\omega _n \tilde{\tau } \sigma }~~ (\sigma \in [-1,0]),~~p_2(\sigma )=\overline{p_1(\sigma )}$ is a basis of $A(\tilde{\tau })$ with $\Lambda _n$ and $q_1(r)=(1,\eta )e^{-i\omega _n \tilde{\tau } r}~~ (r \in [0,1]), ~~q_2(r)=\overline{q_1(r)}$ is a basis of $A^*$ with $\Lambda _n$, where

$$\begin{aligned} \xi =\frac{s/\beta }{d_2 n^2/l^2+i\omega +s},~~~~\eta =\frac{s/\beta }{d_2 n^2/l^2-i\omega +s}. \end{aligned}$$

Let $\Phi =(\Phi _1,\Phi _2)$ and $\Psi ^*=(\Psi ^*_1,\Psi ^*_2)^T$ with

$$\begin{aligned} \Phi _1(\sigma )= & {} \frac{p_1(\sigma )+p_2(\sigma )}{2}=\left( \begin{array}{c} \text {Re}\left( e^{i\omega _n \tilde{\tau } \sigma }\right) \\ \text {Re}\left( \xi \text {e}^{i\omega _n \tilde{\tau } \sigma }\right) \end{array} \right) ,\\ \Phi _2(\sigma )= & {} \frac{p_1(\sigma )-p_2(\sigma )}{2i}=\left( \begin{array}{c} \text {Im}\left( e^{i\omega _n \tilde{\tau } \sigma }\right) \\ \text {Im}\left( \xi \text {e}^{i\omega _n \tilde{\tau }\sigma }\right) \end{array} \right) \end{aligned}$$

for $\theta \in [-1,0]$, and

$$\begin{aligned} \Psi ^* _1(r)= & {} \frac{q_1(r)+q_2(r)}{2}=\left( \begin{array}{c} \text {Re}\left( e^{-i\omega _n \tilde{\tau }\text {r} }\right) \\ \text {Re}\left( \eta \text {e}^{-i\omega _n \tilde{\tau } \text {r} }\right) \end{array} \right) ,\\ \Psi ^* _2(r)= & {} \frac{q_1(r)-q_2(r)}{2i}=\left( \begin{array}{c} \text {Im}\left( e^{-i\omega _n \tilde{\tau }\text { r} }\right) \\ \text {Im}\left( \eta \text {e}^{-i\omega _n \tilde{\tau }\text {r} }\right) \end{array} \right) \end{aligned}$$

for $r \in [0,1]$. Then, we can compute by (3.16)

$$\begin{aligned} D^*_1:= & {} (\Psi ^* _1,\Phi _1),~D^*_2:=(\Psi ^* _1,\Phi _2),\\ ~D^*_3:= & {} (\Psi ^* _2,\Phi _1),~D^*_4:=(\Psi ^* _2,\Phi _2). \end{aligned}$$

Define $(\Psi ^*,\Phi )=(\Psi ^* _j,\Phi _k)=\left( \begin{array}{c} D^*_1~~ D^*_2\\ D^*_3~~ D^*_4 \end{array} \right)$ and construct a new basis $\Psi$ for $P^*$ by

$$\begin{aligned} \Psi =(\Psi _1,\Psi _2)^T=(\Psi ^*,\Phi )^{-1}\Psi ^*. \end{aligned}$$

Then, $(\Psi ,\Phi )=I_2$. In addition, define $f_n:=(\beta ^1_n,\beta ^2_n)$, where

$$\begin{aligned} \beta ^1_n=\left( \begin{array}{c} \cos \frac{n}{l}x\\ 0 \end{array} \right) , ~~~\beta ^2_n=\left( \begin{array}{c} 0\\ \cos \frac{n}{l}x \end{array} \right) . \end{aligned}$$

We also define

$$\begin{aligned} c\cdot f_n=c_1 \beta ^1_n+c_2 \beta ^2_n, ~~\text{ for }~~c=(c_1,c_2)^T\in \mathscr {C}_1. \end{aligned}$$

Thus, the center subspace of linear Eq. (3.12) is given by $P_{CN} \mathscr {C}_1 \oplus P_{S} \mathscr {C}_1$ and $P_{S} \mathscr {C}_1$ denotes the complement subspace of $P_{CN} \mathscr {C}_1$ in $\mathscr {C}_1$,

$$\begin{aligned} <u,v>:=\frac{1}{l\pi } \int _{0}^{l\pi }u_1 \overline{v_1}\mathrm{d}x+ \frac{1}{l\pi } \int _{0}^{l\pi }u_2 \overline{v_2}\mathrm{d}x \end{aligned}$$

for $u=(u_1,u_2), v=(v_1,v_2), u,v\in X$ and $<\phi ,f_0>=(<\phi ,f^1_0>, <\phi ,f^2_0>)^T$.

Let $A_{\tilde{\tau }}$ denote the infinitesimal generator of an analytic semigroup induced by the linear system Eqs. (3.12), and (3.8) can be rewritten as the following abstract form

$$\begin{aligned} \frac{\mathrm{d}U(t)}{\mathrm{d}t}=A_{\tilde{\tau }} U_t+R(U_t,\mu ), \end{aligned}$$

(3.17)

where

$$\begin{aligned} R(U_t,\mu )=\left\{ \begin{array}{ll} 0, &{} \theta \in [-1,0);\\ F(U_t,\mu ), &{} \theta =0. \end{array} \right. \end{aligned}$$

(3.18)

By the decomposition of $\mathscr {C}_1$, the solution above can be written as

$$\begin{aligned} U_t=\Phi \left( \begin{array}{ll} x_1\\ x_2 \end{array} \right) f_n+h(x_1,x_2,\mu ), \end{aligned}$$

(3.19)

where

$$\begin{aligned} \left( \begin{array}{ll} x_1\\ x_2 \end{array} \right) =(\Psi ,<U_t,f_n>), \end{aligned}$$

and

$$\begin{aligned} h(x_1,x_2,\mu ) \in P_{S} \mathscr {C}_1,~ h(0,0,0)=0,~Dh(0,0,0)=0. \end{aligned}$$

In particular, the solution of (3.9) on the center manifold is given by

$$\begin{aligned} U_t= & {} \Phi \left( \begin{array}{ll} x_1(t)\\ x_2(t) \end{array} \right) f_n+h(x_1,x_2,0). \end{aligned}$$

(3.20)

Let $z=x_1-i x_2$, and notice that $p_1=\Phi _1+i\Phi _2$. Then, we have

$$\begin{aligned} \Phi \left( \begin{array}{ll} x_1\\ x_2 \end{array} \right) f_n= & {} (\Phi _1,\Phi _2) \left( \begin{array}{ll} \frac{z+\overline{z}}{2}\\ \frac{i(z-\overline{z})}{2} \end{array} \right) f_n\\= & {} \frac{1}{2}(p_1z+ \overline{p_1} \overline{z})f_n, \end{aligned}$$

and

$$\begin{aligned} h(x_1,x_2,0)=h\left( \frac{z+\overline{z}}{2},\frac{i(z-\overline{z})}{2},0\right) . \end{aligned}$$

Hence, Eq. (3.20) can be transformed into

$$\begin{aligned} U_t= & {} \frac{1}{2}(p_1z+ \overline{p_1} \overline{z})f_n+ h\left( \frac{z+\overline{z}}{2},\frac{i(z-\overline{z})}{2},0\right) \nonumber \\= & {} \frac{1}{2}(p_1z+ \overline{p_1} \overline{z})f_n+ W(z,\overline{z}), \end{aligned}$$

(3.21)

where

$$\begin{aligned} W(z,\overline{z})=h\left( \frac{z+\overline{z}}{2},\frac{i(z-\overline{z})}{2},0\right) . \end{aligned}$$

From [28], z satisfies

$$\begin{aligned} \dot{z}=i\omega _n \tilde{\tau } z +g(z,\overline{z}), \end{aligned}$$

(3.22)

where

$$\begin{aligned} g(z,\overline{z})=(\Psi _1(0)-i\Psi _2(0))\langle F(U_t,0),f_n\rangle .\nonumber \\ \end{aligned}$$

(3.23)

Let

$$\begin{aligned} W(z,\overline{z})= & {} W_{20} \frac{z^2}{2}+W_{11} z \overline{z} +W_{02} \frac{\overline{z}^2}{2}+\cdots , \end{aligned}$$

(3.24)

$$\begin{aligned} g(z,\overline{z})= & {} g_{20} \frac{z^2}{2}+g_{11} z \overline{z} +g_{02} \frac{\overline{z}^2}{2}+\cdots , \end{aligned}$$

(3.25)

from Eqs. (3.21) and (3.24), we have

$$\begin{aligned} u_t(0)= & {} \frac{1}{2} (z+\overline{z})\cos \left( \frac{n x}{l}\right) +W^{(1)}_{20}(0) \frac{z^2}{2}\\&+W^{(1)}_{11}(0) z\overline{z}+W^{(1)}_{02}(0) \frac{\overline{z}^2}{2}+\cdots ,\\ v_t(0)= & {} \frac{1}{2} (\xi z+\overline{\xi }\overline{z})\cos \left( \frac{n x}{l}\right) +W^{(2)}_{20}(0) \frac{z^2}{2}\nonumber \\&+W^{(2)}_{11}(0) z\overline{z}+W^{(2)}_{02}(0) \frac{\overline{z}^2}{2}+\cdots ,\\ u_t(-1)= & {} \frac{1}{2}(z e^{-i\omega _n \tilde{\tau }}+\overline{z} e^{i\omega _n \tilde{\tau }})\cos \left( \frac{n x}{l}\right) \nonumber \\&+W^{(1)}_{20}(-1)\frac{z^2}{2} +W^{(1)}_{11}(-1)z \overline{z}\nonumber \\&+W^{(1)}_{02}(-1)\frac{\overline{z}^2}{2}+\cdots , \end{aligned}$$

and

$$\begin{aligned} \overline{F}_1(U_t,0)= & {} \frac{1}{\tilde{\tau }}F_1=\frac{1}{2} f_{uu} u_t^2(0)+f_{uv}u_t(0) v_t(0)\nonumber \\&-u_t(0) u_t(-1)+\frac{1}{2} f_{vv}v_t^2(0)\nonumber \\&+\frac{1}{6}f_{uuu}u_t^3(0) +\frac{1}{6}f_{uuv}u_t^2(0) v_t(0)\nonumber \\&+\frac{1}{6}f_{uvv} u_t(0) v_t^2(0)\nonumber \\&+\frac{1}{6}f_{vvv} v_t^3(0)+O(4),\end{aligned}$$

(3.26)

$$\begin{aligned} \overline{F}_2(U_t,0)= & {} \frac{1}{\tilde{\tau }}F_2=\frac{1}{2} g_{uu} u_t^2(0)\nonumber \\&+ g_{uv} u_t(0)v_t(0)+\frac{1}{2} g_{vv} v_t^2(0)\nonumber \\&+\frac{1}{6}g_{uuu}u_t^3(0)+\frac{1}{6}g_{uuv}u_t^2(0) v_t(0)\nonumber \\&+\frac{1}{6}g_{uvv} u_t(0) v_t^2(0)\nonumber \\&+\frac{1}{6}g_{vvv} v_t^3(0)+O(4), \end{aligned}$$

(3.27)

with

$$\begin{aligned} f_{uu}= & {} \frac{2 c h}{(c+u_*)^3}+\frac{2 m v_* \alpha }{(m+u_*)^3},\nonumber \\ f_{uv}= & {} -\frac{m \alpha }{(m+u_*)^2}, g_{uu}=-\frac{2 s v_*^2 \beta }{(m+u_*)^3},\nonumber \\ g_{uv}= & {} \frac{2 s v_* \beta }{(m+u_*)^2}, g_{vv}=-\frac{2 s \beta }{m+u_*},\nonumber \\ f_{uuu}= & {} -\frac{6 c h}{(c+u_*)^4}-\frac{6 m v_* \alpha }{(m+u_*)^4},\nonumber \\ f_{uuv}= & {} \frac{2 m \alpha }{(m+u_*)^3}, g_{uuu}=\frac{6 s v_*^2 \beta }{(m+u_*)^4},\nonumber \\ g_{uuv}= & {} -\frac{4 s v_* \beta }{(m+u_*)^3}, g_{uvv}=\frac{2 s \beta }{(m+u_*)^2},\nonumber \\ f_{vv}= & {} f_{uvv}=f_{vvv}=g_{vvv}=0. \end{aligned}$$

(3.28)

Hence,

$$\begin{aligned}&\overline{F}_1(U_t,0)=\cos ^2\left( \frac{n x}{l}\right) \left( \frac{z^2}{2}\chi _{20}+z\overline{z}\chi _{11} +\frac{\overline{z}^2}{2}\overline{\chi }_{02}\right) \nonumber \\&+\frac{z^2\overline{z}}{2} \cos \left( \frac{n x}{l}\right) [W^{(1)}_{11} (0)\nonumber \\&(f_{uu}+\xi f_{uv}-e^{-i \tilde{\tau } \omega _n})+W^{(2)}_{11} (0) f_{uv}\nonumber \\&\quad +W^{(1)}_{20}(0)\frac{f_{uu}+\overline{\xi } f_{uv}-e^{i \tilde{\tau } \omega _n}}{2}\nonumber \\&\quad +W^{(2)}_{20} (0)\frac{f_{uv}}{2}-\frac{1}{2}W^1_{20}(-1)-W^1_{1}(-1)]\nonumber \\&\quad +\frac{z^2\overline{z}}{2}\cos ^3\left( \frac{n x}{l}\right) \nonumber \\&\quad \left[ \frac{1}{8}f_{uuu}+\frac{1}{24} (\overline{\xi } +2 \xi ) f_{uuv}\right] +\cdots , \end{aligned}$$

(3.29)

$$\begin{aligned}&\overline{F}_2(U_t,0)=\cos ^2\left( \frac{n x}{l}\right) \nonumber \\&\quad \times \left( \frac{z^2}{2}\varsigma _{20}+z\overline{z}\varsigma _{11} +\frac{\overline{z}^2}{2}\overline{\varsigma }_{20}\right) \nonumber \\&\quad +\frac{z^2\overline{z}}{2}\cos \frac{nx}{l}\left[ W^1_{11}(0) \left( g_{uu}+\xi g_{uv}\right) \right. \nonumber \\&\quad +W^2_{11}(0) \left( g_{uv}+\xi g_{vv}\right) \nonumber \\&\quad +\frac{1}{2} W^1_{20}(0) \left( g_{uu}+\overline{\xi } g_{uv}\right) \nonumber \\&\quad +\left. \frac{1}{2} W^2_{20}(0) \left( g_{uv}+\overline{\xi } g_{vv}\right) \right] \nonumber \\&\quad +\frac{z^2\overline{z}}{2}\cos ^3\left( \frac{n x}{l}\right) \left[ \frac{1}{8}g_{uuu}+\frac{1}{24} (\overline{\xi } +2 \xi ) g_{uuv}\right. \nonumber \\&\left. \quad +\frac{1}{24} \xi (2 \overline{\xi } +\xi ) g_{uvv}\right] +\cdots , \end{aligned}$$

(3.30)

$$\begin{aligned}&\langle F(U_t,0),f_n \rangle =\tilde{\tau }(\overline{F}_1(U_t,0)f^1_n\nonumber \\&\quad +\overline{F}_2(U_t,0)f^2_n)\nonumber \\&=\frac{z^2}{2}\tilde{\tau }\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) \Gamma +z\overline{z}\tilde{\tau }\left( \begin{array}{c} \chi _{11} \\ \varsigma _{11} \end{array} \right) \Gamma \nonumber \\&\quad +\frac{\overline{z}^2}{2}\tilde{\tau }\left( \begin{array}{c} \overline{\chi }_{20} \\ \overline{\varsigma }_{20} \end{array} \right) \Gamma +\frac{z^2\overline{z}}{2}\tilde{\tau }\left( \begin{array}{c} \kappa _1\\ \kappa _2 \end{array} \right) +\cdots . \end{aligned}$$

(3.31)

with

$$\begin{aligned} \Gamma= & {} \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^3\left( \frac{n x}{l}\right) \mathrm{d}x,\\ \kappa _1= & {} \left[ \left( f_{uu}+\xi f_{uv}-e^{-i \tilde{\tau } \omega _n}\right) W^{(1)}_{11} (0) + f_{uv}W^{(2)}_{11} (0)\right. \nonumber \\&+\frac{1}{2}(f_{uu}+\overline{\xi } f_{uv}-e^{i \tilde{\tau } \omega _n})W^{(1)}_{20}(0)\nonumber \\&+\frac{1}{2}f_{uv}W^{(2)}_{20} (0)\\&\left. +\frac{1}{2}W^1_{20}(-1)+\frac{1}{2}W^1_{1}(-1)\right] \\&\times \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^2\left( \frac{n x}{l}\right) \mathrm{d}x\\&+\left[ \frac{1}{8}f_{uuu}+\frac{1}{24} (\overline{\xi } +2 \xi ) f_{uuv}\right] \\&\times \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^4\left( \frac{n x}{l}\right) \mathrm{d}x,\\ \kappa _2= & {} \left[ (g_{uu}+\xi g_{uv})W^{(1)}_{11} (0) + (g_{uv}+\xi g_{vv})W^{(2)}_{11} (0)\right. \\&+\frac{1}{2}(g_{uu}+\overline{\xi } g_{uv})W^{(1)}_{20}(0)\\&\left. +\frac{1}{2}(g_{uv}+\overline{\xi } g_{vv})W^{(2)}_{20} (0)\right] \\&\times \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^2\left( \frac{n x}{l}\right) \mathrm{d}x\\&+\left[ \frac{1}{8}g_{uuu}+\frac{1}{24} (\overline{\xi } +2 \xi ) g_{uuv}\right. \nonumber \\&\left. +\frac{1}{24} \xi (2 \overline{\xi } +\xi ) g_{uvv}\right] \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^4\left( \frac{n x}{l}\right) \mathrm{d}x \end{aligned}$$

and

$$\begin{aligned} \chi _{20}= & {} \frac{1}{4} \left( f_{uu}+\xi 2 f_{uv}-2 e^{-i \tilde{\tau } \omega _n}\right) \nonumber \\ \chi _{11}= & {} \frac{1}{4} \left( f_{uu}+(\overline{\xi } +\xi ) f_{uv}-e^{-i \tilde{\tau } \omega _n}-e^{i \tilde{\tau } \omega _n}\right) \nonumber \\ \varsigma _{20}= & {} \frac{1}{4} \left( g_{uu}+\xi (2 g_{uv}+\xi g_{vv}\right) \nonumber \\ \varsigma _{11}= & {} \frac{1}{4} \left( g_{uu}+(\overline{\xi } +\xi ) g_{uv}+\overline{\xi } \xi g_{vv}\right) . \end{aligned}$$

(3.32)

Denote

$$\begin{aligned} \Psi _1(0)-i\Psi _2(0):=(\gamma _1~~\gamma _2). \end{aligned}$$

Notice that

$$\begin{aligned} \frac{1}{l\pi } \int _{0}^{l\pi }\cos ^3\left( \frac{n x}{l}\right) \mathrm{d}x=0,~~n\in \mathbb {N}, \end{aligned}$$

and we have

$$\begin{aligned}&(\Psi _1(0)-i\Psi _2(0))<F(U_t,0),f_n>\nonumber \\&\quad =\frac{z^2}{2} (\gamma _1\chi _{20} + \gamma _2\varsigma _{20})\Gamma \tilde{\tau } +z\overline{z}( \gamma _1\chi _{11} + \gamma _2\varsigma _{11})\Gamma \tilde{\tau }\nonumber \\&\qquad +\frac{\overline{z}^2}{2}( \gamma _1\overline{\chi }_{20} + \gamma _2\overline{\varsigma }_{20})\Gamma \tilde{\tau }\nonumber \\&\qquad +\frac{z^2\overline{z}}{2}\tilde{\tau } [\gamma _1 \kappa _1 +\gamma _2 \kappa _2 ]+\cdots , \end{aligned}$$

(3.33)

Then, by (3.23), (3.25) and (3.33), we have $g_{20}=g_{11}=g_{02}=0$, for $n=1,2,3,\cdots$. If $n=0$, we have the following quantities:

$$\begin{aligned} g_{20}= & {} \gamma _1\tilde{\tau } \chi _{20} + \gamma _2\tilde{\tau }\varsigma _{20},\\ g_{11}= & {} \gamma _1\tilde{\tau }\chi _{11}+ \gamma _2\tilde{\tau }\varsigma _{11},\\ g_{02}= & {} \gamma _1\tilde{\tau }\overline{\chi }_{20} + \gamma _2\tilde{\tau }\overline{\varsigma }_{20}. \end{aligned}$$

And for $n\in \mathbb {N}_0, g_{21}=\tilde{\tau }( \gamma _1 \kappa _1 +\gamma _2 \kappa _2)$.

Now, a complete description for $g_{21}$ depends on the algorithm for $W_{20}(0)$ and $W_{11}(0)$ which we shall compute.

From [28], we have

$$\begin{aligned}&\dot{W}(z,\overline{z})=W_{20}z\dot{z}+W_{11}\dot{z} \overline{z} +W_{11} z \dot{\overline{z}} +W_{02}\overline{z} \dot{\overline{z}}+\cdots ,\\&A_{\tilde{\tau }} W(z,\overline{z})=A_{\tilde{\tau }} W_{20} \frac{z^2}{2}+A_{\tilde{\tau }} W_{11} z \overline{z} + A_{\tilde{\tau }} W_{02} \frac{\overline{z}^2}{2}\\&\qquad \qquad \qquad +\,\cdots , \end{aligned}$$

and $W(z,\overline{z})$ satisfies

$$\begin{aligned} \dot{W}(z,\overline{z})= A_{\tilde{\tau }} W+H(z,\overline{z}), \end{aligned}$$

where

$$\begin{aligned}&H(z,\overline{z})=H_{20} \frac{z^2}{2}+W_{11} z \overline{z} +H_{02} \frac{\overline{z}^2}{2}+\cdots \nonumber \\&\quad =X_0F(U_t,0)-\Phi (\Psi ,<X_0 F(U_t,0),f_n>\cdot f_n).\nonumber \\ \end{aligned}$$

(3.34)

Hence, we have

$$\begin{aligned}&(2i\omega _n \tilde{\tau }- A_{\tilde{\tau }})W_{20}=H_{20},\nonumber \\&\quad -A_{\tilde{\tau }}W_{11}=H_{11}, ~~(-2i\omega _n \tilde{\tau }- A_{\tilde{\tau }})W_{02}=H_{02},\nonumber \\ \end{aligned}$$

(3.35)

that is

$$\begin{aligned} W_{20}= & {} (2i\omega _n \tilde{\tau }- A_{\tilde{\tau }})^{-1}H_{20},\nonumber \\ W_{11}= & {} -A_{\tilde{\tau }} ^{-1} H_{11}, ~~W_{02}=(-2i\omega _n \tilde{\tau }- A_{\tilde{\tau }})^{-1}H_{02}.\nonumber \\ \end{aligned}$$

(3.36)

By (3.33), we have that for $\theta \in [-1,0)$,

$$\begin{aligned} H(z,\overline{z})= & {} -\Phi (0) \Psi (0)<F(U_t,0),f_n>\cdot f_n\nonumber \\= & {} -\left( \frac{p_1(\theta )+p_2(\theta )}{2},\frac{p_1(\theta )-p_2(\theta )}{2i}\right) \nonumber \\&\times \left( \begin{array}{c} \Phi _1(0)\\ \Phi _2(0) \end{array} \right) <F(U_t,0),f_n>\cdot f_n\nonumber \\= & {} -\frac{1}{2}[p_1(\theta )(\Phi _1(0)-i\Phi _2(0))\nonumber \\&+p_2(\theta )(\Phi _1(0)+i\Phi _2(0))] \nonumber \\= & {} \langle F(U_t,0),f_n \rangle \cdot f_n-\frac{1}{2}\left[ (p_1(\theta )g_{20}\right. \nonumber \\&+p_2(\theta )\overline{g}_{02})\frac{z^2}{2} + (p_1(\theta )g_{11}+p_2(\theta )\overline{g}_{11})z \overline{z}\nonumber \\&\left. + (p_1(\theta )g_{02}+p_2(\theta )\overline{g}_{20})\frac{\overline{z}^2}{2}\right] +\cdots . \end{aligned}$$

Therefore, by (3.34), for $\theta \in [-1,0)$,

$$\begin{aligned} H_{20}(\theta )= & {} \left\{ \begin{array}{l@{\quad }l} 0 &{} n\in \mathbb {N},\\ -\frac{1}{2}(p_1(\theta )g_{20}+p_2(\theta )\overline{g}_{02})\cdot f_0 &{} n=0, \end{array} \right. \nonumber \\ H_{11}(\theta )= & {} \left\{ \begin{array}{l@{\quad }l} 0 &{} n\in \mathbb {N},\\ -\frac{1}{2}(p_1(\theta )g_{11}+p_2(\theta )\overline{g}_{11})\cdot f_0 &{} n=0, \end{array} \right. \nonumber \\ H_{02}(\theta )= & {} \left\{ \begin{array}{l@{\quad }l} 0 &{} n\in \mathbb {N},\\ -\frac{1}{2}(p_1(\theta )g_{02}+p_2(\theta )\overline{g}_{20})\cdot f_0 &{} n=0, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} H(z,\overline{z})(0)= & {} F(U_t,0)-\Phi (\Psi ,<F(U_t,0),f_n>)\\&\cdot f_n, \end{aligned}$$

where

$$\begin{aligned}&H_{20}(0)\nonumber \\&\quad = \left\{ \begin{array}{ll} \tilde{\tau }\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) \cos ^2\left( \frac{n x}{l}\right) , &{} n\in \mathbb {N},\\ \tilde{\tau }\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) -\frac{1}{2}(p_1(0)g_{20}+p_2(0)\overline{g}_{02})\cdot f_0,&n=0. \end{array} \right. \nonumber \\&H_{11}(0)\nonumber \\&\quad =\left\{ \begin{array}{ll} \tilde{\tau }\left( \begin{array}{c} \chi _{11} \\ \varsigma _{11} \end{array} \right) \cos ^2\left( \frac{n x}{l}\right) , &{} n\in \mathbb {N},\\ \tilde{\tau }\left( \begin{array}{c} \chi _{11} \\ \varsigma _{11} \end{array} \right) -\frac{1}{2}(p_1(0)g_{11}+p_2(0)\overline{g}_{11})\cdot f_0,&n=0. \end{array} \right. \nonumber \\ \end{aligned}$$

(3.37)

By the definition of $A_{\tilde{\tau }}$ and (3.35), we have

$$\begin{aligned} \dot{W}_{20}= & {} A_{\tilde{\tau }}W_{20}=2i\omega _n \tilde{\tau } W_{20}+ \frac{1}{2}(p_1(\theta )g_{20}\\&+p_2(\theta )\overline{g}_{02})\cdot f_n,~~-1\le \theta <0. \end{aligned}$$

That is

$$\begin{aligned} W_{20}(\theta )= & {} \frac{i}{2i\omega _n \tilde{\tau }}(g_{20} p_1(\theta )\\&+\frac{\overline{g}_{02}}{3}p_2(\theta ))\cdot f_n +E_1 e^{2i\omega _n \tilde{\tau } \theta }, \end{aligned}$$

where

$$\begin{aligned}&E_1\nonumber \\&\quad =\left\{ \begin{array}{ll} W_{20}(0) &{} n=1,2,3,\cdots ,\\ W_{20}(0)-\frac{i}{2i\omega _n \tilde{\tau }}(g_{20} p_1(\theta )+\frac{\overline{g}_{02}}{3}p_2(\theta ))\cdot f_0 &{} n=0. \end{array} \right. \end{aligned}$$

Using the definition of $A_{\tilde{\tau }}$ and (3.35), we have that for $-1\le \theta <0$

$$\begin{aligned}&-(g_{20}p_1(0)+\frac{\overline{g}_{02}}{3}p_2(0))\cdot f_0 +2i\omega _n \tilde{\tau } E_1\nonumber \\&-A_{\tilde{\tau }}\left( \frac{i}{2\omega _n \tilde{\tau }} (g_{20}p_1(0)+\frac{\overline{g}_{02}}{3}p_2(0)) \cdot f_0\right) \\&-A_{\tilde{\tau }} E_1-L_{\tilde{\tau }}\left( \frac{i}{2\omega _n \tilde{\tau }} (g_{20} p_1(0)\right. \nonumber \\&\left. +\frac{\overline{g}_{02}}{3} p_2(0)) \cdot f_n+ E_1 e^{2i\omega _n \tilde{\tau } \theta }\right) \\&=\tilde{\tau }\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) -\frac{1}{2}(p_1(0)g_{20}+p_2(0)\overline{g}_{02})\cdot f_0. \end{aligned}$$

As

$$\begin{aligned} A_{\tilde{\tau }} p_1(0)+L_{\tilde{\tau }}(p_1 \cdot f_0)=i\omega _0 p_1(0) \cdot f_0, \end{aligned}$$

and

$$\begin{aligned} A_{\tilde{\tau }} p_2(0)+L_{\tilde{\tau }}(p_2 \cdot f_0)=-i\omega _0 p_2(0) \cdot f_0, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned}&2i\omega _n E_1-A_{\tilde{\tau }} E_1-L_{\tilde{\tau }} E_1 e^{2i\omega _n}\\&\quad =\tilde{\tau }\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) \cos ^2\left( \frac{n x}{l}\right) ,~~n\in \mathbb {N}. \end{aligned} \end{aligned}$$

That is

$$\begin{aligned} E_1=\tilde{\tau }E\left( \begin{array}{c} \chi _{20} \\ \varsigma _{20} \end{array} \right) \cos ^2\left( \frac{n x}{l}\right) \end{aligned}$$

where

$$\begin{aligned} E=\left( \begin{array}{ccc} 2i \omega _n \tilde{\tau }+ d_1 \frac{n^2}{l^2} -a_1-u_* &{} u_*e^{-2i \omega _n \tilde{\tau }} \\ -s/\beta &{} 2i \omega _n \tilde{\tau }+ d_2 \frac{n^2}{l^2} +s\end{array} \right) ^{-1}. \end{aligned}$$

Fig. 1

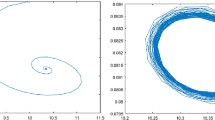
Phase portraits of system (1.5) without delay and diffusion. Left $s =0.2$ and initial condition (0.3, 0.9). Right $s =0.09$ and initial condition (0.3, 0.9)

Fig. 2

For system (1.5) without delay, $s=0.2$, and initial condition is (0.3, 0.9). Left component u(x, t) (stable). Right component v(x, t) (stable)

Similarly, from (3.36), we have

$$\begin{aligned} -\dot{W}_{11}= & {} \frac{i}{2\omega _n \tilde{\tau }}(p_1(\theta )g_{11}+p_2(\theta )\overline{g}_{11})\cdot f_n,\\&~~-1\le \theta <0. \end{aligned}$$

That is

$$\begin{aligned} W_{11}(\theta )=\frac{i}{2i\omega _n \tilde{\tau }}(p_1(\theta ) \overline{g}_{11}-p_1(\theta )g_{11})+E_2. \end{aligned}$$

Similar to the procedure of computing $W_{20}$, we have

$$\begin{aligned} E_2=\tilde{\tau }E^* \left( \begin{array}{c} \chi _{11} \\ \varsigma _{11} \end{array} \right) \cos ^2\left( \frac{n x}{l}\right) , \end{aligned}$$

where

$$\begin{aligned} E^*=\left( \begin{array}{ccc} d_1 \frac{n^2}{l^2} -a_1-u_* &{} u_*\\ -s/\beta &{} d_2 \frac{n^2}{l^2}+s \end{array} \right) ^{-1}. \end{aligned}$$

Thus, we can compute the following quantities which determine the direction and stability of bifurcating periodic orbits:

$$\begin{aligned} c_1(0)= & {} \frac{i}{2\omega _n \tilde{\tau }}\left( g_{20}g_{11}-2|g_{11}|^2- \frac{|g_{02}|^2}{3}\right) +\frac{1}{2}g_{21},\nonumber \\ \mu _2= & {} -\frac{Re(c_1(0))}{Re(\lambda ' (\tau ^j_n))},\nonumber \\ T_2= & {} -\frac{1}{\omega _n \tilde{\tau }}[Im(c_1(0))+\mu _2 Im(\lambda '(\tau ^j_n))],\nonumber \\ \beta _2= & {} 2 Re(c_1(0)). \end{aligned}$$

(3.38)

Then, we have the following theorem.

Fig. 3

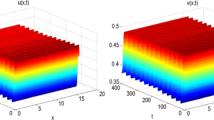
For system (1.5) without delay, $s=0.2, l=2$, and initial condition is (0.3, 0.9). Left component u(x, t) (Turing unstable). Right component v(x, t) (Turing unstable)

Fig. 4

For system (1.5) without delay, $s=0.2, l=0.5$, and initial condition is (0.3, 0.9). Left component u(x, t) (stable). Right component v(x, t) (stable)

Theorem 3.2

For any critical value $\tau ^j_n$, we have

• (i) $\mu _2$ determines the directions of the Hopf bifurcation: if $\mu _2>0$ (resp.<0), then the Hopf bifurcation is forward (resp. backward), that is, the bifurcating periodic solutions exist for $\mu >0$ (resp. $\mu <0$) ;

• (ii) $\beta _2$ determines the stability of the bifurcating periodic solutions on the center manifold: if $\beta _2<0$ (resp. >0), then the bifurcating periodic solutions are orbitally asymptotically stable (resp. unstable) .

• (iii) $T_2$ determines the period of bifurcating periodic solutions: if $T_2>0$ (resp. $T_2<0$), then the period increases (resp. decreases).

4 Numerical simulations

Fix parameters

$$\begin{aligned} \alpha= & {} 0.3,~~h=0.02,\nonumber \\ m= & {} 0.1,~~c=0.5,\nonumber \\ \beta= & {} 0.5. \end{aligned}$$

(4.1)

Hence, $E_*(0.3772,0.9544)$ is the unique positive equilibrium, and $a_1\approx 0.1069, a_2\approx -0.2371, a_1+a_2/\beta \approx -0.3674<0$; then, $\mathbf{(H_1)}$ holds.

For system (1.5) without delay and diffusion, by Theorem (2.1), if $s>a_1$, then equilibrium $E_*(u_*,v_*)$ is locally asymptotically stable, and the system undergoes Hopf bifurcation at $E_*(u_*,v_*)$ when $s=a_1$ (shown in Fig. 1).

Fig. 5

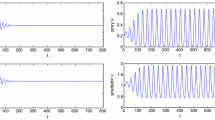
For system (1.5) without delay, $s=0.09$ and initial condition is (0.3, 0.9). Left component u(x, t) (periodic solution). Right component v(x, t) (periodic solution)

Fig. 6

For system (1.5), $\tau =1.5$ and initial condition is (0.3, 0.9). Left component u(x, t) (stable). Right component v(x, t) (stable)

For system (1.5) without delay, we have $\sigma \approx 0.0637$. Set $d_1=0.05, d_2=0.5$ and $l=2$, then $d_1/d_2>\sigma$. By Theorem (2.2) (i) and (ii), $s>a_1$, then equilibrium $E_*(u_*,v_*)$ is locally asymptotically stable and Turing instability will not occur; this is shown in Fig. 2.

For system (1.5) without delay, set $d_1=0.05, d_2=3$, then $d_1/d_2<\sigma$ and $s_-\approx 0.4088$. If set $s=0.2$, then $s\in (a_1,s_-), z_-\approx 0.4683$ and $z_+\approx 1.5691$. If set $l=2$, then there exists a $k=2$ such that $k^2/l^2 \in (z_-,z_+)$; by Theorem (2.2) (iv), $E_*(u_*,v_*)$ is Turing unstable, and this is shown in Fig. 3. If set $l=0.5$, then there doesn’t exist $k\in \mathbb {N}$ such that $k^2/l^2 \in (z_-,z_+)$; by Theorem (2.2) (iii), $E_*(u_*,v_*)$ is locally asymptotically stable, and this is shown in Fig. 4. Set $s=0.09$, by Theorem (2.2) (v), Hopf bifurcation occurs, this is shown in Fig. 5.

Fig. 7

For system (1.5), $\tau =1.7$ and initial condition is (0.3, 0.9). Left component u(x, t) (periodic solution). Right component v(x, t) (periodic solution)

For system (1.5), set $d_1=0.05, d_2=3, l=2$ and $s=0.5$. By direct computation, we have $\mathcal {D}=[0,1,2,3,4,5,6,7,8]$ and $\tau _*=\tau ^0_0 \approx 1.6118$. By Theorem (3.1), we know that if $\tau \in [0,\tau _*)$, then the equilibrium $E_*(u_*,v_*)$ is locally asymptotically stable. This is shown in Fig. 6. By Theorem (3.1), system (1.5) undergoes a Hopf bifurcation at the equilibrium $E_*(u_*,v_*)$ when $\tau =\tau _*$. By Theorem (3.2), we have

$$\begin{aligned} \mu _2\approx & {} 11.5932>0,~~\beta _2\approx -8.0186<0, ~~\text{ and }\\ T_2\approx & {} -3.6610<0. \end{aligned}$$

Hence, the direction of the bifurcation is forward, and the bifurcating period solutions are locally asymptotically stable. In addition, the period of bifurcating periodic solutions decreases. This is shown in Fig. 7.

5 Conclusion

In this paper, we have considered a diffusive modified Leslie–Gower predator–prey model with Michaelis–Menten-type harvesting in prey. The model shows rich and varied dynamics.

For the model without delay, we study the effect of diffusion, including stability and Turing instability of positive equilibrium. When $s>a_1$ and $s\ge \frac{ d_2a_1}{d_1}$, the equilibrium $E_*(u_*,v_*)$ is asymptotically stable and the diffusion has no effect on the system. When $d_1/d_2>\sigma$, then for $s>a_1$ equilibrium $E_*(u_*,v_*)$ is locally asymptotically stable and Turing instability will not occur. When $\frac{d_1}{d_2}<\sigma$, for $a_1<s<s_-$, choose a suitable l (represents the region $\Omega =(0,l\pi )$) such that there exist a $k\in \mathbb {N}$ such that $\frac{k^2}{l^2}\in (z_-, z_+)$, then Turing instability occurs. But when we change l such that there doesn’t exist $k\in \mathbb {N}$ satisfying $k^2/l^2 \in (z_-,z_+), E_*(u_*,v_*)$ is locally asymptotically stable. These results suggest that diffusion coefficients and the region’s size all affect the stability of equilibrium $E_*(u_*,v_*)$.

In addition, the time delay in the resource limitation of the prey plays an important role in coexistence of predator and prey. We obtained that when $\tau$ crosses the critical value $\tau _*$, the stability of the positive equilibrium $P(u_*,v_*)$ changes and Hopf bifurcation occurs. That means the predator and prey coexist and converge to the coexisting equilibrium point when time delay is smaller than the critical value, and the predator and the prey species may coexist in an oscillatory mode when time delay crosses the critical value.