Kinetostatic model of overconstrained lower mobility parallel manipulators

Abstract

The kinetostatic model of overconstrained lower mobility parallel manipulators (PMs) is established in this paper. Based on this model, the actuator wrenches and the constrained wrenches can be completely derived, and the stiffness and the deformation of each leg and the moving platform can be obtained. A novel 2-RPU $+$ UPR (revolute joint-prismatic joint-universal joint+universal joint-prismatic joint-revolute joint) PM is presented to illustrate the approach to solving the kinetostatic of overconstrained PMs. Due to the particular arrangement of the joints in each legs, this PM provides six constraints to the moving platform, whereas three of them are overconstraints. The detailed kinetostatic of this PM is obtained based on the established model. The unified stiffness finite element (FE) model for various PMs is established, and the stiffness of the 2-RPU $+$ UPR PM is verified.

1 Introduction

In recent years, lower mobility parallel manipulators (PMs) have been extensively studied due to their interesting properties and potential engineering values [1–3]. Among them, some overconstrained PMs have drawn particular interests from numerous researchers including mobility, type synthesis, kinematics and singularity analysis [4–9]. In the aspect of overconstrained PMs, Huang et al. [3, 4] investigated the mobility of overconstrained PMs using screw theory and successfully solved the mobility problem of the classical DELASSUS, SARRUS mechanisms as well as the modern 3-RRRH PM with overconstraints using an identical formula. Refaat et al. [5] synthesized asymmetrical 3-degree-of-freedom (DOF) rotational-translational PMs with overconstraints based on Lie group theory. Fang and Tsai [6] synthesized a class of overconstrained PMs using the theory of reciprocal screws. Li et al. [7–9] studied the mobility, kinematics and dynamics of 3-DOF translational PMs with three overconstraints using screw theory. Amine et al. [10] investigated singularity of a 5-DOF overconstrained PM using Grassmann–Cayley algebra and Grassmann geometry. Wu et al. [11] studied the effect of structure parameters on the dynamic characteristics of an overconstrained PRRRP PM.

The kinetostatic analysis is a traditional and a very important topic in mechanism research [12]. In this aspect, Zhang et al. [13] established kinetostatic model for some PMs which have passive legs. In their work, a lumped kinetostatic model was proposed in order to account for joint and link compliances. Cervantes and Rico [14] studied the statics of spatial PMs by means of the principle of virtual work, equipped with a recursive and systematic formulation. In their study, all internal forces and non-working external constraint forces were not considered. Li et al. [22] derived a stiffness matrix of a 3-DOF 3-PUU PM based on an alternative approach considering actuations and constraints, and the compliances subject to both actuators and legs. Hu et al. [16, 17] studied the kinetostatic of some PMs with non-overconstraints. Hong and Choi [18] solved the statics of lower mobility PMs considering feasible controllable loads space. Klimchik et al. [19] presented an advanced stiffness modeling technique for PMs composed of perfect and non-perfect serial chains whose geometry differs from the nominal one. The developed technique contributed both to serial and parallel manipulators under internal and external loadings. Zi et al. [20, 21] studied the dynamics of cooperative multiple mobile cranes, which have the characters of both series and parallel manipulators. In these works, the complete dynamic model of nine input and three-output system was established based on Lagrange equation. Sapio et al. [22] presented a novel approach to effectively address the motion control of holonomically constrained multibody systems, which allows for the simultaneous specification of desired constraint forces.

The previous works concerned with kinetostatic mainly focused on the non-overconstrained PMs, and most of the previous works only solve the actuator wenches applied on the PMs. However, there were few efforts made toward the kinetostatic of overconstrained PMs. In this aspect, Huang [23, 24] solved all the constraint reactions as well as the active forces of PMs with overconstraints via reciprocal-screw theory. Although the study considered reducing the number of unknown constraint reactions, there were still large computing since all the joint reactions were computed based on the loading characteristics of different joints. Due to the complicated coupling and constraints in the overconstrained PMs, there are highly coupled relations between constrained wrenches and the deformations in the legs. The complicated constraints bring difficulties for solving the constrained wrenches. Therefore, how to simplify the action effect of constrained wrenches and reduce the number of unknowns and the number of simultaneous equilibrium equations is the key issue of the kinetostatic for constrained PMs. Based on considering the characteristic of constrained forces, and through solving the coupling relation of the constrained wrenches and the deformations, the kinetostatic issue of constrained PMs is studied in this paper.

The lower mobility PMs have various structures, and this class of manipulators has been widely studied and applied. However, up to now, there is no simple and unified approach for solving the kinetostatic of overconstrained lower mobility PMs. For this reason, this paper aims at establishing a unified and simple kinetostatic model for the lower mobility overconstrained PMs with linear active legs.

In order to illustrate the unified kinetostatic model of overconstrained PMs, a novel overconstrained 2-RPU $+$ UPR PM with two rotations and one translation is presented. For this PM, three constrained forces and three constrained torques are simultaneously existed. Thus, this PM is a good example to illustrate the kinetostatic model for overconstrained PMs .

The remainder of this paper is organized as follows. In Sect. 2, the unified kinetostatic model of the overconstrained PMs is established. In Sect. 3, after a description and constraint analysis of the 2-RPU $+$ UPR PM in Sect. 3.1, the kinematics of this PM is described in Sect. 3.2, and the kinetostatic of this PM is analyzed based on the established kinetostatic model in Sect. 3.3. In Sect. 4, the unified CAD model used for finite element (FE) analysis for the PMs with various structures is established. In Sect. 5, a numerical example concerned with the kinetostatic of the 2-RPU $+$ UPR PM is provided, and the result is verified by the FE model. Finally, some concluding remarks are given in Sect. 6.

2 Unified kinetostatic model of overconstrained PMs

A general n-DOF overconstrained PM with n linear active legs possesses a fixed base B with O as its center, a moving platform m with o as its center, and n XPY-type linear legs $r_{i}$ ($i=1, 2, {\ldots }, n<6)$ with the linear actuators, where X and Y are selected from R, U and S joints. Each of $r_{i}$ connects m at point $a_{i}$ with B at point $A_{i}$.

Let v and ${\varvec{\omega }}$ be the linear and angular velocity of m, respectively. For a general PM with n linear active legs, the inverse actuation velocity can be obtained by following formula [25]:

$$\begin{aligned} {{\varvec{v}}}_r= & {} \mathbf{J}_\alpha \left[ {{\begin{array}{c} {{\varvec{v}}} \\ {{\varvec{\omega }} } \\ \end{array} }} \right] , \quad {{\varvec{v}}}_r=\left[ {\begin{array}{lc} {\begin{array}{c} {v_{r_1 }} \\ \vdots \\ \end{array} } \\ v_{r_n } \\ \end{array}} \right] ,\nonumber \\ \mathbf{J}_\alpha= & {} \left[ {{\begin{array}{cc} {{{\varvec{\delta }} }_1^{\mathrm{T}} }&{} {({{\varvec{e}}}_1 \times {{\varvec{\delta }} }_1 )^{\mathrm{T}}} \\ \vdots &{} \vdots \\ {{{\varvec{\delta }} }_n^{\mathrm{T}} }&{} {({\varvec{e}}_n \times {{\varvec{\delta }} }_n )^{\mathrm{T}}} \\ \end{array} }} \right] \end{aligned}$$

(1a)

where ${{\varvec{\delta }}}_{i}(i=1, 2, {\ldots }, n)$ denotes the unit vector of $r_{i }$ and ${{\varvec{e}}}_{i }$ denotes the vector from o to $a_{i}$. $v_{ri} (1,\ldots ,n)$ are the active velocities of actuators.

The relation between the six dimensional velocity and the n dimensional independent velocity of the moving platform can be expressed as [25]

$$\begin{aligned} \left[ {{\begin{array}{c} {{\varvec{v}}} \\ {\varvec{\omega } } \\ \end{array} }} \right] =\mathbf{J}_o {\dot{\varvec{\theta }}} \end{aligned}$$

(1b)

where $\mathbf{J}_{o}$ is a $6\times n$ form matrix which is defined as velocity decoupling matrix for lower mobility PMs. ${\varvec{\theta }}$ is the vector formed by n independent pose parameters of the moving platform. ${\dot{\varvec{\theta }}}$ is velocity of $\varvec{\theta }$.

Let ${{\varvec{F}}}_{{{\varvec{o}}}}$ and ${{\varvec{T}}}_{{{\varvec{o}}}}$ be the applied force and torque imposed at m. Based on Eqs. (1a), (1b) and the principle of virtue work, it leads

$$\begin{aligned} {\varvec{F}}_r =-\mathbf{J}_o (\mathbf{J}_\alpha \mathbf{J}_o )^{-1}\left[ {{\begin{array}{c} {{\varvec{F}}_{\mathrm{o}} } \\ {{\varvec{T}}_o } \\ \end{array} }} \right] , {\varvec{F}}_r =\left[ {\begin{array}{c} {\begin{array}{c} {F_{r_1 }} \\ \vdots \\ \end{array} } \\ F_{r_n } \\ \end{array}} \right] \end{aligned}$$

(1c)

where $F_{ri}$ (1,..., n) are the actuator wrenches applied to actuators. Equation (1c) is the statics model for solving the actuator wrenches for general PMs. The actuator wrenches for the overconstrained PMs can be solved from Eq. (1c). However, the constrained wrenches are difficult to determine due to the overconstraints existed.

For the overconstrained lower mobility PMs, the constrained wrenches (forces/torques) exist in the legs. The constrained wrenches can be determined by the following rules [25]:

• (a) In each leg of lower mobility PMs, the constrained forces must be perpendicular to all prismatic joints and must be coplanar with all revolute joints, respectively.

• (b) In each leg of lower mobility PMs, the constrained torques must be perpendicular to all revolute joints.

Support that there are m constrained forces and q constrained torques existed in an overconstrained PM. Let $F_{pi }(i=1, 2, {\ldots }, m)$ be the constrained forces in the PM, ${{\varvec{f}}}_{i }(i=1, 2, {\ldots }, m)$ be the unit vector of $F_{pi}$, ${{\varvec{d}}}_{i }(i=1, 2, {\ldots }, m)$ be the vector from o to $F_{pi}$. Let $T_{pi }(i=1, 2, {\ldots }, q)$ be the constrained torques in the PM, and ${\varvec{\tau }}_{i}(i=1, 2, {\ldots }, q)$ be the unit vector of $T_{pi}$.

The constrained wrenches in each leg have the property that they do no work to each joint and thus they do no work to the moving platform. From this concept, it leads to:

$$\begin{aligned}&F_{Pi} {{\varvec{f}}}_i \cdot {{\varvec{v}}}+(F_{Pi} {{\varvec{d}}}_i \times {{\varvec{f}}}_i )\cdot {\varvec{\omega }} =0 (i=1,\ldots ,m) \end{aligned}$$

(2a)

$$\begin{aligned}&T_{Pi} {\varvec{\tau } }_i \cdot {\varvec{\omega } }=0\,\,(i=1, \ldots , q) \end{aligned}$$

(2b)

By combining Eqs. (2a) and (2b), it leads to

$$\begin{aligned} {{\varvec{0}}}_{m+q} =\mathbf{J}_v \left[ {{\begin{array}{c} {\varvec{v}} \\ {\varvec{\omega } } \\ \end{array} }} \right] , \mathbf{J}_v =\left[ {{\begin{array}{cc} {{{\varvec{f}}}_1^T }&{} {({\varvec{d}}_1 \times {{\varvec{f}}}_1 )^{T}} \\ \vdots &{} \vdots \\ {{{\varvec{f}}}_m^T }&{} {({\varvec{d}}_m \times {{\varvec{f}}}_m )^{T}} \\ {{{\varvec{0}}}_{1\times 3} }&{} {{\varvec{\tau } }_1^T } \\ \vdots &{} \vdots \\ {{{\varvec{0}}}_{1\times 3} }&{} {{\varvec{\tau } }_q^T } \\ \end{array} }} \right] \end{aligned}$$

(2c)

Suppose that the moving platform m is elastically suspended by n elastic linear legs and all joints in each leg are rigid body. The applied wrench is balanced by the actuator wrenches and the constrained wrenches in the PM. Thus, the forward statics of the overconstrained PMs can be expressed as follows:

$$\begin{aligned}&\left[ {{\begin{array}{c} {{\varvec{F}}_o } \\ {{\varvec{T}}_o } \\ \end{array} }} \right] =\mathbf{G}_{6\times (m+n+q)}\left[ {\begin{array}{c} {{\varvec{F}}_r } \\ {{\varvec{F}}_p } \\ {\varvec{T}}_p \\ \end{array}} \right] , {\varvec{F}}_r=\left[ {\begin{array}{c} {F_{r_1 } } \\ \vdots \\ F_{r_n } \\ \end{array}} \right] ,\nonumber \\&{\varvec{F}}_p=\left[ {\begin{array}{c} {F_{p_1 }} \\ \vdots \\ F_{p_m } \\ \end{array}} \right] , {\varvec{T}}_p =\left[ {\begin{array}{c} {T_{p_1 } } \\ \vdots \\ T_{p_q } \\ \end{array}} \right] , \mathbf{G}_{6\times (m+n+q)} =\left[ {{\begin{array}{c} {\mathbf{J}_\alpha } \\ {\mathbf{J}_v } \\ \end{array} }} \right] ^{T} \nonumber \\&{} \mathbf{G}_{6\times (m+n+q)} \nonumber \\&\quad =\left[ {{\begin{array}{ccccccccc} {{{\varvec{\delta }} }_1 }&{} \cdots &{} {{{\varvec{\delta }} }_n }&{} {{\varvec{f}}_1}&{} \cdots &{} {{{\varvec{f}}}_m }&{} {{{\varvec{0}}}_{3\times 1} }&{} \cdots &{} {{{\varvec{0}}}_{3\times 1} } \\ {{{\varvec{e}}}_1 \times {{\varvec{\delta }} }_1 }&{} \cdots &{} {{{\varvec{e}}}_n \times {{\varvec{\delta }} }_n }&{} {{\varvec{d}}_1 \times {{\varvec{f}}}_1 }&{} \cdots &{} {{\varvec{d}}_m \times {{\varvec{f}}}_m }&{} {{\varvec{\tau } }_1 }&{} \cdots &{} {{\varvec{\tau } }_q } \\ \end{array} }} \right] , \nonumber \\&\quad m+n+q>6 \end{aligned}$$

(3)

The constrained wrenches for the overconstrained PMs produce complicated deformations in their corresponding legs. Suppose that $F_{p1}, {\ldots },F_{pi},\ldots ,F_{pm}$ produce $s_{1},\ldots , s_{i},\ldots ,s_{m} (s_{i}>$0) deformations, and $T_{p1},\ldots ,T_{pi},\ldots ,T_{pq }$ produce $u_{1},\ldots ,u_{i},\ldots ,u_{q}$ ($u_{1},\ldots ,u_{q}>0)$ deformations respectively. Where $s_{i}(i= 1,\ldots ,m)$ denotes the number of deformations produced by $F_{pi}$, $u_{i}(i= 1,\ldots ,q)$ denotes the number of deformations produced by $T_{pi}$.

Let $F_{p_i ,1} ,\ldots ,F_{p_i ,s_i }$ be the components of $F_{pi}$ corresponding to $s_{i}$ deformations. Let $T_{p_i ,1} ,\ldots ,T_{p_i ,u_i }$ be the components of $T_{pi}$ corresponding to $u_{i}$ deformations.

The relation of $F_{pi}(i=1,\ldots ,m)$ and their components $F_{p_i ,1} ,\ldots ,F_{p_i ,s_i }$can be expressed as follows

$$\begin{aligned} {\begin{array}{ccc} {F_{p_1 ,1} =b_{1,1} F_{p_1 } }&{} \cdots &{} {F_{p_1 ,s_1 } =b_{1,s_1 } F_{p_1 } } \\ &{} \vdots &{} \\ {F_{p_m ,1} =b_{m,1} F_{p_m } }&{} \cdots &{} {F_{p_m ,s_m } =b_{m,s_m } F_{p_m } } \\ \end{array} } \end{aligned}$$

(4a)

where $b_{i,j} (i=1,\ldots m; j=1,\ldots , s_{i})$ denotes the coefficient between $F_{pi}$ and $F_{pi, j}$.

The relation of $T_{pi}(i=1,\ldots ,q)$ and their components $T_{p_i ,1} ,\ldots ,T_{p_i ,u_i }$can be expressed as follows

$$\begin{aligned} {\begin{array}{cccc} {T_{p_1 ,1} =c_{1,1} T_{p_1 } }&{} \cdots &{} {T_{p_1 ,s_1 } =c_{1,u_1 } T_{p_1 } } \\ &{} \vdots &{} \\ {T_{p_q ,1} =c_{q,1} T_{p_q } }&{} \cdots &{} {T_{p_q ,s_q } =c_{q,u_q } T_{p_q } } \\ \end{array} } \end{aligned}$$

(4b)

where $c_{i,j} (i=1,\ldots ,q; j=1,\ldots , u_{i})$ denotes the coefficient between $T_{pi}$ and $T_{pi, j}$.

From Eqs. (4a) and (4b), it leads to

$$\begin{aligned} {\varvec{F}}_w= & {} \mathbf{W}\left[ {\begin{array}{c} {{\varvec{F}}_r} \\ {{\varvec{F}}_{p}} \\ {\varvec{T}}_{p}\\ \end{array}} \right] , \mathbf{W}=\left[ {{\begin{array}{ccc} {\mathbf{E}_{n\times n} }&{} {\mathbf{0}_{n\times m} }&{} {\mathbf{0}_{n\times q} } \\ {\mathbf{0}_{s_1 \times n} }&{} {\mathbf{W}_{f_1 } }&{} {\mathbf{0}_{s_1 \times q} } \\ \vdots &{} \vdots &{} \vdots \\ {\mathbf{0}_{s_m \times n} }&{} {\mathbf{W}_{f_m } }&{} {\mathbf{0}_{s_m \times q} } \\ {\mathbf{0}_{u_1 \times n} }&{} {\mathbf{0}_{u_1 \times m} }&{} {\mathbf{W}_{t_1 } } \\ \vdots &{} \vdots &{} \vdots \\ {\mathbf{0}_{u_q \times n} }&{} {\mathbf{0}_{u_q \times m} }&{} {\mathbf{W}_{t_q } } \\ \end{array} }} \right] , \nonumber \\ {\varvec{F}}_w= & {} \left[ {F_{r_1 } } \ldots {F_{r_n } } {F_{p_1 ,1} } \ldots {F_{p_1 ,s_1 } } \ldots {F_{p_m ,1} } \ldots {F_{p_m ,s_m } } \right. \nonumber \\&\left. \quad {T_{p_1 ,1} } \ldots {T_{p_1 ,u_1 } } \ldots {T_{p_q ,1} } \ldots {T_{p_q ,u_q } } \right] ^{\mathrm{T}} \end{aligned}$$

(4c)

where

$$\begin{aligned} \mathbf{W}_{f_1 }= & {} \left[ {{\begin{array}{cccc} {b_{1,1} }&{} 0&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {b_{1, s_1 } }&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] _{s_1 \times m} ,\ldots ,\\ \mathbf{W}_{f_i }= & {} \left[ {{\begin{array}{cccccc} 0&{} \cdots &{} {b_{i,1} }&{} 0&{} \cdots &{} 0 \\ \vdots &{} &{} \vdots &{} &{} &{} \\ 0&{} \cdots &{} {b_{i,s_i } }&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] _{s_i \times m} ,\ldots ,\\ \mathbf{W}_{{f_m } }= & {} \left[ {{\begin{array}{cccc} 0&{} 0&{} \cdots &{} {b_{m,1} } \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{} 0&{} \cdots &{} {b_{m,s_m } } \\ \end{array} }} \right] _{s_m \times m}\\ \mathbf{W}_{t_1 }= & {} \left[ {{\begin{array}{cccc} {c_{1,1} }&{} 0&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {c_{1,u_1 } }&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] _{u_1 \times q} ,\ldots ,\\ \mathbf{W}_{t_i }= & {} \left[ {{\begin{array}{cccccc} 0&{} \cdots &{} {c_{i,1} }&{} 0&{} \cdots &{} 0 \\ \vdots &{} &{} \vdots &{} &{} &{} \\ 0&{} \cdots &{} {c_{i,u_i } }&{} 0&{} \cdots &{} 0 \\ \end{array} }} \right] _{u_i \times q} ,\ldots ,\\ \mathbf{W}_{t_q }= & {} \left[ {{\begin{array}{cccc} 0&{} 0&{} \cdots &{} {c_{q,1} } \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{} 0&{} \cdots &{} {c_{q,u_q } } \\ \end{array} }} \right] _{u_q \times q} \end{aligned}$$

Here, ${{\varvec{F}}}_{w}$ is a ($n+s_{1}+\cdots +s_{m}+u_{1}+\cdots +u_{q})\times 1$ form vector, W is a ($n+s_{1}+\cdots +s_{m}+u_{1}+\cdots +u_{q})\times (m+n+q)$ form matrix, $\mathbf{E}_{n\times n}$ is an $n\times n$ form unit matrix. $\mathbf{W}_{fi}$ denotes the ith $s_{i}\times m$ form matrix with its ith column components being $b_{i,1},\ldots , b_{i, si}$ in sequence and the other components being 0. $\mathbf{W}_{ti}$ denotes the ith $u_{i}\times q$ form matrix with its ith column components being $c_{i,1},\ldots , c_{i,uq}$ in sequence and the other components being 0.

The active wrenches $F_{ri}(i=1,\ldots , n)$ produce longitudinal deformations, and it leads to

$$\begin{aligned} {\begin{array}{ccc} {F_{r_1 } =k_{r_1 } {{\delta }}d_{r_1 } }&{} \cdots &{} {F_{r_n } =k_{r_n } {{\delta }}d_{r_n } } \\ \end{array} } \end{aligned}$$

(5)

where $k_{ri}(i=1,\ldots , n)$ denotes the coefficient between $F_{ri}$ and ${{\delta }}d_{ri}$.

Let ${{\delta }}d_{p_i ,1} ,\ldots ,{{\delta }}d_{p_i ,s_i } (i=1,\ldots ,m)$ be the deformations produced by $F_{p_i ,1} ,\ldots ,F_{p_i ,s_i }$, respectively. Let ${{\delta }}d_{t_i ,1} ,\ldots ,{{\delta }}d_{t_i ,u_i } (i=1,\ldots ,q)$ be the deformations produced by $T_{p_i ,1} ,\ldots ,T_{p_i ,u_i }$, respectively.

Based on the theory of mechanics of material, the following equations can be obtained

$$\begin{aligned} {\begin{array}{ccc} {F_{p_1 ,1} =k_{f_1 ,1} {{\delta }} d_{f_1 ,1} }&{} \cdots &{} {F_{p_{1,s_1 } } =k_{f_1 ,s_1 } {{\delta }}d_{f_1 ,s_1 } } \\ &{} \vdots &{} \\ {F_{p_m ,1} =k_{f_m ,1} {{\delta }}d_{f_m ,1} }&{} \cdots &{} {F_{p_{m,} s_m } =k_{f_{m,} s_m } {{\delta }}d_{f_{m,} s_m } } \\ \end{array} } \end{aligned}$$

(6a)

where $k_{fi,j} (j=1,\ldots , s_{i})$ denotes the coefficient between ${{\delta }}d_{fi,j}$ and $F_{pi, j}$.

$$\begin{aligned} {\begin{array}{cccc} {T_{p_1 ,1} =k_{t_1 ,1} {{\delta }}d_{t_1 ,1} }&{} \cdots &{} {T_{p_1 ,u_1 } =k_{t_1 ,u_1 } {{\delta }}d_{t_1 ,u_1 } } \\ &{} \vdots &{} \\ {T_{p_q ,1} =k_{t_q ,1} {{\delta }}d_{t_q ,1} }&{} \cdots &{} {T_{p_q ,u_q } =k_{t_q ,u_q } {{\delta }}d_{t_q ,u_q } } \\ \end{array} } \end{aligned}$$

(6b)

where $k_{ti,j} (j=1,\ldots , u_{i})$ denotes the coefficient between ${{\delta }}d_{ti, j}$ and $T_{pi, j}$.

From Eqs. (5), (6a) and (6b), it leads to

$$\begin{aligned} {\varvec{F}}_w= & {} \mathbf{K}_w {{\delta }}{\varvec{d}}_r ,\nonumber \\ \mathbf{K}_w= & {} \hbox {diag}\left[ {k_{r_1 } } \ldots {k_{r_n } } {k_{f_1 ,1} } \ldots {k_{f_1 ,s_1 } } \ldots {k_{f_m ,1} } \ldots \right. \nonumber \\&\left. {k_{f_m ,s_m } } {k_{t_1 ,1} } \ldots {k_{t_1 ,u_1 } } \ldots {k_{t_q ,1} } \ldots {k_{t_q ,u_q }} \right] , \nonumber \\ {{\delta }}{\varvec{d}}_r= & {} \left[ {d_{r_1 } } \ldots {d_{r_n } } {d_{f_1 ,1} } \ldots {d_{f_1 ,s_1 } } \ldots {d_{f_m ,1} } \ldots \right. \nonumber \\&\left. {d_{f_m ,s_m } } {d_{t_1 ,1} } \ldots {d_{t_1 ,u_1 } } \ldots {d_{t_q ,1} } \ldots {d_{t_q ,u_q } } \right] ^{T} \end{aligned}$$

(6c)

where $\mathbf{K}_{\mathrm{w}}$ is a ($n+s_{1}+\cdots +s_{m}+u_{1}+,\cdots +u_{q})\times (n+s_{1}+,\cdots +s_{m}+u_{1}+,\cdots +u_{q})$ form matrix.

Let ${{\delta }}{{\varvec{p}}}=[{{\delta }}x \;\; {{\delta }}y \;\;{{\delta }}z]^{\mathrm{T}}$ and ${{\delta }}{\varvec{\varPhi }}=[{{\delta }}\varPhi _{{\varvec{x}}} \;\; {{\delta }}\varPhi _{{\varvec{y}}} \;\; {{\delta }}\varPhi _{{\varvec{z}}}]^{\mathrm{T}}$ be the linear and angle deformations of moving platform. For the overconstrained PMs, the applied wrench and the deformation of the moving platform can be expressed as:

$$\begin{aligned} \left[ {{\begin{array}{c} {{\varvec{F}}_o } \\ {{\varvec{T}}_o } \\ \end{array} }} \right] =\mathbf{K}_{6\times 6} \left[ {{\begin{array}{c} {{{\delta }} {{\varvec{p}}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] \end{aligned}$$

(7)

Here, $\mathbf{K}_{6\times 6}$ is the stiffness matrix of the overconstrained PMs.

Based on the principle of virtue work, it leads to

$$\begin{aligned} {\varvec{F}}_w^{\mathrm{T}} {{\delta }}{\varvec{d}}_r =\left[ {{\begin{array}{cc} {{\varvec{F}}_o^T }&{} {{\varvec{T}}_o^T } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {{{\delta }}{\varvec{p}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] \end{aligned}$$

(8)

From Eqs. (3), (4c) and (8), it leads to

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {{\varvec{F}}_r^T }&{} {{\varvec{F}}_p^T }&{} {{\varvec{T}}_p^T } \\ \end{array} }} \right] \mathbf{W}^{\mathrm{T}} {{\delta }}{\varvec{d}}_r\nonumber \\&\quad =\left[ {{\begin{array}{ccc} {{\varvec{F}}_r^T }&{} {{\varvec{F}}_p^T }&{} {{\varvec{T}}_p^T } \\ \end{array} }} \right] \mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}} \left[ {{\begin{array}{ccc} {{{\delta }}{{\varvec{p}}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(9)

From Eq. (9), it leads to

$$\begin{aligned} \mathbf{W}^{\mathrm{T}} {{\delta }} {\varvec{d}}_r =\mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}} \left[ {{\begin{array}{c} {{{\delta }}{\varvec{p}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] \end{aligned}$$

(10)

From Eqs. (4c), (6c) and (10), it leads to

$$\begin{aligned} \mathbf{W}^{\mathrm{T}} \mathbf{C}_w {\varvec{F}}_w= & {} \mathbf{W}^{\mathrm{T}} \mathbf{C}_w \mathbf{W}\left[ {\begin{array}{c} {\begin{array}{c} {{\varvec{F}}_r } \\ {{\varvec{F}}_p } \\ \end{array} } \\ {\varvec{T}}_p\\ \end{array}} \right] \nonumber \\= & {} \mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}} \left[ {{\begin{array}{c} {{{\delta }}{\varvec{p}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] , \quad \mathbf{C}_w =\mathbf{K}_w^{-1} \end{aligned}$$

(11)

From Eq. (11), it leads to

$$\begin{aligned} \left[ {\begin{array}{c} {\begin{array}{c} {{\varvec{F}}_r } \\ {{\varvec{F}}_p } \\ \end{array} } \\ {\varvec{T}}_p \\ \end{array}} \right] =\left( {\mathbf{W}^{\mathrm{T}} \mathbf{C}_w \mathbf{W}} \right) ^{\mathrm{-}1}{} \mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}} \left[ {{\begin{array}{c} {{{\delta }}{\varvec{p}}} \\ {{{\delta }}{\varvec{\varPhi } }} \\ \end{array} }} \right] \end{aligned}$$

(12)

Multiplying both sides of Eq. (12) by $\mathbf{G}_{6\times (m+n+q)}$ and combining with Eq. (3), it leads to

$$\begin{aligned} \mathbf{K}_{6\times 6} =\mathbf{G}_{6\times (m+n+q)}\left( {\mathbf{W}^{\mathrm{T}} \mathbf{C}_w \mathbf{W}} \right) ^{\mathrm{-}1}{} \mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}}\nonumber \\ \end{aligned}$$

(13)

Multiplying both sides of Eq. (12) by W and combining with Eqs. (4c) and (7), it leads to

$$\begin{aligned} {\varvec{F}}_w =\mathbf{W}\left( {\mathbf{W}^{\mathrm{T}} \mathbf{C}_w \mathbf{W}} \right) ^{\mathrm{-}1}{} \mathbf{G}_{6\times (m+n+q)}^{\mathrm{T}} \mathbf{C}_{6\times 6}\left[ {{\begin{array}{c} {{\varvec{F}}_o } \\ {{\varvec{T}}_o } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(14)

From Eq. (14), the statics for the overconstrained PMs can be completely solved.

Fig. 1

Sketch of 2-RPU $+$ UPR PM

3 Kinetostatic analysis of the 2-RPU $+$ UPR PM

3.1 Description and constraint analysis of the 2-RPU $+$ UPR PM

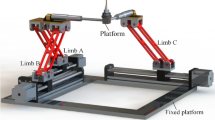
In this section, a novel 2-UPR+UPR PM is presented to illustrate the approach for solving the kinetostatic of overconstrained PMs. The schematic diagram of the 2-RPU $+$ UPR PM is shown in Fig. 1. This manipulator consists of a base B, a moving platform m, two identical RPU-type active legs $r_{i} (i=1, 3)$, and one UPR-type active leg $r_{2}$. Here, B is a regular triangle with O as its center and $A_{i} (i=1, 2, 3)$ as its three vertices. m is a regular triangle with o as its center and $a_{i} (i=1, 2, 3)$ as its three vertices. Each RPU leg connects B to m by a revolute (R) joint followed by a prismatic (P) joint and a universal (U) joint in sequence, where the P joint is driven by a lead screw linear actuator and U joint is composed of two crossed R joints. The UPR leg connects B to the m by a U joint followed by a P joint and an R joint in sequence.

As depicted in Fig. 1, we assign a fixed frame O-XYZ at the centered point O of B, and a moving frame o-xyz on the moving platform at the centered point o of m. Let $\bot$ be a perpendicular constraint, $\Vert$ be a parallel constraint and ${\vert }$ be a collinear constraint. Some conditions ($x\Vert a_{1}a_{3}$, $y\bot a_{1}a_{3}$, $z\bot m$, $X\Vert A_{1}A_{3}$, $Y\bot A_{1}A_{3}$, $\hbox {Z}\bot B)$ are satisfied for the coordinate axes. Let $R_{ij}\,(i=1, 2, 3; j=1, 2, \ldots )$ denotes jth R joint in the ith leg $r_{i}$.

Some geometrical constraints are satisfied for the 2-RPU $+$ UPR PM as follows (see Fig. 1):

$$\begin{aligned}&R_{i1}\bot A_{1}A_{3} , R_{i2}\bot r_{i} , R_{i1}\Vert R_{i2} , R_{i2}\bot R_{i3},\nonumber \\&\quad R_{i3} | a_{1}a_{3} ( i =1,3),R_{21} | A_{2}O , R_{21}\bot R_{22},\nonumber \\&\quad R_{22}\bot r_{2} , R_{22}\Vert R_{23}\Vert a_{1}a_{3} \end{aligned}$$

(15)

Based on the rules (a) and (b) for determining constrained wrenches, for the ith RPU-type leg, one constrained torque $T_{pi}(i=1, 3)$ which is perpendicular to $R_{i1}$, $R_{i2}$ and $R_{i3 }$ and one constrained force $F_{pi}$ which is parallel with $R_{i1}$ and passes through the center of U joint can be determined. In addition, for the UPR-type leg, one constrained torque$T_{p2}$ which is perpendicular to $R_{i1}$, $R_{i2}$ and $R_{i3 }$ and one constrained force $F_{p2}$ which is parallel with $R_{23}$ and passes through the center of U joint can be determined (see Fig. 1). The unit vectors ${\varvec{\tau }}_{i}$ of $T_{pi} (i=1,2, 3)$ and the unit vectors ${{\varvec{f}}}_{ i} (i=1,2, 3)$ of $F_{pi}$ can be determined as follows:

$$\begin{aligned} {\varvec{\tau } }_i= & {} {{\varvec{R}}}_{i2} \times {{\varvec{R}}}_{i3} (i=1, 3),\nonumber \\ {\varvec{\tau } }_2= & {} {{\varvec{R}}}_{i1} \times {{\varvec{R}}}_{i2} , {{\varvec{f}}}_i ={{\varvec{R}}}_{i1}\nonumber \\= & {} {{\varvec{Y}}}\,(i=1, 3), {{\varvec{f}}}_2 ={{\varvec{R}}}_{23} ={{\varvec{x}}} \end{aligned}$$

(16a)

Here, ${{\varvec{R}}}_{ij}$ denotes the vector of $R_{ij}$. From Eqs. (15) and (16a), it leads to

$$\begin{aligned}&T_{p1}\Vert T_{p2}\Vert T_{p3}, F_{p1}\Vert F_{p3}, F_{p1}\bot F_{p2},\nonumber \\&\quad T_{pi}\bot F_{pi}\,\,(i=1, 2, 3) \end{aligned}$$

(16b)

The constrained wrenches in each leg have the property that they do no work to each joint and thus they do no work to m. From this concept, it leads to:

$$\begin{aligned} {{\varvec{0}}}_{6\times 1}= & {} \mathbf{J}_v \left[ {{\begin{array}{c} {{\varvec{v}}} \\ {\varvec{\omega }} \\ \end{array} }} \right] , \mathbf{J}_v =\left[ {{\begin{array}{c@{\quad }c} {{{\varvec{f}}}_1^T }&{} {({{\varvec{d}}}_1 \times {{\varvec{f}}}_1 )^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{12} \times {{\varvec{R}}}_{13} )^{T}} \\ {{{\varvec{f}}}_2^T }&{} {({{\varvec{d}}}_2 \times {{\varvec{f}}}_2 )^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{21} \times {{\varvec{R}}}_{22} )^{T}} \\ {{{\varvec{f}}}_3^T }&{} {({{\varvec{d}}}_3 \times {{\varvec{f}}}_3 )^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{32} \times {{\varvec{R}}}_{33} )^{T}} \\ \end{array} }} \right] ,\nonumber \\ {{\varvec{d}}}_i= & {} {{{\varvec{a}}}}_i -{{{\varvec{o}}}}, {{\varvec{d}}}_2={{\varvec{A}}}_2 -{{{\varvec{o}}}} \end{aligned}$$

(17)

Equation (17) denotes the velocity constraint equation, and $\mathbf{J}_{v}$ denotes the constraint Jacobian for the 2-RPU $+$ UPR PM.

Let $\mathbf{J}_{v,i}(i=1, \ldots ,6)$ be the ith row of matrix $\mathbf{J}_{v}$. From Eqs. (15), (16a), (16b) and (17), it leads to

$$\begin{aligned} \mathbf{J}_{v,2}=\mathbf{J}_{v,4}=\mathbf{J}_{v,6}, (\mathbf{J}_{v,5}-\mathbf{J}_{v,2})/a_{1}a_{3} =\mathbf{J}_{v0,2} \end{aligned}$$

(18)

From Eq. (18), it known that $\mathbf{J}_{v,1}$, $\mathbf{J}_{v,2}$, $\mathbf{J}_{v,3}$, $\mathbf{J}_{v,4}$, $\mathbf{J}_{v,5}$ and $\mathbf{J}_{v,6}$ are linear dependent and the number of independent items is 3. Thus, there are 3 overconstraints in the 2-RPU $+$ UPR PM.

In the 2-RPU $+$ UPR PM, there are 1 base B, 1 moving platform m, 3 cylinders, and 3 piston-rods and thus the number of links is $n=8$. There are 3 prismatic joints, 3 revolute joints, 3 universal joints in this PM, and thus the number of joints is $g=9$. The DOF of this manipulator is calculated as below [3, 4]

$$\begin{aligned} M=6(n-g-1)+\sum _{i=1}^g {k_i } +\rho -\eta =3 \end{aligned}$$

(19)

here, $k_{1} = 1$ is the DOF of revolute joint, $k_{2} = 1$ is the DOF of prismatic joint, $k_{3} = 2$ is the DOF of universal joint. The number of overconstraints is $\rho =3$, and the number of redundancy DOF is $\eta =0$.

Since the constrained wrenches do no work to m, the translation of m must be perpendicular to three constrained forces. Thus, it is easy to determine that this PM has only one translation, which is perpendicular to $R_{11}(F_{p1})$, $R_{23}(F_{p2})$, and $R_{31}(F_{p3})$, the remained two independent motions are two rotations. From the properties of constrained wrenches, it is known that the first rotational axis must be located on the plane determined by $F_{p1}$ and $F_{p3}$, and parallel with $F_{p2}$, the second rotational axis must passes through $F_{p2 }$ and parallel with $F_{pi}\,\,(i=1,3)$.

3.2 Inverse kinematics of the 2-RPU $+$ UPR PM

The unit vectors ${{\varvec{R}}}_{ik}$ of $R_{ik }(i=1,2,3; k=1,2,3)$ for the 2-RPU $+$ UPR PM in $\{B\}$ can be expressed as

$$\begin{aligned} {{\varvec{R}}}_{11}= & {} {{\varvec{R}}}_{{3}1} ={{\varvec{R}}}_{12} ={{\varvec{R}}}_{{3}2} ={{\varvec{R}}}_{21} =\left[ {{\begin{array}{ccc} 0&{} 1&{} 0 \\ \end{array} }} \right] ^{\mathrm{T}},\nonumber \\ {{\varvec{R}}}_{13}= & {} {{\varvec{R}}}_{{3}3} ={{{\varvec{x}}}}, {{\varvec{R}}}_{{2}2} ={{\varvec{R}}}_{{2}3} ={{{\varvec{x}}}} \end{aligned}$$

(20a)

From Eqs. (15) and (20a), we obtain

$$\begin{aligned}&{{\varvec{R}}}_{12} \cdot {{\varvec{R}}}_{13} =0, {{\varvec{R}}}_{32} \cdot {{\varvec{R}}}_{33} =0,\nonumber \\&{{{\varvec{a}}}}_1 {{{\varvec{A}}}}_1 \cdot {{\varvec{R}}}_{11} =0, {{{\varvec{a}}}}_3 {{{\varvec{A}}}}_3 \cdot {{\varvec{R}}}_{31} =0, {{\varvec{R}}}_{21} \cdot {{\varvec{R}}}_{22} =0\nonumber \\ \end{aligned}$$

(20b)

The position vectors of $A_{i} (i=1, 2, 3)$ in $\{B\}$ can be expressed in matrix form as

$$\begin{aligned} {{\varvec{A}}}_1= & {} \frac{1}{2}\left[ {{\begin{array}{c} {qE} \\ {-E} \\ 0 \\ \end{array} }} \right] ,\quad {{\varvec{A}}}_2 =\left[ {{\begin{array}{c} 0 \\ E \\ 0 \\ \end{array} }} \right] ,\nonumber \\ {{\varvec{A}}}_{3}= & {} \frac{1}{2}\left[ {{\begin{array}{c} {-qE} \\ {-E} \\ 0 \\ \end{array} }} \right] , \quad q=3^{1/2} \end{aligned}$$

(21a)

The position vectors of $a_{i} (i=1, 2, 3)$ in $\{m\}$ can be expressed in matrix form as

$$\begin{aligned} { }^m{{{\varvec{a}}}}_1= & {} \frac{1}{2}\left[ {{\begin{array}{c} {qe} \\ {-e} \\ 0 \\ \end{array} }} \right] , \quad { }^m{{{\varvec{a}}}}_2 =\left[ {{\begin{array}{c} 0 \\ e \\ 0 \\ \end{array} }} \right] ,\nonumber \\ { }^m{{{\varvec{a}}}}_3= & {} \frac{1}{2}\left[ {{\begin{array}{c} {-qe} \\ {-e} \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(21b)

here, E is the distance from point O to $A_{i}$, e is the distance from point o to $a_{i}$.

The position vectors of $a_{i} (i=1, 2, 3)$ in $\{B\}$ can be expressed as

$$\begin{aligned} {{\varvec{a}}}_i= & {} \left[ {{\begin{array}{c} {X_{ai} } \\ {Y_{ai} } \\ {Z_{ai} } \\ \end{array} }} \right] ={ }_m^B \mathbf{R}^{m}{{\varvec{a}}}_i +{{\varvec{o}}},\quad { }_m^B \mathbf{R}=\left[ {{\begin{array}{ccc} {x_{_l} }&{} {y_{_l} }&{} {z_{_l} } \\ {x_m }&{} {y_m }&{} {z_m } \\ {x_n }&{} {y_n }&{} {z_n } \\ \end{array} }} \right] ,\nonumber \\ {{\varvec{o}}}= & {} \left[ {{\begin{array}{c} {X_o } \\ {Y_o } \\ {Z_o } \\ \end{array} }} \right] \end{aligned}$$

(21c)

From Eqs. (20a) to (21c), we obtain

$$\begin{aligned}&aex_m /2-ey_m /2+Y_o +E/2=0 \end{aligned}$$

(22a)

$$\begin{aligned}&-aex_m /2-ey_m /2+Y_o +E/2=0 \end{aligned}$$

(22b)

$$\begin{aligned}&(ey_l +X_o )x_l +(ey_m +Y_o -E)x_m\nonumber \\&+(ey_n +Z_o )x_n =0 \end{aligned}$$

(22c)

From Eqs. (22a), (22b) and (22c), we obtain

$$\begin{aligned} x_m =0, \quad X_o =Z_o z_l /z_n , Y_o =(ey_m -E)/2 \end{aligned}$$

(23)

Let the rotational transformation matrix $_m^B \mathbf{R}$ be formed by YZX-type Euler rotations and $\alpha$, $\beta$, and $\lambda$ be three Euler angles about corresponding axes, we obtain

$$\begin{aligned} _m^B \mathbf{R}=\left[ {{\begin{array}{ccc} {c_\alpha c_\beta }&{} {-c_\alpha s_\beta c_\lambda +s_\alpha s_\lambda }&{} {c_\alpha s_\beta s_\lambda +s_\alpha c_\lambda } \\ {s_\beta }&{} {c_\beta c_\lambda }&{} {-c_\beta s_\lambda } \\ {-s_\alpha c_\beta }&{} {s_\alpha s_\beta c_\lambda +c_\alpha s_\lambda }&{} {-s_\alpha s_\beta s_\lambda +c_\alpha c_\lambda } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(24)

here, $s_\phi =\sin \phi , c_\phi =\cos \phi ,\phi$ is one of ($\alpha$, $\beta$, $\lambda$).

From Eqs. (23) and (24), we obtain

$$\begin{aligned} \beta =0 \end{aligned}$$

(25)

From Eqs. (24) and (25), we obtain

$$\begin{aligned} _m^B \mathbf{R}=\left[ {{\begin{array}{ccc} {c_\alpha }&{}\quad {s_\alpha s_\lambda }&{} \quad {s_\alpha c_\lambda } \\ 0&{}\quad {c_\lambda }&{}\quad {-s_\lambda } \\ {-s_\alpha }&{}\quad {c_\alpha s_\lambda }&{} \quad {c_\alpha c_\lambda } \\ \end{array} }} \right] \end{aligned}$$

(26)

From Eqs. (23) and (26), we obtain

$$\begin{aligned} X_o =Z_o \hbox {tg}_\alpha , \quad Y_o =(ec_\lambda -E)/2 \end{aligned}$$

(27)

Equations (26) and (27) are the pose decoupling equations for the 2-RPU $+$ UPR PM. From Eqs. (26) and (27), the position and orientation of this PM can be expressed by $\alpha$, $\lambda$ and $Z_{o}$.

From Eqs. (21), (21b), (21c), (26), and (27), the inverse kinematics can be expressed as follows:

$$\begin{aligned} r_1 ^{2}= & {} Z_0 ^{2}(1+tg_\alpha ^{2})+E^{2}+e^{2}-(E-ec_\lambda )^{2}/4\nonumber \\&-\,Z_0 tg_\alpha (qE+es_\lambda /s_\alpha )\nonumber \\&+\,eE(qs_\alpha s_\lambda -3c_\alpha -c_\lambda )/2 \end{aligned}$$

(28a)

$$\begin{aligned} r_2 ^{2}= & {} Z_0 ^{2}(1+tg_\alpha ^{2})+E^{2}+e^{2}+5(E-ec_\lambda )^{2}/4\nonumber \\&+\,2eZ_0 s_\lambda /c_\alpha -2eEc_\lambda \end{aligned}$$

(28b)

$$\begin{aligned} r_3 ^{2}= & {} Z_0 ^{2}(1+tg_\alpha ^{2})+E^{2}+e^{2}-(E-ec_\lambda )^{2}/4\nonumber \\&+\,Z_0 tg_\alpha (qE-es_\lambda /s_\alpha )-eE(qs_\alpha s_\lambda \nonumber \\&+\,3c_\alpha +c_\lambda )/2 \end{aligned}$$

(28c)

3.3 Kinetostatic analysis of 2-RPU $+$ UPR PM

Based on Eqs. (1b), (26) and (27), it leads to

$$\begin{aligned} \left[ {{\begin{array}{c} {{\varvec{v}}} \\ {\varvec{\omega } } \\ \end{array} }} \right]= & {} \mathbf{J}_o {\dot{\varvec{\theta }}}, \mathbf{J}_o =\left[ {{\begin{array}{ccc} {Z_o \hbox {(sec}_\alpha )^2 }&{} 0&{} {\hbox {tan}_\alpha } \\ 0&{} {-es_\lambda /2}&{} 0 \\ 0&{} 0&{} 1 \\ 0&{} {c_\alpha }&{} 0 \\ 1&{} 0&{} 0 \\ 0&{} {-s_\alpha }&{} 0 \\ \end{array} }} \right] ,\nonumber \\ {\dot{\varvec{\theta }}}= & {} \left[ {{\begin{array}{c} {\dot{\alpha }} \\ {\dot{\lambda }} \\ {\dot{Z}_{\mathrm{o}} } \\ \end{array} }} \right] \end{aligned}$$

(29a)

From Eqs. (1c) and (29a), the actuator forces of the 2-UPR $+$ UPR PM can be expressed as

$$\begin{aligned}&{\varvec{F}}_r=-\mathbf{J}_o (\mathbf{J}_\alpha \mathbf{J}_o )^{-1}\left[ {{\begin{array}{c} {\varvec{F}}_{\mathrm{o}} \\ {{\varvec{T}}_o } \\ \end{array} }} \right] , {\varvec{F}}_r=\left[ {{\begin{array}{c} {F_{r_1 } } \\ {F_{r_2 } } \\ {F_{r_3 } } \\ \end{array} }} \right] , \nonumber \\&\quad \mathbf{J}_\alpha =\left[ {{\begin{array}{ccc} {{{\varvec{\delta }} }_1^{\mathrm{T}} }&{} {({{\varvec{e}}}_1 \times {{\varvec{\delta }} }_1 )^{\mathrm{T}}} \\ {{{\varvec{\delta }} }_2^{\mathrm{T}} }&{} {({{\varvec{e}}}_2 \times {{\varvec{\delta }} }_2 )^{\mathrm{T}}} \\ {{{\varvec{\delta }} }_3^{\mathrm{T}} }&{} {({{\varvec{e}}}_3 \times {{\varvec{\delta }} }_3 )^{\mathrm{T}}} \\ \end{array} }} \right] \end{aligned}$$

(29b)

Equation (29b) can only solve the actuator forces of the 2-UPR+UPR PM.

From Eqs. (3) and (17), it leads to

$$\begin{aligned} \left[ {{\begin{array}{c} {{\varvec{F}}_o } \\ {{\varvec{T}}_o } \\ \end{array} }} \right]= & {} \mathbf{G}_{6\times 9}{\varvec{F}}_ r , \left[ {{\begin{array}{c} {{\varvec{F}}_r } \\ {{\varvec{F}}_p } \\ {{\varvec{T}}_p } \\ \end{array} }} \right] , {\varvec{F}}_r =\left[ {{\begin{array}{c} {F_{r_1 } } \\ {F_{r_2 } } \\ {F_{r_3 } } \\ \end{array} }} \right] ,\nonumber \\ {\varvec{F}}_p= & {} \left[ {{\begin{array}{c} {F_{p_1 } } \\ {F_{p_2 } } \\ {F_{p_3 } } \\ \end{array} }} \right] , {\varvec{T}}_p =\left[ {\begin{array}{c} {\begin{array}{c} {T_{p_1 } } \\ {T_{p_2 } } \\ \end{array} } \\ T_{p_3 } \\ \end{array}} \right] , \nonumber \\ \mathbf{G}_{6\times 9}^{\mathrm{T}}= & {} \left[ {\begin{array}{cc} {\begin{array}{c@{\quad }c} {{{\varvec{\delta }} }_1^{\mathrm{T}} }&{} {({{\varvec{e}}}_1 \times {{\varvec{\delta }} }_1 )^{\mathrm{T}}} \\ {{{\varvec{\delta }} }_2^{\mathrm{T}} }&{} {({{\varvec{e}}}_2 \times {{\varvec{\delta }} }_2 )^{\mathrm{T}}} \\ {{{\varvec{\delta }} }_3^{\mathrm{T}} }&{} {({{\varvec{e}}}_3 \times {{\varvec{\delta }} }_3 )^{\mathrm{T}}} \\ {{{\varvec{f}}}_1^T }&{} {({{\varvec{d}}}_1\times {{\varvec{f}}}_1)^{T}} \\ {{{\varvec{f}}}_2^T }&{} {({{\varvec{d}}}_2\times {{\varvec{f}}}_2)^{T}} \\ {{{\varvec{f}}}_3^T }&{} {({{\varvec{d}}}_3\times {{\varvec{f}}}_3)^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{11} \times {{\varvec{R}}}_{13} )^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{21} \times {{\varvec{R}}}_{23} )^{T}} \\ {{{\varvec{0}}}_{3\times 1}^T }&{} {({{\varvec{R}}}_{31} \times {{\varvec{R}}}_{32} )^{T}} \\ \end{array} } \\ \end{array}} \right] \end{aligned}$$

(29c)

Each constrained force $F_{pi}(i=1,3)$ in the RPU-type leg only produce one deformation, and it leads to

$$\begin{aligned} s_i =1, F_{p_i ,1} =F_{p_i } , \quad b_{i,1} =1 \quad (i=1, 3) \end{aligned}$$

(30a)

For the UPR leg, the constrained forces $F_{p2}$ at U joint can be equivalent to one force $F_{p2,1 }$ at $a_{2}$, which is parallel with $F_{p2}$ and active in the opposite direction. Thus, it leads to

$$\begin{aligned} {{\varvec{F}}}_{p2,1 }={{\varvec{F}}}_{p2}, \quad F_{p2,1 }=-F_{p2}, \quad b_{2,1}=-1 \end{aligned}$$

(30b)

$F_{p2}$ produces only one flexibility deformation. Thus, $s_{2}=1$.

The constrained torque $T_{pi}(i=1,2,3)$ in the ith leg can be decomposed into two elements $T_{pi, 1}$ which is along $r_{i}$, and $T_{pi, 2}$ which is perpendicular to $r_{i}$ (see Fig. 2a, b). Thus, $u_{i} = 2$.

Fig. 2

a The constrained torque situation of RPU leg, b the constrained torque situation of UPR leg

Let ${\varvec{\tau }}_{pi,1}$ and ${\varvec{\tau }}_{pi,2}$ be the unit vector of $T_{pi, 1}$ and $T_{pi,2}$, respectively. From the geometrical constraints in the RPU leg, it leads to

$$\begin{aligned} {\varvec{\tau } }_{p_i ,1} ={{\varvec{\delta }} }_i , {\varvec{\tau } }_{p_i ,2} \bot {{\varvec{\delta }} }_i , {\varvec{\tau } }_i \bot {{{\varvec{R}}}}_{i2} , {\varvec{\tau } }_{p_i ,1} \bot {{{\varvec{R}}}}_{i2} \end{aligned}$$

(31a)

$\varvec{\tau }_{i}$, $\varvec{\tau }_{pi,1 }$ and $\varvec{\tau }_{pi,2 }$ are in the same plane. The following geometrical constraints must be satisfied

$$\begin{aligned} {\varvec{\tau } }_{p_i ,2} \bot {{{\varvec{R}}}}_{i2} , {\varvec{\tau } }_{p_i ,2} ={{\varvec{\delta }} }_i \times {{{\varvec{R}}}}_{i2} \end{aligned}$$

(31b)

From Eq. (31a), $T_{pi,1}$ can be expressed as follows:

$$\begin{aligned} {\varvec{T}}_{p_i ,1} =T_{p_i ,1} {{\varvec{\delta }} }_i , \quad T_{p_i ,1} =c_{i,1} T_{p_i } , c_{i,1} ={\varvec{\tau } }_i \cdot {{\varvec{\delta }} }_i\nonumber \\ \end{aligned}$$

(32a)

From Eq. (31b), $T_{pi,2}$ can be expressed as follows

$$\begin{aligned} {\varvec{T}}_{p_i ,2}= & {} T_{p_i ,2} ({{\varvec{\delta }} }_i \times {{{\varvec{R}}}}_{i2} ), \quad T_{p_i ,2} =T_{p_i } {\varvec{\tau } }_i \cdot {\varvec{\tau } }_{p_i ,2}\nonumber \\= & {} c_{i,2} T_{p_i } , c_{i,2} ={\varvec{\tau } }_i \cdot ({{\varvec{\delta }} }_i \times {{{\varvec{R}}}}_{i2} ) \end{aligned}$$

(32b)

$F_{ri }(i=1, 2, 3)$ produces longitudinal deformation along $r_{i}$. Let ${{\delta }}d_{ri}$ be the longitudinal deformation along $r_{i}$, it leads to

$$\begin{aligned} F_{r_i } =k_{r_i } {{\delta }}d_{r_i } , \quad k_{r_i } =\frac{E_s S_i }{r_i }\quad (i=1, 2, 3) \end{aligned}$$

(33a)

here $E_{s}$ is the modular of elasticity and $S_{i}$ is the area of the ith leg.

$F_{pi,1} (i=1, 3)$ in each RPU leg produces flexibility deformation. Let ${{\delta }}d_{fi,1}$ be the flexibility deformation in the ith leg, and it leads to

$$\begin{aligned} F_{p_i,1}= & {} F_{p_i } =k_{f_i ,1} {{\delta }} d_{f_i ,1} ,\nonumber \\ k_{f_i ,1}= & {} \frac{3E_s I}{r_i^3 }\quad (i=1, 3) \end{aligned}$$

(33b)

where I is the moment inertia.

For the UPR-type leg, $F_{p2,1}$ produces one flexibility deformation ${{\delta }} d_{f2,1}$, thus we obtain

$$\begin{aligned} F_{p_2 ,1} =F_{p_2 } =k_{f_2 ,1} {{\delta }}d_{f_2 ,1}, \quad k_{f_2 ,1} =\frac{3E_s I}{r_2^3 } \end{aligned}$$

(34)

here, I is the moment inertia.

In each leg $r_{i}$, $T_{pi,1}$ and $T_{pi,2}$ produce torsional deformation and bending deformation, respectively. Let ${{\delta }} d_{ti,1}$ be the torsional deformation about $r_{i}$ due to $T_{pi,1}$, ${{\delta }}d_{ti,2}$ be the bending deformation about $r_{i}$ due to $T_{pi, 2}$.

The relation between $T_{pi,1}$ and ${{\delta }} d_{ti,1}$ in the ith leg can be expressed as follows:

$$\begin{aligned}&T_{p_i ,1} = k_{t_i ,1} {{\delta }}d_{t_i ,1} , k_{t_i ,1} =\frac{GI_p }{r_i },\nonumber \\&\quad {{\delta }}d_{t_i ,1}=\frac{r_i T_{p_i ,1} }{GI_p }\quad (i=1, 3) \end{aligned}$$

(35a)

The relation between $T_{pi, 2}$ and ${{\delta }}d_{ti,2}$ in the ith leg can be expressed as follows:

$$\begin{aligned}&T_{p_i ,2} =k_{t_i ,2} {{\delta }}d_{t_i ,2} , k_{t_i ,2} =\frac{E_s I}{r_i },\nonumber \\&\quad {{\delta }}d_{t_i ,2} =\frac{r_i T_{p_i ,2} }{E_s I}\quad (i=1,3) \end{aligned}$$

(35b)

here, G is the shear modulus and $I_{p}$ is the polar moment of inertia.

From Eqs. (30a) to (32b), it leads to

$$\begin{aligned}&{\varvec{F}}_w=\mathbf{W}_{12\times 9}\left[ {{\begin{array}{c} {{\varvec{F}}_a } \\ {{\varvec{F}}_p } \\ {{\varvec{T}}_p } \\ \end{array} }} \right] ,\nonumber \\&\mathbf{W}_{12\times 9}=\left[ {{\begin{array}{ccc} {\mathbf{E}_{3\times 3} }&{} {\mathbf{0}_{3\times 3} }&{} {\mathbf{0}_{3\times 3} } \\ {\mathbf{0}_{1\times 3} }&{} {\mathbf{W}_{f_1 } }&{} {\mathbf{0}_{1\times 3} } \\ {\mathbf{0}_{1\times 3} }&{} {\mathbf{W}_{f_2 } }&{} {\mathbf{0}_{1\times 3} } \\ {\mathbf{0}_{1\times 3} }&{} {\mathbf{W}_{f_3 } }&{} {\mathbf{0}_{1\times 3} } \\ {\mathbf{0}_{2\times 3} }&{} {\mathbf{0}_{2\times 3} }&{} {\mathbf{W}_{t_1 } } \\ {\mathbf{0}_{2\times 3} }&{} {\mathbf{0}_{2\times 3} }&{} {\mathbf{W}_{t_2 } } \\ {\mathbf{0}_{2\times 3} }&{} {\mathbf{0}_{2\times 3} }&{} {\mathbf{W}_{t_3 } } \\ \end{array} }} \right] , \nonumber \\&{\varvec{F}}_w =\left[ {F_{r_1 } } {F_{r_2 } } {F_{r_3 } } {F_{p_1 ,1} } {F_{p_2 ,1} } {F_{p_3 ,1} }\right. \nonumber \\&\qquad \qquad \left. {T_{p_1 ,1} } {T_{p_1 ,2} } {T_{p_2 ,1} } {T_{p_2 ,2} } {T_{p_3 ,1} } {T_{p_3 ,2} } \right] ^{\mathrm{T}}, \nonumber \\&{} \mathbf{W}_{f_{1} } =\left[ {{\begin{array}{ccc} 1&{} 0&{} 0 \\ \end{array} }} \right] , \mathbf{W}_{f_{2} } =\left[ {{\begin{array}{ccc} 0&{} {-1}&{} 0 \\ \end{array} }} \right] , \nonumber \\&{} \mathbf{W}_{f_{3} } =\left[ {{\begin{array}{ccc} 0&{} 0&{} 1 \\ \end{array} }} \right] , \nonumber \\&{} \mathbf{W}_{t_{1} } =\left[ {{\begin{array}{ccc} {c_{1,1} }&{} 0&{} 0 \\ {c_{1,2} }&{} 0&{} 0 \\ \end{array} }} \right] , \mathbf{W}_{t_{2} } =\left[ {{\begin{array}{ccc} 0&{} {c_{2,1} }&{} 0 \\ 0&{} {c_{2,2} }&{} 0 \\ \end{array} }} \right] , \nonumber \\&{} \mathbf{W}_{t_{3} } =\left[ {{\begin{array}{ccc} 0&{} 0&{} {c_{3,1} } \\ 0&{} 0&{} {c_{3,2} } \\ \end{array} }} \right] , \end{aligned}$$

(36)

From Eqs. (6c), (33a),(33b), (34), (35a) and (35b), it leads to

$$\begin{aligned} {\varvec{F}}_w= & {} \mathbf{K}_w {{\delta }} {\varvec{d}}_r , \nonumber \\ \mathbf{K}_w= & {} \hbox {diag}(k_{r_1 } ,k_{r_2 } ,k_{r_3 } ,k_{f_1 ,1} ,k_{f_2 ,1} ,k_{f_3 ,1} ,k_{t_1 ,1} ,k_{t_1 ,2} ,\nonumber \\&\qquad \qquad k_{t_2 ,1} ,k_{t_2 ,2} ,k_{t_3 ,1} ,k_{t_3 ,2} ) \end{aligned}$$

(37)

After $\mathbf{G}_{6\times 9}$, $\mathbf{W}_{12\times 9}$ and $\mathbf{K}_{w}$ for the 2-RPU $+$ UPR PM are derived from Eqs. (29c) and (33a) to Eq. (37). The kinetostatic of this PM can be solved from Eqs. (12), (13) and (14).

4 Unified CAD model for FE analysis

Apart from the analytical approach, based on the powerful geometric modeling capability and the simulation function of CAD software, a unified CAD solid model of PMs with linear legs can be generated to carry out a finite element (FE) analysis for kinetostatic analysis.

For the PMs with linear legs, there are various XPY(X and Y are selected from R, U and S joints) legs, establishing a unified 3D assembly manipulator and the corresponding FE model which is applicative for various PMs is a significant and work.

Without loss of generality, a CAD solid model with three linear legs is used to illustrate the unified FE model. In this model, a 3-SPS structure is selected as the original PM (see Fig. 3). This structure is composed of a moving platform, a base platform, three liner legs, and six equivalent spherical joints. To generate various PMs, S joint is designed as adjustable joints. In this structure, S joint is constructed by three lockable R joints (see Fig. 3). Let $R_{ij}$ ($i=1, 2, 3; j=1,2,\ldots ,6)$ denotes the jth R joint in the ith leg $r_{i}$. In each leg, $R_{i1}$ and $R_{i6}$ are perpendicularly connected with the base and the moving platform, respectively. $R_{i2}$ is perpendicular with $R_{i1}$ and $R_{i3}$. $R_{i5}$ is perpendicular with $R_{i4}$ and $R_{i6}$. $R_{i3}$ and $R_{i4}$ are perpendicular with the linear leg $r_{i}$. The linear leg $r_{i}(i=1, 2, 3)$ can be seen as the P joints.

In the CAD environment, by locking some R joints using some special commands of the CAD software, the S joints can be converted into U joints or R joints and thus the SPS-type leg can be converted into XPY(X and Y are selected from R, U and S joints)-type leg. Then the PMs with various topology can be easily obtained. For example, by locking $R_{i1}$, $R_{i2}$, and then setting $R_{i3}$ parallel to the opposite sides of the base in each leg, the typical 3-RPS PM [26] can be obtained. By locking $R_{i2}$, $R_{i5}(i=1, 2, 3)$, and then setting $R_{i3}\bot R_{i1}$, $R_{i4}\bot R_{i6}$ and $R_{i3}\Vert R_{i4} (i=1, 2, 3)$, the 4-DOF 3-UPU PM [4] with 3 translations and 1 rotation can be obtained. By locking $R_{i1}$, $R_{i6}(i=1, 2, 3)$, setting $R_{i2}$, $R_{i5}$ parallel to the opposite sides of the base and moving platform respectively and then setting $R_{i3}\Vert R_{i4}$, the Tsai’s 3-UPU PM [2] can be obtained. In fact, other PMs can be easily obtained based on their corresponding geometrical constraints and the original 3-SPS structure.

Fig. 3

The unified 3D 3-SPS model

After the CAD model of the expected PM is established, we process some routine processes such as material parameters setting and the finite element mesh generation and then run the simulation, the simulation results can be obtained easily. To simulate the stiffness with different configurations, we can set the lengths of P joint according to the inverse kinematics obtained from the analytical model and click the reconstruct button to update the established model, and then the expected configurations can be obtained automatically.

The merit of this approach lies in that the FE model of PMs with different topologies can easily obtained without reconstructing their CAD model.

5 Analytic solved example

5.1 Stiffness calculation based on the theoretical model

The numerical results of the 2-RPU $+$ UPR PM can be easily calculated using the established analytic model. Set $E=1.20/q$, $e=0.60/q$ m, ${{\varvec{F}}}_{o}=[-20 -30 -60]^{\mathrm{T} }\hbox {N}$, ${{\varvec{T}}}_{o}=[0\, 0\, 0]^{\mathrm{T} } \hbox {N}\,.\,\hbox {m}$, $E_{s}=2.11\times 10^{11 }\hbox {Pa}$, $E_{s}I=8345.5\hbox {N} \, \hbox {m}^{2}$, $A=3.14\times (0.015)^{2}\hbox {m}^{2}$. $G=80\times 10^{9}\hbox {Pa}$, $I_{p}=3.14\times (0.03)^{4}/32\hbox {m}^{4}$.

Set the pose parameters of the moving platform of the 2-RPU $+$ UPR PM as $\alpha =0^{\mathrm{o}}$, $\beta =0^{\mathrm{o}}$, $Z_{o}=1.30\hbox {m}$. By means of Eqs. (28a) to (28c) and MATLAB, the inverse kinematics for the 2-RPU $+$ UPR PM are solved as:

$$\begin{aligned} r_{1}=1.3342\mathrm{m}, r_{2}=1.400\mathrm{m}, r_{3}=1.3342\mathrm{m} \end{aligned}$$

From Eq. (29b), the actuator forces applied to actuators can be solved as follows:

$$\begin{aligned} F_{r}=[-1.7105 \;21.5385 \;42.7617]^{\mathrm{T}}\mathrm{N} \end{aligned}$$

From Eqs. (13), (29c) and Eqs. (33a) to (36), the stiffness matrix of the 2-RPU $+$ UPR PM is solved as

$$\begin{aligned} \mathbf{K}=10^{8}\times \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.1125&{}0&{}0&{}0&{}0.1461&{}0.0194\\ 0&{}0.1462&{}-0.3652&{}-0.1265&{}0&{}0\\ 0&{}-0.3652&{}3.0254&{}-0.0492&{}0&{}0\\ 0&{}-0.1265&{}-0.0492&{}0.1730&{}0&{}0\\ 0.1461&{}0&{}0&{}0&{}0.1902&{}0.0254\\ 0.0194&{}0&{}0&{}0&{}0.0254&{}0.0036\\ \end{array}} \right] \end{aligned}$$

(38)

From Eq. (37), the actuator forces applied to actuators and the constrained forces/torques in this PM can be solved as follows:

$$\begin{aligned} F_{w}= & {} [-1.7105\;\;21.5385\;\;42.7617\;\;20.3462\\&10.0000\;\;0\;\;-17.6479\;\;2.0051 -0.4627\\&1.8600\;\;0.7435\;\;2.0051\;\;0.4627]^{\mathrm{T}} \end{aligned}$$

From the calculated ${{\varvec{F}}}_{r}$ and ${{\varvec{F}}}_{w}$, it can be seen that the actuator forces applied to actuators solved by two statics models are identical.

5.2 FE model analysis of the 2-RPU $+$ UPR PM

By locking $R_{i1}(i=1, 2, 3), R_{i2}$ and $R_{i6} (i=1, 3)$, then setting $R_{13}\Vert R_{33}\Vert R_{14}\Vert R_{34}$, $R_{13}\bot A_{1}A_{3}$, $R_{15}|R_{35}|a_{1}a_{3}$ in the unified CAD model, the 2-RPU+2-UPR PM can be obtained.

In the 3D assembly model, the dimension and material parameters are given according to the parameters used in analytical model. Assume a force $F_{o}=[-20\; -30\; -60]^{\mathrm{T}}\hbox {N}$ applied on the center of m. The simulated results based on FE model for the deformation of m are solved as shown in Fig. 4.

Fig. 4

Solved results of elastic deformations of FE model of the 2-RPU $+$ UPR PM

The simulated results based on analytic approach and FE model for the deformation of m are listed in Table 1.

Table 1 The comparison of the elastic deformation of m derived from analytic approach and FE model

It is well known that the solved results of FE model are greatly depend on some key factors such as material parameter, FE dimension and type, reasonable boundary constraints and connection constraints. Thus, the FE analysis is a numerical technique for solving approximate solutions. From the result, it can be seen that the results obtained by the FE model is basically coincident with that of analytical ones, which is acceptable for stiffness analysis.

5.3 Stiffness characteristics analysis

In this section, the minimum and maximum eigenvalues of the stiffness matrix are used to describe the stiffness distribution [15]. The eigenscrew problem of stiffness matrix can be expressed as follows [27]:

$$\begin{aligned} \mathbf{K}{\Delta }{{\varvec{e}}}_i =\lambda _i {\varvec{e}}_i , {\varvec{\Delta } }=\left[ {{\begin{array}{cc} {\mathbf{0}_{3\times 3} }&{} {\mathbf{E}_{3\times 3} } \\ {\mathbf{E}_{3\times 3} }&{} {\mathbf{0}_{3\times 3} } \\ \end{array} }} \right] \end{aligned}$$

(39)

where $\lambda _{i}$ and the corresponding ${{\varvec{e}}}_{i}$ are the eigenvalue and eigenvector of $\mathbf{K} \Delta$, respectively. The transformation matrix $\Delta$ interchanges the first and last three components of six dimension vector.

A numerical approach [15] is applied to evaluate the stiffness properties throughout the workspace. In the numerical example, the workspace is partitioned in to a finite number of elements. For the sake of generality, the following illustrates the distribution of the stiffness values in one plane which is parallel with the Base.

Based on the established kinematics model, the workspace can be solved (see Fig. 5).

Fig. 5

Workspace of the 2-RPU $+$ UPR PM

Fig. 6

The distribution of the stiffness in the plane of Z = 1.3 m, a the distribution of maximum stiffness, b The distribution of minimum stiffness

From Fig. 5, it can be seen that the workspace is symmetrical about the plane $X=0$, which is in accord with the characteristic of the structure of the 2-RPU $+$ UPR PM.

Based on Eq. (39) and the stiffness model of the 2-RPU $+$ UPR PM, the distributions for the maximum and minimum stiffness in the plane of $Z=1.3\,\hbox {m}$ for the 2-RPU $+$ UPR PM are illustrated in Fig. 6a and b, respectively.

It can be observed that, similar to the reachable workspace, the distribution of minimum and maximum stiffness in the plane of Z = 1.3 m for the 2-RPU $+$ UPR PM is symmetrical about the $X=0$ plane. In addition, the lowest value of maximum and minimum stiffness occurs around the boundary of the workspace, since the manipulator approaches singular when it comes near the workspace boundary.

In what follows, the stiffness behavior is investigated through the eigenscrew decomposition of the stiffness matrix of the 2-RPU $+$ UPR PM. The eigenscrew decomposition of stiffness matrix can be expressed as [27]:

$$\begin{aligned}&{} \mathbf{K}=\sum _{i=1}^6 {k_i {{\varvec{w}}}_i {{\varvec{w}}}_i^T}\quad , k_i =\frac{\lambda _i }{2h_i },\nonumber \\&\quad h_i =\frac{1}{2}{{\varvec{w}}}_i^T \Delta {{\varvec{w}}}_i , {{\varvec{w}}}_i =\left[ {{\begin{array}{c} {{{\varvec{n}}}_i } \\ {{\varvec{\rho }} _i \times {{\varvec{n}}}_i +h_i {{\varvec{n}}}_i } \\ \end{array} }} \right] \end{aligned}$$

(40)

where the spring wrench ${{\varvec{w}}}_{i}$ is the unitization of ${{\varvec{e}}}_{i}(i=1,\ldots , 6)$, $h_{i}$ is the pitch of ${{\varvec{w}}}_{i}$, ${{\varvec{n}}}_{i }$and ${\varvec{\rho }}_{i}$ are the direction and position vectors of the ith spring, respectively.

Table 2 Parameters of springs based on the eigenscrew decomposition

Applying the eigenscrew decomposition to the stiffness matrix obtained in Eq. (38), the corresponding six eigenvalue values [$\lambda$], the six eigenscrew pitches [h], and the corresponding six eigenscrews [w] can be solved as follows:

$$\begin{aligned} \left[ \lambda \right]= & {} \hbox {diag}\left( \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -2.5243&1.9816&1.4232&-0.9537&0.2490&-0.1759 \end{array} \right] \right) \times 10^{6}, \nonumber \\ \left[ h \right]= & {} \hbox {diag}\left( \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -0.0086&0.0086&0.0347&-0.0347&0.0557&-0.055 \end{array} \right] \right) , \nonumber \\ {\left[ {{{\varvec{w}}}} \right] }= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0.0027&{}-0.0027&{}-0.0799&{}0.0799&{}-0.9899&{}-0.9899\\ -0.0906&{}-0.0906&{}-0.7798&{}-0.7798&{}0.1025&{}-0.1025\\ 0.9959&{}0.9959&{}0.6209&{}0.6209&{}-0.0977&{}0.0977\\ -0.0547&{}-0.0547&{}0.9002&{}0.9002&{}-0.1717&{}0.1717\\ -0.0040&{}0.0040&{}-0.1513&{}0.1513&{}-1.2786&{}-1.2786\\ -0.0088&{}0.0088&{}-0.0181&{}0.0181&{}-0.1707&{}-0.1707\\ \end{array} \right] \end{aligned}$$

(41)

The interpretation of stiffness matrix K based on eigenscrew decomposition is elaborated in Table 2, which indicates that K can be interpreted by a body suspended by six screw springs with directions along the eigenscrews of K as shown in Fig. 7. For each spring, the spring constant is determined by $\lambda _{i}/2h_{i}$, the geometrical connection of the spring is determined by the eigenscrews ${{\varvec{w}}}_{i}$, and the pitch of the eigenscrew is determined by $-2\pi h_{i}$. It can be seen from Table 2 that the six screws can be divided into three groups with each group having two springs. In each group, the two springs have the pitches with equal magnitude and opposite sign.

Fig. 7

Physical interpretation of the stiffness matrix based on eigenscrew decomposition

From Fig. 7, it can be seen that the rigid body is suspended by six screw springs which are distributed in space. The six screws are reciprocal, and any twist along one spring only leads to a wrench along the same twist for the elastic system, which will not affect any other directions. The six screw springs system yielded by the eigenscrew decomposition reflects the eigenstructure of the stiffness matrix.

6 Conclusions

The main contribution of this paper lies in the establishment of the kinetostatic analysis model of overconstrained PMs. A novel 2-UPR $+$ UPR PM is proposed to illustrate the approach for solving the kinetostatic of overconstrained PMs. Since the overconstrained wrenches existed in each leg, the forces and deformations situation become complex than non-overconstrained PM. In the 2-UPR+UPR PM, there are six constrained wrenches which produce multiple deformations. The detailed forces and deformations are solved based on the established kinetostatic model. The kinetostatic of 2-UPR+UPR PM is calculated using conventional model and the established model. The results show that the actuator forces applied to actuators used by two kinetostatic models are identical. In addition, a unified FE model for the PMs with linear legs is established and a statics simulation of the 2RPU $+$ UPR PM is carried out, which verifies the correctness of the analytic model. Furthermore, the distribution of the stiffness in the prescribed workspace is described, and the eigenscrew decomposition of the stiffness matrix is carried out to have an insight view of the stiffness characteristic of the 2-UPR $+$ UPR PM. The method proposed in this paper is particularly useful in kinetostatic analysis for overconstrained PMs.