Dynamic Modelling of Lower Mobility Parallel Manipulators

Abstract

This paper deals with the dynamic modelling of lower mobility parallel manipulators using the screw theory. The proposed approach is developed by considering both the permitted and restricted virtual displacements of a parallel manipulator, leading to the evaluation of intensities of the wrenches of actuations and constraints applied on the moving platform. By introducing the complementary part in terms of generalized constraint forces/torques, it completes the dynamic model of lower mobility parallel manipulators, and provides a feasible way to investigate the dynamic interactions between the limbs and the moving platform.

1 Introduction

With the wide applications of parallel kinematic machines (PKM) in industry, high-speed pick-and-place operations and high-speed drilling/milling in situ for example, more and more attentions have been paid to the improvement of dynamic behaviors of the system with the goal to achieve higher accuracy and productivity. In spite of a number of commercial software that have been available on market, a general, complete and precise formulation of rigid-body dynamics of parallel kinematic machines is still in need since it is helpful to gain deep insight into dynamic performance evaluation, motor sizing, trajectory planning and control algorithm development.

In this paper, the application of dynamic model for design purpose as that stated in [1] is addressed by introducing a novel modelling approach for lower mobility parallel manipulators based on the principle of virtual work [2], which is capable of evaluating the reactions in terms of both actuation and constraint imposed on the moving platform simultaneously. The proposed method is developed drawing on the generalized Jacobian and the acceleration analysis of parallel manipulators presented in our previous works [2, 3].

Hereby, the virtual displacements related to the permitted and restricted motions can be naturally defined, and the inertial and resulting gravity wrenches of a rigid body are formulated in a body-fixed frame. Then, the virtual work of individual rigid bodies can be lumped together, resulting in analytical expressions of the actuation and constraint forces/moments.

2 Kinematic Analysis

The kinematic analysis of a non-redundant actuated and non-overconstrained f-DOF ($2 \le f \le 6$) parallel mechanism is briefly reviewed [2, 3].

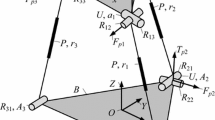
As shown in Fig. 1, a global frame ${\mathcal{K}}$ is placed on the base and an instantaneous frame ${\mathcal{K}^{\prime}}$ keeping parallel to ${\mathcal{K}}$ is established on the platform. In order to evaluate the tensor of inertia of the jth ($j = 1, \ldots ,n_{i} - 1$) body in limb i, a body-fixed frame ${\mathcal{K}}_{j,i}^{L}$ is attached to body j with its z-axis coincident with the $\left( {j_{a} { + }1} \right)\text{th}$ ($j_{a} = j$) joint axis. A body-fixed frame ${\mathcal{K}}_{p}^{L}$ is placed on the platform. Considering the effects of constraints, $6 - n_{i}$ 1-DOF virtual joints are added in limb i by making an assumption that all of them are active ones. Then, referring to [2, 3], the joint velocity and the accelerator of the platform can be given as

Fig. 1.

Coordinate frames in the ith limb of a parallel mechanism

$$ \dot{\varvec{\theta }}_{i} = \varvec{J}_{i}^{ - 1} {\mathbf{\$ }}_{t} = \varvec{J}_{i}^{ - 1} \varvec{W}^{{ - {\text{T}}}} \varvec{\varLambda \dot{\varvec{q}}} = \varvec{P}_{i}^{{}} \dot{\varvec{q}},\quad \varvec{P}_{i}^{{}} = \varvec{J}_{i}^{ - 1} \varvec{W}^{{ - {\text{T}}}}\varvec{\varLambda},\quad {\varvec{A}} = {\varvec{J}}_{i} {\varvec{\ddot{\theta}}}_{i} + {\dot{\varvec{\theta}}}_{i}^{\text{T}} {\varvec{H}}_{i} {\dot{\varvec{\theta}}}_{i} $$

(1)

$$ \dot{\varvec{\theta }}_{i} = \left( {\begin{array}{*{20}c} {\dot{\varvec{\theta }}_{a,i}^{\text{T}} } & {\dot{\varvec{\theta }}_{c,i}^{\text{T}} } \\ \end{array} } \right)^{\text{T}} ,\;\;\dot{\varvec{\theta }}_{a,i}^{{}} = \left( {\begin{array}{*{20}c} {\dot{\theta }_{a,1,i} } & \ldots & {\dot{\theta }_{{a,n_{i} ,i}} } \\ \end{array} } \right)^{\text{T}} ,\;\;\dot{\varvec{\theta }}_{c,i}^{{}} = \left( {\begin{array}{*{20}c} {\dot{\theta }_{c,1,i} } & \ldots & {\dot{\theta }_{{c,6 - n_{i} ,i}} } \\ \end{array} } \right)^{\text{T}} $$

$$ \dot{\varvec{q}} = \left( {\begin{array}{*{20}c} {\dot{\varvec{q}}_{a}^{\text{T}} } & {\dot{\varvec{q}}_{c}^{\text{T}} } \\ \end{array} } \right)^{\text{T}} ,\quad \varvec{q}_{a}^{{}} = \left( {\begin{array}{*{20}c} {\dot{q}_{a,1} } & \ldots & {\dot{q}_{a,f}^{{}} } \\ \end{array} } \right)^{\text{T}} ,\quad \varvec{q}_{c}^{{}} = \left( {\begin{array}{*{20}c} {\dot{q}_{c,1} } & \ldots & {\dot{q}_{c,6 - f}^{{}} } \\ \end{array} } \right)^{\text{T}} $$

where $\dot{\theta }_{{a,j_{a} ,i}}$($j_{a} = 1, \ldots ,n_{i}$)/$\dot{\theta }_{{c,j_{c} ,i}}$($j_{c} = 1, \ldots ,6 - n_{i}$) are the joint rates of the $j_{a} \text{th}$/$j_{c} \text{th}$ joint in limb i; $\dot{q}_{a,\chi }$($\chi = 1, \ldots ,f$)/$\dot{q}_{c,\vartheta }$($\vartheta = 1, \ldots ,6 - f$) denote the joint rates of the $\chi {\text{th}}$/$\vartheta {\text{th}}$ actuated joint; The definition and expression of $\varvec{J}_{i}$, $\varvec{W}$, $\varvec{\varLambda}$, ${\mathbf{H}}_{i}$ can be found in [3, 4]. From Eq. (1), the twist of permissions [2] and the accelerator of the jth body in limb i can be expressed as

$$ {\mathbf{\$ }}_{t,j,i} = \varvec{J}_{a,j,i}^{{}} \varvec{P}_{j,i}^{{}} \dot{\varvec{q}},\quad {\varvec{A}}_{j,i} = {\varvec{J}}_{a,j,i} {\varvec{\ddot{\theta}}}_{a,j,i} + {\dot{\varvec{\theta }}}_{a,j,i}^{\text{T}} {\varvec{H}}_{a,j,i} {\dot{\varvec{\theta }}}_{a,j,i} ,\quad i = 1,2, \ldots ,l,\;j = 1, \ldots ,n_{i} - 1 $$

(2)

$$ {\varvec{J}}_{a,j,i} = \left[ {\begin{array}{*{20}c} {{\mathbf{\hat{\$ }}}_{ta,1,i} } & \ldots & {{\mathbf{\hat{\$ }}}_{{ta,j_{a} ,i}} } \\ \end{array} } \right],\quad \varvec{P}_{j,i}^{{}} = \varvec{G}_{j,i}^{{}} \varvec{W}^{{ - {\text{T}}}}\varvec{\varLambda},\quad\varvec{\theta}_{a,j,i}^{{}} = \left( {\begin{array}{*{20}c} {\theta_{1,i} } & \ldots & {\theta_{{j_{a} ,i}} } \\ \end{array} } \right)^{\text{T}} $$

where $\varvec{G}_{j,i}^{{}}$ is a ($j_{a} \times 6$) matrix formed by the first $j_{a}$ rows of $\varvec{J}_{i}^{ - 1}$; $\varvec{H}_{a,j,i} \in {\mathbb{R}}^{{6 \times j_{a} \times j_{a} }}$ is the corresponding Hessian matrix extracted from $\varvec{H}_{i}$ [3]. Since Eq. (2) is formulated in ${\mathcal{K}^{\prime}}$, when ${\mathbf{\$ }}_{t,j,i}$/${\mathbf{\$ }}_{t}$ and $\varvec{A}_{j,i}$/$\varvec{A}$ are evaluated with respect to ${\mathcal{K}}_{j,i}^{L}$/${\mathcal{K}}_{p}^{L}$, the adjoint transformation should be applied.

$$ {\mathbf{\$ }}_{t,j,i}^{L} = {\text{Ad}}_{{g_{j,i} }} {\mathbf{\$ }}_{t,j,i}^{{}} = \varvec{T}_{j,i} \dot{\varvec{q}},\;\;{\mathbf{\$ }}_{t}^{L} = {\text{Ad}}_{{g_{p} }} {\mathbf{\$ }}_{t}^{{}} = \varvec{T}_{p} \dot{\varvec{q}} $$

(3)

$$ {\varvec{A}}_{j,i}^{L} = {\text{Ad}}_{{g_{j,i} }} {\varvec{A}}_{j,i} ,\;\;{\varvec{A}}_{{}}^{L} = {\text{Ad}}_{{g_{p} }} {\varvec{A}} $$

(4)

$$ \varvec{T}_{j,i} = {\text{Ad}}_{{g_{j,i} }} \varvec{J}_{a,j,i}^{{}} \varvec{P}_{j,i}^{{}} = \left[ {\begin{array}{*{20}c} {\varvec{T}_{a,j,i} } & {\varvec{T}_{c,j,i} } \\ \end{array} } \right],\;\;\varvec{T}_{p} = {\text{Ad}}_{{g_{p} }} \varvec{W}^{{ - {\text{T}}}}\varvec{\varLambda}= \left[ {\begin{array}{*{20}c} {\varvec{T}_{a,p} } & {\varvec{T}_{c,p} } \\ \end{array} } \right] $$

(5)

$$ {\text{Ad}}_{{g_{j,i} }} = \left[ {\begin{array}{*{20}c} {\varvec{R}_{j,i} } & {\left[ {\varvec{r}_{j,i} \times } \right]\varvec{R}_{j,i} } \\ {\mathbf{0}} & {\varvec{R}_{j,i} } \\ \end{array} } \right],\;\;{\text{Ad}}_{{g_{p} }} = \left[ {\begin{array}{*{20}c} {\varvec{R}_{p} } & {\left[ {\varvec{r}_{p} \times } \right]\varvec{R}_{p} } \\ {\mathbf{0}} & {\varvec{R}_{p} } \\ \end{array} } \right] $$

$$ \varvec{T}_{a,j,i} = \left[ {\begin{array}{*{20}c} {{\mathbf{\$ }}_{Pa,j,i}^{\left( 1 \right)} } & \ldots & {{\mathbf{\$ }}_{Pa,j,i}^{\left( f \right)} } \\ \end{array} } \right],\;\;\varvec{T}_{c,j,i} = \left[ {\begin{array}{*{20}c} {{\mathbf{\$ }}_{Pc,j,i}^{\left( 1 \right)} } & \ldots & {{\mathbf{\$ }}_{Pc,j,i}^{{\left( {6 - f} \right)}} } \\ \end{array} } \right] $$

$$ \varvec{T}_{a,p} = \left[ {\begin{array}{*{20}c} {{\mathbf{\$ }}_{Pa,p}^{\left( 1 \right)} } & \ldots & {{\mathbf{\$ }}_{Pa,p}^{\left( f \right)} } \\ \end{array} } \right],\;\;\varvec{T}_{c,p} = \left[ {\begin{array}{*{20}c} {{\mathbf{\$ }}_{Pc,p}^{\left( 1 \right)} } & \ldots & {{\mathbf{\$ }}_{Pc,p}^{{\left( {6 - f} \right)}} } \\ \end{array} } \right] $$

where $\varvec{R}_{{j\text{,}i}}$($\varvec{R}_{p}$) is the orientation matrix of ${\mathcal{K}^{\prime}}$ with respect to ${\mathcal{K}}_{j,i}^{L}$(${\mathcal{K}}_{p}^{L}$) and $\left[ {\varvec{r}_{{j\text{,}i}} { \times }} \right]$($\left[ {\varvec{r}_{p} { \times }} \right]$) is the skew-symmetric matrix of the vector $\varvec{r}_{{j\text{,}i}}$($\varvec{r}_{p}$). The columns of $\varvec{T}_{j,i}$ and $\varvec{T}_{p}$ are nothing but partial screws [5].

3 Dynamic Modelling

First, the inertial wrench of a rigid body evaluated in different reference frames is investigated. The inertial wrench $\varvec{\$ }_{wI}^{C}$ can be expressed in ${\mathcal{K}}^{L}$ as

$$ \mathbf{\$ }_{wI}^{L} = {\text{Ad}}_{{g_{C} }}^{{ - {\text{T}}}} \mathbf{\$ }_{wI}^{C} = - {\varvec{m}}_{{}}^{L} {\varvec{A}}_{{}}^{L} {\text{ + ad}}^{\text{T}} (\mathbf{\$ }_{t}^{L} ){\varvec{m}}_{{}}^{L} \mathbf{\$ }_{t}^{L} $$

(6)

$$ {\varvec{m}}_{{}}^{L} = {\text{Ad}}_{{g_{C} }}^{{ - {\text{T}}}} {\varvec{m}}_{{}}^{C} {\text{Ad}}_{{g_{C} }}^{ - 1} ,\;\;{\text{ad}}^{\text{T}} (\mathbf{\$ }_{t}^{L} ) = {\text{Ad}}_{{g_{C} }}^{{ - {\text{T}}}} {\text{ad}}^{\text{T}} (\mathbf{\$ }_{t}^{C} ){\text{Ad}}_{{g_{C} }}^{\text{T}} $$

where ${\varvec{m}}_{{}}^{C}$ is the tensor of inertia. Hence, the inertial wrench of the jth body in limb i, $\mathbf{\$ }_{wI,j,i}^{L}$, and the inertial wrench of the platform, $\mathbf{\$ }_{wI,p}^{L}$, can be obtained by adding subscript ‘j, i’ and ‘p’ to the corresponding terms in Eq. (6), respectively.

Suppose that the parallel mechanism is subject to the effect of a gravity field, then the gravity wrenches of the jth body in limb i, $\mathbf{\$ }_{wG,j,i}^{L}$, and the platform, $\mathbf{\$ }_{wG,p}^{L}$, evaluated in ${\mathcal{K}}_{j,i}^{L}$ and ${\mathcal{K}}_{p}^{L}$, can be obtained through adjoint transformation, respectively. Then, the overall wrench $\mathbf{\$ }_{w,p}^{L}$ ($\mathbf{\$ }_{w,j,i}^{L}$) evaluated in ${\mathcal{K}}_{p}^{L}$ (${\mathcal{K}}_{j,i}^{L}$) can be expressed as

$$ \mathbf{\$ }_{w,p}^{L} = \mathbf{\$ }_{wI,p}^{L} + \mathbf{\$ }_{wG,p}^{L} ,\;\;\mathbf{\$ }_{w,j,i}^{L} = \mathbf{\$ }_{wI,j,i}^{L} + \mathbf{\$ }_{wG,j,i}^{L} $$

(7)

Finally, the principle of virtual work states

$$ \delta w = \sum\limits_{i = 1}^{l} {\sum\limits_{j = 1}^{{n_{i} - 1}} {\left( {{\mathbf{\$ }}_{w,j,i}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{t,j,i}^{L} } } + \left( {{\mathbf{\$ }}_{w,p}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{t,p}^{L} + {\mathbf{\mathcal{F}}}^{\text{T}} {\dot{\mathbf{\mathit{q}}}} = 0 $$

(8)

$$ {\mathbf{\mathcal{F}}} = \left( {\begin{array}{*{20}c} {{\mathbf{\mathcal{F}}}_{a}^{\text{T}} } & {{\mathbf{\mathcal{F}}}_{c}^{\text{T}} } \\ \end{array} } \right)^{\text{T}} ,\;\;{\mathbf{\mathcal{F}}}_{a} = \left( {\begin{array}{*{20}c} {{\mathcal{F}}_{a,1} } & \ldots & {{\mathcal{F}}_{a,f} } \\ \end{array} } \right)^{\text{T}} ,\;\;{\mathbf{\mathcal{F}}}_{c} = \left( {\begin{array}{*{20}c} {{\mathcal{F}}_{c,1} } & \ldots & {{\mathcal{F}}_{c,6 - f} } \\ \end{array} } \right)^{\text{T}} $$

where ${\mathcal{F}}_{a,\chi }$ ($\chi = 1, \ldots ,f$) and ${\mathcal{F}}_{c,\vartheta }$ ($\vartheta = 1, \ldots ,6 - f$) denote the intensities of the wrenches of actuations and constraints. Then, we have

$$ {\mathcal{F}}_{a,\chi } = - \sum\limits_{i = 1}^{l} {\sum\limits_{j = 1}^{{n_{i} - 1}} {\left( {{\mathbf{\$ }}_{w,j,i}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{Pa,j,i}^{\left( \chi \right)} } } - \left( {{\mathbf{\$ }}_{w,p}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{Pa,p}^{\left( \chi \right)} ,\quad \chi = 1, \ldots ,f $$

(9)

$$ {\mathcal{F}}_{c,\vartheta } = - \sum\limits_{i = 1}^{l} {\sum\limits_{j = 1}^{{n_{i} - 1}} {\left( {{\mathbf{\$ }}_{w,j,i}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{Pc,j,i}^{\left( \vartheta \right)} } } - \left( {{\mathbf{\$ }}_{w,p}^{L} } \right)^{\text{T}} {\mathbf{\$ }}_{Pc,p}^{\left( \vartheta \right)} ,\quad \vartheta = 1, \ldots ,6 - f $$

(10)

${\mathcal{F}}_{a,\chi }$ (${\mathcal{F}}_{c,\vartheta }$) can be physically interpreted as the superposition of the projection of the overall wrench of a rigid body on the direction of corresponding partial screw.

4 Example

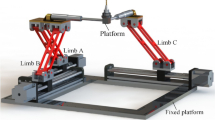
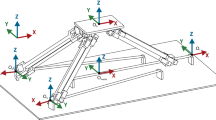
A 3-DOF R(2RPS-RP)-UPS parallel mechanism within a 5-DOF hybrid robot is taken as an example (see Fig. 2). The geometric parameters for this example are given in Table 1. While, the definitions of body-fixed frames and inertial parameters obtained from 3D software are listed in Table 2. Assume that the trajectory of the reference point A is

Fig. 2.

Schematic diagram of the R(2RPS-RP)-UPS parallel mechanism within the TriMule robot

Table 1. Dimensional parameters (unit: m)

Table 2. Definitions of body-fixed frames and inertial parameters

$$ \left\{ \begin{aligned} & x = - r\sin \psi \left( t \right) + x_{0} \hfill \\ & y = r\cos \psi \left( t \right) + y_{0} \hfill \\ & z = z_{0} \hfill \\ \end{aligned} \right. $$

(11)

$$ r = 0.45\;{\text{m}},\;\;x_{0} = 0,\;\;y_{0} = - 0.145\;{\text{m,}}\;\;z_{0} = 0.75\;{\text{m}} $$

where $\left( {\begin{array}{*{20}c} {x_{0} } & {y_{0} } & {z_{0} } \\ \end{array} } \right)^{\text{T}}$ is the initial value of A; $\psi \left( t \right)$ is the motion rule as the same as that given in [2]. The variations of ${\mathcal{F}}_{a,\chi }$ ($\chi = 1,2,3$) and ${\mathcal{F}}_{c,\vartheta }$ ($\vartheta = 1,2,3$) versus time can be obtained using Eqs. (9) and (10) (see Fig. 3). Moreover, the results of ${\mathcal{F}}_{a,\chi }$ are also compared with those obtained by a commercial software.

Fig. 3.

Variations of the actuated torques (Figure a, b, c) versus time compared with commercial software and constrained moment and forces (Figure d, e, f) versus time

It has to be pointed out that for the convenience of dynamic modeling and computational efficiency, some assumptions are made in the proposed method with little loss of accuracy: (i) the inertia of S joints and lead-screw assemblies in active limbs are neglected; (ii) all active limbs are assumed to be axially symmetrical, leading to the inertia matrices being diagonal. However, the inertia parameters of all components are taken into account in the software. From the comparison study, it can be found that although the numerical results of two models are not exactly the same, the residuals are rather small. Therefore, the effectiveness of the proposed approach is demonstrated.

5 Conclusion

This paper presents a general and systematic approach for dynamic modelling of lower mobility parallel manipulators. A calculation of both the intensities of the wrenches of actuations and constraints is derived, which is formulated in a compact form as the superposition of the projection of the overall wrench of a rigid body on the direction of corresponding partial screw. Compared with other methods in literatures, this approach completes the dynamic model by developing the complementary part in terms of generalized constraint forces/torques.