Effects of time delay on an active vibration control of a forced and Self-excited nonlinear beam

Abstract

Loop delays are taken into our consideration when positive position feedback controller is used to control the vibrations of forced and self-excited nonlinear beam. External excitation is a harmonic excitation caused by support motion of the cantilever beam. Self-excitation is caused by fluid flow and modeled by a nonlinear damping with a negative linear part (Rayleigh’s function). The multiple timescales perturbation technique is applied to obtain a first-order approximate solution. Effects of time delay on the system are extensively studied, and optimal conditions for the system operation are deduced. The equilibrium solution curves are plotted for several values of controller parameters. The stability of the steady-state solution is investigated using frequency-response equations. The analytical results are validated by numerical integration of the original closed-loop system model equations, time histories and Poincaré map for the system. We realized that all predictions from analytical solutions are in good agreement with the numerical simulation.

1 Introduction

Many closed-loop control systems contain loop delays “time delays”. Time delays are inevitable in any active control system as a result of measuring system states, processing the control algorithms, control interfaces, transport delay and actuation delay. The presence of time delays imposes strict limitations on the control system. With delays in measurement, the controller receives “outdated” information about process behavior. Also, the control action cannot be applied “on time” as a result of delays in actuation. Thus, time delay reduces the compensation efficiency to the effect of disturbances. So controller design and operation become complicated. Time delays can affect the stability of the system. Thus, the control system with time delays became a subject of researchers interest. Control issues in systems with loop delays have been studied extensively [1]. A saturation-based controller has been used to suppress a nonlinear beam vibration where time delay was taken into consideration and the effects of time delay on the system behavior were studied [2]. Time- delayed position feedback controller was used to reduce the horizontal vibration of a magnetically levitated body subjected to multi-force excitations, and the effects of time delay were investigated to indicate the safe region of system operation [3]. The effect of time delays on the saturation control of the first-mode vibration of a stainless-steel beam have been studied [4]. The delayed feedback control has been applied to suppress or stabilize the vibration of the primary system in a two- degree-of-freedom dynamical system with a parametrically excited pendulum [5]. Xu et al. [6] and others improved a nonlinear saturation controller by using quadratic velocity coupling term with time delay instead of the original quadratic position coupling term in the controller, and they added a negative time-delay velocity feedback to the primary system and then utilized this controller to suppress high-amplitude vibrations of a flexible, geometrically nonlinear beam-like structure. The authors in [7–13] have been studied extensively the vibration control of many systems with the time delay by using different controllers. An active linear absorber based on positive position feedback control strategy has been developed and applied to suppress the high-amplitude response of a flexible beam subjected to a primary external excitation [14]. Positive position feedback controller has been modified, and a new active vibration control technique was developed and applied to piezoelectrically controlled systems [15]. An active vibration control of clamp beams using positive position feedback controller with a sensor /moment pair actuator has been investigated [16]. Authors in [17] have used a nonlinear saturation controller to control the vibrations of a nonlinear beam with self- and external excitations, and they concluded that the closed-loop system might lose stability when the two type excitations interacted near the fundamental resonance zone.

An active vibration control of a nonlinear beam with self- and external excitations by using positive position feedback (PPF) controller is investigated in this work. Loop delays are taken into our consideration. External excitation is a harmonic excitation caused by support motion of the cantilever beam. Self-excitation is caused by fluid flow and modeled by a nonlinear damping with a negative linear part (Rayleigh’s function). Systems with self-excitation are common in applications of solid or fluid mechanics. Multiple timescales perturbation (MTSP) technique is applied to obtain a first-order approximate solution. Effects of time delays on the system are studied extensively. In our study, time margin of the system is deduced for many values of controller parameters to deduce the optimal conditions for system operation. Where time margin is the amount of time delay that system can bear without being unstable. The equilibrium solution curves were plotted for various values of controller parameters. The stability of the steady-state solution was investigated using frequency-response equations. Analytical results using MTSP technique are verified by numerical integration of the original closed-loop system model equations, time histories and Poincaré map for the system. We found that all predictions from analytical solutions are in good agreement with the numerical simulation.

2 Model of the structure

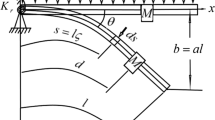
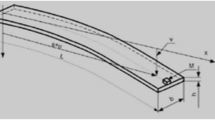
The model of the beam and its characteristic parameters are presented in Fig. 1 and Fig. 2 presents the block diagram of the closed loop system. The physical parameter’s values are given in [17]. The cantilever beam is mounted on an armature of an electrodynamic shaker which is a source of external excitation along the x-axis. This model can be used practically to describe the wing of a plane such that the wing of the plane is suspended to external excitation from plane body and self-excitation from the wind flow. The external excitation is written as

$$\begin{aligned} x=x_0\sin (\varOmega t). \end{aligned}$$

(1)

Fig. 1

Model of the nonlinear beam with self- and external excitations

Fig. 2

Block diagram of the closed-loop system

The differential equation of the beam (the plant) is given by [17] in the dimensionless form as follows:

$$\begin{aligned}&{}\ \ {}\ddot{x}_1+(-\alpha _1\dot{x}_1+\beta _1\dot{x}_1^3)+\omega _1^2x_1+\gamma _1x_1^3\nonumber \\&\qquad +\delta (x_1\dot{x}_1^2+x_1^2\ddot{x}_1)\nonumber \\&\quad =x_0\mu \varOmega ^2\sin (\varOmega t)+\lambda _1 f_c(t). \end{aligned}$$

(2)

Self-excitation is represented by a nonlinear damping with a negative linear part (Rayleigh’s function). A control force $f_c(t)$ is added to right-hand side of differential Eq. (2). Positive position feedback controller (PPF) is coupled to the beam. The equation governing the dynamics of this controller (PPF) is suggested as

$$\begin{aligned} \ddot{x}_2+\alpha _2\dot{x}_2+\omega _2^2x_2=\lambda _2f_f(t). \end{aligned}$$

(3)

In this work, time delays in the control signal and the feedback signal are taken into our consideration, so the control signal $f_c(t)$ and feedback signal $f_f(t)$ are given by

$$\begin{aligned} f_c(t)=x_2(t-\tau _1)\ \ \text {and}\ \ f_f(t)=x_1(t-\tau _2). \end{aligned}$$

(4)

So the closed-loop system equations are

$$\begin{aligned}&\ddot{x}_1(t)+(-\alpha _1\dot{x}_1(t)+\beta _1\dot{x}_1^3(t))+\omega _1^2x_1(t)\nonumber \\&\qquad +\,\gamma _1x_1^3(t)+\delta (x_1(t)\dot{x}_1^2(t)+x_1^2\ddot{x}_1(t))\nonumber \\&\quad =x_0\mu \varOmega ^2\sin (\varOmega t)+\lambda _1x_2(t-\tau _1), \end{aligned}$$

(5)

$$\begin{aligned}&\ddot{x}_2(t)+\alpha _2\dot{x}_2(t)+\omega _2^2x_2(t)=\lambda _2x_1(t-\tau _2). \end{aligned}$$

(6)

3 Perturbation analysis

Approximate analytical solution is obtained by using multiple scales perturbation technique (MSPT) [18]. Assume that the system is weakly nonlinear. We obtain first-order approximate solutions of Eqs. (5) and (6) by seeking the solution in the forms:

$$\begin{aligned}&x_1(t,\varepsilon )=x_{10}(T_0,T_1)+\varepsilon x_{11}(T_0,t_1), \end{aligned}$$

(7)

$$\begin{aligned}&x_2(t,\varepsilon )=x_{20}(T_0,T_1)+\varepsilon x_{21}(T_0,T_1), \end{aligned}$$

(8)

$$\begin{aligned}&x_1(t-\tau _2,\varepsilon )=x_{10\tau _2}(T_0,T_1)+\varepsilon x_{11\tau _2}(T_0,T_1), \end{aligned}$$

(9)

$$\begin{aligned}&x_2(t-\tau _1,\varepsilon )=x_{20\tau _1}(T_0,T_1)+\varepsilon x_{21\tau _1}(T_0,T_1) \end{aligned}$$

(10)

where $\varepsilon$ is a small dimensionless perturbation parameter ($\varepsilon<<1$), $T_0=t$ and $T_1=\varepsilon t$ are the fast and slow timescales, respectively. Time derivatives are as follows:

$$\begin{aligned}&\left. \begin{aligned}&\frac{d}{dt}={{D}_{0}}+\varepsilon {{D}_{1}}+\cdots , \\&\frac{{{d}^{2}}}{d{{t}^{2}}}={{D}_{0}}^{2}+2\varepsilon {{D}_{0}}{{D}_{1}}+\cdots \end{aligned} \right\} \end{aligned}$$

(11)

where ${{D}_{j}}=\dfrac{\partial }{\partial {{T}_{j}}},\ j=0,1$. To obtain a uniformly valid approximate solution of this problem we order the dimensionless parameters of the system by the formal small parameter $\varepsilon$ as follows:

$$\begin{aligned}&\left. \begin{aligned}&\alpha _1=\varepsilon \hat{\alpha }_1,\beta _1=\varepsilon \hat{\beta }_1,\gamma _1=\varepsilon \hat{\gamma }_1,\delta =\varepsilon \hat{\delta },\\&\mu =\varepsilon \hat{\mu },\lambda _1=\varepsilon \hat{\lambda }_1,\alpha _2=\varepsilon \hat{\alpha }_2\lambda _2=\varepsilon \hat{\lambda }_2. \end{aligned} \right\} \end{aligned}$$

(12)

Substitute equations from (7) to (12) into Eqs. (5) and (6), and thereafter, equate coefficients of like powers of $\varepsilon$. We obtain the following set of ordinary differential equations:

$$\begin{aligned}&\left( D_0^2+\omega _1^2\right) x_{10}=0, \end{aligned}$$

(13)

$$\begin{aligned}&\left( D_0^2+\omega _2^2\right) x_{20}=0. \end{aligned}$$

(14)

$$\begin{aligned}&\left( D_{0}^{2}+\omega _1^2\right) x_{11}=\varOmega ^2\hat{\mu }x_0\sin (\varOmega t)-\hat{\gamma }_1x_{10}^3+\hat{\lambda }_1x_{20\tau _1}\nonumber \\&\quad +\hat{\alpha }_1D_0x_{10}-\hat{\delta }x_{10}(D_0x_{10})^2\nonumber \\&\quad -\hat{\beta }_1(D_0x_{10})^3-2D_0D_1x_{10}\nonumber \\&\quad -\hat{\delta }x_{10}^2D_0^2x_{10}, \end{aligned}$$

(15)

$$\begin{aligned}&\left( D_0^2+\omega _2^2\right) x_{21}=\hat{\lambda }_2x_{10\tau _2}-\hat{\alpha }_2D_0x_{20}-2D_0D_1x_{20}. \end{aligned}$$

(16)

The general solution of Eqs. (13) and (14) can be expressed in the forms:

$$\begin{aligned}&x_{10}(T_0,T_1)=A(T_1)e^{i\,\omega _1T_0}+\bar{A}(T_1)e^{-i\omega _1T_0} \end{aligned}$$

(17)

$$\begin{aligned}&x_{20}(T_0,T_1)=B(T_1)e^{i\,\omega _2T_0}+\bar{B}(T_1)e^{-i\omega _2T_0} \end{aligned}$$

(18)

where the overbar denotes the complex conjugate functions. The coefficients $A(T_1)$, $B(T_1)$ are unknown functions of $T_1$. These coefficients will be determined later by eliminating the secular and small devisor terms. From (17) and (18), we get

$$\begin{aligned}&x_{10\tau _2}(T_0,T_1)=A_{\tau _2}(T_1)e^{i\omega _1(T_0-\tau _2)}\nonumber \\&\quad +\bar{A}_{\tau _2}(T_1)e^{-i\omega _1(T_0-\tau _2)} \end{aligned}$$

(19)

$$\begin{aligned}&x_{20\tau _1}(T_0,T_1)=B_{\tau _1}(T_1)e^{i\omega _2(T_0-\tau _1)}\nonumber \\&\quad +\bar{B}_{\tau _1}(T_1)e^{-i\omega _2(T_0-\tau _1)}. \end{aligned}$$

(20)

Expanding $A_{\tau _2}$ and $B_{\tau _1}$ in Taylor series, we get

$$\begin{aligned}&A_{\tau _2}(T_1)=A(T_1-\varepsilon \tau _2)\cong A(T_1)-\varepsilon \tau _2A'(T_1)\nonumber \\&\quad +O(\varepsilon ^2), \end{aligned}$$

(21)

$$\begin{aligned}&B_{\tau _1}(T_1)=B(T_1-\varepsilon \tau _1)\cong B(T_1)-\varepsilon \tau _1B'(T_1)\nonumber \\&\quad +O(\varepsilon ^2) \end{aligned}$$

(22)

where prime denotes derivative w.r.t. $T_1$ . Substituting Eqs. (17–22) into (15) and (16), respectively, we get

$$\begin{aligned}&\left( D_0^2+\omega _1^2\right) x_{11}=\left( i\hat{\alpha }_1\omega _1A+2\hat{\delta }\omega _1^2A^2\bar{A}-3i\hat{\beta }_1\omega _1^3A^2\bar{A}\right. \nonumber \\&\quad -3\hat{\gamma }_1A^2\bar{A}-2i\omega _1D_1A\Big )e^{i\omega _1T_0}\nonumber \\&\quad +\left( 2\hat{\delta }\omega _1^2A^3+i\hat{\beta }_1\omega _1^3A^3- A^3\hat{\gamma }_1\right) e^{3i\omega _1T_0}\nonumber \\&\quad +\left( \hat{\lambda }_1B-\varepsilon \tau _1\hat{\lambda }_1D_1B\right) e^{- i\omega _2(\tau _1-T_0)}\nonumber \\&\quad -\frac{1}{2}i\hat{\mu }x_0\varOmega ^2e^{i\varOmega T_0}+cc, \end{aligned}$$

(23)

$$\begin{aligned}&\left( D_0^2+\omega _2^2\right) x_{21}=-\Big (i\hat{\alpha }_2\omega _2B+2i\omega _2D_1B\Big )e^{i\omega _2T_0}\nonumber&\\&\quad +\Big (\hat{\lambda }_2A-\varepsilon \tau _2\hat{\lambda }_2D_1A\Big )e^{-i\omega _1(\tau _2- T_0)}+cc \end{aligned}$$

(24)

where cc stands for the complex conjugate of the preceding terms. The particular solution of (23) and (24) is

$$\begin{aligned}&x_{11}=-\frac{\left( 2\hat{\delta }\omega _1^2A^3+i\hat{\beta }_1\omega _1^3A^3-A^3\hat{\gamma }_1\right) }{8\omega _1^2}e^{3i\omega _1T_0}\nonumber \\&\quad +\frac{(\hat{\lambda }_1B-\varepsilon \tau _1\hat{\lambda }_1D_1B)}{\left( \omega _1^2-\omega _2^2\right) }e^{-i\omega _2(\tau _1-T_0)}\nonumber \\&\quad -\frac{i\hat{\mu }x_0\varOmega ^2}{2(\omega _1^2-\varOmega ^2)}e^{i\varOmega T_0}+cc, \end{aligned}$$

(25)

$$\begin{aligned}&x_{21}=-\frac{(\hat{\lambda }_2A-\varepsilon \tau _2\hat{\lambda }_2D_1A)}{\left( \omega _1^2-\omega _2^2\right) }e^{-i\omega _1(\tau _2-T_0)}+cc. \end{aligned}$$

(26)

From (25) and (26), the resonance cases in this approximation order are

• (I) Primary resonance: $\varOmega =\omega _1$.

• (II) Internal resonance: $\omega _2=\omega _1$.

• (III) Simultaneous resonance: $\varOmega =\omega _1$ and $\omega _2=\omega _1$

Simultaneous resonance case ($\varOmega =\omega _1$ and $\omega _2=\omega _1$) is studied in this work. Closeness of simultaneous resonance can be described using detuning parameters $\sigma _1$ and $\sigma _2$ as follows:

$$\begin{aligned}&\left. \begin{aligned}&\varOmega =\omega _1+\sigma _1=\omega _1+\varepsilon \hat{\sigma }_1,\\&\omega _2=\omega _1+\sigma _2=\omega _1+\varepsilon \hat{\sigma }_2\end{aligned}\right\}&\end{aligned}$$

(27)

Insert (27) into the secular and small devisor terms in (23) and (24) to find the solvability conditions

$$\begin{aligned}&\frac{-i\hat{\mu }x_0\varOmega ^2}{2}e^{i(\omega _1+\varepsilon \hat{\sigma }_1)T_0}+\Big (i\hat{\alpha }_1\omega _1A+2\hat{\delta }\omega _1^2A^2\bar{A}\nonumber \\&\quad -3i\hat{\beta }_1\omega _1^3A^2\bar{A}-3\hat{\gamma }_1A^2\bar{A}-2i\omega _1D_1A\Big )e^{i\omega _1T_0}\nonumber \\&\quad +\Big (\hat{\lambda }_1B-\varepsilon \tau _1\hat{\lambda }_1D_1B\Big )e^{-i\tau _1\omega _2}e^{i(\omega _1+\varepsilon \hat{\sigma }_2)T_0}=0 \end{aligned}$$

(28)

$$\begin{aligned}&\Big (\hat{\lambda }_2A-\varepsilon \tau _2\hat{\lambda }_2D_1A\Big )e^{-i\tau _2\omega _1}e^{i(\omega _2- \varepsilon \hat{\sigma }_2)T_0}\nonumber \\&\quad -\Big (i\hat{\alpha }_2\omega _2B+2i\omega _2D_1B\Big )e^{i\omega _2T_0}=0 \end{aligned}$$

(29)

Divide (28) and (29) by $e^{i\omega _1T_0}$ and $e^{i\omega _2T_0}$ respectively, to obtain

$$\begin{aligned}&i\hat{\alpha }_1\omega _1A+2\hat{\delta }\omega _1^2A^2\bar{A}-3i\hat{\beta }_1\omega _1^3A^2\bar{A}-3\hat{\gamma }_1A^2\bar{A}\nonumber \\&\quad -2i\omega _1D_1A-\frac{i\hat{\mu }x_0\varOmega ^2}{2}e^{i\varepsilon \hat{\sigma }_1T_0}\nonumber \\&\quad +\big (\hat{\lambda }_1B-\varepsilon \tau _1\hat{\lambda }_1D_1B\big )e^{-i\tau _1\omega _2}e^{i\varepsilon \hat{\sigma }_2T_0}=0, \end{aligned}$$

(30)

$$\begin{aligned}&\big (\hat{\lambda }_2A-\varepsilon \tau _2\hat{\lambda }_2D_1A\big )e^{-i\tau _2\omega _1}e^{-i\varepsilon \hat{\sigma }_2T_0}\nonumber \\&\quad -\big (i\hat{\alpha }_2\omega _2B+2i\omega _2D_1B\big )=0. \end{aligned}$$

(31)

To analyze the solution of (30) and (31), express A and B in polar form as follows:

$$\begin{aligned}&A=\frac{a_1}{2}e^{i\beta _1},\ \ D_1A=\frac{a'_1}{2}e^{i\beta _1}+i\frac{a_1\beta '_1}{2}e^{i\beta _1}, \end{aligned}$$

(32)

$$\begin{aligned}&B=\frac{a_2}{2}e^{i\beta _2},\ \ D_1B=\frac{a'_2}{2}e^{i\beta _2}+i\frac{a_2\beta '_2}{2}e^{i\beta _2} \end{aligned}$$

(33)

where $a_1$ and $a_2$ are the steady-state displacement amplitudes of the beam and controller, respectively, and $\beta _1,\,\beta _2$ are the phases of the motion.

By inserting (32) and (33) into (30) and (31), returning each scaled parameter back to its real value and separating real and imaginary parts, we get

$$\begin{aligned}&\omega _1a_1\dot{\beta }_1+\tfrac{1}{4}\delta \omega _1^2a_1^3-\tfrac{3}{8}\gamma _1a_1^3+\tfrac{1}{2}\mu \,x_0\varOmega ^2\sin (\varphi _1) \nonumber \\&\quad +\tfrac{1}{2}\tau _1\lambda _1a_2\dot{\beta }_2\sin (\varphi _2-\tau _1\omega _2)\nonumber \\&\quad +\tfrac{1}{2}\big (\lambda _1a_2-\tau _1\lambda _1\dot{a}_2\big )\cos (\varphi _2-\tau _1\omega _2)=0, \end{aligned}$$

(34)

$$\begin{aligned}&\tfrac{1}{2}\alpha _1\omega _1a_1-\tfrac{3}{8}\omega _1^3\beta _1a_1^3-\omega _1\dot{a}_1-\tfrac{1}{2}\mu \,x_0\varOmega ^2\cos (\varphi _1)\nonumber \\&\quad +\tfrac{1}{2}\big (\lambda _1a_2-\tau _1\lambda _1\dot{a}_2\big )\sin (\varphi _2-\tau _1\omega _2) \nonumber \\&\quad -\tfrac{1}{2}\tau _1\lambda _1a_2\dot{\beta }_2\cos (\varphi _2-\tau _1\omega _2)=0, \end{aligned}$$

(35)

$$\begin{aligned}&\omega _2a_2\dot{\beta }_2-\tfrac{1}{2}\tau _2\lambda _2a_1\dot{\beta }_1\sin (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\tfrac{1}{2}\big (\lambda _2a_1-\tau _2\lambda _2\dot{a}_1\big )\cos (\varphi _2+\tau _2\omega _1)=0, \end{aligned}$$

(36)

$$\begin{aligned}&\tfrac{1}{2}\alpha _2\omega _2a_2+\omega _2\dot{a}_2-\tfrac{1}{2}\big (\tau _2\lambda _2\dot{a}_1-\lambda _2a_1\big )\sin (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\tfrac{1}{2}\tau _2\lambda _2a_1\dot{\beta }_1\cos (\varphi _2+\tau _2\omega _1)=0, \end{aligned}$$

(37)

where dot represents derivative w.r.t t. Hence,

$$\begin{aligned} \left. \begin{aligned}&\varphi _1=\varepsilon \hat{\sigma }_1T_0-\beta _1=\sigma _1t-\beta _1,\\&\varphi _2=\varepsilon \hat{\sigma }_2T_0-\beta _1+\beta _2=\sigma _2t-\beta _1+\beta _2.&\end{aligned}\right\} \end{aligned}$$

(38)

Differentiate (38) w.r.t. t to obtain

$$\begin{aligned}&\dot{\beta }_1=\sigma _1-\dot{\varphi }_1\ \ \text {and}\ \ \dot{\beta }_2=\big (\dot{\varphi }_2-\dot{\varphi }_1+\sigma _1-\sigma _2\big ). \end{aligned}$$

(39)

Insert (39) into Eqs. (34–37) and extract values of $\dot{a}_1,\,\dot{a}_2,\,\dot{\varphi }_1$ and $\dot{\varphi }_2$, and then, the autonomous amplitude-phase modulating equations are

$$\begin{aligned}&\dot{a}_1=\eta _1+\eta _2\cos (\varphi _1)+\eta _3\cos (\varphi _1+\psi ) \nonumber \\&\quad +\eta _4\sin (\varphi _2+\tau _2\omega _1)+\eta _5\cos (\psi )\nonumber \\&\quad +\eta _6\sin (\psi )+\eta _7\sin (\varphi _2-\tau _1\omega _2), \end{aligned}$$

(40a)

$$\begin{aligned}&\dot{\varphi }_1=\eta _8-\frac{\eta _2}{a_1}\sin (\varphi _1)-\frac{\eta _3}{a_1}\sin (\varphi _1+\psi )\nonumber \\&\quad +\frac{\eta _4}{a_1}\cos (\varphi _2+\tau _2\omega _1)+\eta _9\cos (\psi )\nonumber \\&\quad +\eta _{10}\sin (\psi )+\dfrac{\eta _7}{a_1}\cos (\varphi _2-\tau _1\omega _2), \end{aligned}$$

(40b)

$$\begin{aligned}&\dot{a}_2=\eta _{11}+\eta _{12}\sin (\varphi _1-\varphi _2+\tau _2\omega _2) \nonumber \\&\quad +\eta _{13}\sin (\varphi _1-\varphi _2-\tau _2\omega _1) \nonumber \\&\quad +\eta _{14}\sin (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\eta _{15}\cos (\varphi _2+\tau _2\omega _1)+\eta _{16}\cos (\psi )\nonumber \\&\quad +\eta _{17}\sin (\varphi _2-\tau _1\omega _2)+\eta _{18}\cos (\varphi _2-\tau _1\omega _2), \end{aligned}$$

(40c)

$$\begin{aligned}&\dot{\varphi }_2=\eta _{19}-\frac{\eta _{13}}{a_2}\cos (\varphi _1-\varphi _2-\tau _2\omega _1)-\frac{\eta _{2}}{a_1}\sin (\varphi _1)\nonumber \\&\quad -\frac{\eta _{12}}{a_2}\cos (\varphi _1-\varphi _2+\tau _1\omega _2)\nonumber \\&\quad -\frac{\eta _3}{a_1}\sin (\varphi _1+\psi )+\eta _{20}\cos (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\eta _{21}\sin (\varphi _2+\tau _2\omega _1)+\eta _{22}\sin (\varphi _2-\tau _1\omega _2)\nonumber \\&\quad +\eta _{23}\cos (\varphi _2-\tau _1\omega _2)+\eta _{24}\sin (\psi )\nonumber \\&\quad +\eta _{25}\cos (\psi ) \end{aligned}$$

(40d)

where $\psi =\tau _2\omega _1+\tau _1\omega _2$ and the coefficients $\eta _{i},\,i=1,2,\cdots ,25$ are defined in the “Appendix”.

4 Equilibrium solution

The steady-state response of both the beam and the controller can be obtained as follows

$$\begin{aligned}&\dot{a}_1=\dot{a}_2=\dot{\varphi }_1=\dot{\varphi }_2=0. \end{aligned}$$

(41)

Substituting by (41) into (39), we get

$$\begin{aligned}&\dot{\beta }_1=\sigma _1,\ \ \dot{\beta }_2=\sigma _1-\sigma _2. \end{aligned}$$

(42)

Substituting by (41) and (42) into (34) to (37), we get

$$\begin{aligned}&\omega _1a_1\sigma _1+\tfrac{1}{4}\delta \omega _1^2a_1^3-\tfrac{3}{8}\gamma _1a_1^3+\tfrac{1}{2}\mu \,x_0\varOmega ^2\sin (\varphi _1)\nonumber \\&\quad +\tfrac{1}{2}\tau _1\lambda _1a_2(\sigma _1-\sigma _2)\sin (\varphi _2-\tau _1\omega _2)\nonumber \\&\quad +\tfrac{1}{2}\lambda _1a_2\cos (\varphi _2-\tau _1\omega _2)=0, \end{aligned}$$

(43)

$$\begin{aligned}&\tfrac{1}{2}\alpha _1\omega _1a_1-\tfrac{3}{8}\omega _1^3\beta _1a_1^3-\tfrac{1}{2}\mu \,x_0\varOmega ^2\cos (\varphi _1)\nonumber \\&\quad +\tfrac{1}{2}\lambda _1a_2\sin (\varphi _2-\tau _1\omega _2)\nonumber \\&\quad -\tfrac{1}{2}\tau _1\lambda _1a_2(\sigma _1-\sigma _2)\cos (\varphi _2-\tau _1\omega _2)=0, \end{aligned}$$

(44)

$$\begin{aligned}&\omega _2a_2(\sigma _1-\sigma _2)-\tfrac{1}{2}\tau _2\lambda _2a_1\sigma _1\sin (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\tfrac{1}{2}\lambda _2a_1\cos (\varphi _2+\tau _2\omega _1)=0, \end{aligned}$$

(45)

$$\begin{aligned}&\tfrac{1}{2}\alpha _2\omega _2a_2+\tfrac{1}{2}\lambda _2a_1\sin (\varphi _2+\tau _2\omega _1)\nonumber \\&\quad +\tfrac{1}{2}\tau _2\lambda _2a_1\sigma _1\cos (\varphi _2+\tau _2\omega _1)=0. \end{aligned}$$

(46)

From (45) and (46), we can extract values of $\sin (\varphi _2)$ and $\cos (\varphi _2)$ as follows

$$\begin{aligned}&\sin (\varphi _2)=\eta _{26}\sin (\tau _2\omega _1)-\eta _{27}\cos (\tau _2\omega _1), \end{aligned}$$

(47)

$$\begin{aligned}&\cos (\varphi _2)=-\eta _{26}\cos (\tau _2\omega _1)-\eta _{27}\sin (\tau _2\omega _1). \end{aligned}$$

(48)

Substitute $\sin (\varphi _2)$ and $\cos (\varphi _2)$ in (43) and (44) and extract values of $\sin (\varphi _1)$ and $\cos (\varphi _1)$, and we get

$$\begin{aligned}&\sin (\varphi _1)=\eta _{28}+\eta _{29}\cos (\psi )+\eta _{30}\sin (\psi ), \end{aligned}$$

(49)

$$\begin{aligned}&\cos (\varphi _1)=\eta _{31}-\eta _{30}\cos (\psi )+\eta _{29}\sin (\psi ) \end{aligned}$$

(50)

By squaring and adding (45) and (46), we get the first closed-form equation

$$\begin{aligned} \tfrac{1}{4}a_2^2\omega _2^2\Big (\alpha _2^2+4(\sigma _1-\sigma _2)^2\Big )=\tfrac{1}{4}a_1^2\lambda _2^2\big (1+\sigma _1^2\tau _2^2\big ). \end{aligned}$$

(51)

By squaring and adding (49) and (50), we get the second closed-form equation

$$\begin{aligned}&(\eta _{28}+\eta _{29}\cos (\psi )+\eta _{30}\sin (\psi ))^2\nonumber \\&\quad +(\eta _{31}+\eta _{29}\sin (\psi )-\eta _{30}\cos (\psi ))^2=1 \end{aligned}$$

(52)

where $\eta _i,\,i=26,\cdots ,31$ are defined in the “Appendix”. Eqs. (51) and (52) are the frequency response equations that describe the system steady-state solution behavior for the practical case, i.e. ($a_1\ne 0,\,a_2\ne 0$).

5 Stability analysis

Stability of equilibrium solution is investigated by using Jacobian matrix J of the right-hand side of Eq. (40). To derive the stability criteria, we need to examine the behavior of small deviations from the equilibrium solutions. Thus, we assume that:

$$\begin{aligned} \left. \begin{aligned}&a_1=a_{11}+a_{10},&a_2&=a_{21}+a_{20},\\&\varphi _1=\varphi _{11}+\varphi _{10}&\varphi _2&=\varphi _{21}+\varphi _{20},\\&\dot{a}_1=\dot{a}_{11},&\dot{a}_2&=\dot{a}_{21}\\&\dot{\varphi }_1=\dot{\varphi }_{11},&\dot{\varphi }_2&=\dot{\varphi }_{21}. \end{aligned}\right\} \end{aligned}$$

(53)

Such that $a_{10}$, $\varphi _{10}$, $a_{20}$, $\varphi _{20}$ denote values of $a_1,$ $\varphi _1$, $a_2$, $\varphi _2$ at equilibrium solution. And $a_{11}$, $\varphi _{11}$, $a_{21}$, $\varphi _{21}$ are perturbations, which are assumed to be small compared to $a_{10}$, $\varphi _{10}$, $a_{20}$, $\varphi _{20}$. Substituting (53) into (40) and keeping linear terms in $a_{11}$, $\varphi _{11}$, $a_{21}$, $\varphi _{21}$, we get

$$\begin{aligned}&\dot{a}_{11}=r_{11}a_{11}+r_{12}\varphi _{11}+r_{13}a_{21}+r_{14}\varphi _{21} \end{aligned}$$

(54)

$$\begin{aligned}&\dot{\varphi }_{11}=r_{21}a_{11}+r_{22}\varphi _{11}+r_{23}a_{21}+r_{24}\varphi _{21} \end{aligned}$$

(55)

$$\begin{aligned}&\dot{a}_{21}=r_{31}a_{11}+r_{32}\varphi _{11}+r_{33}a_{21}+r_{34}\varphi _{21} \end{aligned}$$

(56)

$$\begin{aligned}&\dot{\varphi }_{21}=r_{41}a_{11}+r_{42}\varphi _{11}+r_{43}a_{21}+r_{44}\varphi _{21} \end{aligned}$$

(57)

The characteristic determinant of Eqs. (54) to (57) can be expressed as follows

$$\begin{aligned} \left| \begin{array}{cccc} r_{11}-\lambda &{} r_{12} &{} r_{13} &{} r_{14}\\ r_{21} &{} r_{22}-\lambda &{} r_{23} &{} r_{24}\\ r_{31} &{} r_{32} &{} r_{33}-\lambda &{} r_{34}\\ r_{41} &{} r_{42} &{} r_{43} &{} r_{44}-\lambda \end{array}\right| =0. \end{aligned}$$

(58)

Thus, the stability of the steady-state solution depends on the eigenvalues of the Jacobian matrix [J], which can be obtained from (58) where $r_{ij}$, i.e., $i=1,2,3,4$ and $j=1,2,3,4$ are given in the “Appendix”.

6 Analytical and numerical results

In this section, the steady-state response of the closed-loop system composed of the beam and the PPF controller is discussed analytically and numerically. The dimensionless parameters of the beam take the values $\alpha _1=0.01$, $\beta _1=0.05$, $\omega _1=3.06309$, $\gamma _1=14.4108$, $\delta =3.2746$ and $\mu =0.89663$, and the amplitude and frequency of excitation vary, respectively, in the ranges $x_0\in (0,0.1)$ and $\varOmega \in (1.5,4.5)$ approximately. The PPF controller parameters are chosen as $\alpha _2=0.05$, $\omega _2=\omega _1+\sigma _2$, $\sigma _2=0$, $\lambda _1=0.5$ and $\lambda _2=0.5$ unless specifying otherwise. In the obtained figures, solid lines correspond to stable solutions, while dashed lines correspond to unstable solutions and the numerical results for steady-state solutions are plotted as small circles.

Fig. 3

Amplitude-delay $\tau _1$ response curve for a beam and b controller at $\tau _2=0$

Fig. 4

a Time history and b Poincaré map of the beam at $\tau _1=0.04$ and $\lambda _1=0.5$

Fig. 5

a Time history and b Poincaré map of the beam at $\tau _1=0.12$ and $\lambda _1=0.5$

Fig. 6

Amplitude-delay $\tau _1$ response curve for a beam and b controller at $\tau _2=0.02$

Fig. 7

Frequency responses curves for different values of $\mu$: a the main system b the controller

The system without control was studied extensively by [17]. Figure 3 shows the amplitude-delay $\tau _1$ response curve at $\tau _2=0$ for different values of $\lambda _1$. It can be seen that the stability region of the solution decreases when control signal gain $\lambda _1$ increases. For the amplitude-delay $\tau _1$ response curve at $\lambda _1=0.5$, in the interval AB the roots of the characteristic equation are conjugate complex roots with negative real part, so the solution is stable and the beam vibrates periodically. However, in interval BC, two roots of the characteristic equation are conjugate complex roots with positive real part which corresponds to unstable focus, so the solution is unstable. So interval AB represents the time delay that system can bear without being unstable ”time margin”. The behavior of the beam at $\lambda _1=0.5$ is studied extensively in Figs. 4 and 5 by using time history and Poincaré map at different values of $\tau _1$.

Interval AB in Fig. 3 is studied extensively in Fig. 4 by studying the point $\tau _1=0.04$ as a sample from this interval.

Figure 4a, b studies the beam response at $\tau _1=0.04$ by using time history and Poincaré map, respectively. Figure 4a, b shows that the beam passes through a transient region into a steady-state region and that the steady- state solution is stable. Figure 4a shows another comparison between the numerical solution using numerical integration of Eqs. (5), (6) and analytical solution using MSPT. The dashed black lines represent the modulation of beam displacement amplitudes $a_1$ which resulted from numerical solution of Eqs. (40); in addition, the continuous blue lines represent the time history of beam displacement amplitude which resulted from numerical solution of Eqs. (5), (6). The simulation results show that Eqs. (40) describe transient and steady-state amplitudes with great precision. This comparison is used in this work with all time-histories in order to verify our results.

Interval BC in Fig. 3 is studied extensively in Fig. 5 by studying the beam response at $\tau _1=0.12$ as a sample from this interval. Figure 5a, b studies the beam response at $\tau _1=0.12$ by using time history and Poincaré map, respectively. Figure 5a, b shows that the beam vibrates a quasi-periodic motion and stability analysis shows that solution is unstable.

Amplitude-delay $\tau _1$ response curve at $\tau _1=0.02$ is presented in Fig. 6 for the beam and controller, respectively, at different values of $\lambda _1$. From Figs. 3, 6 we deduced that the time margin of the solution depends on the overall delay of the system $\tau _1+\tau _2$. So we can exchange values of $\tau _1$ and $\tau _2$ for a constant value of $\sigma _1$ to get the same time margin. It can be seen that, when control signal gain $\lambda _1$ increases, the displacement amplitude of the beam decreases and the time margin decreases.

The frequency response curve for beam and controller under different values of $\tau _1$ and $\tau _2$ is presented in Fig. 7. The figure shows that there is a good vibration suppression bandwidth indicated by the dotted rectangle in the figure and the system response is stable. Increasing values of $\tau _1$ and/or $\tau _2$ “within time margins which are indicated by Figs. 3, 6” has no effect on vibration suppression bandwidth but changes only the peak displacement amplitudes for the beam and controller. Figure 8 verifies the results of Fig. 7 numerically at $\tau _1=\tau _2=0.02$. It can be seen that the numerical simulation results are in good agreement with analytical solution result. From previous results, if overall time delay in the system is small then we can increase values of $\lambda _1$ and $\lambda _2$ to increase the vibration suppression bandwidth.

Fig. 8

Numerical simulation of FRC of a beam and b controller at $\tau _1=\tau _2=0.02$

Figure 9a, b presents the frequency response of the beam and controller, respectively, at $\tau _2=0.03$ when $\tau _1$ changes within the permissible time margin. Effect of changing $\tau _1$ on the peak displacement amplitudes is obvious in the figure.

In this work, it is assumed that the beam vibrates in the presence of external harmonic excitation close to its natural frequency. From previous results, there is a good vibration suppression bandwidth around excitation frequency especially when overall time delay in the system is small as seen in Figs. 7, 9. However, if excitation frequency turns to make the beam out of the indicated vibration suppression bandwidth, we can tune controller natural frequency to be ($\varOmega =\omega _2$), i.e., as indicated by [3]. If excitation frequency increases, i.e., beam turns to vibrate with the right peak displacement amplitude, it is advisable to increase controller natural frequency. If excitation decreases, i.e., beam turns to vibrate with the left peak displacement amplitude, it is advisable to decrease controller natural frequency. This tuning process can be applied practically if the rate of change of excitation frequency can be accompanied by tuning controller natural frequency, i.e., $\varOmega =\omega _2$. This idea is explained explicitly in the following parts.

Fig. 9

a Beam response and b controller response versus $\sigma _1$ and $\tau _1$ at $\tau _2=0.03$

Figure 10 studies amplitude-delay $\tau _1$ response curve at different values of $\sigma _2$. We use this figure to know the time margin at these values of $\sigma _2$. From this figure, we can observe that, in case of $\sigma _1=\sigma _2=0.1$, the displacement amplitudes of the beam and controller increase slightly, but the time margin increases; in case of $\sigma _1=\sigma _2=-0.1$, the displacement amplitudes of the beam and controller are smaller than the previous case, but the time margin decreases.

Fig. 10

Amplitude-delay $\tau _1$ response curve for a beam and b controller at different values of $\sigma _1=\sigma _2$

Fig. 11

Frequency responses curves of a beam and b controller for different values $\sigma _2$

In addition, Fig. 11 studies the effect of controller natural frequency on FRC of beam and controller at $\tau _1=\tau _2=0.01$, respectively. This figure shows that minimum beam steady-state displacement amplitude occurs when $\sigma _1=\sigma _2$, i.e., ($\varOmega =\omega _2$). So it is recommended to tune the controller natural frequency to be equal to excitation frequency for dynamical systems which are subjected to the variable excitation frequency. This tuning process can be applied practically if the rate of change of excitation frequency can be accompanied by tuning controller natural frequency, i.e., $\varOmega =\omega _2$. However, the existence of long time delay can prevent this tuning for negative values of because this can lead system to instability as shown in Fig. 10.

Figure 12 presents the force–amplitude response curve of the beam and controller, respectively. Figure 12a shows the force–amplitude response curve for the uncontrolled beam and two cases (A, B) for controlled beam. In case A, the overall time delay in the closed-loop system is large, so we used small values for $\lambda _1$ and $\lambda _2$ to protect the system from instability. So parameters values in case A are $\tau _1=\tau _2=0.04$ and $\lambda _1=\lambda _2=0.5$. If the controlled beam response in case A is compared with the uncontrolled beam response, we will find that the beam response in case A is better than the response of the uncontrolled beam. If overall time delay in the closed-loop system is small, we can get a better response than that of case A by using larger values of $\lambda _1$ and $\lambda _2$. So parameters values in case B are $\tau _1=\tau _2=0.005$ and $\lambda _1=\lambda _2=3$. Vibration suppression in case B is better than case A, but we cannot use case B if overall time delay in the closed-loop system is small. All analytical results in Fig. 12 are verified numerically by using small circles with the same color of the corresponding analytical result.

Fig. 12

Force–amplitude response curve of a beam and b controller at ($\sigma _1=\sigma _2=0$)

Fig. 13

Time history of the uncontrolled beam at $\sigma _1=0$

Fig. 14

Time response of a beam and b controller at $\sigma _1=\sigma _2=0$, $\tau _1=0.02$ and $\tau _2=0.01$

Fig. 15

Time response of a beam and b controller at $\sigma _1=\sigma _2=0$, $\tau _1=0.04$ and $\tau _2=0.03$

Fig. 16

Time response of a beam and b controller at $\sigma _1=\sigma _2=0.1$, $\tau _1=0.04$ and $\tau _2=0.03$

Figure 13 shows the time history of the uncontrolled beam at $\sigma _1=0$. Figure 14 shows the time history of the beam and controller at $\sigma _1=\sigma _2=0$, $\tau _1=0.02$ and $\tau _2=0.01$. Figure 15 shows the time history of the beam and controller at $\sigma _1=\sigma _2=0$, $\tau _1=0.04$ and $\tau _2=0.03$. From Figs. 14, 15, we see that when time delays increase within the time margin the transient state for the system increases and the system approximately reaches the same steady-state displacement amplitudes. Time history for the beam and controller at $\sigma _1=\sigma _2=0.1$, $\tau _1=0.04$ and $\tau _2=0.03$ is shown in Fig. 16. The transient region in Fig. 16 is less than the transient region in Fig. 15. The steady-state displacement amplitude decreases when control and/or feedback gains increase. Also, we can see that the steady- state displacement amplitudes of the beam in Figs. 14 to 16 are much smaller than the steady-state displacement amplitude of the uncontrolled beam in Fig. 13.

7 Conclusion

The model of a beam and its characteristic parameters are presented [17]. In this paper, the time delays, in the control signal and the feedback signal, are taken into our consideration for different values of controller parameters. We are interested in determining the time margin which is the amount of time delay that system can bear without being unstable. The analytic solution is investigated using MTSP method [18]. A comparison of the analytic results and the solutions obtained by Runge–Kutta fourth-order accuracy numerical method is illustrated which prove a good agreement. Theoretical results showed that the time margin depends on the overall delay of the system $\tau _1+\tau _2$. The proposed control with time delay shows that the time margin decreases when control and feedback gains “$\lambda _1$ and/or $\lambda _2$” increase; however, increasing control and feedback gains can widen the vibration suppression bandwidth. The choice of $\lambda _1$ and/or $\lambda _2$ values depends on the overall delay of the system $\tau _1+\tau _2$. There is a good vibration suppression bandwidth and stable system operation if time delays change within the specified time margin. Increasing values of $\tau _1$ and/or $\tau _2$ within the specified time margins have no effect on vibration suppression bandwidth but changes only the peak displacement amplitudes for the beam and controller. Apart from the considered resonance case, there are two peak displacement amplitudes of the beam. This problem can be solved by tuning the controller natural frequency such that $\varOmega =\omega _2$. So the minimum beam steady-state displacement amplitude occurs at $\sigma _2=\sigma _1$. From this result, we can recommend tuning the controller natural frequency to be equal to the excitation frequency. This recommendation can be applied to the dynamical systems which are subjected to variable excitation frequency out the original vibration suppression bandwidth around $\sigma _1=0$ when the rate of change in excitation frequency can be accompanied by tuning controller natural frequency, i.e., $\varOmega =\omega _2$ and loop delay $\tau _1+\tau _2$ is small. The time margin increases monotonically as controller natural frequency is increased. The transient response region increases as time delays increase.

Appendix

$$\begin{aligned} \dfrac{1}{\rho }= & {} \big (\lambda _1^2\lambda _2^2\tau _1^2\tau _2^2+8\lambda _1\lambda _2\tau _1\tau _2\omega _1\omega _2\cos (\psi )\\&\quad +16\omega _1^2\omega _2^2\big ),\\ \eta _1= & {} a_1\rho \big (\lambda _1^2\lambda _2^2\tau _1^2\tau _2+2\omega _1^2\omega _2^2(4\alpha _1-3\alpha _1^2\beta _1\omega _1^2)\big ),\\ \eta _2= & {} -\rho \big (8\mu \varOmega ^2x_0\omega _1\omega _2^2\big ),\\ \eta _3= & {} -\rho \big (2\mu \varOmega ^2x_0\lambda _1\lambda _2\tau _1\tau _2\omega _2\big ),\\ \eta _4= & {} \rho \big (a_2\lambda _1^2\lambda _2\tau _1\tau _2\omega _2(2+\alpha _2\tau _1)\big ),\\ \eta _5= & {} \frac{1}{2}\rho \big (a_1\lambda _1\lambda _2\tau _1\omega _1\omega _2(8+4\alpha _1\tau _2-3a_1^2\beta _1\tau _2\omega _1^2)\big ),\\ \eta _6= & {} \frac{1}{2}\rho \big (a_1^3\lambda _1\lambda _2\tau _1\tau _2\omega _2(-3\gamma _1+2\delta \omega _1^2)\big ),\\ \eta _7= & {} \rho \big (4a_2\lambda _1\omega _1\omega _2^2(2+\alpha _2\tau _1)\big ),\\ \eta _8= & {} \rho \big (\lambda _1^2\lambda _2^2\sigma _1\tau _1^2\tau _2^2+2\omega _1\omega _2^2\big (8\sigma _1\omega _1+a_1^2(-3\gamma _1\\&+\,2\delta \omega _1^2)\big )\big ),\\ \eta _9= & {} \frac{1}{2}\rho \big (\lambda _1\lambda _2\tau _1\tau _2\omega _2\big (16\sigma _1\omega _1+a_1^2(-3\gamma _1+2\delta \omega _1^2)\big )\big ),\\ \eta _{10}= & {} \frac{1}{2}\rho \big (\lambda _1\lambda _2\tau _1\omega _1\omega _2\big (8-4\alpha _1\tau _2+3a_1^2\beta _1\tau _2\omega _1^2\big )\big ),\\ \eta _{11}= & {} \rho a_2\big (\lambda _1^2\lambda _2^2\tau _1\tau _2^2-8\alpha _2\omega _1^2\omega _2^2\big )\big ),\\ \eta _{12}= & {} \rho \mu \varOmega ^2x_0\lambda _1\lambda _2^2\tau _1\tau _2^2,\\ \eta _{13}= & {} 4\rho \mu \varOmega ^2x_0\lambda _2\tau _2\omega _1\omega _2,\\ \eta _{14}= & {} \rho a_1\lambda _2\omega _1^2\omega _2\big (-8+4\alpha _1\tau _2-3a_1^2\beta _1\tau _2\omega _1^2\big ),\\ \eta _{15}= & {} \rho a_1^3\lambda _2\tau _2\omega _1\omega _2\big (-3\gamma _1+2\delta \omega _1^2\big ),\\ \eta _{16}= & {} -2\rho a_2\lambda _1\lambda _2\tau _2\omega _1\omega _2(-2+\alpha _2\tau _1),\\ \eta _{17}= & {} \frac{1}{4}\rho a_1\lambda _1\lambda _2^2\tau _1\tau _2\omega _1(8-4\alpha _1\tau _2+3a_1^2\beta _1\tau _2\omega _1^2),\\ \eta _{18}= & {} \frac{1}{4}\rho a_1^3\lambda _1\lambda _2^2\tau _1\tau _2^2(-3\gamma _1+2\delta \omega _1^2),\\ \eta _{19}= & {} \rho \big (\lambda _1^2\lambda _2^2\sigma _2\tau _1^2\tau _2^2+2\omega _1\omega _2^2\big (8\sigma _2\omega _1+a_1^2(-3\gamma _1\\&\quad +\,2\delta \omega _1^2)\big )\big ),\\ \eta _{20}= & {} \dfrac{1}{a_1a_2}\rho \lambda _2\omega _2\big (4(-2+\alpha _1\tau _2)\omega _1^2a_1^2-3\beta _1\tau _2\omega _1^4a_1^4\\&\quad \lambda _1^2\tau _1(2+\alpha _2\tau _1)\tau _2a_2^2\big ),\\ \end{aligned}$$

$$\begin{aligned} \eta _{21}= & {} \dfrac{1}{a_2}\rho \lambda _2\tau _2\omega _1\omega _2a_1^3\big (3\gamma _1-2\delta \omega _1^2\big ),\\ \eta _{22}= & {} \dfrac{1}{4a_2}\rho \lambda _1\lambda _2^2\tau _1\tau _2^2\big (3\gamma _1-2\delta \omega _1^2\big )a_1^3,\\ \eta _{23}= & {} \dfrac{1}{4a_1a_2}\rho \lambda _1\omega _1\big (\lambda _1^2\tau _1\tau _2a_1^2\big (-8+4\alpha _1\tau _2\\&-\,3\beta _1\tau _2\omega _1^2a_1^2\big )+16(2+\alpha _2\tau _1)\omega _2^2a_2^2\big ),\\ \eta _{24}= & {} \frac{1}{2}\rho \lambda _1\lambda _2\omega _1\omega _2\big (-8\tau _2+\tau _1\big (8-4\alpha _1\tau _2-4\alpha _2\tau _2\\&+\,3a_1^2\beta _1\tau _2\omega _1^2\big )\big ),\\ \eta _{25}= & {} \frac{1}{2}\rho \lambda _1\lambda _2\tau _1\tau _2\omega _2\big (16\sigma _2\omega _1+a_1^2(-3\gamma _1+2\delta \omega _1^2)\big ),\\ \eta _{26}= & {} \dfrac{a_2(-2\sigma _2+\sigma _1(2+\alpha _2\tau _2))\omega _2}{a_1\lambda _2(1+\sigma _1^2\tau _2^2)},\\ \eta _{27}= & {} \dfrac{a_2(\alpha _2+2\sigma _1(-\sigma _1+\sigma _1)\tau _2)\omega _2}{a_1\lambda _2(1+\sigma _1^2\tau _2^2)},\\ \eta _{28}= & {} \dfrac{a_1\big (-8\sigma _1\omega _1+a_1^2(3\gamma _1-2\delta \omega _1^2)\big )}{4\mu \varOmega ^2x_0},\\ \eta _{29}= & {} \dfrac{a_2^2\lambda _1\omega _2}{\mu \varOmega ^2a_1x_0\lambda _2(1+\sigma _1^2\tau _2^2)}\Big ((\sigma _1-\sigma _2)(2+\alpha _2\tau _1\big )\\&\quad +\,\sigma _1\tau _2(\alpha _2-2(\sigma _1-\sigma _2)^2\tau _1)\Big ),\\ \eta _{30}= & {} \dfrac{a_2^2\lambda _1\omega _2}{\mu \varOmega ^2a_1x_0\lambda _2(1+\sigma _1^2\tau _2^2)}\Big [\alpha _2\big (1\\&+\,\sigma _1\tau _1\tau _2(\sigma _2-\sigma _1)\big )\\&-\,2(\sigma _1-\sigma _2)\big (-\sigma _2\tau _1+\sigma _1(\tau _1+\tau _2)\big )\Big ],\\ \eta _{31}= & {} \dfrac{4a_1\alpha _1\omega _1-3a_1^3\beta _1\omega _1^3}{4\mu \varOmega ^2x_0},\\ r_{11}= & {} \frac{1}{2}\rho \Big [2\lambda _1^2\lambda _2^2\tau _1^2\tau _2\\&+\,\lambda _1\lambda _2\tau _1\omega _2\Big (12\omega _1a_{10}^2\tau _2\cos (\psi )(2+\alpha _1\tau _2)\\&+\,\big (3\gamma _1\sin (\psi )-2\delta \omega _1^2\sin (\psi )+3\beta _1\omega _1^3\cos (\psi )\big )\Big )\\&+\,4\omega _1^2\omega _2^2(4\alpha _1-9a_{10}^2\beta _1\omega _1^2)\Big ],\\ r_{12}= & {} 2\rho \mu \varOmega ^2x_0\omega _2\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{10}+\psi )\\&+\,4\omega _1\omega _2\sin (\varphi _{10})\big ),\\ r_{13}= & {} \rho \lambda _1\omega _2(2+\alpha _2\tau _1)\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}+\tau _2\omega _1)\\&+\,4\omega _1\omega _2\sin (\varphi _{20}-\tau _1\omega _2)\big ),\\ r_{14}= & {} a_{20}\lambda _1\omega _2(2+\alpha _2\tau _1)\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}+\tau _2\omega _1)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}-\tau _1\omega _2)\big ), \end{aligned}$$

$$\begin{aligned} r_{21}= & {} -\dfrac{\omega _2\rho }{a_{10}^2}\Big [\dfrac{r_{14}}{\omega _2\rho }+2\mu \varOmega ^2x_0\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{10}+\psi )\\&+\,4\omega _1\omega _2\sin (\varphi _{10})\big )\\&+\,a_{10}^3\big \{3\gamma _1\lambda _1\lambda _2\tau _2\tau _2\big (\cos (\psi )+4\omega _1\omega _2\big )\\&-\,\omega _1^2\big (\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \cos (\psi )+3\beta _1\omega _1\sin (\psi )\big )\\&+\,8\delta \omega _1\omega _2\big )\big \}\Big ],\\ r_{22}= & {} \dfrac{2\rho }{a_{10}}\mu \varOmega ^2x_0\omega _2\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{10}+\psi )\\&+\,4\omega _1\omega _2\cos (\varphi _{10})\big ),\\ r_{23}= & {} \dfrac{1}{a_{10}}\rho \lambda _1\omega _2(2+\alpha _2\tau _1)\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}+\tau _2\omega _1)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}-\tau _1\omega _2)\big ),\\ r_{24}= & {} -\dfrac{a_{20}}{a_{10}}r_{13},\\ r_{31}= & {} -\dfrac{\rho \lambda _2}{4}\Big [-4\omega _2(-2+\alpha _1\tau _2)\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}\\&-\,\tau _1\omega _2)+4\omega _1\omega _2\sin (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,3a_{10}^2\tau _2\big (3\gamma _1\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}+\tau _2\omega _1)\big )+\omega _1^2\big (-\lambda _1\lambda _2\tau _1\tau _2 \end{aligned}$$

$$\begin{aligned}&\quad \big (2\delta \cos (\varphi _{20}-\tau _1\omega _2)-3\beta _1\omega _1\sin (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,4\omega _1\omega _2\big (-2\delta \cos (\varphi _{20}+\tau _2\omega _1)\\&+\,3\beta _1\omega _1\sin (\varphi _{20}+\tau _2\omega _1)\big )\big )\big )\Big ],\\ r_{32}= & {} \rho \mu \varOmega ^2x_0\lambda _2\tau _2\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{10}-\varphi _{20}+\tau _1\omega _2)\\&+\,4\omega _1\omega _1\cos (\varphi _{10}-\varphi _{20}-\tau _2\omega _1)\big ),\\ r_{33}= & {} \rho \big (\lambda _1^2\lambda _2^2\tau _1\tau _2^2-8\alpha _2\omega _1^2\omega _2^2\\&-\,2\lambda _1\lambda _2\tau _2\omega _1\omega _2(-2+\alpha _2\tau _2)\cos (\psi )\big ),\\ r_{34}= & {} -\frac{1}{4}\rho \lambda _2\Big [4\mu \varOmega ^2x_0\tau _2\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{10}-\varphi _{20}\\&+\,\tau _1\omega _2)+4\omega _1\omega _2\cos (\varphi _{10}-\varphi _{20}-\tau _2\omega _1)\big )\\&+\,a_{10}\big \{-4\omega _1(-2+\alpha _1\tau _2)\\&\quad \big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,a_{10}^2\tau _2(-3\gamma _1\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\sin (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,\omega _1^2\big (\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \sin (\varphi _{20}-\tau _1\omega _2)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,4\omega _1\omega _2\big (2\delta \sin (\varphi _{20}+\tau _2\omega _1)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}+\tau _2\omega _1)\big )\big )\big )\big \}\Big ], \end{aligned}$$

$$\begin{aligned} r_{41}= & {} \dfrac{\rho }{4a_{10}^2a_{20}}\Big [4a_{10}^2\lambda _2\omega _1(-2+\alpha _1\tau _2)\\&\quad \big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,4a_{10}^3a_{20}\omega _2\big (-3\gamma _1\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\psi )\\&+\,4\omega _1\omega _2\big )+\omega _1^2\big (\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \cos (\psi )\\&+\,3\beta _1\omega _1\sin (\psi )\big )+8\delta \omega _1\omega _2\big )\big )\\&-\,4a_{20}\omega _2\big (a_{20}\lambda _1(2+\alpha _2\tau _1)(\lambda _1\lambda _2\tau _1\tau _2 \,\hbox {cos}(\varphi _{20}+\tau _2 \omega _1)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,2\mu \varOmega ^2x_0\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{10}+\psi )\\&+\,4\omega _1\omega _2\sin (\varphi _{10})\big )\big )\\&-\,3a_{10}^4\lambda _2\tau _2\big (-3\gamma _1\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\sin (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,\omega _1^2\big (\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \sin (\varphi _{20}-\tau _1\omega _2)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,4\omega _1\omega _2\big (2\delta \sin (\varphi _{20}+\tau _2\omega _1)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}+\tau _2\omega _1)\big )\big )\big )\Big ],\\ r_{42}= & {} \dfrac{\rho \mu \varOmega ^2x_0}{a_{10}a_{20}}\Big [2a_{20}\omega _2\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{10}+\psi ) \end{aligned}$$

$$\begin{aligned}&+\,4\omega _1\omega _2\cos (\varphi _{10})\big )\\&+\,a_{10}\lambda _2\tau _2\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{10}-\varphi _{20}+\tau _1\omega _2)\\&+\,4\omega _1\omega _2\sin (\varphi _{10}-\varphi _{20}-\tau _2\omega _1)\big )\Big ],\\ r_{43}= & {} \dfrac{\rho }{4a_{10}a_{20}^2}\Big [4\mu \varOmega ^2a_{10}x_0\lambda _2\tau _2\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{10}\\&-\varphi _{20}+\tau _1\omega _2)\\&+\,4\omega _1\omega _2\cos (\varphi _{10}-\varphi _{20}-\tau _2\omega _1)\big )\\&-\,4a_{10}^2\lambda _2\omega _1\big (-2+\alpha _1\tau _2)\big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}\\&+4\omega _1 \omega _2 \cos (\varphi _{20}+\tau _2 \omega _1)-\tau _1\omega _2)\big )\\&+\,4a_{20}^2\lambda _1\omega _2(2+\alpha _2\tau _1)\\&\quad \big (\lambda _1\lambda _2\tau _1\tau _2\cos (\varphi _{20}+\tau _2\omega _1)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,a_{10}^4\lambda _2\tau _2\big (-3\gamma _1\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\sin (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,\omega _1^2\big (\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \sin (\varphi _{20}-\tau _1\omega _2)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,4\omega _1\omega _2\big (2\delta \sin (\varphi _{20}+\tau _2\omega _1)\\&+\,3\beta _1\omega _1\cos (\varphi _{20}+\tau _2\omega _1)\big )\big )\big )\Big ],\\ \end{aligned}$$

$$\begin{aligned} r_{44}= & {} \dfrac{\rho }{4a_{10}a_{20}}\Big [-4\mu \varOmega ^2a_{10}x_0\lambda _2\tau _2\big (\lambda _1\lambda _2\tau _1\tau _2\\&\quad \sin (\varphi _{10}-\varphi _{20}+\tau _1\omega _1)+4\omega _1\omega _2\sin (\varphi _{10}\\&-\,\varphi _{20}-\tau _2\omega _1)\big )-4a_{10}^2\lambda _2\omega _1(-2+\alpha _1\tau _2)\\&\quad \big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\sin (\varphi _{20}+\tau _2\omega _1)\big )\\&-\,4a_{20}^2\lambda _1\omega _2(2+\alpha _2\tau _1)\big (\lambda _1\lambda _2\tau _1\tau _2\sin (\varphi _{20}\\&+\,\tau _2\omega _1)+4\omega _1\omega _2\sin (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,a_{10}^4\lambda _2\tau _2\big (3\gamma _1\big (\lambda _1\lambda _2\tau _2\tau _2\cos (\varphi _{20}-\tau _1\omega _2)\\&+\,4\omega _1\omega _2\cos (\varphi _{20}+\tau _2\omega _1)\big )\\&+\,\omega _1^2\big (-\lambda _1\lambda _2\tau _1\tau _2\big (2\delta \cos (\varphi _{20}-\tau _1\omega _2)\\&-\,3\beta _1\omega _1\sin (\varphi _{20}-\tau _1\omega _2)\big )\\&+\,4\omega _1\omega _2\big (-2\delta \cos (\varphi _{20}+\tau _2\omega _1)\\&+\,3\beta _1\omega _1\sin (\varphi _{20}+\tau _2\omega _1)\big )\big )\big )\Big ]. \end{aligned}$$