Primary and secondary resonance analyses of a cantilever beam carrying an intermediate lumped mass with time-delay feedback

Abstract

Time-delay displacement and velocity feedback of different types of active control in a cantilever beam carrying an lumped mass is investigated in this paper. Based on Euler–Bernoulli beam theory, the nonlinear governing equation is studied with damping, harmonic distribution, displacement delay, velocity delay and two time delays. The multiple scales perturbation method is applied to obtain the frequency response equations near primary, superharmonic and subharmonic resonances. A thorough study on the stability is proposed, with a particular emphasis on delay feedback. The results show that the hardening and softening behaviors of the system depend on the location of lumped mass. Furthermore, the displacement feedback gain coefficient only makes the peak amplitude move to the low frequency, yet velocity feedback coefficient and their time delays can be used to effectively enhance the stability and quench the nonlinear vibration of the cantilever beam. Thus, reasonable selection of the control system parameters can effectively improve the level of vibration control for the mechanical system.

1 Introduction

The study of a cantilever beam with an intermediate lumped mass at an arbitrary position subjected to base excitation can find applications in robotic manipulators, components of high-speed machinery, structural buildings and many other structural elements [1,2,3,4,5]. If internal resonance is involved in such a system, the response and stability analysis will be more complicated. Therefore, the study of instability has attracted much attention in recent years [6,7,8,9,10]. For example, Nayfeh and Younis [11] studied the dynamics of electrically actuated microbeams under secondary, superharmonic and subharmonic resonances and found that a dynamic pull-in instability can occur at an electric load much lower than a pure DC voltage. Ekici and Boyaci [12] examined the nonlinear vibrations of microbeams using the multiple scales method and solved the equation of motion for two cases of subharmonic and superharmonic resonances. It was found that nonideal boundary conditions have a certain influence on the vibration of microbeams. Mehran et al. [13] studied the nonlinear forced vibration of a cantilever beam with an intermediate lumped mass and found that the frequency response of the cantilever beam is strongly influenced by the damping and excitation levels. Eftekhari et al [14, 15] investigated the dynamical behaviors of an aeroelastic panel and pointed out that for linear systems, a nonlinear feedback force should be used to obtain bifurcation boundary and produce limit cycle oscillation as the system response. Oveissi et al [16] and Toghraie et al [17] all studied the vibration and instability of axially moving carbon nanotubes conveying fluids and found that the stationary CNT conveying fluid is more stable than all cases of the axially moving CNT conveying fluid.

In addition to the study of a cantilever beam with an intermediate lumped mass, the control of various nonlinear systems [18,19,20,21,22] has been investigated recently. Because the flexibility of active control and time delay [23,24,25,26,27] are more common and unavoidable in controlled systems, many researchers are working on nonlinear systems with time delay. For example, Hu et al. [28] studied the resonance of a harmonic forced Duffing oscillator with time-delay feedback using a multiple scales method. They found that appropriate choices of the feedback gain coefficient and the time delay value enable better vibration control. Hu and Wang [29] considered the primary and subharmonic resonances of a harmonic forced Duffing oscillator with time delay and discussed the stability of periodic motion. In Refs. [30,31,32,33,34,35,36,37], the authors studied time-delay controllers and found that the time delay can be used as a control parameter to suppress the vibration of the dynamic system. Alhazza et al. [38,39,40] studied the nonlinear vibrations of a cantilever beam when excited externally and parametrically with linear and nonlinear time-delay feedback control. They found that time-delay control could feasibly reduce the system vibrations. Daqaq et al. [41] studied the nonlinear vibration of a piezoelectric-coupled cantilever beam by time-delay acceleration feedback control. They demonstrated that when the excitation frequency is very close to the least-damped delay frequency and the excitation amplitude is sufficiently large, the homogeneous solution emanating from the delayed feedback locks onto the particular solution resulting from the primary excitation.

Although many studies have been carried out on the stability of systems under time-delay control, to the best of the author’s knowledge, a rigorous analysis of cantilever beams carrying a lumped mass has not been presented. In this paper, the nonlinear behavior of a cantilever beam carrying a lumped mass with both delayed displacement and velocity feedbacks is investigated. Based on Euler–Bernoulli beam theory, the nonlinear governing equation is studied with damping, harmonic distribution, displacement delay, velocity delay and two time delays. The primary and secondary resonances of this control system are determined using multiple scales analysis. All subharmonic and superharmonic conditions are obtained. The steady-state frequency response curves of the system in each case are given, and the amplitude-stable and unstable portions of the frequency response are determined. Then, comprehensive sensitivity studies are carried out for different time-delay parameters (displacement feedback gain coefficient, velocity feedback gain coefficient, displacement feedback and velocity feedback), and the effects of different parameters on the nonlinear system behavior are compared.

2 Mathematical model

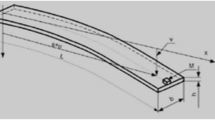
In this section, a cantilever beam carrying an intermediate lumped mass is shown in Fig. 1. The cantilever beam with a length l and a mass per unit length m has a lumped mass located at a distance d from its base. The cantilever beam is connected to a joint rotation spring of $K_r$ at the base and is subjected to a harmonic distribution load of amplitude P. We use the total kinetic and potential energy of the beam to obtain the corresponding Lagrangian:

$$\begin{aligned} L=\frac{ml}{2}\left[ {\begin{array}{l} c_1 \left( {\frac{\hbox {d}u}{\hbox {d}\tau }} \right) ^{2}+\frac{c_3 u^{2}}{l^{2}}\left( {\frac{\hbox {d}u}{\hbox {d}\tau }} \right) ^{2}+\frac{c_4 u^{2}}{l^{2}}\left( {\frac{\hbox {d}u}{\hbox {d}\tau }} \right) ^{2}\\ +\frac{c_5 u^{4}}{l^{4}}\left( {\frac{\hbox {d}u}{\hbox {d}\tau }} \right) ^{2}+\frac{c_6 u^{4}}{l^{4}}\left( {\frac{\hbox {d}u}{\hbox {d}\tau }} \right) ^{2} \\ -\left( {\frac{EI}{ml^{4}}} \right) \left( {c_2 u^{2}+\frac{c_7 u^{4}}{l^{2}}+\frac{c_8 u^{6}}{l^{4}}} \right) \\ \end{array}} \right] \end{aligned}$$

where $u\left( \tau \right)$ denotes the time dependence of the beam displacement. E and I represent the Young’s modulus of elasticity and the moment of inertia, respectively.

The constant values $c_1 -c_8$ are defined as follows:

$$\begin{aligned} \begin{array}{l} c_1 =\int _0^1 {\phi ^{2}} \hbox {d}\varsigma +\rho \phi ^{2}\left( \eta \right) ;\,\,c_2 =\int _0^1 {{\phi }''^{2}} \hbox {d}\varsigma ;\,\,\\ c_3 =\int _0^1 {\left( {\int _0^\varsigma {{{\phi }}'^{2}\hbox {d}\chi } } \right) } ^{2}\hbox {d}\varsigma ; \\ c_4 =\rho \left[ {\left( {\int _0^\varsigma {{{\phi }}'^{2}\hbox {d}\chi } } \right) ^{2}} \right] _{\varsigma =\eta } ;\,\,\\ c_5 =\int _0^1 {\left[ {\left( {\int _0^\varsigma {{{\phi }}'^{2}\hbox {d}\chi } } \right) \left( {\int _0^\varsigma {{{\phi }}'^{4}\hbox {d}\chi } } \right) } \right] } \hbox {d}\varsigma ; \\ c_6 =\rho \left[ {\left( {\int _0^\varsigma {{{\phi }}'^{2}\hbox {d}\chi } } \right) \left( {\int _0^\varsigma {{{\phi }}'^{4}\hbox {d}\chi } } \right) } \right] _{\varsigma =\eta } ;\,\,\\ c_7 =\int _0^1 {{{\phi }}'^{2}} {\phi }''^{2}\hbox {d}\varsigma ;\,\,c_8 =\int _0^1 {{{\phi }}'^{4}} {\phi }''^{2}\hbox {d}\varsigma \\ \end{array} \end{aligned}$$

where $\phi \left( \varsigma \right)$ is the eigenfunction of the beam, which is written as [24] $\phi \left( \zeta \right) =\frac{\sin \beta \zeta -U\sinh \beta \zeta -V\left( {\cos \beta \zeta -\cosh \beta \zeta } \right) }{r}$

Here, $r(r=\phi \left( 1 \right) )$ is the scaling factor, $\beta$ is a dimensionless frequency parameter defined by $\beta ^{4}=\frac{m\omega _0^2 l^{4}}{EI}$, and $\omega _0$ is the natural frequency of the beam. U and V are, respectively, defined as $U=\frac{lK_r \,-\,2EI\beta \sin \beta \left( {\cos \beta \,+\,\cosh \beta } \right) }{lK_r \,+\,2EI\beta \sinh \beta \left( {\cos \beta \,+\,\cosh \beta } \right) }$, $V=\frac{\sin \beta \,+\,U\sinh \beta }{\cos \beta \,+\,\cosh \beta }$.

The dimensionless parameters $\eta =\frac{d}{l},\,\,\varsigma =\frac{s}{l},\,\,\rho =\frac{M}{ml}$ represent the distance, span length and mass ratio, respectively. $\rho$ is the mass density per unit length.

By employing the Euler-Lagrange equation, the dimensionless governing equation of motion for the dynamics is as follows [17]:

$$\begin{aligned}&\ddot{u}+u+\mu \dot{u}+\alpha _1 u^{3}+\alpha _2 u^{5}+\beta _1 u^{2}\ddot{u}+\beta _1 u\dot{u}^{2}\nonumber \\&\quad +\beta _2 u^{4}\ddot{u}+\beta _2 u^{3}\dot{u}^{2}=F\cos \left( {\Omega t} \right) \end{aligned}$$

(1)

where $\mu$ is the damping coefficient. The coefficients $\alpha _1 ,\,\,\alpha _2 ,\,\,\beta _1$ and $\beta _2$ are defined as $\alpha _1 =\frac{2c_7 }{c_2 },\,\,\alpha _2 =\frac{2c_8 }{c_2 },\,\beta _1 =\frac{c_3 c_4 }{\beta ^{4}c_1 },\,\,\beta _2 =\frac{c_5 c_6 }{\beta ^{4}c_1 }$. $t=\tau \sqrt{\frac{EIc_2 }{l^{4}c_1 m}}$, $F=\frac{P}{\int _0^1 {\phi ^{2}\hbox {d}\varsigma } }$, and $\Omega =\frac{\omega }{\omega _0 }$ is the dimensionless excitation frequency.

Fig. 1

Schematic of a cantilever beam carrying a lumped mass under harmonic loading

By integrating the time-delayed displacement and velocity feedback controller into system (1), Eq. (2) becomes the following:

$$\begin{aligned}&\ddot{u}+u+\mu \dot{u}+\alpha _1 u^{3}+\alpha _2 u^{5}+\beta _1 u^{2}\ddot{u}+\beta _1 u\dot{u}^{2}\nonumber \\&\quad +\beta _2 u^{4}\ddot{u}+\beta _2 u^{3}\dot{u}^{2}=F\cos \left( {\Omega t} \right) +g_p u\left( {t-\tau _1 } \right) \nonumber \\&\quad +g_d \dot{u}\left( {t-\tau _2 } \right) \end{aligned}$$

(2)

where $g_p$, $g_d$, $\tau _1$ and $\tau _2$ are the displacement feedback coefficient, velocity feedback coefficient and time delays of the displacement and velocity feedbacks, respectively.

3 Multiple scales method

3.1 Primary resonance

In this section, we use the multiple scales method to obtain an accurate analytical solution of a cantilever beam. To obtain the primary resonance of the system, supposing a small perturbation parameter $\varepsilon$, Eq. (2) can be rewritten as follows:

$$\begin{aligned}&\ddot{u}+u\nonumber \\&\quad = \varepsilon \left( {\begin{array}{l} -\mu \dot{u}-\alpha _1 u^{3}-\alpha _2 u^{5}-\beta _1 u^{2}\ddot{u}\\ beta _1 u\dot{u}^{2} -\beta _2 u^{4}\ddot{u}+\beta _2 u^{3}\dot{u}^{2} \\ +F\cos \left( {\Omega t} \right) +g_p u\left( {t-\tau _1 } \right) \\ +g_d \dot{u}\left( {t-\tau _2 } \right) \\ \end{array}} \right) \end{aligned}$$

(3)

We assume that the frequency of the actuation is close to the fundamental frequency:

$$\begin{aligned} \Omega =1+\varepsilon \sigma \end{aligned}$$

(4)

where $\sigma$ is the nonlinear detuning parameter. Let $T_n =\varepsilon ^{n}t,\left( {n=0,\,1,\,\,2} \right)$ and the displacement be $u_0 \left( t \right) =u_0 \left( {T_0 ,T_1 ,T_2 } \right)$. Equation (3) can be expanded Eqs. (5) and (6):

$$\begin{aligned} u\left( t \right)= & {} u_0 (T_0 ,T_1 ,T_2 )+\varepsilon u_1 (T_0 ,T_1 ,T_2 )\nonumber \\&+\,\varepsilon ^{2}u_2 (T_0 ,T_1 ,T_2 )\cdot \cdot \cdot \,\, \end{aligned}$$

(5)

$$\begin{aligned} u\left( {t-\tau _i } \right)= & {} u_0 (T_0 -\tau _i ,T_1 -\varepsilon \tau _i ,T_2 -\varepsilon ^{2}\tau _i )\nonumber \\&+\,\varepsilon u_1 (T_0 -\tau _i ,T_1 -\varepsilon \tau _i ,T_2 -\varepsilon ^{2}\tau _i ) \nonumber \\&+\,\varepsilon ^{2}u_2 (T_0 -\tau _i ,T_1 - \varepsilon \tau _i ,T_2 - \varepsilon ^{2}\tau _i )\cdots \,\,,\nonumber \\&\quad \,i=1,2 \end{aligned}$$

(6)

The time derivatives are defined as follows:

$$\begin{aligned} \frac{d}{dt}= & {} D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 +\cdot \cdot \cdot \,\, \end{aligned}$$

(7)

$$\begin{aligned} \frac{d^{2}}{dt^{2}}= & {} D_0 ^{2}+2\varepsilon D_0 D_1 +\varepsilon ^{2}\left( {D_1 ^{2}+2D_0 D_2 } \right) +\cdot \cdot \cdot \nonumber \\ \end{aligned}$$

(8)

By substituting Eqs. (5-8) into Eq. (3) and equating the coefficients of $\varepsilon$, we have

$$\begin{aligned}&\varepsilon ^{0}:\,\,D_0^2 u_0 +u_0 =0\,\, \end{aligned}$$

(9)

$$\begin{aligned}&\varepsilon ^{1}:\,D_0^2 u_1 +u_1 =-\mu D_0 u_0 -2D_0 D_1 u_0 \,-\alpha _1 u_0^3 \nonumber \\&\quad -\alpha _2 u_0^5 -\beta _1u_0^2 D_0^2 u_0 -\beta _1u_0 \left( {D_0 u_0 } \right) ^{2} \nonumber \\&\quad -\beta _2 u_0^4 \left( {D_0^2 u_0 } \right) -\beta _2 u_0^3 \left( {D_0 u_0 } \right) ^{2}+g_p u_{0\tau _1 } \nonumber \\&\quad +g_d D_0 u_{0\tau _2 } +F\cos \left( {\Omega t} \right) \end{aligned}$$

(10)

The general solution of Eq. (9) is

$$\begin{aligned} u_0 =A(T_1 ,T_2 )e^{iT_0 }+\bar{{A}}(T_1 ,T_2 )e^{-iT_0 }\,\, \end{aligned}$$

(11a)

and

$$\begin{aligned} u_{0\tau _i }= & {} A(T_1 -\varepsilon \tau _1 ,T_2 -\varepsilon ^{2}\tau _2 )e^{i\left( {T_0 -\tau _i } \right) }\nonumber \\&+\,\,\bar{{A}}(T_1 -\varepsilon \tau _1 ,T_2 -\varepsilon ^{2}\tau _{22} )e^{-i\left( {T_0 -\tau _i } \right) }\,\, \end{aligned}$$

(11b)

where A and $\bar{{A}}$ are the complex amplitude and complex conjugate of A, respectively.

Given the fact that $\varepsilon$ is very small compared to unity, after expansion by Taylor’s

formula, we get

$$\begin{aligned}&A(T_1 -\varepsilon \tau _1 ,T_2 -\varepsilon ^{2}\tau _2 )\nonumber \\&\quad = A(T_1 ,T_2 )-\varepsilon \tau _j D_1 A(T_1 ,T_2 )\nonumber \\&\qquad -\varepsilon ^{2}\tau _j D_2 A(T_1,T_2)+\cdots \cong A(T_1 ,T_2 ) \end{aligned}$$

(12)

Substituting Eqs. (11, 12) into Eq. (10),

$$\begin{aligned}&D_0^2 u_1 +\omega _0^2 u_1 \nonumber \\&\quad =\frac{1}{2}Fe^{i\Omega T_0 }-\alpha _1 A^{3}e^{3iT_0 }\nonumber \\&\qquad -\,\,\alpha _2 A^{5}e^{5iT_0 }-5\alpha _2 A^{4}\bar{{A}}e^{3iT_0 } \nonumber \\&\qquad +\,2\beta _1 A^{3}e^{3iT_0 }+2\beta _2 A^{5}e^{5iT_0 }+6\beta _2 A^{4}\bar{{A}}e^{3iT_0 } \nonumber \\&\qquad +\left( {\begin{array}{l} -3\alpha _1 A^{2}\bar{{A}}-10\alpha _2 A^{3}\bar{{A}}^{2}-i\mu A+2\beta _1 A^{2}\bar{{A}} \\ +8\beta _2 A^{3}\bar{{A}}^{2}-2i\dot{A}\\ +g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 } \\ \, \\ \end{array}} \right) e^{iT_0 } \nonumber \\&\qquad +\,c.c\, \end{aligned}$$

(13)

where c.c represents the complex conjugate of all terms.

Eliminating the secular term in Eq. (13), the following expression is obtained:

$$\begin{aligned}&-\,3\alpha _1 A^{2}\bar{{A}}-10\alpha _2 A^{3}\bar{{A}}^{2}-i\mu A+2\beta _1 A^{2}\bar{{A}}\nonumber \\&\quad +\,8\beta _2 A^{3}\bar{{A}}^{2}-2i\dot{A}+\frac{1}{2}Fe^{i\sigma T_1 }+g_p Ae^{-i\tau _1 }\nonumber \\&\quad +ig_d Ae^{-i\tau _2 }=0\, \end{aligned}$$

(14)

By assuming $A=\frac{ae^{i\theta }}{2}$, substituting it into Eq. (14), and separating the real and imaginary parts, we have the result

$$\begin{aligned} \dot{a}= & {} -\frac{\mu a}{2}+\frac{F}{2}\sin \gamma -\frac{ag_p }{2}\sin \left( {\tau _1 } \right) +\frac{ag_d }{2}\cos \left( {\tau _2 } \right) \nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} a\dot{\gamma }= & {} a\sigma +\frac{F}{2}\cos \gamma -\frac{3\alpha _1 a^{3}}{8}-\frac{5\alpha _2 a^{5}}{16}+\frac{\beta _1 a^{3}}{4} \nonumber \\&+\,\frac{\beta _2 a^{5}}{4}+\frac{ag_p }{2}\cos \left( {\tau _1 } \right) +\frac{ag_d }{2}\sin \left( {\tau _2 } \right) \end{aligned}$$

(16)

where $\gamma =\sigma T_1 -\theta$.

Letting $\dot{a}=a\dot{\gamma }=0$, we obtain the frequency response equation

$$\begin{aligned} \frac{F^{2}}{4}= & {} \left( {\frac{\mu a}{2}+\frac{ag_p }{2}\sin \left( {\tau _1 } \right) -\frac{ag_d }{2}\cos \left( {\tau _2 } \right) } \right) ^{2}\, \nonumber \\&+\,\left( a\sigma -\frac{3\alpha _1 a^{3}}{8}-\frac{5\alpha _2 a^{5}}{16}+\frac{\beta _1 a^{3}}{4}+\frac{\beta _2 a^{5}}{4}\right. \nonumber \\&\left. +\frac{ag_p }{2}\cos \left( {\tau _1 } \right) +\frac{ag_d }{2}\sin \left( {\tau _2 } \right) \right) ^{2} \end{aligned}$$

(17)

The peak value of the primary resonance can be obtained by Eq. (17)

$$\begin{aligned} a_{\max } =\frac{F}{2\mu _0 } \end{aligned}$$

(18)

here $\mu _0 =\frac{\mu +g_p \sin \tau _1 -g_d \cos \tau _2 }{2}$.

The corresponding peak amplitude of uncontrolled system is

$$\begin{aligned} \bar{{a}}_{\max } =\frac{F}{\mu } \end{aligned}$$

(19)

Since the analytical solution of the nonlinear vibration system is usually difficult to solve, the study of the time-delay control performance of the nonlinear vibration system cannot simply adopt the form of the response amplitude ratio similar to the linear vibration system. Therefore, the attenuation ratio of the peak amplitude of primary resonance response, denoted by R, is defined by the ratio of the peak amplitude of primary resonance vibrations with and without the attachment. The vibration control performance is evaluated by using the attenuation rate [42]. The attenuation ratio is expressed as follows:

$$\begin{aligned} R=\frac{a_{\max } }{\bar{{a}}_{\max } } = \frac{1}{1+\frac{g_p \sin \tau _1 -g_d \cos \tau _2 }{\mu }} \end{aligned}$$

(20)

As can be seen from Eq. (20) that a small value of R indicates a large reduction in amplitude which indicates that the level of vibration control is effectively improved. A smaller attenuation rate can be obtained by selecting an appropriate feedback gain factors and time delays.

For simplicity, two delays are expressed as $\tau _1 =\tau$ and $\tau _2 =\phi +\tau$. As the phase of velocity is ahead of displacement by $\frac{\pi }{2}$, the phase difference $\phi$ can be assumed as $\frac{\pi }{2}$ [43]. Equation (20) can be rewritten as

$$\begin{aligned} R=\frac{1}{1+\frac{\left( {g_p +g_d } \right) \sin \tau }{\mu }} \end{aligned}$$

(21)

The stability of solutions is determined by the eigenvalues of the corresponding Jacobian matrix of Eqs. 15 and 16. The eigenvalue is the root of the following equation

$$\begin{aligned}&\lambda ^{2}+2\mu _0 \lambda +\mu _0^2 +\left( {\sigma _0 -v_0 a^{2}-v_1 a^{4}} \right) \nonumber \\&\quad \left( {\sigma _0 -3v_0 a^{2}-5v_1 a^{4}} \right) =0 \end{aligned}$$

(22)

The sufficient condition of system stability is

$$\begin{aligned} f\left( {\sigma _0 } \right)= & {} \mu _0^2 +\left( {\sigma _0 -v_0 a^{2}-v_1 a^{4}} \right) \nonumber \\&\quad \left( {\sigma _0 -3v_0 a^{2}-5v_1 a^{4}} \right)>0, \quad \mu _0 >0\nonumber \\ \end{aligned}$$

(23)

When the critical equation $f\left( {\sigma _0 } \right) =0$ has no real solution, the value of $f\left( {\sigma _0 } \right)$ is always positive. Then, the expression is as

$$\begin{aligned} \mu _0^2\ge & {} v_0^2 a_{\max }^4 +4v_0 v_1 a_{\max }^6 +4v_1^2 a_{\max }^8 \nonumber \\\ge & {} v_0^2 a^{4}+4v_0 v_1 a^{6}+4v_1^2 a^{8} \end{aligned}$$

(24)

where $v_0 =\frac{3\alpha _1 }{8}-\frac{\beta _1 }{4}$, $v_1 =\frac{5\alpha _2 }{16}-\frac{\beta _2 }{4}$.

Substituting Eq. (18) into Eq. (24), the region of the stable vibration control parameters is satisfied as

$$\begin{aligned}&\left( {\mu +g_{\tau 1} \sin \tau } \right) ^{10}\ge 4v_0^2 F^{4}\left( {\mu +g_{\tau 1} \sin \tau } \right) ^{4}\nonumber \\&\quad +\,16v_0 v_1 F^{6}\left( {\mu +g_{\tau 1} \sin \tau } \right) ^{2}+16v_1^2 F^{8}, \mu _0 >0\nonumber \\ \end{aligned}$$

(25)

When the critical equation $f\left( {\sigma _0 } \right) =0$ has two real solutions, the stable vibration region is

$$\begin{aligned}&g_{\tau 2} \cos \tau \nonumber \\&\quad \ge \frac{8v_0 F^{2}\mu ^{2}+3v_1 F^{4}{+}2\sqrt{4v_0^2 F^{4}\mu ^{4}{+}4v_0 v_1 F^{6}\mu ^{2}+v_1^2 F^{8}-\mu ^{10}}}{8\mu ^{4}}\nonumber \\&\qquad -\,2\sigma , \quad \mu _0 >0 \end{aligned}$$

(26)

or

$$\begin{aligned}&g_{\tau 3} \cos \tau \nonumber \\&\quad \le -\frac{\sqrt{4v_0^2 F^{4}\mu ^{4}+4v_0 v_1 F^{6}\mu ^{2}+v_1^2 F^{8}-\mu ^{10}}}{4\mu ^{4}}\nonumber \\&\qquad -\,2\sigma , \quad \mu _0 >0 \end{aligned}$$

(27)

where $g_{\tau i} =\left( {g_p +g_d } \right) ,\,i=1,\,2,\,3$.

In a word, if the critical equation has no real solution, the optimal design of the control parameters meets $\min \frac{1}{1+\frac{g_{\tau 1} \sin \tau }{\mu }}$ and Eq. (25). If the critical equation has two real solution, the optimal design of the control parameters satisfies $\min \frac{1}{1+\frac{\left( {g_p +g_d } \right) \sin \tau }{\mu }}$ and Eq. (26), or $\min \frac{1}{1+\frac{\left( {g_p +g_d } \right) \sin \tau }{\mu }}$ and Eq. (27).

Obviously, when nonlinear control parameters, excitation amplitude, damping coefficient, time delays and natural frequency of the system are known, feedback gain coefficients, attenuation ratio and also the optimal time delays can be obtained.

3.2 Secondary resonance

To investigate the superharmonic and subharmonic resonances of a cantilever beam with time delay, Eq. (2) can be rewritten as follows:

$$\begin{aligned}&\ddot{u}+u= \nonumber \\&\quad \,\,\varepsilon \left( {\begin{array}{l} -\mu \dot{u}-\alpha _1 u^{3}-\alpha _2 u^{5}-\beta _1 u^{2}\ddot{u}-\beta _1 u\dot{u}^{2}\\ -\beta _2 u^{4}\ddot{u}-\beta _2 u^{3}\dot{u}^{2} \\ +g_p u\left( {t-\tau _1 } \right) +g_d \dot{u}\left( {t-\tau _2 } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,F\cos \left( {\Omega t} \right) \end{aligned}$$

(28)

By substituting Eqs. (5)–(8) into Eq. (28) and equating the coefficients of $\upvarepsilon$, we have

$$\begin{aligned}&\varepsilon ^{0}:\,\,D_0^2 u_0 +u_0 =F\cos \left( {\Omega t} \right) \, \end{aligned}$$

(29)

$$\begin{aligned}&\varepsilon ^{1}:\,D_0^2 u_1 +u_1 =-\mu D_0 u_0 -2D_0 D_1 u_0 \,-\alpha _1 u_0^3 \nonumber \\&\quad -\alpha _2 u_0^5 -\beta _1 \,u_0^2 D_0^2 u_0 -\beta _1 u_0 \left( {D_0 u_0 } \right) ^{2} \nonumber \\&\quad -\beta _2 u_0^4 \left( {D_0^2 u_0 } \right) -\beta _2 u_0^3 \left( {D_0 u_0 } \right) ^{2}\nonumber \\&\quad +g_p u_{0\tau _1 } +g_d D_0 u_{0\tau _2} \end{aligned}$$

(30)

The general solution of Eq. (22) is

$$\begin{aligned} u_0 =A(T_1 ,T_2 )e^{iT_0 }+\Lambda (T_1 ,T_2 )e^{i\Omega T_0 }+c.c\,\, \end{aligned}$$

(31)

where $\Lambda =\frac{F}{2\left( {1-\Omega ^{2}} \right) }$.

Substituting Eq. (31) into (30), we obtain Eq. (32), which is presented in Appendix A. All the conditions of the secondary resonances of the control system (2) can be recognized, and the corresponding amplitude–frequency response equation is studied in the next section.

3.2.1 Superharmonic resonances of $\omega \approx \frac{1}{2}\omega _0$, $\omega \approx \frac{1}{3}\omega _0$ and $\omega \approx \frac{1}{5}\omega _0$

Here, we assume that the frequency of actuation is close to one-half of the fundamental frequency:

$$\begin{aligned} \hbox {2}\Omega =1 + \varepsilon \sigma \end{aligned}$$

(33)

Substituting Eq. (33) into Eq. (32), the secular terms are collected, and then, we have

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2 \nonumber \\&\quad +\,e^{2i\sigma T_1 }\left( -5\Lambda ^{4}\bar{{A}}\alpha _2 +7\Lambda ^{4}\bar{{A}}\Omega ^{2}\beta _2\right. \nonumber \\&\quad \left. -\,2\Lambda ^{4}\bar{{A}}\Omega \beta _2 +\Lambda ^{4}\bar{{A}}\beta _2 \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(34)

By assuming $A=\frac{ae^{i\theta }}{2}$ and separating the real and imaginary parts, the frequency response equation of the steady-state solutions is obtained

$$\begin{aligned}&\left( {-\frac{5a\Lambda ^{4}\alpha _2 }{2}+\frac{7a\Lambda ^{4}\Omega ^{2}\beta _2 }{2}-a\Lambda ^{4}\Omega \beta _2 +\frac{a\Lambda ^{4}\beta _2 }{2}} \right) ^{2} \nonumber \\&\quad =\,\left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\,\,\nonumber \\&\qquad +\,\left( {\begin{array}{l} a\sigma -3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2} \end{aligned}$$

(35)

Similarly, when $\hbox {3}\Omega = 1 +\varepsilon \sigma$ is substituted into Eq. (32), one obtains

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2\nonumber \\&\quad +\,e^{i\sigma T_1 }\left( {\begin{array}{l} -\Lambda ^{3}\alpha _1 -5\Lambda ^{5}\alpha _2 -20A\Lambda ^{3}\bar{{A}}\alpha _2 +2\Lambda ^{3}\Omega ^{2}\beta _1 \\ +6\Lambda ^{5}\Omega ^{2}\beta _2 +18A\Lambda ^{3}\bar{{A}}\Omega ^{2}\beta _2 +6A\Lambda ^{3}\bar{{A}}\beta _2 \\ \end{array}} \right) \nonumber \\&\quad +\,e^{-i\sigma T_1 }\left( -10A^{2}\Lambda ^{3}\alpha _2 +\,9A^{2}\Lambda ^{3}\Omega ^{2}\beta _2 \right. \nonumber \\&\quad \left. -\,6A^{2}\Lambda ^{3}\Omega \beta _2 +5A^{2}\Lambda ^{3}\beta _2 \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(36)

Similarly, the frequency response equation of the steady-state solutions is obtained:

$$\begin{aligned}&\left( {\begin{array}{l} -\Lambda ^{3}\alpha _1 -5\Lambda ^{5}\alpha _2 -\frac{5a^{2}\Lambda ^{3}\alpha { }_2}{2}\\ +2\Lambda ^{3}\Omega ^{2}\beta _1 +6\Lambda ^{5}\Omega ^{2}\beta _1 +\frac{9a^{2}\Lambda ^{3}\Omega ^{2}\beta _2 }{4} \\ +\frac{a^{2}\Lambda ^{3}\beta _2 }{4}-\frac{3a^{2}\Lambda ^{3}\Omega \beta _2 }{2} \\ \end{array}} \right) ^{2}\cdot \nonumber \\&\quad \left( {\begin{array}{l} -\Lambda ^{3}\alpha _1 -5\Lambda ^{5}\alpha _2 -\frac{\hbox {1}5a^{2}\Lambda ^{3}\alpha { }_2}{2}\\ +2\Lambda ^{3}\Omega ^{2}\beta _1 +6\Lambda ^{5}\Omega ^{2}\beta _1 +\frac{\hbox {27}a^{2}\Lambda ^{3}\Omega ^{2}\beta _2 }{4} \\ +\frac{\hbox {11}a^{2}\Lambda ^{3}\beta _2 }{4}-\frac{3a^{2}\Lambda ^{3}\Omega \beta _2 }{2} \\ \end{array}} \right) ^{2} \nonumber \\&\quad =\left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\,\,\nonumber \\&\quad \left( {\begin{array}{l} -\Lambda ^{3}\alpha _1 -5\Lambda ^{5}\alpha _2 -\frac{\hbox {1}5a^{2}\Lambda ^{3}\alpha { }_2}{2}+2\Lambda ^{3}\Omega ^{2}\beta _1 \\ +6\Lambda ^{5}\Omega ^{2}\beta _1 +\frac{\hbox {27}a^{2}\Lambda ^{3}\Omega ^{2}\beta _2 }{4}+\frac{\hbox {11}a^{2}\Lambda ^{3}\beta _2 }{4} \\ -\frac{3a^{2}\Lambda ^{3}\Omega \beta _2 }{2} \\ \end{array}} \right) ^{2} \nonumber \\&\qquad +\,\left( {\begin{array}{l} a\sigma -3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2}\nonumber \\&\quad \left( {\begin{array}{l} -\Lambda ^{3}\alpha _1 -5\Lambda ^{5}\alpha _2 -\frac{5a^{2}\Lambda ^{3}\alpha { }_2}{2} \\ +2\Lambda ^{3}\Omega ^{2}\beta _1 +6\Lambda ^{5}\Omega ^{2}\beta _1 \\ +\frac{9a^{2}\Lambda ^{3}\Omega ^{2}\beta _2 }{4}+\frac{a^{2}\Lambda ^{3}\beta _2 }{4} \\ -\frac{3a^{2}\Lambda ^{3}\Omega \beta _2 }{2} \\ \end{array}} \right) ^{2} \end{aligned}$$

(37)

When $\hbox {5}\Omega = 1 + \varepsilon \sigma$, one obtains

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2 \nonumber \\&\quad +\,e^{i\sigma T_1 }\left( {-\Lambda ^{\mathrm{5}}\alpha _2 +\hbox {2}\Lambda ^{\mathrm{5}}\Omega ^{2}\beta _2 } \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(38)

Then, the steady-state responses of the system are:

$$\begin{aligned}&\left( {-\Lambda ^{5}\alpha _2 +2\Lambda ^{5}\Omega ^{2}\beta _2 } \right) ^{2}= \nonumber \\&\quad \,\left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\,\,\nonumber \\&\qquad +\,\left( {\begin{array}{l} a\sigma -3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2} \end{aligned}$$

(39)

3.2.2 Subharmonic resonances of $\omega \approx 2\omega _0$, $\omega \approx 3\omega _0$ and $\omega \approx 5\omega _0$

In this section, three cases of subharmonic resonances are studied.

Case 1: when $\Omega = 2 + \varepsilon \sigma$, one obtains

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2 \nonumber \\&\quad +\,e^{2i\sigma T_1 }\left( {\begin{array}{l} -\hbox {10}\Lambda ^{\mathrm{2}}\bar{{A}}^{\mathrm{3}}\alpha _2 +\hbox {5}\Lambda ^{\mathrm{2}}\bar{{A}}^{\mathrm{3}}\Omega ^{2}\beta _2 -\hbox {6}\Lambda ^{\mathrm{2}}\bar{{A}}^{\mathrm{3}}\beta _2 \\ +\hbox {9}\Lambda ^{\mathrm{2}}\bar{{A}}^{\mathrm{3}}\beta _2 \\ \end{array}} \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(40)

Then, the frequency response equation of the steady-state solutions is obtained:

$$\begin{aligned}&\left( {-\frac{5a^{\mathrm{3}}\Lambda ^{\mathrm{2}}\alpha _2 }{\hbox {4}}+\frac{\hbox {5}a^{\mathrm{3}}\Lambda ^{\mathrm{2}}\Omega ^{2}\beta _2 }{\hbox {8}}-\frac{\hbox {3}a^{\mathrm{3}}\Lambda ^{\mathrm{2}}\beta _2 }{\hbox {4}}+\frac{\hbox {9}a^{\mathrm{3}}\Lambda ^{\mathrm{2}}\beta _2 }{\hbox {8}}} \right) ^{2} \nonumber \\&\quad =\left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\,\,\nonumber \\&\qquad +\,\left( {\begin{array}{l} \frac{a\sigma }{\hbox {2}}-3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2} \end{aligned}$$

(41)

Case 2: when $\Omega = 3 + \varepsilon \sigma$, one obtains

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2 +e^{i\sigma T_1 }\nonumber \\&\qquad \left( {\begin{array}{l} -\hbox {3}\Lambda \bar{{A}}^{2}\alpha _1 -30\Lambda ^{3}\bar{{A}}^{2}\alpha _2 -20A\Lambda \bar{{A}}^{3}\alpha _2 \\ +\,\bar{{A}}^{2}\Lambda \Omega ^{2}\beta _1 +15\Lambda ^{3}\Omega ^{2}\bar{{A}}^{2}\beta _2 +4A\Lambda \bar{{A}}^{3}\Omega ^{2}\beta _2 \\ -\,2\Lambda \Omega \bar{{A}}^{2}\beta _1 -6\Lambda ^{3}\Omega \bar{{A}}^{2}\beta _2 -4A\Lambda \bar{{A}}^{3}\Omega \beta _2 \\ +\,3\Lambda \bar{{A}}^{2}\beta _1 +15\Lambda ^{3}\bar{{A}}^{2}\beta _2 +16A\Lambda \bar{{A}}^{3}\beta _2 \\ \end{array}} \right) \nonumber \\&\quad +\,e^{-i\sigma T_1 }\left( -5A^{4}\Lambda \alpha _2 +A^{4}\Lambda \Omega ^{2}\beta _2 \right. \nonumber \\&\quad \left. -\,2A^{4}\Lambda \Omega \beta _2 +7A^{4}\Lambda \beta _2 \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(42)

and the amplitude-frequency curve equation is

$$\begin{aligned}&\left( {\begin{array}{l} -\frac{3\Lambda a^{2}\alpha _1 }{4}-\frac{15\Lambda ^{3}a^{2}\alpha _2 }{2}-\frac{15\Lambda a^{4}\alpha _2 }{16}+\frac{\Lambda a^{2}\Omega ^{2}\beta _1 }{4} \\ +\frac{15\Lambda ^{3}a^{2}\Omega ^{2}\beta _2 }{4}+\frac{3\Lambda a^{4}\Omega ^{2}\beta _2 }{16}-\frac{\Lambda a^{2}\Omega \beta _1 }{2}-\frac{3\Lambda ^{3}a^{2}\Omega \beta _2 }{2} \\ -\frac{\Lambda a^{4}\Omega \beta _2 }{8}+\frac{3\Lambda a^{2}\beta _1 }{4}+\frac{15\Lambda ^{3}a^{2}\beta _2 }{4}+\frac{9\Lambda a^{4}\beta _2 }{16} \\ \end{array}} \right) ^{2}\cdot \nonumber \\&\left( {\begin{array}{l} -\frac{3\Lambda a^{2}\alpha _1 }{4}-\frac{15\Lambda ^{3}a^{2}\alpha _2 }{2}-\frac{25\Lambda a^{4}\alpha _2 }{16}+\frac{\Lambda a^{2}\Omega ^{2}\beta _1 }{4} \\ +\frac{15\Lambda ^{3}a^{2}\Omega ^{2}\beta _2 }{4}+\frac{5\Lambda a^{4}\Omega ^{2}\beta _2 }{16}-\frac{\Lambda a^{2}\Omega \beta _1 }{2}-\frac{3\Lambda ^{3}a^{2}\Omega \beta _2 }{2} \\ -\frac{3\Lambda a^{4}\Omega \beta _2 }{8}+\frac{3\Lambda a^{2}\beta _1 }{4}+\frac{15\Lambda ^{3}a^{2}\beta _2 }{4}+\frac{23\Lambda a^{4}\beta _2 }{16} \\ \end{array}} \right) ^{2} \nonumber \\&\quad = \left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\nonumber \\&\qquad \left( {\begin{array}{l} -\frac{3\Lambda a^{2}\alpha _1 }{4}-\frac{15\Lambda ^{3}a^{2}\alpha _2 }{2}-\frac{25\Lambda a^{4}\alpha _2 }{16} \\ +\frac{\Lambda a^{2}\Omega ^{2}\beta _1 }{4}+\frac{15\Lambda ^{3}a^{2}\Omega ^{2}\beta _2 }{4}+\frac{5\Lambda a^{4}\Omega ^{2}\beta _2 }{16} \\ -\frac{\Lambda a^{2}\Omega \beta _1 }{2}-\frac{3\Lambda ^{3}a^{2}\Omega \beta _2 }{2}-\frac{3\Lambda a^{4}\Omega \beta _2 }{8} \\ +\frac{3\Lambda a^{2}\beta _1 }{4}+\frac{15\Lambda ^{3}a^{2}\beta _2 }{4}+\frac{23\Lambda a^{4}\beta _2 }{16} \\ \end{array}} \right) ^{2} \nonumber \\&\quad +\left( {\begin{array}{l} \frac{a\sigma }{3}-3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2}\nonumber \\&\qquad \left( {\begin{array}{l} -\frac{3\Lambda a^{2}\alpha _1 }{4}-\frac{15\Lambda ^{3}a^{2}\alpha _2 }{2} \\ -\frac{15\Lambda a^{4}\alpha _2 }{16}+\frac{\Lambda a^{2}\Omega ^{2}\beta _1 }{4} \\ +\frac{15\Lambda ^{3}a^{2}\Omega ^{2}\beta _2 }{4}+\frac{3\Lambda a^{4}\Omega ^{2}\beta _2 }{16} \\ -\frac{\Lambda a^{2}\Omega \beta _1 }{2}-\frac{3\Lambda ^{3}a^{2}\Omega \beta _2 }{2} \\ -\frac{\Lambda a^{4}\Omega \beta _2 }{8}+\frac{3\Lambda a^{2}\beta _1 }{4} \\ +\frac{15\Lambda ^{3}a^{2}\beta _2 }{4}+\frac{9\Lambda a^{4}\beta _2 }{16} \\ \end{array}} \right) ^{2} \end{aligned}$$

(43)

Case 3: when $\Omega = 5 + \varepsilon \sigma$, one obtains

Fig. 2

Amplitude–frequency curve of the system for the primary resonance with different delays and feedback gain coefficients

$$\begin{aligned}&-\,6A\Lambda ^{2}\alpha _1 -3A^{2}\bar{{A}}\alpha _1 -30A\Lambda ^{4}\alpha _2 -60A^{2}\Lambda ^{2}\bar{{A}}\alpha _2\nonumber \\&\quad -\,10A^{3}\bar{{A}}^{2}\alpha _2 +2A\Lambda ^{2}\Omega ^{2}\beta _1 \nonumber \\&\quad +\,18A\Lambda ^{4}\Omega ^{2}\beta _2 +18A^{2}\Lambda ^{2}\bar{{A}}\Omega ^{2}\beta _2 -i\mu A\nonumber \\&\quad +\,2A\Lambda ^{2}\beta _1 +2A^{2}\bar{{A}}\beta _1 +6A\Lambda ^{4}\beta _2 \nonumber \\&\quad +\,30A^{2}\Lambda ^{2}\bar{{A}}\beta _2 +8A^{3}\bar{{A}}^{2}\beta _2 \nonumber \\&\quad +\,e^{i\sigma T_1 }\left( {\begin{array}{l} -5\Lambda \bar{\hbox {A}}^{4}\alpha _2 +\Lambda \Omega ^{2}{\bar{\hbox {A}}}^{4}\beta _2 -2\Lambda \Omega {\bar{\hbox {A}}}^{4}\beta _2 \\ +7\Lambda {\bar{\hbox {A}}}^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\quad -\,2i\dot{A}+g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 }=0 \end{aligned}$$

(44)

Similarly, the frequency response equation is obtained:

$$\begin{aligned}&\left( {-\frac{5\Lambda a^{4}\alpha _2 }{16}+\frac{\Lambda \Omega ^{2}a^{4}\beta _2 }{16}-\frac{\Lambda \Omega a^{4}\beta _2 }{8}+\frac{7\Lambda a^{4}\beta _2 }{16}} \right) ^{2} \nonumber \\&\quad =\left( {\frac{\mu a}{2}+\frac{ag_p \sin \tau _1 }{2}-\frac{ag_d \cos \tau _2 }{2}} \right) ^{2}\,\,\nonumber \\&\quad +\left( {\begin{array}{l} \frac{a\sigma }{5}-3a\Lambda ^{2}\alpha _1 -\frac{3a^{3}\alpha _1 }{8}-15a\Lambda ^{4}\alpha _2 \\ -\frac{15a^{3}\Lambda ^{2}\alpha _2 }{2}-\frac{5a^{5}\alpha _2 }{16}+a\Lambda ^{2}\Omega ^{2}\beta _1 \\ +9a\Lambda ^{4}\Omega ^{2}\beta _2 +\frac{9a^{3}\Lambda ^{2}\Omega ^{2}\beta _2 }{4}+a\Lambda ^{2}\beta _1 \\ +\frac{a^{3}\beta _1 }{4}+3a\Lambda ^{4}\beta _2 +\frac{15a^{3}\Lambda ^{2}\beta _2 }{4}+\frac{a^{5}\beta _2 }{4} \\ +\frac{ag_p \cos \tau _1 }{2}+\frac{ag_d \sin \tau _2 }{2} \\ \end{array}} \right) ^{2} \end{aligned}$$

(45)

Fig. 3

Phase–amplitude response with zero initial conditions

Fig. 4

Time–amplitude response with zero initial conditions

Fig. 5

Variation of R with time delay for different feedback gain coefficients at $\mu =0.06$ and $F=0.1$

4 Results and discussion

To investigate the nonlinear behavior of the control system (2), the primary amplitude–frequency response Eq. (17) of a cantilever beam carrying an intermediate lumped mass is considered. The influences of the feedback gain coefficients $g_p ,\,g_d$ and delay feedback $\tau _1 ,\,\tau _2$ on the amplitude–frequency curve of the main system can be calculated with $\alpha _1 =0.3331,\alpha _2 =0.1299,\beta _1 =0.3338$ and $\beta _2 =0.1319$ [44]. In all figures of this article, a solid line indicates the stable solution, and the dashed line indicates the unstable solution. The effects of the different parameters on the primary resonance are studied, and the corresponding amplitude–frequency curves are illustrated in Fig. 2. Figure 2a, b shows the influence of the excitation amplitude and the dimensionless damping coefficient on the amplitude of the steady-state response of the system without a time delay. Obviously, the primary resonant frequency curve is shifted to the right, exhibiting hard spring and multivalued characteristics. With an increase in F, the response area broadens and the maximum amplitude of the vibration increases. When the damping increases, the peak amplitude decreases, the migratory nature of the resonance frequency decreases, and the curve with the characteristics of a hard spring and multivalued areas is significantly reduced. From Fig. 2a, b, we can see that the excitation amplitude has little effect on the shape of the stable resonance frequency, but the damping coefficient has an important influence on the stability behavior of the system. Obviously, the conclusions are in good agreement with Refs. [13, 45]. Figure 2c shows that as the displacement feedback gain coefficient increases, the peak amplitude moves to the left, and the vibration peak amplitude, the response spring characteristic, and the stability of the system’s nonlinearity do not change. However, as shown in Fig. 2d, with the increase in the velocity feedback gain coefficient, the peak amplitude obviously decreases, and it remarkably changes the stability of the system. To compare the control effects of the displacement and velocity feedback gain coefficients, different gain coefficient values are chosen, as shown in Fig. 2e. An increase in $g_p$ makes the peak amplitude move to a low frequency, and the increase in $g_d$ can effectively suppress the vibration amplitude of the nonlinear system. These results are consistent with those shown in Fig. 2c, d. Therefore, vibration control of a nonlinear system can be achieved by optimizing the selection of the velocity feedback gain coefficient. Figure 2f–h shows the effect of time delays on the frequency response of the system. Figure 2f, g shows that both the displacement time delay $\tau _1$ and the velocity time delay $\tau _2$ can suppress the vibration amplitude of the nonlinear system. The effectiveness of the time delay is further studied in Fig. 2h. Four cases are shown: without time delay, only displacement time delay, only velocity time delay and with two time delays. The results show that velocity delay has a more obvious effect on the nonlinear vibration of the system and that the two time delays have a better suppressive effect on system control at lower frequencies. Obviously, with the change in the time delay and feedback gain coefficient, the effect of nonlinear suppression is enhanced. It is also observed that the results of this paper agree well with those in Refs. [24,25,26]. Therefore, choosing an appropriate time delay and feedback gain coefficient can improve the control effect and stability of the nonlinear system. To further illustrate the validity of the results, the phase diagram and the time–amplitude response diagram are shown in Figs. 3 and 4 with zero initial conditions when $g_p =0.01$, $g_d =0.01$, $\tau _{1}=0.05\pi$, $\tau _2 =0.05\pi$. It can be seen from the figures that the vibration response of the system eventually tends toward stability.

Fig. 6

Amplitude–frequency curves of the system for the superharmonic case of $\omega \approx \frac{1}{2}\omega _0$ with different delays and feedback gain coefficients

Fig. 7

Amplitude–frequency curves of the system for the superharmonic case of $\omega \approx \frac{1}{3}\omega _0$ with different delays and feedback gain coefficients

Fig. 8

Amplitude–frequency curves of the system for the superharmonic case of $\omega \approx \frac{1}{5}\omega _0$ with different delays and feedback gain coefficients

Fig. 9

Amplitude–frequency curves of the system for subharmonic case of $\omega \approx 2\omega _0$ with different delays and feedback gain coefficients

Fig. 10

Amplitude–frequency curves of the system for subharmonic case of $\omega \approx 3\omega _0$ with different delays and feedback gain coefficients

Fig. 11

Amplitude–frequency curves of the system for subharmonic case of $\omega \approx 5\omega _0$ with different delays and feedback gain coefficients

The relations between the attenuation ratio and time delay with different feedback gain coefficients are presented in Fig. 5. The figure states that reasonable selection of time delays for different feedback gain coefficients gives a small value of the attenuation rate R. The smaller R, the better vibration control of system. Obviously, $\frac{\pi }{2}$ is one of the optimal time delays.

For the superharmonic case of $\omega =\frac{1}{2}\omega _0$, the effects of F and $\mu$ are illustrated in Fig. 6a, b. The only stable response for this case is zero amplitude (which is presented by a solid line), while the other curves are unstable. The effects of the feedback gain coefficient and time delay are shown in Fig. 6c–h. The results show that these parameters only have a certain influence on the system resonance bandwidth. Similarly, Figs. 7 and 8 are plotted for the superharmonic case of $\omega =\frac{1}{3}\omega _0$ and $\omega =\frac{1}{5}\omega _0$. Moreover, when $\omega \approx \frac{1}{5}\omega _0$, the control effect is more obvious. This result is consistent with the primary resonance result.

A similar parametric study is performed for all the cases ($\omega \approx 2\omega _0 ,\,\omega \approx 3\omega _0$ and $\omega \approx 5\omega _0 )$ of the subharmonic resonances, and their results are shown in Figs. 9, 10 and 11, respectively. It can be seen from the figures that each curve has two branches corresponding to two different values of the amplitude. In the two branches, the large amplitude is stable, and the small amplitude is unstable. The displacement feedback gain coefficient only makes the peak amplitude of system move to a low frequency, but the velocity feedback gain coefficient can change the amplitude and the bandwidth when subharmonic resonance occurs.

We now turn our attention to the influence of location of the concentrated mass on the primary resonance of the system. According to Ref. [44], the values of dimensionless parameters are taken as $\alpha _1 =0.3331,\,\alpha _2 =0.1299,\,\beta _1 =0.1850$ and $\beta _2 =0.4306$. The amplitude–frequency curves of the system for tip mass subjected to base excitation are plotted in Fig. 12. It is noticed that the system shows softening behavior which is different from Fig. 2. The results also reveal that the increase of displacement feedback gain coefficient only makes the peak amplitude of system move to a low frequency. Yet velocity feedback coefficient and their time delays are able to effectively restrain the amplitude of the system. Furthermore, velocity feedback coefficient is significant for the stability of the system, but the displacement feedback gain coefficient only causes a translation of stable points of the system. These results are consistent well with those in Fig. 2.

Fig. 12

Amplitude–frequency curve of the system for the primary resonance of tip mass with different delays and feedback gain coefficients

5 Conclusion

In this paper, we presented an analysis of the dynamics of a cantilever beam carrying an lumped mass with time-delay displacement and velocity feedback. The multiple scales method is used to approximate the primary, superharmonic and subharmonic resonance conditions of the control system and to investigate their stability. The variation of the amplitude–frequency response curve of the system under different time delays was discussed and solved numerically. The results show that the system exhibits a hard spring characteristic for a lumped mass at an intermediate position, whereas it shows softening behavior for tip mass. The delayed displacement and velocity feedback control terms have significant effects on the resonance stability and peak amplitude. A specific time delay control can effectively reduce the amplitude of the resonance. Moreover, by comparing the feedback gain coefficient and time delay, it is found that under the same conditions, the control effects of the velocity feedback gain coefficient and the velocity time delay are relatively good. When four control variables exist at the same time, the control effect of the system is better.

Appendix A

$$\begin{aligned}&\varepsilon ^{1}:\,\,D_0^2 u_1 +u_1 =+e^{-5i\Omega T_0 }\left( {-\alpha _2 \Lambda ^{5}+2\Lambda ^{5}\beta _2 \Omega ^{2}} \right) \nonumber \\&\qquad +\,e^{5i\Omega T_0 }\left( {-\alpha _2 \Lambda ^{5}+2\Lambda ^{5}\beta _2 \Omega ^{2}} \right) +e^{-5iT_0 }\left( {-\alpha _2 A^{5}+2A^{5}\beta _2 } \right) \nonumber \\&\qquad +\,e^{5iT_0 }\left( {-\alpha _2 A^{5}+2A^{5}\beta _2 } \right) \nonumber \\&\qquad +\,e^{-3i\Omega T_0 }\left( {\begin{array}{l} -\alpha _1 \Lambda ^{3}-20A\bar{{A}}\alpha _2 \Lambda ^{3}-5\alpha _2 \Lambda ^{5}+2\beta _1 \Omega ^{2}\Lambda ^{3}+12A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,6\beta _2 \Lambda ^{5}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{3i\Omega T_0 }\left( {\begin{array}{l} -\alpha _1 \Lambda ^{3}-20A\bar{{A}}\alpha _2 \Lambda ^{3}-5\alpha _2 \Lambda ^{5}+2\beta _1 \Omega ^{2}\Lambda ^{3}+12A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,6\beta _2 \Lambda ^{5}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-i\Omega T_0 }\left( {\begin{array}{l} -\,6A\bar{{A}}\alpha _1 \Lambda -30A^{2}\bar{{A}}^{2}\alpha _2 \Lambda -3\alpha _1 \Lambda ^{3}-60A\bar{{A}}\alpha _2 \Lambda ^{3}-10\alpha _2 \Lambda ^{5} \\ +\,2A\bar{{A}}\beta _1 \Lambda \Omega ^{2}+2\beta _1 \Lambda ^{3}\Omega ^{2}+6A^{2}\bar{{A}}^{2}\beta _2 \Lambda \Omega ^{2}+30A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,8\beta _2 \Lambda ^{5}\Omega ^{2}+2A\bar{{A}}\beta _1 \Lambda +18A^{2}\bar{{A}}^{2}\beta _2 \Lambda +18A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{i\Omega T_0 }\left( {\begin{array}{l} -\,6A\bar{{A}}\alpha _1 \Lambda -30A^{2}\bar{{A}}^{2}\alpha _2 \Lambda -3\alpha _1 \Lambda ^{3}-60A\bar{{A}}\alpha _2 \Lambda ^{3}-10\alpha _2 \Lambda ^{5} \\ +\,2A\bar{{A}}\beta _1 \Lambda \Omega ^{2}+2\beta _1 \Lambda ^{3}\Omega ^{2}+6A^{2}\bar{{A}}^{2}\beta _2 \Lambda \Omega ^{2}+30A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,8\beta _2 \Lambda ^{5}\Omega ^{2}+2A\bar{{A}}\beta _1 \Lambda +\,18A^{2}\bar{{A}}^{2}\beta _2 \Lambda +18A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{4iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}+2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ +e^{-i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}-2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-4iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}+2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ +\,e^{-i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}-2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{3iT_0 }\left( {\begin{array}{l} -A^{3}\alpha _1 -5A^{4}\bar{{A}}\alpha _2 -20A^{3}\alpha _2 \Lambda ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega ^{2}+2A^{3}\beta _1 +6A^{4}\bar{{A}}\beta _2 \\ +\,18A^{3}\beta _2 \Lambda ^{2} \\ +e^{2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ +e^{-2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}-6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-3iT_0 }\left( {\begin{array}{l} -A^{3}\alpha _1 -5A^{4}\bar{{A}}\alpha _2 -20A^{3}\alpha _2 \Lambda ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega ^{2}+2A^{3}\beta _1 +6A^{4}\bar{{A}}\beta _2 \\ +\,18A^{3}\beta _2 \Lambda ^{2} \\ +e^{2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ +e^{-2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}-6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{iT_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \bar{{A}}-10A^{3}\bar{{A}}^{2}\alpha _2 -6A\alpha _1 \Lambda ^{2}-60A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-30A\alpha _2 \Lambda ^{4}+2A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +\,18A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+18A\Lambda ^{4}\beta _2 \Omega ^{2}+2A^{2}\bar{{A}}\beta _1 +2A\Lambda ^{2}\beta _1 +8A^{3}\bar{{A}}^{2}\beta _2 \\ +\,30A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \omega _0^2 +6A\Lambda ^{4}\beta _2 +g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 } \\ +e^{4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ +e^{-4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{iT_0 }e^{2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2}+15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2} \\ 16A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\Lambda ^{2}\beta _1 \Omega +6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega +4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \end{aligned}$$

$$\begin{aligned}&\qquad +\,e^{iT_0 }e^{-2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2}+15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2} \\ 16A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\Lambda ^{2}\beta _1 \Omega -6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega -4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }\left( {\begin{array}{l} -3A^{2}\alpha _1 \bar{{A}}-10A^{3}\bar{{A}}^{2}\alpha _2 -6A\alpha _1 \Lambda ^{2}-60A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-30A\alpha _2 \Lambda ^{4} \\ +\,2A\Lambda ^{2}\beta _1 \Omega ^{2}+18A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+18A\Lambda ^{4}\beta _2 \Omega ^{2}+2A^{2}\bar{{A}}\beta _1 \\ +\,2A\Lambda ^{2}\beta _1 +8A^{3}\bar{{A}}^{2}\beta _2 +30A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +6A\Lambda ^{4}\beta _2 \\ +e^{4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ +e^{-4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }e^{2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+16A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\Lambda ^{2}\beta _1 \Omega \\ +6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega +4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }e^{-2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+16A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\Lambda ^{2}\beta _1 \Omega \\ -\,6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega -4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{2iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+2A^{2}\beta _1 \Lambda \Omega +4A^{3}\bar{{A}}\beta _2 \Lambda \Omega +6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{-i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-2A^{2}\beta _1 \Lambda \Omega -4A^{3}\bar{{A}}\beta _2 \Lambda \Omega -6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ +e^{-3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-2iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+2A^{2}\beta _1 \Lambda \Omega +4A^{3}\bar{{A}}\beta _2 \Lambda \Omega +6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{-i\Omega T_0 }\left( {\begin{array}{l} -3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-2A^{2}\beta _1 \Lambda \Omega -4A^{3}\bar{{A}}\beta _2 \Lambda \Omega -6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ +e^{-3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ \end{array}} \right) \end{aligned}$$

(32)