Introduction

In recent decades, cable-stayed structures have become increasingly popular for modern long-span bridges. The long-span cable-stayed bridge is a high-order statically indeterminate structure composed of cable stays, deck beams and bridge towers [1]. The cable stays in cable-stayed bridges suspend the deck from the towers; they are elastic and flexible, with extremely low damping properties. With the ever-increasing span lengths of cable-stayed bridges, stay cables are getting longer and longer and thus more prone to excessive vibration under complex external excitations due to vehicles, rain, snow, and temperature, among others [2]. Monitoring studies of active cable-stayed bridges show that the cables are prone to large-scale vibration even under the action of breeze and drizzle. This effect is generally attributed to the parametric vibration induced by the excitation of stiffening beams or bridge towers. The resulting fatigue stress in the cable–beam anchorage area may accelerate fatigue damage to the cable, and in severe cases endanger the operational safety and performance of the bridge [3]. Therefore, it is very important to understand the stay cable’s parametric vibration mechanism and dynamic response characteristics.

Traditionally, investigations into the parametric vibration of stay cables have focused separately on the beam and cables [4,5,6,7]. In other studies that consider the overall structure, the cable–beam coupling, consisting of a beam and a cable, has also often been used to investigate cable parametric vibration [8,9,10,11,12]. Extensive research has been conducted on the different forms of cable end excitation, including ideal excitation [13], vertical harmonic support excitation [14], wind and support motion excitation [6], white noise and narrow band random excitation [15], in-plane transverse uniformly distributed Gaussian white noise [16], random and periodic combined support motion excitation [17], filtered Gaussian white noise [18], and seismic and sea wave excitation [19]. In practice, the different excitations applied to cables are neither harmonic nor periodic but random in nature. Therefore, it is crucial to analyze the random response of stay cables.

Modeling parametric vibration under random excitation of the stay cable, Zhou et al. [3] apply fourth-order cumulant-neglect closure together with C-type Gram–Charlier expansion with a fourth-order closure to obtain the statistical moments, power spectral density (PSD) and probability density function (PDF) of the dynamic response of an inclined shallow cable with linear viscous dampers under stochastic excitation. In Brouwers’ [20] theoretical analysis of the non-stationary response of a randomly parametrically excited oscillator, the amplitude and phase are described by fluctuation equations in which time is the independent variable and Fokker–Planck equations are applied to derive the probability density of amplitude and phase. Nielsen and Sichani [21] analyze the stochastic response and chaotic behavior of a shallow cable using two comparable stochastic models. Narayanan and Kumar [22] develop a modified path integral procedure based on a non-Gaussian transition PDF, which is the product of a Gaussian PDF and a series of Hermite polynomials, to solve the Fokker–Planck equation and predict the stochastic and chaotic response of a number of nonlinear systems subjected to external and parametric random excitations. In their study of the random vibration of stay cables under Gaussian white noise and narrowband random excitation, Gu et al. [23] derive Gaussian and first-order non-Gaussian closed-form solutions by employing the statistical moment truncation method to solve the moment equation. Brzakala and Herbut [24] test a projection method based on the finite dimensional polynomial subspace as an effective alternative to popular perturbation methods, the method of moments, or the Monte Carlo simulation. Taking a different approach, Fu et al. [25] apply the stochastic averaging method and stochastic dynamic programming principle to determine stochastic optimal control of the stayed cable under fluctuating wind load. Based on nonlocal strain gradient theory, Rastehkenari [26] investigate the dynamic response of a functionally graded nanobeam supported by viscoelastic foundation to a stationary random excitation. Most recently, using the direct eigenvalue analysis approach based on response moment stability, Floquet theorem, Fourier series and matrix eigenvalue analysis, Ying et al. [27] analyze stochastic stability control of parameter-excited vibration of the inclined stay cable with multiple modes of coupling and under random and periodic combined support excitation.

The literature review reveals that despite the richness and profundity of investigations into the parametric vibration of stay cables under random excitations, there is limited research available in the open literature on the vibration characteristics of the cable parameters from the angle of random orbit. Most existing studies are based on the Fokker–Planck–Kolmogorov (FPK) equation and study cable parametric vibration from the perspective of transition probability density, ignoring the effect of the synergistic vibration of the bridge deck beam and cannot directly solve the vibration response time history. Therefore, in order to more accurately grasp the vibration characteristics of the stayed cable, and consider the geometric nonlinearity of the staying cable, the inclination angle and the synergistic vibration effect of the bridge deck beam, the aim of this study is to provide one method which can directly solve the response time history of the cable–beam coupling structure. To this end, based on the cable–beam coupling vibration model under random excitation established, the coupled motion equations of stay cable and bridge deck beam are derived and transformed into a random system of state equations by phase space transformation. Following in the next section, the Milstein–Platen method is used as a first attempt to solve the coupled random vibration time history of the cable–beam structure. An iterative method for solving the time history of the random vibration of the cable-deck beam is applied to avoid the influence of the parametric diffusion coefficient on the numerical forma, which is of great significance to the vibration analysis of the cable–beam coupling system. The proposed model is then validated by a detailed case study. The random displacement, statistical moment characteristics, PSD and probability density change of the cable are analyzed from the random track angle, and the results are compared with the Gauss truncation method. Finally, a comparative study is illustrated with the help of a numerical example to investigate the effects of damping ratio, initial tension, initial disturbance of stiffening beam and random excitation intensity on the vibration of the cable. The results of the analysis are thoroughly discussed, and the paper ends with the conclusions drawn from the analysis based on the key findings.

Cable–Beam Coupled Vibration Model Under Random Excitation

Model Description

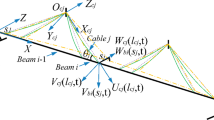
The effect of the coordinated vibration of the cable and the deck beam is modeled using the cable–beam coupled system shown in Fig. 1. The cable and beam are supported on one end and attached to each other at the other end. For the purposes of this study, the subscripts c and b denote the variables of the cable and the deck beam, respectively. The structure parameters for the system (shown in Fig. 1) are denoted as follows: m, l, c, E, I, A and θ are the masses per unit length, lengths, damping coefficients, elastic modulus, moment of inertia, cross-sectional area, and cable inclination angle, respectively. The following assumptions are made: (1) since the dead weight of the cable is often small and the tension is large, the sag effect of the cable is very small. In the chord vibration direction, the stay cable is only subjected to its self-weight load uniformly distributed along the cable length, and the weight redistribution of the cable caused by gravity sag and thermal expansion and contraction is ignored; (2) the constitutive relationship of the stay cable complies with Hooke's law, and the influence of factors such as the bending stiffness, torsion stiffness and shear stiffness of the stay cable are ignored; (3) under the excitation of Gaussian white noise, the stay cable remains elastic.

Fig. 1
figure 1

Coupled vibration model

Full size image

Modern long-span cable-stayed bridges mostly adopt dense cable structure systems. To improve the bending rigidity of the entire bridge, the design stiffness of the pylon is relatively large. Therefore, the influence of the vibration of the pylon is ignored in the model, and the boundary between the pylon and the cable regarded as a hinged connection. Consolidation is often used at the junction of the bridge tower and the bridge deck beam to reduce the stress on the bridge deck beam. Supported by the cable at various points, the bridge deck beam behaves like a continuous beam with multi-span elastic support, and is prone to producing vertical random excitation f(t) when subjected to external excitations such as wind, snow, and vehicles, etc. Therefore, the bridge deck beam can be regarded as a Bernoulli–Euler beam: one end is consolidated with the boundary and the other end is hinged with the cable. The vertical vibration displacement is vb. The cable is hinged with the bridge tower and the bridge deck beam, and uc and vc are the longitudinal and transverse in-plane dynamic displacements, respectively.

Vibration Equation

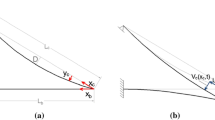
The respective motion trajectories of the cable and deck beam are described by the local coordinate systems o-xbyb and o-xcyc, as shown in Fig. 1. Assuming that the static linear shape of the cable is a parabola, the linear equation for the sag of the stayed cable is

$$y_c = \frac{m_c gl_c \cos \theta }{{2H}}\left( {x_c - \frac{x_c^2 }{{l_c }}} \right),$$
(1)

where H is the horizontal component of the cable force and g is the gravitational acceleration. It is worth noting that the precise line type of the cables of the long-span cable-stayed bridge is actually a catenary. In order to facilitate the calculation, the author selects a quadratic parabola as the initial line type of the cable.

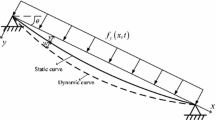
Based on D'Alembert's principle and cable static equilibrium, the in-plane lateral vibration differential equation of the stayed cable is established as [28]:

$$m_c \frac{\partial^2 v_c }{{\partial t^2 }} + c_c \frac{\partial v_c }{{\partial t}} - \left[ {1 - \frac{8d^2 }{{l_c^2 }}\left( {1 - \frac{2x_c }{{l_c }}} \right)^2 } \right] \cdot \left\{ {H\frac{\partial^2 v_c }{{\partial x_c^2 }} + \left( {h + f\left( t \right)\sin \theta } \right)\left( {\frac{d^2 y_c }{{dx_c^2 }} + \frac{\partial^2 v_c }{{\partial x_c^2 }}} \right)} \right\}{ = }f\left( t \right)\cos \theta \delta \left( x \right)$$
(2)

in which mc, lc and θ are the masses per unit length, length and inclination angle of cable, respectively, vc and yc are the functions of the position coordinate xc and time t, h is the horizontal component of the cable dynamic tension, d is the sag of the cable at the midspan, f(t) is the Gaussian white noise random excitation, and δ(x) is the Dirac function.

The first mode of the stay cable is the predominant vibration mode under end axial excitation and thus is usually the only mode taken into account [29]. Thus, the in-plane lateral vibration displacement of the stay cable is

$$v_c \left( {x,t} \right) = V_b \left( t \right)\phi_b \left( {l_b } \right){\text{cos}}\theta \left( {1 - \frac{x_c }{{l_c }}} \right) + V_c \left( t \right)\phi_c \left( {x_c } \right),$$
(3)

where V is the modal displacement and \({\phi }_{c}\left({x}_{c}\right)\) and \({\phi }_{b}\) are the mode functions of the stay cable and bridge deck beam, respectively; moreover, \({\phi }_{\mathrm{c}}\left({x}_{\mathrm{c}}\right)=\mathrm{sin}(\pi {x}_{\mathrm{c}}/{l}_{\mathrm{c}})\). As can clearly be seen, Eq. (3) includes the cable displacement caused by the vibration of the bridge deck beam so that the dynamic effect on the structure system can be considered.

In addition, the tangential dynamic tension of the cable T can be expressed by the stress–strain relationship of the cable as follows:

$$T = E_c A_c \varepsilon = E_c A_c \frac{{ds^{\prime} - ds}}{ds},$$
(4)

where \(\varepsilon\) is the axial strains of the stay cable, and \(s^{\prime}\) and s are the in-plane arc length coordinates of the stay cable in its present and initial configurations, respectively. The elements of s can be expressed as:

$$ds = \sqrt {\left( {dx_c + \frac{\partial u_c }{{\partial s}}dx_c } \right)^2 + \left( {dy_c + \frac{\partial v_c }{{\partial s}}dy_c } \right)^2 } = \sqrt {1 + (\frac{dy_c }{{dx_c }})^2 } {\text{d}}x_c .$$
(5)

If f is the additional tangential dynamic tension of the stay cable, then the following equation is obtained by combining Eq. (1) and Eq. (5):

$$\frac{dx_c }{{ds}} = \frac{h}{f} = \left[ {1 + \left( {\frac{dy_c }{{dx_c }}} \right)^2 } \right]^{ - \frac{1}{2}} \approx 1 - \frac{8d^2 }{{l_c^2 }}\left( {{1 - }\frac{{{2}x_c }}{l_c }} \right)^2$$
(6)

Considering the second-order amount of the cable, the strain ε caused by the lateral vibration of the cable can be obtained as

$$\varepsilon = \frac{{ds^{\prime} - ds}}{ds} \approx {{\left[ {\frac{\partial u_c }{{\partial s}}\frac{\partial x_c }{{\partial s}} + \frac{\partial v_c }{{\partial s}}\frac{\partial y_c }{{\partial s}} + \frac{1}{2}\left( {\frac{\partial v_c }{{\partial s}}} \right)^2 } \right]} / {\left[ {1 + \left( {\frac{dy_c }{{dx_c }}} \right)^2 } \right]}}$$
(7)

Then based on Eqs. (6) and (7), the horizontal dynamic tension h of the stay cable can be obtained as

$$h = f/\left[ {1 + \left( {\frac{{dy_c }}{{dx_c }}} \right)^2 } \right] = E_c A_c {\text{ }}\int_0^{l_c } {\left[ {\frac{{\partial u_c }}{{\partial x}} + \frac{{\partial v_c }}{{\partial x}}\frac{{\partial y_c }}{{\partial x}} + \frac{1}{2}\left( {\frac{{\partial v_c }}{{\partial x}}} \right)^2 } \right]} dx_c /\int_0^{l_c } {\sqrt {\left[ {1 + \left( {\frac{{dy_c }}{{dx_c }}} \right)^2 } \right]^3 } } dx_c ,$$
(8)

where the longitudinal displacement of any point on the cable is expressed as

$$u_c \left( {x_c ,t} \right) = - V_b \left( t \right)\phi_b \left( {l_b } \right)\sin \theta \left( {1 - \frac{x_c }{{l_c }}} \right).$$
(9)

To calculate h, first take out the denominator part of Eq. (8) for separate analysis, as represented by le and expanded according to Taylor's formula at \(y^{\prime} = 0\). Finally, take the first three terms of the expansion and integrate them to get:

$$l_e = \int_0^{l_c } {\sqrt {\left[ {1 + \left( {\frac{dy_c }{{dx_c }}} \right)^2 } \right]^3 } } dx_c \approx l_c \left( {1 + \frac{8d^2 }{{l_c^2 }}} \right).$$
(10)

Subsequently, h can be calculated by substituting Eqs. (1), (3), (9) and (10) into Eq. (8):

$$h = \frac{{E_c A_c }}{{l_e }}\left[ {\frac{{\left( {V_b \left( t \right)\phi _b \left( {l_b } \right)\cos \theta } \right)^2 }}{{2l_c }} + \frac{{\pi ^2 V_c^2 }}{{4l_c }} + \frac{{16dV_c }}{{\pi l_c }} + V_b \left( t \right)\phi _b \left( {l_b } \right)\sin \theta } \right].$$
(11)

Simplifying the bridge deck beam as a Bernoulli–Euler cantilever beam (Xia and Fujino 2016), its partial differential equation of motion is

$$E_b I_b \frac{\partial^4 v_b }{{\partial x_b^4 }} + N\frac{\partial^2 v_b }{{\partial x_b^2 }} + m_b \frac{\partial^2 v_b }{{\partial t^2 }} + c_b \frac{\partial v_b }{{\partial t}} - f(t)\delta \left( {x_b - l_b } \right) = 0,$$
(12)

in which N is the axial force of the beam and \(N=\left(h+H\right)\mathrm{cos}\theta\). If the vertical vibration displacement vb is separated into variables, and only the first-order vibration mode of the bridge deck beam considered:

$$v_b \left( {x_b ,t} \right) = V_b \left( t \right)\phi_b \left( {x_b } \right),$$
(13)

where the mode functions of bridge deck beam \({\phi }_{b}\) is:

$$\phi_b \left( {x_b } \right) = A_1 \sin \left( {\beta_b x_b } \right) + A_2 {\text{cos}}\left( {\beta_b x_b } \right) + A_3 {\text{sinh}}\left( {\beta_b x_b } \right) + A_4 {\text{cosh}}\left( {\beta_b x_b } \right)$$
(14)

then the boundary conditions of the bridge deck beam \(\phi _b (0) = \phi _b^{\prime} (0) = \phi _b^{\prime\prime} (0) = 0\) can be introduced into Eq. (14) to obtain the value of each constant:

\(A_1 = - A_3 ,\;A_2 = - A_4 ,\;A_4 = - A_3 \frac{{\left( {\sin \beta_b l_b + \sinh \beta_b l_b } \right)}}{{\left( {\cos \beta_b l_b + \cosh \beta_b l_b } \right)}}\) where \(\beta_b\)satisfies the transcendental equation:

$$\frac{E_c A_c \sin^2 \theta }{{E_b I_b l_c }} = \beta_b^3 \frac{1 + \cos \beta_b l_b \cosh \beta_b l_b }{{\cos \beta_b l_b \sinh \beta_b l_b - \sin \beta_b l_b \cosh \beta_b l_b }}$$

Let A3 = 1, then the values of A1, A2, and A4 can be obtained from the above relationship.

The Galerkin method [30] is used to model truncation of the vibration equations of the cable and the bridge deck beam, and the vibration Eqs. (15) and (16) of the cable-deck beam coupling system under random excitation can then be obtained as follows:

$$\mathop {V_c }\limits^{ \bullet \bullet } + m_1 \mathop {V_b }\limits^{ \bullet \bullet } + m_2 \mathop {V_c }\limits^\bullet + m_3 \mathop {V_b }\limits^\bullet + \left( {m_4 + \beta f\left( t \right)} \right)V_c + m_5 V_b + m_6 V_c^2 + m_7 V_b^2 + m_8 V_b V_c + m_9 V_c^3 + m_{10} V_c V_b^2 + \gamma_1 f\left( t \right) = 0,$$
(15)
$$\mathop {V_b }\limits^{ \bullet \bullet } + h_1 \mathop {V_b }\limits^\bullet + h_2 V_b + h_3 V_c V_b + h_4 V_b^2 + h_5 V_b V_c^2 + h_6 V_b^3 + \gamma_2 f\left( t \right) = 0,$$
(16)

where

\(m_1 = \frac{{2\phi_b \left( {l_b } \right)\cos \theta }}{\pi },\;m_2 = \frac{c_c }{{m_c }},\;m_3 = \frac{{2c_c \phi_b \left( {l_b } \right)\cos \theta }}{\pi m_c },\;m_4 = \frac{H\pi^2 }{{m_c l_c^2 }}\alpha_1 + \frac{512E_c A_c d}{{m_c l_c^3 l_e \pi^2 }}\alpha_2\)

\(m_5 = \frac{{32E_c A_c \phi_b \left( {l_b } \right)\sin \theta d}}{m_c l_c^2 l_e \pi }\alpha_2 ,\;m_6 = \frac{8E_c A_c \pi d}{{m_c l_c^3 l_e }}\alpha_2 ,\;m_7 = \frac{{16E_c A_c \phi_b^2 \left( {l_b } \right)\cos^2 \theta d}}{m_c l_c^3 l_e \pi }\alpha_2\)

\(m_8 = \frac{{E_c A_c \phi_b \left( {l_b } \right)\sin \theta \pi^2 }}{m_c l_c^2 l_e }\alpha_1 ,\;m_9 = \frac{E_c A_c \pi^4 }{{4m_c l_c^3 l_e }}\alpha_1 ,\;m_{10} = \frac{{E_c A_c \phi_b^2 \left( {l_b } \right)\cos^2 \theta \pi^2 }}{2m_c l_c^3 l_e }\alpha_1\)

\(\alpha _1 = 1 - \frac{{8d^2 }}{{3l_c }} + \frac{{16d^2 }}{{\pi ^2 l_c }},\;\alpha _2 = 1 - \frac{{8d^2 }}{{l_c }} + \frac{{64d^2 }}{{\pi ^2 l_c^2 }},\;\beta = \frac{{\pi ^2 \sin ^2 \theta }}{{m_c l_c^2 }}\alpha _1 ,\;\gamma _1 = \frac{{32\sin \theta d}}{{\pi m_c l_c^2 }}\alpha _2 ,\;\gamma _2 = - \frac{1}{{m_b }}\)

\(h_1 = \frac{c_b }{{m_b }},\;h_2 = \frac{E_b I_b \beta_b^4 + HQ\cos \theta } {m_b },\;h_3 = \frac{16Qd\cos \theta E_c A_c }{{\pi l_c l_e m_b }},\;h_4 = \frac{{\cos \theta Q\phi_b \left( {l_b } \right)E_c A_c \sin \theta }}{l_e m_b }\)

\(h_5 = \frac{\cos \theta QE_c A_c \pi^2 }{{4l_e l_c m_b }},\;h_6 = \frac{{\cos^3 \theta Q\phi_b^2 \left( {l_b } \right)E_c A_c }}{2l_e l_c m_b }\)

$$Q = \beta_b^2 \left\{ {\frac{{A_1 \left[ {\cos \left( {\beta_b l_b } \right) - 1} \right] - A_2 \sin \left( {\beta_b l_b } \right) + A_3 \left[ {\cosh \left( {\beta_b l_b } \right) - 1} \right] + A_4 \sinh \left( {\beta_b l_b } \right)}}{{A_1 \left[ {1 - \cos \left( {\beta_b l_b } \right)} \right] + A_2 \sin \left( {\beta_b l_b } \right) + A_3 \left[ {\cosh \left( {\beta_b l_b } \right) - 1} \right] + A_4 \sinh \left( {\beta_b l_b } \right)}}} \right\}.$$

Solution of Vibration Equation

As an important highlight of this paper, in this section, the Milstein–Platen method is used as a first attempt to solve the coupled random vibration time history of the cable–beam structure under random excitation. The phase space transformation method is first adopted to convert the above-mentioned cable-deck beam coupled vibration Eqs. (15) and (16) set into a random state equation. Introducing the state vector \(\left\{ Y \right\} = \left\{ {\begin{array}{*{20}c} {Y_1 } & {Y_2 } \\ \end{array} } \right\} = [\begin{array}{*{20}c} {q_1 } & {q_2 } & {q_3 } & {q_4 ]^T } \\ \end{array}\)superscript T denotes the transpose operation), the phase space change method is as follows:

$$\left\{ \begin{gathered} Y_1 = (V_c ,\mathop {V_c }\limits^\bullet )^T = \left( {q_1 ,q_2 } \right)^T \hfill \\ Y_2 = (V_b ,\mathop {V_b }\limits^\bullet )^T = \left( {q_3 ,q_4 } \right)^T \hfill \\ \end{gathered} \right.,$$
(17)
$$\frac{{d\left\{ Y \right\}}}{dt} = \left\{ {M\left( {q_i ,t} \right)} \right\} + \left\{ {N\left( {q_i ,t} \right)} \right\}dW,$$
(18)

where \(\left\{ {M\left( {q_i ,t} \right)} \right\}\)and \(\left\{ {N\left( {q_i ,t} \right)} \right\}\)are the drift vector and diffusion vector, respectively; i = 1, 2, 3, 4; W(\(\tau\)) is a zero mean unit intensity Gaussian white noise with spectral density K, and the autocovariance function:

$$E\left[W\left(t\right)W\left(t+\tau \right)\right]=\delta \left(\tau \right),$$

in which E[] denotes the mathematical expectation.

The Stradonovich equation equivalent of Eq. (18) is

$$d\left\{ Y \right\} = \left\{ {M\left( {q_i ,t} \right)} \right\}dt + \left\{ {N\left( {q_i ,t} \right)} \right\} \circ d\tilde{B}_t ,$$
(19)

where \(\tilde{B}_t\) is the Wiener process with covariance function:

$$E\left[ {\tilde{B}_{t_1 } \tilde{B}_{t_2 } } \right] = 2\pi K\delta_{t_1 t_2 } .$$

The Itô-differential equation equivalent to the Stradonovich Eq. (19) can be obtained by introducing the Wong–Zakai correction term on the basis of the original equation, namely

$$d\left\{ Y \right\} = \left\{ {\tilde{M}\left( {q_i ,t} \right)} \right\}dt + \sqrt {2\pi K} \left\{ {N\left( {q_i ,t} \right)} \right\}dB_t ,$$
(20)
$$\tilde{M}\left( {q_i ,t} \right) = M\left( {q_i ,t} \right) + \pi KN\left( {q_i ,t} \right)\frac{\partial }{\partial Y}N\left( {q_i ,t} \right),$$
(21)

where Bt is the unit Wiener process, i = 1, 2, 3, 4.

Then, substituting Eqs. (15) and (16) into Eq. (19), the Itô state equations for the coupled vibration of the cable–beam under random excitation can be obtained as

$$\left\{ \begin{aligned} dq_1 = q_2 dt \\ dq_2 = (m_1 h_1 q_4 + m_1 h_2 q_3 + m_1 h_3 q_1 q_3 + m_1 h_4 q_3^2 + m_1 h_5 q_1^2 q_3 + m_1 h_6 q_3^3 \\ & - m_2 q_2 - m_3 q_4 - m_4 q_1 - m_5 q_3 - m_6 q_1^2 - m_7 q_3^2 - m_8 q_1 q_3 - m_9 q_1^3 - m_{10} q_1 q_3^2 )dt \\ & + \sqrt {2\pi K} \left( { - \beta q_1 - \gamma_1 } \right)dB_{\text{t}} \\ dq_3 = q_4 dt \\ dq_4 = \left( { - h_1 q_4 - h_2 q_3 - h_3 q_1 q_3 - h_4 q_3^2 - h_5 q_1^2 q_3 - h_6 q_3^3 } \right)dt + \left( { - \sqrt {2\pi K} \gamma_2 } \right)dB_{\text{t}} \\ \end{aligned} \right..$$
(22)

At present, most researches start from the perspective of transition probability density, and are used to transform the Itô state equations of the cable into the FPK equation of the cable vibration, and then the Gauss truncation method is used to solve the equation and only the statistical characteristics of the parametric vibration response of the stay cable can be obtained. Since the external random excitation applied in this research is Gaussian white noise, the state response Y(t) of the system is a Markov process. Therefore, the transition probability density of Y(t) (denoted as p) still needs to satisfy the FPK equation:

$$\begin{gathered} \frac{\partial p}{{\partial t}} = - \sum_i \frac{\partial }{\partial q_i }\left[ {a_i \left( {Y,t} \right)p} \right] + \frac{1}{2}\sum_i \sum_j \frac{\partial^2 }{{\partial q_i \partial q_j }}\left[ {a_{ij} \left( {Y,t} \right)p} \right] \\ a_i \left( {Y,t} \right) = M_i \left( {Y,t} \right) \\ a_{ij} \left( {Y,t} \right) = \pi KN\left( {q_i ,t} \right)N^T \left( {q_i ,t} \right) \\ i = 1,\begin{array}{*{20}c} {} \\ \end{array} 2,\begin{array}{*{20}c} {} \\ \end{array} 3,\begin{array}{*{20}c} {} \\ \end{array} 4;\begin{array}{*{20}c} {} \\ \end{array} j = 1,\begin{array}{*{20}c} {} \\ \end{array} 2,\begin{array}{*{20}c} {} \\ \end{array} 3,\begin{array}{*{20}c} {} \\ \end{array} 4. \\ \end{gathered}$$
(23)

Substituting Eq. (22) into Eq. (23), the FPK equation of the cable–beam coupling system can be obtained as

$$\begin{gathered} \frac{\partial p}{{\partial t}} = - [\partial q_2 p/\partial q_1 + \partial (m_1 h_1 q_4 + m_1 h_2 q_3 + m_1 h_3 q_1 q_3 + m_1 h_4 q_3^2 + m_1 h_5 q_1^2 q_3 + m_1 h_6 q_3^3 - m_2 q_2 - m_3 q_4 - m_4 q_1 - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} m_5 q_3 - m_6 q_1^2 - m_7 q_3^2 - m_8 q_1 q_3 - m_9 q_1^3 - m_{10} q_1 q_3^2 )p/\partial q_2 + \partial q_4 p/\partial q_3 + \partial ( - h_1 q_4 - h_2 q_3 - h_3 q_1 q_3 - h_4 q_3^2 \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - h_5 q_1^2 q_3 - h_6 q_3^3 )p/\partial q_4 ] + \pi K(\partial^2 \left( {\beta q_1 + \gamma_1 } \right)^2 p/\partial q_2^2 + 2\partial^2 \left( {\gamma_2 \beta q_1 + \gamma_1 \gamma_2 } \right)p/\partial q_2 \partial q_4 + \gamma_2^2 \partial^2 p/\partial q_4^2 ). \hfill \\ \end{gathered}$$
(24)

Since Eq. (22) contains the diffusion term \(\sqrt {2\pi K} \left( { - \beta q_1 - \gamma_1 } \right)\), the multiplicative white noise excitation term will affect the stability of the solution process, resulting in the Gauss truncation method being unable to solve the stay cable vibration time history. Therefore, as the main contribution of this paper, the Milstein–Platen method [31, 32] is introduced to directly transform the Itô state Eq. (22) into iterative format that can be solved numerically. The Milstein–Platen iteration format is

$$\left\{ \begin{gathered} y_{n + 1}^{\left( i \right)} = y_n^{\left( i \right)} + m\left( {y_n^{\left( i \right)} ,t} \right)\Delta t + \sqrt {2\pi K} n\left( {y_n^{\left( i \right)} ,t} \right)\Delta W_n + \pi Kn\left( {y_n^{\left( i \right)} ,t} \right)\frac{{\partial n\left( {y_n^{\left( i \right)} ,t} \right)}}{{\partial y_n^{\left( i \right)} }}\left[ {\left( {\Delta W_n } \right)^2 - \Delta t} \right] \hfill \\ n\left( {y_n^{\left( i \right)} ,t} \right)\frac{{\partial n\left( {y_n^{\left( i \right)} ,t} \right)}}{{\partial y_n^{\left( i \right)} }} \approx \frac{1}{{\sqrt {\Delta t} }}\sqrt {2\pi K} [n\left( {s_n^{\left( i \right)} ,t} \right) - n\left( {y_n^{\left( i \right)} ,t} \right)] \hfill \\ s_n^{\left( i \right)} = y_n^{\left( i \right)} + m\left( {y_n^{\left( i \right)} ,t} \right)\Delta t + \sqrt {2\pi K} n\left( {y_n^{\left( i \right)} ,t} \right)\Delta t \hfill \\ \Delta W_j = W_j - W_{j - 1} ,j = 1,2,3, \ldots ,N \hfill \\ \end{gathered} \right.,$$
(25)

where \(y_n^{\left( i \right)}\),\(m\left( {y_n^{\left( i \right)} ,t} \right)\) and \(n\left( {y_n^{\left( i \right)} ,t} \right)\) are the ith element for vectors \(\left\{ Y \right\}\),\(\left\{ {M\left( {q_i ,t} \right)} \right\}\) and \(\left\{ {N\left( {q_i ,t} \right)} \right\}\) in the nth iteration, respectively; N is obtained by three initial conditions: start time t0, end time tn, time step \(\Delta t\),\(N=({t}_{n}-{t}_{0})/\Delta t\);\(\Delta {W}_{j}\) is an independent random increment, and satisfies \(\Delta {W}_{j}\sim \sqrt{\Delta t}N\left(\mathrm{0,1}\right)\). The initial value of i is 1 and when i is equal to N, the iteration is terminated. The calculation iteration format of Eq. (22) is then

$$\left\{ \begin{gathered} q_{n + 1}^{\left( 1 \right)} = q_n^{\left( 2 \right)} \Delta t \hfill \\ q_{n + 1}^{\left( 2 \right)} { = [}m_1 h_1 q_n^{(4)} + m_1 h_2 q_n^{(3)} + m_1 h_3 q_n^{(1)} q_n^{(3)} + m_1 h_4 (q_n^{(2)} )^2 + m_1 h_5 (q_n^{(1)} )^2 q_n^{(3)} { + }m_1 h_6 (q_n^{(3)} )^3 - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} m_2 q_n^{(2)} - m_3 q_n^{(4)} - m_4 q_n^{(1)} - m_5 q_n^{(3)} - m_6 (q_n^{(1)} )^2 - m_7 (q_n^{(3)} )^2 - m_8 q_n^{(1)} q_n^{(3)} - m_9 (q_n^{(1)} )^3 - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} m_{10} q_n^{(1)} (q_n^{(3)} )^2 ]\Delta t - \sqrt {2\pi K} (\beta q_n^{(1)} + \gamma_1 )\Delta W_n + \sqrt {\frac{\pi K}{{2\Delta t^2 }}} \beta (q_n^{(2)} - s_n^{(2)} )[\left( {\Delta W_n } \right)^2 - \Delta t] \hfill \\ q_{n + 1}^{(3)} = q_n^{(4)} \Delta t \hfill \\ q_{n + 1}^{\left( 4 \right)} = [ - h_1 q_n^{\left( 4 \right)} - h_2 q_n^{\left( 3 \right)} - h_3 q_n^{\left( 1 \right)} q_n^{\left( 3 \right)} - h_4 (q_n^{\left( 3 \right)} )^2 - h_5 (q_n^{\left( 1 \right)} )^2 q_n^{\left( 3 \right)} - h_6 (q_n^{\left( 3 \right)} )^3 ]\Delta t - \sqrt {2\pi K} \gamma_2 \Delta W_n \hfill \\ s_n^{\left( 2 \right)} = q_n^{\left( 2 \right)} + (m_1 h_1 q_n^{\left( 4 \right)} + m_1 h_2 q_n^{\left( 3 \right)} + m_1 h_3 q_n^{\left( 1 \right)} q_n^{\left( 3 \right)} + m_1 h_4 (q_n^{\left( 2 \right)} )^2 + m_1 h_5 (q_n^{\left( 1 \right)} )^2 q_n^{\left( 3 \right)} + m_1 h_6 (q_n^{\left( 3 \right)} )^3 \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - m_2 q_n^{\left( 2 \right)} - m_3 q_n^{\left( 4 \right)} - m_4 q_n^{\left( 1 \right)} - m_5 q_n^{\left( 3 \right)} - m_6 (q_n^{\left( 1 \right)} )^2 - m_7 (q_n^{\left( 3 \right)} )^2 - m_8 q_n^{\left( 1 \right)} q_n^{\left( 3 \right)} - m_9 (q_n^{\left( 1 \right)} )^3 \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - m_{10} q_n^{\left( 1 \right)} (q_n^{\left( 3 \right)} )^2 )\Delta t - \sqrt {2\pi K\Delta t} \left( {\beta q_n^{\left( 1 \right)} + \gamma_1 } \right) \hfill \\ \end{gathered} \right.,$$
(26)

in which the \(q_n^{\left( 1 \right)}\), \(q_n^{\left( 2 \right)}\) and \(q_n^{\left( 4 \right)}\) are the iterative terms of cable displacement, cable speed, bridge deck displacement and bridge deck speed, respectively. \(s_n^{\left( 2 \right)}\) is a correction term for multiplicative white noise excitation, which can reduce the influence of random parametric excitation on iteration. Starting from \(q_n^{\left( i \right)}\), iteratively solve \(q_{n + 1}^{\left( i \right)}\) (i = 1,2,3,4) step by step. After the state vector is obtained, the time-domain and frequency-domain characteristics of the coupled vibration of the cable–beam structure can be obtained.

Based on the above-mentioned process, the time history of the cable–deck beam coupling vibration under random excitation can be successfully obtained. The method introduced in this section overcomes the problem that other methods can only obtain the probability statistical information, so that the influence of the multiplicative excitation on the system can be effectively eliminated, which is of great significance to the vibration analysis of the cable–beam coupling system.

Case Analysis

Verification of Milstein–Platen Iterative Method

Taking the longest stay cable of a long-span cable-stayed bridge as an example, the initial displacement of the cable and beam is set to 0.01 m. The structural parameters are shown in Table 1.

Table 1 The parameter value of the structure
Full size table

Based on the relationship between Gaussian white noise and Wiener process, namely \({{dB_{\text{t}} } / {dt}} = W(t)\), it can be seen that the ideal white noise process has infinite energy. As shown by Zhu and Cai [30], within a small time step Δt, the white noise can be discretized into the following form:

$$\begin{array}{*{20}c} {E\left[ {W\left( {t_i } \right)} \right] = 0} & {E\left[ {W^2 \left( {t_i } \right)} \right] = \frac{2\pi K}{{\Delta t}}} & {E\left[ {W\left( {t_i } \right)W\left( {t_j } \right)} \right] = 0,i \ne j} \\ \end{array} .$$
(27)

Considering two moments, then:

$$W\left( {t_i + \tau } \right) = W\left( {t_i } \right) + \left[ {W\left( {t_{i + 1} } \right) - W\left( {t_i } \right)} \right]\frac{\tau }{\Delta t}.$$
(28)

According to the reciprocal theorem method, random excitation can be degenerated into ideal excitation [33]. It is worth noting that the introduction of ideal excitation here is only used to compare with the problem of random excitation and verify the correctness of the method proposed in this paper. The ideal excitation is set to \(p(t) = A\sin \varpi t\), where A and \(\varpi\) are, respectively, the amplitude and circle frequency of the equivalent ideal excitation; moreover,

$$\varpi = \frac{\pi }{{\sum_{i \ne j} {\max \left| {W\left( i \right) - W\left( j \right)} \right| \cdot \Delta t} }}.$$
(29)

The relevant parameters are selected as follows: the white noise intensity K is 135.66N2/Hz, the load time is 300 s, and the random excitation peak value is 2.48 × 107 N. The time history comparison between random excitation and equivalent ideal excitation is shown in Fig. 2. As shown by Fig. 2, the size of the random excitation force varies randomly and irregularly with time, with strong uncertainty, while the ideal excitation force has obvious periodicity, and its magnitude is determined. Obviously, the vibration of bridge deck beam is random in engineering practice, and if the bridge deck beam is simplified as ideal excitation, it cannot truly reflect the end excitation of the cable. Therefore, it can be seen that studying the parametric vibration of stay cables under random excitation has broader engineering practical significance.

Fig. 2
figure 2

Time history comparison between two excitation modes

Full size image

In order to verify the accuracy of the Milstein–Platen method for solving the vibration equations, it is compared with the traditional FPK method, with the mean square error of the statistical distance under the transition probability density used as the comparison index. When Eq. (24) is multiplied by \({q}_{1}^{i}{q}_{2}^{j}{q}_{3}^{k}{q}_{4}^{l}\) (i, j, k and l are all non-negative integers), and then the entire state space is integrated with the boundary condition P(-∞,t) = P(+ ∞,t) = 0, the moment equation of the state vector \(\left\{Y\right\}\) can be obtained, where p = p(q,t) is the PDF of the diffusion process. The r-th order (r = i + j + k + l) statistical moment equation of the state vector {Y} is:

$$\begin{gathered} \mathop {m_{i,j,k,l} }\limits^\bullet = im_{i - 1,j + 1,k,l} + j[(m_1 h_1 - m_3 )m_{i,j - 1,k,l + 1} + (m_1 h_2 - m_5 )m_{i,j - 1,k + 1,l} + (m_1 h_3 - m_8 )m_{i + 1,j - 1,k + 1,l} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + m_1 h_4 m_{i,j - 1,k + 2,l} + m_1 h_5 m_{i + 2,j - 1,k + 1,l} + m_1 h_6 m_{i,j - 1,k + 3,l} - m_2 m_{i,j,k,l} - m_4 m_{i + 1,j - 1,k,l} - m_6 m_{i + 2,j - 1,k,l} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} - m_7 m_{i,j - 1,k + 2,l} - m_9 m_{i + 3,j - 1,k,l} - m_{10} m_{i + 1,j - 1,k + 2,l} ] + km_{i,j,k - 1,l + 1} - l(h_1 m_{i,j,k,l} + h_2 m_{i,j,k + 1,l - 1} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + h_3 m_{i + 1,j,k + 1,l - 1} + h_4 m_{i,j,k + 2,l - 1} + h_5 m_{i + 2,j,k + 1,l - 1} + h_6 m_{i,j,k + 3,l - 1} ) + \pi K[j(j - 1)(\beta^2 m_{i + 2,j - 2,k,l} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} + 2\beta \gamma_1 m_{i + 1,j - 2,k,l} + \gamma_1^2 m_{i,j - 2,k,l} ) + 2jl(\gamma_2 \beta m_{i + 1,j - 1,k,l - 1} + \gamma_1 \gamma_2 m_{i,j - 1,k,l - 1} ) + l(l - 1)\gamma_2^2 m_{i,j,k,l - 2} ], \hfill \\ \end{gathered}$$
(30)

where \({m}_{i,j,k,l}=E\left[{q}_{1}^{i}{q}_{2}^{j}{q}_{3}^{k}{q}_{4}^{l}\right]\), which is the r = i + j + k + l moment of q1, q2, q3 and q4. It can be seen that Eq. (30) contains nonlinear terms and coupling terms. Therefore, higher moments are generated in the rth order moment equation, with the result that the moment equation cannot be closed. In other words, Eq. (30) is a non-closed nonlinear differential equation.

Therefore, the Gaussian statistical moment truncation method [25] is used next to convert Eq. (30) into a closed differential equation. The logarithm calculation of the mean square error (MSE) is as follows:

$$Y\left[ {q_i } \right] = Ln\left( {E\left[ {q_i^2 } \right]} \right).$$
(31)

The changing trend for the logarithm of the MSE over time is shown in Fig. 3, where the MSE of the cable vibration displacement quickly stabilized in a relatively short period of time. The reason for this is that the initial moment of the external excitation is an assault. In the stable vibration region, the logarithmic MSE calculated by the Gaussian truncation method is [3.32 m -2.51 m], and [-2.79 m -2.52 m] by the Milstein–Platen method, indicating the calculation results of the two methods are basically consistent. As time goes by, the absolute error between the two continues to decrease. Therefore, from the perspective of random orbit, the Milstein–Platen method is clearly the correct choice to solve the cable displacement time history under random excitation, which is consistent with the calculation results of the Gaussian truncation method.

Fig. 3
figure 3

Comparison of logarithm MSE and error curve of cable displacement

Full size image

Time-History Analysis of Cable–Beam Vibration Under Random Excitation

Based on the iterative format derived from Eq. (26), a program is compiled to analyze the time history characteristics of the displacement of the cable and beam under random excitation. The time history curves of cable and beam displacement are shown in Fig. 4.

Fig. 4
figure 4

Displacement time history curves of cable and beam

Full size image

It can be seen from Fig. 4 that the parametric vibration of the stay cable presents an obvious "beat vibration" phenomenon under the action of random excitation. Under random excitation, the "beat vibration" amplitude of the cable changes randomly, the absolute value of its amplitude within 300 s is 0.27 m ~ 0.61 m, and the "beat vibration" period is 9.1 s. Under the equivalent ideal excitation effect, the amplitude of the "beat" is relatively unchanged, with a maximum amplitude of 0.5 m and a period of 10 s, which is relatively close to the period of the beat under random excitation. It can be seen that under random excitation, the amplitude of the stay cable has obvious uncertainty.

Regarding the vibration displacement of the bridge deck beam under random excitation, it exhibits irregular changes as can be seen in Fig. 4c. The bridge deck beam undergoes relatively stable periodic vibration near the balance plane, but the maximum amplitude does not exceed 0.02 m. According to Fig. 4d, under equivalent ideal excitation, the bridge deck beam makes a relatively stable periodic vibration at the equilibrium position, and its amplitude is -0.02 m ~ 0.02 m. These indicate that when coupled vibration occurs in the structural system, there is energy transfer between the stayed cable and the bridge deck beam.

To further grasp the statistical characteristics of cable vibration, the mean square response curve of cable vibration displacement under the two excitation modes are shown in Fig. 5.

Fig. 5
figure 5

The statistical characteristic curve of cable vibration displacement

Full size image

From Fig. 5a, b, it can be seen that under random excitation and equivalent ideal excitation, the vibration of the stayed cable at the initial moment has non-stationary transient characteristics. During random excitation, the average value of cable displacement oscillates repeatedly in the range of -8 mm ~ 12 mm, and reaches a stable state after 12 s, and then gradually approaches zero. The average value of the cable's displacement during ideal excitation reciprocates in the range of -16 mm ~ 21 mm, and reaches a stable state after 10 s, and finally gradually approaches zero. It can be seen that whether it is random excitation or ideal excitation, the average value of the displacement response of the cable eventually tends to zero.

It can be seen from Fig. 5c that the MSE of the cable's displacement during ideal excitation first increases sharply, then the oscillation decreases, and finally tends to be stable; while randomly excited, the MSE of the cable's displacement increases sharply at first, then slowly increases in an oscillating manner, and finally stabilizes, stabilizing at 0.2 m after 100 s. Under the two excitation modes, the mean square deviation of the cable displacement is obviously different. The reason is that the ideal excitation is a deterministic effect, while the random excitation has a strong uncertainty.

Analysis of Frequency Domain Characteristics of Cable Vibration

To further analyze the frequency domain characteristics of cable vibration, firstly, based on the vibration time history results of the stay cable, the fast Fourier change is used to calculate the random response power–frequency curve of the cable, and the result is shown in Fig. 6a; the Welch method is used to divide the cable response data sequence into different periods, and the improved periodogram method is then applied to estimate and average each section and obtain the PSD curve, as shown in Fig. 6b. Finally, the non-parametric test is performed on the results to obtain the PDF and the cumulative distribution function (CDF) for the random vibration displacement of the cable, as shown in Fig. 7a, b.

Fig. 6
figure 6

Random response power and PSD curve of cable

Full size image
Fig. 7
figure 7

PDF and CDF curve of random response for cable

Full size image

It can be seen from Fig. 6a that under random excitation and ideal excitation, the power–frequency of the cable displacement response presents a nonlinear trend that first increases and then becomes stable. The power peak of the cable response occurs near f1 = 43.3 Hz and f2 = 45.6 Hz, which dominate the entire response, and the power–frequency curve of the stay cable is smoother under ideal excitation. Further, as shown by Fig. 6b, under the two excitation modes, the PSDs of the cable response show a trend of nonlinear oscillation decreasing, and the PSD of the randomly excited drop cable is slightly higher than that of the ideal excitation. Compared with the main peak, the attenuation of the first side lobe of the PSD of the cable response under random excitation is -22.1 dB, and the peak attenuation of the side lobe is -3.17 dB/oct, which corresponding to ideal excitation are -22.8 dB and -3.17 dB/oct, respectively. Thus, whether it is random excitation or ideal excitation, the frequency of the power peak response of the stay cable is basically the same as the attenuation of the PSD sidelobe peak. However, the difference between the first side lobe peak and the main peak of the cable PSD under the two excitations is not the same.

It can be seen from Fig. 7a that under the two excitation modes, the PDF of the cable response first increases and then decreases, and its distribution trend satisfies the Gaussian distribution, with a confidence interval of about 0.98, and conforms to the Markov property. Compared with the ideal excitation, the tail area of the PDF curve of the cable response under random excitation is expanded from [-0.5 m ~ 0.5 m] to [-0.525 m ~ 0.525 m]. However, the peak value of the relative probability density decreases from 9.1% to 7.5%. The main reasons are as follows: First, the amplitude of the cable under random excitation changes, which causes the amplitude of the cable at the same time to be greater than the ideal excitation, and the system absorbs excess energy due to load uncertainty. Second, the probability density of the reciprocating and balanced positions of the ideal excitation cable is greater than the random excitation, and the periodic random excitation of the "beat" movement of the cable is greater than the ideal excitation. Further, as shown by Fig. 7b, under the two conditions, the CDF curve of the cable response shows a nonlinear increase. In [− 0.5 m ~ 0 m], the random excitation is slightly larger than the ideal excitation, while in [0 m ~ 0.5 m], the ideal excitation is slightly larger than the random excitation.

Analysis of Coupled Vibration Factors of Cable and Beam

To analyze the effect of cable self-damping, initial perturbation of the bridge deck beam, and initial tension and external excitation intensity on cable amplitude, the influence of these different factors can be obtained by adjusting the structural parameters of the cable and bridge deck beam.

Influence of Cable Self-Damping

The cable damping ratio varies between 0.01 and 0.1, and the initial displacement of the stay cable and the bridge deck beam are set to zero. The maximum amplitude change curve of the stay cable under different cable damping ratio conditions is calculated as shown in Fig. 8.

Fig. 8
figure 8

The relationship curve between cable amplitude and cable damping ratio

Full size image

The results show that with the gradual increase in the cable damping ratio, the cable amplitude exhibits a nonlinear decreasing trend under both random excitation and ideal excitation, and the cable displacement response under random excitation is greater than the ideal excitation response. When the damping ratio increases from 0.01 to 0.04, the cable amplitude change rate is 16.7%, and when the damping ratio increases from 0.06 to 0.1, the cable amplitude change rate decreases to 8.9%. It can also be seen that the larger the cable damping ratio, the smaller the cable amplitude. However, when the damping ratio continues to increase, the amplitude decay of the cable vibration tends to ease, and the damping ratio of the cable itself restrains the cable amplitude to a limited extent.

Influence of Initial Disturbance of Bridge Deck Beam

The initial disturbance of the bridge deck beam is set to 0.01 ~ 0.1 m, the initial displacement of the cable is set to zero, and the influence of the self-damping of the cable is ignored. The change curve of the maximum amplitude of the cable under different initial disturbance conditions of the beam is shown in Fig. 9.

Fig. 9
figure 9

The relationship curve between cable amplitude and initial disturbance of beam

Full size image

Figure 9 shows that as the initial disturbance of the beam increases, the amplitude of the cable presents a nonlinear increasing trend, and the maximum amplitude of the cable under the random excitation is greater than the ideal excitation. When the initial disturbance of the bridge deck beam increases from 0.01 m to 0.03 m, the maximum amplitude of the stay cable under random excitation increases from 0.65 m to 1.11 m. Under ideal excitation, the maximum amplitude of the stay cable increases from 0.51 m to 1.01 m. It can be seen that the greater the initial disturbance of the bridge deck beam, regardless of whether this occurs under random excitation or ideal excitation conditions, the greater the amplitude of the stayed cable. Therefore, in engineering practice, it is necessary to control the disturbance of the bridge deck as much as possible.

Effect of Initial Tension

The initial tension range is 6.4 × 107 N ~ 7 × 107 N, and the initial displacement of the cable is set to zero. The maximum amplitude change curve of the cable under different initial tension conditions is shown in Fig. 10.

Fig. 10
figure 10

The relationship curve between cable amplitude and initial tension

Full size image

It can be seen from Fig. 10 that as the initial cable force increases, the maximum amplitude of the cable first decreases sharply and then tends to relax, and the amplitude of the cable under random excitation is greater than under the ideal excitation. When the initial tension of the cable is increased from 6.4 × 107 N to 6.8 × 107 N, the cable amplitude reduction rate is 56.9% under random excitation and 65.2% under ideal excitation. When the initial tension of the cable is further increased from 6.8 × 107 N to 7.0 × 107 N, the amplitude reduction rate is only 5.2% for random excitation, and 11.2% for ideal excitation. It can be seen that the initial tension has a great influence on the vibration of the stay cable, and the amplitude is greater under random than ideal excitation.

At the same time, it also can be seen that with greater initial tension of the cable, the sag effect decreases, that is, the Irvine parameter \({\lambda }_{I}^{2}\) decreases:

$$\lambda_I^2 = \left( \frac{mgl}{H} \right)^2 \frac{E_c A_c l}{{HL_e }}.$$
(32)

Conversely, with a smaller initial cable force, the cable sag effect increases, and the random excitation term \({\gamma }_{1}\) in Eq. (15) will increase accordingly, which is equivalent to increasing the external excitation intensity, resulting in an increase in the vibration intensity of the cable.

Effects of External Excitation Intensity

For Gaussian external excitation intensity of the bridge deck beam in the range 0N2/Hz ~ 165.6N2/Hz, and the initial displacement of the cable and bridge deck beam set to zero, Fig. 11 shows the relationship curve between the amplitude of the cable and the external excitation intensity.

Fig. 11
figure 11

The relationship curve between cable amplitude and external noise

Full size image

It can be seen from Fig. 11 that as the intensity of the external excitation increases, the maximum response of the cable shows a nonlinear increasing trend. When the external excitation intensity is 45.6N2/Hz, the maximum response of the cable is 0.37 m, and when the external excitation intensity is 165.6N2/Hz, the maximum amplitude of the cable increases to 0.68 m. It can also be seen that the greater the intensity of the random excitation, the greater the vibration amplitude of the cable.

Summary and Conclusions

After establishing a parametric vibration model of the cable–beam coupling under random excitation, the Milstein–Platen method is used as a first attempt to solve the coupled random vibration time history of the cable–beam structure. As the main contribution, the method proposed in this study overcomes the issue that other methods can only obtain the probability statistical information and offers a way to directly solve the coupled random vibration time history of the cable–beam structure. The cable random displacement, statistical moment characteristics, PSD and probability density changes are analyzed from the random track angle, and the results are compared with the Gaussian truncation method. The cable damping ratio, initial perturbation of the stiffened beam, initial tension, and the influence of external excitation intensity on the amplitude of the cable are also studied. The research results are very meaningful for studying the cable–beam coupling and provide a theoretical basis for vibration control of long-span cable-stayed bridges. Based on the analysis conducted in this study, the following conclusions can be drawn:

From the perspective of random orbit, the Milstein–Platen method can be used to discretize the given Itô state equations of cable–beam coupled vibration under random excitation and effectively solve the cable displacement time history. The case study shows that the result calculated by the Milstein–Platen method is consistent with that calculated by the traditional Gaussian truncation method.

The phenomenon of “quasi-beat vibration” appears in the cable vibration under random excitation, and vibration amplitude changes randomly with time. There is energy transfer in the coupling system, and when the cable–beam structure undergoes coupling vibration, the bridge deck beam creates relatively stable periodic vibration.

With the passage of time, whether it is random excitation or ideal excitation, the mean value of the vibration displacement response of the stay cable tends to zero. Under the two excitation modes, the mean square error stabilization time of the displacement response of the stay cable is not the same, but it tends to be stable in the end.

Under random excitation and ideal excitation, the frequency and power spectral density side lobe peak attenuation corresponding to the power peak of the stay cable response are basically the same, but the difference between the first side lobe peak and the main peak of the stay cable under the two excitation modes is not same.

As the damping ratio increases, the damping efficiency of the cable itself decreases; the initial disturbance of the bridge deck beam has a greater impact on the cable vibration. The greater the initial disturbance of the bridge deck beam, the greater the cable vibration displacement; The greater the tension of the cable, the vibration amplitude of the cable shows a non-linear decrease, but when the tension of the cable is further increased, the amplitude of the vibration of the cable tends to be attenuated; the greater the intensity of the random excitation, the greater the amplitude of the cable.