Bright hump solitons for the higher-order nonlinear Schrödinger equation in optical fibers

Abstract

Under investigation is the higher-order nonlinear Schrödinger equation with the third-order dispersion (TOD), self-steepening (SS) and self-frequency shift, which can be used to describe the propagation and interaction of ultrashort pulses in the subpicosecond or femtosecond regime. Through the introduction of an auxiliary function, bilinear form is derived. Bright one- and two-soliton solutions are obtained with the Hirota method and symbolic computation. From the one-soliton solutions, we present the parametric regions for the existence of single- and double-hump solitons, and find that they are affected by the coefficients of the group velocity dispersion (GVD) and TOD. Besides, propagation of the one single- or double-hump soliton is observed. We analytically obtain the amplitudes for the single- and double-hump solitons, and calculate the interval between the two peaks for the double-hump soliton. Moreover, soliton amplitudes are related to the coefficients of the GVD, TOD and SS, while the interval between the two peaks for the double-hump soliton is dependent on the coefficients of the GVD and TOD. Interactions are seen between the (i) two single-hump solitons, (ii) two double-hump solitons, and (iii) single- and double-hump solitons. Those interactions are proved to be elastic via the asymptotic analysis.

1 Introduction

It has been theoretically predicted [1, 2] and experimentally observed [3, 4] that the bright (dark) optical solitons can exist in the anomalous (normal) dispersion regime. Since then, optical solitons have attracted some attention because of their potential applications in the optical communication systems and all-optical switching devices [5]. Optical solitons can stably propagate over a long distance due to the balance between the linear dispersion and nonlinear effects [5]. In the picosecond regime, the nonlinear Schrödinger (NLS) equation with the group velocity dispersion (GVD) and self-phase modulation (SPM) [5]

$$\begin{aligned} iU_Z+\alpha U_{TT}+\chi|U|^2U=0 \end{aligned}$$

(1)

can model the propagation and interaction of optical solitons in the mono-mode fibers. Hereby, U is the slowly varying envelope of the electric field, Z is the normalized distance along the direction of propagation, T is retarded time, the subscripts represent the partial derivatives, the real parameters α and χ are, respectively, related to the GVD and SPM [5].

In the subpicosecond or femtosecond regime, Eq. (1) is inadequate since the optical solitons become shorter [6–9]. Higher-order effects including the third-order dispersion (TOD), self-steepening (SS) and stimulated Raman scattering (SRS) need to be considered for the ultrashort pulses [10–12]. Among them, the TOD produces the asymmetrical temporal broadening for the ultrashort pulses, the SS, which is also called the Kerr dispersion, leads to the asymmetrical spectral broadening for the ultrashort pulses, and the SRS causes a self-frequency shift for the ultrashort pulse [10–14]. Besides, optical solitons with the non-Kerr law nonlinearity or perturbation terms have been considered in Refs. [15–24]. For example, Refs. [15, 16] have, respectively, investigated two variable-coefficient NLS equations with non-Kerr law nonlinearity, and derived the bright and dark one-soliton solutions when the coefficients are Riemann integrable. Ref. [17] has discussed the adiabatic parameter dynamics of Gaussian optical solitons with the local and non-local perturbation terms through the collective variables method. Dynamics of optical solitons for the improved NLS equation with the Kerr law, power law, parabolic law, dual-power law or log law nonlinearity has been investigated [18, 19]. Ref. [20] has studied the NLS equation with the power law nonlinearity and Hamiltonian perturbation terms, and obtained the bright and dark one-soliton solutions. Ref. [21] has researched the Schrödinger–Hirota equation with the power law nonlinearity in the dispersive optical, and derived the soliton solutions and complexitons. Ref. [22] has discussed the dynamics of dark solitons for the variable-coefficient NLS equation with the power law nonlinearity. Ref. [23] has considered the dynamics of the dark solitons for the generalized NLS equation with the parabolic law and dual-power law nonlinearities. Lie symmetry approach has been used to obtained the stationary one-soliton solutions for the NLS equation with the Kerr law, power law, parabolic law or the dual-power law nonlinearity [24].

In this paper, we will only take the TOD, SS and SRS into account, and investigate the following higher-order NLS (HNLS) equation [25–33]:

$$\begin{aligned} &{iu_z+\alpha_1u_{tt}+ \alpha_2|u|^2u} \\ &{\quad{}+i \bigl[\alpha_3u_{ttt}+ \alpha_4 \bigl(|u|^2u \bigr)_t+ \alpha_5u \bigl(|u|^2 \bigr)_t \bigr]=0,} \end{aligned}$$

(2)

where u is the slowly varying envelope of the electric field, z is the normalized distance along the direction of propagation, t is retarded time, the real parameters α ₁, α ₂, α ₃, α ₄ and α ₅ are relevant to the GVD, SPM, TOD, SS and SRS, respectively. Equation (2) can be used to describe the propagation and interaction of ultrashort pulses in optical fibers [10–14, 25]. Specially, when α ₃=α ₄=α ₅=0, Eq. (2) reduces to Eq. (1) [5]; when α ₃=α ₅=0, to the modified NLS equation [25, 34]; when 3α ₂ α ₃=α ₁ α ₄ and α ₄+α ₅=0, to the Hirota equation [25, 35]; when 3α ₂ α ₃=α ₁ α ₄ and α ₄+2α ₅=0, to the Sasa–Satsuma equation [25, 31].

Equation (2) has been investigated analytically in some aspects [26–33]: Painlevé analysis, Lax pair and soliton solutions have been investigated for Eq. (2), with the discussion on the all-soliton communication links [26]; one-soliton solutions have been obtained for Eq. (2) with α ₁=α ₂=α ₃=1 and 3α ₄+2α ₅>0 [27]; dark soliton solution for Eq. (2) has been discussed and derived through the coupled amplitude-phase formulation [28], and dark one- and two-soliton solutions for Eq. (2) with α ₁=−1, α ₂=2, α ₃=−1, α ₄=6 and α ₅=−6 (α ₅=−3) have been constructed [29]; a class of soliton solutions has been derived for Eq. (2) with α ₁=1, α ₂=2, α ₃=−1, α ₄=−6 and α ₅=3, and those solitons have been found to be stable in a certain domain of the parameter [30]; via the inverse scattering transform, one-soliton solutions have been explicitly given for Eq. (2) with α ₁=1/2, α ₂=1, α ₃=1, α ₄=6 and α ₅=−3, and propagation of the one soliton with the double humps has been observed [31]; N-soliton solutions for Eq. (2) with 3α ₂ α ₃=α ₁ α ₄ and α ₄+α ₅=0 have been presented through the Darboux transformation, with the indication that the interaction between neighboring solitons can be restrained to some extent, helping to increase the bit-rate in optical telecommunication systems [32]; bilinear form and one-soliton solutions have been obtained for Eq. (2) with α ₁=α ₂=0, α ₃=1, α ₄=6 and α ₅=−3 [33].

However, to our knowledge, propagation and interaction of the bright single- and double-hump solitons have not been investigated for Eq. (2) with 3α ₂ α ₃=α ₁ α ₄ and α ₄+2α ₅=0. Therefore, in this paper, we will obtain the bilinear form through an auxiliary function, and construct the bright hump one- and two-soliton solutions with the Hirota method [36] and symbolic computation [37–40]. In Sect. 3, based on those solutions, we will investigate the propagation and interaction of bright single- and double-hump solitons analytically and graphically. For the one-soliton solutions, we will give the parametric regions for the existence of single- and double-hump solitons. For the two-soliton solutions, we will find that the interactions can exist between (i) two single-hump solitons, (ii) two double-hump solitons, and (iii) one single-hump and one double-hump solitons. Besides, we will carry out the asymptotic analysis on the two-soliton solutions to prove that the interaction are elastic. Our conclusions will be listed in Sect. 4.

2 Bilinear form and bright soliton solutions

2.1 Bilinear form

Introducing the dependent variable transformation,

$$\begin{aligned} u=\frac{g}{f}, \end{aligned}$$

(3)

where g is the complex differentiable function with respect to z and t, and f is a real one, we transform Eq. (2) with 3α ₂ α ₃=α ₁ α ₄ and α ₄+2α ₅=0 into the following form:

$$\begin{aligned} &{i\frac{D_zg\cdot f}{f^2}+\alpha_1 \biggl(\frac{D_t^2g\cdot f}{f^2}- \frac{g}{f}\frac{D_t^2f\cdot f}{f^2} \biggr)} \\ &{\quad{}+\frac{\alpha_1\alpha_4}{3\alpha_3}\frac{g}{f} \frac {gg^*}{f^2}} \\ &{\quad{}+i\biggl(\alpha_3\frac{D_t^3g\cdot f}{f^2}-3 \alpha_3\frac{D_tg\cdot f}{f^2}\frac{D_t^2f\cdot f}{f^2}} \\ &{\quad{}+\frac{3\alpha_4}{2}\frac{D_tg\cdot f}{f^2}\frac{gg^*}{f^2}+ \frac{\alpha_4}{2}\frac{D_tg^*\cdot f}{f^2}\frac{g^2}{f^2}\biggr)=0,} \end{aligned}$$

(4)

with ∗ as the complex conjugate, while D _z and D _t being the Hirota operators [36] defined as

$$\begin{aligned} &{D_z^m\,D_t^n a(z,t) \cdot b(z,t)} \\ &{\quad= \biggl(\frac{\partial}{\partial z}-\frac{\partial}{\partial z'} \biggr)^m \biggl(\frac{\partial}{\partial t}-\frac{\partial}{\partial t'} \biggr)^n} \\ &{\qquad{}\times a(z,t)b\bigl(z',t' \bigr)\big|_{z'=z,t'=t},} \end{aligned}$$

where a(z,t) and b(z,t) are the differentiable functions, z′ and t′ are the independent variables, and m and n are the nonnegative integers.

Through the exchange formula [36], we can derive

$$\begin{aligned} \bigl(D_tg^*\cdot f\bigr)g^2=(D_tg\cdot f)gg^*-\bigl(D_tg\cdot g^*\bigr)gf. \end{aligned}$$

(5)

Via Expression (5), Eq. (4) becomes as follows:

$$\begin{aligned} &{\frac{ (iD_z+\alpha_1D_t^2+i\alpha_3D_t^3 )g\cdot f}{f^2}} \\ &{\quad{}-\frac{3\alpha_3D_t^2f\cdot f-2\alpha_4gg^*}{f^2} \biggl(\frac{\alpha_1g}{3\alpha_3f}+i \frac{D_tg\cdot f}{f^2} \biggr)} \\ &{\quad{}-\frac{g}{f}\frac{ (3i\alpha_3\alpha_4D_t+2\alpha _1\alpha_4 )g\cdot g^*}{6\alpha_3f^2}=0.} \end{aligned}$$

(6)

Setting

$$\begin{aligned} 3\alpha_3D_t^2f\cdot f-2 \alpha_4gg^*=0, \end{aligned}$$

(7)

we have

$$\begin{aligned} &{\frac{ (iD_z+\alpha_1D_t^2+i\alpha_3D_t^3 )g\cdot f}{f^2}} \\ &{\quad{}-\frac{g}{f}\frac{ (3i\alpha_3\alpha_4D_t+2\alpha _1\alpha_4 )g\cdot g^*}{6\alpha_3f^2}=0.} \end{aligned}$$

(8)

Note that Eq. (8) is not a bilinear form but a trilinear one. Therefore, we need to introduce one auxiliary function and obtain the bilinear form for Eq. (2) as follows:

$$\begin{aligned} &{ \bigl(iD_z+\alpha_1D_t^2+i \alpha_3D_t^3 \bigr)g\cdot f-gh=0,} \end{aligned}$$

(9a)

$$\begin{aligned} &{ (3i\alpha_3\alpha_4D_t+2 \alpha_1\alpha_4 )g\cdot g^*-6\alpha_3fh=0,} \end{aligned}$$

(9b)

$$\begin{aligned} &{3\alpha_3D_t^2f\cdot f-2 \alpha_4gg^*=0,} \end{aligned}$$

(9c)

with h as an auxiliary function of z and t to be determined.

2.2 Bright soliton solutions

In order to obtain the bright soliton solutions, g, f and h are expanded with respect to a formal parameter ε as follows:

$$\begin{aligned} &{g=\varepsilon g_1+\varepsilon^3 g_3+\varepsilon^5 g_5+\varepsilon^7 g_7+\cdots,} \end{aligned}$$

(10a)

$$\begin{aligned} &{f=1+\varepsilon^2 f_2+\varepsilon^4 f_4+\varepsilon^6 f_6+\varepsilon^8 f_8+\cdots,} \end{aligned}$$

(10b)

$$\begin{aligned} &{h=\varepsilon^2 h_2+\varepsilon^4 h_4+\varepsilon^6 h_6+\varepsilon^8 h_8+\cdots,} \end{aligned}$$

(10c)

where g _j ’s (j=1,3,5,…), f _k ’s and h _k ’s (k=2,4,6,…) are the differentiable functions with respect to z and t. Substituting Expressions (10a)–(10c) into Bilinear Form (9a)–(9c) and collecting the coefficients of each order of ε yield the recursion relations for g _j ’s (j=1,3,5,…), f _k ’s and h _k ’s (k=2,4,6,…), through which the bright soliton solutions for Eq. (2) can be derived.

2.2.1 Bright one-soliton solutions

To obtain the bright one-soliton solutions, we truncate Expressions (10a)–(10c) as g=εg ₁+ε ³ g ₃, f=1+ε ² f ₂+ε ⁴ f ₄ and h=ε ² h ₂+ε ⁴ h ₄. Setting that

$$\begin{aligned} g_1=e^{kt+wz+\eta}, \end{aligned}$$

(11)

where k and η are two complex parameters and w is a complex one to be determined, and through Bilinear Form (9a)–(9c), we have

$$\begin{aligned} \begin{aligned} &{f_2=\beta e^{\theta+\theta^*},\qquad h_2=\gamma e^{\theta+\theta^*},\qquad g_3=\delta e^{2\theta+\theta^*},} \\ &{f_4=\zeta e^{2\theta+2\theta^*},\qquad h_4=\vartheta e^{2\theta +2\theta^*},} \\ &{\theta=kt+wz+\eta,} \\ &{w=i\alpha_1k^2-\alpha_3k^3, \qquad\zeta=\delta\delta^*,\qquad \vartheta=0,} \\ &{\beta=\frac{\alpha_4}{3\alpha_3(k+k^*)^2},\qquad \gamma=\frac{\alpha_4[2\alpha_1+3i\alpha_3(k-k^*)]}{6\alpha_3},} \\ &{\delta=\frac{\gamma}{2 (3i\alpha_3k+\alpha_1 )(k+k^*)^2}.} \end{aligned} \end{aligned}$$

(12)

Without loss of generality, with ε=1 and Expression (3), the bright one-soliton solutions for Eq. (2) are

$$\begin{aligned} u=\frac{g_1+g_3}{1+f_2+f_4}. \end{aligned}$$

(13)

2.2.2 Bright two-soliton solutions

Similarly, we truncate Expressions (10a)–(10c) as g=εg ₁+ε ³ g ₃+ε ⁵ g ₅+ε ⁷ g ₇, f=1+ε ² f ₂+ε ⁴ f ₄+ε ⁶ f ₆+ε ⁸ f ₈ and h=ε ² h ₂+ε ⁴ h ₄+ε ⁶ h ₆+ε ⁸ h ₈. Setting that

$$\begin{aligned} \begin{aligned} &{g_1=e^{\theta_1}+e^{\theta_2}, \qquad \theta_j=k_jt+w_jz+ \eta_j,} \\ &{w_j=i\alpha_1k_j^2- \alpha_3k_j^3,} \end{aligned} \end{aligned}$$

(14)

where k _j ’s and η _j ’s are complex parameters (j=1,2), and through Bilinear Form (9a)–(9c), we have

$$\begin{aligned} \begin{aligned} &{f_2=\beta_1e^{\theta_1+\theta_1^*}+ \beta_2e^{\theta_1+\theta_2^*}+\beta _3e^{\theta_2+\theta_1^*}+ \beta_4e^{\theta_2+\theta_2^*},} \\ &{h_2=\gamma_1e^{\theta_1+\theta_1^*}+ \gamma_2e^{\theta_1+\theta _2^*}+\gamma_3e^{\theta_2+\theta_1^*}+ \gamma_4e^{\theta_2+\theta_2^*}\, ,} \\ &{g_3=\delta_1e^{2\theta_1+\theta_1^*}+ \delta_2e^{2\theta_1+\theta _2^*}+\delta_3e^{2\theta_2+\theta_1^*}+ \delta_4e^{2\theta_2+\theta _2^*}} \\ &{\phantom{g_3=} {}+\delta_5e^{\theta_1+\theta_2+\theta_1^*}+ \delta_6e^{\theta _1+\theta_2+\theta_2^*},} \\ &{f_4=\zeta_1e^{2\theta_1+2\theta_1^*}+ \zeta_2e^{2\theta_1+2\theta _2^*}+\zeta_3e^{2\theta_2+2\theta_1^*}} \\ &{\phantom{f_4=} {}+ \zeta_4e^{2\theta_2+2\theta _2^*}+\zeta_5e^{\theta_1+\theta_2+\theta_1^*+\theta_2^*}+\zeta _6e^{\theta_1+\theta_2+2\theta_1^*}} \\ &{\phantom{f_4=} {}+\zeta_7e^{\theta_1+\theta_2+2\theta _2^*}+\zeta_8e^{2\theta_1+\theta_1^*+\theta_2^*}+\zeta _9e^{2\theta_2+\theta_1^*+\theta_2^*},} \\ &{h_4=\vartheta_1e^{\theta_1+\theta_2+\theta_1^*+\theta_2^*}+\vartheta _2e^{\theta_1+\theta_2+2\theta_1^*}+\vartheta_3e^{\theta_1+\theta _2+2\theta_2^*}} \\ &{\phantom{h_4=} {}+\vartheta_4e^{2\theta_1+\theta_1^*+\theta_2^*}+ \vartheta _5e^{2\theta_2+\theta_1^*+\theta_2^*},} \\ &{g_5=\mu_1e^{2\theta_1+\theta_2+\theta_1^*+\theta_2^*}+ \mu_2e^{\theta _1+2\theta_2+\theta_1^*+\theta_2^*}} \\ &{\phantom{g_5=} {}+\mu_3e^{2\theta_1+\theta_2+2\theta _1^*}+\mu_4e^{\theta_1+2\theta_2+2\theta_1^*}} \\ &{\phantom{g_5=} {}+ \mu_5e^{2\theta _1+\theta_2+2\theta_2^*}+\mu_6e^{\theta_1+2\theta_2+2\theta_2^*},} \\ &{f_6=\iota_1e^{\theta_1+2\theta_2+\theta_1^*+2\theta_2^*}+\iota _2e^{\theta_1+2\theta_2+2\theta_1^*+\theta_2^*}} \\ &{\phantom{f_6=} {}+\iota_3e^{2\theta_1+\theta_2+\theta_1^*+2\theta_2^*}+\iota _4e^{2\theta_1+\theta_2+2\theta_1^*+\theta_2^*},} \\ &{h_6=\kappa_1e^{\theta_1+2\theta_2+\theta_1^*+2\theta_2^*}+\kappa _2e^{\theta_1+2\theta_2+2\theta_1^*+\theta_2^*}} \\ &{\phantom{h_6} {}+\kappa_3e^{2\theta_1+\theta_2+\theta_1^*+2\theta _2^*}+ \kappa_4e^{2\theta_1+\theta_2+2\theta_1^*+\theta_2^*},} \\ &{g_7=\lambda_1e^{2\theta_1+2\theta_2+\theta_1^*+2\theta_2^*}+\lambda _2e^{2\theta_1+2\theta_2+2\theta_1^*+\theta_2^*},} \\ &{f_8=\chi e^{2\theta_1+2\theta_2+2\theta_1^*+2\theta_2^*},} \\ &{h_8=\rho e^{2\theta_1+2\theta_2+2\theta_1^*+2\theta_2^*},} \end{aligned} \end{aligned}$$

(15)

where the corresponding parameters in Expressions (15) can be seen in the Appendix. Without loss of generality, with ε=1 and Expression (3), the bright two-soliton solutions for Eq. (2) are

$$\begin{aligned} u=\frac{g_1+g_3+g_5+g_7}{1+f_2+f_4+f_6+f_8}. \end{aligned}$$

(16)

3 Soliton propagation and interactions

Based on Solutions (13) and (16), we will discuss the propagation and interaction of the bright single- and double-hump solitons analytically and graphically. More on the solitonic interaction can be seen, e.g., in Refs. [41–45].

3.1 Soliton propagation

On the basis of Solutions (13), we have

$$\begin{aligned} &{|u|^2=\biggl \vert \frac{g_1+g_3}{1+f_2+f_4}\biggr \vert ^2} \\ &{\phantom{|u|^2}=\frac{e^{\theta+\theta^*} [1+(\delta+\delta^*)e^{\theta+\theta ^*}+\delta\delta^*e^{2\theta+2\theta^*} ]}{ (1+\beta e^{\theta+\theta^*}+\zeta e^{2\theta+2\theta^*} )^2},} \\ &{\phantom{|u|^2}=\frac{e^{\theta+\theta^*} [1+(\delta+\delta^*)e^{\theta+\theta ^*}+\delta\delta^*e^{2\theta+2\theta^*} ]}{ (1+\beta e^{\theta+\theta^*}+\delta\delta^* e^{2\theta+2\theta^*} )^2},} \end{aligned}$$

(17a)

$$\begin{aligned} &{\bigl(|u|^2\bigr)_t=\frac{(k+k^*)e^{\theta+\theta^*}(1-\delta\delta^*e^{2\theta +2\theta^*})}{ (1+\beta e^{\theta+\theta^*}+\delta\delta^* e^{2\theta+2\theta^*} )^3}} \\ &{\phantom{\bigl(|u|^2\bigr)_t=} {}\times \bigl[1+\bigl(2\delta+2\delta^*-\beta\bigr)e^{\theta+\theta ^*}+\delta \delta^*e^{2\theta+2\theta^*} \bigr].} \end{aligned}$$

(17b)

Via Expression (12), we derive

$$\begin{aligned} &{\bigl(2\delta+2\delta^*-\beta\bigr)^2-4\delta\delta^*} \\ &{\quad=-\frac{3\alpha_4^2 [\alpha_1^2+3i\alpha_1\alpha_3(k-k^*)-3\alpha _3^2(k^2-kk^*+k^{*2}) ]}{4(k+k^*)^2(\alpha_1+3i\alpha_3k)^2(\alpha _1-3i\alpha_3k^*)^2}.} \end{aligned}$$

(18)

When

$$\begin{aligned} \alpha_1^2+3i\alpha_1\alpha_3 \bigl(k-k^*\bigr)-3\alpha _3^2\bigl(k^2-kk^*+k^{*2} \bigr)\geq0, \end{aligned}$$

(19)

we find that

$$\begin{aligned} \bigl(2\delta+2\delta^*-\beta\bigr)^2-4\delta\delta^*\leq0. \end{aligned}$$

(20)

From Expressions (17a), (17b) and (20), we conclude that |u|² has only one maximum value at

$$\begin{aligned} e^{\theta+\theta^*}=1/|\delta|. \end{aligned}$$

(21)

Substituting Expression (21) into (17a), we derive

$$\begin{aligned} |u|^2=\frac{\delta+\delta^*+2|\delta|}{ (\beta+2|\delta| )^2} . \end{aligned}$$

(22)

When

$$\begin{aligned} \alpha_1^2+3i\alpha_1\alpha_3 \bigl(k-k^*\bigr)-3\alpha_3^2\bigl(k^2-kk^*+k^{*2} \bigr)<0\, , \end{aligned}$$

(23)

we find that

$$\begin{aligned} \bigl(2\delta+2\delta^*-\beta\bigr)^2-4\delta\delta^*>0. \end{aligned}$$

(24)

From Expressions (17a), (17b) and (24), we conclude that |u|² has two equal maximum values at

$$\begin{aligned} e^{\theta+\theta^*}=\frac{\beta-2\delta-2\delta^*\pm\sqrt{(2\delta +2\delta^*-\beta)^2-4\delta\delta^*}}{2\delta\delta^*}. \end{aligned}$$

(25)

Substituting Expression (25) into (17a), we obtain

$$\begin{aligned} |u|^2=\frac{1}{4(\beta-\delta-\delta^*)}. \end{aligned}$$

(26)

Therefore, parametric regions for the existence of single- and double-hump solitons are presented as follows:

Single-hump soliton:

$$\begin{aligned} \alpha_1^2+3i\alpha_1\alpha_3 \bigl(k-k^*\bigr)-3\alpha _3^2\bigl(k^2-kk^*+k^{*2} \bigr)\geq0, \end{aligned}$$

(27a)

Double-hump soliton:

$$\begin{aligned} \alpha_1^2+3i\alpha_1\alpha_3 \bigl(k-k^*\bigr)-3\alpha _3^2\bigl(k^2-kk^*+k^{*2} \bigr)<0. \end{aligned}$$

(27b)

Moreover, by virtue of Expressions (22) and (26), amplitudes for the single- and double-hump solitons are, respectively, expressed as

$$\begin{aligned} \varDelta_S=\frac{\sqrt{\delta+\delta^*+2|\delta|}}{\beta+2|\delta|}\quad\text{and} \quad \varDelta_D=\frac{1}{2\sqrt{\beta-\delta-\delta^*}}. \end{aligned}$$

(28)

Besides, the interval between the two peaks for the double-hump soliton is

$$\begin{aligned} L=\ln\frac{\beta-2\delta-2\delta^*+\sqrt{(\beta-2\delta-2\delta ^*)^2-4\delta\delta^*}}{\beta-2\delta-2\delta^*-\sqrt{(\beta-2\delta -2\delta^*)^2-4\delta\delta^*}}. \end{aligned}$$

(29)

Substituting Expressions (12) into (28) and (29), we find that the amplitudes Δ _S and Δ _D are related to the coefficients of the GVD, TOD and SS (i.e., α ₁, α ₃ and α ₄), while the interval L is dependent on the coefficients of the GVD and TOD (i.e., α ₁ and α ₃).

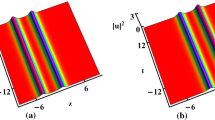
With the different coefficients of the GVD, i.e., α ₁=2 in Fig. 1(a), while α ₁=0.5 in Fig. 1(b), the single- and double-hump solitons can both propagate stably, and the interval between the two peaks for the double-hump soliton keeps invariant during the propagation. Moreover, we can derive the single- or double-hump soliton when the coefficients of the GVD and TOD (i.e., α ₁ and α ₃) satisfy Condition (27a) or (27b). From Fig. 2, we find that adjusting the coefficients of the GVD and TOD (i.e., α ₁ and α ₃) will lead to the change of the interval between the two peaks for the double-hump soliton.

Fig. 1

(a) Single-hump soliton via Solutions (13) with α ₁=2, α ₃=1, α ₄=6, k=1 and η=0; (b) double-hump soliton via Solutions (13) with α ₁=0.5, α ₃=1, α ₄=6, k=1 and η=0

Fig. 2

Double-hump solitons via Solutions (13) at z=0 with (a) α ₁=0.5 (α ₁=0.1), α ₃=1, α ₄=6, k=1 and η=0 for the solid (dashed) line; (b) α ₁=0.5, α ₃=1 (α ₃=0.6), α ₄=6, k=1 and η=0 for the solid (dashed) line

3.2 Soliton interactions

In order to investigate the soliton interactions, we will carry out the asymptotic analysis on Solutions (16):

Before the interaction (z→−∞):

$$\begin{aligned} &{u^{1-}\rightarrow\frac{e^{\theta_1}+\delta_1e^{2\theta_1+\theta _1^*}}{1+\beta_1e^{\theta_1+\theta_1^*}+\zeta_1e^{2\theta_1+2\theta _1^*}},} \\ &{\quad\bigl(\theta_1+\theta_1^*\sim0,\quad \theta_2+\theta _2^*\rightarrow-\infty\bigr),} \end{aligned}$$

(30a)

$$\begin{aligned} &{u^{2-}\rightarrow\frac{\mu_3e^{\theta_2}+\lambda_2e^{2\theta_2+\theta _2^*}}{\zeta_1+\iota_4e^{\theta_2+\theta_2^*}+\chi e^{2\theta_2+2\theta_2^*}},} \\ &{\quad\bigl(\theta_2+\theta_2^*\sim0,\quad \theta_1+\theta _1^*\rightarrow+\infty\bigr),} \end{aligned}$$

(30b)

where u ¹⁻ and u ²⁻ denote the asymptotic expressions for the two solitons before the interaction, respectively.

After the interaction (z→+∞):

$$\begin{aligned} &{u^{1+}\rightarrow\frac{\mu_6e^{\theta_1}+\lambda_1e^{2\theta_1+\theta _1^*}}{\zeta_4+\iota_1e^{\theta_1+\theta_1^*}+\chi e^{2\theta_1+2\theta_1^*}},} \\ &{\quad\bigl(\theta_1+\theta_1^*\sim0,\quad \theta_2+\theta _2^*\rightarrow+\infty\bigr),} \end{aligned}$$

(31a)

$$\begin{aligned} &{u^{2+}\rightarrow\frac{e^{\theta_2}+\delta_4e^{2\theta_2+\theta _2^*}}{1+\beta_4e^{\theta_2+\theta_2^*}+\zeta_4 e^{2\theta_2+2\theta_2^*}},} \\ &{\quad\bigl(\theta_2+\theta_2^*\sim0,\quad \theta_1+\theta _1^*\rightarrow-\infty\bigr),} \end{aligned}$$

(31b)

where u ¹⁺ and u ²⁺ denote the asymptotic expressions for the two solitons after the interaction, respectively.

Similarly, by virtue of the procedure to obtain the amplitudes for the single- and double-hump solitons in Sect. 3.1, and through some calculations, we have

$$\begin{aligned} &{\varDelta^{1-}_S=\varDelta^{1+}_S= \frac{\sqrt{\delta_1+\delta_1^*+2|\delta _1|}}{\beta_1+2|\delta_1|},} \end{aligned}$$

(32a)

$$\begin{aligned} &{\varDelta^{2-}_S=\varDelta^{2+}_S= \frac{\sqrt{\delta_4+\delta_4^*+2|\delta _4|}}{\beta_4+2|\delta_4|},} \end{aligned}$$

(32b)

$$\begin{aligned} &{\varDelta^{1-}_D=\varDelta^{1+}_D= \frac{1}{2\sqrt{\beta_1-\delta_1-\delta _1^*}},} \end{aligned}$$

(32c)

$$\begin{aligned} &{\varDelta^{2-}_D=\varDelta^{2+}_D= \frac{1}{2\sqrt{\beta_4-\delta_4-\delta _4^*}},} \end{aligned}$$

(32d)

where $\varDelta^{1-}_{S}$ (or $\varDelta^{1-}_{D}$) and $\varDelta^{2-}_{S}$ (or $\varDelta^{2-}_{D}$), respectively, are the amplitudes for two single-hump (or double-hump) solitons before the interaction, and $\varDelta^{1+}_{S}$ (or $\varDelta^{1+}_{D}$) and $\varDelta^{2+}_{S}$ (or $\varDelta^{2+}_{D}$), after the interaction, β ₁, β ₄, δ ₁ and δ ₄ can be seen in the appendix. Expressions (32a)–(32d) indicate that the interaction between the two solitons is elastic.

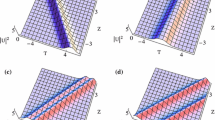
From Figs. 3, 4, 5, for the given α ₁ and α ₃, the interactions can exist between the (i) two single-hump solitons when k ₁ and k ₂ both satisfy Condition (27a), (ii) two double-hump solitons when k ₁ and k ₂ both satisfy Condition (27b), and (iii) single- and double-hump solitons when k ₁ and k ₂, respectively, satisfy Conditions (27a) and (27b). Besides, we find that the amplitudes and velocities for two solitons after the interactions do not change except for some phase shifts, i.e., those interactions in Figs. 3–5 are all elastic. Moreover, from Conditions (27a), (27b), we know that the single- and double-hump solitons are affected by the coefficients of the GVD and TOD (i.e., α ₁ and α ₃), and therefore, the three types of the interactions between the two solitons will be also affected by the coefficients of the GVD and TOD (i.e., α ₁ and α ₃), e.g., the interaction might change from the one between the two single-hump solitons to the one between the two double-hump solitons when we adjust α ₁ and α ₃.

Fig. 3

(a) Interaction between the two single-hump solitons via Solutions (16) with α ₁=0.5, α ₃=1, α ₄=6, k ₁=1+i, k ₂=1+1.5i and η ₁=η ₂=0; (b) corresponding trajectories of (a) at: z=−3 (solid line) and z=3 (dashed line)

Fig. 4

(a) Interaction between the two double-hump solitons via Solutions (16) with α ₁=0.5, α ₃=1, α ₄=6, k ₁=1, k ₂=1.5 and η ₁=η ₂=0; (b) corresponding trajectories of (a) at: z=−7 (solid line) and z=7 (dashed line)

Fig. 5

(a) Interaction between the single- and double-hump solitons via Solutions (16) with α ₁=0.5, α ₃=1, α ₄=6, k ₁=1+i, k ₂=1 and η ₁=η ₂=0; (b) corresponding trajectories of (a) at: z=−10 (solid line) and z=10 (dashed line)

4 Conclusions

In this paper, we have investigated the higher-order nonlinear Schrödinger equation [i.e., Eq. (2) with 3α ₂ α ₃=α ₁ α ₄ and α ₄+2α ₅=0], which can be used to describe the propagation and interaction of the ultrashort pulses in the subpicosecond or femtosecond regime. Via the Hirota method and an auxiliary function, we have derived Bilinear Form (9a)–(9c), and constructed the bright hump one- and two-soliton solutions [i.e., Solutions (13) and (16)]. Based on Solutions (13), we have presented Conditions (27a), (27b), through which people can see that the existence of single- and double-hump solitons can be affected by the coefficients of the GVD and TOD (i.e., α ₁ and α ₃). We have observed the propagation of one single- or double-hump soliton, as shown in Figs. 1 and 2, and obtained the amplitudes for the single- and double-hump solitons [i.e., Δ _S and Δ _D in Expression (28)] and interval between the two peaks for the double-hump soliton [i.e., L in Expression (29)]. Besides, we have found that Δ _S and Δ _D are related to the coefficients of the GVD, TOD, and SS (i.e., α ₁, α ₃, and α ₄), while L is dependent on the coefficients of the GVD and TOD (i.e., α ₁ and α ₃). We have carried out the asymptotic analysis on Solutions (16) to prove that the interactions are elastic [i.e., Expressions (30a), (30b)–(32a)–(32d)], and worked out that the elastic interactions can exist between the (i) two single-hump solitons, as shown in Fig. 3, (ii) two double-hump solitons, as shown in Fig. 4, and (iii) single- and double-hump solitons, as seen in Fig. 5.

Appendix

The corresponding parameters in Expressions (15) are as follows:

$$\begin{aligned} &{\beta_1=\frac{\alpha_4}{3\alpha_3(k_1+k_1^*)^2},}\\ &{\gamma_1= \frac{\alpha_4[2\alpha_1+3i\alpha_3(k_1-k_1^*)]}{6\alpha_3},} \\ &{\beta_2=\frac{\alpha_4}{3\alpha_3(k_1+k_2^*)^2},}\\ &{\gamma_2= \frac{\alpha_4[2\alpha_1+3i\alpha_3(k_1-k_2^*)]}{6\alpha_3},} \\ &{\beta_3=\frac{\alpha_4}{3\alpha_3(k_2+k_1^*)^2},}\\ &{\gamma_3=\frac{\alpha_4[2\alpha_1+3i\alpha_3(k_2-k_1^*)]}{6\alpha_3},} \\ &{\beta_4=\frac{\alpha_4}{3\alpha_3(k_2+k_2^*)^2},}\\ &{\gamma_4=\frac{\alpha_4[2\alpha_1+3i\alpha_3(k_2-k_2^*)]}{6\alpha_3},} \\ &{\delta_1=\frac{\gamma_1}{2 (3i\alpha_3k_1+\alpha_1 )(k_1+k_1^*)^2},} \\ &{\delta_2=\frac{\gamma_2}{2 (3i\alpha_3k_1+\alpha_1 )(k_1+k_2^*)^2},} \\ &{\delta_3=\frac{\gamma_3}{2 (3i\alpha_3k_2+\alpha_1 )(k_2+k_1^*)^2},} \\ &{\delta_4=\frac{\gamma_4}{2 (3i\alpha_3k_2+\alpha_1 )(k_2+k_2^*)^2},} \\ &{\delta_5=\frac{\gamma_1+\gamma_3}{2 [3i\alpha_3(k_1+k_2)+\alpha _1 ](k_1+k_1^*)(k_2+k_1^*)}} \\ &{\phantom{\delta_5=} {}+\frac{\alpha_4(k_1-k_2)^2}{3\alpha _3(k_1+k_1^*)^2(k_2+k_1^*)^2},} \\ &{\delta_6=\frac{\gamma_2+\gamma_4}{2 [3i\alpha_3(k_1+k_2)+\alpha _1 ](k_1+k_2^*)(k_2+k_2^*)}} \\ &{\phantom{\delta_6=} {}+\frac{\alpha_4(k_1-k_2)^2}{3\alpha _3(k_1+k_2^*)^2(k_2+k_2^*)^2},} \\ &{\zeta_1=\delta_1\delta_1^*,\qquad \zeta_2=\delta_2\delta_3^*,}\\ &{\zeta_3=\delta_3\delta_2^*,\qquad \zeta_4=\delta_4\delta_4^*,} \end{aligned}$$

$$\begin{aligned} \zeta_5&=\frac{\alpha_4(\delta_5+\delta_6+\delta_5^*+\delta_6^*)-3\alpha _3\beta_1\beta_4(k_1-k_2+k_1^*-k_2^*)^2}{3\alpha _3(k_1+k_2+k_1^*+k_2^*)^2} \\ &\quad{}-\frac{3\alpha_3\beta_2\beta _3(k_1-k_2-k_1^*+k_2^*)^2}{3\alpha_3(k_1+k_2+k_1^*+k_2^*)^2}, \end{aligned}$$

$$\begin{aligned} &{\zeta_6=\frac{\alpha_4(\delta_5+\delta_1^*+\delta_2^*)-3\alpha_3\beta _1\beta_3(k_1-k_2)^2}{3\alpha_3(k_1+k_2+2k_1^*)^2},} \\ &{\zeta_7=\frac{\alpha_4(\delta_6+\delta_3^*+\delta_4^*)-3\alpha_3\beta _2\beta_4(k_1-k_2)^2}{3\alpha_3(k_1+k_2+2k_2^*)^2},} \\ &{\zeta_8=\frac{\alpha_4(\delta_1+\delta_2+\delta_5^*)-3\alpha_3\beta _1\beta_2(k_1^*-k_2^*)^2}{3\alpha_3(2k_1+k_1^*+k_2^*)^2},} \\ &{\zeta_9=\frac{\alpha_4(\delta_3+\delta_4+\delta_6^*)-3\alpha_3\beta _3\beta_4(k_1^*-k_2^*)^2}{3\alpha_3(2k_2+k_1^*+k_2^*)^2},} \\ &{\vartheta_1=\frac{i\alpha_4}{2}\bigl[\bigl(\delta_5- \delta _5^*\bigr) \bigl(k_1+k_1^*\bigr)+ \bigl(\delta_5+\delta_5^*\bigr) \bigl(k_2-k_2^* \bigr)} \\ &{\phantom{\vartheta_1=} {}+\bigl(\delta_6+ \delta_6^*\bigr) \bigl(k_1-k_1^*\bigr)+ \bigl(\delta_6-\delta _6^*\bigr) \bigl(k_2+k_2^* \bigr)\bigr]} \\ &{\phantom{\vartheta_1=} {}+\frac{\alpha_1\alpha_4}{3\alpha_3}\bigl( \delta_5+\delta _6+\delta_5^*+ \delta_6^*\bigr)} \\ &{\phantom{\vartheta_1=} {}-(\beta_1 \gamma_4+\beta_2\gamma_3+\beta_3 \gamma_2+\beta _4\gamma_1),} \\ &{\vartheta_2=\frac{\gamma_1\gamma_3(k_1-k_2)^2}{2(\alpha_1-3i\alpha _3k_1^*)(k_1+k_1^*)^2(k_2+k_1^*)^2},} \\ &{\vartheta_3=\frac{\gamma_2\gamma_4(k_1-k_2)^2}{2(\alpha_1-3i\alpha _3k_2^*)(k_1+k_2^*)^2(k_2+k_2^*)^2},} \\ &{\vartheta_4=\frac{\gamma_1\gamma_2(k_1^*-k_2^*)^2}{2(\alpha_1+3i\alpha _3k_1)(k_1+k_1^*)^2(k_1+k_2^*)^2},} \\ &{\vartheta_5=\frac{\gamma_3\gamma_4(k_1^*-k_2^*)^2}{2(\alpha_1+3i\alpha _3k_2)(k_2+k_1^*)^2(k_2+k_2^*)^2},} \\ &{\mu_1=\frac{\gamma_1\gamma_2(k_1-k_2)^2(4\alpha_1\sigma_2-3i\alpha _3\sigma_3)}{2\sigma_1(\alpha_1+3i\alpha_3k_1)},} \\ &{\mu_2=\frac{\gamma_3\gamma_4(k_1-k_2)^2(4\alpha_1\sigma_4-3i\alpha _3\sigma_5)}{2\sigma_1(\alpha_1+3i\alpha_3k_2)},} \\ &{\sigma_1=\bigl(k_1+k_1^* \bigr)^2\bigl(k_1+k_2^*\bigr)^2 \bigl(k_2+k_1^*\bigr)^2\bigl(k_2+k_2^* \bigr)^2} \\ &{\phantom{\sigma_1=} {}\times \bigl[2\alpha_1+3i \alpha_3(k_1+k_2) \bigr] \bigl[2 \alpha_1-3i\alpha_3\bigl(k_1^*+k_2^* \bigr) \bigr],} \\ &{\sigma_2=k_2\bigl(k_2+k_2^* \bigr)+k_1^*\bigl(k_2+k_1^* \bigr)-k_2^*\bigl(k_1^*-k_2^*\bigr),} \\ &{\sigma_3=\bigl(k_1^*+k_2^*\bigr) \bigl(k_1^*-k_2^*\bigr)^2- \bigl(k_2-k_1^*\bigr) \bigl(k_2+k_1^* \bigr)^2} \\ &{\phantom{\sigma_3=} {}-\bigl(k_2-k_2^* \bigr) \bigl(k_2+k_2^*\bigr)^2,} \\ &{\sigma_4=k_1\bigl(k_1+k_1^* \bigr)+k_1^*\bigl(k_1^*-k_2^* \bigr)+k_2^*\bigl(k_1-k_2^*\bigr),} \\ &{\sigma_5=\bigl(k_1^*+k_2^*\bigr) \bigl(k_1^*-k_2^*\bigr)^2- \bigl(k_1-k_1^*\bigr) \bigl(k_1+k_1^* \bigr)^2} \\ &{\phantom{\sigma_5=} {}-\bigl(k_1-k_2^* \bigr) \bigl(k_1+k_2^*\bigr)^2,} \\ &{\mu_3=\frac{\delta_1\delta_3(\alpha_1+3i\alpha_3k_2)(k_1-k_2)^2[2\alpha _1+3i\alpha_3(k_1-k_1^*)]}{(\alpha_1-3i\alpha _3k_1^*)(k_1+k_1^*)^2[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\mu_4=\frac{\delta_1\delta_3(\alpha_1+3i\alpha_3k_1)(k_1-k_2)^2[2\alpha _1+3i\alpha_3(k_2-k_1^*)]}{(\alpha_1-3i\alpha _3k_1^*)(k_2+k_1^*)^2[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\mu_5=\frac{\delta_2\delta_4(\alpha_1+3i\alpha_3k_2)(k_1-k_2)^2[2\alpha _1+3i\alpha_3(k_1-k_2^*)]}{(\alpha_1-3i\alpha _3k_2^*)(k_1+k_2^*)^2[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\mu_6=\frac{\delta_2\delta_4(\alpha_1+3i\alpha_3k_1)(k_1-k_2)^2[2\alpha _1+3i\alpha_3(k_2-k_2^*)]}{(\alpha_1-3i\alpha _3k_2^*)(k_2+k_2^*)^2[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\iota_1=\frac{\alpha_4\mu_6\mu_6^*}{3\alpha_3\delta_4\delta _4^*(k_1+k_1^*)^2},\qquad\iota_2= \frac{\alpha_4\mu_3\mu_5^*}{3\alpha _3\delta_1\delta_2^*(k_1+k_2^*)^2},} \\ &{\iota_3=\frac{\alpha_4\mu_5\mu_3^*}{3\alpha_3\delta_2\delta _1^*(k_2+k_1^*)^2},\qquad \iota_4= \frac{\alpha_4\mu_2\mu_2^*}{3\alpha_3\delta_3\delta _3^*(k_2+k_2^*)^2},} \\ &{\kappa_1=\frac{\iota_1(k_1+k_1^*)^2[2\alpha_1+3i\alpha _3(k_1-k_1^*)]}{2},} \\ &{\kappa_2=\frac{\iota_2(k_1+k_2^*)^2[2\alpha_1+3i\alpha _3(k_1-k_2^*)]}{2},} \\ &{\kappa_3=\frac{\iota_3(k_2+k_1^*)^2[2\alpha_1+3i\alpha _3(k_2-k_1^*)]}{2},} \\ &{\kappa_4=\frac{\iota_4(k_2+k_2^*)^2[2\alpha_1+3i\alpha _3(k_2-k_2^*)]}{2},} \\ &{\lambda_1=\frac{3\alpha_3\delta_2\iota_1(k_1-k_2)^2[2\alpha_1+3i\alpha _3(k_1-k_1^*)]}{\alpha_4[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\lambda_2=\frac{3\alpha_3\delta_3\iota_4(k_1-k_2)^2[2\alpha_1+3i\alpha _3(k_2-k_2^*)]}{\alpha_4[2\alpha_1+3i\alpha_3(k_1+k_2)]},} \\ &{\chi=\frac{\iota_1\iota_4}{\beta_1\beta_4},\quad\rho=0.} \end{aligned}$$