A joint color image encryption and compression scheme based on hyper-chaotic system

Abstract

For the low security and compression performance of the existing joint image encryption and compression technology, an improvement algorithm for joint image compression and encryption is proposed. The algorithm employs the discrete cosine transformation dictionary to sparsely represent the color image and then combines it with the encryption algorithm based on the hyper-chaotic system to achieve image compression and encryption simultaneously. Through the experimental analysis, the algorithm proposed in this paper has a good performance in security and compression.

1 Introduction

Along with the rapid growth of transmitting images over public networks, the network bandwidth and security have received a lot of attention. Compressing images to save bandwidth and encrypting images to protect privacy have become hot research areas.

The traditional method is compressing the image before the encryption is done. Encryption and compression are unrelated. However, such traditional method will sacrifice flexibility and calculation simplicity. A better way is the joint operation of compression and encryption in a single process. However, the contradiction between the image compression and encryption makes the joint operation difficult. Researches have been working on the joint operation of image compression and encryption to achieve better performance on compression and encryption [1–11].

For the joint operation of compression and encryption, the most common method is embedding the encryption into compression [1, 2] thus to get a balance in image compression and encryption. For the different compression methods, the joint algorithms of compression and encryption are divided into different situations at the present stage. (1) Using the compression method of Joint Photographic Experts Group (JPEG) or related discrete cosine transformation (DCT), the encryption is embedded into the compression process. By means of encrypting DCT coefficient, some joint encryption and compression schemes [3–5] are proposed. As the perceptual information concentrates at low-frequency DCT coefficients, some selective encryption schemes are proposed. Reference [3] proposed to encrypt the DC coefficient and the sign bit of all AC coefficients using a spatiotemporal chaotic system. However, Wu and Kuo stated that selective encryption is not suitable for DCT-based compression algorithm [6]. Moreover, they proposed some perceptual attacks to restore perceptual image. In full encryption, Yuen and Wong proposed chaos-based joint image compression and encryption algorithm using DCT [5]. In their scheme, the DCT coefficients of the whole image are separated to encrypt. However, compression performance is not high. (2) Compared with the JPEG, JPEG2000 based on wavelet transformation has a better compression performance. So there are a lot of image compression and encryption algorithms based on JPEG2000 and related wavelet transformation [7–9]. In Ref. [7], only low-frequency region of the wavelet transform is encrypted. The security need to be improved. Reference [8] presented a new private key cryptosystem based on the finite-field wavelet. However, the compression performance was not analyzed. Yang et al. [9] encrypted the image between wavelet transformation and SPIHT coding. However, the compression performance is lower than that of only compression using wavelet transformation. (3) Due to the certain resemblance in the sense of secrecy between cryptographic ciphers and entropy coders, some joint encryption and compression schemes based on entropy coding compression method are proposed [10–12]. In these methods, encryption is embedded in entropy coding. Reference [10] proposed to embed encryption in Huffman coding based on multiple Huffman tables. References [11, 12] proposed to embed encryption in arithmetic coding. However, in these schemes, encryption is an additional feature but not the primary concern. Therefore, the security may not be satisfactory. References [10, 11] suffers known-plaintext attack [13, 14]. (4) Using compression technique based on sparse decomposition, the joint encryption and compression algorithms are proposed. Image sparse representation provides a new way to solve the distortion problem of reconstructed image for low bit rate image compression. Wu [15] proposed the joint encryption and compression algorithm using sparse decomposition, Secure Hash Algorithm-1(SHA-1) and chaotic map. However, the scheme needs a large amount of calculation in the generation of over-complete dictionary. Therefore, the scheme does not suitable for the real-time transmission of images. Rebollo-Neira [16, 17] proposed the idea of encryption image folding in which orthogonal projection matrix is used to transform the coefficients into orthogonal complementary space of the host image, and then the coefficients are folded into the host image. The algorithm can obtain reconstructed image with better quality at high compression ratio. However, the experimental results presented in the paper are just an ideal state of the data, and there are some problems for the algorithm. The algorithm does not compress the additional data required in decompression and decryption, so it takes up a lot of network resources in transmission. In addition, the compressed and encrypted images carry some information of the original images. When using the error key to decompress and decrypt the image, we can obtain the original outline information. That will create a serious security hole in the algorithm. In order to solve these problems, according to the idea of encryption image folding proposed in Refs. [16, 17], a joint color image encryption and compression scheme based on hyper-chaotic system is proposed by this paper.

In order to improve the security of the joint color image encryption and compression scheme, we design the hyper-chaos-based scrambling and diffusion scheme. Conventional cryptographic techniques, such as International Data Encryption Algorithm (IDEA) or Advanced Encryption Standard (AES), are not suitable for image encryption due to the bulky data capacity and high correlation among pixels in image files [18, 19]. Owing to simplicity in implementation, high speed and good cryptography properties of chaos, the chaotic encryption algorithm has caused widespread concern since it was first proposed by the UK mathematician Matthews in 1989 [20]. With the chaotic system used in the image encryption, high-dimensional chaotic system with high complexity is subjected to the value more and more [21–24]. As high-dimensional chaotic system, hyper-chaotic system has greater complexity. Its pseudorandomness and long-term unpredictability is stronger. In several existing hyper-chaos-based encryption algorithms, due to their inappropriate cryptographic structure, the security is not good. Reference [25] proposed a fast color image encryption algorithm based on hyper-chaotic systems. In Ref. [26], a novel image encryption algorithm with only one round diffusion process based on hyper-chaotic system was proposed. By applying known-plaintext and chosen-plaintext attacks, Ref. [27] broke it. In Ref. [28], a novel image encryption scheme based on improved hyper-chaotic sequences was proposed. Reference [29] evaluated the security of Ref. [28] and broke it. In this paper, the security is improved based on hyper-chaotic system in three aspects: the hyper-chaos-based scrambling method is used to scramble the effective coefficients’ position to remove the relativity among pixels within the block; the sparse coefficients are controlled by the hyper-chaotic system to encrypt the coefficients; the hyper-chaos-based diffusion method is used in the folded image to encrypt the final data. Moreover, Huffman coding is used to compress the additional position information required in decompression and decryption to save network bandwidth.

The rest of paper is organized as follows. Section 2 introduces the scrambling and diffusion encryption algorithms based on hyper-chaotic system. Section 3 describes the joint image encryption and compression scheme of color image based on hyper-chaotic system. Section 4 gives the test results and analysis of our improved scheme. Finally, Sect. 5 makes a conclusion for this paper.

2 The encryption algorithm based on hyper-chaotic system

In this paper we design the system of differential equations like Eq. (1), the Lyapunov exponents are 0.81, 0.31, 0, -24.11. The state of the system is hyper-chaos which has a high complexity.

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{{\text {d}}y_1 }{{\text {d}}t}=16(y_2 -y_1 ) \\ \displaystyle \frac{{\text {d}}y_2 }{{\text {d}}t}=45y_4 -2y_2 +47.6y_1 -y_1 y_3 -y_3 y_4 \\ \displaystyle \frac{{\text {d}}y_3 }{{\text {d}}t}=-4y_3 +y_2 y_4 +y_1 y_2 \\ \displaystyle \frac{{\text {d}}y_4 }{{\text {d}}t}=-y_2 -y_4 -0.05y_1 y_3 \\ \end{array} \right. \end{aligned}$$

(1)

2.1 The generation of pseudorandom sequence

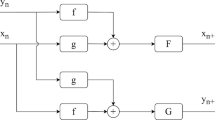
In order to make a full use of the chaotic sequence generated by hyper-chaotic system, different bits of different dimension of chaotic sequence are selected as a key sequence. The structure of pseudorandom sequence generator is shown in Fig. 1.

Fig. 1

The structure of pseudorandom sequence generator

Assuming the color image size is $M\times N$, Fig. 1 illustrates the concrete steps of generating pseudorandom sequence. The steps are as follows.

(1) Generate the hyper-chaotic sequence.

Set the initial value (y10 , y20 , y30 , y40) of the hyper-chaotic system Eq. (1) to iterate $(M\times N)/3+1000$ times. In order to eliminate transient effect of the chaotic sequence and enhance their sensitivity to initial conditions, we get rid the first 1000 groups value of the chaotic sequence then get the sequences $y_{\textit{1}},y_{\textit{2}},y_{\textit{3}},y_{\textit{4}.}$

(2) Discretize the hyper-chaotic sequence.

For each value $y_{i_j } ,i=1,2,3,4,j=1,2,\ldots M\times N\div 3$, we get the decimal part of chaotic sequence by Eq. (2).

$$\begin{aligned} \Delta y_{i_j } =y_{i_j } -\left\lfloor {y_{i_j } } \right\rfloor \end{aligned}$$

(2)

$\left\lfloor x \right\rfloor$ returns the value of x to the nearest integers, less than or equal to x. Use Eq. (3) to discretize the decimal part and get the integers sequence $Y_{\textit{1}}$, $Y_{\textit{2}},Y_{\textit{3}},Y_{\textit{4}.}$

$$\begin{aligned} Y_{i_j } =\hbox {mod}\left( \left\lfloor {\Delta y_{i_j } \times 10^{14}} \right\rfloor ,65536\right) \end{aligned}$$

(3)

(3) Select different bits of each hyper-chaotic sequence to generate key sequence.

The integer $Y_{i_j }$ can be represented as the form shown in Eq. (4).

$$\begin{aligned} Y_{i_j }= & {} w_{{ij}_{15}} \times 2^{15}+w_{{ij} _{{14} }} \times 2^{14}+\cdots +w_{{ij} _{1 }} \times 2^{1}\nonumber \\&+\,w_{{ij} _{0 }} ,(w_{{ij} _{0 }}\ldots w_{{ij} _{{15} }} \in \{0,1\}) \end{aligned}$$

(4)

In order to reduce the correlation among the three pseudorandom sequences and enhance the rate of reusing, we select different bits of sequences $Y_{1}$, $Y_{2}$, $Y_{3}$ and $Y_{4.}$.

The key sequence Key1 comes from the 0th to the 7th bit of $Y_{1_j } ,Y_{2_j } ,Y_{3_j }$, and its expression is shown as Eq. (5).

$$\begin{aligned} \left\{ \begin{array}{l} key1(k)=w_{1j_7 } \times 2^{7}+w_{1j_6 } \times 2^{6}+w_{1j_5 } \times 2^{5}\\ \quad +\,w_{1j_4 } \times 2^{4}+w_{1j_3 } \times 2^{3}+w_{1j_2 } \times 2^{2}+w_{1j_1 }\\ \quad \times 2^{1}+w_{1j_0 } \\ key1(k+1)=w_{2j_7 } \times 2^{7}+w_{2j_6 } \times 2^{6}+w_{2j_5 } \times 2^{5}\\ \quad +\,w_{2j_4 }\times 2^{4}+w_{2j_3 } \times 2^{3}+w_{2j_2 } \times 2^{2}+w_{2j_1 } \\ \quad \times 2^{1}+w_{2j_0 } \\ key1(k+2)=w_{3j_7 } \times 2^{7}+w_{3j_6 } \times 2^{6}+w_{3j_5 } \times 2^{5}\\ \quad +\,w_{3j_4 } \times 2^{4}+w_{3j_3 }\times 2^{3}+w_{3j_2 } \times 2^{2}+w_{3j_1 }\\ \quad \times 2^{1}+w_{3j_0 } \\ \end{array} \right. \end{aligned}$$

(5)

The key sequence Key2 comes from the 4th to the 11th bit of $Y_{3_j } ,Y_{4_j } ,Y_{1_j }$, and its expression is shown as Eq. (6).

$$\begin{aligned} \left\{ \begin{array}{l} key2(k)=w_{3j_{11} } \times 2^{7}+w_{3j_{10} } \times 2^{6}+w_{3j_9 } \times 2^{5}\\ \quad +\,w_{3j_8 } \times 2^{4}+w_{3j_7 } \times 2^{3}+w_{3j_6 } \times 2^{2}+w_{3j_5 }\\ \quad \times \, 2^{1}+w_{3j_4 } \\ key2(k+1)=w_{4j_{11} } \times 2^{7}+w_{4j_{10} } \times 2^{6}+w_{4j_9 }\\ \quad \times 2^{5}+w_{4j_8 } \times 2^{4}+w_{4j_7 } \times 2^{3}+w_{4j_6 } \times 2^{2}\\ \quad +\,w_{4j_5 }\times 2^{1}+w_{4j_4 } \\ key2(k+2)=w_{1j_{11} } \times 2^{7}+w_{1j_{10} } \times 2^{6}+w_{1j_9 }\\ \quad \times \, 2^{5}+w_{1j_8 } \times 2^{4}+w_{1j_7 } \times 2^{3}+w_{1j_6 } \times 2^{2}\\ \quad +\,w_{1j_5 } \times 2^{1}+w_{1j_4 } \\ \end{array}\right. \end{aligned}$$

(6)

The key sequence Key3 comes from the 8th to the 15th bit of $Y_{2_j } ,Y_{3_j } ,Y_{4_j }$, and its expression is shown as Eq. (7).

$$\begin{aligned} \left\{ \begin{array}{l} key3(k)=w_{2j_{15} } \times 2^{7}+w_{2j_{14} } \times 2^{6}+w_{2j_{13} } \times 2^{5}\\ \quad +\,_{2j_{12} } \times 2^{4}+w_{2j_{11} } \times 2^{3}+w_{2j_{10} } \times 2^{2}+w_{2j_9 }\\ \quad \times 2^{1}+w_{2j_8 } \\ key3(k+1)=w_{3j_{15} } \times 2^{7}+w_{3j_{14} } \times 2^{6}+w_{3j_{13} }\\ \quad \times \, 2^{5}+w_{3j_{12} } \times 2^{4}+w_{3j_{11} } \times 2^{3}+w_{3j_{10} } \times 2^{2}\\ \quad +\,w_{3j_9 } \times 2^{1}+w_{3j_8 } \\ key3(k+2)=w_{4j_{15} } \times 2^{7}+w_{4j_{14} } \times 2^{6}+w_{4j_{13} }\\ \quad \times \, 2^{5}+w_{4j_{12} } \times 2^{4}+w_{4j_{11} } \times 2^{3}+w_{4j_{10} } \times 2^{2}\\ \quad +\,w_{4j_9 } \times 2^{1}+w_{4j_8 } \\ \end{array} \right. \end{aligned}$$

(7)

The relation of j and k in Eqs. (5), (6) and (7) is $k=j\times 3-2$. While finishing the above three steps, we can get the pseudorandom sequence key1, key2 andkey3 which can be used to encrypt the image.

NIST SP800-22 tests [30] are used to detect the deviation of a sequence from a true random sequence. For each test, if the P value is greater than a predefined threshold $\alpha$, then the sequence is considered to pass the test. Commonly, the value of $\alpha$ is 0.01. For the three pseudorandom sequences key1, key2 and key3, we take 100 groups key stream with the length of $10^{6}$ bits to count the pass rate of SP800 test, and the result is shown in Table 1.

Table 1 The SP800 test on key stream

From Table 1 we can know that the pseudorandom sequence generator proposed in this paper can generate the key stream with good randomness.

2.2 The diffusion algorithm of image encryption based on hyper-chaos

According to the independence of color image’s channel, this paper processes the three channels of image pixel respectively. The specific structure of image encryption is shown in Fig. 2:

Fig. 2

The structure of image encryption

The pseudorandom sequence generator proposed in Sect. 2.1 is used to generate three key streams key1, key2 and key3. The concrete steps of encryption are as follows:

(1) Divide the channel.

Load the original image P and divide it into three channels $P_{R}, P_{G }$ and $P_{B}$. In the encryption, the pixel values of three channels are processed separately.

(2) Perform diffusion algorithm with row-major.

Diffuse image P using the row-major diffusion. Take an example of $P_{R,}$ the process of row-major diffusion is shown in Fig. 3a. We use key1 to diffuse $P_{R }$ and get the cipher image $C'_{R}$, the equation of diffusion is shown in Eq. (8). We take the same method to $P_{G }$ and $P_{B }$ with the key2 and key3. The cipher image after row-major diffusion is denoted as C$^{{\prime }}$.

$$\begin{aligned} \left\{ \begin{array}{l} {C^{\prime }}_R (i,j)={C^{\prime }}_R (i,j-1)\oplus \hbox {mod}(P_R (i,j)\\ \quad +\,key1((i-1)\times N+j),256),j!=1 \\ {C^{\prime }}_R (i,j)={C^{\prime }}_R (i-1,N)\oplus \hbox {mod}(P_R (i,j)\\ \quad +\,key1((i-1)\times N+j),256),i!=1,j=1 \\ {C^{\prime }}_R (i,j)=P_R (M,N)\oplus \hbox {mod}(P_R (i,j)\\ \quad +\,key1((i-1)\times N+j),256),i=1,j=1 \\ \end{array} \right. \end{aligned}$$

(8)

Fig. 3

The diffusion process of encryption a the diffusion process of row-major and b the diffusion process of column major

(3) Perform the diffusion algorithm with column major.

Diffuse image $C'$ using the column major diffusion. Take an example of $C'_{R,}$ the process of column major diffusion is shown in Fig. 3b. In order to save the time of generating key streams, we reuse key1, key2, key3. Meanwhile, we need ensure one key stream is not reused in each channel. Therefore, we assign key2 to diffuse $C'_{R}$, key3 to diffuse $C'_{G}$ and key1 to diffuse $C'_{B}$. Use Eq. (9) to diffuse $C'_{R }$ and get the cipher image $C''_{R}$. We take the same method for $C'_{G }$ and $C'_{B }$ to get the cipher image $C''_{G}$ and $C''_{B}$ . The cipher image after column major diffusion is denoted as $C^{\prime \prime }$.

$$\begin{aligned} \left\{ \begin{array}{l} {C^{\prime \prime }}_R (i,j)={C^{\prime \prime }}_R (i+1,j)\oplus \hbox {mod}({C^{\prime }}_R (i,j)\\ \quad +\,key2((i-1)\times N+j),256),i!=M \\ {C^{\prime \prime }}_R (i,j)={C^{\prime \prime }}_R (1,j+1)\oplus \hbox {mod}({C^{\prime }}_R (i,j)\\ \quad +\,key2((M-i+1)+(N-j)\times M),256),\\ \quad i=M,j!=N \\ {C^{\prime \prime }}_R (i,j)={C^{\prime }}_R (1,1)\oplus \hbox {mod}({C^{\prime }}_R (i,j)\\ \quad +\,key2(1),256),i=M,j=N \\ \end{array} \right. \end{aligned}$$

(9)

After finishing all the steps, we can finally get the encrypted image $C^{{\prime \prime }}$.

2.3 The scrambling algorithm based on the cat map with parameters

In this paper, we use the cat map with parameters to scramble the image. The equation of cat map with parameters is shown in Eq. (10), ($x_{n},y_{n})$ represents the position of the pixel before scrambling, and ($x_{n+1},y_{n+1})$ represents the position of the pixel after scrambling.

$$\begin{aligned}&\left( \begin{array}{c} x_{n+1} \\ y_{n+1} \end{array} \right) =A\left( \begin{array}{c} x_n \\ y_n \end{array} \right) (\hbox {mod}\, N)\quad \nonumber \\&\hbox {where }A=\left( \begin{array}{cc} 1&{} a \\ b&{} {ab+1} \end{array} \right) \end{aligned}$$

(10)

Take an example of R Channel, the parameters $a_{R},b_{R }$ used in cat map are shown in Eq. (11). Using the same equation like Eq. (11), we can get the parameters of cat map in G and B Channel scrambling.

$$ \begin{aligned} \left\{ \begin{array}{l} a_R =({C^{\prime \prime }}_R (1,1) \& 0xF0)>>4 \\ b_R ={C^{\prime \prime }}_R (1,1) \& 0x0F \end{array} \right. \end{aligned}$$

(11)

One characteristic of cat map is that the value of the first position on the top left corner will not be changed during the scrambling. In order to increase the security of encryption system, we need to hide the value of first pixel of each channel in the cipher image by using the key stream. Take an example of R Channel, the position (i, j) used to hide the first pixel can be calculated by Eq. (12), and then the pixel value of position (1, 1) is interchanged with (i, j).

$$\begin{aligned} \left\{ \begin{array}{l} i=\hbox {mod}(key1(M\times N/(3\times 2)),M) \\ j=\hbox {mod}(key2(M\times N/(3\times 2)),M) \end{array} \right. \end{aligned}$$

(12)

This section is the basis of the third section. In the third section, the encryption algorithm proposed in this section is embedded into the compression, so as to realize compression and encryption for image simultaneously.

3 The design of joint image encryption and compression scheme

The structure of the joint color image encryption and compression algorithm is shown in Fig. 4. The main steps for algorithm are obtaining R, G, B channel of the original image, encrypting and compressing data of each channel and adjusting the data length of each channel. Because the pixel distribution is different for each channel of color image, the compression ratio of each channel maybe is different. Therefore, we need adjust the data length of each channel. The adjusting method is as follows: get the average length of the three-channel data; if the channel length is greater than the average length, we store the extra data in the channel whose length is less than the average height. That realizes the sharing of the channels’ space, so as to increase the compression ratio of color image.

Fig. 4

The structure of color image compression and encryption

For the module of compression and encryption of each channel, the structure is shown in Fig. 5. From Fig. 5, the algorithm in the module of compression and encryption of each channel takes the DCT dictionary to sparsely represent the image, embeds the encryption algorithm into the process of the compression from three aspects: (1) scramble the position information of the effective coefficients, which can destroy the relationship between atoms in DCT dictionary and effective coefficients. So the algorithm can eliminate relativity among pixels in the wrong reconstructed image blocks. It can also eliminate the vulnerability by which we can get the outline information with a wrong key. (2) Use hyper-chaotic system to control the coefficients transformation to encrypt the coefficients. (3) Use the diffusion algorithm to encrypt the folded image, but not encrypt the information blocks, which can guarantee the security of image and do not destroy the data structure of the information block. Through three ways of encryption, the cipher image has high security.

Fig. 5

The structure of image compression and encryption on single channel

3.1 The construction of DCT dictionary

Supposing the size of the image is $M\times N$, the concrete steps to generate DCT dictionary are as follows:

• (1) Use the cosine transformation to get the initial orthogonal matrix V, the element $v_{i,j}$ in matrix V can be expressed as Eq. (13). The symbol i and j denote the row and column of elements.

  $$\begin{aligned} v_{i,j} =\cos \left( \frac{\pi (2i-1)(j-1)}{2M}\right) \end{aligned}$$

  (13)

• (2) Normalize the matrix V to get the matrix V. The element $v'_{i,j }$ can be calculated by Eq. (14).

  $$\begin{aligned} v^{\prime }_{i,j} =p_j v_{i,j} , \mathrm{where}\;\;p_j =\frac{1}{\left\| {v_{:,j} } \right\| } \end{aligned}$$

  (14)

  The symbol $p_j ,(j=1,\;2,\ldots ,N)$ is the normalization factor, and its value is the reciprocal of the length of the jth column vector in matrix V.

• (3) Take Kronecker product of matrix $V^{\prime }$ to get the matrix D whose size is $M^{2}\times N^{2},D=V\otimes V^{\prime },\otimes$ represents the Kronecker product. Take the matrix A of size $m \times n$ and matrix B of size $p \times q$ as an example, its calculation process is as follows.

  $$\begin{aligned}&A\otimes B=\left( \begin{array}{cccc} {a_{11} B}&{} {a_{12} B}&{} {\cdots }&{} {a_{1n} B} \\ {a_{21} B}&{} {a_{22} B}&{} {\cdots }&{} {a_{2n} B} \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ {a_{m1} B}&{} {a_{m2} B}&{} {\cdots }&{} {a_{mn} B} \\ \end{array}\right) \nonumber \\&\quad =\left( \begin{array}{cccccccc} {a_{11} b_{11} }&{} {\cdots }&{} {a_{11} b{ }_{1q}}&{} {a_{12} b_{11} }&{} {\cdots }&{} {a_{12} b_{1q} }&{} {\cdots }&{} {a_{1n} b_{1q} } \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ {a_{11} b_{p1} }&{} {\cdots }&{} {a_{11} b_{pq} }&{} {a_{12} b_{p1} }&{} {\cdots }&{} {a_{12} b_{pq} }&{} {\cdots }&{} {a_{1n} b_{pq} } \\ {a_{21} b_{11} }&{} {\cdots }&{} {a_{21} b{ }_{1q}}&{} {a_{22} b_{11} }&{} {\cdots }&{} {a_{22} b_{1q} }&{} {\cdots }&{} {a_{2n} b_{1q} } \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ {a_{21} b{ }_{p1}}&{} {\cdots }&{} {a_{21} b{ }_{pq}}&{} {a_{22} b_{p1} }&{} {\cdots }&{} {a_{22} b_{pq} }&{} {\cdots }&{} {a_{2n} b_{pq} } \\ {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots }&{} {\cdots } \\ {a_{m1} b{ }_{p1}}&{} {\cdots }&{} {a_{m1} b{ }_{pq}}&{} {a_{m2} b{ }_{p1}}&{} {\cdots }&{} {a_{m2} b{ }_{pq}}&{} {\cdots }&{} {a_{mn} b{ }_{pq}} \\ \end{array} \right) \nonumber \\ \end{aligned}$$

  (15)

Finally we can get the over-complete dictionary D which is used to sparsely represent the image, each column $d_l ,l=1,2,\ldots N^{2}$ of D is called atom.

3.2 The relationship between DCT dictionary and DCT

By definition, there is a certain relationship between the DCT dictionary and DCT. Equation (16) is the definition of two-dimensional DCT, and f(x, y) denotes the image pixel value in position (x, y).

$$\begin{aligned} F(u,v)= & {} \frac{2}{\sqrt{MN}}c(u)c(v)\sum _{x=1}^M \sum _{y=1}^N f(x,y)\nonumber \\&\times \cos \frac{(2x-1)u\pi }{2M}\cos \frac{(2y-1)v\pi }{2N} \end{aligned}$$

(16)

where $c(u),c(v)=\left\{ \begin{array}{l} 1/\sqrt{2},\quad u,v=1 \\ 1,\quad \quad \quad \mathrm{others}\quad \\ \end{array} \right.$.

The inverse DCT is shown in Eq. (17).

$$\begin{aligned} f(x,y)= & {} \frac{2}{\sqrt{MN}}\sum _{u=1}^{M-1} \sum _{v=1}^{N-1} F(u,v)c(u)c(v)\nonumber \\&\times \cos \frac{(2x-1)u\pi }{2M} \cos \frac{(2y-1)v\pi }{2N} \end{aligned}$$

(17)

We represent the two-dimensional image data as a one-dimensional vector f( : ). The relationship among DCT coefficients, the original image pixels, and the DCT dictionary D is shown in Eq. (18):

$$\begin{aligned} f(:)=\sum _{u=1}^M {\sum _{v=1}^N {F(u,v)} d_{(u-1)\times N+v} } \end{aligned}$$

(18)

From Eq. (18) we can know that the DCT coefficients of image are the projection coefficients of image or residuals in the over-complete DCT dictionary. There is a certain relationship between the position of the DCT coefficients and the DCT dictionary atoms column. Combining sparse representation with compression feature of DCT, DCT coefficients carrying less information can be omitted. Finally, we can compress the image by coding some coefficients.

3.3 Properties of orthogonal projection matrix

Using the properties of orthogonal projection matrix, this paper embeds the effective coefficients into the host image to compress the image. In this section, we describe the definition and properties of the orthogonal projection matrix.

Supposing $\varphi \in C^{n}$ is a sub space, $P\in C^{n,n}$ denotes the orthogonal projection of $C^{n }$ to $\varphi$, when P satisfies the following properties.

(1) $\psi (P)=\varphi ;$ (2) $P^{2}=P$; (3) $P^{H}=P$. $P^{H }$ represents the transpose of P matrix. $\psi (P)$ is the value of P space.

When a subspace $\varphi \in C^{n}$ is given, for any vector $v\in C^{n}$, there is an orthogonal decomposition on the subspace $\varphi$.

$$\begin{aligned} v=v_1 +v_2 \equiv Pv+(I-P)v \end{aligned}$$

(19)

where $v_1 \equiv Pv\in \varphi ,v_2 \equiv (I-P)v\in \varphi ^{\bot },\varphi ^{\bot }$ represents the orthogonal complement space of $\varphi$, I is the unit matrix. We do the following deformation for Eq. (19):

$$\begin{aligned} Pv= & {} P(v_1 +v_2 )\equiv P(Pv+(I-P)v) \\= & {} P^{2}v+P(I-P)v \\= & {} Pv+0 \end{aligned}$$

Then we can get the equation like Eq. (20).

$$\begin{aligned} P(v_1 +v_2 )=v_1 \end{aligned}$$

(20)

From Eq. (19) we know that the projection on $\varphi \in C^{n}$ of the sum of $v_{1}$ and $v_{2 }$ is $v_{1}$, vector $v_1$ is in space of $\varphi \in C^{n}$ and vector $v_2$ is in space of $\varphi ^{\bot }$.

Set $\varphi$ be r-dimensional subspace, the matrix $D=[d_1 ,\ldots d_r ]$ be orthonormal basis vectors of $\varphi$ in space of $C^{n,n}$. Equation (21) is the equation to get the orthogonal projection matrix P .

$$\begin{aligned} P=DD^{H} \end{aligned}$$

(21)

This paper takes the host image as subspace $\varphi$, forms the matrix D using the atoms of the DCT dictionary and then uses the matrix $(I-P)$ to transform the sparse coefficients into the orthogonal complement space of host image. Finally the host image can be recovered by Eq. (20).

3.4 The image compression and encryption algorithm

Taking an example of the image I, its size is $M\times N$, the concrete steps of image compression and encryption algorithm are as follows. Figure 6 shows the main procedures of compression and encryption in our proposed scheme.

(1) Divide the image into blocks and make discrete cosine transform on each block. In order to facilitate storing the position information of coefficient, we take $8\times 8$ as the size of block. If the width and length of the image are not a multiple of 8, they should be made up with 0. We mark each block as $I_{x,y} ,x=1,\ldots ,M/8,\;y=1,\ldots ,N/8$. For each block $I_{x,y}$, we can get the coefficient block $c_{x,y} ,x=1,\ldots ,M/8,y=1,\ldots ,N/8$ after discrete cosine transform.

(2) Choose the effective coefficients according to the expected PSNR value. The expected PSNR value represents reconstructed image quality of the user’s expectation. The principles of selecting coefficients are as follows.

Fig. 6

Procedures of image compression and encryption

1) Take the absolute value of the matrix $c_{x,y}$ and sort the elements by column in ascending order. We can get the sorted matrix $c\_sort_{x,y}$, and the index matrix $i\_sort_{x,y}$ which records the corresponding elements positions of matrix $c\_sort_{x,y}$ in $c_{x,y}$.

2) Get the matrix $c\_sum\_sort_{x,y}$ by calculating the square of the each element in the $c\_sort_{x,y}$. Then make the element value of (i, j) equal to the sum of values of elements contained in the row number from 1 to i of the $j_{th}$ column in the matrix $c\_sum\_sort_{x,y}$.

3) Compare the elements in the matrix $c\_sum\_sort_{x,y}$ with the threshold $\Theta =64\times (255^{2}/(10^{{\hbox {PSNR}}/10}))$. The value PSNR represents the expected PSNR value. If the value is greater than the threshold $\Theta$, reserve the corresponding coefficient in $c_{x,y}$ according to the index matrix $i\_sort_{x,y}$. Otherwise, the coefficient is set to 0. Finally we get the matrix $c_{x,y}^{\prime }$.

Fig. 7

Code rule for the position of nonzero coefficient

Fig. 8

The coding format for information block

(3) Read the nonzero coefficients in $c_{x,y}^{\prime }$ into an array named as coefficients, and calculate the length of coefficients as len_coefficients. We use matrix $CIndex_{x,y} ,x=1,\ldots ,M/8,y=1,\ldots ,N/8$ to store the position of the nonzero coefficients.

(4) Scramble the CIndex matrix using scrambling algorithm proposed in Sect. 2.3. As we all known, DCT has the property that the outline information of image can be obtained by the high frequency coefficients. According to this property of DCT and its relationship with the DCT dictionary, we can use the position of nonzero coefficients and the DCT dictionary to get outline information of image. In order to improve the security, the CIndex matrix is scrambled.

(5) Code the CIndex matrix after scrambling. For the $8\times 8$ block matrix, its position can be represented by three bits. So a coefficient’s position can be represented by one byte. The specific code rule for the position of nonzero coefficient is shown in Fig. 7. The seventh bit is the flag used to represent whether the position information belongs to the same block. The fourth to sixth bits are used to store the row coordinate of the coefficients in the block. The first to third bits are used to store the column coordinate of the coefficients in the block. The zeroth bit is idle. Finally, we use Huffman coding to compress the position information.

(6) Choose the host image blocks. The coefficients get by step (2) usually are the large float number. It will need a large space if we store it directly. In this paper we use the method proposed in EIF algorithm $^{ 10}$, and embed the sparse coefficient into the host image blocks through the matrix transformation. The required number of host image blocks is $n=\mathrm{ceil}(\frac{len\_coefficients}{64})$, ceil(x) returns the value of x to the nearest integers less than or equal to x. Get $n\quad c_{x,y}^{\prime }$ blocks in row-major order, and do the inverse discrete cosine transform on the n chosen $c_{x,y}^{\prime }$ blocks to get the host image blocks $Host_{p,q}$ ($p=1,\ldots M/8,q=1,..8n/M$) used to embed coefficients.

(7) Represent the embedded coefficients under the controlling of hyper-chaotic system. The following is the detail.

1) For the $Host_{p,q}$, get the related atomic space $D_{p,q }$ by $CIndex_{p,q}$, and the number of atoms is $num\_d_{p,q}$. We can obtain the orthogonal projection matrix $P\_matrix_{p,q }$ by using Eq. (20).

2) Generate a random matrix $Random_{p,q}$ with size of 64$\times$(64-num_dp,q) by the hyper-chaotic system in Eq. (1). In order to reduce the error, the values of the matrix are controlled in [-0.5, 0.5].

3) Use Eq. (22) to represent the embedded coefficients $F_{p,q}$.

$$\begin{aligned} F_{p,q}= & {} (I-P\_matrix{ }_{p,q})\times Random_{p,q}\nonumber \\&\times coefficients(x+1:x+64\nonumber \\&-num\_d_{p,q} ) \end{aligned}$$

(22)

Fig. 9

The structure of image decryption and decompression

where $x=(p-1)\times N\times 8+(q-1)\times 64$.

(8) Embed the embedded coefficients into host image blocks. Add the data $F_{p,q}$ generated from step (7) to $Host_{p,q}$, and we will get the folded data $Fold_{p,q}$.

(9) Encrypt the folded data. Use Eq. (23) to convert the folded data into integers between 0 and 255 forming $F'$. $F'$ is encrypted using the encryption algorithm proposed in Sect. 2.2, and then the cipher data P’ can be obtained.

$$\begin{aligned} F^{\prime }_{p,q} (\hbox {i},\hbox {j})=\frac{Fold_{p,q} (\hbox {i},\hbox {j})}{Max-Min}\times 255 \end{aligned}$$

(23)

where the symbol Max and Min represent the maximum and the minimum value in Fold respectively, i, j are row and column value.

(10) Combine cipher data $P'$ and information block, the final encrypted and compressed image P can be obtained. The information block includes some information used in decryption, such as position information. The structure of information block is as shown in Fig. 8.

From Fig. 8, P_height is used to store the length of single channel image data which can be used to recover the data of each channel in color image; Len_coefficients represents length of coefficients in step (3) and the Max and Min are the values in step (9). Flag is used to mark the positive or negative of Min. len_huf represents the length of encoded position information using Huffman coding; Huf_code is the coded position information using Huffman coding; I_height and I_width are used to store the length and width of original plaintext image, and used to judge the correct reconstructed image size in decompression; “...” represents the random number added for data alignment.

Fig. 10

Procedures of image decompression and decryption algorithm

3.5 The decompression and decryption algorithm of cipher image

Decryption and decompression algorithm is the reverse process of encryption and compression. The structure of decompression and decryption of single channel data is shown in Fig. 9.

From Fig. 9, the concrete steps for decompression the decryption algorithm are as follows. Figure 10 shows the main procedures of decompression and decryption in our proposed scheme.

(1) Read the header information of P and then separate the information block and the folded data from cipher image.

(2) From the information block, get the information Max, Min and Huf_code required in the decompression process. After decoding the Huffman coding data, we can get the position index matrix, and take reverse scrambling operation to obtain position information CIndex matrix .

(3) Decrypt the folded image. The decryption process is the reverse of diffusion algorithm. Then use Eq. (24) to transform the data into the original range, and get the folded data Fold.

$$\begin{aligned} Fold_{p,q} (i,j)=\frac{P^{\prime }_{p,q} (\hbox {i},j)}{255}\times (Max-Min) \end{aligned}$$

(24)

where i, j are row and column value.

(4) Separate the embedded coefficient F from the folded image Fold by Eq. (25).

$$\begin{aligned} \left\{ \begin{array}{l} Host_{p,q} =P\_matrix_{p,q} \times Fold_{p,q} \\ F_{p,q} =Fold_{p,q} -Host_{p,q} \\ \end{array} \right. \end{aligned}$$

(25)

(5) Obtain the original coefficients by Eq. (26).

$$\begin{aligned}&coefficients(x+1:x+64-num\_d_{p,q} )\nonumber \\&\quad =\left( {(I-P\_matrix{ }_{p,q})\times Random_{p,q} } \right) ^{-1}\nonumber \\&\qquad \,\times F_{p,q} \end{aligned}$$

(26)

The symbol $(.)^{-1}$ represents the inverse matrix.

(6) Through the position matrix CIndex, DCT dictionary and the array coefficients, we can get the approximate image block $I^{\sim }_{x,y}$, and the calculation equation is shown in Eq. (27):

$$\begin{aligned} I^{\sim }_{x,y} =\sum _{k=1}^{numel(CIndex_{x,y} )} {d_l \times coefficients_z } \end{aligned}$$

(27)

The symbol numel (.) denotes the number of the elements in the matrix, the relationship between l and z is shown in Eq. (28).

$$\begin{aligned} :\left\{ \begin{array}{l} z=\sum _{i=1}^{x-1} {\mathop {\sum }\limits _{j=1}^{N/8} {numel(CIndex_{i,j} )} }\\ \qquad \, +\mathop {\sum }\limits _{j=1}^{y-1} {numel(CIndex_{x,j} )} \\ l=(CIndex_{\left( {x,y} \right) _k .i\_value} -1)\times N\\ \qquad +\,CIndex_{\left( {x,y} \right) _k .j\_value} \\ \end{array} \right. \end{aligned}$$

(28)

(7) Finally, we get the approximate image $I^{\sim }$ of the original I.

4 The experimental results and performance analysis

For the new compression and encryption scheme, we conducted the security test and compression performance test. The compression and encryption is implemented in MATLAB 2012b running on a personal computer with 2.8 GHz CPU and 2 GB memory.

4.1 Experimental results

Due to the different distribution of the image pixels, the compression performances of different images are different. In this paper, we take several standard test images to illustrate the performance of compression and encryption algorithm. The expected signal-to-noise ratio (PSNR) represents the quality of reconstructed image users expect. Take an example of color image Lena with size of $1024\times 1024$, we set the initial values to be [0,1,0,2], and the results of image compression and encryption under different parameters are shown in Fig. 11.

Fig. 11

The cipher images of Lena $1024 \times 1024$ with different parameters: a the original image of Lena and b the cipher image with expected PSNR = 45 and c the cipher image with expected PSNR = 40 and d the cipher image with expected PSNR = 35 and e the cipher image with expected PSNR = 30 and f the cipher image with expected PSNR = 25

Fig. 12

The decompression and decryption images of Lena cipher image: a the decompression and decryption image with [0, 1, 0, 2] and b the decompression and decryption image with [0, 1, 0, 2+1e$-$14]

Fig. 13

The cipher images of pepper $512 \times 512$ with different parameters: a the original image of pepper and b the cipher image with expected PSNR = 45 and c the cipher image with expected PSNR = 40 and d the cipher image with expected PSNR = 35 and e the cipher image with expected PSNR = 30 and f the cipher image with expected PSNR = 25

Fig. 14

The decompression and decryption image of pepper cipher image: a the decompression and decryption image with [0, 1, 0, 2] and b the decompression and decryption image with [0, 1, 0, 2+1e$-$14]

Figure 11 shows cipher images with different expected PSNR values of the color image Lena with size $1024\times 1024$. Taking an example of the cipher image with expected PSNR 30, Fig. 12 shows the decompression and decryption image at the initial values [0,1,0,2] and [0,1,0,2+1$-$14e]. The PSNR value of Fig. 12a is 35.27, and the PSNR value of Fig. 10b is $-$3.66.

Figure 13 shows cipher images with different expected PSNR values of the color image pepper with size $512\times 512$. Taking an example of the cipher image with expected PSNR 30, Fig. 14 shows the decompression and decryption image at the initial values [0,1,0,2] and [0,1,0,2+1$-$14e]. The PSNR value of Fig. 14a is 31.79, and the PSNR value of Fig. 14b is $-$4.49.

4.2 Performance analysis of image compression and encryption algorithm

4.2.1 Compression ratio and PSNR test

The compression ratio CR is computed by Eq. (29), I_height and I_width denote the height and width of the original image, respectively. And C_height and C_width denote the height and width of the cipher image, respectively.

$$\begin{aligned} \textit{CR}=\frac{I\_height\times I\_width}{C\_height\times C\_width} \end{aligned}$$

(29)

The peak PSNR is calculated by Eq. (30), and it is usually used to judge the quality of reconstructed image after image processing. The higher the quality is, the larger PSNR value is. $f_{i,j}$ in Eq. (30) denotes the original pixel value in position (i, j), and $\hat{f_{i,j}}$ denotes the processed pixel value in position (i, j).

$$\begin{aligned} \mathrm{PSNR}= & {} 10\times \log _{10}\nonumber \\&\left[ {\left( \frac{255^{2}}{\frac{1}{M\times N} \mathop {\sum }\limits _{i=1}^M {\mathop {\sum }\limits _{j=1}^N {\left( f_{i,j} -\hat{f_{i,j} }\right) ^{2}} } }\right) } \right] \end{aligned}$$

(30)

Table 2 lists the compression ratio and the PSNR values for different images with different parameters.

Table 2 The CR and PSNR values for different images with different parameters

Table 3 The MSSIM for different images with different parameters

Table 4 The compression performance of different algorithms

From Table 2, we can know that the compression ratio of images is different for different pixels distribution. We can also know that, if the compression ratio is higher, the quality is lower. Table 2 results reflect the flexibility of the algorithm proposed in this paper. And we can compress and encrypt image according to the different requirement.

4.2.2 MSSIM test

Structural similarity (SSIM) [31] index is a novel method for measuring the similarity between the two images aiming at improving the traditional metrics such as PSNR by considering human visual system (HVS). SSIM index is defined in Eq. (31).

$$\begin{aligned} \mathrm{SSIM}(x,y)=\frac{(2\mu _x \mu _y +c_1 )(2\sigma _{xy} +c_2 )}{({\mu _x} ^{2}+{\mu _y }^{2}+c_1 )({\sigma _x} ^{2}+{\sigma _y }^{2}+c_2 )} \end{aligned}$$

(31)

In Eq. (31), x and y represent the windows of two images of size $m\times m,\mu _x$ and $\mu _y$ represent the average values of x and $y,{\sigma _x} ^{2}$ an ${\sigma _y} ^{2}$ represent the variance of x and y, respectively, $\sigma _{xy}$ represents the covariance of x and y. From Ref. [16], $c_1 =(k_1 L)^{2},c_2 =(k_2 L)^{2},k_1 =0.01,k_2 =0.03$, L is the gray level of pixel value.

In this paper, we use the mean SSIM (MSSIM) as a supplement to evaluate the decompressed image quality. MSSIM is defined in Eq. (32). Table 3 lists the MSSIM results for different images.

$$\begin{aligned} \mathrm{MSSIM}(X,Y)=\frac{1}{n}\sum _{i=1}^n {\mathrm{SSIM}(x_i ,y_i )} \end{aligned}$$

(32)

where X and Y represent the original image and the reconstructed image, respectively; $x_i$ and $y_i$ are the image contents at the ith local window; n is the number of local windows. The smaller the MSSIM is, the greater the difference of two images is.

From Tables 2 and 3, with the increasing demand for compression ratio, the variation trends of PSNR and MSSIM are identical. This shows that the higher the compression ratio is, the lower the quality of the reconstructed image is.

4.2.3 Compression performance comparison

Table 4 lists the compression performance of different algorithms, where ‘–’ indicates that the compression performance of images were not analyzed in the references.

Table 5 The time for different images with different parameters

The results of the Refs. [1, 8] and [10] in Table 4 are all based on gray image compression and encryption algorithm. The algorithm proposed in this paper is based on the color image. For each channel of a color image, the pixels distribution is different. So the image size in each channel of a color image after compression and encryption may not be the same, which will affect the compression performance of the color image. From Table 4, we can know that the compression and encryption algorithm proposed in this paper has a good performance in compression ratio and image quality.

4.2.4 The performance test in time

Table 5 shows the compression and encryption time, decompression and decryption time for different images at different expected PSNR.

As shown in Table 5, the lower the quality of reconstructed image is, the less the time required is. Image compression and encryption technology not only ensures the security of the image information, but also reduces the amount of network resources during transmission. The time taken in encryption and compression is acceptable.

Fig. 15

The histogram of Lena plain image and cipher image: a the histogram of Lena and b the histogram of Lena cipher image

Fig. 16

The histogram of pepper plain image and cipher image: a the histogram of pepper and b the histogram of pepper cipher image

4.3 Security analysis of image compression and encryption algorithm

(1) The analysis of key space

The key space of the proposed algorithm depends on the chosen chaotic system for encryption. In our algorithm, if the precision of initial values is $10^{-14}$, the size of the key space is $10^{14\times 4}$, which is greater than $2^{186}$. It is enough to resist brute-force attack on the basis of existing computing power.

(2) Resistance to statistical attack

In order to prevent the attacker to obtain the characteristics pixels of the image, resistance to statistical analysis is the most basic principle of image encryption algorithm. Being strong against statistical attack means that the cipher must require some random properties [25]. This is shown by a test on the histograms of the cipher image, the correlations of adjacent pixels in the cipher image and information entropy analysis.

1) The histogram analysis

Take color images Lena and pepper for example; when expected PSNR is 30, three-channel pixel histograms are shown in Figs. 15, 16.

Figures 15 and 16 show that the pixels of cipher images can be uniformly distributed in [0, 255]. The pixels distribution has nothing to do with the original image, which can effectively resist the statistical analysis.

2) Correlation of two adjacent pixels

For image data, there is strong correlation between adjacent pixels. Therefore, a good encryption algorithm should remove it to improve the resistance against statistical analysis. The calculation of correlation is as follows.

$$\begin{aligned} C_r =\frac{N\mathop {\sum }\limits _{j=1}^N {(x_j y_j )} -\left( \mathop {\sum }\limits _{j=1}^N {x_j } \right) \left( \mathop {\sum }\limits _{j=1}^N {y_j } \right) }{\left( N\mathop {\sum }\limits _{j=1}^N {x_j^2 } -\left( \mathop {\sum }\limits _{j=1}^N {x_j } \right) ^{2}\right) \left( N\mathop {\sum }\limits _{j=1}^N {y_j^2 } -\left( \mathop {\sum }\limits _{j=1}^N {y_j } \right) ^{2}\right) } \end{aligned}$$

(33)

When expected PSNR is 40, the test results are shown in Table 6.

Table 6 shows that the adjacent pixels of plain image are highly correlated, but the cipher pixels are little correlated with each other. The data illustrates that our scheme can effectively destroy the correlation of pixels.

Table 7 gives the comparison of correlation coefficient of adjacent pixels.

From Table 7, compared with the results in Refs. [16, 17], our scheme shows superior performance.

Take color images Lena and pepper for example, when expected PSNR is 40, three-channel pixels distributions are shown in Figs. 17, 18.

Fig. 17

Pixels distribution of Lena image and the corresponding cipher image: a the distribution of original R channel, b the distribution of original G channel, c the distribution of original B channel, d the distribution of encrypted R channel, e the distribution of encrypted G channel and f the distribution of encrypted B channel

Fig. 18

Pixels distribution of peppers image and the corresponding cipher image: a the distribution of original R channel, b the distribution of original G channel, c the distribution of original B channel, d the distribution of encrypted R channel and e the distribution of encrypted G channel, f the distribution of encrypted B channel

From Figs. 17, 18, we can know that the pixels distribution of original image is uneven, and there is a strong correlation between pixels. But the correlation between pixels is completely destroyed in the cipher image and we cannot get the pixels information by the adjacent pixels.

3) Information entropy test

The information entropy is an indicator of measuring the random system’s complexity. The higher the entropy is, the more complexity of the system is. The image pixels are treated as random events, we use Eq. (34) to calculate the information entropy of the image.

$$\begin{aligned} H(S)=\sum _s P(S_i)\log _2\frac{1}{P(S_i)} \end{aligned}$$

(34)

Table 6 Correlation coefficient of adjacent pixels

Table 7 Comparison of correlation coefficient of adjacent pixels

From Eq. (34), we can know that the ideal entropy value is 8 if the image pixels can be expressed by 8 bits. Table 8 lists the entropies of cipher images with different parameters.

As is apparent from Table 8, the information entropy of cipher images are closed to the ideal value, which can illustrate that the cipher image has a good randomness. With the compression ratio increasing, the information entropies are decreasing, which accords with the nature of compression and encryption.

Table 9 shows the entropy comparison.

From Table 9, the information entropy of our scheme is better than those of the existing algorithms mentioned in Refs. [16, 17].

(3) Avalanche effect

The avalanche effect for image compression and encryption algorithm means the proportion of the bits changed in the cipher image when the initial keys are changed a little. Table 10 lists the avalanche effect of different images. The initial values are [0,1,0,2] and [0,1,0, 2+1e$-$14]. The symbol ’–’ represents that the image sizes do not match when the initial keys have a little change, which better explains little change on initial keys has more influence on cipher image.

Table 8 Entropy test

Table 9 Entropy comparison

Table 10 Avalanche effect test

Table 11 NPCR and UACI value

Table 12 Sensitivity to key

The ideal value of avalanche effect is 0.5. From Table 10, we can know that the image compression algorithm proposed in this paper has a good avalanche effect.

(4) Resistance to differential attack

Differential attack is one type of classical cryptanalysis methods based on strong characteristics. The attacker may observe the change of decryption by the tiny change of plaintext to find the correlation between plain image and cipher image. If tiny change of original image can bring great changes to cipher image, the effect of differential attack will be reduced. Generally, we use number of pixels change rate (NPCR) and unified average changing intensity (UACI) to describe this variation. NPCR defined by formula (35) is to obtain the difference between two images by evaluating the number of pixel difference. UACI defined by formula (37) is to obtain the difference between two images by evaluating the change of visual effect.

$$\begin{aligned} \mathrm{NPCR}=\frac{\mathop {\sum }\limits _{i,j}D(i,j)}{W\times H}\times 100\,\% \end{aligned}$$

(35)

D(i, j) is the difference value of the corresponding pixel of the two images. It is defined as:

$$\begin{aligned} D(i, j)=\left\{ \begin{array}{ll} 1&{} \quad C_1 (i, j)\ne C_2 (i, j)\\ 0&{} \quad C_1 (i, j)= C_2 (i, j) \end{array} \right. \end{aligned}$$

(36)

where $C_{1}$ and $C_{2 }$are two encrypted images, whose corresponding original images have only one-pixel difference.

$$\begin{aligned} \mathrm{UACI}= & {} \frac{1}{W\times H} \left[ \sum _{i,j}\frac{|C_1 (i, j)-C_2 (i, j)|}{255}\right] \nonumber \\&\times 100\,\% \end{aligned}$$

(37)

The theoretical values of NPCR and UACI are 99.6 and 33 %, respectively.

In our test, one bit change is introduced with the other values unchanged to get another image. We encrypt two images when expected PSNR is 40. The NPAR and UACI of the two cipher image are evaluated, and the result is shown in Table 11.

From Table 11, NPAR and UACI values are close to the theoretical values. The algorithm can resist to differential attack.

(5) Sensitivity analysis of key

A good encryption scheme should be sensitive to the key. If it is sensitive to the key, a small change of the key will lead to be very different of the cipher text. Figures 12b and 14b show that the decrypted image with a tiny change ($10^{-14}$) to the right key. We can find that the tiny modification of $10^{-14}$ to the key will lead to the failure of the decryption. So our scheme is extremely sensitive to the key.

The sensitivity to the key can also be quantified by NPCR an UACI defined by Eqs. (35) and (37).

The tiny modification of $10^{-14}$ to the key is used in encryption to get another image. We change four initial values respectively. So there are four key pairs: [1, 1, 0, 1] and [1+1e$-$14, 1, 0, 1], [1, 1, 0, 1] and [1, 1+1e$-$14, 0, 1], [1, 1, 0, 1] and [1, 1, 0+1e$-$14, 1], [1, 1, 0, 1] and [1, 1 ,0, 1+1e$-$14]. Table 12 shows the NPCR and UACI value with a tiny change in keys when expected PSNR is 40.

The symbol ‘–’ represents that the image sizes do not match when the initial keys have a little change, which better explains little change on initial keys has more influence on cipher image.

Table 13 Comparison between Ref. [37] and our pseudorandom sequence generator

Table 12 results show our new schemes have a satisfied performance on sensitivity to key.

(6) Cryptanalysis related to hyper-chaos-based schemes

Recently, many hyper-chaos-based image encryption schemes are proposed. However, due to the failed design of the encryption process, such as permutation or diffusion, many of these algorithms are broken [27, 29, 32–36]. This weakness in the design of image encryption process, not hyper-chaos itself, leads to the insecurity of the cryptosystems. For the design of image encryption process in our proposed scheme, the test results show it has high security.

Reference [37] proposed pseudorandom sequence generator based on the Chen chaotic system. However, it is insecure and Ref. [38] analyzed the security weakness of the proposed generator. The discretization process of the proposed generator, not the chaos system itself, leads to the dependence among output values of a chaotic system that yielded a smaller key space. Moreover, Chen chaotic system is not a hyper-chaotic system. For pseudorandom sequence generator of our proposed scheme, we discretize the hyper-chaotic sequence by getting the decimal part of chaotic sequence and select different bits of sequences to obtain the key sequence, which avoids the dependence among output values of a chaotic system. The comparison of the key space between our pseudorandom sequence generator and the pseudorandom sequence generator of Ref. [37] after broken by Ref. [38] is shown in Table 13. From Table 13, the key space of our pseudorandom sequence generator is larger than that of Ref. [37] after broken by Ref. [38]. The key space of our pseudorandom sequence generator is enough to resist brute-force attack on the basis of existing computing power. In addition, the kolmogorov entropy and approximate entropy of our pseudorandom sequence generator and the pseudorandom sequence generator of Ref. [37] are shown in Table 13. Kolmogorov entropy can be used to measure the randomness of binary sequence. The higher the kolmogorov entropy value, the better the randomness. Approximate entropy measures the probability of the key sequence to produce the new pattern. The greater probability means the greater approximate entropy and more random sequence.

From Table 13, the kolmogorov entropy and approximate entropy of our pseudorandom sequence generator are better than these of Ref. [37].

The characteristics of hyper-chaos such as nonlinearity and random-like behaviors make hyper-chaotic systems suited to generate pseudorandom sequences. In our scheme, hyper-chaos is used to construct pseudorandom sequence generator. The characteristics of hyper-chaos such as nonlinearity and random-like behaviors make hyper-chaotic systems suited to generate pseudorandom sequences. Compared with the general chaos system, hyper-chaotic system has more complex chaotic behaviors, its pseudorandomness and long-term unpredictability is stronger. The ability to resist many attacks such as phase-space reconstruction attack is better. Table 14 shows the approximate entropy of chaotic sequence about Logistic map, Chen chaotic system and our hyper-chaotic system.

Table 14 Approximate entropy

From Table 14, the approximate entropy of our hyper-chaotic system is larger than that of Logistic map and Chen chaotic system. It shows the superiority of hyper-chaos.

In the same conditions, the hyper-chaos-based cryptosystem has bigger key space. Therefore, in general, hyper-chaos can contribute to the improvement of the security of the key stream produced by the pseudorandom sequence generators. If hyper-chaos-based key stream can be used effectively, it can help to improve the security of image encryption algorithm.

5 Conclusion

In this paper, the image is compressed by folding the color image using the nature of the orthogonal projection matrix and the relationship among image data, DCT dictionary and DCT. The diffusion and scrambling image encryption algorithm based on the hyper-chaotic system is designed to encrypt the image. In the process of the folded compression, the image is encrypted from three aspects: Firstly, a scrambling method for the position of effective coefficients is proposed to reach the goal of eliminating the correlation between pixels in one block. Then in order to encrypt the coefficients, the sparse coefficients are controlled by the hyper-chaotic system, and finally, a diffusion method for the folded image is proposed to encrypt the final data. The proposed algorithm can compress and encrypt the image based on the requirements of the quality of reconstructed images, with some flexibility. The key space is large enough to resist brute-force attacks. The test results show that the proposed compression and encryption algorithm has high security and good performance in compression.