1 Introduction

Nowadays, with the development and perfection of the computer, network, communication and multimedia technologies, network has gradually become a common form of acquirement and transmitting information resources, and it’s possess such advantages as convenience and swiftness. Meanwhile, information security becomes a factor that cannot be ignored. At present, digital image play an important role in multimedia images and it is widely applied in military, political, commercial, medical and other fields, which have high confidentiality requirements. Therefore, it has important practical application value to research the digital image encryption.

Compared with traditional information carriers, digital image has follow features: (1) big data capacity; (2) large correlation between neighborhood pixels; (3) the big data redundancy. These inherent characteristics bring a result that the traditional encryption algorithm cannot effectively encrypt digital image. Since chaotic system have the performances of sensitivity of initial value randomness and ergodicity, there are widely used in the field of digital image encryption [1,2,3]. Ever since Matthews introduced chaotic encryption for the first time in 1989 [4], soon afterwards, all kinds of image encryption algorithms using chaotic system have been proposed [5,6,7,8,9,10,11,12]. Li C et.al presented an image encryption algorithm based on 1D tent chaotic map [5]. Secure image encryption algorithm using a novel chaos through S-Box is designed by Ünal Çavuşoğlu [6]. Zhu H et.al proposed an image encryption algorithm through 2D compound homogeneous hyper-chaotic system and local binary pattern [7]. Luo Y et.al presented a parallel digital image encryption algorithm based on a piecewise linear chaotic map and a 4D hyper-chaotic map [8]. The chaotic sequence is used to scrambling or diffusion of image pixels in algorithm [5,6,7,8].

Subsequently, to improve security properties of the image encryption system, DNA molecule is introduced to image encryption algorithm. Since Zhang et.al proposed an image scheme using DNA addition and chaotic system in 2010 [13], based on DNA operation and chaotic system, the various image encryption schemes are designed. Wang X Y et.al introduced an image encryption algorithm through DNA sequence operation and 2D logistic map [14]. A combined DNA operations and chaotic system image cryptosystem by Hu T et.al [15]. Zhang Li Min et.al [16] proposed a novel color image encryption scheme by employing fractional-order hyper-chaotic system and DNA operations. These encryption methods implement digital image encryption, but do not reduce the storage, processing and transmission costs.

To overcome these weaknesses, people try to use CS to effectively decrease the cost of storage, processing and transmission. In 2006, Cande and Donoho proposed CS theory, and they proved that if the signal is sparse or compressible [17], it can sample signal much smaller than the data sampling rate specified by Nyquist’s theorem, and the high probability signal can be accurately reconstructed. At present, reconstruction algorithms for compression sensing include: Orthogonal Matching Pursuit (OMP) [18], Compressive Sampling Matching Pursuit (CSMP) [19], Subspace Pursuit (SP) [20], Gradient Pursuit (GP) [21], Basis Pursuit (BP) [22], Least Angle Regression (LARS) [23], Gradient Projection for Sparse Reconstruction (GPSR) [21] and Bayesian algorithm [24].

Initially, Rachin and Baron certified that CS did not fit to Shannon’s definition of perfect confidentiality, and it just possessed the computational for confidentiality [25]. In 2013, Ramezani et.al proposed that the CS has perfect confidentiality under certain conditions [26], and then it became the important theoretical basis of application CS for encryption algorithm. Consequently, numerous of image encryption schemes based on CS are presented [27,28,29,30,31,32,33]. Liu X et.al proposed a new optical image encryption scheme by using Arnold transformation and CS [27]. Robust multispectral double-image encryption based on CS was introduced by Kim B et.al [28]. Zhou N et.al presented an image compression-encryption algorithm by 2D CS and hyper-chaotic system, this algorithm overcame low-dimensional chaotic system bearing security risk and reduced the possible transmission burden [29]. Chai X et.al [30] proposed an image encryption algorithm through CS and chaotic system. The algorithm in references [27, 28] do not used the chaotic system, and the randomness of the measurement matrix is not well. For the algorithm in [29, 30] only compresses and scrambles the image, does not to diffusion operation, and the security performance is not high. In the encryption schemes [31,32,33], the key space is not large enough, and is susceptible to brute-force attack. Therefore, these digital image encryption methods have respectively shortcoming. We proposed to scramble and diffusion through hyper-chaotic sequence and CS encryption scheme, which not only can reduce the cost of the storage, processing and transmission, but also improve the security of encryption algorithm.

In this paper, we focus on applying the hyper-chaotic sequence and CS to compress and encrypt digital image, and the security features and CS reconstruction performances are analysed. The rest of this paper is organized as follows: In Section 2, principal definitions and theories are introduced. The combined image compression and encryption algorithm are detail described In Section 3. In Section 4, the cryptographic features and reconstruction performances are analysed. Finally, the main conclusion in Section 5 is given.

2 Principle of the Algorithm

2.1 Compressive Sensing

The main idea of CS can be expressed as: firstly, the high dimensional signal is obtained by a transforming to obtain cardinality independent of the measurement matrix, and then project it to low dimensional space. Finally, the original signal is reconstructed by using a small number of high probability signals in the projection.

Assumption one dimensional signal x = [x(1), x(2),…, x(N)]T, the linear combination of its orthogonal basis is as follows:

$$ x=\varPsi S=\sum \limits_{i=1}^N{S}_i{\varPsi}_i, $$
(1)

where Ψ, Ψi, S,Ψ are basis matrix, column vector, N × 1 column vector and the sparse coefficient of x respectively. If S has K non-zero coefficients and N-K zero coefficients, x is deemed to be sparse. The common sparse transform algorithms mainly consist of discrete cosine transform (DCT) [34], Fourier transform and discrete wavelet transform (DWT) [35].

The sparse signal x is measured through the measurement matrix Φ∈RM × N, and the corresponding measured value y is obtained by

$$ y=\varPhi x=\varPhi \varPsi S=\varTheta S, $$
(2)

where Θ = ΦΨ is Μ × N matrix.

The signal reconstruction is essentially a linear equation solving process. The number of unknowns is more than equations in Eq. (2), so, the Eq. (2) has a group of multiple solutions. Because of the coefficients S are sparse, the minimum norm l0 to reconstruction signal can be solved, if the measurement matrix Φ and sparse transform matrix Ψ are meet to (Restricted Isometry Property) RIP. For all x∈ ∑k, the existing δk∈(0,1) is used to:

$$ \left(1-{\delta}_k\right){\left\Vert x\right\Vert}_2^2\le {\left\Vert Ax\right\Vert}_2^2\le \left(1+{\delta}_k\right){\left\Vert x\right\Vert}_2^2, $$
(3)

where x is k-order sparse signal. δk is RIP constant, and matrix A∈RM × N is meet k-order RIP.

The signal can be accurately reconstructed by

$$ \overset{\wedge }{S}=\mathrm{argmin}{\left\Vert S\right\Vert}_0,s.t.y=\varTheta S, $$
(4)

where ‖•‖0 is vector norm l0,and it is the number of non-zero elements in the vector x.

In this paper, the measurement matrix Φ is obtained by 3D-SIMM hyper-chaotic sequence and Hadmard matrix, the corresponding detailed steps as follows.

  1. (a)

    Setting the 3D-SIMM hyper-chaotic system initial values, let the Eq. (5) iteration m + M times, then discard front m times values, a sequence X of length M is obtained.

  2. (b)

    The index sequence s is obtained by the elements of X stored in order from high to low. According to s to rearrange natural sequence n = [1, 2,…., M], the sequence n1 of length M is obtained.

  3. (c)

    The Hadmard matrix is generated using seed as follows

$$ \left[\begin{array}{l}-1\\ {}1\end{array}\begin{array}{r}1\\ {}-1\end{array}\right], $$
(5)

the size of M × N measurement matrix Φ is obtained by n1 select M rows.

2.2 Hyper-Chaotic System

The high dimensional chaotic map 3D-SIMM is defined by [36].

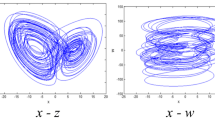
$$ \Big\{{\displaystyle \begin{array}{l}{x}_{i+1}=a\sin \left(b{z}_i\right)\sin \left(c/{x}_i\right)\\ {}{y}_{i+1}=a\sin \left(b{x}_{i+1}\right)\sin \left(c/{y}_i\right)\\ {}{z}_{i+1}=a\sin \left(b{y}_{i+1}\right)\sin \left(c/{z}_i\right)\end{array}}, $$
(6)

where a, b, c are parameters of 3D-SIMM chaotic system. When parameters (a = 1, b = 2π, c = 11.5) and initial values are (0.4, 0.8, 0.6), we can get the phase diagrams of 3D-SIMM chaotic system in x-y plane as shown in Fig. 1(a). Fixed the parameters b, c and initial conditions, let a∈[0, 5], b∈ [1, 8] and c∈ [0, 15]. The Lyapunov exponent spectrum (LEs) and bifurcation diagram (BD) are shown in Fig. 1 (b), (c), (d), (e), (f) and (g). It shows that the 3D-SIMM is hyper-chaotic system when other parameters remain unchanged and parameter a∈[0.33, 5], b∈ [2, 8] and c∈ [0, 15].

Fig. 1
figure 1

(a) Phase diagram in x-y plane, (b) LEs with b = 2π, c = 11.5, a∈ [0, 5], (c) BD with b = 2π, c = 11.5, a∈ [0, 5], (d) LEs with a = 1, c = 11.5, b∈ [1, 8], (e) BD with a = 1, c = 11.5, b∈ [1, 8], (f) LEs with a = 1, b = 2π, c∈ [0, 15], (g) BD with a = 1, b = 2π, c∈ [0, 15]

Full size image

The experiment investigation shows that 3D-SIMM chaotic system has extremely strong randomness and sensitivity to initial conditions and parameters, which indicates that it can generate more random of chaotic sequences. Hence, it can improve security of cryptosystem, if it is applied to encryption image.

2.3 Improved Arnold Matrix Transformation

Convert the plaintext image P to 1D row vector A of size MN. The new position (p, q) is obtained by Arnold matrix transformation for any point position (1, j) of vector A, as following formula

$$ \left[\begin{array}{l}p\\ {}q\end{array}\right]=\left[\begin{array}{l}1\\ {}b\end{array}\begin{array}{c}a\\ {} ab+1\end{array}\right]\left[\begin{array}{l}1\\ {}j\end{array}\right], $$
(7)

So we can get

$$ p=1+ aj, $$
(8)
$$ q=b+\left( ab+1\right)j, $$
(9)

The pixel transformation between (1, j) and (1, q) is realized through the pseudo- random variables a and b from Eq. (8). Consider ab + 1as a new random number, and set it as f. Eq. (10) turns to

$$ q=b+ aj. $$
(10)

The improved Arnold matrix transformation can scramble image pixels by Eq. (10). The improved algorithm not only has less running time, but also has superior scrambling effect.

3 The encryption and Decryption Algorithm

3.1 Encryption Algorithm

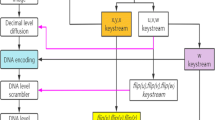
Encryption algorithm includes sparse, CS calculation, scramble and diffusion. The entire process is shown in Fig. 2, and the corresponding specific encryption steps are list as follows.

  1. Step 1:

    In order to compress the image, the pixel matrix needs to be sparse. For a N × N image I, the same size of sparse coefficient matrix I1 is obtained by discrete wavelet transform (DWT).

  2. Step 2:

    Setting the 3D-SIMM hyper-chaotic system initial values, let the Eq. (6) iteration m + M times, then discard front m times values, a sequence X of length M is obtained. The measurement matrix Φ with the size M × N is generated by Section 2.1.

  3. Step 3:

    The spare image is compressed with the measurement matrix Φ, the compressed result image I2 with size of M × M is generated by CS calculations according to.

Fig. 2
figure 2

Encryption process

Full size image
$$ {I}_2=\varPhi {\left(\varPhi {I}_1\right)}^{\hbox{'}}, $$
(11)
  1. Step 4:

    The compression image I2 is quantified so that all pixel values are between 0 and 256.

  2. Step 5:

    To generate scramble chaotic sequence, let the Eq. (6) iteration m + M × M times, then discard front m times values, the two sequences X and Y of length M × M are gained, then make the random number a = X, b = Y as setting in Section 2.3.

  3. Step 6:

    Scramble the quantified image I2 Firstly, let the quantified image I2 convert to one dimension M × M vector, then scrambled result I3 is generated by improved Arnold matrix transformation in Section 2.3.

  4. Step 7:

    The scrambled vector is restored to a M × M matrix and the matrix is transposed.

  5. Step 8:

    To generate diffusion chaotic sequence, let et the Eq.(5) iterate n + M × M times, and discard front n times values, we get two sequences y and z of length M × M, Y and Z are generated by as follows operation for sequences y and z,

$$ Y=\operatorname{mod}\left( floor\left(y\ast pow2(10)\right),256\right), $$
(12)
$$ Z=\operatorname{mod}\left( floor\left(z\ast pow2(10)\right),256\right). $$
(13)
  1. Step 9:

    Pseudo-random vectors S1 and S2 of forward diffusion algorithm and reverse diffusion algorithm are obtained by Eq. (12) and (13).

  2. Step 10:

    Perform pixel diffusion on the results of the transpose, and the diffusion results are generated according to

$$ {C}_i=\left({C}_{i-1}+{S}_i+{P}_i\right)\operatorname{mod}256, $$
(14)
$$ {C}_i=\left({C}_{i+1}+{S}_i+{P}_i\right)\operatorname{mod}256, $$
(15)

where Eq. (14) is forward diffusion, Eq. (15) is reverse diffusion.

  1. Step 11:

    The encrypted image C is obtained by restore diffusion vector as matrix.

3.2 Decryption Scheme

The Fig. 3 shows the decryption process. The detailed decryption process of the proposed algorithm is described as follows.

  1. Step 1:

    Input encrypted image.

  2. Step 2:

    To restore the diffusion pixel values, the pseudo-random vectors generated by step 10 of the application encryption process, then diffusion processing is governed by

Fig. 3
figure 3

Decryption process

Full size image
$$ {P}_i=\left(2\times 256+{C}_i-{C}_{i+1}-{S}_i\right)\operatorname{mod}256, $$
(16)
$$ {P}_i=\left(2\times 256+{C}_i-{C}_{i-1}-{S}_i\right)\operatorname{mod}256. $$
(17)
  1. Step 3:

    The results of the reverse diffusion are transposed.

  2. Step 4:

    The scrambled result is obtained by doing the opposite of the scrambling processing as encryption step 6.

  3. Step 5:

    For the result of the recover scrambling to Orthogonal Matching Pursuit (OMP) reconstruction. The image information before compression is obtained by two OMP reconstruction calculations.

  4. Step 6:

    Decrypted image received by inverse discrete wavelet transform (IDWT) is used to the reconstruction results.

3.3 Discussion

In this paper, we aim at the low safety features, high costs of storage and transmission, an image compression and encryption algorithm is designed. The proposed algorithm’s highlight contributions and list them as follows.

Firstly, the theory of CS is used to compress image for reducing the costs of transmission and storage, so that the encrypted image can be transmitted and stored quickly and efficiently. The measurement matrix Φ is generated by hyper-chaotic sequence and Hadmard matrix, which can be satisfied with (Restricted Isometry Property) RIP. And it would be improved the compression and reconstruction characteristics effectively.

Secondly, the improve Arnold matrix algorithm is applied in scrambling process. Compared with the Arnold matrix transformation, improved Arnold matrix algorithm has good image scrambling effect and less running time. What’s more, using the Modular operation to diffuse the pixels of image, which would be improved the security performance of encryption algorithm.

4 Experimental Analyses

In this section, to verify the encryption and decryption effects of the designed algorithm, we have employed three different 256 × 256 images “Lena”, “finger”, “aerial” and three different 512 × 512 images “bridge”, “airfield”, “dollar” are tested in MATLAB R2014a. In order to compare with other encryption algorithms, we just analyzed the safety performance of Lena image in security analysis parts.

4.1 Encrypted and Decrypted Image

Secret key is composed of 3D-SIMM chaotic system parameters a, b, c, initial values ×0, y0, z0 and iterations times m, n. Set a = 1, b = 2π, c = 11.5, ×0 = 0.4, y0 = 0.8, z0 = 0.6, m = 100, n = 500, the compression rate is 0.8. The three different images Lena (256 × 256), finger (256 × 256) and bridge (512 × 512) are shown in Fig. 4(a), (d) and (g), and corresponding encrypted and decryption images are shown in Fig. 4(b), (e), (h), (c), (f) and (i), respectively. Visually, decryption image is a bit lower in resolution than the original image, but we can get most of the mainly information of original image. Therefore, we proposed algorithm can compress and encrypt image effectively.

Fig. 4
figure 4

Encryption and decryption test of Lena image, (a) original Lena image, (b) encrypted Lena image, (c) decrypted Lena image, (d) original finger image, (e) encrypted finger image, (f) decrypted finger image, (g) original bridge image, (h) encrypted bridge image, (i) decrypted bridge image

Full size image

4.2 The effect of the Compression Ratio on Simulation

In this section, the compression performance of the new compression and encryption algorithm is analyzed by Mean Structural Similarity (MSSIM) and Peak Signal to Noise Ratio (PSNR) at different compression ratios (CR). The CR is defined as follows

$$ CR=\frac{C_M\times {C}_N}{I_M\times {I}_N}, $$
(18)

where IM and IN are height and width of original image. CM and CN are height and width of encrypted image, respectively.

4.2.1 Mean Structural Similarity (MSSIM)

The MSSIM is used to estimate the characteristic of the encryption algorithm, and it is defined by

$$ l\left(X,Y\right)=\frac{2{\mu}_X{\mu}_Y+{C}_1}{\mu_X^2+{\mu}_Y^2+{C}_1}, $$
(19)
$$ c\left(X,Y\right)=\frac{2{\sigma}_X{\sigma}_Y+{C}_2}{\sigma_X^2+{\sigma}_Y^2+{C}_2}, $$
(20)
$$ s\left(X,Y\right)=\frac{\sigma_{XY}+{C}_3}{\sigma_X{\sigma}_Y+{C}_3}, $$
(21)
$$ \mathrm{SSIM}\left(X,Y\right)=l\left(X,Y\right)\times c\left(X,Y\right)\times s\left(X,Y\right), $$
(22)
$$ \mathrm{MSSIM}\left(X,Y\right)=\frac{1}{M}\sum \limits_{k=1}^M\mathrm{SSIM}\left({x}_k,{y}_k\right), $$
(23)

where μ is the mean of image structural. σ means image variance structural, c1, c2 and c3 are small constants to avoid denominator of 0. M is the total number of image blocks. Here, parameters C1 = (K1 × L)2, C2 = (K2 × L)2, C3 = C2/2, K1 = 0.001, K2 = 0.003, M = 64, L = 255. The MSSIM values under the different CR are listed in Table 1. According to the data of the Table 1, we know that the MSSIM values will be changed when compression ratio is changed, which effectively compress and encrypt image according to different practical application needs.

Table 1 MSSIM values under the different CR
Full size table

4.2.2 Peak Signal to Noise Ratio (PSNR)

Peak Signal-to-noise Ratio (PSNR) is used to evaluate the performance of reconstruction algorithm to restore image. The formula for calculating PSNR is as follows:

$$ MSE=\frac{1}{rc}\sum \limits_{i=1}^r\sum \limits_{j=1}^c{\left({e}_{ij}-{e}_{ij}^{\hbox{'}}\right)}^2, $$
(24)
$$ PSNR={\log}_{10}\left(\frac{255^2}{MSE}\right), $$
(25)

where r and c are length and height of the image, MSE is mean error between the original and the restore image. eij and e’ ij are pixels of original and restore image in i, j position. The larger the value of the PSNR means that the higher the similarity of original image and the reconstructed image. The PSNR values of different CR are listed in Table 2. Compared with the PSNR values of references [30, 37] are listed in Table 3. From Table 2 and Table 3, we can get that PSNR values are close to 30 when CR>0.4. Therefore, the reconstruction result is also good for a small of compression.

Table 2 PSNR values under the different CR
Full size table
Table 3 PSNR values of different algorithms
Full size table

4.3 Statistic Analysis

4.3.1 Histograms analysis

As we can be seen from the Fig. 5 that the histogram before encryption has a lot of fluctuations, whereas the encrypted histogram is very flat and almost uniform. Therefore, the attacker would not get any useful information from the histograms, so this algorithm has the ability to prevent statistical attacks.

Fig. 5
figure 5

Histogram of image with before and after encryption, (a) the histogram of Lena image before encryption, (b) the histogram of Lena image after encryption, (c) the histogram of finger before encryption, (d) the histogram of finger after encryption, (e) the histogram of bridge before encryption, (f) the histogram of bridge after encryption

Full size image

4.3.2 Correlation between adjacent pixels

Generally, the correlation between neighborhood pixels before image encryption is extremely large, while the after encryption image should not has correlation between adjacent pixels. The correlation values are calculated by.

$$ {r}_{xy}=\frac{\operatorname{cov}\left(x,y\right)}{\sqrt{D(x)D(y)}}, $$
(26)
$$ \operatorname{cov}\left(x,y\right)=E\left\{\left[x-E(x)\right]\left[y-E(y)\right]\right\}, $$
(27)
$$ E(x)=\frac{1}{N}\sum \limits_{i=1}^N{x}_i, $$
(28)
$$ D(x)=\frac{1}{N}\sum \limits_{i=1}^N{\left[{x}_i-E(x)\right]}^2, $$
(29)

where E(x) and D(x) are average and variance of x respectively, and N is the all number of pixels of the image.

In this test, we randomly selected 2000 pairs of neighborhood pixels at different directions. From the Fig. 6, we can see that adjacent pixels of original image at different directions are dense on line y = x, but adjacent pixels of original image at different directions are distributed in the rectangular (lower-left coordinate (0, 0), and upper-right coordinate (255, 255)) region, which illustrates the original image has highly correlation in all directions, encrypted image don’t have correlation in all directions. The correlation coefficients of before and after Lena image encryption neighborhood pixels in different directions are listed in Table 4. It is obvious that the correlation before encryption of Lena image is highly, on the contrary, the correlation of after encryption the three directions decreased a lot, which proves that the proposed encryption scheme can effectively dislocate the pixel position.

Fig. 6
figure 6

Correlation before and after Lena image encryption in different directions, (a) before image encryption in horizontal, (b) before image encryption in vertical, (c) before image encryption in diagonal, (d) after image encryption in horizontal, (e) after image encryption in vertical, (f) after image encryption in diagonal

Full size image
Table 4 Correlation coefficient of plaintext Lena image and ciphertext Lena image
Full size table

4.4 Information Entropy Analysis

Information entropy is mainly used to test the randomness of image information. The larger the entropy value, the greater the uncertainly and the less the visual information. The information entropy value can be obtained by is defined by

$$ H=-\sum \limits_{i=0}^Lp(i){\log}_2p(i), $$
(30)

where L represent gray scale of the image, and p(i) is the probability of gray value i occurrence. For L = 256 Gy image, the theoretical value of information entropy H is 8. When the compression ratios take different values, the values of information entropy are listed in Table 5. Compared with the information entropy of references [11, 38, 39] are listed in Table 6. According to the data of the Table 5 and 6, the values of information entropy under different compression rates are almost equal to the theoretical value of 8, which shows that encrypted image proposed has superior randomness and can avoid the attack of information entropy.

Table 5 Information entropy at different compression ratio
Full size table
Table 6 Information entropy with the different algorithms
Full size table

4.5 Key space Analysis

For a good encryption system, the key space of encryption algorithm should be large enough to prevent brute force attack. The secret key of the presented scheme includes: (1) the parameters a, b and c; (2) the initial values ×0, y0 and z0; (3) the number of throw away hyper-chaotic sequences m and n. When keys a, b, c, ×0, y0 and z0 are calculated with precision of 10−15, the secret key space about is (1015)6 = 1090 > 2298. Therefore, the key space of our algorithm is large enough to guard against violent attacks. Compare the key space with other encryption methods in Table 7.

Table 7 Comparison of key space different encryption algorithms
Full size table

4.6 Key sensitivity Analysis

In sensitivity test of secret key, we get the decryption images are shown in Fig. 7 when the key minor changes. It shows that the decrypted image is extremely differently from original image, therefore, we designed algorithm is extremely sensitive to the key.

Fig. 7
figure 7

The sensitivity test results of key, (a) x0 + 10−16, (b) y0 + 10−16, (b) z0 + 10−16, (d) a + 10−14, (e) b + 10−14, (f) c + 10−14, (g) n + 1, (h) CR-0.2, (i) m + 1

Full size image

From the Fig. 7, we find that if the key slight change, the decrypted image information is extremely different original image, which due to the DWT in the algorithm. Due to DWT’s layered wavelet transform and high and low frequency filtering. Like DCT transform will not appear pixel value missing phenomenon.

4.7 Robustness Analysis

4.7.1 Noise Attack

Because of the encrypted image is disturbed by noise in the transmission process. So we added the Gaussian noise and salt & Pepper noise to the encrypted image for carry out anti-noise test. Three different variances of Gaussian noise are added to the encrypted Lena image, and corresponding recover results are shown in Fig. 8 (a), (b) and (c). The Lena cipher image is attacked by salt & Pepper noise with the variances are 0.0001, 0.0002 and 0.0003, and the test results as shown in Fig. 8 (d), (e) and (f). Among them, the quality of the decrypted images becomes worse and worse with the increase of noise variance. However the main image information can be obtained. This proves that the proposed encryption scheme has strong anti-noise capability.

Fig. 8
figure 8

Decrypted image with Gaussian noise at different variances, (a) Gaussian noise with variance of 0.001, (b) Gaussian noise with variance of 0.002, (c) Gaussian noise with variance of 0.003, (d) Salt & pepper noise with variance of 0.0001, (e) Salt & pepper noise with variance of 0.0002, (f) Salt & pepper noise with variance of 0.0003

Full size image

4.7.2 Cropping Attack

The cropping attack is an important evaluate standard of cryptosystem. In order to test resist cropping attack of the proposed algorithm, we let encrypted Lena image with three different data losses as shown in Fig. 9(a), (b) and (c), the decrypted images are shown in Fig. 9(d), (e) and (f), respectively. It shows that even though the encrypted image is cropped off, the main information of image can be recovered. Moreover, our algorithm could resist cropping attack to a certain degree.

Fig. 9
figure 9

Cropping attack test results, (a) with 10 × 10 encrypted Lena image cut, (b) with 20 × 10 encrypted Lena image cut, (c) with 10 × 30 encrypted Lena image cut, (d) recovered image (a), (e) recovered image (b), (f) recovered image (c)

Full size image

5 Conclusions

In this paper, based on compression sensing (CS) and 3D hyper-chaotic map, an efficient digital image compression and encryption algorithm is proposed. The dynamic analysis shows that hyper-chaotic map possess more complex dynamic characteristics and randomness, which improved security features of encryption algorithm. The compression performance and reconstruction results indicate that the compression characteristics of CS theory is used to cryptosystem, it effectively reduce the amount of image data for storage and transmission. The safety performances analysis demonstrates that the proposed algorithm can resist lots of common attacks, including brute-force, statistical and others attack. The robustness analysis illustrates that the designed algorithm could resist cropping and noise attacks to a certain degree. Therefore, the designed image compressive and encryption method can effectively encrypt and compress image, which provides experimental basis and theoretical guidance for the safe transmission of image information. In future work, we intend to propose more encryption and CS algorithms and continuously improve safety features.