1 Introduction

In order to understand human locomotion which is one of the most complicated motions in the nature (Alberto et al. 2014), investigating bipedal walking robots is shown to be an appropriate means. Although human motion is controlled by the neuromuscular system, except for part of a stride (Philippe et al. 2013), McGeer (1990) showed that some legged mechanisms could exhibit stable human-like walking on a range of shallow ramps without actuation.

The compass-like biped robot investigated by Garcia et al. (1997) is assumed to be the simplest model capable of mimicking bipedal gait. The dynamics of the model has been studied widely by several researchers (Garcia et al. 1997; Goswami et al. 1998; Asano et al. (2015); Gritli et al. 2012; Gan et al. 2014; Wang et al. 2015). Moreover, several control strategies have been applied to get a desired motion from the bipedal walkers. The control parameter is usually the torque at the joints (Khosravi et al. 1987) and is identified by different control algorithms and techniques. Linear control, based on linearization of the equations of motion around the vertical stance (Garcia et al. 2002), variable structure control (Li and Ge 2013), optimal control (Liu et al. 2013), and shaping discrete event dynamics (Piiroinen and Dankowicz 2002) are the main techniques that have been applied to biped robots by investigators.

The basic idea in controlling biped walking robots is choosing a proper control input in order to get a desired behavior. Another common desired feature for bipedal walking with chaotic behavior is a stable periodic motion. Using chaos control techniques, this desired behavior can be extracted from the nature of the chaotic system through detection of UPOs embedded in the chaotic attractor (Abedini et al. 2012). Since the desired trajectory is already included in the dynamics of the system, the resulting behavior would be more natural and the system can be stabilized with less control effort.

Although there is an acceptable amount of research on controlling bipedal walkers with chaotic behavior, there are still few works on stabilization of UPOs of the system via applying chaos control algorithms. Chaos control with the aim of stabilization of UPOs has several major advantages due to dynamical properties of the system. Because of the ergodicity of the chaotic attractor, a trajectory eventually comes close to the neighborhood of a hyperbolic fixed point in the chaotic region, but never converges to the specific point (Baker and Gollub 1996). This enables us to drive the system to periodic orbits embedded in the chaotic attractor with small perturbations (Starrett and Tagg 1995; Ott 1990; Shirazi and Ghafari 2003; Danca et al. 2013; Pourtakdoust and Fazelzadeh 2003). Such a controller is more robust because the basin of attraction for chaotic region is bigger than the basin for a periodic orbit (Garcia et al. 1997). This has been shown via numerical study of the model (Garcia et al. 1997). A thorough investigation of the basin of attraction of the simplest walking model is given by Schwab and Wisse (2001). Moreover, the control strategy has more flexibility since there is an infinite set of UPOs within the chaotic attractor (Buhl and Kennel 2007) that enables us to generate various stable patterns by driving the system to any of these UPOs arbitrarily. In other words, using the already existed periodic orbits in the chaotic attractor as the desired trajectory would lead to such advantages.

In the literature, several works have been presented to stabilize UPOs of chaotic systems. However, for chaotic behavior of biped walking model, chaos control is not extensively treated and only few works are found (Gritli et al. 2015). One of the most famous chaos control algorithms is OGY method proposed by Ott et al. in 1998 based on the linearization of the Poincaré map near the fixed point in the chaotic attractor (Ott 1990). In Suzuki et al. (2005), the authors have applied OGY algorithm to a compass-like biped with masses on knees assuming the hip actuation torque as the controlling signal. The delayed feedback control method has been accomplished to parametric excitation walking to suppress bifurcation in a passive planar biped model with semicircular feet by Harata et al. (2012). Gritli et al. (2015) have suggested an OGY-based control method to stabilize UPOs of a chaotic semi-passive biped walking robot. This method is based on the linearization of the nonlinear model around a desired passive hybrid limit cycle, and according to the linearized model, they derive an analytical expression of a constrained controlled Poincaré map (Gritli et al. 2015). Kurz and Stergiou (2005) have proposed a biologically inspired ANN algorithm to rapidly drive the trajectories to a stable periodic orbit. Actually the neural network proposed in Kurz and Stergiou (2005) gives the proper spring stiffness for a single ramp incline and is said to be applied to the system after several steps. Nevertheless, the control parameter and therefore the desired trajectory are calculated regardless of the existing UPOs within the chaotic attractor. This is one of the main features of chaos control algorithm which was mentioned above and would have several advantages. This would lessen the control effort and make the controller flexible enough to get various behaviors from the system. The control parameter is not adjustable enough, and setting up a spring in the hip joint in the middle of walking seems not to be applicable. Furthermore, adding up the spring from the beginning actually changes the dynamics of the system and the chaotic characteristics of the model that have already been resulted through numerical manipulations. That is why a more commonly used parameter which is the torque applied at the hip is considered as the control parameter here.

In this investigation, firstly, the dynamic model of the system is introduced. Choosing a proper Poincaré section, the bifurcation diagram and a spectrum of the Lyapunov exponents are plotted. This preliminary analysis would show the chaotic behavior of the system and the region of chaotic attractor in the phase space, and then, UPOs of the chaotic system are achieved. After that, extending the Kurz’s algorithm (Kurz and Stergiou 2005), an ANN-based control structure is designed to stabilize the obtained UPOs of the chaotic biped walking model. Choosing the torque in the hip as the control actuator is thought to be more applicable and more similar to what occurs in human locomotion. The neural network is designed so that the controller can be turned on at any time during the locomotion. The parameters of the ANN are varied in order to see their effects on the performance of the walking biped. This would give design hints for an experimental set and the applicability of the proposed controller. Moreover, the robustness of the controller to possible perturbations is simulated by a toe-off impulse and the results are shown. To illustrate the performance and effectiveness of the proposed controller, the chaotic behavior of the biped walking model is also stabilized via the OGY method and the corresponding results are compared with those attained by the ANN-based controller.

The main contributions of this work can be stated as follows:

  1. 1.

    The unstable periodic orbits of different orders for the chaotic passive biped are detected

  2. 2.

    An ANN-based controller is designed to stabilize these orbits with actuation at hip joint.

  3. 3.

    The performance of the controller is compared with the famous OGY method (Ott 1990).

  4. 4.

    A parametric study of ANN is performed to provide insights in designing the controller.

The article is organized as follows: The dynamic model of the system is introduced in Sect. 2. In Sects. 3 and 4, chaotic behavior and UPO of the system are detected. A controller based on artificial neural networks is designed and utilized to control the biped from a chaotic behavior to a periodic motion in Sect. 5. The simulation results are illustrated in Sect. 6. Also, the OGY method is used to control the chaotic motion of the biped model in this section and a comparison between the performances of the ANN-based and OGY controllers is accomplished. Conclusions are given in the last section of this paper.

2 Chaotic Biped Walking Model

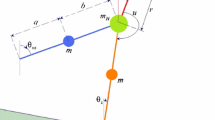
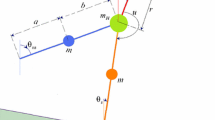
The simplest walking model shown in Fig. 1 is a biped robot with two rigid legs joints by a frictionless hinge at the hip. There is a point mass at the hip, M, and two point masses at the feet tips, m. The feet masses are much smaller than the hip so that the hip motion is not affected by the swinging leg motion. During each step, the stance leg acts as an inverted pendulum while the other leg oscillates until the heel contact. At this moment, the system has a plastic impact without any slip or bounce and passes a double-support phase instantaneously (Garcia et al. 1997).

Fig. 1
figure 1

Schematic of the walking model with a hip mass and two point masses at the feet tip (Garcia et al. 1997) (after the heel strike the stance leg and the swing leg switch)

Full size image

The legs are assumed to be able to pass the foot-scuff situation, and the swing leg is able to momentarily pass through the ramp surface when the stance leg is nearly vertical. These assumptions are made to avoid scuffing problems for straight-legged walkers.

The degrees of freedom are chosen to be \(\theta\) and \(\varphi\) that show the stance leg angle with the vertical direction to the ramp surface and the angle between stance and swing leg, respectively. The governing equation in the single-support phase is derived by the Lagrange method. Substituting the Lagrangian of the system in the Lagrange equations and applying the simplifying assumption \(\left( {\frac{m}{M} < < 1} \right)\), the dimensionless governing equations become

$$\begin{aligned} & \ddot{\theta } - \sin (\theta - \gamma ) = 0 \\ & \ddot{\theta } - \ddot{\varphi } + \dot{\theta }^{\,2} \sin \varphi - \cos (\theta - \gamma )\sin \varphi = 0 \\ \end{aligned}$$
(1)

in which the dimensionless time \(t^{\prime } = \sqrt {{\raise0.7ex\hbox{$l$} \!\mathord{\left/ {\vphantom {l g}}\right.\kern-0pt} \!\lower0.7ex\hbox{$g$}}} t\). Also, l and g indicate the length of each leg and the gravitational constant, respectively. During the single-support phase, the above equation governs the motion of the biped. When the swing leg contacts the surface, the following geometric condition is satisfied

$$\varphi \, - \,2\,\theta = \,0$$
(2)

The collision occurs, and solving differential Eq. (1) should be stopped. The conservation of angular momentum should be satisfied for the whole system about the new stance leg tip and for the new swing leg around the hip. Considering the toe-off impulse denoted by P, the transition rule (Kurz and Stergiou 2005) for heel strike moment is as follows:

$$\left[ {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \varphi \\ {\dot{\varphi }} \\ \end{array} } \right]^{ + } = \left[ {\begin{array}{*{20}c} { - 1} & 0 & 0 & 0 \\ 0 & {\cos 2\theta } & 0 & 0 \\ { - 2} & 0 & 0 & 0 \\ 0 & {\cos 2\theta (1 - \cos 2\theta )} & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} \theta \hfill \\ {\dot{\theta }} \hfill \\ \varphi \hfill \\ {\dot{\varphi }} \hfill \\ \end{array} } \right]^{\, - } + \left[ {\begin{array}{*{20}c} 0 \\ {\sin 2\theta } \\ 0 \\ {(1 - \cos 2\theta )\sin 2\theta } \\ \end{array} } \right]P$$
(3)

The states of the system just after and just before the impact are identified by ‘+’ and ‘−’ subscripts, respectively. The set of differential algebraic Eqs. (1)–(3) are the governing equations of the simplest walking model.

3 Detection of Chaos in Biped Walking Model

In order to have a better understanding of the nonlinear dynamics model, Poincaré section is used to monitor the variation in the states of the system stroboscopically. The Poincaré section reduces the dimensions of the system by one and helps to find out the main characteristics of the behavior of the system (Baker and Gollub 1996). The states of the biped would be recorded right after the heel strike (Eq. 2). Since there are special relations between the variables at this moment in which Eq. (3) is the governing equation of the motion, the Poincaré map of the system would be 2D.

$$\left[ {\begin{array}{*{20}l} \theta \hfill \\ {\dot{\theta }} \hfill \\ {\varphi = 2\theta } \hfill \\ {\dot{\varphi } = (1 - cos2\theta )\dot{\theta })} \hfill \\ \end{array} } \right] \Rightarrow \left[ {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \right]$$
(4)

The Poincaré map of the biped model can be stated as

$$z_{n + 1} = f\left( {z_{n} ,\gamma ,\tau } \right)$$
(5)

in which \(z_{n} = \left[ {\theta \dot{\theta }} \right]^{T}\) is the state of the system at nth step and \(\tau\) is the dimensionless torque, \(\tau = {T \mathord{\left/ {\vphantom {T {ml^{2} }}} \right. \kern-0pt} {ml^{2} }}\), in which T is the input torque and applied at hip joint during the step. The torque applied at the hip joint is to be varied at each intersection of the trajectory with Poincaré section, that is at the beginning of heel strike. Then, it will remain unchanged during the step till the next heel strike. A limit cycle trajectory on phase space which shows periodic behavior corresponds to a point. Numerous scattered points on a subspace of Poincaré section show chaotic behavior and are called chaotic attractor. It has been shown that there are infinite numbers of hyperbolic fixed points embedded in chaotic attractors. Hyperbolic fixed points correspond to UPOs in phase space, and the objective of chaos control is to stabilize these UPOs.

The behavior of the system depends on the initial conditions \(z_{0} = \left[ {\theta_{0} \dot{\theta }_{0} } \right]^{T}\) and the parameters \(\gamma\) and \(\tau\). To have a better understanding of this dependence, the bifurcation diagram of the model is drawn and shown in Fig. 2 in which \(\theta_{\text{st}}\) indicates the value of \(\theta\) at Poincaré section.

Fig. 2
figure 2

Bifurcation diagram of the system with respect to the ramp slope \(\gamma\)

Full size image

One of the most widespread methods for chaos prediction is calculation of Lyapunov exponent of the system. The procedure of this calculation can be seen in Sprott and Sprott (2003). According to this procedure (Sprott and Sprott 2003), the Lyapunov exponent spectrum of the biped is calculated according to Eq. (6) and shown in Fig. 3 versus slope angle \(\gamma\).

$$\lambda = \frac{1}{n}\ln \left( {\frac{{\left\| {f^{(n)} ({\mathbf{z}}_{{\mathbf{0}}} + {\varvec{\upvarepsilon}}) - f^{(n)} ({\mathbf{z}}_{{\mathbf{0}}} )} \right\|}}{{\left\| {\varvec{\upvarepsilon}} \right\|}}} \right)$$
(6)
Fig. 3
figure 3

Lyapunov exponent spectrum of the biped model with respect to the slope angle \(\gamma\)

Full size image

As known, a positive Lyapunov exponent is interpreted as a chaotic behavior while a negative one would show the absence of chaos (Sprott and Sprott 2003).

The obtained results from Lyapunov exponent are in acceptable competence with the bifurcation diagram.

4 Detection of Unstable Periodic Orbits

Based on attained data illustrated in Figs. 2 and 3, we can say that the passive biped walking model (\(\tau = 0\)) starts exhibiting chaotic behavior for \(\gamma\) > 0.0187 rad. Within this region, we can detect UPOs for which

$$z_{n}^{*} = f\left( {z_{n}^{*} ,\gamma ,\tau = 0} \right)$$
(7)

Detection of these points is not easy, obviously due to the hyperbolic (unstable) nature of these fixed points. There are various ways to detect these points. To this end, we used the iterative method proposed in Bu et al. (2004).

For the Poincaré map of (5), we have

$$z_{n + 1} = f\left( {z_{n} ,\gamma ,\tau } \right) + Q\left( {f\left( {z_{n} ,\gamma ,\tau } \right) - z_{n} } \right)$$
(8)

in which

$$Q = \left( {cI - J\left( {z_{n} } \right)} \right)\left( {f\left( {z_{n} ,\gamma ,\tau } \right) - z_{n} } \right)^{ - 1}$$
(9)

converges to the fixed point of the Poincaré map. J(z n ) is the Jacobian function which should be calculated numerically, \(- 1 < c < 1\) is a constant, and I is the identity matrix. The initial condition is chosen to be the fixed point found by the previous method. Setting this as the initial condition, the fixed point of the map for \(\gamma\) = 0.0187 rad and \(\tau = 0\) is found to be

$$z^{ * } = \left[ {\begin{array}{*{20}c} {\theta^{ * } } \\ {\dot{\theta }^{ * } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {0.25340} \\ { - 0.24530} \\ \end{array} } \right]$$
(10)

The detected UPO is of order 1; however, the same procedure can be used for detection of UPOs of higher orders, namely period-2 behavior by merely considering Poincaré map of corresponding order in (8).

The reason why we considered UPOs of different orders is to indicate the value of ‘chaos control’ approach in which many different step length combinations are readily available (Garcia et al. 1997) and can be stabilized to provide different behaviors.

5 Chaos Control of Biped Model based on Artificial Neural Networks

Artificial neural networks (ANN) can be used to control chaos in biped motion using the data from Poincaré map and the detected unstable periodic orbit (UPO). Since the system is nonlinear and discontinuous, there is no analytic formulation of Poincaré map or its inverse. The idea is to force the trajectory to follow the stable manifold of the hyperbolic fixed point by applying necessary torque, \(\tau\), at the hip.

The neural network would get the value of \(z = \begin{bmatrix}\theta & \dot{\theta } \end{bmatrix}^{T}\) in the current step and the desired one, \(z^{*} = \begin{bmatrix}\theta^{*} & \dot{\theta}^{*} \end{bmatrix}^{T}\), in the next step as inputs and the hip torque \(\tau\) as the output. So, basically the network has 4 inputs and one output. The number of input neurons can be increased as will be discussed in the next subsection.

The network is trained using a set of data gathered from Poincaré map of the system in chaotic state. For each set of input target, initial conditions are chosen from within the basin of attraction of the chaotic attractor. This would be the first pair of input values. A random amount of torque is applied to the hip, and the z value at the next step would be the second pair of input values. The applied torque is the target value.

The trained network will be used to control the chaotic motion by getting the current state of the biped right after the heel strike, z, and the fixed point of the Poincaré map, z *, as inputs. The output would be the suggestion of the trained network for the necessary torque applied to the hip joint during the step so that the system converges to periodic behavior. However, the torque will not be applied unless the trajectory is close enough to the periodic orbit. That is the main idea behind the chaos control which is leading the system to the unstable periodic orbit with the least control effort. Moreover, the applied torque should not exceed a maximum limit. Then, the applied toque is determined as

$$\tau = \left\{ {\begin{array}{*{20}l} {\tau_{\text{net}} ,\quad } \hfill & {{\text{if}}\quad \left\| {z_{n} - z^{*} } \right\| < \eta \quad {\text{and}}\quad \left| {\tau_{\text{net}} } \right| \le \tau_{\hbox{max} } } \hfill \\ {\text{sgn} \left( {\tau_{\text{net}} } \right)\tau_{\hbox{max} } ,} \hfill & {{\text{if}}\quad \left\| {z_{n} - z^{*} } \right\| < \eta \quad {\text{and}}\quad \left| {\tau_{\text{net}} } \right| > \tau_{\hbox{max} } } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(11)

in which \(\tau_{\text{net}}\) is the network output, \(\tau_{\hbox{max} }\) is the maximum torque. The critical distance between the trajectory and UPO inside which the actuation is applied is denoted by \(\eta\). The state of the system at Poincaré section is denoted by \(z_{n}\) and the corresponding UPO by z *.

5.1 Effect of ANN Parameters on Biped Performance

An understanding of how the ANN parameters affect the performance of the controller is necessary if we want to extend the model or possibly apply the results for an experimental set. Some of these parameters are chosen and changed to see their effects on biped performance. To evaluate the biped performance, three different parameters are considered. These parameters are maximum slope angle, dimensionless response time, and maximum disturbance level.

  1. (a)

    Maximum Slope Angle (\(\gamma_{\hbox{max} }\))

The simulation results show that the biped would have no stable walking for slope angle \(\gamma\) > 0.0187 rad. So, the maximum slope angle on which the biped can continue walking can be considered as one of the performance parameters.

Furthermore, the approximate percent relative error \(\varepsilon_{a}^{\gamma }\) is defined between the maximum slope angles of the controlled and the uncontrolled systems as \(\varepsilon_{a}^{\gamma } = \left| {{{(\gamma^{\hbox{max} } - 0.0187)} \mathord{\left/ {\vphantom {{(\gamma^{\hbox{max} } - 0.0187)} {0.0187}}} \right. \kern-0pt} {0.0187}}} \right| \times 100\) and determined for various cases. The maximum slope angle of the controlled system is indicated by \(\gamma^{\hbox{max} }\), and that of the uncontrolled system is considered as \(\gamma\) = 0.0187 rad.

  1. (b)

    Dimensionless Response Time (\(t_{\text{res}}^{\prime }\))

When the controller starts working, it takes some time for the biped to transmit from chaotic state to a periodic situation. Since the state of the system is viewed only after heel strikes and the amount of torque is unchanged for the whole step, it takes several steps for the controller to stabilize a periodic orbit. The dimensionless response time which can be defined as the number of steps or the amount of time before the motion becomes periodic is considered to be another performance parameter.

  1. (c)

    Maximum Disturbance Level (\(P_{\hbox{max} }\))

Chaos controllers are claimed to be robust due to stability of chaotic attractors. To evaluate the maximum disturbance level that the controlled biped can tolerate, a toe-off impulse, denoted by P in Eq. (3), is applied to the biped after it is led to a periodic motion. The maximum value of P that biped can withstand without falling over is considered to be another performance parameter.

The ANN parameters for which the performance of biped is evaluated are stated in the following. These ANN parameters are chosen as transfer function, number of input neurons, number of neurons in hidden layer, number of hidden layers, training method. For investigating the effect of each parameter, the biped performance results are listed for comparison. Except for the results of maximum slope angle, the simulations are done for slope angle of \(\gamma\) = 0.0187 rad.

5.1.1 Effect of Transfer Function

The effect of transfer function is investigated by choosing three different functions for hidden layer. The definition of these functions is stated in Table 1. In this paper, we simply refer to hyperbolic sigmoid function as sigmoid function.

Table 1 Transfer functions used for evaluation of biped performance (Hagan et al. 2002)
Full size table

The number of neurons in hidden layer is four, and there are also four inputs. The results are listed in Table 2.

Table 2 Effect of the hidden layer transfer function on the performance of the controlled biped
Full size table

5.1.2 Number of Input Neurons

According to Hausdorff et al. (2000), human locomotion has a neural memory of past locomotive states. Inspired by that, Kurz and Stergiou (2005) suggested that the states of previous steps are the input values to the neural network. The control parameter we have considered, \(\tau\), can change in every step, unlike the case of Kurz and Stergiou (2005) in which the stiffness of the spring added at the hip joint is unchanged for the whole walk. Therefore, in order to consider the information of previous steps, the states and also the torques applied in each step are considered to be the inputs for the network.

Considering N last steps of the biped walk, there would be 3N + 1 input neurons, including 2N state values of the current and previous steps, two state values of the next (desired) step value, and N − 1 torque values that led the biped to this position. The schematic of the network is shown in Fig. 4.

Fig. 4
figure 4

Schematic of the artificial neural network using the data from last N steps of the biped

Full size image

Training of the network for each case is similar to the one explained in Sect. 5 except that the data should be gathered for N + 1 successive steps along with the random torque applied at each step. The torque applied for transition between the last two steps is the target value. The network for each value of N = 1, 2, …, 7 was trained, and the performance parameters were evaluated. A hidden layer with 6 neurons is considered. The transition function is chosen to be sigmoid for hidden layer and linear for the output layer. The maximum slope angle, \(\gamma_{\hbox{max} }\), the dimensionless response time, \(t_{\text{res}}^{\prime }\), the relative step number, and the maximum disturbance level, P max, are shown according to N in Table 3. The data for N last steps of the biped are the input values for 3N + 1 input neurons. For the values N > 5, the controller was unable to control chaos for \(\gamma\) = 0.0187 rad.

Table 3 Effect of no. of neurons in the first layers on the performance of controlled biped
Full size table

5.1.3 Number of Neurons in Hidden Layer

The number of neurons in the hidden layer seems to have an important effect on neural network function fitting. We have changed this parameter to see its effect on the chaos controller performance. The results are for the case of N = 1 which means there are four inputs, one hidden layer with sigmoid transfer function, and the output layer with one neuron and linear transfer function (Table 4).

Table 4 Effect of no. of neurons in the hidden layer N hid on the performance of controlled biped
Full size table

5.1.4 Number of Hidden Layers

The number of hidden layers is increased to see whether they affect the biped performance. To see the effect of each parameter, other parameters remained constant. For this case, the number of neurons in hidden layer(s) is 4, with sigmoid transfer function. The results are listed in Table 5.

Table 5 Effect of no. of hidden layer L hid on the performance of controlled biped
Full size table

5.1.5 Training Method

There are several commonly used training methods in backpropagation algorithm (Hagan et al. 2002). The size of data set for training the network is 100, and other parameters are like those mentioned in the part of transfer function effect. The biped performance according to each of these methods is shown in Table 6. The methods are referred to as’trainlm (Levenberg–Marquardt backpropagation), ‘trainbfg’ (BFGS quasi-Newton backpropagation), ‘trainscg’ (scaled conjugate gradient backpropagation) and ‘traincgp’ (conjugate gradient backpropagation) (Hagan et al. 2002).

Table 6 Effect of training method on the performance of controlled biped
Full size table

5.2 Discussion on ANN Parameters Effects

There are parameters other than the ones considered here that can affect the results shown in Tables 3, 4, 5, and 6 such as the initial conditions for biped motion and initially selected weights and biases. But these results can give quite useful guidelines and intuitions for designing ANN chaos controller. The results show that:

  1. 1.

    Increasing the number of input neurons does not necessarily improve the performance of the biped. This number effectively plays the role of memory of the controller.

  2. 2.

    It is shown that increasing the number of hidden layers to two improves the performance parameters, but it will have a negative effect if it becomes more.

  3. 3.

    Changing the transfer functions would have dramatic effects on the performance. The network controller with hard limit function returns the same amount of hip torque for any input value, but can still control the chaotic motion. The sigmoid function in the hidden layer seems to be the best choice as suggested by many authors (Hagan et al. 2002).

  4. 4.

    The training methods used in the backpropagation algorithm also have significant effects on the performance parameters. The best choice seems to be the commonly used Levenberg–Marquardt backpropagation method.

  5. 5.

    The performance parameters do not vary with the same trend. The response time and maximum disturbance level have better correlation in variation and are more sensitive to ANN parameter compared to maximum slope angle.

  6. 6.

    An optimum set of parameters for the network can be suggested from these results which are: a network with four inputs, two hidden layers with four neurons and sigmoid transfer function and an output layer with one neuron and linear transfer function. The training method for backpropagation is suggested to be Levenberg–Marquardt.

6 Simulation Results

The variations of biped state and the applied torque according to the footsteps are shown for some ANN parameters in Figs. 5, 6, and 7. To show the disturbance tolerance of the chaos controller, a toe-off impulse is applied at the 80th step after the biped has already been controlled so as to have periodic motion. The simulations are done for \(\gamma\) = 0.0187 rad, \(\tau_{\hbox{max} }\) = 0.02 s−2, and \(\eta\) = 0.01.

Fig. 5
figure 5

Variation of \(\theta\) value and the hip torque \(\tau\) value generated by a network with N = 7 and hard limit transfer function

Full size image
Fig. 6
figure 6

Variation of \(\theta\) value and the hip torque \(\tau\) value generated by a network with N = 1 and sigmoid transfer function in a hidden layer with 10 neurons

Full size image
Fig. 7
figure 7

Variation of \(\theta\) value and the hip torque \(\tau\) value generated by a network with N = 1 and sigmoid transfer function in a hidden layer with 4 neurons trained with Levenberg–Marquardt backpropagation method

Full size image

As shown in these figures, the proposed ANN-based controller is able to stabilize the chaotic behavior of the biped model to its UPO.

6.1 Chaos Control of Biped Model based on the OGY Method

To show the superiority of the proposed ANN-based controller, the OGY method as a conventional chaos control technique is selected to control the chaotic behavior of the biped model. The formulation of the OGY controller is based on the following two key ideas: (1) designing controller by the discrete system model based on linearization of the Poincaré map and (2) applying the control action only at the instants when the trajectory returns to some neighborhood of the desired state or given orbit (Ott 1990).

Consider that the discrete dynamical system or the Poincaré map of a continuous system is expressed by

$$z_{\,n\, + \,1} = \,f\,(z_{\,n} \,,\,p)$$
(12)

where z n is introduced in Eq. (5) and p is the accessible parameter of the system that can be changed in the neighborhood of p *. p * is the value of the accessible parameter p corresponding to the UPO or its intersection with the section indicated by z* as the hyperbolic fixed point. The map (11) can be linearized in the neighborhood of this orbit by Ott (1990)

$$z_{n + 1} - z^{*} = J(z_{n} - z^{*} ) + g(p_{n} - p^{\,*} )$$
(13)

in which

$$\begin{aligned} J & = \left. {\frac{\partial f(z,p)}{\partial z}} \right|_{{\,(z^{*} ,p^{\,*} )}} \\ g & = \left. {\frac{\partial f(z,p)}{\partial p}} \right|_{{\,(z^{*} ,p^{\,*} )}} \\ \end{aligned}$$
(14)

J is the Jacobian of the system at the fixed point and g shows the differentiation of the function with respect to parameter p at the same point. The values of J and g can be calculated either by numerical differentiation or by linearization methods like the one described in detection of periodic orbits.

Let \(\lambda_{\text{s}}\) and \(\lambda_{\text{u}}\) be the stable and unstable eigenvalues of the map (\(\left| {\lambda_{\text{u}} } \right| > 1 > \left| {\lambda_{\text{s}} } \right|\)), and the eigenvectors \(e_{\text{s}}\) and \(e_{\text{u}}\) show the stable and unstable directions along which the trajectories are attracted to and repelled from the fixed point. Then, the contra variant vectors \(f_{\text{s}}\) and \(f_{\text{u}}\) can be defined such that (Ott 1990)

$$\begin{aligned} f_{u} .e_{u} & = f_{s} .e_{s} = 1 \\ f_{u} .e_{s} & = f_{s} .e_{u} = 0 \\ \end{aligned}$$
(15)

Based on the OGY method, as soon as the trajectory gets close enough to the fixed point, so that \(0 < \left\| {z_{\,n} - z^{*} } \right\| < h\), the parameter p is varied so that the trajectory will be located on the stable manifold of the fixed point in the next step which means

$$f_{u}^{T} (z_{n + 1} - z^{*} ) = f_{u}^{T} (J(z_{n\,} - z^{*} ) + g(p_{n} - p^{*} )) = 0$$
(16)

and the control law would be (Ott 1990)

$$\left\{ {\begin{array}{*{20}l} {p_{n} = p^{*} - \frac{{f_{u}^{T} J(z_{n} - z^{*} )}}{{f_{u}^{T} g}}\quad } \hfill & {{\text{if}}\quad 0 < \left\| {z_{n} - z^{*} } \right\| < h} \hfill \\ {p_{n} = 0\quad } \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(17)

Using the UPO detected and attained in Sect. 4, the Poincaré map is linearized in the neighborhood of the point for \(\gamma = 0.0187\) and \(\tau = 0\) as

$$z_{n + 1} - z^{*} = \left[ {\begin{array}{*{20}c} { - 7.2383} & { - 8.4847} \\ {5.01633} & {6.16318} \\ \end{array} } \right](z_{n} - z^{*} ) + \left[ {\begin{array}{*{20}c} { - 0.2642} \\ {0.07397} \\ \end{array} } \right]\tau$$
(18)

Applying the control law (16), the chaotic system would be controlled on the detected periodic orbit and the biped continues a periodic motion with repeated steps as shown in Fig. 8.

Fig. 8
figure 8

Variation of \(\theta\) value and the hip torque \(\tau\) value attained from the implementation of the OGY controller

Full size image

It should be noted that the footfall and the step number mentioned as the x-labels in Figs. 5, 6, 7 and 8, respectively, are identical. Comparing the results obtained by the proposed ANN-based controller and the OGY method, it can be said that the control effort needed by the OGY controller is more than that attained by the neural network controller for stabilizing the same periodic orbit. OGY method is a theoretically more reliable method for controlling chaos, but it requires a rather accurate detection of periodic orbit and linearization of Poincaré map to give good results. On the other hand, there is no analytical tool to investigate the stability of neural network controller and it depends on network’s parameters. But the neural network controller is shown to be more flexible in getting various behaviors from the system and robust to possible perturbations which were not seen by the OGY controller applied to the biped model.

7 Conclusions

Chaos detection and chaos control of a biped walking model have been investigated in this study. The unstable periodic orbits within the chaotic attractor have been detected. Based on artificial neural networks, a chaos control scheme has been proposed to stabilize the achieved UPO of the chaotic system. The control input has been considered as the torque applied at the hip. The effects of changing ANN parameters on the biped performance have been studied through numerical results. The results can be used to design an optimum ANN chaos controller. Investigating the effects of various ANN parameters showed that the transfer function and the training methods have significant effects on the biped performance. The number of neurons and layers did not seem to have exact correlation with the performance, but some suggestions for optimum values could be extracted from the numerical results. Furthermore, to control the chaotic behavior of the biped model, the OGY method has been also utilized and the obtained results are compared with those attained from the ANN-based controller. The simulation results illustrated that the proposed ANN-based controller is flexible and robust to a noise like toe-off impulses at heel strikes.