1 Introduction

Traffic congestion produces significantly negative effect on urban residents’ daily lives, such as increased travel time, more energy consumption, excessive air pollution, etc. The traditional method of alleviating traffic congestion is to increase road supply. However, this method doesn’t always work due to either limited budget or space. Traffic control is an effective method to relieve congestion. It optimizes the temporal and spatial distribution of traffic flow by regulating the green ratios of intersections in the network. To this end, it is essential to understand the formation mechanism of traffic congestion. Phase diagram is a powerful method to investigate the intrinsic evolution mechanism. Numerous traffic models have been developed to reveal the intrinsic features of various instability diagrams observed in real traffic. It would be favorable to take effective control strategy to maximize the network efficiency if the traffic dynamics could be understood by studying the phase transition.

Phase transitions under various congested traffic had been investigated (see, for instance, [1–16]). In these studies, two kinds of models are applied, that is, macroscopic models [1–11] and microscopic models [12–16]. In these models, almost all the observed spatio-temporal traffic patterns have been reproduced by varying the inflow of upstream freeway and the bottleneck strength (e.g., on-ramp). The empirical traffic patterns include the moving local clusters (MLC), the stop-and go waves (SG), the oscillating congested traffic (OCT), widening synchronized pattern (WSP), pinned localized cluster (PLC), homogeneous congested traffic (HCT), etc.

Until now, studies mainly focused on the phase transitions of traffic flow nearby the on-ramp. Traffic phase transitions under open system are seldom investigated except for cellular automaton models. Under the open boundary condition, Nagatani [17] performed a numerical study on the transitions of traffic states and density waves by fluctuating a leading car. Tian et al [18] demonstrated that the single-lane lattice model could reproduce rich congested traffic patterns. However, most of the road networks are made up of two-lane or multi-lane. To our knowledge, it is unknown whether the empirical observations could be reproduced in two-lane density difference lattice hydrodynamic model under open boundary condition. Therefore, it is necessary to study the traffic states in the two-lane lattice model to test the validity of lattice model.

The remaining context is organized as follows. The two-lane density difference lattice hydrodynamic model and its linear stability condition are given in Sect. 2. Applying the nonlinear method, the KdV equation is deduced in Sect. 3. Numerical simulations are conducted in Sect. 4. Firstly, we simulate the soliton wave under period condition. Then, under the open boundary condition, we present the phase diagram including different kinds of traffic congestion states. Finally, we reproduce the spatial and time evolution of various congested traffic state in detail. Section 5 concludes the whole study.

2 Extended lattice hydrodynamic model for two-lane traffic

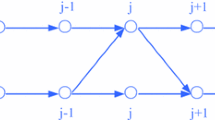
The lattice hydrodynamic model was firstly proposed by Nagatani [19, 20]. Based on the intelligent transportation system, the lattice model has been extended by considering various influence factors [21–33]. Nagatani [34] further gave the two-lane lattice hydrodynamical model. Figure 1 exhibits the schematic diagram of the traffic flow on a two-lane highway. If density at the \(j-1\)th site of the second lane is higher than that at the \(j\)th site of the first lane, then lane changing occurs from the second lane to the first lane with the rate \(\gamma \big |\rho _0^2V'(\rho _0)\big |(\rho _{2,j-1}(t)-\rho _{1,j}(t))\), where \(\gamma \) is a fixed dimensionless coefficient, constant \(\left| \rho _0^2V'(\rho _0)\right| \) is introduced in order to be dimensionless, \(\rho _0\) is the average density, \(\rho _{1,j}\) and \(\rho _{2,j}\) are the densities on the first lane and second lane at site \(j\). Accordingly, the lane-change rate in the opposite case is \(\gamma \big |\rho _0^2V'(\rho _0)\big |(\rho _{1,j}(t)-\rho _{2,j+1}(t))\).

Fig. 1
figure 1

The schematic model of traffic flow on a two-lane highway

Full size image

The lattice hydrodynamic model for two-lane traffic is formulated by the following equation [34]. The continuity equation for the first lane is

$$\begin{aligned}&\partial _t\rho _{1,j}(t)+\rho _0(\rho _{1,j}(t)v_{1,j}(t)-\rho _{1,j-1}(t)v_{1,j-1}(t))\nonumber \\&\quad =\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{2,j+1}(t)-2\rho _{1,j}(t)+\rho _{2,j-1}(t)).\nonumber \\ \end{aligned}$$
(1)

Similarly, the continuity equation on the second lane is

$$\begin{aligned}&\partial _t\rho _{2,j}(t)+\rho _0(\rho _{2,j}(t)v_{2,j}(t)-\rho _{2,j-1}(t)v_{2,j-1}(t))\nonumber \\&\quad =\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{1,j+1}(t)-2\rho _{2,j}(t)+\rho _{1,j-1}(t)),\nonumber \\ \end{aligned}$$
(2)

where \(\rho \) and \(v\) are the local velocity, respectively. To simplify the expression, time \(t\) will be omitted hereafter.

Then, the continuity equation Eq. (3) for two-lane traffic is obtained by adding Eq. (1) and Eq. (2) together

$$\begin{aligned}&\partial _t\rho _{j}+\rho _0(\rho _{j}v_{j}-\rho _{j-1}v_{j-1})\nonumber \\&\quad =\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{j+1} -2\rho _{j}+\rho _{j-1}), \end{aligned}$$
(3)

where \(\rho _j=\frac{\rho _{1,j}+\rho _{2,j}}{2}, \rho _jv_j=\frac{\rho _{1,j}v_{1,j}+\rho _{2,j}v_{2,j}}{2}\), and \(V_e(\rho _j)=\frac{V(\rho _{1,j})+V(\rho _{2,j})}{2}\).

Assume the evolution equation of traffic is immune to lane-change, the evolution equation for two-lane traffic is obtained.

$$\begin{aligned} \partial _t(\rho _j v_j)=a\rho _0V_e(\rho _{j+1})-a\rho _j v_j. \end{aligned}$$
(4)

Due to the significant role of density difference plays on the traffic stability, we suggest taking the density difference into Nagatani’s two-lane lattice hydrodynamic model. Mathematically, the corresponding density difference model is described below.

$$\begin{aligned}&\partial _t\rho _{j}+\rho _0(\rho _{j}v_{j}-\rho _{j-1}v_{j-1})\nonumber \\&\quad =\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{j+1} -2\rho _{j}+\rho _{j-1}) \ \mathrm and \end{aligned}$$
(5)
$$\begin{aligned}&\partial _t(\rho _j v_j)=a\rho _0V_e(\rho _{j+1})-a\rho _j v_j\nonumber \\&\qquad +\,\lambda (\rho _{j}-\rho _{j+1})/\rho _0, \end{aligned}$$
(6)

where \(\lambda \) is the react coefficient of density difference between the leading and the following lattice.

By eliminating velocity \(v\) in Eqs. (5) and (6), we get the following density equation

$$\begin{aligned}&\partial ^2_t\rho _j+a\rho _0^2(V_e(\rho _{j+1})-V_e(\rho _j))\nonumber \\&\quad -\,a\gamma \left| \rho _0^2V'(\rho _0)\right| (\rho _{j+1}-2\rho _{j}+\rho _{j-1})\nonumber \\&\quad +\, a\partial _t\rho _j-\lambda (\rho _{j+1}-2\rho _j+\rho _{j-1})\nonumber \\&\quad -\,\gamma \left| \rho _0^2V'(\rho _0)\right| (\partial _t\rho _{j+1}-2\partial _t\rho _j+\partial _t\rho _{j-1})=0.\nonumber \\ \end{aligned}$$
(7)

In Eq. (7), the optimal velocity function is given by

$$\begin{aligned} V_e(\rho )\!=\!\frac{v_{max}}{2}\tanh \left( \frac{2}{\rho _0}\!-\!\frac{\rho }{\rho _0^2}\!-\!\frac{1}{\rho _c}\right) \!+\!\tanh \left( \frac{1}{\rho _c}\right) ,\nonumber \\ \end{aligned}$$
(8)

where \(v_{max}\) is the maximal velocity. It can be concluded that \(V_e(\rho )\) is the optimal velocity function which decreases monotonically, bounds upper and inflects the point at \(\rho =\rho _c\) when \(\rho _0=\rho _c\). For convenience, we will simplify \(V_e(\rho )\) as \(V(\rho )\) hereafter.

As verified in [27], the uniform traffic flow is stable, if the following condition holds

$$\begin{aligned} a>-\frac{2\rho _0^2V'(\rho _0)}{1+2\gamma }+\frac{1}{\rho _0^2V'(\rho _0)}\frac{2\lambda }{1+2\gamma }. \end{aligned}$$
(9)

When \(\lambda =0\), the stable condition of Nagatani’s two-lane model is obtained:

$$\begin{aligned} a>-\frac{2\rho _0^2V'(\rho _0)}{1+2\gamma }. \end{aligned}$$
(10)

3 Nonlinear stability analysis

We apply the reductive perturbation method to obtain the KdV equation. By introducing slow scales for space variable \(n\) and time variable \(t\), we define the slow variables \(X\) and \(T\) for \(0<\varepsilon \ll 1\) below.

$$\begin{aligned} X =\varepsilon (j + bt), \quad T =\varepsilon ^3t. \end{aligned}$$
(11)

Set the density \(\rho _j(t)\) as

$$\begin{aligned} \rho _j(t)=\rho _c+\varepsilon ^2 R(X,T), \end{aligned}$$
(12)

substituting Eqs. (11) and (12) into Eq (7) and making the Taylor expansions to the sixth order of \(\varepsilon \), we obtain the following expression:

$$\begin{aligned}&\varepsilon ^3[ab+am]\partial _XR+\varepsilon ^4\left[ b^2+\frac{1}{2}am+\gamma am-\lambda \right] \partial ^2_XR\nonumber \\&\quad +\,\varepsilon ^5\left[ a\partial _TR+\left( \frac{1}{6}am+\gamma mb\right) \partial ^3_XR+\frac{1}{2}as\partial _XR^2\right] \nonumber \\&\quad +\,\varepsilon ^6\left( 2b\partial _X\partial _TR+\left( \frac{1}{24}am+\frac{1}{12}\gamma am-\frac{1}{12}\lambda \right) \partial ^4_XR\right. \nonumber \\&\quad \left. +\,\frac{1}{4}as\partial ^2_XR^2\right) =0, \end{aligned}$$
(13)

where \(m=\rho ^2_0V', n=\rho ^2_0V''', s=\rho ^2_0V''\). For simplicity, we rewrite Eq. (13) as the following version

$$\begin{aligned}&\varepsilon ^3f_1\partial _XR\!+\!\varepsilon ^4f_2\partial ^2_XR\!+\!\varepsilon ^5(\partial _TR\!+\!f_3\partial ^3_XR+f_4R\partial _XR) \nonumber \\&\quad +\, \varepsilon ^6(f_5\partial _X\partial _TR\!+\!f_6\partial ^4_XR\!+\!f_7\partial ^2_XR^2)\!=\!0, \end{aligned}$$
(14)

where \(f_i (i=1,2,\cdots , 7)\) are the coefficients (see Table 1 for detail formulations).

Table 1 The formulations of coefficient \(f_i\ (i=1,2,\cdots , 7)\)
Full size table

By eliminating the third- and fourth-order terms of \(\varepsilon \) from Eq. (12), we obtain the simplified equation:

$$\begin{aligned}&\varepsilon ^5[\partial _TR+g_1\partial ^3_XR+g_2\partial _XR^2]\nonumber \\&\quad +\, \varepsilon ^6[g_3\partial ^2_XR+g_4\partial ^4_XR+g_5\partial ^2_XR^2]=0. \end{aligned}$$
(15)

The coefficients \(g_i\) are listed in Table 2.

$$\begin{aligned}&\varepsilon ^5\left[ \partial _TR+\left( \frac{1}{6}m+\frac{\gamma mb}{a}\right) \partial ^3_XR+\frac{1}{2}s\partial _XR^2\right] \nonumber \\&\quad +\,\varepsilon ^6\left[ \frac{1}{2}b(1+2\gamma )\partial ^2_XR+\left( \frac{1}{24}m+\frac{1}{12}\gamma m-\frac{\lambda }{12a}\right. \right. \nonumber \\&\quad \left. \left. -\,\frac{bm}{3a}-\frac{2}{a^2}\gamma mb^2\right) \partial ^4_XR+\left( \frac{s}{4}-\frac{bs}{a}\right) \partial ^2_XR^2\right] =0.\nonumber \\ \end{aligned}$$
(16)

In order to obtain the standard KdV equation, we make the following transformation \(T=\sqrt{g_1}T', X=\sqrt{g_1}X', R=\frac{1}{g_2}R'\). Then, we obtain the regularized KdV equation with correction term \(O(\varepsilon )\) on the right-hand side of Eq. (16)

$$\begin{aligned} \partial _{T'}R'+\partial ^3_{X'}R'+\partial _{X'}R'+\varepsilon M[R']=0, \end{aligned}$$
(17)

where \(M[R']=(\frac{g_3}{\sqrt{g_1}}\partial ^2{X'}R'+\frac{g_4}{{g_1}^{3/2}}\partial ^4_{X'}R'+\frac{g_5}{g_2\sqrt{g_1}}\partial ^2_{X'}R'^2)\). Ignoring the \(O(\varepsilon )\) terms in Eq. (17), we get the KdV equation with the soliton solution

$$\begin{aligned} R'_0(X',T')=Asech^2\left[ \sqrt{\frac{A}{12}(X'-\frac{A}{3}T')}\right] , \end{aligned}$$
(18)

where \(A\) is the amplitude of soliton solutions of the KdV equation. Supposing \(R'(X',T')=R'_0(X',T')+\varepsilon R'_1(X',T')\), in order to determine \(A\), it is necessary to consider the solvability condition.

$$\begin{aligned} (R'_0,M[R'_0])\equiv \int \limits ^{+\infty }_{-\infty }dXR'_0M[R'_0]=0, \end{aligned}$$
(19)

with \(M[R'_0]=M[R']\). Then, we get \(A\) through integral operation

$$\begin{aligned} A=\frac{21g_1g_2g_3}{24g_1g_5-5g_2g_4}. \end{aligned}$$
(20)
Table 2 The formulations of coefficient \(g_i\ (i=1,2,\cdots , 5)\).
Full size table

4 Numerical simulation

In this section, we use the difference form obtained from Eq. (7) to conduct numerical simulation.

$$\begin{aligned} \rho _j(t+2\tau )&= 2\rho _j(t+\tau )-\rho _j(t)\nonumber \\&-\,a\tau ^2\gamma \rho _0^2V'(\rho _0)(\rho _{j+1}(t)-2\rho _j(t)\nonumber \\&+\,\rho _{j-1}(t))-a\tau (\rho _j(t+\tau )-\rho _{j}(t))\nonumber \\&+\,\lambda \tau ^2(\rho _{j+1}(t)-2\rho _j(t)+\rho _{j-1}(t))\nonumber \\&-\,\tau \gamma \rho _0^2V'(\rho _0)(\rho _{j+1}(t+\tau )-\rho _{j+1}(t)\nonumber \\&-\,2\rho _{j}(t+\tau )+2\rho _{j}+rho_{j-1}(t+\tau )\nonumber \\&-\,\rho _{j-1}(t))-a\tau ^2\rho _0^2(V(\rho _{j+1}(t))\nonumber \\&-\,V(\rho _{j}(t))). \end{aligned}$$
(21)

4.1 Soliton simulations in metastable region

Under the condition of periodical boundary, the initial conditions of the numerical simulation are set as follows: the lattice number \(N=100\), and the density is assumed to be a piece-wise function at the average density.

$$\begin{aligned}&\rho _j(0)=\rho _0,\ \ j\in [1,N],\end{aligned}$$
(22)
$$\begin{aligned}&\rho _j(1)=\left\{ \begin{array}{r@{\quad }l} \rho _0: &{} j\in [1,N], j\ne n_1, j\ne n_2 \\ \rho _0+\Delta \rho : &{}j=n_1\\ \rho _0-\Delta \rho : &{} j=n_2\end{array}\right. , \end{aligned}$$
(23)

where \(n_1=49, n_2=50, \Delta \rho \) is the initial disturbance. \(v_{max}=2, \rho _0=0.2, \Delta \rho =0.02, a=1.05, \gamma =0.1, \lambda =0.1, \tau =0.05\). We conduct a numerical simulation for the traffic to generate the soliton wave in metastable region. The soliton solution derived from the KdV equation is different from the kink solution derived from mKdV equation. When the selected perturbation \(\Delta \rho =0.02\) is added to the uniform traffic system, the typical soliton density wave is observed in Fig. 2. The soliton waves propagate backward with constant velocity. This is consistent with the nonlinear analysis result. Figure 2b is the density profile corresponding to Fig. 2a.

Fig. 2
figure 2

Schematic phase diagrams for the expected traffic patterns as a function of the upstream traffic density \(\rho _{up}\) and the downstream boundary perturbation \(\rho _{down}\).

Full size image

4.2 Phase diagram of two-lane hydrodynamic traffic flow model

In the case of open boundary, we investigate the traffic behavior described in Eqs. (5) and (6). We consider a two-lane section road with one entrance and one exit. The whole road is composed of \(N\) lattices, and the lattice \(N\) locates at the downstream exit. The density of lattice \(N\) fluctuates randomly. The system starts with a homogeneous traffic flow with density \(\rho _h\). The boundary condition can be described as:

$$\begin{aligned} \rho _0(t)=\rho _1(t),\ \ \ \rho _N(t)=\rho _f+\rho _f(2R(t)-1), \end{aligned}$$
(24)

where \(\rho _f\) is the density of lattice \(N, R(t)\) is the random number between 0 and 1. \(\rho _N(t)\) is the density of downstream boundary. The simulation parameters are \(a=0.5, v_{max}=2, \rho _0=0.25, \rho _c=0.25, \tau =0.1, \gamma =0.1, \lambda =0.2, N=400\).

We execute the simulation by varying the initial density \(\rho _h (\rho _{up})\) and the amplitude of \(\rho _f (\rho _{down})\). We derive the phase diagram in \((\rho _{up}, \rho _{down})\) space. As shown in Figure 2, the traffic state is not affected by the initial density \(\rho _h\). The emergences of MLC, TSG, OCT, and HCT traffic states only depend on the amplitude of the lattice \(N\). At first, the traffic is free flow before density \(\rho _f\) reaches 0.17. When \(\rho _f=0.17\), a single moving cluster (MLC) occurs. With the increase of density \(\rho _{up}\), the TSG, OCT, TSG and MLC traffic states appear one by one. After that, traffic flow achieves another stable state in high density region, i.e., the homogeneous congested traffic (HCT).

4.3 Phase transitions under open boundary condition with random fluctuations

In this section, we explore the spatial and temporal evolution of the traffic flow in detail. The upstream traffic density takes \(\rho _h=0.1\), the other parameters are the same as that in Sect. 4.2. Figure 3 (a–g) show the space–time evolution of density wave with \(\rho _f=0.16, 0.17, 0.18, 0.24, 0.36, 0.38\),  and  \(0.39\), respectively.

Fig. 3
figure 3

The solitary wave. a The spatiotemporal evolution after \(t=10,000\) s. b Density profile corresponding to (a) at \(t=10,000\) s

Full size image

As displayed in Fig. 4, when \(\rho _f\) is less than the critical value \(\rho _f=0.17\), traffic flow is stable, and the random disturbance of lattice \(N\) cannot trigger traffic congestion. As time proceeds, it is shown from Fig. 4a that the traffic is still free flow over the whole space except for the downstream boundary.

Fig. 4
figure 4

The spatiotemporal evolutions of density for the variation of \(\rho _f\). a The free traffic (FT). b The moving localized cluster of the compression wave. c, e The triggered stop and go traffic (TSG). d The oscillating congested traffic (OCT). f The moving localized cluster of the expansion wave (MLC). g The homogeneous congested traffic (HCT)

Full size image

When the density \(\rho _f\) reaches the critical value \(\rho _f=0.17\), the first phase transition between free flow and congested traffic appears. Then a single moving local cluster (MLC) of compression wave arises just after the first phase transition shown in Fig. 4b. The density wave is a compression wave and propagates backward, which corresponds to the moving localized clusters observed by Helbing. The transition of traffic state from MLC to TSG at \(\rho _f=0.18\). Compared with MLC, TSG (pattern (c)) has a series of block clusters moving upstream with free traffic between each other.

The number of density wave increases with respect to \(\rho _f\), and the traffic changes from the TSG state to OCT state. When \(\rho _f\) reaches a critical value \(\rho _f=0.24\), the number of density wave reaches the maximum value. Pattern (d) exhibits one of the OCT traffic state with the maximum number of density wave. After that, the number of density wave decreases gradually with \(\rho _f\) increases in further. The transition of traffic state occurs from OCT (see pattern (e)) to TSG at \(\rho _f=0.36\).

The pattern (f) shows the moving localized clusters (MLC) which occurs just before the transition from metastable traffic phase to stable traffic phase. This density wave is a single expansion wave and propagates backward. Pattern (f) is not a compression wave but an expansion wave, which distinguishes pattern (f) from pattern (b). After the state transition from congested traffic to stable traffic in high density regimes, i.e., \(\rho _f>0.38\), the traffic density is high and generally constant (about \(\rho =0.325\)) over space except for the neighborhood of the downstream boundary. According to the optimal velocity function Eq. (8), the corresponding velocity is very low (equals about to 0.166). This traffic state is the homogeneous congested traffic (HCT). Both the pattern (a) FT and pattern (g) HCT are stable, but HCT is different from FT since the vehicle speed is very low in HCT.

5 Conclusions

In this manuscript, we have derived the KdV equation from two-lane hydrodynamic traffic model. Using the reductive method, soliton solution near the neutral line is obtained from the KdV equation. Under periodic boundary condition, numerical simulations are conducted to verify the nonlinear theoretical result. It can be found that the simulation results are in good agreement with analytical results.

In further, we presented the phase diagram under open system through numerical simulation. The traffic states of MLC, TSG, OCT, and HCT are given in the phase diagram. From the phase diagram, we have found that the transitions of traffic states are not related with the upstream initial density but with the fluctuation of lattice \(N\).

Finally, we have reproduced the evolution of density profile of different kinds for different traffic states in detail. These simulation results show that the lattice hydrodynamic traffic flow could predict the appearance of traffic states and transitions between them.