1 Introduction

With the development of soliton theory, the study of optical solitons has been attractive and active, and great progress has been made in both experimental and theoretical investigations [1–19]. In recent years, soliton interactions are of particular interest because of their applications to nonlinear optics, plasma physics, multi-component Bose–Einstein condensates, and biophysics [20–24]. In the context of nonlinear optics, spatial soliton interactions are usually described by the coupled nonlinear Schrödinger (CNLS) equations [1, 25–29].

In the present study, we will examine spatial soliton interactions in the following CNLS equations [30, 31]:

$$\begin{aligned} \frac{\partial u}{\partial z}&= i\,\frac{\beta }{2}\frac{\partial ^{2} u}{\partial x^{2}}-i\,\frac{\Delta k}{2}u\nonumber \\&+\,\frac{1}{\beta }\Big (a_{1}|u|^{2}u+b_{1}|v|^{2}v+c_{1}v^{2}u^{*}\nonumber \\&+\,d_{1}u^{2}v^{*}+e_{1}|u|^{2}v+k_{1}|v|^{2}u\Big ),\end{aligned}$$
(1a)
$$\begin{aligned} \frac{\partial v}{\partial z}&= i\,\frac{\beta }{2}\frac{\partial ^{2} v}{\partial x^{2}}+i\,\frac{\Delta k}{2}v\nonumber \\&+\,\frac{1}{\beta }\Big (a_{2}|v|^{2}v+b_{2}|u|^{2}u+c_{2}u^{2}v^{*}\nonumber \\&+\,d_{2}v^{2}u^{*}+e_{2}|v|^{2}u+k_{2}|u|^{2}v\Big ), \end{aligned}$$
(1b)

where \(u(z,x)\) and \(v(z,x)\) are the envelopes of two orthogonally polarized modes. \(z\) and \(x\) denote the transverse and propagation coordinates, respectively. \(\beta =\frac{c}{w n_{2}^{L}[001]}\), and \(\Delta k\) represents the phase mismatch. \(a_{1}\) and \(a_{2}\) represent the self-phase modulation. \(k_{1}\) and \(k_{2}\) represent the cross-phase modulation. \(c_{1}\) and \(c_{2}\) represent the four-wave mixing. \(b_{1}\), \(b_{2}\), \(d_{1}\), \(d_{2}\), \(e_{1}\), and \(e_{2}\) occur only in anisotropic media and require phase matching. In particular, \(b_{1}\) and \(b_{2}\) contain only the fields orthogonal to the polarizations that are being considered and do in fact correspond to the generation of orthogonal components. In Ref. [30], stationary solutions for Eq. (1) have been identified. The effects of refractive anisotropy and induced birefringence on spatial soliton collisions in an AlGaAs slab waveguide have been studied numerically, and the interaction dynamics as a function of crystal orientation and for varying degrees of linear birefringence have been investigated [31].

However, to our knowledge, a systematic study on the coefficient constraints of \(a_{j}\), \(b_{j}\), \(c_{j}\), \(d_{j}\), \(e_{j}\), and \(k_{j}\,(j=1,2)\) has not been reported in the existing literatures. This paper will mainly focus on the following two points: First, the coefficient constraints of \(a_{j}\), \(b_{j}\), \(c_{j}\), \(d_{j}\), \(e_{j}\), and \(k_{j}\), which are the key points of this paper, will be obtained. Second, according to the different types of coefficient constraints of Eq. (1), soliton interactions will be classified as either elastic or inelastic. The conditions for elastic and inelastic interactions will be discussed. Numerical simulations will approximately reflect the analytic results and reveal the mechanisms for all-optical switching and soliton amplification.

The structure of the present paper will be as follows. In Sect. 2, with the aid of symbolic computation, the bilinear forms and analytic two-soliton solutions for Eq. (1) will be derived by use of the Hirota method, and the coefficient constraints of Eq. (1) will be obtained. In Sect. 3, asymptotic analysis will be made, discussion on the inelastic interactions will be performed, and numerical simulations will be demonstrated in order to verify the correctness of the analytic results. Finally, our conclusions will be given in Sect. 4.

2 Bilinear forms and soliton solutions for Eq. (1)

Firstly, we introduce the dependent variable transformations [32]

$$\begin{aligned} u(z,x)=\frac{g(z,x)}{f(z,x)}, \ \ v(z,x)=\frac{h(z,x)}{f(z,x)}, \end{aligned}$$
(2)

where \(g(z,x)\) and \(h(z,x)\) are the complex differentiable functions, and \(f(z,x)\) is a real one. After some symbolic manipulations, the bilinear forms for Eq. (1) can be obtained as

$$\begin{aligned}&\Big (D_{z}-\frac{i}{2}\beta \,D_{x}^{2}+\frac{i}{2}\Delta k\Big )g\cdot f =0,\end{aligned}$$
(3a)
$$\begin{aligned}&\Big (D_{z}-\frac{i}{2}\beta \,D_{x}^{2}-\frac{i}{2}\Delta k\Big )h\cdot f =0, \end{aligned}$$
(3b)
$$\begin{aligned}&\frac{i}{2}\beta ^{2} D_{x}^{2}f\cdot f = \Big (a_{1}\,|g|^{2}+d_{1}gh^{*}+e_{1}hg^{*}+k_{1}\,|h|^{2}\Big ), \nonumber \\ \end{aligned}$$
(3c)
$$\begin{aligned}&\frac{i}{2}\beta ^{2} D_{x}^{2}f\cdot f = \Big (a_{2}\,|h|^{2}+d_{2}hg^{*}+e_{2}gh^{*}+k_{2}\,|g|^{2}\Big ), \nonumber \\ \end{aligned}$$
(3d)
$$\begin{aligned}&b_{1}h^{*}+ c_{1}g^{*}=0, \end{aligned}$$
(3e)
$$\begin{aligned}&b_{2}g^{*}+ c_{2}h^{*}=0, \end{aligned}$$
(3f)

where the asterisk denotes the complex conjugate. In order to insure that \(g\) and \(h\) are not collinear, we should assume that \(b_{1}=c_{1}=b_{2}=c_{2}=0\). Hirota’s bilinear operators \( D_{z} \) and \( D_{x}\) [33] are defined by

$$\begin{aligned} D_{z}^{m}\,D_{x}^{n}(a\cdot b)&= \left( \frac{\partial }{\partial z} - \frac{\partial }{\partial z^{\prime }} \right) ^{m}\,\left( \frac{\partial }{\partial x} - \frac{\partial }{\partial x^{\prime }} \right) ^{n}\nonumber \\&\quad a (z,x)\, b(z^{\prime },x^{\prime })\bigg |_{z^{\prime }= z, x^{\prime }= x}. \end{aligned}$$
(4)

Bilinear forms (3) can be solved by the following power series expansions for \( g(z,x) \), \( h(z,x) \), and \( f(z,x) \):

$$\begin{aligned} g(z,x)&= \varepsilon \,g_{1}(z,x) + \varepsilon ^{3}\,g_{3}(z,x) \nonumber \\&+\, \varepsilon ^{5}\,g_{5}(z,x) + \cdots , \end{aligned}$$
(5a)
$$\begin{aligned} h(z,x)&= \varepsilon \,h_{1}(z,x) + \varepsilon ^{3}\,h_{3}(z,x)\nonumber \\&+\, \varepsilon ^{5}\,h_{5}(z,x) + \cdots ,\end{aligned}$$
(5b)
$$\begin{aligned} f(z,x)&= 1 + \varepsilon ^{2}\,f_{2}(z,x) + \varepsilon ^{4}\,f_{4}(z,x)\nonumber \\&+\, \varepsilon ^{6}\,f_{6}(z,x) + \cdots , \end{aligned}$$
(5c)

where \( \varepsilon \) is a formal expansion parameter. Substituting expressions (5) into bilinear forms (3) and equating coefficients of the same powers of \( \varepsilon \) to zero yield the recursion relations for \( g_{n}(z,x) \)’s, \( h_{n}(z,x) \)’s, and \( f_{n}(z,x) \)’s. Then, soliton solutions for Eq. (1) can be obtained.

To obtain the two-soliton solutions for Eq. (1), we assume that

$$\begin{aligned} g_{1}(z,x) = \gamma _{1}\,e^{\theta _{1}}+\gamma _{3}\,e^{\theta _{2}},\ h_{1}(z,x) = \gamma _{2}\,e^{\theta _{1}}+\gamma _{4}\,e^{\theta _{2}}, \end{aligned}$$
(6)

where \(\theta _{1}=m\,z+p\,x=(m_{1}+i\,m_{2})\,z+(p_{1}+i\,p_{2})\,x\) and \(\theta _{2}=n\,z+w\,x=(n_{1}+i\,n_{2})\,z+(w_{1}+i\,w_{2})\,x\). \(\gamma _{1}\), \(\gamma _{2}\), \(\gamma _{3}\), \(\gamma _{4}\), \(m_{1}\), \(m_{2}\), \(p_{1}\), \(p_{2}\), \(n_{1}\), \(n_{2}\), \(w_{1}\), and \(w_{2}\) are all real constants. Substituting \( g_{1}(z,x) \) and \( h_{1}(z,x) \) into bilinear forms (3), and after some calculations, we can get the relations of the soliton parameters:

$$\begin{aligned}&m_{1}=-\beta \,p_{1}\,p_{2},\ \ m_{2}=\frac{\beta }{2}\left( p_{1}^{2}-p_{2}^{2}\right) , \\&\!\!\!\!n_{1}=-\beta \,w_{1}\,w_{2},\ \ n_{2}=\frac{\beta }{2}\left( w_{1}^{2}-w_{2}^{2}\right) , \ \ \Delta k=0, \end{aligned}$$

and

$$\begin{aligned} f_{2}(z,x)&= A_{1}e^{\theta _{1}+\theta _{1}^{*}}+A_{2}e^{\theta _{2}+\theta _{2}^{*}}\\&\quad +\, A_{3}e^{\theta _{2}+\theta _{1}^{*}}+A_{4}e^{\theta _{1}+\theta _{2}^{*}},\\ g_{3}(z,x)&= B_{1}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}}+B_{2}e^{\theta _{1}+\theta _{2}+\theta _{2}^{*}},\\ h_{3}(z,x)&= B_{3}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}}+B_{4}e^{\theta _{1}+\theta _{2}+\theta _{2}^{*}},\\ f_{4}(z,x)&= E_{1}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}+\theta _{2}^{*}}, \\ g_{n}(z,x)&= 0, \ \ h_{n}(z,x)=0\ \ (n =5,7,...), \\ f_{n}(z,x)&= 0\ \ (n =6,8,...). \end{aligned}$$

In the process of solving \(f_{2}(z,x)\), we obtain the following two coefficient constraints of Eq. (1),

$$\begin{aligned} \begin{aligned}&\gamma _{1}=\frac{\gamma _{2}\gamma _{3}}{\gamma _{4}}, c_{1}=-\frac{b_{1} \gamma _4}{\gamma _3}, c_{2}=-\frac{b_{2} \gamma _1}{\gamma _2},\\&a_{1}=k_{2}+\frac{(a_{2}-k_{1})\gamma _4^{2}}{\gamma _3^2}+\frac{\left( d_{2}-d_{1}-e_{1}+e_{2}\right) \gamma _4}{\gamma _3}, \end{aligned}\nonumber \\ \end{aligned}$$
(7)

and

$$\begin{aligned} k_{1}=a_{2},\ \ k_{2}=a_{1}, \ \ d_{2}=e_{1}, \ \ e_{2}=d_{1}. \end{aligned}$$
(8)

In both of these constraints, the constants \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(B_{1}\), \(B_{2}\), \(B_{3}\), \(B_{4}\), and \(E_{1}\) can be determined, and two-soliton solutions for Eq. (1) can be derived. Furthermore, those two coefficient constraints (7) and (8) of Eq. (1) are the only possible to derive the soliton solutions.

With the coefficient constraint (7) of Eq. (1), the soliton solutions for Eq. (1) are similar with the known results in Refs. [34, 35], and are not discussed in more details here. With the coefficient constraint (8) of Eq. (1), we derive

$$\begin{aligned}&A_{1}=\frac{k_{2} \gamma _1^2+d_{2}\gamma _1 \gamma _2 +e_{2}\gamma _1 \gamma _2 +a_{2} \gamma _2^2}{8 p_{1}^2},\nonumber \\&A_{3}=\frac{k_{2} \gamma _1 \gamma _3+e_{2} \gamma _2 \gamma _3+d_{2} \gamma _1 \gamma _4+a_{2} \gamma _2 \gamma _4}{2 S^2},\nonumber \\&A_{2}=\frac{k_{2} \gamma _3^2+d_{2}\gamma _3 \gamma _4 +e_{2}\gamma _3 \gamma _4 +a_{2} \gamma _4^2}{8 w_1^2},\nonumber \\&A_{4}=\frac{k_{2} \gamma _1 \gamma _3+d_{2} \gamma _2 \gamma _3+e_{2} \gamma _1 \gamma _4+a_{2} \gamma _2 \gamma _4}{2 S^{*2}},\nonumber \\&B_{1}=\frac{R\big \{R \left( k_{2}\gamma _1+e_{2} \gamma _2 \right) \gamma _1\gamma _3-[S\gamma _2\gamma _3-2p_{1} \gamma _1 \gamma _4 ] \left( a_{2}\gamma _2+d_{2} \gamma _1 \right) \big \}}{8 (p_{1} S)^2},\nonumber \\&B_{2}=\frac{R \big \{R \left( k_{2} \gamma _3+e_{2} \gamma _4\right) \gamma _1 \gamma _3+ \left[ S^{*} \gamma _1 \gamma _4-2 w_1 \gamma _2 \gamma _3\right] \left( d_{2} \gamma _3+a_{2} \gamma _4\right) \big \}}{8 (w_1 S^{*})^2},\nonumber \\&B_{3}=\frac{R \big \{R\left( e_{1} \gamma _1+k_{1} \gamma _2\right) \gamma _2 \gamma _4-\left[ S \gamma _1 \gamma _4-2 p_{1} \gamma _2 \gamma _3\right] \left( k_{2} \gamma _1+d_{1} \gamma _2\right) \big \}}{8 (p_{1} S)^2},\nonumber \\&B_{4}=\frac{R\big \{R \left( e_{1} \gamma _3+k_{1} \gamma _4\right) \gamma _2 \gamma _4+\left[ S^{*} \gamma _2 \gamma _3-2 w_1 \gamma _1 \gamma _4\right] \left( k_{2} \gamma _3+d_{1} \gamma _4\right) \big \}}{8 (w_1 S^{*})^2},\nonumber \\&E_{1}=\frac{8 A_3 A_4 \left( p_2-w_2\right) ^2-8 A_1 A_2 \left( p_{1}-w_1\right) ^2+P+Q}{8 \left( p_{1}+w_1\right) ^2} \end{aligned}$$
(9)

with

$$\begin{aligned} R&= p-w,\ \ S=p^{*}+w,\\ P&= B_4^{*} d_{1} \gamma _1+B_4 e_{1} \gamma _1+B_2 d_{1} \gamma _2+B_2^{*} e_{1} \gamma _2 \\&+\,B_3^{*} d_{1} \gamma _3+B_3 e_{1} \gamma _3+B_1 d_{1} \gamma _4+B_1^{*} e_{1} \gamma _4,\\ Q&= \left( B_2+B_2^{*}\right) a_{1}\gamma _1+\left( B_4+B_4^{*}\right) k_{1} \gamma _2\\&+\left( B_1+B_1^{*}\right) a_{1}\gamma _3+\left( B_3+B_3^{*}\right) k_{1} \gamma _4. \end{aligned}$$

Without loss of generality, we set \( \varepsilon =1\), and the two-soliton solutions can be expressed as

$$\begin{aligned}&u(z,x)=\frac{g(z,x)}{f(z,x)}=\frac{g_{1}(z,x) + g_{3}(z,x)}{1 + f_{2}(z,x)+f_{4}(z,x)}\nonumber \\&\quad =\frac{\gamma _{1}e^{\theta _{1}}+\gamma _{3}e^{\theta _{2}}+ B_{1}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}}+B_{2}e^{\theta _{1}+\theta _{2}+\theta _{2}^{*}}}{1+ A_{1}e^{\theta _{1}+\theta _{1}^{*}}+ A_{2}e^{\theta _{2}+\theta _{2}^{*}}+ A_{3}e^{\theta _{2}+\theta _{1}^{*}}+ A_{4}e^{\theta _{1}+\theta _{2}^{*}}+E_{1}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}+\theta _{2}^{*}}},\end{aligned}$$
(10)
$$\begin{aligned}&v(z,x)=\frac{h(z,x)}{f(z,x)}=\frac{h_{1}(z,x) + h_{3}(z,x)}{1 + f_{2}(z,x)+f_{4}(z,x)}\nonumber \\&\quad =\frac{\gamma _{2}e^{\theta _{1}}+\gamma _{4}e^{\theta _{2}}+ B_{3}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}}+B_{4}e^{\theta _{1}+\theta _{2}+\theta _{2}^{*}}}{1+ A_{1}e^{\theta _{1}+\theta _{1}^{*}}+ A_{2}e^{\theta _{2}+\theta _{2}^{*}}+ A_{3}e^{\theta _{2}+\theta _{1}^{*}}+ A_{4}e^{\theta _{1}+\theta _{2}^{*}}+E_{1}e^{\theta _{1}+\theta _{2}+\theta _{1}^{*}+\theta _{2}^{*}}}. \end{aligned}$$
(11)

3 Discussion

According to solutions (10) and (11), we will perform asymptotic analysis, discuss interactions between spatial solitons with different coefficient constraints of Eq. (1), and analyze the influence of parameters for spatial soliton interactions.

3.1 Asymptotic analysis

  1. (1)

    Before interactions (\(z\rightarrow -\infty \))

    1. (a)

      \(\theta _{1}+ \theta _{1}^{*}\sim 0,\ \theta _{2}+ \theta _{2}^{*}\rightarrow -\infty \)

      $$\begin{aligned}&u^{1-} \rightarrow \frac{\gamma _{1}e^{\theta _{1}}}{1+ A_{1}e^{\theta _{1}+\theta _{1}^{*}}}=\frac{\gamma _{1}}{2\sqrt{A_{1}}}\nonumber \\&\quad \times e^{i(p_{2}x+p_{1}^{2}z-p_{2}^{2}z)}\nonumber \\&\quad \times \text {sech} \left( p_{1}x-2p_{1}p_{2}z+\frac{1}{2}\text {ln}A_{1}\right) , \end{aligned}$$
      (12)
      $$\begin{aligned}&v^{1-} \rightarrow \frac{\gamma _{2}e^{\theta _{1}}}{1+ A_{1}e^{\theta _{1}+\theta _{1}^{*}}}=\frac{\gamma _{2}}{2\sqrt{A_{1}}}\nonumber \\&\quad \times e^{i(p_{2}x+p_{1}^{2}z-p_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( p_{1}x-2p_{1}p_{2}z+\frac{1}{2}\text {ln}A_{1}\right) . \end{aligned}$$
      (13)
    2. (b)

      \(\theta _{2}+ \theta _{2}^{*}\sim 0,\ \theta _{1}+ \theta _{1}^{*}\rightarrow +\infty \)

      $$\begin{aligned}&u^{2-} \rightarrow \frac{B_{1}e^{\theta _{2}}}{A_{1}+E_{1}e^{\theta _{2}+\theta _{2}^{*}}}=\frac{B_{1}}{2\sqrt{E_{1}A_{1}}}\nonumber \\&\quad \times e^{i(w_{2}x+w_{1}^{2}z-w_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( w_{1}x-2w_{1}w_{2}z+\frac{1}{2}\text {ln}\frac{E_{1}}{A_{1}}\right) ,\end{aligned}$$
      (14)
      $$\begin{aligned}&v^{2-} \rightarrow \frac{B_{3}e^{\theta _{2}}}{A_{1}+ E_{1}e^{\theta _{2}+\theta _{2}^{*}}}=\frac{B_{3}}{2\sqrt{E_{1}A_{1}}}\nonumber \\&\quad \times e^{i(w_{2}x+w_{1}^{2}z-w_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( w_{1}x-2w_{1}w_{2}z+\frac{1}{2}\text {ln}\frac{E_{1}}{A_{1}}\right) . \end{aligned}$$
      (15)
  2. (2)

    After interactions (\(z\rightarrow +\infty \))

    1. (a)

      \(\theta _{1}+ \theta _{1}^{*}\sim 0,\ \theta _{2}+ \theta _{2}^{*}\rightarrow +\infty \)

      $$\begin{aligned}&u^{1+} \rightarrow \frac{B_{2}e^{\theta _{1}}}{A_{2}+ E_{1}e^{\theta _{1}+\theta _{1}^{*}}}=\frac{B_{2}}{2\sqrt{E_{1}A_{2}}}\nonumber \\&\quad \times e^{i(p_{2}x+p_{1}^{2}z-p_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( p_{1}x-2p_{1}p_{2}z+\frac{1}{2}\text {ln}\frac{E_{1}}{A_{2}}\right) , \end{aligned}$$
      (16)
      $$\begin{aligned}&v^{1+} \rightarrow \frac{B_{4}e^{\theta _{1}}}{A_{2}+ E_{1}e^{\theta _{1}+\theta _{1}^{*}}}=\frac{B_{4}}{2\sqrt{E_{1}A_{2}}}\nonumber \\&\quad \times e^{i(p_{2}x+p_{1}^{2}z-p_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( p_{1}x-2p_{1}p_{2}z+\frac{1}{2}\text {ln}\frac{E_{1}}{A_{2}}\right) . \end{aligned}$$
      (17)
    2. (b)

      \(\theta _{2}+ \theta _{2}^{*}\sim 0,\ \theta _{1}+ \theta _{1}^{*}\rightarrow -\infty \)

      $$\begin{aligned}&u^{2+} \rightarrow \frac{\gamma _{3}e^{\theta _{2}}}{1+A_{2}e^{\theta _{2}+\theta _{2}^{*}}}\nonumber \\&\quad =\frac{\gamma _{3}}{2\sqrt{A_{2}}}e^{i(w_{2}x+w_{1}^{2}z-w_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( w_{1}x-2w_{1}w_{2}z+\frac{1}{2}\text {ln}A_{2}\right) , \end{aligned}$$
      (18)
      $$\begin{aligned}&v^{2+} \rightarrow \frac{\gamma _{4}e^{\theta _{2}}}{1+ A_{2}e^{\theta _{2}+\theta _{2}^{*}}}=\frac{\gamma _{4}}{2\sqrt{A_{2}}}\nonumber \\&\quad \times e^{i(w_{2}x+w_{1}^{2}z-w_{2}^{2}z)}\nonumber \\&\quad \times \text {sech}\left( w_{1}x-2w_{1}w_{2}z+\frac{1}{2}\text {ln}A_{2}\right) . \end{aligned}$$
      (19)

We can substitute the parameters \(A_{1}\), \(A_{2}\), \(B_{1}\), \(B_{2}\), \(B_{3}\), \(B_{4}\), and \(E_{1}\) into expressions (12)–(19) and then, investigate spatial soliton interactions. Although Eq. (1) admits two-soliton solutions, the soliton interactions in both coefficient constraints (7) and (8) of Eq. (1) are of different nature. Under the condition of the coefficient constraint (7) of Eq. (1), the solitons demonstrate the standard elastic interactions, which is a known result [36], and we will not discuss it in this case. Next, we will discuss the properties of inelastic interactions with coefficient constraints (8) of Eq. (1).

3.2 Inelastic interactions with the coefficient constraint (8) of Eq. (1)

Substituting expressions (9) into expressions (12)–(19), we can obtain that

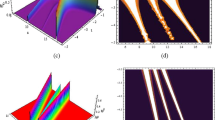
$$\begin{aligned}&|u^{1-}|\ne |u^{1+}|,\ \ \ |v^{1-}|\ne |v^{1+}|,\\&\!\!\!|u^{2-}|\ne |u^{2+}|,\ \ \ |v^{2-}|\ne |v^{2+}|. \end{aligned}$$

Hereby, the interactions between spatial solitons are inelastic with the coefficient constraint (8) of Eq. (1). That is, there is an energy exchange between two solitons after the interactions. In Fig. 1, the parameters are chosen as \(p_{1}=1.8\), \(p_{2}=-1\), \(w_{1}=-1.5\), \(w_{2}=1\), \(\gamma _{1}=1\), \(\gamma _{2}=2\), \(\gamma _{3}=4\), \(\gamma _{4}=1\), \(\beta =0.5\), \(a_{1}=0.5\), \(d_{1}=0.1\), \(e_{1}=0.3\), \(k_{1}=1.5\), \(a_{2}=1.5\), \(d_{2}=0.3\), \(e_{2}=0.1\), and \(k_{2}=0.5\). Two bright solitons propagate stably without shape changing before interactions. During the interactions, the solitons merge as one soliton with higher amplitude, and the solitons are compressed. After the interactions, one of the soliton amplitudes increases, and the other one decreases.

Fig. 1
figure 1

Soliton interactions between two solitons via solutions (10) and (11). Parameters are: \(p_{1}=1.8\), \(p_{2}=-1\), \(w_{1}=-1.5\), \(w_{2}=1\), \(\gamma _{1}=1\), \(\gamma _{2}=2\), \(\gamma _{3}=4\), \(\gamma _{4}=1\), \(\beta =0.5\), \(a_{1}=0.5\), \(d_{1}=0.1\), \(e_{1}=0.3\), \(k_{1}=1.5\), \(a_{2}=1.5\), \(d_{2}=0.3\), \(e_{2}=0.1\), and \(k_{2}=0.5\)

Full size image

The distinct feature of the inelastic interaction process is that the interacting dynamical behavior allows one of the solitons to get suppressed, while the other one to get enhanced. The energy exchange phenomenon between two solitons occurs, but the total energy of two solitons is conserved, and the exchange phenomenon satisfies the energy conservation of solitons before and after interactions. The features of energy exchange give possible applications for all-optical switching and soliton amplification. For the soliton amplification, the amplifier does not require any external amplification medium, and the amplification process does not introduce any noise. Moreover, the switching rate and signal-to-noise ratio for the all-optical switching or soliton amplifier can be controlled through adjusting the parameters related to solutions (10) and (11) with the coefficient constraint (8) of Eq. (1).

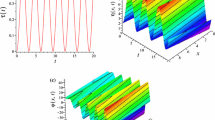
The solitons can also be inputted in phase as shown in Fig. 2. During the propagation, the interactions between solitons show the periodical changes. The two solitons attract and repel each other periodically and form the bound solitons. The bound solitons exchange their energy periodically. By changing the value of \(a_{j}\), \(d_{j}\), \(e_{j}\), and \(k_{j}\), we can change the amplitudes of spatial solitons in Fig. 3. In the above analysis, the value of \(a_{2}\), \(d_{2}\), \(e_{2}\), and \(k_{2}\) is both positive. In fact, as long as \(k_{2} \gamma _1^2+d_{2}\gamma _1 \gamma _2 +e_{2}\gamma _1 \gamma _2 +a_{2} \gamma _2^2\) is positive, the value of \(a_{2}\), \(d_{2}\), \(e_{2}\), and \(k_{2}\) can be negative.

Fig. 2
figure 2

Soliton interactions between two solitons via solutions (10) and (11). Parameters are: \(p_{1}=1.1\), \(p_{2}=0.15\), \(w_{1}=1.5\), \(w_{2}=0.15\), \(\gamma _{1}=-1\), \(\gamma _{2}=2\), \(\gamma _{3}=4\), \(\gamma _{4}=1\), \(\beta =0.5\), \(a_{1}=0.5\), \(d_{1}=0.1\), \(e_{1}=0.3\), \(k_{1}=1.5\), \(a_{2}=1.5\), \(d_{2}=0.3\), \(e_{2}=0.1\), and \(k_{2}=0.5\)

Full size image
Fig. 3
figure 3

Soliton interactions between two solitons via solutions (10) and (11). Parameters are: \(p_{1}=1.8\), \(p_{2}=-1\), \(w_{1}=-1.5\), \(w_{2}=1\), \(\gamma _{1}=1\), \(\gamma _{2}=2\), \(\gamma _{3}=4\), \(\gamma _{4}=1\), \(\beta =0.5\), \(a_{1}=0.3\), \(d_{1}=0.1\), \(e_{1}=0.3\), \(k_{1}=1.0\), \(a_{2}=1.0\), \(d_{2}=0.3\), \(e_{2}=0.1\), and \(k_{2}=0.3\)

Full size image

3.3 Numerical simulations’ results

To verify the correctness of the analytic results, the numerical simulation based on split-step Fourier method will be investigated. Figures for \(v\) solutions are not discussed in this subsection for the sake of simplicity. The propagation of spatial solitons is shown in Fig. 4. The stable soliton can be obtained, and the interaction between spatial solitons is inelastic in Fig. 4a. After the interaction, the spatial solitons exchange their energy. One of the spatial solitons is amplified, and the all-optical switching function is achieved. Those results are in agreement with the analytic results in Figs. 1, 2, and 3.

Fig. 4
figure 4

Numerical simulations of soliton interactions between two solitons. The corresponding initial conditions are \(u=\text {sech}(x+5)\text {exp}(15ix)+0.8\text {sech}[0.8(x-5)] \text {exp}(-10ix)\)

Full size image

4 Conclusions

In conclusion, the CNLS equations [see Eq. (1)], which can be used to describe the propagation of spatial solitons in an AlGaAs slab waveguide, have been investigated analytically. With the help of symbolic computation and Hirota method, bilinear forms (3) and two-soliton solutions (10) and (11) for Eq. (1) have been obtained. The soliton interactions have been studied through the asymptotic analysis. Attention needs to be paid to the following issues:

  1. 1.

    The key point of this paper lies in the obtaining of two coefficient constraints (7) and (8) of Eq. (1), which can divide the soliton interactions into two classes: elastic and inelastic interactions. In the condition of coefficient constraint (7) of Eq. (1), the soliton interaction has been elastic. With coefficient constraint (8) of Eq. (1), the soliton interaction has been inelastic.

  2. 2.

    For the inelastic interaction, there has been an energy exchange between two solitons after the interactions (see Fig. 1). The features of energy exchange give the possible applications for all-optical switching and soliton amplification. Numerical simulations have been made to support the correctness of the conclusions. For the all-optical switching, the switching rate and signal-to-noise ratio can be controlled through adjusting the parameters for solutions (10) and (11). For the soliton amplification, the amplifier does not require any external amplification medium, and the amplification process does not introduce any noise.

  3. 3.

    Either soliton interactions are elastic or inelastic, the bound solitons can be formed (see Fig. 2). The period and intensity of soliton interaction can be controlled with the changing value of wave numbers \(p_{1}\), \(p_{2}\), \(w_{1}\), and \(w_{2}\). The bound states of solitons can also be controlled when the amplitude of the initial incident pulse changes.

The investigation of this paper provides a theoretical foundation for studying the elastic or inelastic interactions in CNLS equations. Results may lead to exciting applications in nonlinear optics, particularly in the design of birefringence-managed switching architecture.