Synchronization of hybrid impulsive and switching dynamical networks with delayed impulses

Abstract

In this paper, the exponential synchronization problem is investigated for a class of hybrid impulsive and switching dynamical networks (HISDNs). Different from the existing results concerning synchronization of HISDNs, impulsive input delays are considered in our model. Moreover, in our model, the impulsive instances and system switching instances do not need to be coincident. By using the Razumikhin theorem and the mathematical induction method, several sufficient synchronization criteria are obtained in terms of linear matrix inequalities. The obtained criteria reveal that the frequency of impulsive occurrence, impulsive input delays, can heavily affect the synchronization performance. Finally, an example is provided to illustrate the effectiveness of the obtained results.

1 Introduction

With the development of science and technology, our daily life is increasingly dependant on complex dynamical networks, such as the internet, the Word Wide Web, communication networks, and social networks [2, 6]. Complex dynamical networks that consist of a large number of nodes and links between the nodes have been studied in many field of mathematics, engineering, biology, and social science [7, 14, 20, 23, 25, 28, 43]. As one of the most important collective behaviors, synchronization has received considerable attention in many fields, since synchronization of coupled dynamical networks has potential applications in various fields including information science, parallel image processing, secure communication, and neural networks [16, 30–32, 37, 42, 48].

As we all know, when signals or waves propagate between nodes, time delay can often occur due to the finite speed of switching and transmitting signals, which may result in oscillatory behavior or system instability [26, 29, 35]. On the other hand, time delay also emerges due to intrinsic factors, for example, in a neuronal system, information can be transmitted between neurons via synapses, and the electric activity of neuron and collective behaviors of neurons can be modulated by autapse. Autapse can change the excitability and fluctuation of membrane potential, and its effect can be described by time-delayed feedback terms, which is thought as another potential origin of time delay [21, 24, 27]. Moreover, the authors showed that coupled time delay also plays an important role in enhancing synchronization in the network in [22]. So, when modeling real-world complex dynamical networks, time delays are necessary to be taken into account. In the past decade, there have been many excellent results concerning synchronization and stability of delayed complex networks [12, 16, 34, 36, 39–41, 48]. For example, the authors of [12] discussed the stability of delayed impulsive and switching neural networks. In [41], the synchronization problem was studied for a class of switched neural networks with mixed delays via impulsive control.

In network environment, complex dynamical networks may be affected more or less by uncertainties such as unmodeled dynamics, link failure, and new link creation that may happen at times, and then the switching between different topologies is inevitable [19]. Hence, it is important to consider the switching when modeling real-world dynamical networks. Recently, synchronization problem of switched complex networks has become a hot issue [13, 16, 29, 30, 36, 44, 47, 48]. One useful method to investigate the synchronization problem of switched complex networks is the dwell time approach, By using the dwell time approach, in [33], the synchronization problem of switched complex networks was investigated. In [16], by using the average dwell time approach, synchronization of complex networks with switching topology was investigated where some subnetworks are not self-synchronized. In [48], based on the switched system point view and the average dwell time approach, synchronization of complex networks with switching topology was studied.

On the other hand, in real life, many biological and electronic networks are often subjected to instantaneous disturbances and experience abrupt changes at certain instants, which may be caused by frequency switching or other sudden noise, i.e., they exhibit impulsive effects [18, 44]. Due to the serious effects on the dynamical behaviors caused by impulses and switching, it is necessary to consider simultaneously both impulsive and switching effects when modeling the real-world dynamical networks [12, 44]. Recently, impulsive switched systems (networks) have gained increasingly attention, since they provide a natural and convenient unified framework for mathematical modeling of switching and impulsive phenomena [1, 8, 10, 12, 17, 34, 38, 49]. For example, in [44], the synchronization problem was investigated for a class of coupled switched neural networks with mode-dependent impulsive effects by using the average dwell time approach and the comparison principle. In [10, 12], asymptotic synchronization of HISDNs with arbitrary switching law was investigated by using feedback control. In [17], robust exponential stability of impulsive switched systems with switching delays was studied by the Razumikhin approach. However, in most existing results on impulsive switched systems, it is implicitly assumed that impulsive effects occur at the switching points [1, 10, 12, 17, 38, 40]. Obviously this assumption is conservative and impractical. As was shown in [41, 44], impulsive effects can be activated not only at the instants coinciding with the system switching but also at the instants when there is no system switching.

Moreover, all the results mentioned above on HISDNs did not take into account the impulsive input delays. In fact, for a impulsive dynamical network, it is not practical to ignore the impulsive input delays. As was demonstrated in [4], when applying the impulsive control strategy, communication and sampling delays often occur in the transmission of impulsive information in network environments. For instance, in networked control systems, sensor-to-controller delay and controller-to-actuator delay are unavoidable, which can be modeled as impulses with time delays [4]. Therefore, it is very important to consider impulsive input delays in impulsive systems. Recently, delayed impulses have received increasing attention [4, 5, 45]. For example, in [45], synchronization of stochastic dynamical networks under delayed impulsive control was investigated. These works provide a way to investigate stability or synchronization of delayed impulsive systems. Unfortunately, up to now, with respect to the HISDNs, impulsive input delays have been largely overlooked primarily due to its mathematical difficulty in analyzing the coexistence of coupling terms, internal delays, switching and delayed impulsive effects despite their importance in modeling realistic complex dynamical networks. In order to shorten the gaps mentioned above and extend the application of HISDNs, in this paper, both impulsive input delays and switching effects are considered. Moreover, the impulsive effects can be activated not only at the instants coinciding with the system switching but also at the instants when there is no system switching.

Based on the above discussion, in this paper, we consider a more general HISDNs with delayed impulses, and several sufficient criteria are derived to ensure exponential synchronization of HISDNs by means of the time-dependent Lyapunov function method combined with the Razumikhin theorem. The contributions of this paper can be listed as follows: (1) both impulsive input delays and switching are considered simultaneously in our model; (2) the impulsive effects can be activated not only at the instants coinciding with the system switching but also at the instants when there is no system switching; (3) by constructing a time-dependent Lyapunov function, several synchronization criteria are derived in terms of LMIs, which can be applied to large-scale systems.

Notations Throughout this paper, $\mathbb {N}^{+}$ and $\mathbb {R}^{n}$ denote, respectively, the set of nonnegative integers and the n-dimensional space. $\mathbb {R}^{m\times n}$ denotes $m\times n$ real matrix. For vector $x\in \mathbb {R}^{n}$, |x| and $x^{T}$ denote, respectively, the Euclidean norm and its transpose. We use $\lambda _{\max }(\cdot )$ (respectively $\lambda _{\min }(\cdot )$) to denote the maximum (respectively the minimum) eigenvalue of a real matrix. The asterisk $\star$ in a matrix is used to denote a term that is induced by symmetry. For matrix $A\in \mathbb {R}^{n\times n}$, $|A|=\sqrt{\lambda _{\max }(A^{T}A)}$. The notation $A\le B$ (respectively $A<B$) means that the matrix $A-B$ is negative semidefinite (respectively negative definite). $I_{n}$ is the identity matrix of order n. $PC([-\tau ,0];\mathbb {R}^{n})$ denotes the family of piecewise continuous function from $[-\tau ,0]$ to $\mathbb {R}^{n}$ with the norm $\Vert \phi \Vert _{\tau }=\sup _{-\tau \le \theta \le 0}|\phi (\theta )|$. Dini derivative $D^{+}W(t)$ is defined as $D^{+}W(t)=\lim _{h\rightarrow 0^{+}}(W(t+h)-W(t))/h$.

2 Model and preliminaries

Consider the following HISDNs model:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)=C_{\sigma (t)}x_{i}(t)+B_{\sigma (t)} g_{1}(\sigma (t),x_{i}(t))\\ \quad \quad \quad \quad +D_{\sigma (t)} g_{2}(\sigma (t),x_{i}(t-\tau (t)))\\ \quad \quad \quad \quad +\vartheta \sum \nolimits ^{N}_{j=1}a_{ij}^{\sigma (t)}\varGamma _{\sigma (t)} x_{j}(t),t\ne t_{k},k\in \mathbb {N}^{+},\\ x_{i}(t_{k}^{+})=x_{i}(t_{k}^{-})+\mu _{\sigma (t_{k})}x_{i}((t_{k}-d_{k})^{-}), \end{array}\quad \right. \end{aligned}$$

(1)

where $x_{i}(t)=[x_{i1}(t),\ldots ,x_{in}(t)]^{T}$ denotes the state vector of the i-th node; $\vartheta$ is the coupling strength; $\tau (t)$ is the time-varying delay satisfying $0\le \tau (t)\le \tau$; $\sigma (t):[0,\infty )\rightarrow \mathfrak {M}=\{1,2,\ldots ,m\}$ is the switching signal, which is a piecewise constant function continuous from the right. The switching sequence $0<T_{1}<T_{2}<\cdots <T_{k}<\cdots$ satisfies $\lim _{k\rightarrow \infty }T_{k}=\infty$. For each fixed $\sigma (t)=r\in \mathfrak {M}$, $\mu _{r}\in \mathbb {R}^{n\times n}$ represents the corresponding mode-dependent impulsive gain; $C_{r}\in \mathbb {R}^{n\times n}$, $B_{r}\in \mathbb {R}^{n\times n}$, $D_{r}\in \mathbb {R}^{n\times n}$, $g_{1}(r,x_{i}(t))=[g_{11}(r,x_{i1}(t)),\ldots ,$ $g_{1n}(r,x_{in}(t))]^{T}\in \mathbb {R}^{n}$, $g_{2}(r,x_{i}(t))=[g_{21}(r,x_{i1}(t)),\ldots ,$ $g_{2n}(r,x_{in}(t))]^{T}\in \mathbb {R}^{n}$, $\varGamma _{r}\in \mathbb {R}^{n\times n}>0$ is the diagonal inner coupling matrix; $A_{r}\in \mathbb {R}^{N\times N}$ is the outer coupling configuration matrix which represents the structure of the network in which $a_{ij}^{r}$ is defined as follows: if there is a connection from node j to node i ($j\ne i$), then $a_{ij}^{r}\ne 0$; otherwise, $a_{ij}^{r}=0$. The diagonal entries of matrix $a_{ii}^{r}$ are determined by the following coupling condition:

$$\begin{aligned} a_{ii}^{r}=-\sum \limits _{j=1,j\ne i}^{N}a_{ij}^{r},\quad i=1,2,\ldots ,N,\quad r\in \mathfrak {M}. \end{aligned}$$

(2)

The initial conditions are assumed to be $x_{i}(t)=\phi _{i}(t)\in PC([-\tau ,0];\mathbb {R}^{n}), i=1,2,\ldots ,n$. $d_{k}$ is the impulsive delay at instant $t_{k}$ satisfying $0\le d_{k}\le d$, where d is a positive scalar. The impulsive time instants $t_{k}$ satisfy $0<t_{1}<t_{2}<\cdots <t_{k}<\cdots ,$ $\lim _{k\rightarrow \infty }t_{k}=\infty$. $x_{i}(t_{k}^{+})$ and $x_{i}(t_{k}^{-})$ denote the limit from the right and the left at time $t_{k}$, respectively. Without loss of generality, in this paper, we assume that $x_{i}(t_{k})=x_{i}(t_{k}^{+})$.

Remark 1

Recently, in [44], the synchronization problem of coupled switched neural networks with mode-dependent impulsive effects was investigated by using the average dwell time approach and the comparison principle. In [10, 12], asymptotic synchronization of HISDNs was investigated by using feedback control in order to improve the security of communication. It should be mentioned that impulsive input delays have not been considered in [10, 12, 44]. In fact, to our best knowledge, in existing results concerning HISDNs, impulsive input delays have been largely overlooked. In our model (1), impulsive input delays are considered, which make our model more general.

Remark 2

In model (1), the impulsive instances and system switching instances don’t need to be coincident. It means that the impulsive effects may occur at the switching instance $T_{k}$, e.g., there exits a positive integer $q_{1}$ such that $t_{q_{1}}=T_{k}$, and the impulsive effects may occur in the switching interval $(T_{k-1},T_{k})$, e.g., there exit some positive integer $q_{2}$ such that $T_{k-1}<t_{q_{2}}<T_{k}$. In most existing results concerning on HISDNs, it is implicitly assumed that the impulsive effects occur at instants coinciding with mode switching [10, 12, 15, 40].

We assume that the isolated node of the network (1) is in the form of:

$$\begin{aligned} \dot{s}(t)&=C_{\sigma (t)}s(t)+B_{\sigma (t)} g_{1}(\sigma (t),s(t))\nonumber \\&\quad +\,D_{\sigma (t)} g_{2}(\sigma (t),s(t-\tau (t))), \end{aligned}$$

(3)

where $s(t)=[s_{1}(t),\ldots ,s_{n}(t)]^{T}$ denotes the state vector of the isolate node with the initial condition $s(t)=\varphi (t)\in PC([-\tau ,0];\mathbb {R}^{n})$. Moreover, s(t) can be either an equilibrium point, or a periodic orbit, or a chaotic orbit in the phase space.

Let $e_{i}(t)=x_{i}(t)-s(t)$, then the following error dynamical system can be obtained:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{e}_{i}(t)=C_{\sigma (t)}e_{i}(t)+B_{\sigma (t)} g_{1}(\sigma (t),e_{i}(t))\\ \quad \quad \quad \quad +\,D_{\sigma (t)} g_{2}(\sigma (t),e_{i}(t-\tau (t)))\\ \quad \quad \quad \quad +\,\vartheta \sum \nolimits ^{N}_{j=1}a_{ij}^{\sigma (t)}\varGamma _{\sigma (t)} e_{j}(t),t\ne t_{k},k\in \mathbb {N}^{+},\\ e_{i}(t_{k}^{+})=e_{i}(t_{k}^{-})+\mu _{\sigma (t_{k})}e_{i}((t_{k}-d_{k})^{-}), \end{array} \right. \end{aligned}$$

(4)

where $g_{1}(\sigma (t),e_{i}(t))=g_{1}(\sigma (t),x_{i}(t))-g_{1}(\sigma (t),s(t))$, $g_{2}(\sigma (t),e_{i}(t-\tau (t)))=g_{2}(\sigma (t),x_{i}(t-\tau (t))) -g_{2}(\sigma (t),s(t-\tau (t)))$.

Let $e(t)=[e_{1}^{T}(t),e_{2}^{T}(t),\ldots ,e_{N}^{T}(t)]^{T}$, $\mathbf {G}_{1}(\sigma (t),e(t))=[g_{1}^{T}(\sigma (t),e_{1}(t)),\ldots ,g_{1}^{T}(\sigma (t),e_{N}(t))]^{T}$, $\mathbf {G}_{2}(\sigma (t),e(t-\tau (t)))=[g_{2}^{T}(\sigma (t),e_{1}(t-\tau (t))),\ldots ,g_{2}^{T}(e_{N}(\sigma (t),t-\tau (t)))]^{T}$, $\mathbf {C}_{\sigma (t)}=I_{N}\otimes C_{\sigma (t)}$, $\mathbf {B}_{\sigma (t)}=I_{N}\otimes B_{\sigma (t)}$, $\mathbf {D}_{\sigma (t)}=I_{N}\otimes D_{\sigma (t)}$, $\mathbf {A}_{\sigma (t)}=\vartheta (A_{\sigma (t)}\otimes \varGamma _{\sigma (t)})$, $\mathfrak {U}_{\sigma (t_{k})}=I_{N}\otimes \mu _{\sigma (t_{k})}$, then the system in (4) can be rewritten as:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{e}(t)=\mathbf {C}_{\sigma (t)}e(t)+\mathbf {B}_{\sigma (t)}\mathbf {G}_{1}(\sigma (t),e(t))\\ \quad \quad \quad \quad +\,\mathbf {D}_{\sigma (t)} \mathbf {G}_{2}(\sigma (t),e(t-\tau (t)))\\ \quad \quad \quad \quad +\,\mathbf {A}_{\sigma (t)}e(t),\quad t\ne t_{k},k\in \mathbb {N}^{+},\\ \varDelta e(t_{k})=\mathfrak {U}_{\sigma (t_{k})}e((t_{k}-d_{k})^{-}), \end{array} \right. \end{aligned}$$

(5)

where $\varDelta e(t_{k})=e(t_{k}^{+})-e(t_{k}^{-})$. The initial value of error system (5) is prescribed as $e(t)=\varPhi (t)=[(\phi _{1}(t)-\varphi (t))^{T},\ldots ,(\phi _{N}(t)-\varphi (t))^{T}]^{T}\in PC([-\tau ,0];\mathbb {R}^{nN})$.

In order to overcome the difficulties caused by the switching, we define an indicator function $\pi (t)=[\pi _{1}(t),$ $\ldots ,\pi _{m}(t)]^{T}$ [41], where

$$\begin{aligned} \pi _{r}(t)=\left\{ \begin{array}{ll} 1, \quad \text {when}\quad \sigma (t)=r,\\ 0, \quad \text {otherwise}, \end{array}r\in \mathfrak {M}. \right. \end{aligned}$$

(6)

It is easy to see that $\sum \limits _{r=1}^{m}\pi _{r}(t)=1$. And then the system (5) can be rewritten as:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{e}(t)=\sum \nolimits _{r=1}^{m}\pi _{r}(t)[\mathbf {C}_{r}e(t)+\mathbf {B}_{r}\mathbf {G}_{1}(r,e(t))\\ \quad \quad \quad \quad +\,\mathbf {D}_{r} \mathbf {G}_{2}(r,e(t-\tau (t)))\\ \quad \quad \quad \quad +\,\mathbf {A}_{r}e(t)],\quad t\ne t_{k},k\in \mathbb {N}^{+},\\ \varDelta e(t_{k})=\sum \nolimits _{r=1}^{m}\pi _{r}(t_{k})\mathfrak {U}_{r}e((t_{k}-d_{k})^{-}). \end{array} \right. \end{aligned}$$

(7)

In order to derive our main results, the following basic definition, lemmas and assumptions are needed.

Definition 1

The complex dynamical network in (1) is said to be globally exponentially synchronized to the objective state s(t), if there exist $\epsilon >0$, $\varrho _{1}>0$ such that when $\Vert \varPhi (t)\Vert _{\tau }\le \varrho _{1}$ holds for some $\varrho >0$, the following condition is satisfied:

$$\begin{aligned} |x_{i}(t)-s(t)|\le \varrho e^{-\epsilon (t-t_{0})},i=1,2,\ldots ,N,\quad \forall t\ge t_{0}.\nonumber \\ \end{aligned}$$

(8)

Assumption 1

There exist two positive integers $\delta _{1}$ and $\delta _{2}$ such that for $k\in \mathbb {N}^{+}$, $\delta _{1}\le t_{k}-t_{k-1}\le \delta _{2}$.

Assumption 2

The nonlinearities $g_{1}(.,.)$ and $g_{2}(.,.)$ with $g_{1}(.,0)=0$ and $g_{2}(.,0)=0$ satisfy the following Lipschitz condition:

$$\begin{aligned}&|g_{1}(\sigma (t),x)-g_{1}(\sigma (t),y)|\le K_{\sigma (t)}|x-y|,\end{aligned}$$

(9)

$$\begin{aligned}&|g_{2}(\sigma (t),x)-g_{2}(\sigma (t),y)|\le L_{\sigma (t)}|x-y|, \end{aligned}$$

(10)

$\forall x,y\in \mathbb {R}^{n}$, $\forall t\in [0,+\infty )$. For every fixed $\sigma (t)=r\in \mathfrak {M}$, $K_{r}$ and $L_{r}$ are positive constants.

Lemma 1

[46]: Let $x,y\in \mathbb {R}^{n}$, $Q\in \mathbb {R}^{n\times n}$ be a positive semidefinite matrix, then the following inequality holds

$$\begin{aligned} 2x^{T}Qy\le x^{T}Qx+y^{T}Qy. \end{aligned}$$

Lemma 2

[46]: Assume that $\varOmega ,X_{1}$ and $X_{2}$ are constant matrices with appropriate dimensions, $0\le \varpi (t)\le 1$, then

$$\begin{aligned} \left\{ \begin{array}{ll} \varOmega +X_{1}<0,\\ \varOmega +X_{2}<0, \end{array} \right. \end{aligned}$$

(11)

is equivalent to

$$\begin{aligned} \varOmega +(1-\varpi (t))X_{1}+\varpi (t)X_{2}<0. \end{aligned}$$

(12)

Lemma 3

[3]: The following linear matrix inequality

$$\begin{aligned} \left[ \begin{array}{ccc} Q(x)&{}S(x)\\ S^{T}(x)&{}R(x)\\ \end{array} \right] >0, \end{aligned}$$

where $Q^{T}(x)=Q(x)$, $R^{T}(x)=R(x)$, is equivalent to either of the following conditions:

• 1) $Q(x)>0, R(x)-S^{T}(x)Q^{-1}(x)S(x)>0$;

• 2) $R(x)>0, Q(x)-S(x)R^{-1}(x)S^{T}(x)>0$.

Lemma 4

[9]: For any real matrices E and G and any real positive definite matrix P with compatible dimensions

$$\begin{aligned} EG+G^{T}E^{T}\le EPE^{T}+G^{T}P^{-1}G. \end{aligned}$$

(13)

3 Main results

In this section, the exponential synchronization of HISDNs with delayed impulses is investigated by using the Razumikhin theorem and the mathematical induction method. For this purpose, we need the following lemma to give an estimate of the solutions of the system (5) on $[t_{0}-\tau ,t_{0}+d]$.

Lemma 5

Consider system (5) and assume that Assumptions 1 and 2 hold and $(\ell -1)\delta _{1}< d\le \ell \delta _{1}$ for some positive integer $\ell$. Then, we have

$$\begin{aligned} |e(t)|\le \varrho _{0}\Vert \varPhi \Vert _{\tau },t\in [t_{0}-\tau ,t_{0}+d], \end{aligned}$$

(14)

where $\varrho _{0}=\alpha _{2}^{\ell }e^{\alpha _{1}d}$, $\alpha _{1}=\max _{r}\{|\mathbf {A}_{r}+\mathbf {C}_{r}|+K_{r}|\mathbf {B}_{r}|+L_{r}|\mathbf {D}_{r}|,r\in \mathfrak {M}\}$, $\alpha _{2}=\max _{r}\{1+|\mathfrak {U}_{r}|,r\in \mathfrak {M}\}$.

Proof

Since $(\ell -1)\delta _{1}< d\le \ell \delta _{1}$, the maximum number of impulse times in the interval $(t_{0},t_{0}+d]$ is $\ell$. We assume that the impulsive instants on $(t_{0},t_{0}+d]$ are $t_{\omega },\omega =1,2,\ldots ,\ell _{0}\le \ell$.

When $t+\theta \in [t_{0}-\tau ,t_{0}]$, $|e(t+\theta )|\le \Vert \varPhi \Vert _{\tau }$.

When $t+\theta \in [t_{0},t_{1})$,

$$\begin{aligned}&|e(t+\theta )|\nonumber \\&\quad =|e(t_{0})+\int ^{t+\theta }_{t_{0}}\sum _{r=1}^{m}\pi _{r}(t)[(\mathbf {A}_{r}+\mathbf {C}_{r})e(s)\nonumber \\ {}&\qquad +\mathbf {B}_{r}\mathbf {G}_{1}(r,e(s))+\mathbf {D}_{r} \mathbf {G}_{2}(r,e(s-\tau (s)))]\mathrm{d}s|\nonumber \\ {}&\le |e(t_{0})|+\int ^{t+\theta }_{t_{0}}\sum _{r=1}^{m}\pi _{r}(t)[|\mathbf {A}_{r}+\mathbf {C}_{r}||e(s)|\nonumber \\ {}&\quad +K_{r}|\mathbf {B}_{r}||e(s)|+L_{r}|\mathbf {D}_{r}||e(s-\tau (s))|]\mathrm{d}s\nonumber \\ {}&\le \Vert \varPhi \Vert _{\tau }+\int ^{t}_{t_{0}}\sum _{r=1}^{m}\pi _{r}(t)(|\mathbf {A}_{r}+\mathbf {C}_{r}|+K_{r}|\mathbf {B}_{r}|\nonumber \\ {}&\qquad +L_{r}|\mathbf {D}_{r})|)\Vert e(s)\Vert _{\tau }\mathrm{d}s. \end{aligned}$$

(15)

For $t\in [t_{0},t_{1})$, it follows from (15) that

$$\begin{aligned} \Vert e(t)\Vert _{\tau }&\le \Vert \varPhi \Vert _{\tau }+\int ^{t}_{t_{0}}\sum _{r=1}^{m}\pi _{r}(t)(|\mathbf {A}_{r}+\mathbf {C}_{r}|+K_{r}|\mathbf {B}_{r}|\nonumber \\ {}&\quad +L_{r}|\mathbf {D}_{r})|)\Vert e(s)\Vert _{\tau }\mathrm{d}s\nonumber \\&\le \Vert \varPhi \Vert _{\tau }+\int ^{t}_{t_{0}}\alpha _{1}\Vert e(s)\Vert _{\tau }\mathrm{d}s. \end{aligned}$$

(16)

Applying the Gronwall inequality gives

$$\begin{aligned} \Vert e(t)\Vert _{\tau }&\le \Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t-t_{0})},t\in [t_{0},t_{1}). \end{aligned}$$

(17)

Moreover

$$\begin{aligned} |e(t_{1})|&=|e(t_{1}^{-})+\varDelta e((t_{1}^{-})|\nonumber \\ {}&=|e(t_{1}^{-})+\sum _{r=1}^{m}\pi _{r}(t_{1})\mathfrak {U}_{r}e((t_{1}-d_{1})^{-})|\nonumber \\ {}&\le [1+\sum _{r=1}^{m}(\pi _{r}(t_{1})|\mathfrak {U}_{r}|)]\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t_{1}-t_{0})}\nonumber \\ {}&\le \alpha _{2}\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t_{1}-t_{0})}. \end{aligned}$$

(18)

Hence, $|e(t)|\le \alpha _{2}\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t-t_{0})}$, $t\in [t_{0},t_{1}]$. Repeating the above argument, for $t\in [t_{0},t_{\ell _{0}}]$, one has

$$\begin{aligned} |e(t)|\le \alpha _{2}^{\ell _{0}}\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t-t_{0})}. \end{aligned}$$

(19)

Since there are no impulses on $(t_{l_{0}},t_{0}+d]$, we can obtain

$$\begin{aligned} |e(t)|&\le \Vert e(t_{\ell _{0}})\Vert _{\tau }e^{\alpha _{1}(t-t_{\ell _{0}})}\nonumber \\ {}&\le \alpha _{2}^{\ell _{0}}\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t_{\ell _{0}}-t_{0})}e^{\alpha _{1}(t-t_{l_{0}})}\nonumber \\ {}&\le \alpha _{2}^{\ell _{0}}\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}(t-t_{0})}\nonumber \\ {}&\le \alpha _{2}^{\ell }\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}d}. \end{aligned}$$

(20)

From (19) and (20), for any $t\in [t_{0}-\tau ,t_{0}+d]$, we have

$$\begin{aligned} |e(t)|\le \alpha _{2}^{\ell }\Vert \varPhi \Vert _{\tau }e^{\alpha _{1}d}. \end{aligned}$$

(21)

Thus, the proof is complete. $\square$

Theorem 1

Suppose that Assumptions 1 and 2 hold and the impulsive input delays $d_{k}$ satisfy $0\le d_{k}\le d$. If for a prescribed positive scalar $u\in (0,1)$, there exist positive constants $\lambda _{0}$, $\lambda _{1}$, $\beta _{r}$ and $\varsigma _{r},r\in \mathfrak {M}$, and positive definite matrices $P_{1},P_{2}\in \mathbb {R}^{nN\times nN}$ such that $\forall r\in \mathfrak {M}$, the following LMIs hold:

$$\begin{aligned}&\lambda _{0}I_{nN}\le P_{j}\le \lambda _{1}I_{nN} \end{aligned}$$

(22)

$$\begin{aligned}&\left( \frac{\beta _{r}}{u}+\frac{\ln u}{\delta _{2}}\right) P_{j}+P_{j}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{j}+P_{j}\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P_{j}\nonumber \\&\quad +\,2\lambda _{r}K_{r}|\mathbf {B}_{r}|I_{nN} +\lambda _{r}L_{r}|\mathbf {D}_{r}|I_{nN}+\frac{P_{1} -P_{2}}{\delta _{h}}<0\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}&\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}-\beta _{r}P_{j}<0 \end{aligned}$$

(24)

$$\begin{aligned}&\left[ \begin{array}{ccc} \varPi _{r}P_{1}&{}(I_{nN}+\mathfrak {U}_{r})^{T}P_{2}&{}0\\ \star &{}-P_{2}&{}P_{2}\mathfrak {U}_{r}\\ \star &{}\star &{}-\varsigma _{r}I_{nN} \end{array} \right] <0, \end{aligned}$$

(25)

where $\varPi _{r}=-(u-\varsigma _{r}\frac{\alpha _{4}^{2}}{\lambda _{0}})$, $j=1,2$, $h=1,2$, $\alpha _{4}=d\alpha _{1}+\ell \alpha _{3}$, $\alpha _{3}=\max _{r}\{|\mathfrak {U}_{r}|,r\in \mathfrak {M}\}$, and the other parameters are as defined in Lemma 5. Then the HISDNs in (1) is exponentially synchronized under the arbitrary switching signals.

Proof

From (23), (24) and (25), there exist small enough scalars $\varepsilon _{0}$ and $\varepsilon _{1}\in (0,1-u)$ such that (22) and the following LMIs hold:

$$\begin{aligned}&\left( \varepsilon _{0}+\frac{\beta _{r}}{u}+\frac{\ln (u+\varepsilon _{1})}{\delta _{2}}\right) P_{j}+P_{j}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{j}+P_{j}\mathbf {A}_{r}\nonumber \\&\quad +\,\mathbf {A}_{r}^{T}P_{j}+2\lambda _{r}K_{r}|\mathbf {B}_{r}|I_{nN} +\lambda _{r}L_{r}|\mathbf {D}_{r}|I_{nN}\nonumber \\&\quad +\frac{P_{1}-P_{2}}{\delta _{h}}<0, \end{aligned}$$

(26)

$$\begin{aligned}&\quad \lambda _{r}L_{r}| \mathbf {D}_{r}|I_{nN}-\beta _{r}e^{-\varepsilon _{0}\tau }P_{j}<0, \end{aligned}$$

(27)

$$\begin{aligned}&\quad \left[ \begin{array}{ccc} \tilde{\varPi }_{r}P_{1}&{}(I_{nN}+\mathfrak {U}_{r})^{T}P_{2}&{}0\\ \star &{}-P_{2}&{}P_{2}\mathfrak {U}_{r}\\ \star &{}\star &{}-\varsigma _{r}I_{nN} \end{array} \right] <0, \end{aligned}$$

(28)

where $\tilde{\varPi }_{r}=-(u-\varsigma _{r}\frac{\tilde{\alpha }_{4}^{2}}{\lambda _{0}})$, $\tilde{\alpha }_{4}=d\alpha _{1} e^{\frac{\varepsilon _{0}(\tau +d)}{2}}+\ell \alpha _{3}e^{\varepsilon _{0}d}$. We introduce the following piecewise linear functions $\rho :[t_{0},\infty )\rightarrow (0,1]$:

$$\begin{aligned} \rho (t)=\frac{t_{k}-t}{t_{k}-t_{k-1}},t\in [t_{k-1},t_{k}),k\in \mathbb {N}^{+}. \end{aligned}$$

It is easy to see that

$$\begin{aligned} \rho (t_{k}^{-})=0,\quad \rho (t_{k})=\rho (t_{k}^{+})=1,k\in \mathbb {N}^{+}. \end{aligned}$$

(29)

Consider the following time-dependent Lyapunov function for system (5):

$$\begin{aligned} V(t)&=e^{T}(t)[(1-\rho (t))P_{1}+\rho (t)P_{2}]e(t). \end{aligned}$$

(30)

For simpleness, set $P(t)=(1-\rho (t))P_{1}+\rho (t)P_{2}$.

For any given scalar $\varrho$, choose $\varrho _{1}>0$ such that $\lambda _{1}(\varrho _{0}\varrho _{1})^{2}<u\lambda _{0}\varrho$. By Lemma 5, we have $|e(t)|\le \varrho _{0}\Vert \varPhi \Vert _{\tau }$ $\le \varrho _{0}\varrho _{1}$ for $t\in [t_{0}-\tau ,t_{0}+d]$.

In the following, we will prove that

$$\begin{aligned} V(t)\le \lambda _{0}\varrho ^{2}e^{-\varepsilon _{0}(t-t_{0}-d)},\quad t\in [t_{0}-\tau ,+\infty ). \end{aligned}$$

(31)

We assume that the impulsive time sequence on $(t_{0}+d,+\infty )$ is $\{t_{k}\},k=1,2,\ldots$ For any given $t\in [t_{k},t_{k+1})$, set $W(t)=e^{\varepsilon _{0}(t-t_{0}-d)}V(t)$. We claim that

$$\begin{aligned} W(t)<\lambda _{0}\varrho ^{2},\quad t\in [t_{0}-\tau ,+\infty ). \end{aligned}$$

(32)

In the following, we will use the mathematical induction method to show that (32) holds.

Firstly, we will prove that

$$\begin{aligned} W(t)<\lambda _{0}\varrho ^{2},\quad t\in [t_{0}-\tau ,t_{1}). \end{aligned}$$

(33)

We divide the proof of (33) into the following two steps:

Step 1: From Lemma 5, when $t\in [t_{0}-\tau ,t_{0}+d]$,

$$\begin{aligned} W(t)&=e^{\varepsilon _{0}(t-t_{0}-d)}e^{T}(t)P(t)e(t)\le \lambda _{1}|e(t)|^{2}\nonumber \\ {}&\le \lambda _{1}\varrho _{0}^{2}\Vert \varPhi \Vert _{\tau }^{2}\le \lambda _{1}(\varrho _{0}\varrho _{1})^{2}\le u\lambda _{0}\varrho ^{2}. \end{aligned}$$

(34)

Step 2: In the following, we will prove that

$$\begin{aligned} W(t)<\lambda _{0}\varrho ^{2},\quad t\in (t_{0}+d,t_{1}). \end{aligned}$$

(35)

If it is not true, there exists $t\in (t_{0}+d,t_{1})$ such that $W(t)\ge \lambda _{0}\varrho ^{2}$. Set $t^{*}=\inf \{t\in [t_{0}+d,t_{1});W(t)\ge \lambda _{0}\varrho ^{2}\}$. Then we have $W(t^{*})=\lambda _{0}\varrho ^{2}$. Set $t_{*}=\sup \{t\in [t_{0}+d,t^{*}):W(t)\le u\lambda _{0}\varrho ^{2}\}$, then $W(t_{*})=u\lambda _{0}\varrho ^{2}$. Therefore, for $t\in [t_{*},t^{*}],$

$$\begin{aligned} W(t)\ge u\lambda _{0}\varrho ^{2}\ge uW(t+\theta ),\theta \in [-\tau ,0]. \end{aligned}$$

(36)

When $t\in [t_{*},t^{*}]$, we have

$$\begin{aligned} D^{+}V(t)= & {} 2e^{T}(t)P(t)\sum _{r=1}^{m}\pi _{r}(t)[\mathbf {C}_{r}e(t) \nonumber \\&+\,\mathbf {B}_{r}\mathbf {G}_{1}(r,e(t))\nonumber \\&+\,\mathbf {D}_{r}\mathbf {G}_{2}(r,e(t-\tau (t))+\mathbf {A}e(t)]\nonumber \\&+\,e^{T}(t)\dot{P}(t)e(t). \end{aligned}$$

(37)

In view of Lemma 1, (22) and Assumption 2, the following inequalities can be obtained:

$$\begin{aligned} 2e&^{T}(t)P(t)\mathbf {B}_{r}\mathbf {G}_{1}(r,e(t))\nonumber \\ {}&\le 2\lambda _{1}|e(t)|\sqrt{|\mathbf {B}_{r}\mathbf {G}_{1}(r,e(t))|^{2}}\nonumber \\ {}&\le 2\lambda _{1}K_{r}|\mathbf {B}_{r}|e^{T}(t)e(t), \end{aligned}$$

(38)

$$\begin{aligned} 2e&^{T}(t)P(t)\mathbf {D}_{r}\mathbf {G}_{2}(r,e(t-\tau (t)))\nonumber \\ {}&\le 2\lambda _{1}\sqrt{|e(t)|^{2}}\sqrt{|\mathbf {D}_{r}\mathbf {G}_{2}(r,e(t-\tau (t)))|^{2}}\nonumber \\ {}&\le 2\lambda _{1}L_{r}|\mathbf {D}_{r}|\sqrt{|e(t)|^{2}}\sqrt{|e(t-\tau (t)))|^{2}}\nonumber \\ {}&\le \lambda _{1}L_{r}|\mathbf {D}_{r}|e^{T}(t)e(t)\nonumber \\ {}&\quad +\lambda _{1}L_{r}|\mathbf {D}_{r}|e^{T}(t-\tau (t))e(t-\tau (t)). \end{aligned}$$

(39)

From (38) and (39), we have

$$\begin{aligned} D^{+}V(t)&\le \sum _{r=1}^{m}\pi _{r}(t)\{e^{T}(t)[P(t)\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P(t)\nonumber \\ {}&\quad +P(t)\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P(t)+2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}\nonumber \\ {}&\quad +\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+\dot{P}(t)]e(t)\nonumber \\ {}&\quad +\lambda _{1}L_{r}|\mathbf {D}_{r}|e^{T}(t-\tau (t))e(t-\tau (t))\}. \end{aligned}$$

(40)

It follows from (40) that for $t\in [t_{*},t^{*}]$,

$$\begin{aligned} D^{+}&W(t)\nonumber \\ {}&=e^{\varepsilon _{0}(t-t_{0}-d)}(\varepsilon _{0}V(t)+D^{+}V(t))\nonumber \\ {}&\le e^{\varepsilon _{0}(t-t_{0}-d)}[\sum _{r=1}^{m}\pi _{r}(t)\varepsilon _{0}V(t)+D^{+}V(t)]\nonumber \\ {}&\quad +\sum _{r=1}^{m}\pi _{r}(t)\beta _{r}(\frac{1}{u}W(t)-W(t-\tau (t)))\nonumber \\ {}&\quad -\sum _{r=1}^{m}\pi _{r}(t)u_{1}W(t)+u_{1}W(t)\nonumber \\ {}&\le e^{\varepsilon _{0}(t-t_{0}-d)}\sum _{r=1}^{m}\pi _{r}(t)\{\varepsilon _{0}V(t)+e^{T}(t)[P(t)\mathbf {C}_{r}\nonumber \\ {}&\quad +\mathbf {C}_{r}^{T}P(t)+P(t)\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P(t)\nonumber \\ {}&\quad +2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+\dot{P}(t)]e(t)\nonumber \\ {}&\quad +\lambda _{1}L_{r}|\mathbf {D}_{r}|e^{T}(t-\tau (t))e(t-\tau (t))\nonumber \\ {}&\quad +\frac{\beta _{r}}{u}V(t)-\beta _{r}e^{-\varepsilon _{0}\tau }V(t-\tau (t))-u_{1}V(t)\}\nonumber \\ {}&\quad +u_{1}W(t)\nonumber \\ {}&\le e^{\varepsilon _{0}(t-t_{0}-d)}\sum _{r=1}^{m}\pi _{r}(t)\{e^{T}(t)[(\varepsilon _{0}+\frac{\beta _{r}}{u}-u_{1})P(t)\nonumber \\ {}&\quad +P(t)\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P(t)+P(t)\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P(t)\nonumber \\ {}&\quad +2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+\dot{P}(t)]e(t)\}\nonumber \\ {}&\quad +e^{\varepsilon _{0}(t-t_{0}-d)}\sum _{r=1}^{m}\pi _{r}(t)e^{T}(t-\tau (t))[\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}\nonumber \\ {}&\quad -\beta _{r}e^{-\varepsilon _{0}\tau }P(t)]e(t-\tau (t))+u_{1}W(t), \end{aligned}$$

(41)

where $u_{1}=-\frac{\ln (u+\varepsilon _{1})}{\delta _{2}}$.

From the definition of P(t), we have

$$\begin{aligned} \dot{P}(t)=\frac{1}{t_{k}-t_{k-1}}(P_{1}-P_{2}). \end{aligned}$$

(42)

In view of Assumption 1, one has

$$\begin{aligned} \frac{1}{\delta _{2}}\le \frac{1}{t_{k}-t_{k-1}}\le \frac{1}{\delta _{1}}. \end{aligned}$$

(43)

Then, there exists a function $\pi (t):(0,+\infty )\rightarrow [0,1]$ such that

$$\begin{aligned} \frac{1}{t_{k}-t_{k-1}}=(1-\pi (t))\frac{1}{\delta _{1}}+\pi (t)\frac{1}{\delta _{2}}. \end{aligned}$$

(44)

From (41) to (44), we have

$$\begin{aligned}&\left( \varepsilon _{0}+\frac{\beta _{r}}{u}-u_{1}\right) P(t)+P(t)\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P(t)+P(t)\mathbf {A}_{r}\nonumber \\&\quad +\,\mathbf {A}_{r}^{T}P(t)+2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+\dot{P}(t)\nonumber \\&\quad =2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+(1-\rho (t))[(\varepsilon _{0}\nonumber \\&\quad +\,\frac{\beta _{r}}{u}-u_{1})P_{1}+P_{1}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{1}+P_{1}\mathbf {A}_{r} +\mathbf {A}_{r}^{T}P_{1}]\nonumber \\&\quad +\,\rho (t)[(\varepsilon _{0}+\frac{\beta _{r}}{u}-u_{1})P_{2}+P_{2}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{2}\nonumber \\&\quad +\,P_{2}\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P_{2}]+(1-\pi (t))\frac{P_{1}-P_{2}}{\delta _{1}}\nonumber \\&\quad +\,\pi (t)\frac{P_{1}-P_{2}}{\delta _{2}}. \end{aligned}$$

(45)

From Lemma 2, we know that (26) is equivalent to

$$\begin{aligned}&\left( \varepsilon _{0}+\frac{\beta _{r}}{u}+\frac{\ln (u+\varepsilon _{1})}{\delta _{2}}\right) P_{j}+P_{j}\mathbf {C}_{r}\nonumber \\&\quad +\,\mathbf {C}_{r}^{T}P_{j}+P_{j}\mathbf {A}_{r}\nonumber \\&\quad +\,\mathbf {A}_{r}^{T}P_{j}+2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}\nonumber \\&\quad +\,(1-\pi (t))\frac{P_{1}-P_{2}}{\delta _{1}}+\pi (t)\frac{P_{1}-P_{2}}{\delta _{2}}<0. \end{aligned}$$

(46)

Similarly, we know that (46) is equivalent to

$$\begin{aligned}&2\lambda _{1}K_{r}|\mathbf {B}_{r}|I_{nN}+\lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}+(1-\rho (t))[(\varepsilon _{0}\nonumber \\ {}&\quad +\frac{\beta _{r}}{u}-u_{1})P_{1}+P_{1}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{1}+P_{1}\mathbf {A}_{r} +\mathbf {A}_{r}^{T}P_{1}]\nonumber \\ {}&\quad +\rho (t)[(\varepsilon _{0}+\frac{\beta _{r}}{u}-u_{1})P_{2}+P_{2}\mathbf {C}_{r}+\mathbf {C}_{r}^{T}P_{2}\nonumber \\&\quad +P_{2}\mathbf {A}_{r}+\mathbf {A}_{r}^{T}P_{2}]+(1-\pi (t))\frac{P_{1}-P_{2}}{\delta _{1}}\nonumber \\ {}&\quad +\pi (t)\frac{P_{1}-P_{2}}{\delta _{2}}<0. \end{aligned}$$

(47)

Then, we obtain that (45) is negative definition. And similarly , from (27), one can obtain

$$\begin{aligned} \lambda _{1}L_{r}|\mathbf {D}_{r}|I_{nN}-\beta _{r}e^{-\varepsilon _{0}\tau }P(t-\tau (t))<0. \end{aligned}$$

(48)

From (41), (47) and (48), we can obtain

$$\begin{aligned} D^{+}W_{r}(t)<u_{1}W_{r}(t), t\in [t_{*},t^{*}]. \end{aligned}$$

(49)

It leads to

$$\begin{aligned} W_{r}(t^{*})\le W_{r}(t_{*})e^{u_{1}\delta _{2}}\le u\lambda _{0}\varrho ^{2}e^{u_{1}\delta _{2}}<\lambda _{0}\varrho ^{2}. \end{aligned}$$

(50)

This is a contradiction. Therefore, (33) holds.

Secondly, we assume that for some $k\in \mathbb {N}^{+}$

$$\begin{aligned} W(t)<\lambda _{0}\varrho ^{2},t\in [t_{0}-\tau ,t_{k}). \end{aligned}$$

(51)

Then, we will prove that

$$\begin{aligned} W(t)<\lambda _{0}\varrho ^{2},\quad t\in [t_{k},t_{k+1}). \end{aligned}$$

(52)

By (51), we have

$$\begin{aligned} |e(t)|^{2}\le \varrho ^{2}e^{-\varepsilon _{0}(t-t_{0}-d)},t\in [t_{0}-\tau ,t_{k}). \end{aligned}$$

(53)

Since $\delta _{1}\le t_{k}-t_{k-1}\le \delta _{2}$, and similar to Lemma 5, there are at most $\ell$ impulse time on the interval $[t_{k}-d_{k},t_{k})$. We assume that impulsive instants are $t_{k_{\jmath }},\jmath =1,2,\ldots ,\ell _{0}\le \ell$. By (15), (16) and (53), we get

$$\begin{aligned} |e(t&_{k}^{-})-e((t_{k}-d_{k})^{-})|\nonumber \\ {}&=|\int _{t_{k}-d_{k}}^{t_{k}}\dot{e}(s)\mathrm{d}s-\sum _{\jmath =1}^{\ell _{0}}\varDelta e(t_{k_{\jmath }})|\nonumber \\ {}&\le \int _{t_{k}-d_{k}}^{t_{k}}|\dot{e}(s)|\mathrm{d}s+\sum _{j=1}^{\ell _{0}}|\varDelta e(t_{m_{\jmath }})|\nonumber \\&\le \int _{t_{k}-d_{k}}^{t_{k}}\alpha _{1}\Vert e(s)\Vert _{\tau }\mathrm{d}s+\sum _{\jmath =1}^{\ell _{0}}\alpha _{3}|e((t_{k_{\jmath }}-d_{k_{\jmath }})^{-})|\nonumber \\ {}&\le (d\alpha _{1}e^{\frac{\varepsilon _{0}(d+\tau )}{2}}+\ell _{0}\alpha _{3}e^{\varepsilon _{0}d})\varrho e^{-\frac{\varepsilon _{0}}{2}(t_{k}-t_{0}-d)}\nonumber \\ {}&\le \tilde{\alpha }_{4}\varrho e^{-\frac{\varepsilon _{0}}{2}(t_{k}-t_{0}-d)}. \end{aligned}$$

(54)

From the definition of P(t), one can obtain that $V(t_{k})=V(t_{k}^{+})=e^{T}(t_{k}^{+})P_{2}e(t_{k}^{+})$ and $V(t_{k}^{-})=e^{T}(t_{k}^{-})P_{1}e(t_{k}^{-})$. Set $\varDelta \tilde{e}(t_{k})=e((t_{k}-d_{k})^{-})-e(t_{k}^{-})$. Pre- and post-multiplying (28) by diag$\{e^{T}(t^{-}_{k}),I_{nN},I_{nN}\}$ and its transpose, respectively, we have

$$\begin{aligned} \left[ \begin{array}{ccc} \tilde{\varPi }_{r}V(t_{k}^{-}) &{}\varTheta _{12}&{}0\\ \star &{}-P_{2}&{}P_{2}\mathfrak {U}_{r}\\ \star &{}\star &{}-\varsigma _{r}I_{nN} \end{array} \right] <0, \end{aligned}$$

(55)

where $\varTheta _{12}=e^{T}(t_{k}^{-})(I_{nN}+\mathfrak {U}_{r})^{T}P_{2}$.

It follows from (51) that

$$\begin{aligned} \left[ \begin{array}{ccc} \varTheta _{11} &{}\varTheta _{12}&{}0\\ \star &{}-P_{2}&{}P_{2}\mathfrak {U}_{r}\\ \star &{}\star &{}-\varsigma _{r}I_{nN} \end{array} \right] <0, \end{aligned}$$

(56)

where $\varTheta _{11}=-(u-\lambda _{0}\varsigma _{r}\tilde{\alpha }_{4}^{2})\varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)}$.

Then, by (54), (56) and Lemma 3, we further obtain

$$\begin{aligned}&\left[ \begin{array}{cc} \varTheta _{11}&{}\varTheta _{12}\\ \star &{}-P_{2} \end{array} \right] +\varsigma _{r}\left[ \begin{array}{cc} \varDelta \tilde{e}^{T}(t_{k}^{-})\\ 0 \end{array} \right] \left[ \begin{array}{cc} \varDelta \tilde{e}(t_{k}^{-})&0 \end{array} \right] \nonumber \\&\quad +\varsigma _{r}^{-1}\left[ \begin{array}{cc} 0\\ P_{2}\mathfrak {U}_{r} \end{array} \right] \left[ \begin{array}{cc} 0&\mathfrak {U}_{r}^{T}P_{2} \end{array} \right] <0, \end{aligned}$$

(57)

By Lemma 4, for any scalars $\varsigma _{r}>0$,

$$\begin{aligned}&\left[ \begin{array}{cc} \varDelta \tilde{e}^{T}(t_{k}^{-})\\ 0 \end{array} \right] \left[ \begin{array}{cc} 0&\mathfrak {U}_{r}^{T}P_{2} \end{array} \right] + \left[ \begin{array}{cc} 0\\ P_{2}\mathfrak {U}_{r} \end{array} \right] \left[ \begin{array}{cc} \varDelta \tilde{e}^{T}(t_{k}^{-})&0 \end{array} \right] \nonumber \\ {}&\quad \le \varsigma _{r}\left[ \begin{array}{cc} \varDelta \tilde{e}^{T}(t_{k}^{-})\\ 0 \end{array} \right] \left[ \begin{array}{cc} \varDelta \tilde{e}(t_{k}^{-})&0 \end{array} \right] \nonumber \\ {}&\quad +\varsigma _{r}^{-1}\left[ \begin{array}{cc} 0\\ P_{2}\mathfrak {U}_{r} \end{array} \right] \left[ \begin{array}{cc} 0&\mathfrak {U}_{r}^{T}P_{2} \end{array} \right] <0. \end{aligned}$$

(58)

Combining (57) and (58), and noting $e(t_{k})=e(t_{k}^{-})+\mathfrak {U}_{r}e((t_{k}-d_{k})^{-})$, we have

$$\begin{aligned} \left[ \begin{array}{cc} -u\lambda _{0}\varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)}&{}e^{T}(t_{k})P_{2}\\ \star &{}-P_{2} \end{array} \right] <0. \end{aligned}$$

(59)

Then, by Lemma 3, we have

$$\begin{aligned} V(t_{k})&=V(t_{k}^{+})=e^{T}(t_{k}^{+})P_{2}e(t_{k}^{+})\\\nonumber&=e^{T}(t_{k})P_{2}e^{T}(t_{k})<u\lambda _{0}\varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)} \end{aligned}$$

(60)

which means that

$$\begin{aligned} |e(t_{k})|^{2}\le \varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)} \end{aligned}$$

(61)

Thus, we obtain $W_{\sigma (t_{k}})<u\lambda _{0}\varrho ^{2}<\lambda _{0}\varrho ^{2}$. Therefore, if (52) is not true, there exists $t\in [t_{k},t_{k+1})$ such that $W(t)\ge \lambda _{0}\varrho ^{2}$. Set $t^{*}=\inf \{t\in [t_{k},t_{k+1}) :W(t)\ge \lambda _{0}\varrho ^{2}\}$ and $t_{*}=\sup \{t\in [t_{k},t^{*}) :W(t)\le u\lambda _{0}\varrho ^{2}\}$. Then (52) can be obtained by using the similar argument in the proof of (35) directly and therefore the claim in (32) holds by the mathematical induction method. This completes the proof. $\square$

Remark 3

Recently, the exponential stability problem was studied for nonlinear time delay systems with delayed impulses in [4], in which the switching effect was ignored. Compared with [4], the differences are as follows.

(1) Model Difference Firstly, in this paper, the synchronization problem is studied for a class of coupled switched dynamical networks with delayed impulses. Secondly, the switching and delayed impulsive effects are considered simultaneously in this paper, which can render more dynamic behaviors of systems.

(2) Method Difference In [4], the Lyapunov function method and the Razumikhin scheme were used to deal with the delayed impulses. In this paper, by constructing a time-dependent Lyapunov function and combining the Razumikhin scheme with the mathematical induction method, the synchronization problem of HISDNs with impulsive input delay is investigated. In this paper, the time-dependent Lyapunov function plays a key role in deriving our main results. The latter Remark 5 shows this point in detail.

If there are no impulsive input delays in (1), then model (1) reduces to the following HISDNs:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)=C_{\sigma (t)}x_{i}(t)+B_{\sigma (t)} g_{1}(\sigma (t),x_{i}(t))\\ \quad \quad \quad \quad +\,D_{\sigma (t)} g_{2}(\sigma (t),x_{i}(t-\tau (t)))\\ \quad \quad \quad \quad +\,\vartheta \sum \nolimits ^{N}_{j=1}a_{ij}^{\sigma (t)}\varGamma _{\sigma (t)} x_{j}(t),t\ne t_{k},k\in \mathbb {N}^{+},\\ x_{i}(t_{k}^{+})=x_{i}(t_{k}^{-})+\mu _{\sigma (t_{k})}x_{i}((t_{k})^{-}). \end{array} \right. \end{aligned}$$

(62)

For HISDNs in (62), the following corollary can be obtained directly.

Corollary 1

Suppose that Assumptions 1 and 2 hold. If for a prescribed positive scalar $u\in (0,1)$, there exist positive constants $\lambda _{0}$, $\lambda _{1}$, $\beta _{r}$, $r\in \mathfrak {M}$, and positive definite matrices $P_{1},P_{2}\in \mathbb {R}^{nN\times nN}$ such that for $\forall r\in \mathfrak {M}$, the LMIs (22)–(24) hold and

$$\begin{aligned} \left[ \begin{array}{cc} -uP_{1}&{}(I_{nN}+\mathfrak {U}_{r})^{T}P_{2}\\ \star &{}-P_{2} \end{array} \right] <0, \end{aligned}$$

(63)

where $j=1,2$, $h=1,2$. Then the HISDNs in (62) is exponentially synchronized under the arbitrary switching signals.

Remark 4

Recently, the synchronization problem was investigated for a class of coupled switched neural networks with mode-dependent impulsive effects by using the average dwell time approach and the comparison principle in [44]. It should be pointed out that the impulsive input delay was neglected in [44]. On the other hand, there are two theorems in [44], in which $|u_{r}+1|<1,\forall r\in \mathfrak {M}$ and $|u_{r}+1|>1,\forall r\in \mathfrak {M}$ are considered, respectively. However, our results can be applied to these two cases simultaneously. Hence, the model considered here is more general than the model in [44] and the results have wider applications than the results in [44].

If there are no switching signals in (1), then model (1) reduces to the following complex dynamical network with delayed impulses:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)=Cx_{i}(t)+B g_{1}(x_{i}(t))+Dg_{2}(x_{i}(t-\tau (t)))\\ \quad \quad \quad \quad +\,\vartheta \sum \nolimits ^{N}_{j=1}a_{ij}\varGamma x_{j}(t),t\ne t_{k},k\in \mathbb {N}^{+},\\ x_{i}(t_{k}^{+})=x_{i}(t_{k}^{-})+\mu _{k}x_{i}((t_{k}-d_{k})^{-}). \end{array} \right. \end{aligned}$$

(64)

Then, the following corollary can be obtained:

Corollary 2

Suppose that Assumptions 1 and 2 hold and the impulsive input delays $d_{k}$ satisfy $0\le d_{k}\le d$. If for a prescribed positive scalar $u\in (0,1)$, there exist positive constants $\lambda _{0}$, $\lambda _{1}$, $\varsigma$, $\beta$ and positive definite matrices $P_{1},P_{2}\in \mathbb {R}^{nN\times nN}$ such that (22) and the following LMIs hold:

$$\begin{aligned}&\left( \frac{\beta }{u}+\frac{\ln u}{\delta _{2}}\right) P_{j}+P_{j}\mathbf {C}+\mathbf {C}^{T}P_{j}+P_{j}\mathbf {A}+\mathbf {A}^{T}P_{j}\nonumber \\&\quad +\,2\lambda _{1}K|\mathbf {B}|I_{nN}+\lambda _{1}L|\mathbf {D}|I_{nN}+\frac{P_{1}-P_{2}}{\delta _{h}}<0, \end{aligned}$$

(65)

$$\begin{aligned}&\lambda _{1}L|\mathbf {D}|I_{nN}-\beta P_{j}<0, \end{aligned}$$

(66)

$$\begin{aligned}&\left[ \begin{array}{ccc} -\left( u-\varsigma \frac{\alpha _{4}^{2}}{\lambda _{0}}\right) P_{1}&{}(I_{nN}+\mathfrak {U}_{k})^{T}P_{2}&{}0\\ \star &{}-P_{2}&{}P_{2}\mathfrak {U}_{k}\\ \star &{}\star &{}-\varsigma I_{nN} \end{array} \right] <0,\nonumber \\ \end{aligned}$$

(67)

where $j=1,2$, $h=1,2$, $\mathbf {C}=I_{N}\otimes C$, $\mathbf {B}=I_{N}\otimes B$, $\mathbf {D}=I_{N}\otimes D$, $\mathbf {A}=\vartheta (A\otimes \varGamma )$, $\mathfrak {U}_{k}=I_{N}\otimes \mu _{k}$ $\alpha _{4}=d\alpha _{1}+\ell \alpha _{3}$, $\alpha _{1}=|\mathbf {A}+\mathbf {C}|+K|\mathbf {B}|+L|\mathbf {D}|$, $\alpha _{3}=\max _{1\le \jmath \le \ell _{k}}\{|\mathfrak {U}_{k_{j}}|\}$. $k_{\jmath }$ is the number of impulsive instants in the interval $[t_{k}-d_{k},t_{k})$, and $\mathfrak {U}_{k_{j}}$ are the corresponding impulsive gain and $\ell _{k}$ is the number of impulses in $[t_{k}-d_{k},t_{k})$. The other parameters are as defined in Lemma 5 and Theorem 1. Then the impulsive dynamical networks in (64) is exponentially synchronized.

Remark 5

Recently, the delayed impulsive control problem was studied for complex dynamical networks with stochastic disturbances in [45]. However, it can be seen that we focus on revealing the relationship among impulses, switching and time delay. On the other hand, in [45], a time-independent Lyapunov function $V_{0}(t)=e^{T}(t)e(t)$ was used to prove the main results. In this paper, a time-dependent Lyapunov function $V(t)=e^{T}(t)[(1-\rho (t))P_{1}+\rho (t)P_{2}]e(t)$ have been used to prove the main results. There are three important features of the time-dependent Lyapunov function that are worth mentioning: Firstly, when $P_{1}=P_{2}=I_{nN}$, V(t) reduces to $V_{0}(t)$, which shows that the time-independent Lyapunov function method in [45] can be viewed as a special case of the time-dependent Lyapunov function method. Secondly, according to (22–25) in Theorem 1, one can find that the results obtained by using V(t) have better conservativeness than the results obtained by using $V_{0}(t)$. Thirdly, the time-independent Lyapunov function $V_{0}(t)$ cannot be applied to our results. The reason is as follows. In the proof of this paper, the inequality $|e(t_{k})|^{2}\le \varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)}$ is of vital importance. However, if we use $V_{0}(t)$ to prove our main results, the following inequality will be obtained:

$$\begin{aligned} V_{0}(t_{k})=&e^{T}(t_{k})e(t_{k})\nonumber \\ =&[e(t_{k}^{-})+\mu _{\sigma (t_{k})}(e(t_{k}^{-})+)\varDelta \tilde{e}(t_{k})]^{T}\nonumber \\ {}&\times [e(t_{k}^{-})+\mu _{\sigma (t_{k})}(e(t_{k}^{-})+)\varDelta \tilde{e}(t_{k})]\nonumber \\ \le&2(1+\mu _{\sigma (t_{k})})^{2}|e(t_{k}^{-})|^{2}+2\mu _{\sigma (t_{k})}^{2}|\varDelta \tilde{e}(t_{k})|^{2}\nonumber \\ \le&[2(1+\mu _{r})^{2}+2\mu _{r}^{2}\tilde{\alpha }_{4}]\varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)}\nonumber \\ \le&\varrho ^{2}e^{-\varepsilon _{0}(t_{k}-t_{0}-d)}. \end{aligned}$$

(68)

Then the following condition will be imposed according to the method in [45]: $2(1+\mu _{r})^{2}+2\mu _{r}^{2}\tilde{\alpha }_{4}<1$, which means that $|1+u_{r}|\le \frac{\sqrt{2}}{2}$. However, in this paper, the impulsive strength applies to not only $|u_{r}+1|<1$ but also $|u_{r}+1|>1$. Thus, by using the time-dependent Lyapunov function method, our results are less conservative than the results in [45].

4 Numerical example

In this section, an example is given to illustrate the effectiveness of the main results obtained in this paper.

Example 1

Consider a HISDNs with 100 nodes as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)=C_{\sigma (t)}x_{i}(t)+B_{\sigma (t)} g_{1}(\sigma (t),x_{i}(t))\\ \quad \quad \quad \quad +\,D_{\sigma (t)} g_{2}(\sigma (t),x_{i}(t-\tau (t)))\\ \quad \quad \quad \quad +\,\vartheta \sum \nolimits ^{100}_{j=1}a_{ij}^{\sigma (t)}\varGamma _{\sigma (t)} x_{j}(t),t\ne t_{k},k\in \mathbb {N}^{+},\\ x_{i}(t_{k}^{+})=x_{i}(t_{k}^{-})+\mu _{\sigma (t_{k})}x_{i}((t_{k}-d_{k})^{-}), \end{array} \right. \nonumber \\ \end{aligned}$$

(69)

where $\vartheta =0.3$, $d_{k}=0.2$, $\mathfrak {M}=\{1,2\}$, $\mu _{1}=-0.8$ and $\mu _{2}=0.15$, $g_{1}(1,x_{i}(t))=g_{2}(1,x_{i}(t))=g_{1}(2,x_{i}(t))=g_{2}(2,x_{i}(t))=(\frac{x_{i1}^{2}(t)}{x_{i1}^{2}(t)+1},\frac{x_{i2}^{2}(t)}{x_{i2}^{2}(t)+1})^{T}$, $\tau (t)=\frac{e^{t}}{1+e^{t}}+1$,

$$\begin{aligned}&C_{1}=\left[ \begin{array}{cc}0.5&{}-3.1\\ 1.9&{}-1.3\end{array}\right] ,\quad C_{2}=\left[ \begin{array}{cc}-0.4&{}0.3\\ 0.4&{}-0.3\end{array}\right] ,\quad \\&B_{1}=\left[ \begin{array}{cc}-0.1&{}0\\ 0.1&{}0.1\end{array}\right] ,\quad B_{2}=\left[ \begin{array}{cc}-0.2&{}0.2\\ 0&{}0.2\end{array}\right] \\&D_{1}=\left[ \begin{array}{cc}0.4&{}0.2\\ 0&{}0.03\end{array}\right] ,\quad D_{2}=\left[ \begin{array}{cc}0.3&{}0\\ 0&{}0.5\end{array}\right] ,\\&\varGamma _{1}=\left[ \begin{array}{cc}1&{}0\\ 0&{}1\end{array}\right] ,\quad \varGamma _{2}=\left[ \begin{array}{cc}1.1&{}0\\ 0&{}0.9\end{array}\right] \\&A_{1}=\left[ \begin{array}{cccccc}-99&{}1&{}1&{}\cdots &{}1&{}1\\ 1&{}-99&{}1&{}\cdots &{}1&{}1\\ 1&{}1&{}-99&{}\cdots &{}1&{}1\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 1&{}1&{}1&{}\cdots &{}-99&{}1\\ 1&{}1&{}1&{}\cdots &{}1&{}-99\end{array}\right] ,\\&A_{2}=\left[ \begin{array}{cccccc}-2&{}1&{}0&{}\cdots &{}0&{}1\\ 1&{}-2&{}1&{}\cdots &{}0&{}0\\ 0&{}1&{}-2&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}-2&{}1\\ 1&{}0&{}0&{}\cdots &{}1&{}-2\end{array}\right] . \end{aligned}$$

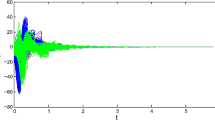
Here, we obtain $K_{1}=K_{2}=L_{1}=L_{2}=1$. Fix $u=0.85\in (0,1),\lambda _{0}=0.1$, $\lambda _{1}=0.4$, $\beta _{1}=\beta _{2}=1$, $\varsigma _{1}=0.13$, $\varsigma _{2}=0.27$. By solving (22–25), we have $\delta _{1}>0.1382$ and $\delta _{2}<1.066$. Figure 1a gives the impulsive sequences $u_{\sigma (t_{k})}$, and Fig. 1b gives the switching signal $\sigma (t)$. From Fig. 1, one can find that the impulsive effects can be activated not only at the instants coinciding with the system switching but also at the instants when there is no system switching. Figure 2 gives the synchronization errors $e_{i}(t)$, from which, it can be seen that the simulation confirms the theoretical results well.

Fig. 1

a The impulsive sequences $u_{\sigma (t_{k})}$ where $u_{1}=-0.8$, $u_{2}=0.15$; b the switching signal $\sigma (t)$

Fig. 2

a The synchronization errors of $e_{i1}(t)$ of the HISDNs in (69); b the synchronization errors of $e_{i2}(t)$ of the HISDNs in (69)

5 Conclusion

In this paper, synchronization of HISDNs with delayed impulsive effects has been investigated, where the impulsive instances and system switching instances don’t need to be coincident. Based on the Razumikhin theorem and the mathematical induction method, several synchronization criteria have been obtained in term of LMIs such that the addressed systems can be synchronized to a desired state. Finally, a numerical example has been given to illustrate the effectiveness of our results. In the future, it is interesting to investigate synchronization of HISDNs with stochastic disturbances.