1 Introduction

Vibro-impact systems, as typical nonlinear dynamical systems, widely exist in the field of engineering and physics [1–3]. The behaviors of these vibro-impact systems are complex and unusual because they behave as continuous dynamical systems between two successive impacts and develop a discrete behavior when reaching a constraint. There have been considerably extensive efforts to investigate the response of vibro-impact systems on different aspects. For example, the stability and bifurcation of the vibrations of vibro-impact systems under deterministic excitation were studied by many researchers, e.g., [4–7]. Several non-smooth coordinate transformation techniques were also developed and studied for vibro-impact vibration [8–12]. In particular, the stochastic response of vibro-impact systems has received more and more attention in the past decades [13–24]. In these investigations, the stochastic averaging method was extensively adopted using different impact models. The model with instantaneous repetitive impacts was used in quite a few researches  [13–18]. For this impact model, a restitution factor is used between impact and rebound velocities to describe the energy loss according to the Newton’s law. By contrast, a Hertzian contact model with the well-known 3/2-power law was also used to describe impacts [19]. Besides, Monte Carlo simulation was adopted to investigate the response probability density function (PDF) of vibro-impact systems using the model with instantaneous repetitive impacts [20]. In addition, a numerical path integration method was developed together with the Zhuravlev–Ivanov coordinate transformation for obtaining the response PDF of stochastic vibro-impact systems with high energy losses at impacts [21]. Recently, a solution procedure has been proposed to obtain the stationary PDF of lightly vibro-impact systems for different cases of Gaussian white noises [22–24]. The solution procedure consists of Zhuravlev non-smooth coordinate transformation [2, 13], the exponential–polynomial closure (EPC) method [25–27] and the methodology on the PDF solution of a function of variables [28]. The PDF solutions obtained with the proposed solution procedure agree with the simulated results, especially in the tail regions.

Although extensive work has been done on the stochastic response of vibro-impact systems, the above studies are limited to the cases of Gaussian white noise, an irregularly continuous random excitation. In fact, the case of Poisson impulses is also worth being studied because this type of excitation represents a discrete sequence of random impulses arriving at random times. Poisson impulses can more adequately model some natural loadings in practice [29], e.g., ice impacts [30]. However, the stochastic response of vibro-impact systems has been scarcely addressed in the presence of Poisson impulses. Most relevant work on Poisson impulses is concerned with the response of smooth nonlinear systems under Poisson impulses. The response PDF solution is governed by the generalized Fokker–Planck–Kolmogorov (FPK) equation (i.e., the Kolmogorov–Feller equation) [31–34]. The generalized FPK equation is too complex in its form to be exactly solved in most cases [35–37]. Most problems have to rely on approximation methods, such as perturbation method [31, 32], Petrov–Galerkin method [38], path integration technique [39–42] and finite difference approach [43]. As the statistical response moments of nonlinear systems are concerned, equivalent linearization methods [44–50] and cumulant-neglect closure methods [51–53] are extensively investigated. When the response of nonlinear systems is nearly Gaussian, these two methods can present adequate values for the statistical moments.

In this paper, a recently proposed solution procedure is extended to the case of Poisson impulses [22–24]. This study considers a one-sided constraint is located at the equilibrium position of the system and the system collides with the constraint by instantaneous repetitive impacts. The solution procedure consists of three steps. First, the Zhuravlev non-smooth coordinate transformation is utilized to convert the original vibro-impact system into a new system without any barrier by introducing an additional damping term. Second, the PDF of the new system is obtained with the EPC method by solving the generalized FPK equation. Last, the PDF of the original system is formulated in terms of the methodology on seeking the PDF of a function of random variables. Different nonlinearity degrees and excitation intensities are considered in four illustrative examples to show the effectiveness of the proposed solution procedure. When the polynomial order is six, the PDF obtained with the proposed solution procedure agrees well with the simulated result for both displacement and velocity, especially in the tail regions.

2 Problem formulation

2.1 A vibro-impact Duffing system

A single-degree-of-freedom vibro-impact Duffing system under Poisson impulses can be expressed as

$$\begin{aligned}&\ddot{y}+c\dot{y}+ky+\mu y^3=\xi (t),~~y>0 \end{aligned}$$
(1)
$$\begin{aligned}&\dot{y}_{+}=-r\dot{y}_{-},~~y=0,~0<r\le 1 \end{aligned}$$
(2)

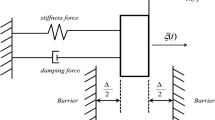
where \(\ddot{y}\), \(\dot{y}\) and y are the acceleration, velocity and displacement, respectively; c is the damping coefficient; k is the linear stiffness coefficient; \(\mu \) is the nonlinearity coefficient in displacement; \(\xi (t)\) is an excitation process of zero-mean Poisson impulses; r is the restitution factor; \(\dot{y}_{-}\) and \(\dot{y}_{+}\) are impact and rebound velocities, respectively. Correspondingly, Fig. 1a illustrates a vibro-impact Duffing system with a zero offset constraint. The constraint is located at the static equilibrium position of the system.

Fig. 1
figure 1

A vibro-impact system under Poisson impulses: a a Duffing system with a zero offset constraint; b representative Poisson impulses between 0 and 20 s in the case of \(\lambda =1\), \(\lambda E[Y^2]=0.1\) and Y is a zero-mean Gaussian variable

Full size image

In this paper, \(\xi (t)\) represents an excitation process of Poisson impulses as follows

$$\begin{aligned} \xi (t)=\sum _{k=1}^{N(T)}Y_{k}\delta (t-\tau _k) \end{aligned}$$
(3)

where N(T) is the total number of impulses arriving in the time interval \((-\infty ,T ]\). \(Y_k\) is the random amplitude of the kth impulse arriving at time \(\tau _k\). \(\delta (t)\) is the Dirac delta function. N(T) is assumed to yield the Poisson law with a constant impulse arrival rate \(\lambda \). The impulse amplitudes \(Y_k\) are independent and identically distributed (i.i.d.) random variables. These impulses are also independent of the impulse arrival time \(\tau _k\). The nth cumulant function of \(\xi _(t)\) is a multiplication of \((n-1)\) Dirac delta functions

$$\begin{aligned} \kappa _{n}[\xi (t_1),\ldots ,\xi (t_n)]=\lambda E[Y^n]\delta (t_2\!-\!t_1)\ldots \delta (t_n\!-\!t_1)\nonumber \\ \end{aligned}$$
(4)

Figure 1b shows a typical excitation process of Poisson impulses in the case of \(\lambda =1\) and \(\lambda E[Y^2]=0.1\), in which Y is a zero-mean Gaussian variable.

2.2 Non-smooth coordinate transformation

First, Eqs. (1) and (2) are combined into one equation by the Zhuravlev non-smooth coordinate transformation so that the new equation can be further handled by the generalized FPK equation. The transformation procedure is given in details in Refs. [2, 13] as follows

$$\begin{aligned} y=|z|=zsgn({z}),~\dot{y}=\dot{z}sgn({z}),~\ddot{y}=\ddot{z}sgn({z}) \end{aligned}$$
(5)

where \(\ddot{z}\), \(\dot{z}\) and z are the acceleration, velocity and displacement of the converted system, respectively; \(sgn(\bullet )\) is the sign function as follows

$$\begin{aligned} sgn(z)=\left\{ \begin{array}{l} 1, ~~~~~~ z>0\\ 0, ~~~~~~ z=0\\ -1,~~~~ z<0\\ \end{array} \right. \end{aligned}$$
(6)

Therefore, the last two items of Eq. (5) are formulated due to the fact that \({\text {d}}(sgn(z))/{\text {d}}t=0\).

Equation (2) presents the condition for each impact. Based on Eq. (5), Eq. (2) is reformulated into the below condition using the new variable

$$\begin{aligned} \dot{z}_{+}=r\dot{z}_{-}~~at~~z=0 \end{aligned}$$
(7)

where \(\dot{z}_{-}\) and \(\dot{z}_{+}\) are impact and rebound velocities before and after each impact for the converted system, respectively. After that, the reduction in the converted velocity jump is evaluated by an amount proportional to (\(1-r\)).

Subsequently, an additional impulsive damping term, as a substitute of Eq. (7), is introduced into the equation of motion for the converted system. Using this additional damping term, the equation of motion and the impact condition are integrated into one equation. In Refs. [2, 13], the Dirac delta function is used to introduce this velocity jump into the equation of motion as an additional impulsive damping term. The additional damping term due to impacts is approximately evaluated as

$$\begin{aligned}&(\dot{z}_{+}-\dot{z}_{-})\delta (t-t_i)=(1-r)\dot{z}\delta \nonumber \\&\quad (t-t_i), ~~{\text {given}}~{\text {that}}~~|\dot{z}_{+}|<|\dot{z}|<|\dot{z}_{-}| \end{aligned}$$
(8)

In Eq. (8), \(t_i\) is the time instant of each impact, which is implicitly determined by initial condition, system parameters and excitation intensity. Directly using the term with \(t_i\) in the transformed equation of motion leads to a complicated equation which is difficult to be solved. In order to remove the time instant \(t_i\) from the expression of the additional impulsive damping term, the transformation of variables from the time domain to the space domain is established by the following way.

It should be addressed that the restitution factor is assumed to be close to unity in the following transformation procedure. Therefore, (\(1-r\)) can be treated as a small parameter. In such a case, the response of the converted system may have much less significant discontinuities in its time derivative. Consequently, the response can be approximately treated as a continuous process. This assumption permits the vibro-impact problem to be handled by some conventional approximate methods [16, 54], e.g., FPK equation methods, equivalent linearization methods and stochastic averaging methods.

Since the response of the vibro-impact system can be approximated by a continuous process as explained above, the displacement in the vicinity of each impact can be approximated as follows

$$\begin{aligned} z(t)=z(t_i)+\dot{z}(t_i)(t-t_i) \end{aligned}$$
(9)

where \(z(t_i)\) is the displacement at the time instant of impacts \(t_i\). That is, \(z(t_i)\) is the location of equilibrium position and \(z(t_i)=0\). Subsequently, Eq. (9) is further written as

$$\begin{aligned} t-t_i=z(t)/\dot{z}(t_i) \end{aligned}$$
(10)

Considering Eq. (8), the Dirac delta function is applied to Eq. (10) in a small interval of the vicinity of each impact

$$\begin{aligned} \delta (t-t_i)=\delta (z(t)/\dot{z}(t_i)) \end{aligned}$$
(11)

Furthermore, the Dirac delta function has a property that \(\delta (z(t)/\dot{z}(t_i))=|\dot{z}|\delta (z)\), and Eq. (8) further reads

$$\begin{aligned} (1-r)\dot{z}\delta (t-t_i)=(1-r)\dot{z}|\dot{z}|\delta (z) \end{aligned}$$
(12)

After that, the time instant of each impact \(t_i\) is removed from the expression of the additional impulsive damping term. Equations (1) and (2) finally are integrated into one equation as follows

$$\begin{aligned} \ddot{z}+c\dot{z}+kz+\mu z^3+(1-r)\dot{z}|\dot{z}|\delta (z)=sgn(z)\xi (t)\nonumber \\ \end{aligned}$$
(13)

Some remarks are worth addressing on this non-smooth coordinate transformation procedure. This transformation procedure is performed by an approximate way. First, for Eq. (5), it is justified in autonomous conservative cases, when the barrier is eliminated completely, and the external load does not lead to multiple strikes against the barrier per one cycle of vibration. Therefore, the examined cases of this paper should approximately satisfy this requirement. Second, as Eq. (8) is concerned, the interval before and after an instantaneous impact is very small, and the restitution factor is assumed to be close to unity. In such a case, the magnitude of velocity is expected to be nearly uniform. Thus, \(\dot{z}\) is approximately adopted in Eq. (8) replacing \(\dot{z}_{+}\) and \(\dot{z}_{-}\) in the expression. Last, in general, introducing Dirac delta function into nonlinear differential equations complicates mathematical justification of the modeling [55]. It is an important issue on how delta function participates in these nonlinear differential equations. Grace et al. [11] presented a good interpretation of such a manipulation with delta function. In the transformation manipulation, \(\delta (z)\) is treated as a specific distribution applied to some testing function rather than the conventional Dirac delta function. It is because the term with the conventional Dirac delta function in Eq. (13) cannot be justified due to the discontinuous factor \(\dot{z}|\dot{z}|\) at \(z=0\). Herein, \(\delta (z)\) is used to take the value of the testing function at the one adjacent side of zero but not exactly at zero. In such a case, the term \((1-r)\dot{z}|\dot{z}|\delta (z)\) can present an approximate description for the energy loss at the barrier. Similarly, this specific definition of delta function has been used in some references, e.g.,  [1, 56–58].

2.3 Exponential–polynomial closure method

In this section, Eq. (13) is further handled by the generalized FPK equation which is approximately solved by the EPC method. Letting \(x_1=z\), \(x_2=\dot{z}\) , Eq. (13) can be formulated in a set of two first-order differential equations

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=-cx_2-kx_1-\mu x^3_1-(1-r)x_2|x_2|\delta (x_1)+sgn(x_1)\xi (t) \end{array} \right. \nonumber \\ \end{aligned}$$
(14)

The response \(\{x_1,x_2\}^T\) is approximated by a Markov process, and its PDF, i.e., \(p(x_1,x_2,t)\), is governed by the following generalized FPK equation

The generalized FPK equation is expressed in an infinite series form [34]

$$\begin{aligned}&\frac{\partial p(x_1,x_2,t)}{\partial t}=-x_2\frac{\partial p(x_1,x_2,t)}{\partial x_1}\nonumber \\&\quad +\,\frac{\partial }{\partial x_2}\{[cx_2+kx_1+\mu x^3_1\nonumber \\&\quad +\,(1-r)x_2|x_2|\delta (x_1)]p(x_1,x_2,t)\}\nonumber \\&\quad +\,\lambda \sum ^{\infty }_{j=1}\frac{(-1)^j}{j!}[sgn(x_1)]^jE[Y^j]\frac{\partial ^j p(x_1,x_2,t)}{\partial x_2^j}\nonumber \\ \end{aligned}$$
(15)

where \(E[\bullet ]\) denotes the expectation of \((\bullet )\). The FPK equation or the generalized FPK equation is a partial differential equation. It describes the time evaluation of the probability density function of the response of a system. For a linear system and a few specific single-degree-of-freedom nonlinear systems, some closed-form solutions (mostly stationary solutions) are available. When considering the non-stationary response of nonlinear systems, the FPK equation and generalized FPK equation are too complicated in their forms to be exactly solved. Although some numerical methods can be used, e.g., finite element method, finite difference method and path integration method, the associated solution procedure is still a tough and time-consuming task [59, 60]. In those methods, the spatial and temporal discretization of the initial-boundary value problem has to properly be handled. Meanwhile, some adequate associated techniques also need to be developed for solving the resulting non-symmetric system of linear, algebraic equations. On the other hand, other previous methods for stationary cases are also difficult to be extended directly for non-stationary cases.

In this paper, the EPC method is used to study the stationary PDF solution of vibro-impact systems. Therefore, the term on the left-hand side of Eq. (15) vanishes and Eq. (15) is reduced to be

$$\begin{aligned}&-x_2\frac{\partial p(x_1,x_2)}{\partial x_1}+\frac{\partial }{\partial x_2}\{[cx_2+kx_1+\mu x^3_1\nonumber \\&\quad +\,(1-r)x_2|x_2|\delta (x_1)]p(x_1,x_2)\}\nonumber \\&\quad -\,\lambda [sgn(x_1)]E[Y]\frac{\partial p(x_1,x_2)}{\partial x_2}\nonumber \\&\quad +\,\frac{1}{2!}\lambda E[Y^2]\frac{\partial ^2 p(x_1,x_2)}{\partial x^2_2}\nonumber \\&\quad -\,\frac{1}{3!}\lambda [sgn(x_1)]E[Y^3]\frac{\partial ^3 p(x_1,x_2)}{\partial x^3_2}\nonumber \\&\quad +\,\frac{1}{4!}\lambda E[Y^4]\frac{\partial ^4 p(x_1,x_2)}{\partial x^4_2}+\cdots =0 \end{aligned}$$
(16)

Equation (16) is too complicated in its form to be solved exactly, and the solution has to rely on some approximate methods. Herein, the EPC method is used and an approximate PDF solution \({\mathop {p}\limits ^{\sim }}(x_1,x_2;\mathbf{a})\) to Eq. (16) is assumed to be

$$\begin{aligned} {\mathop {p}\limits ^{\sim }}(x_1,x_2;\mathbf{a})=C\exp \{Q_n(x_1,x_2; \mathbf{a})\} \end{aligned}$$
(17)

where C is a normalization constant; \(\exp {\{\cdot \}}\) is an exponential function; \(\mathbf a\) is an unknown parameter vector containing \(N_p\) entries. The polynomial \(Q_n(x_1,x_2;\mathbf{a})\) is expressed as

$$\begin{aligned} Q_n(x_1,x_2;\mathbf{a})=\sum _{i=1}^{n}\sum _{j=0}^{i}a_{ij}x_{1}^{i-j}x_{2}^{j} \end{aligned}$$
(18)

which is an nth-degree polynomial in \(x_1\) and \(x_2\). It is also required that

$$\begin{aligned} \lim _{x_i\rightarrow \pm \infty }Q_n(x_1,x_2;\mathbf{a})= -\infty , i=1,2 \end{aligned}$$
(19)

Substituting \({\mathop {p}\limits ^{\sim }}(x_1,x_2;\mathbf{a})\) for \(p(x_1,x_2)\) leads to the following residual error

$$\begin{aligned}&\Delta (x_1,x_2;\mathbf{a})=-x_2\frac{\partial {\mathop {p}\limits ^{\sim }}}{\partial x_1}+\frac{\partial }{\partial x_2}\left\{ \left[ cx_2+kx_1+\mu x^3_1\right. \right. \nonumber \\&\quad + \left. \left. (1-r)x_2|x_2|\delta (x_1)\right] {\mathop {p}\limits ^{\sim }}\right\} \nonumber \\&\quad -\,\lambda [sgn(x_1)]E[Y]\frac{\partial {\mathop {p}\limits ^{\sim }}}{\partial x_2}+\frac{1}{2!}\lambda E[Y^2]\frac{\partial ^2{\mathop {p}\limits ^{\sim }}}{\partial x_2^2}\nonumber \\&\quad -\,\frac{1}{3!}\lambda [sgn(x_1)] E[Y^3]\frac{\partial ^3 {\mathop {p}\limits ^{\sim }}}{\partial x_2^3}+\frac{1}{4!}\lambda E[Y^4]\frac{\partial ^4{\mathop {p}\limits ^{\sim }}}{\partial x_2^4} \end{aligned}$$
(20)

Furthermore, only the terms up to fourth-order derivative are retained from Eq. (16) for analysis. It is based on the assumption that higher-order terms have relatively small magnitudes compared with the lower-order terms. When the impulse arrival rate is moderate or high, this assumption is usually satisfied. In such a case, the approximate solution is expected to work well.

Substituting Eq. (17) into Eq. (20), the residual error is formulated as

$$\begin{aligned} \Delta (x_1,x_2;\mathbf{a})=F(x_1,x_2;\mathbf{a}){\mathop {p}\limits ^{\sim }}(x_1,x_2; \mathbf{a}) \end{aligned}$$
(21)

where

$$\begin{aligned} F(x_1,x_2;\mathbf{a})= & {} -x_2\frac{\partial Q_n}{\partial x_1}+[cx_2+kx_1+\mu x^3_1\nonumber \\&+\,(1-r)x_2|x_2|\delta (x_1)]\frac{\partial Q_n}{\partial x_2}\nonumber \\&-\,\lambda [sgn(x_1)]E[Y]\frac{\partial Q_n}{\partial x_2}\nonumber \\&+\,\frac{1}{2!}\lambda E[Y^2]\left[ \frac{\partial ^2 Q_n}{\partial x_2^2}+\left( \frac{\partial Q_n}{\partial x_2}\right) ^2 \right] \nonumber \\&-\,\frac{1}{3!}\lambda [sgn(x_1)]E[Y^3]\nonumber \\&\times \,\left[ \frac{\partial ^3 Q_n}{\partial x^3_2}+3\frac{\partial Q_n}{\partial x_2}\frac{\partial ^2 Q_n}{\partial x^2_2}+\left( \frac{\partial Q_n}{\partial x_2}\right) ^3\right] \nonumber \\&+\,\frac{1}{4!}\lambda E[Y^4]\left[ \frac{\partial ^4 Q_n}{\partial x_2^4}+4\frac{\partial Q_n}{\partial x_2}\frac{\partial ^3 Q_n}{\partial x_2^3}\right. \nonumber \\&+\,3\left( \frac{\partial ^2 Q_n}{\partial x_2^2}\right) ^2\nonumber \\&\left. +\,6\left( \frac{\partial Q_n}{\partial x_2}\right) ^2\frac{\partial ^2 Q_n}{\partial x_2^2}+\left( \frac{\partial Q_n}{\partial x_2}\right) ^4\right] \nonumber \\&+\,c+2(1-r)|x_2|\delta (x_1) \end{aligned}$$
(22)

If the residual error is zero, the approximate PDF solution can fully satisfy the reduced generalized FPK equation with some lower-order terms. However, the residual error generally cannot be zero because \({\mathop {p}\limits ^{\sim }}(x_1,x_2;\mathbf{a})\) is a nonzero exponential function and \(F(x_1,x_2;\mathbf{a})\) is not zero in general cases.

Therefore, another set of mutually independent functions \(H_s(x_1,x_2)\) spanning space \(\mathfrak {R}^{N_p}\) is further introduced to make the projection of \(F(x_1,x_2;\mathbf{a})\) on \(\mathfrak {R}^{N_p}\) vanish, which leads to

$$\begin{aligned} \int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }F(x_1,x_2;\mathbf{a})H_s(x_1,x_2)dx_1dx_2=0\nonumber \\ \end{aligned}$$
(23)

Selecting \(H_s(x_1,x_2)\) as:

$$\begin{aligned} H_s(x_1,x_2)=x_1^{m-l}x_2^{l}f_1(x_1)f_2(x_2) \end{aligned}$$
(24)

where \(m=1,2,\ldots ,n\); \(l=0,1,2,\ldots ,m\) and \(s=\frac{1}{2}(m+2)(m-1)+l+1\). This means that the reduced generalized FPK equation is satisfied in a weak sense.

A convenient and effective selection for \(f_1(x_1)\) and \(f_2(x_2)\) is the PDF obtained with equivalent linearization method or Gaussian closure method under Gaussian excitation with the same intensity \(\lambda E[Y^2]\) as follows

$$\begin{aligned} f_1(x_1)=\frac{1}{\sqrt{2\pi }\sigma _1} \exp \left\{ -\frac{x_1^2}{2\sigma ^2_1}\right\} \end{aligned}$$
(25)
$$\begin{aligned} f_2(x_2)=\frac{1}{\sqrt{2\pi }\sigma _2} \exp \left\{ -\frac{x_2^2}{2\sigma ^2_2}\right\} \end{aligned}$$
(26)

According to Eqs. (23) through (26), nonlinear algebraic equations are formulated for the unknown parameter \(\mathbf{a}\). The conventional Newton–Raphson method is adopted to solve the nonlinear algebraic equations. The initial stationary solution of \(\mathbf{a}\) can be adopted with the result of equivalent linearization method. In general, the EPC method uses an even-order polynomial in Eq. (18) because the even-order polynomial can easily satisfy Eq. (19) with a negative coefficient for its highest order terms. In addition, the EPC method with a complete set of fourth- or sixth-order polynomial usually can present a satisfactory PDF solution compared with available exact solutions or simulation results. At present, it is still a difficult mathematical problem on how to guarantee that the EPC method with a complete set of fourth- or sixth-order polynomials is enough to solve nonlinear systems with needed accuracy. A feasible way is to numerically show the convergence of the PDF solution as the polynomial order increases from two to either four or six, even to higher orders.

2.4 Probability density function formulation

After \({\mathop {p}\limits ^{\sim }}(x_1,x_2;\mathbf{a})\) is obtained for \({\mathop {p}\limits ^{\sim }}(z,\dot{z})\), the PDF solution of the original system can be also formulated according to Eq. (5). Herein \({\mathop {p}\limits ^{\sim }}_Y(y)\) and \({\mathop {p}\limits ^{\sim }}_{\dot{Y}}(\dot{y})\) denote the PDFs of displacement and velocity of the original system, respectively. Their formulations follow the procedure given in Ref. [28] about the PDF distribution of a function of random variables.

First, let us consider the PDF of y, namely \({\mathop {p}\limits ^{\sim }}_Y(y)\). Because y is a function of z with the relationship given in Eq. (5), the relationship can be simply expressed as

$$\begin{aligned} y=|z|=g(z) \end{aligned}$$
(27)

where \(g(\cdot )\) is a general function of z. In Ref. [28],

$$\begin{aligned} {\mathop {p}\limits ^{\sim }}_Y(y)=\sum _j\frac{{\mathop {p}\limits ^{\sim }}_Z[g^{-1}_j(y)]}{\left| \frac{dg(u)}{du}\right| _{u=g^{-1}_j(y)}} \end{aligned}$$
(28)

with the summation being over all inverse points \(z=g^{-1}_j(y)\) that map from z to y. \(g^{-1}(\cdot )\) is the inverse function of \(g(\cdot )\); \({\mathop {p}\limits ^{\sim }}_Z(z)=\int ^{+\infty }_{-\infty }{\mathop {p}\limits ^{\sim }}(z,\dot{z}){\text {d}}\dot{z}\) and it is the approximate PDF of z. \(g_j(\cdot )\) is a piecewise function as

$$\begin{aligned} y=|z|=g(z)=\left\{ \begin{array}{l} z, ~~~~~~ z>0\\ 0, ~~~~~~ z=0\\ -z,~~~~ z<0\\ \end{array} \right. \end{aligned}$$
(29)

In terms of Eqs. (28) and (29),

$$\begin{aligned} {\mathop {p}\limits ^{\sim }}_Y(y)={\mathop {p}\limits ^{\sim }}_Z^{+}(y) +{\mathop {p}\limits ^{\sim }}_Z^{-}(-y), y>0 \end{aligned}$$
(30)

where \({\mathop {p}\limits ^{\sim }}_Z^{+}(\cdot )\) and \({\mathop {p}\limits ^{\sim }}_Z^{-}(\cdot )\) are the PDFs located at the positive domain and the negative domain of z, respectively. Furthermore, it is defined that \({\mathop {p}\limits ^{\sim }}_Y(0)=2{\mathop {p}\limits ^{\sim }}_Z(0)\) because Eq. (28) is null for \(z=0\).

Second, let us consider the PDF of \(\dot{y}\), namely \({\mathop {p}\limits ^{\sim }}_{\dot{Y}}(\dot{y})\). Because \(\dot{y}\) is a function of multiple random variables with the relationship in Eq. (5), it is defined in a similar manner

$$\begin{aligned} \dot{y}=\dot{z}sgn(z)=h(z,\dot{z}) \end{aligned}$$
(31)

where \(h(\cdot )\) is also a general function of z and \(\dot{z}\). \({\mathop {p}\limits ^{\sim }}_{\dot{Y}}(\dot{y})\) can be formulated in terms of its cumulative distribution function \(F_{\dot{Y}}(\dot{y})\).

$$\begin{aligned} F_{\dot{Y}}(\dot{y})=\int \!\!\!\int _{h(z,\dot{z})\le \dot{y}}^{}{\mathop {p}\limits ^{\sim }}(z,\dot{z}){\text {d}}z{\text {d}}\dot{z} \end{aligned}$$
(32)

The cumulative distribution function further reads in a piecewise integral form

$$\begin{aligned} F_{\dot{Y}}(\dot{y})= & {} \int _0^{+\infty }{\text {d}}z\int _{-\infty }^{\dot{y}} {\mathop {p}\limits ^{\sim }}(z,\dot{z}){\text {d}}\dot{z}\nonumber \\&+\int _{-\infty }^0dz \int _{-\dot{y}}^{+\infty }{\mathop {p}\limits ^{\sim }}(z,\dot{z}){\text {d}}\dot{z} \end{aligned}$$
(33)

Therefore, the PDF of \(\dot{y}\) is obtained by taking the derivative with respect to \(\dot{y}\) on Eq. (33)

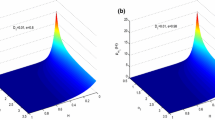
$$\begin{aligned} {\mathop {p}\limits ^{\sim }}_{\dot{Y}}(\dot{y})=\int _0^{+\infty } {\mathop {p}\limits ^{\sim }}(z,\dot{y}){\text {d}}z+\int _{-\infty }^0 {\mathop {p}\limits ^{\sim }}(z,-\dot{y}){\text {d}}z \end{aligned}$$
(34)

In this paper, the complete sets of second-, fourth- and sixth-order polynomials are adopted in the EPC method, respectively. For the forms of Eqs. (30) and (34), the integrals of the exponential function with the complete sets of fourth- and sixth-order polynomials are very hard to be explicitly obtained. Therefore, the numerical integration is used on Eqs. (30) and (34) to directly obtain the values of the PDF solutions. The non-Gaussian behaviors of the PDF solutions are compared and discussed in illustrative examples.

3 Illustrative examples

In this section, four illustrative examples are further studied to show the effectiveness of the proposed solution procedure. According to Eqs. (1), (2) and (4), the parameters of the Duffing system are given as follows: \(c=0.1\), \(k=1\), \(r=0.98\), \(\lambda =1.0\) and Y is a zero-mean Gaussian variable. Therefore, \(E[Y]=0\) and \(E[Y^3]=0\) in Eq. (22). Other parameters are various in each example and listed in Table 1. A Monte Carlo simulation (MCS) is also conducted, and the simulation procedure following the techniques introduced in Refs. [20, 32, 45]. A sample size of \(1\times 10^7\) is adopted to provide adequate evaluation on the tail of the PDF solution.

Table 1 Parameter settings in the parametric study
Full size table

3.1 Case 1: Lightly nonlinear system with a low-level excitation intensity

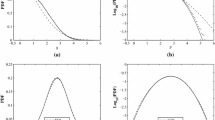
Case 1 is about a lightly nonlinear system under Poisson impulses with a low-level excitation intensity by setting \(\mu =0.1\) and \(\lambda E[Y^2]=0.1\). EPC (\(n=2\)) denotes the PDF solution obtained with the proposed solution procedure when the polynomial order equals two in the EPC method. Similarly, EPC (\(n=4\)) and EPC (\(n=6\)) denote the PDF solutions obtained with the proposed solution procedure when the polynomial order equals four and six, respectively. MCS denotes the simulated result given with Monte Carlo simulation. These symbols are also used in the same manner in the following cases.

The numerical analysis shows that EPC (\(n=2\)) is the same as that given by equivalent linearization method in the case of Gaussian white noise. Therefore, EPC (\(n=2\)) denotes the result obtained by a Gaussian PDF in terms of Eqs. (30) and (34). It can be regarded as a special Gaussian PDF in the case of vibro-impact vibration. Figure 2a, b presents a comparison on the PDF solution of displacement. Both EPC (\(n=2\)) and EPC (\(n=6\)) are close to MCS showing that the PDF distribution of displacement is almost Gaussian. However, EPC (\(n=4\)) differs a lot from the simulation in the tail as shown in Fig. 2b. By contrast, in the case of velocity as shown in Fig. 2c, d, EPC (\(n=6\)) agrees well with MCS and they differ significantly from EPC (\(n=2\)) (denoting a Gaussian PDF). This difference indicates that the PDF distribution of velocity becomes non-Gaussian. EPC (\(n=4\)) differs from the simulation result unlike EPC (\(n=2\)) and EPC (\(n=6\)) .

Fig. 2
figure 2

Comparison of PDFs in Case 1: a PDFs of displacement; b logarithmic PDFs of displacement; c PDFs of velocity; d logarithmic PDFs of velocity

Full size image

The reasons of the non-Gaussian PDF distribution formulation are as follows. When the nonlinearity in displacement is light and the excitation intensity is low, the cubic terms in Eqs. (1) and (13) have small magnitudes. Meanwhile, the impulse arrival rate is moderate, in which Poisson impulses approach Gaussian white noise. Furthermore, the restitution factor is close to unity. Under these situations, the lightly nonlinear system behaves more like a linear system under Gaussian white noise. Therefore, the PDF of displacement is almost Gaussian. On the other hand, as Eq. (14) shows, Poisson impulses are imposed in the differential equation of velocity, which inevitably has an effect on the PDF distribution of velocity. This leads the PDF distribution of velocity to becoming non-Gaussian in the tail region. In the following three cases, the effects of the nonlinearity in displacement and the excitation intensity are examined by increasing their magnitudes, respectively. It is expected that the PDF solutions of the response become more non-Gaussian when these parameters increase in their magnitudes.

In addition, a complete set of eighth-order polynomial has been also used to examine the convergence of the EPC method in each case (i.e., EPC \(n=8\)). However, the conventional Newton–Raphson method solving Eq. (23) becomes non-convergent for EPC (\(n=8\)) in the four examined cases. It seems that the nonlinear algebraic equations with the set of eighth-order polynomial are hardly solved by the conventional Newton–Raphson method. On the other hand, extensive computational efforts are also taken during each iteration for EPC (\(n=8\)). An adequate solution technique to solve the nonlinear algebraic equations is worth further investigating for the EPC method in such cases.

3.2 Case 2: Lightly nonlinear system with a high-level excitation intensity

In Case 2, the excitation intensity increases from 0.1 in Case 1 to 1.0 to show the effect of the excitation intensity. The nonlinearity coefficient in the displacement term is unchanged as \(\mu =0.1\). Figure 3a, b gives a comparison on the PDF solution of displacement in this case. Different from Case 1, the comparison shows that EPC (\(n=2\)) differs significantly from the simulated result showing that the PDF of displacement becomes non-Gaussian due to the increase in excitation intensity. When the excitation intensity increases, the response of the system correspondingly increases in its magnitude and the nonlinear displacement term becomes larger. Compared with EPC (\(n=2\)), EPC (\(n=4\)) provides an improved result for the PDF of displacement, but it still differs a lot from the simulation result as shown in Fig. 3b. In such a case, EPC (\(n=6\)) coincides well with the simulated result, especially in the tail region as shown in Fig. 3b. In the case of velocity as shown in Fig. 3c, d, EPC (\(n=2\)) and EPC (\(n=4\)) are different from MCS, whereas EPC (\(n=6\)) agrees well with the simulated result. In this case, the PDF distribution of velocity is also non-Gaussian.

Fig. 3
figure 3

Comparison of PDFs in Case 2: a PDFs of displacement; b logarithmic PDFs of displacement; c PDFs of velocity; d logarithmic PDFs of velocity

Full size image

3.3 Case 3: Highly nonlinear system with a low-level excitation intensity

In the third case, the large nonlinearity coefficient is used as \(\mu =1.0\) and the level of excitation intensity is low with \(\lambda E[Y^2]=0.1\). This case shows the effect of the nonlinear displacement term on the PDF solutions. Figure 4a, b exhibits the obtained PDF distributions of displacement using each method. Compared with Case 1, EPC (\(n=2\)) departs from the simulated result due to the increase in the nonlinearity coefficient. The highly nonlinear term leads displacement to exhibiting a more non-Gaussian behavior. Similar to Case 2, EPC (\(n=4\)) gave a better result compared to EPC (\(n=2\)). In such a case, EPC (\(n=6\)) agrees well with the simulated result. In the case of velocity as shown in Fig. 4c, d, the PDF distribution of velocity is non-Gaussian because EPC (\(n=2\)) differs from the simulated result. Comparatively, EPC (\(n=6\)) is in good agreement with the simulated result, which is better than EPC (\(n=2\)) and EPC (\(n=4\)).

Fig. 4
figure 4

Comparison of PDFs in Case 3: a PDFs of displacement; b logarithmic PDFs of displacement; c PDFs of velocity; d logarithmic PDFs of velocity

Full size image

3.4 Case 4: Highly nonlinear system with a high-level excitation intensity

In the last case, a highly nonlinear system under Poisson impulses with a high-level excitation intensity is studied by setting \(\mu =1.0\) and \(\lambda E[Y^2]=1.0\). As shown in Fig. 5a, b , the simulated result differs a lot from EPC (\(n=2\)) (i.e., a Gaussian PDF) in the case of displacement. This significant difference is formulated due to both the highly nonlinear displacement term and high-level excitation intensity which drive the system behave in a highly nonlinear manner. In such a case, both EPC (\(n=4\)) and EPC (\(n=6\)) can present a satisfactory PDF solution compared with the simulated result, especially in the tail region. In the case of velocity in Fig. 5c, d, the similar observation to those of the above cases can be found. EPC (\(n=2\)) differs from MCS, whereas EPC (\(n=4\)) and EPC (\(n=6\)) agree well with the simulated result. In this case, the PDF distribution of velocity also shows a non-Gaussian behavior. Furthermore, EPC (\(n=6\)) is more accurate than EPC (\(n=4\)) as shown in Fig. 5a, d.

Fig. 5
figure 5

Comparison of PDFs in Case 4: a PDFs of displacement; b logarithmic PDFs of displacement; c PDFs of velocity; d logarithmic PDFs of velocity

Full size image

4 Conclusions

A recently proposed solution procedure is extended to the case of a lightly vibro-impact system under external Poisson impulses. The system has a one-sided constraint located at the equilibrium position of the system with instantaneous repetitive impacts. The solution procedure consists of three steps. First, the Zhuravlev non-smooth coordinate transformation is utilized to convert the original vibro-impact system into a new system without any barrier by introducing an additional damping term. Second, the PDF of the new system is obtained with the exponential–polynomial closure method by solving the generalized FPK equation. Last the PDF of the original system is formulated in terms of the methodology on seeking the PDF of a function of random variables. Different nonlinearity degrees and excitation intensities are used in four numerical examples to show the effectiveness of the proposed solution procedure. The numerical results show that the PDFs obtained with the proposed solution procedure agree well with the simulated results when the polynomial order equals six. The tail region of the PDF is also approximated well for both displacement and velocity.