Further results on sampled-data control for master–slave synchronization of chaotic Lur’e systems with time delay

Abstract

This paper is concerned with the problem of sampled-data control for master–slave synchronization of chaotic Lur’e systems with time delay. The sampling periods are assumed to be arbitrary but bounded. A new Lyapunov functional is constructed, in which the information on the nonlinear function and the actual sampling pattern have been taken fully into account. By employing the Lyapunov functional and a tighter bound technique to estimate the derivative of the Lyapunov functional, a less conservative exponential synchronization criterion is established by analyzing the corresponding synchronization error systems. Furthermore, the derived condition is employed to design a sampled-data controller. The desired controller gain matrix can be obtained by means of the linear matrix inequality approach. Simulations are provided to show the effectiveness and the advantages of the proposed approach.

1 Introduction

The problem of master–slave synchronization for chaotic systems has arisen a great attention since the master–slave concept has been proposed for achieving the synchronization of coupled chaotic systems in [1–4]. This stems from its potential applications in secure communication, image processing, biological systems, chemical reaction, and information science (see e.g., [5–7]). It has been shown that many nonlinear systems can be represented in the form of Lur’e systems [8–10]. Thus, the problem of master–slave synchronization of chaotic Lur’e systems has been widely studied, and many important results have been proposed. For example, the robust synthesis problem of master–slave synchronization has been investigated for Lur’e systems in [11]. In [12], the problem of master–slave synchronization has been studied for Lur’e systems via a time delay feedback control. By employing the free-weighting matrix approach, some improved delay-dependent synchronization criteria have been obtained in [13] and [14]. In [15], the problem of designing time-varying delay feedback controllers for master–slave synchronization of Lur’e systems has been investigated based on Lyapunov functional approach, and some LMI-based synchronization criteria have been obtained for two cases of time-varying delays. These results were extended to the fault-tolerant master–slave synchronization of Lur’e systems in [16]. The master–slave synchronization problem has been investigated for Lur’e systems via delayed PD controller in [17].

It is well known that time delays exist in many physical processes, such as nuclear reactors, chemical processes, and biological systems, and may lead to instability or significantly deteriorate the performance of the systems. Thus, a great attention has also been paid to the synchronization of chaotic Lur’e systems with time delays. For example, in [18], an adaptive approach has been proposed for the master–slave synchronization of chaotic Lur’e systems with time-varying delays based on the invariant principle of functional differential equations. The master–slave synchronization problem has been investigated for coupled time delay Lur’e systems with parameter mismatch in [19], where a general methodology has been proposed to derive some delay-dependent quasi-synchronization conditions.

Also, sampled-data control systems have received much attention during the last decades due to the fact that modern control systems usually employ digital controllers instead of the traditional controllers implemented by analog circuits [20–24]. The approach proposed in [25], which requires multiple steps to synchronize chaos, is too difficult to application. Based on the input delay approach proposed in [20], the sampled-data control was employed to investigate for master–slave synchronization of chaotic Lur’e systems in [26], where sufficient conditions have been derived for global asymptotic synchronization of chaotic Lur’e systems. Nevertheless, in [26], the enlargement of the integral term and the neglect of some useful information lead to conservativeness of the derived results. The information that the change rate of the time-varying delay transformed by sampling instants is equal to 1 was firstly taken into account in [27], but the discontinuous characteristic of delay at the sampling instant was ignored. In [28, 29, 32], some improved results have been obtained by constructing a class of piecewise Lyapunov functionals. In [31], the synchronization problem was investigated for chaotic Lur’e systems with quantized sampled-data controller, and a new controller design method was obtained. All of the above literatures are focused on delay-free chaotic Lur’e systems. For chaotic Lur’e systems with time delay, the master–slave synchronization problem has been investigated based on sampled-data control, and some exponential synchronization criteria were derived in [30]. However, the information on nonlinear function have not been taken into account in the construction of Lyapunov functional in [30]. Also, there are some enlargements in evaluating the derivative of Lyapunov functional. Therefore, the results given in [30] are conservative, which motivates the study of this paper.

This paper revisits the problem of sampled-data control for master–slave synchronization of chaotic Lur’e systems with time delay. A new Lyapunov functional is constructed for the corresponding synchronization error systems, in which the information on the nonlinear function and the actual sampling pattern has been taken fully into account. A tight bound technique is proposed to estimate the derivative of the Lyapunov functional, which yields a less conservative exponential synchronization criterion. The derived condition is employed to design a sampled-data controller, and the desired controller gain matrix can be obtained by means of the linear matrix inequality approach. The Chua’s circuit is applied to verify the effectiveness of the proposed approach.

Notation: Throughout this paper, the superscripts T and $-1$ mean the transpose and the inverse of a matrix, respectively; ${\mathbb {R}}^n$ denotes the $n$-dimensional Euclidean space; ${\mathbb {R}}^{n\times m}$ is the set of all $n\times m$ real matrices; $\Vert \cdot \Vert$ refers to the Euclidean vector norm or the induced matrix 2-norm; $P>0$ ($\ge \!\!0$) means that P is a real symmetric and positive-definite (semi-positive-definite) matrix; I stands for an appropriately dimensioned identity matrix; diag{$\cdots$} denotes a block-diagonal matrix; and the symmetric terms in a symmetric matrix are denoted by $*$. Matrices, if not explicitly stated, are assumed to have compatible dimensions.

2 System description

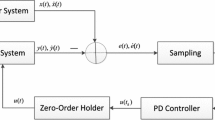
Consider the master–slave synchronization scheme as follow:

$$\begin{aligned} \mathcal {M}:{}&\left\{ \begin{aligned} \dot{x}(t)&=Ax(t)+Bx(t-d)+W\varphi (Dx(t))\nonumber \\ p(t)&=Cx(t) \end{aligned}\right. \\ \mathcal {S}:{}&\left\{ \begin{aligned} \dot{z}(t)&=Az(t)+Bz(t-d)+W\varphi (Dz(t))+u(t)\nonumber \\ q(t)&=Cz(t) \end{aligned}\right. \\ {\mathcal {C}}:{}&u(t)=K(p(t_k)-q(t_k)),\,t_k\leqslant {t}<t_{k+1} \end{aligned}$$

(1)

which comprises master system ${\mathcal {M}}$, slave system ${\mathcal {S}}$, and controller ${\mathcal {C}}$. ${\mathcal {M}}$ and ${\mathcal {S}}$ with $u(t)=0$ are identical chaotic Lur’e systems with time delay, where x(t), $z(t)\in {\mathbb {R}}^n$ are state vectors and p(t), $q(t)\in {\mathbb {R}}^l$ are outputs of subsystems. $u(t) \in {\mathbb {R}}^n$ is the control input of the slave system; $A \in {\mathbb {R}}^{n\times n}$, $B \in {\mathbb {R}}^{n\times n}$, $C \in {\mathbb {R}}^{l\times n}$, $D \in {\mathbb {R}}^{n_h\times n}$, and $W \in {\mathbb {R}}^{n\times n_h}$ are known constant matrices; $K \in {\mathbb {R}}^{n\times {l}}$ is the sampled-data controller to be designed later; $d>0$ represents the time delay; $\varphi (\cdot ):{\mathbb {R}}^{n_h} \rightarrow {\mathbb {R}}^{n_h}$ is a diagonal nonlinearity with $\varphi _i(\cdot )$ belonging to sector $[0,\,f_i]$ for $i=1,2,\ldots ,n_h$.

For sampled-data control, only discrete measurements of p(t) and q(t) can be utilized for synchronization purposes, i.e., we only get the measurements $p(t_k)$ and $q(t_k)$ at the sampling instant $t_k$. It is assumed that the control signal is generated by using a zero-order hold with a sequence of hold times $0\leqslant t_0<t_1<\cdots <{t}_k<\cdots <\lim _{k\rightarrow +\infty }t_k=+\infty$. The sampling periods are arbitrary but bounded, i.e.,

$$\begin{aligned} t_{k+1}-t_{k}=h_k\leqslant h \end{aligned}$$

(2)

for all $k\geqslant 0$, where $h>0$ is the upper bound of the sampling periods.

Defining $r(t)=x(t)-z(t)$ yields the following synchronization error system:

$$\begin{aligned} \dot{r}(t)&=Ar(t)+Br(t-d)+W\eta (Dr(t))-KCr(t_k),\nonumber \\&\qquad t_k\leqslant {t}<t_{k+1} \end{aligned}$$

(3)

where $\eta (Dr(t))=\varphi (D(r(t)+z(t)))-\varphi (Dz(t))$.

Since $\varphi _i(\cdot )$ belongs to sector $[0,\,f_i]$, it can be derived that for any $i=1,2,\ldots ,n_h$, and $\forall {r}, z$,

$$\begin{aligned} 0\leqslant \frac{\eta _i(d_i^{\mathrm {T}}r)}{d_i^{\mathrm {T}}r}=\frac{\varphi _i(d_i^{\mathrm {T}}(r+z))-\varphi _i(d_i^{\mathrm {T}}r)}{d_i^{\mathrm {T}}r}\leqslant f_i,\,d_i^{{\mathrm {T}}}r\ne 0 \end{aligned}$$

(4)

where $d_i^{\mathrm {T}}$ denotes the ith row vector of D.

It is easily obtained from (4) that for any $i=1,2,\ldots ,n_h$, and $\forall {r}$,

$$\begin{aligned} \eta _i(d_i^{\mathrm {T}}r)\left[ \eta _i(d_i^{\mathrm {T}}r)-f_id_i^{\mathrm {T}}r\right] \leqslant 0. \end{aligned}$$

(5)

Next, we present the following definition and lemmas, which will be used to derive our main result.

Definition 1

The master system ${\mathcal {M}}$ and the slave system ${\mathcal {S}}$ in (1) are said to be exponentially synchronous if the synchronization error system (3) is exponentially stable, that is, there exist two constants $\alpha >0$ and $\beta >0$ such that

$$\begin{aligned} ||{r(t)}||\leqslant \beta \mathrm{e}^{-\alpha t}||{r_{0}}||_{c},\,\forall t\geqslant 0 \end{aligned}$$

(6)

where $||{r_{t}}||_{c}=\sup _{{-d}\leqslant \theta \leqslant 0}\{||{r(t+\theta )}||,||{\dot{r}(t+\theta )}||\}$.

Lemma 1

[33] For $R>0$, and a vector function $x:\left[ {\alpha , \beta } \right] \rightarrow {{\mathbb {R}}^n}$ such that the integrations concerned are well defined, the following inequality holds:

$$\begin{aligned}&\left( \int _\alpha ^\beta x(s){\mathrm {d}}s \right) ^{\mathrm {T}} R \int _\alpha ^\beta x(s){\mathrm {d}}s\nonumber \\&\quad \le (\beta -\alpha ) \int _\alpha ^\beta x(s)^{\mathrm {T}} R x(s){\mathrm {d}}s \end{aligned}$$

(7)

Lemma 2

For a scalar $\tau >0$, matrices $R>0$ and Y, the following inequality holds:

$$\begin{aligned} \frac{1}{\tau } R \ge Y+Y^{\mathrm {T}}-\tau Y^{\mathrm {T}}R^\mathrm {-1}Y \end{aligned}$$

(8)

Proof

It is noted that

$$\begin{aligned} \frac{1}{\tau } (R-{\tau }Y)^{\mathrm {T}}R^\mathrm {-1}(R-{\tau }Y) \ge 0, \end{aligned}$$

(9)

then, it is easy to obtain from (9) that

$$\begin{aligned} \frac{1}{\tau } R -Y-Y^{\mathrm {T}}+\tau Y^{\mathrm {T}}R^\mathrm {-1}Y \ge 0. \end{aligned}$$

(10)

Rearranging the terms in (10), we can get (8) and this completes the proof. $\square$

Lemma 3

[30] Consider the synchronization error system (3). Then the following inequality holds:

$$\begin{aligned} ||r(t)||^2\leqslant \theta _1||r(t_k)||^2+\theta _2\int \limits _{t_k-d}^{t_k}||r(\alpha )||^2\,{\mathrm {d}}\alpha ,\,t_k\leqslant {t}<t_{k+1} \end{aligned}$$

(11)

where

• $\theta _1={}5(1+||KC||^2h^2)\mathrm{e}^{5(||A||^2+||W||^2||FD||^2+||B||^2)h^2}$

• $\theta _2={}5||B||^2h\mathrm{e}^{5(||A||^2+||W||^2||FD||^2+||B||^2)h^2}$

• $F={\mathrm {diag}}\{f_{1},\,f_{2},\ldots ,f_{n_h}\}$

Our goal in this paper is to design a sampled-data controller ${\mathcal {C}}$ in (1) such that the master system ${\mathcal {M}}$ and the slave system ${\mathcal {S}}$ in (1) are exponentially synchronous.

3 Main results

In this section, we shall present the result of the master–slave synchronization for chaotic Lur’e system (1). Firstly, we discuss system (1) with a given controller gain. In this case, the following criterion is obtained.

Theorem 1

Given a scalar $\alpha >0$, the master system $\mathcal {M}$ and the slave system $\mathcal {S}$ in (1) are exponentially synchronous if there exist matrices $P>0$, $Q>0$, $Z>0$, $U>0$, $\begin{bmatrix}R_1&R_2\\*&R_3\end{bmatrix}>0$, $X_1$, $X_2$, $X_3$, $X_4$, $X_5$, $G_1$, $G_2$, $G_3$, Y, $N=\begin{bmatrix}N_1&N_2&N_3&N_4\end{bmatrix}$, $H=\begin{bmatrix}H_1&H_2&H_3&H_4\end{bmatrix}$, and diagonal matrices $\Lambda >0$, $V_1>0$, and $V_2>0$ such that (12) and (13) is feasible for $\bar{h}=0, h$

$$\begin{aligned} \varXi _1(\bar{h})={}&\begin{bmatrix} \varXi _{11}+\varTheta _{11}&\varXi _{12}+\varTheta _{12}&\varXi _{13}+\varTheta _{13}&\varXi _{14}+\varTheta _{14}&G_1W+D^{\mathrm {T}}FV_1&\varXi _{16}\\ *&\varXi _{22}+\bar{h}U&\varXi _{23}+\varTheta _{23}&\bar{h}X_3+2N_2^{\mathrm {T}}&-\Lambda D+ G_2W&G_2B \\ *&*&\varXi _{33}+\varTheta _{33}&\varXi _{34}+\varTheta _{34}&G_3W&G_3B\\ *&*&*&\varXi _{44}+\varTheta _{44}&0&0 \\ *&*&*&*&-2V_1&0\\ *&*&*&*&*&\varXi _{66} \\ \end{bmatrix}<0 \end{aligned}$$

(12)

$$\begin{aligned} \varXi _2(\bar{h})={}&\begin{bmatrix} \varXi _{11}&\varXi _{12}&\varXi _{13}&\varXi _{14}&G_1W+D^{\mathrm {T}}FV_2&\varXi _{16}&\sqrt{\bar{h}}H_1^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_1^{\mathrm {T}}&0\\ *&\varXi _{22}&\varXi _{23}&2N_2^{\mathrm {T}}&-\Lambda D+G_2W&G_2B&\sqrt{\bar{h}}H_2^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_2^{\mathrm {T}}&0\\ *&*&\varXi _{33}&\varXi _{34}&G_3W&G_3B&\sqrt{\bar{h}}H_3^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_3^{\mathrm {T}}&0\\ *&*&*&\varXi _{44}&0&0&\sqrt{\bar{h}}H_4^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_4^{\mathrm {T}}&\sqrt{\bar{h}}Y^{\mathrm {T}}\\ *&*&*&*&-2V_2&0&0&0&0\\ *&*&*&*&*&\varXi _{66}&0&0&0\\ *&*&*&*&*&*&-\mathrm{e}^{-2\alpha h}U&0&0\\ *&*&*&*&*&*&*&-3\mathrm{e}^{-2\alpha h}U&0\\ *&*&*&*&*&*&*&*&-\mathrm{e}^{2\alpha h}R_1\\ \end{bmatrix}<0 \end{aligned}$$

(13)

where

$$\begin{aligned} \varXi _{11}= & {} 2\alpha {P}+Q-{X_1-X_1^{\mathrm {T}}}-\frac{\mathrm{e}^{-2\alpha d}}{d}Z+H_1+H_1^{\mathrm {T}}\\&+\,G_1A+ A^{\mathrm {T}}G_1^{\mathrm {T}}+2\alpha D^{\mathrm {T}}F\Lambda D-\bar{h}N_1-\bar{h}N_1^{\mathrm {T}},\\ \varXi _{12}= & {} P+H_2-G_1+A^{\mathrm {T}}G_2^{\mathrm {T}}+D^{\mathrm {T}}F\Lambda {D}-\bar{h}N_2,\\ \varXi _{13}= & {} X_1-X_2+H_3-H_1^{\mathrm {T}}\\&-\,G_1KC+ A^{\mathrm {T}}G_3^{\mathrm {T}}-\bar{h}N_3-\bar{h}N_1^{\mathrm {T}},\\ \varXi _{14}= & {} -X_3+H_4+2N_1^{\mathrm {T}}-\bar{h}N_4,\\ \varXi _{16}= & {} \frac{\mathrm{e}^{-2\alpha d}}{d}Z+G_1B,\\ \varXi _{22}= & {} dZ-G_2-G_2^{\mathrm {T}},\\ \varXi _{23}= & {} -H_2^{\mathrm {T}}-G_2KC-G_3^{\mathrm {T}}-\bar{h}N_2^{\mathrm {T}},\\ \varXi _{33}= & {} X_2+X_2^{\mathrm {T}}-H_3-H_3^{\mathrm {T}}-G_3KC- C^{\mathrm {T}}K^{\mathrm {T}}G_3^{\mathrm {T}}\\&-\,\mathrm{e}^{-2\alpha h}\bar{h}R_3-\bar{h}N_3-\bar{h}N_3^{\mathrm {T}},\\ \varXi _{34}= & {} -X_4-\mathrm{e}^{-2\alpha h}R_2^{\mathrm {T}}-H_4+2N_3^{\mathrm {T}}-\bar{h}N_4,\\ \varXi _{44}= & {} -{X_5-X_5^{\mathrm {T}}}-{\mathrm{e}^{-2\alpha h}}(Y+Y^{\mathrm {T}})+2N_4+2N_4^{\mathrm {T}},\\ \varXi _{66}= & {} -\mathrm{e}^{-2\alpha d}Q-\frac{\mathrm{e}^{-2\alpha d}}{d}Z,\\ \varTheta _{11}= & {} 2\alpha \bar{h}{(X_1+X_1^{\mathrm {T}})}+\bar{h}X_3+\bar{h}X_3^{\mathrm {T}}+\bar{h}R_1\\&+\,\bar{h}N_1+\bar{h}N_1^{\mathrm {T}},\\ \varTheta _{12}= & {} \bar{h}(X_1+X_1^{\mathrm {T}})+\bar{h}N_2,\\ \varTheta _{13}= & {} 2\alpha \bar{h}(-X_1+X_2)+ \bar{h}X_4^{\mathrm {T}}+\bar{h}R_2+\bar{h}N_3+\bar{h}N_1^{\mathrm {T}},\\ \varTheta _{14}= & {} 2\alpha \bar{h}X_3+\bar{h}({X_5+X_5^{\mathrm {T}}})+\bar{h}N_4,\\ \varTheta _{23}= & {} \bar{h}(-X_1+X_2)+\bar{h}N_2^{\mathrm {T}},\\ \varTheta _{33}= & {} 2\alpha \bar{h}\left( -X_2-X_2^{\mathrm {T}}\right) \\&+\,\bar{h}R_3+\mathrm{e}^{-2\alpha h}\bar{h}R_3+\bar{h}N_3+\bar{h}N_3^{\mathrm {T}},\\ \varTheta _{34}= & {} 2\alpha \bar{h}X_4+\bar{h}N_4,\\ \varTheta _{44}= & {} 2\alpha \bar{h}(X_5+X_5^{\mathrm {T}}). \end{aligned}$$

Proof

Choose the following Lyapunov functional candidate for the synchronization error system (3):

$$\begin{aligned} V(t)=\sum \limits _{i=1}^{7}V_i(t),\,t\in [t_k,\,t_{k+1}) \end{aligned}$$

(14)

where

and

$$\begin{aligned} {}&\bar{X}=\left[ \begin{array}{ccc} {X_1+X_1^{\mathrm {T}}}{}&{}-X_1+X_2 &{} X_3\\ *&{} -X_2-X_2^{\mathrm {T}}&{} X_4\\ *&{} *&{} {X_5+X_5^{\mathrm {T}}}\\ \end{array}\right] . \end{aligned}$$

It is noted that $V_5(t)$, $V_6(t)$, and $V_7(t)$ vanish before $t_k$ and after $t_k$, i.e., $\lim _{t\rightarrow {t}_k}V(t)=V(t_k)$, then it can be obtained that V(t) is a continuous function in time. Calculating the derivative of V(t) along the trajectories of system (3) yields

$$\begin{aligned} \dot{V}_1(t)&={}2\mathrm{e}^{2\alpha t}r(t)^{\mathrm {T}}P\dot{r}(t)+2\alpha \mathrm{e}^{2\alpha t}r(t)^{\mathrm {T}}Pr(t), \end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_2(t)&={}\mathrm{e}^{2\alpha t}r(t)^{\mathrm {T}}Q r(t)-\mathrm{e}^{2\alpha t}\mathrm{e}^{-2\alpha d}r(t-d)^{\mathrm {T}}Q\nonumber \\&\qquad \times r(t-d), \end{aligned}$$

(16)

$$\begin{aligned} \dot{V}_3(t)&={}d\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}Z\dot{r}(t)-\int \limits ^{t}_{t-d}\mathrm{e}^{2\alpha s}\dot{r}(s)^{\mathrm {T}}Z\dot{r}(s)\, {\mathrm {d}}s \nonumber \\&\leqslant {}d\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}Z\dot{r}(t)-\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t-d}\mathrm{e}^{-2\alpha d}\dot{r}(s)^{\mathrm {T}}Z\nonumber \\&\qquad \times \dot{r}(s)\,{\mathrm {d}}s , \end{aligned}$$

(17)

$$\begin{aligned} \dot{V}_4(t)&={}2\mathrm{e}^{2\alpha t}(r(t)^{\mathrm {T}}{D^{\mathrm {T}}}F-\eta (Dr(t))^{\mathrm {T}})\Lambda {D}\dot{r}(t)\nonumber \\&\quad + 4\alpha \mathrm{e}^{2\alpha t}\sum \limits _{i=1}^{n_h}\lambda _{i}\int \limits ^{d_i^{\mathrm {T}} r}_{0}(f_i s- \eta _i(s)){\mathrm {d}}s\nonumber \\&\leqslant {}2\mathrm{e}^{2\alpha t}(r(t)^{\mathrm {T}}{D^{\mathrm {T}}}F-\eta (Dr(t))^{\mathrm {T}})\Lambda {D}\dot{r}(t)\nonumber \\&\quad +2\alpha \mathrm{e}^{2\alpha t} {r}(t)^{\mathrm {T}}D^{\mathrm {T}}F\Lambda D{r}(t) , \end{aligned}$$

(18)

$$\begin{aligned} \dot{V}_5(t)&=(t_{k+1}-t)\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}U\dot{r}(t)-\int \limits ^{t}_{t_k}\mathrm{e}^{2\alpha s}\dot{r}(s)^{\mathrm {T}}\nonumber \\&\quad \ U\dot{r}(s)\,{\mathrm {d}}s\nonumber \\&\leqslant {}(t_{k+1}-t)\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}U\dot{r}(t)\nonumber \\&\quad -\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}\mathrm{e}^{-2\alpha h} \dot{r}(s)^{\mathrm {T}}U\dot{r}(s)\,{\mathrm {d}}s, \end{aligned}$$

(19)

$$\begin{aligned} \dot{V}_6(t) ={}&-\int \limits ^{t}_{t_k}\mathrm{e}^{2\alpha s}\begin{bmatrix}r(s)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(s)\\ r(t_k)\end{bmatrix}\,{\mathrm {d}}s\nonumber \\&+(t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}\nonumber \\ \leqslant {}&-\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}\mathrm{e}^{-2\alpha h}\begin{bmatrix}r(s)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(s)\\ r(t_k)\end{bmatrix}\,{\mathrm {d}}s\nonumber \\&+(t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}\nonumber \\ ={}&-\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}\mathrm{e}^{-2\alpha h}r(s)^{\mathrm {T}}R_1r(s)\,{\mathrm {d}}s\nonumber \\&-2\mathrm{e}^{2\alpha t}r(t_k)^{\mathrm {T}}\mathrm{e}^{-2\alpha h}R_2^{\mathrm {T}}\int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\nonumber \\ {}&-\mathrm{e}^{2\alpha t}(t-t_k)r(t_k)^{\mathrm {T}}\mathrm{e}^{-2\alpha h}R_3r(t_k)\nonumber \\&+(t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix} , \end{aligned}$$

(20)

$$\begin{aligned} \dot{V}_7(t)={}&-\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}\bar{X} \begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}\nonumber \\&+2\alpha (t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}\bar{X} \begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}\nonumber \\ {}&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}\bar{X}\begin{bmatrix}\dot{r}(t)\\ 0\\ r(t)\end{bmatrix}\nonumber \\ \leqslant {}&-\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}\bar{X}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}\nonumber \\&+2\alpha (t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}\bar{X}\begin{bmatrix}r(t)\\ r(t_k)\\ \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\end{bmatrix}\nonumber \\ {}&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}r(t)^{\mathrm {T}}(X_1+X_1^{\mathrm {T}})\dot{r}(t)\nonumber \\&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}r(t_k)^{\mathrm {T}}(-X_1+X_2)^{\mathrm {T}}\dot{r}(t)\nonumber \\ {}&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}\,{\mathrm {d}}sX_3^{\mathrm {T}}\dot{r}(t)\nonumber \\&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}r(t)^{\mathrm {T}}X_3r(t)\nonumber \\ {}&+2(t_{k+1}-t)\mathrm{e}^{2\alpha t}r(t_k)^{\mathrm {T}}X_4r(t)\nonumber \\&+2(t_{k+1}-t) \mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}\,{\mathrm {d}}s(X_5+X_5^{\mathrm {T}})r(t), \end{aligned}$$

(21)

where $F={\mathrm {diag}}\{f_{1},\,f_{2},\cdots ,f_{n_h}\}$. $\square$

Applying Lemmas 1 and 2, we have

$$\begin{aligned}&-\int \limits ^{t}_{t-d}{}\mathrm{e}^{-2\alpha d}\dot{r}(s)^{\mathrm {T}}Z\dot{r}(s)\,{\mathrm {d}}s\nonumber \\&\quad \leqslant {}\begin{bmatrix}r(t)\\ r(t-d)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}-\frac{\mathrm{e}^{-2\alpha d}}{d}Z&\frac{\mathrm{e}^{-2\alpha d}}{d}Z\\ *&-\frac{\mathrm{e}^{-2\alpha d}}{d}Z\end{bmatrix}\begin{bmatrix}r(t)\\ r(t-d)\end{bmatrix} \end{aligned}$$

(22)

and

$$\begin{aligned}&-\int \limits ^{t}_{t_k}\mathrm{e}^{-2\alpha h}r(s)^{\mathrm {T}}{}R_1r(s)\,{\mathrm {d}}s \leqslant \nonumber \\&\qquad -\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}\,{\mathrm {d}}s\frac{\mathrm{e}^{-2\alpha h}}{t-t_k}R_1\int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\nonumber \\&\quad {\leqslant }{\mathrm{e}^{-2\alpha h}}\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}\,{\mathrm {d}}s(-2Y+(t-t_k)(Y^{\mathrm {T}}R_1^{-1}Y))\nonumber \\&\qquad \times \int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s . \end{aligned}$$

(23)

Applying (22) and (23) to (18) and (20), respectively, we can get

$$\begin{aligned} \dot{V}_3(t)&\leqslant {}d\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}Z\dot{r}(t)\nonumber \\&\quad +\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t-d)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}-\frac{\mathrm{e}^{-2\alpha d}}{d}Z&\frac{\mathrm{e}^{-2\alpha d}}{d}Z\\ *&-\frac{\mathrm{e}^{-2\alpha d}}{d}Z\end{bmatrix}\nonumber \\&\quad \times \begin{bmatrix}r(t)\\ r(t-d)\end{bmatrix} \end{aligned}$$

(24)

and

$$\begin{aligned} \dot{V}_6(t)&\leqslant {}\mathrm{e}^{2\alpha t}\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}\,{\mathrm {d}}s{\mathrm{e}^{-2\alpha h}}(-2Y\nonumber \\&\qquad +(t-t_k)(Y^{\mathrm {T}}R_1^{-1}Y))\int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\nonumber \\ {}&\quad \quad -2\mathrm{e}^{2\alpha t}r(t_k)^{\mathrm {T}}\mathrm{e}^{-2\alpha h}R_2^{\mathrm {T}}\int \limits ^{t}_{t_k}r(s)\,{\mathrm {d}}s\nonumber \\ {}&\quad -\mathrm{e}^{2\alpha t}(t-t_k)r(t_k)^{\mathrm {T}}\mathrm{e}^{-2\alpha h}R_3r(t_k)\nonumber \\ {}&\quad +(t_{k+1}-t)\mathrm{e}^{2\alpha t}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}^{\mathrm {T}}\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}\begin{bmatrix}r(t)\\ r(t_k)\end{bmatrix}. \end{aligned}$$

(25)

Furthermore, based on the Schur complement [34], it can be found that for any appropriately dimensioned matrices H and N,

$$\begin{aligned} \begin{bmatrix}H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}H&H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N&H^{\mathrm {T}}\\\ *&N^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N&N^{\mathrm {T}}\\ *&*&\mathrm{e}^{-2\alpha h}U\end{bmatrix}\geqslant 0 \end{aligned}$$

(26)

which implies

$$\begin{aligned}&\int \limits ^{t}_{t_k}\begin{bmatrix}\phi (t)\\g(s)\phi (t)\\\dot{r}(s)\end{bmatrix}^{\mathrm {T}} \begin{bmatrix}H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}H&H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N&H^{\mathrm {T}}\\\ *&N^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N&N^{\mathrm {T}}\\ *&*&\mathrm{e}^{-2\alpha h}U\end{bmatrix}\nonumber \\&\qquad \begin{bmatrix}\phi (t)\\ g(s)\phi (t)\\ \dot{r}(s)\end{bmatrix}{\mathrm {d}}s\geqslant 0 \end{aligned}$$

(27)

where $\phi (t)=\begin{bmatrix}r(t)^{\mathrm {T}}&\dot{r}(t)^{\mathrm {T}}&r(t_k)^{\mathrm {T}}&\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}{\mathrm {d}}s\end{bmatrix}^{\mathrm {T}}$ and $g(s)={t+t_k-2s}$.

From (27), we can get that

$$\begin{aligned}&-\int \limits ^{t}_{t_k}\mathrm{e}^{-2\alpha h}\dot{r}(s)^{\mathrm {T}}{}U\dot{r}(s){\mathrm {d}}s\nonumber \\&\quad \leqslant {}(t-t_k)\phi (t)^{\mathrm {T}}H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}H\phi (t)\nonumber \\&\quad \quad +\frac{(t-t_k)^3}{3}\phi (t)^{\mathrm {T}}N^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N\phi (t)\nonumber \\ {}&\quad \quad +\,2\phi (t)^{\mathrm {T}}H^{\mathrm {T}}(r(t)-r(t_k))+4\phi (t)^{\mathrm {T}}N^{\mathrm {T}}\nonumber \\ {}&\quad \quad \times \int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}{\mathrm {d}}s-2(t-t_k)\phi (t)^{\mathrm {T}}N^{\mathrm {T}}(r(t)+r(t_k)) . \end{aligned}$$

(28)

Applying the above inequality to (19), we obtain that

$$\begin{aligned} \dot{V}_5(t) \leqslant {}&\mathrm{e}^{2\alpha t}(t-t_k)\phi (t)^{\mathrm {T}}H^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}H\phi (t)\nonumber \\&+ \mathrm{e}^{2\alpha t}\frac{(t-t_k)^3}{3}\phi (t)^{\mathrm {T}}N^{\mathrm {T}}\mathrm{e}^{2\alpha h}U^{-1}N\phi (t)\nonumber \\ {}&+2\mathrm{e}^{2\alpha t}\phi (t)^{\mathrm {T}}H^{\mathrm {T}}(r(t)-r(t_k))\nonumber \\&+4\mathrm{e}^{2\alpha t}\phi (t)^{\mathrm {T}}N^{\mathrm {T}}\int \limits ^{t}_{t_k}r(s)^{\mathrm {T}}{\mathrm {d}}s\nonumber \\ {}&-2\mathrm{e}^{2\alpha t}(t-t_k)\phi (t)^{\mathrm {T}}N^{\mathrm {T}}(r(t)+r(t_k))\nonumber \\&{}+(t_{k+1}-t)\mathrm{e}^{2\alpha t}\dot{r}(t)^{\mathrm {T}}U\dot{r}(t) . \end{aligned}$$

(29)

On the other hand, according to system (3), for any appropriately dimensioned matrices $G_1, G_2,$ and $G_3$, the following equation holds:

$$\begin{aligned} \nonumber \ {}&2\mathrm{e}^{2\alpha t}\left[ r(t)^{\mathrm {T}}G_1+\dot{r}(t)^{\mathrm {T}}G_2+{r}(t_k)^{\mathrm {T}}G_3\right] [-\dot{r}(t)\\ {}&\quad +Ar(t)+Br(t-d)+W\eta (Dr(t))-KCr(t_k)]=0 . \end{aligned}$$

(30)

In addition, it can be derived form (5) that, for any matrices $V_j={\mathrm {diag}}\{v_{j1},\,v_{j2},\cdots ,v_{j{n_h}}\}\geqslant 0$, $j=1,2$, the following inequality holds,

$$\begin{aligned}&2\mathrm{e}^{2\alpha t}\frac{t_{k+1}-t}{h_k}{}\left[ r(t)^{\mathrm {T}}D^{\mathrm {T}}FV_1\eta (Dr(t))\right. \nonumber \\&\qquad \left. -\eta (Dr(t))^{\mathrm {T}}V_1\eta (Dr(t))\right] +2\mathrm{e}^{2\alpha t}\frac{t-t_k}{h_k}{}\nonumber \\&\qquad \times \left[ r(t)^{\mathrm {T}}D^{\mathrm {T}}FV_2\eta (Dr(t))-\eta (Dr(t))^{\mathrm {T}}V_2\eta (Dr(t))\right] \nonumber \\&\quad \geqslant 0. \end{aligned}$$

(31)

Then, adding the left-hand side of (30) and (31) to $\dot{V}(t)$, we obtain from (16), (17), (19), (21), (24), (25), and (29) that for $t\in [t_k,\,t_{k+1})$,

$$\begin{aligned}&\dot{V}(t)\leqslant \mathrm{e}^{2\alpha t}\chi (t)^{\mathrm {T}}\left[ \frac{t_{k+1}-t}{h_k}\varXi _1(h_k)\right. \nonumber \\&\left. +\frac{t-t_k}{h_k}\hat{\varXi }_2(h_k)\right] \chi (t) \end{aligned}$$

(32)

where

$\chi (t)=\begin{bmatrix}\phi (t)^{\mathrm {T}}&\eta (Dr(t))^{\mathrm {T}}&r(t-d)^{\mathrm {T}}\end{bmatrix}^{\mathrm {T}}$ and

$$\begin{aligned} \hat{\varXi }_2(h_k)&=\begin{bmatrix} \varXi _{11}&\varXi _{12}&\varXi _{13}&\varXi _{14}&G_1W+D^{\mathrm {T}}SV_2&\varXi _{16}\\ *&\varXi _{22}&\varXi _{23}&2N_2^{\mathrm {T}}&-\Lambda D+G_2W&G_2B \\ *&*&\varXi _{33}&\varXi _{34}&G_3W&G_3B\\ *&*&*&\varXi _{44}&0&0\\ *&*&*&*&-2V_2&0\\ *&*&*&*&*&\varXi _{66} \\ \end{bmatrix}\\&\quad +{h_k}\begin{bmatrix} H_1^{\mathrm {T}}\\ H_2^{\mathrm {T}}\\ H_3^{\mathrm {T}}\\ H_4^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}\mathrm{e}^{2\alpha h}U^{-1}\begin{bmatrix} H_1^{\mathrm {T}}\\ H_2^{\mathrm {T}}\\ H_3^{\mathrm {T}}\\ H_4^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}^{\mathrm {T}}\\&+{}\frac{h_k^3}{3}\begin{bmatrix} N_1^{\mathrm {T}}\\ N_2^{\mathrm {T}}\\ N_3^{\mathrm {T}}\\ N_4^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}\mathrm{e}^{2\alpha h}U^{-1}\begin{bmatrix} N_1^{\mathrm {T}}\\ N_2^{\mathrm {T}}\\ N_3^{\mathrm {T}}\\ N_4^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}^{\mathrm {T}}\\&+{h_k}\begin{bmatrix} 0\\ 0\\ 0\\ Y^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}\mathrm{e}^{-2\alpha h}R_1^{-1}\begin{bmatrix} 0\\ 0\\ 0\\ Y^{\mathrm {T}}\\ 0\\ 0\\ \end{bmatrix}^{\mathrm {T}} . \end{aligned}$$

Noticing that

$$\begin{aligned} \varXi _1(h_k)=\frac{h_k}{h}\varXi _1(h)+\frac{h-h_k}{h}\varXi _1(0) \end{aligned}$$

(33)

and

$$\begin{aligned} \hat{\varXi }_2(h_k)=\frac{h_k}{h}\hat{\varXi }_2(h)+\frac{h-h_k}{h}\hat{\varXi }_2(0) , \end{aligned}$$

(34)

we get from (12) that

$$\begin{aligned} \varXi _1(h_k)<0 . \end{aligned}$$

(35)

Similarly, it can be obtained from (13) that

$$\begin{aligned} \hat{\varXi }_2(h_k)<0 \end{aligned}$$

(36)

by means of the Schur complement. Thus, we obtain from (32), (35) and (36) that

$$\begin{aligned} \dot{V}(t)<0,\,t\in [t_k,\,t_{k+1}) . \end{aligned}$$

(37)

Thus, it follows that for $t\in [t_k,\,t_{k+1})$,

$$\begin{aligned} V(t)\leqslant V(t_{k})\leqslant V(t_{k-1}) \leqslant \cdots \leqslant V(0) . \end{aligned}$$

(38)

From Lemma 3 and (38), it can be concluded that for $t_k\leqslant {t}<t_{k+1}$

$$\begin{aligned} ||r(t)||^2&\leqslant \theta _1||r(t_k)||^2+\theta _2\int \limits _{t_k-d}^{t_k}||r(\alpha )||^2\,{\mathrm {d}}\alpha \nonumber \\&=\frac{\theta _1}{\lambda _{\min }(P)\mathrm{e}^{2\alpha {t}_k}}\mathrm{e}^{2\alpha {t}_k}\lambda _{\min }(P)||r(t_k)||^2\nonumber \\&\quad +\frac{\theta _2}{\lambda _{\min }(Q)\mathrm{e}^{2\alpha {t}_k}}\mathrm{e}^{2\alpha {t}_k}\lambda _{\min }(Q)\int \limits _{t_k-d}^{t_k}||r(\alpha )||^2\,{\mathrm {d}}\alpha \nonumber \\&\leqslant \frac{\theta _1}{\lambda _{\min }(P)\mathrm{e}^{2\alpha {t}_k}}\mathrm{e}^{2\alpha {t}_k}r({t}_k)^{\mathrm {T}}Pr({t}_k)\nonumber \\&\quad +\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)\mathrm{e}^{2\alpha {t}_k}}\int \limits _{t_k-d}^{t_k}\mathrm{e}^{2\alpha s}r(s)^{\mathrm {T}}Qr(s)\,{\mathrm {d}}s\nonumber \\&\leqslant \frac{\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }{\mathrm{e}^{2\alpha {t}_k}}(V_1(t_k)+V_2(t_k))\nonumber \\&\leqslant \frac{\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }{\mathrm{e}^{2\alpha {t}_k}}V(t_k)\nonumber \\&\leqslant \frac{\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }{\mathrm{e}^{2\alpha {t}_k}}V(0)\nonumber \\&={\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }{\mathrm{e}^{-2\alpha {t}}}{\mathrm{e}^{2\alpha (t-{t}_k)}}V(0)\nonumber \\&\leqslant {\mathrm{e}^{2\alpha h}}{\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }{\mathrm{e}^{-2\alpha {t}}}V(0) . \end{aligned}$$

(39)

In addition, we can get that

$$\begin{aligned} V(0)={}&r(0)^{\mathrm {T}}Pr(0)+\int \limits ^{0}_{-d}\mathrm{e}^{2\alpha s}r(s)^{\mathrm {T}}Qr(s)\,{\mathrm {d}}s\nonumber \\&+\int \limits ^{0}_{-d}\int \limits ^{0}_{\theta }\mathrm{e}^{2\alpha s}\dot{r}(s)^{\mathrm {T}}Z\dot{r}(s)\,{\mathrm {d}}s\,{\mathrm {d}}\theta \nonumber \\&+2\sum \limits _{i=1}^{n_h}\lambda _{i}\int \limits ^{d_i^{\mathrm {T}} r(0)}_{0}(f_i s- \eta _i(s)){\mathrm {d}}s\nonumber \\ \leqslant {}&r(0)^{\mathrm {T}}Pr(0)+\int \limits ^{0}_{-d}r(s)^{\mathrm {T}}Qr(s)\,{\mathrm {d}}s\nonumber \\&+d\int \limits ^{0}_{-d}\dot{r}(s)^{\mathrm {T}}Z\dot{r}(s)\,{\mathrm {d}}s+2\sum \limits _{i=1}^{n_h}\lambda _{i}\int \limits ^{d_i^{\mathrm {T}} r(0)}_{0}f_i s {\mathrm {d}}s\nonumber \\ \leqslant {}&(\lambda _{\max }(P)+\lambda _{\max }(D^{\mathrm {T}}\Lambda FD))||r(0)||^2\nonumber \\&+d\lambda _{\max }(Q)\sup _{{-d}\leqslant \theta \leqslant 0}||{r(\theta )}||^2\nonumber \\&+d^2\lambda _{\max }(Z)\sup _{{-d}\leqslant \theta \leqslant 0}||{\dot{r}(\theta )}||^2\nonumber \\ \leqslant {}&\theta _3\left( \sup _{{-d}\leqslant \theta \leqslant 0}\{||{r(\theta )}||,||{\dot{r}(\theta )}||\}\right) ^2 \end{aligned}$$

(40)

where

$$\begin{aligned} \theta _3= & {} \lambda _{\max }(P)+\lambda _{\max }(D^{\mathrm {T}}\Lambda FD)+d\lambda _{\max }(Q)\\&+\,d^2\lambda _{\max }(Z) . \end{aligned}$$

From (39) and (40), we get

$$\begin{aligned} ||r(t)||\leqslant {\mathrm{e}^{\alpha h}}\sqrt{{\max \left\{ \frac{\theta _1}{\lambda _{\min }(P)},\,\frac{\theta _2\mathrm{e}^{2\alpha d}}{\lambda _{\min }(Q)}\right\} }\theta _3}\mathrm{e}^{-\alpha t}||r_{0}||_c.\nonumber \\ \end{aligned}$$

(41)

Thus, it can be concluded from Definition 1 that the master system $\mathcal {M}$ and the slave system $\mathcal {S}$ in (1) are exponentially synchronous. This concludes the proof.

Remark 1

Theorem 1 provides a new synchronization criterion for the master system ${\mathcal {M}}$ and the slave system S in (1). It should be pointed out that it is very important to consider the synchronization control design problem under a bigger sampling period since a longer sampling period will lead to lower communication channel occupation, fewer actuation of the controller, and less signal transmission [26, 27].

Remark 2

Compared with the results in [30], the less conservative of the criteria provided in this paper relies on the constructed Lyapunov functional and the method of estimation of its derivative. First, $V_4(t)$ is considered in this paper, while this term is neglected in [30]. Second, Lemma 2 is used to handle the term $-\int _{t_k}^t r(s)R_1r(s)ds$ instead of using Jenson inequality. Finally, in bounding $-\int \nolimits ^{t}_{t_k}\mathrm{e}^{-2\alpha h}\dot{r}(s)^{\mathrm {T}}{}U\dot{r}(s){\mathrm {d}}s$, the function, g(s), is firstly proposed and a free-matrix N is introduced. When setting $N=0$, (29) reduces to (28) in [30]. It should be noted that the Theorem 1 provides less conservative result than the ones obtained in [30] but at an increasing computation burden because of introducing the free-matrix N and the Lyapunov functional $V_4(t)$.

Next, Theorem 1 is extended to design a sampled-data controller to assure that system $\mathcal {M}$ and the slave system $\mathcal {S}$ in (1) are exponentially synchronous. Setting $G_1=\varepsilon G$, $G_2=G$, $G_3=\gamma G$ in (12) and (13) and letting $L=GK$, we have the following result.

Theorem 2

Given scalars $\alpha >0$, $\varepsilon$, and $\gamma$, the master system ${\mathcal {M}}$ and the slave system $\mathcal {S}$ in (1) are exponentially synchronous if there exist matrices $P>0$, $Q>0$, $Z>0$, $U>0$, $\begin{bmatrix}R_1&R_2\\ *&R_3\end{bmatrix}>0$, $X_1$, $X_2$, $X_3$, $X_4$, $X_5$, G, L, Y, $N=\begin{bmatrix}N_1&N_2&N_3&N_4\end{bmatrix}$, $H=\begin{bmatrix}H_1&H_2&H_3&H_4\end{bmatrix}$, and diagonal matrices $\Lambda >0$, $V_1>0$, and $V_2>0$ such that (42) and (43) is feasible for $\bar{h}=0, h$

$$\begin{aligned} {}&\begin{bmatrix} \hat{\varXi }_{11}+\varTheta _{11}&\hat{\varXi }_{12}+\varTheta _{12}&\hat{\varXi }_{13}+\varTheta _{13}&\varXi _{14}+\varTheta _{14}&\varepsilon GW+D^{\mathrm {T}}FV_1&\hat{\varXi }_{16}\\ *&\hat{\varXi }_{22}+\bar{h}U&\hat{\varXi }_{23}+\varTheta _{23}&\bar{h}X_3+2N_2^{\mathrm {T}}&-\Lambda D+GW&GB \\ *&*&\hat{\varXi }_{33}+\varTheta _{33}&\varXi _{34}+\varTheta _{34}&\gamma GW&\gamma GB\\ *&*&*&\varXi _{44}+\varTheta _{44}&0&0 \\ *&*&*&*&-2V_1&0\\ *&*&*&*&*&\varXi _{66} \end{bmatrix}<0 \end{aligned}$$

(42)

$$\begin{aligned} {}&\begin{bmatrix} \hat{\varXi }_{11}&\hat{\varXi }_{12}&\hat{\varXi }_{13}&\varXi _{14}&\varepsilon GW+D^{\mathrm {T}}FV_2&\hat{\varXi }_{16}&\sqrt{\bar{h}}H_1^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_1^{\mathrm {T}}&0\\ *&\hat{\varXi }_{22}&\hat{\varXi }_{23}&2N_2^{\mathrm {T}}&-\Lambda D+GW&GB&\sqrt{\bar{h}}H_2^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_2^{\mathrm {T}}&0\\ *&*&\hat{\varXi }_{33}&\varXi _{34}&\gamma GW&\gamma GB&\sqrt{\bar{h}}H_3^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_3^{\mathrm {T}}&0\\ *&*&*&\varXi _{44}&0&0&\sqrt{\bar{h}}H_4^{\mathrm {T}}&{\bar{h}}\sqrt{\bar{h}}N_4^{\mathrm {T}}&\sqrt{\bar{h}}Y^{\mathrm {T}}\\ *&*&*&*&-2V_2&0&0&0&0\\ *&*&*&*&*&\varXi _{66}&0&0&0\\ *&*&*&*&*&*&-\mathrm{e}^{-2\alpha h}U&0&0\\ *&*&*&*&*&*&*&-3\mathrm{e}^{-2\alpha h}U&0\\ *&*&*&*&*&*&*&*&-\mathrm{e}^{2\alpha h}R_1\\ \end{bmatrix}<0 \end{aligned}$$

(43)

where

$$\begin{aligned} \hat{\varXi }_{11}= & {} 2\alpha {P}+Q-{X_1-X_1^{\mathrm {T}}}-\frac{\mathrm{e}^{-2\alpha d}}{d}Z+H_1\\&+\,H_1^{\mathrm {T}}+\varepsilon GA+\varepsilon A^{\mathrm {T}}G^{\mathrm {T}}\\&+\,2\alpha D^{\mathrm {T}}F\Lambda D -\bar{h}N_1-\bar{h}N_1^{\mathrm {T}},\\ \hat{\varXi }_{12}= & {} P+H_2-\varepsilon G+A^{\mathrm {T}}G^{\mathrm {T}}+D^{\mathrm {T}}F\Lambda D-\bar{h}N_2,\\ \hat{\varXi }_{13}= & {} X_1-X_2+H_3-H_1^{\mathrm {T}}\\&-\,\varepsilon LC+\gamma A^{\mathrm {T}}G^{\mathrm {T}}-\bar{h}N_3-\bar{h}N_1^{\mathrm {T}},\\ \hat{\varXi }_{16}= & {} \frac{\mathrm{e}^{-2\alpha d}}{d}Z+\varepsilon GB,\\ \hat{\varXi }_{22}= & {} dZ-G-G^{\mathrm {T}},\\ \hat{\varXi }_{23}= & {} -H_2^{\mathrm {T}}-LC-\gamma G^{\mathrm {T}}-\bar{h}N_2^{\mathrm {T}},\\ \hat{\varXi }_{33}= & {} X_2+X_2^{\mathrm {T}}-H_3-H_3^{\mathrm {T}}-\gamma LC\\&-\,\gamma C^{\mathrm {T}}L^{\mathrm {T}}-\mathrm{e}^{-2\alpha h}\bar{h}R_3-\bar{h}N_3-\bar{h}N_3^{\mathrm {T}},\\ \end{aligned}$$

and the other parameters are defined in Theorem 1. Furthermore, the controller gain matrix in (1) is given by

$$\begin{aligned} K=G^{-1}L . \end{aligned}$$

(44)

4 Numerical example and simulation

In this section, a numerical example will be provided to demonstrate the effectiveness and the benefits of the proposed method.

Example 1

Consider the following Chua’s circuit [35]

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_1(t)=a(x_2(t)-m_1{x}_1(t)+g({x}_1(t)))-cx_1(t-d)\\ \dot{x}_2(t)={x}_1(t)-{x}_2(t)+{x}_3(t)-cx_1(t-d)\\ \dot{x}_3(t)=-b{x}_2(t)+c(2x_1(t-d)-x_3(t-d))\\ p(t)=x_1(t) \end{array}\right. \nonumber \\ \end{aligned}$$

(45)

with the nonlinear characteristics

$$\begin{aligned} g({x}_1(t))=\frac{1}{2}(m_1-m_0)(|{x}_1(t)+1|-|{x}_1(t)-1|) \end{aligned}$$

and parameters $m_0=-1/7$, $m_1=2/7$, $a=9$, $b=14.28$, $c=0.1$, $d=1$.

It is obvious that this circuit can be rewritten as the time delay Lur’e system with

$$\begin{aligned} A={}&\begin{bmatrix}-am_1&a&0\\ 1&-1&1\\ 0&-b&0 \end{bmatrix}, B=\begin{bmatrix}-c&0&0\\ -c&0&0\\ 2c&0&-c \end{bmatrix}\\ W={}&\begin{bmatrix}a(m_1-m_0)&0&0\\ 0&0&0\\ 0&0&0 \end{bmatrix}, D=\begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}\\ C={}&\begin{bmatrix}1&0&0 \end{bmatrix} \end{aligned}$$

with $\varphi _1({x}_1(t))=\frac{1}{2}(|{x}_1(t)+1|-|{x}_1(t)-1|)$ belonging to sector $[0,\,1]$, and $\varphi _2({x}_2(t))=\varphi _3({x}_3(t))=0$.

Applying Theorem 2 with $\varepsilon =0.5$ and $\gamma =2$, for different $\alpha$, the maximum values of the upper bound h are obtained and summarized in Table 1, along with the results given in [30]. From Table 1, it can be seen that the criterion proposed in this paper can get larger h than [30]. On the other hand, for given largest sampling interval h, the corresponding maximum decay rate $\alpha$ is obtained and listed in Table 2, which shows that our approach can achieve faster synchronization than [30] under the same h. It can be also concluded that a smaller sampling period can achieve a faster synchronization of the master and slave systems.

Table 1 Maximum values of the upper bound h for different $\alpha$

Table 2 Maximum values of $\alpha$ for different upper bound h

Choosing $\alpha =0.2$ and $h=0.3919$, and using Matlab LMI Toolbox to solve the LMIs (12) and (13), we can get the following gain matrix in (1):

$$\begin{aligned} K=\begin{bmatrix} 3.6620&0.6363&-2.4233\end{bmatrix}^{\mathrm {T}} \end{aligned}$$

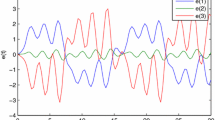
that is, for any sampling period $h_k\leqslant 0.3919$, the master and slave systems are exponentially synchronized by the given sampled-data controller. The initial conditions of the master and slave systems are chosen as $x(t)=\begin{bmatrix}0.5&0.3&0.2 \end{bmatrix}^{\mathrm {T}}$ and $z(t)=\begin{bmatrix}-0.3&-0.1&0.4 \end{bmatrix}^{\mathrm {T}}$, $t\in [-1,\,0]$, and the response curves of error system (3) are given in Figs. 1 and 2 under the obtained controller gain matrix. It can be seen from Fig. 1 that the synchronization error is tending to zero, which implies that the synchronization of the master and slave systems can be achieved by the designed sampled-data controller.

Fig. 1

State response of error system (3)

Fig. 2

Input response of error system (3)

Fig. 3

State response of error system (43)

Fig. 4

Input response of error system (43)

Choosing $c=0$, the Chua’s circuit (45) reduces to a Lur’e system without time delay, which has been discussed in [26–32]. It was reported in [26–32] that the maximum values of the upper bound h, which assure the synchronization of the master and slave systems, are 0.17, 0.21, 0.33, 0.3914, 0.3981, 0.45, and 0.48, respectively. While utilizing Theorem 2 with $\alpha =0$ given in this paper, the maximum value of h is 0.5463, and the corresponding gain matrix is

$$\begin{aligned} K=\begin{bmatrix} 2.8724&0.2754&-1.9238 \end{bmatrix}^{\mathrm {T}} \end{aligned}$$

Obviously, the criterion given in this paper can provided larger upper bound of h than [26–32]. Choosing the initial conditions of the master and slave systems as $x(0)=\begin{bmatrix}0.7&-0.3&0.4\end{bmatrix}^{\mathrm {T}}$ and $z(0)=\begin{bmatrix}-0.7&-0.5&0.5 \end{bmatrix}^{\mathrm {T}}$, the response curves of error system (43) under the obtained controller, are given in Figs. 3 and 4, which show that the synchronization error is tending to zero.

5 Conclusions

In this paper, the problem of master–slave synchronization for chaotic Lur’e systems with time delay has been investigated via a sampled-data control approach. A new Lyapunov functional has been constructed for the synchronization error systems, in which the information about the actual sampling pattern and the nonlinear function has been taken fully into account. A tighter bounding technique is proposed to handle the derivative of the Lyapunov functional, which yields a less conservative synchronization criterion. The derived criterion is extended to design a sampled-data controller and the desired controller gain matrix has been given. Finally, the Chua’s circuit has been applied to verify the effectiveness of the proposed approach.