Sampled-Data Synchronization of Chaotic Lur’e Systems with Stochastic Sampling

Abstract

In this paper, we study the problem of master–slave synchronization for chaotic Lur’e systems with sampled-data control. The sampling intervals are assumed to satisfy a Bernoulli distributed white noise sequence with fixed and given occurrence probability. By applying an input-delay approach, the probabilistic sampling system is transformed into a continuous time-delay system with stochastic parameters in the system matrices. Based on Lyapunov functional approach, a sufficient condition of exponentially mean-square synchronization is obtained by analyzing the corresponding synchronization error systems. The controller gains are designed by solving a set of linear matrix inequalities. Finally, two numerical examples are given to demonstrate the effectiveness of the proposed method.

1 Introduction

Since the concept for synchronization of coupled chaotic systems was first proposed by Pecora and Caroll [18], chaos synchronization has become a very hot topic in the nonlinearity community, and a variety of alternative schemes for ensuring the control and synchronization of chaotic systems have been proposed due to its potential applications in various fields such as secure communication, physics, automatic control and chemical and biological systems [17]. It has been shown that a lot of nonlinear systems, such as neural networks, n-scroll attractors, Chua’s circuits and hyper-chaotic attractors can be represented in the form of Lur’e systems [10, 12, 29]. Therefore, a number of control schemes for synchronization of chaotic Lur’e systems have been proposed such as state-feedback control [5, 6, 8, 40], dynamic output feedback control [20], impulsive control [1, 2, 13], PD control [7, 30], adaptive control [11, 14] and so on.

With the rapid development of modern high-speed computers, modern control systems tend to be controlled by digital controllers for better scalability, reliability, flexibility, and cost-effectiveness [31–34]. The sampled-data controllers, which only need the samples of the state variables of the master–slave systems at discrete time instants, are proposed to synchronize chaos systems. Lu et al. [15] investigated the problem of synchronization of chaotic Lur’e system by using the input-delay approach combined with the free-weighting matrix technique. Compared with the control design method in [15], the result presented in [38] is less conservative by using an improved free-weighting matrix method. Recently, the work in [3, 41] has improved the results by employing some discontinuous Lyapunov functional. Compared with the time-independent Lyapunov functional introduced in [15, 38], the discontinuous Lyapunov functional suggested in [3, 41] can capture more information about the actual sampling pattern and provide less conservative results. The sampled-data synchronization of chaotic Lur’e system was further studied in [26, 37]. In [27], the problem of sampled-data control for master–slave synchronization schemes that consist of identical chaotic Lur’e systems with time delays was studied. Xiao et al. [28] studied the synchronization problem of chaotic Lur’e system by adopting the quantized sampled-data control. The problem of secure communication via synchronization of Lur’e systems using samped-data controller was investigated in [24].

It should be noted that, for analysis and design of the above-mentioned control systems [3, 15, 24, 26–28, 37, 38, 41], only the information of variation range and/or variation rate of the time delay was employed. However, the uncertain sampling may happen when the sampler contains uncertainties or the mathematical model is not ideally consistent with the sampling equipment in some practical systems. One example is the case of deadbeat control for MW (megawatt) class PWM (pulse width modulation) inverter system [21]. Another example is the stochastic effects of short tandem repeat (STR) typing [22]. Therefore, the necessity of the controller design problem using sampled-data with the stochastically varying sampling interval has been highlighted and many important results have been reported [4, 9, 19, 23, 25, 35, 36, 39]. To the best of the authors’ knowledge, the problem of sampled-data synchronization for Lur’e systems considering both the information of variation range of the time delay and the information of probability of the time-varying delay in an interval has not been investigated in the existing literatures.

Motivated by above discussions, in this paper, attention is focused on the synchronization problem of chaotic Lur’e systems with stochastic sampled-data control. Unlike previous studies in [3, 15, 24, 26–28, 37, 38, 41], the sampling period considered here is assumed to be time-varying that switches between two different values in a random way with a given probability. It is also assumed to satisfy Bernoulli distribution, which can be further extended to the case with multiple stochastic sampling periods [9]. By applying an input-delay approach, the probabilistic sampling system is transformed into a continuous time-delay system with stochastic parameters in the system matrices. Based on Lyapunov stability theory combined with lower bound lemma, a delay-dependent condition is established such that the master and slave system can be exponentially mean-square synchronized. Moreover, a controller gain is obtained by solving a set of linear matrix inequalities. The effectiveness of the proposed theoretical result is demonstrated by numerical simulations.

Throughout this paper, $I$ denotes the identity matrix with appropriate dimensions, ${\mathcal {R}}^n$ denotes the $n$ dimensional Euclidean space, and ${\mathcal {R}}^{m\times n}$ is the set of all $m \times n$ real matrices, $\parallel . \parallel$ refers to the Euclidean vector norm and the induced matrix norm. For symmetric matrices $A$ and $B$, the notation $A > B$(respectively, $A \ge B$) means that the matrix $A-B$ is positive definite (respectively, nonnegative). ${\mathcal {E}}\{x\}$ and ${\mathcal {E}}\{x|y\}$ mean the expectation of $x$ and expectation of $x$ conditional of $y$, respectively.

2 Problem Formulation and Preliminaries

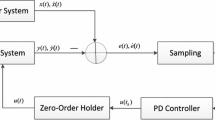
Consider the following master–slave type of Lur’e systems with sampled-data control [3, 15, 24, 26–28, 37, 38, 41]:

$$\begin{aligned}&{\mathcal {M}}:\left\{ \begin{aligned} \dot{x}(t)&=Ax(t)+Hf(Dx(t)), \\ p(t)&=Cx(t), \end{aligned} \right. \end{aligned}$$

(1)

$$\begin{aligned}&{\mathcal {S}}:\left\{ \begin{aligned} \dot{y}(t)&=Ay(t)+Hf(Dy(t))+u(t) , \\ q(t)&=Cy(t), \end{aligned} \right. \end{aligned}$$

(2)

$$\begin{aligned}&{\mathcal {U}}:u(t)=-K(p(t_k)-q(t_k)),\; t_k \le t \le t_{k+1} \end{aligned}$$

(3)

which consists of master system ${\mathcal {M}}$, the slave system ${\mathcal {S}}$, and controller ${\mathcal {U}}$; the master and slave systems are delayed Lur’e systems with state vectors $x(t),y(t) \in {\mathcal {R}}^n$, respectively, $A \in {\mathcal {R}}^{n\times n}, H \in {\mathcal {R}}^{n\times n_h},C \in {\mathcal {R}}^{l\times n},D \in {\mathcal {R}}^{n_h\times n}$ are known constant matrices, $u(t)\in {\mathcal {R}}^n$ is the slave system control input, and $K \in {\mathcal {R}}^{n\times l}$ is the sampled-data controller gain matrix to be designed. It is assumed that $f(\cdot ):{\mathcal {R}}^{n_h} \rightarrow {\mathcal {R}}^{n_h}$ is a diagonal nonlinearity with $f(\cdot )$ belonging to sector $[k_i^-, k_i^+]$ for $i=1,2,\ldots ,m$.

For the sampled-data synchronization, only discrete measurements of $p(t)$ and $q(t)$ can be used for synchronization purposes, that is, we only have the measurements $p(t_k )$ and $\hbox {q}(t_k)$ at the sampling instant $t_k$. In this paper, the control signal is assumed to be generated by using a zero-order-hold (ZOH) function with a sequence of hold times $0 \le t_0<t_1<\cdots <t_k \cdots < \mathop {\lim }\limits _{\mathrm{{k}} \rightarrow \infty } {t_k} = + \infty$.

Define $d_k(t)=(t-t_k)$, then $t_k=t-(t-t_k)=t-d_k(t)$, $t_k \le t < t_{k+1}$.

Define the error signal $e(t)=y(t)-x(t),$ we have

$$\begin{aligned} \dot{e}(t) = Ae(t)+Hg(De(t),x(t))+KCe(t-d_k(t)), \end{aligned}$$

(4)

where

$$\begin{aligned} g(De(t),x(t))=f(De(t)+Dx(t))-f(Dx(t)). \end{aligned}$$

The nonlinearity $g(De(t),x(t))$ belongs to the sector $[k_i^-,k_i^+],i=1,2\ldots ,m$, then

$$\begin{aligned} \left[ g_i(d_{i}e(t),x(t))-k_i^-d_{i}e(t)\right] \left[ g_i(d_{i}e(t),x(t))-k_i^+d_{i}e(t)\right] \le 0, \forall e(t),x(t) \in {\mathcal {R}}^n.\nonumber \\ \end{aligned}$$

(5)

As pointed out in [4, 19, 25, 35, 36], in an environment, the sampling period itself might be a stochastic variable due to unpredictable environmental changes. To reflect such a reality, in this paper, the sampling of each control signal is allowed to randomly switch between to different values $c_1$ and $c_2$ with $c_2>c_1>0$, and the probability of the occurrence of each is known, that is,

$$\begin{aligned} \text {Prob}\{c=c_1\}=\alpha , \text {Prob}\{c=c_2\}=1-\alpha . \end{aligned}$$

From the definition of $d_k(t)$, it is obvious that $d_k(t)$ is a sawtooth function with randomness, and its value lies in the interval $[0,c_2]$. We divide the intervals $[0,c_2]$ into two interval $[0,c_1]$ and $(c_1,c_2]$ and introduce the following stochastic variable $\delta (t)$:

$$\begin{aligned} \delta (t) = \left\{ {\begin{array}{ll} 1,&{}\quad 0 \le d_k(t) \le c_1 \\ 0, &{}\quad c_1 \le d_k(t) \le c_2. \\ \end{array}} \right. \end{aligned}$$

(6)

We are assumed that $\delta (t)$ is a Bernoulli distributed sequence with $Prob\{\delta (t) = 1 \} = \delta _0$, and $Prob\{\delta (t) = 0 \}=1-\delta _0$, where $\delta _0=\alpha +\frac{c_1}{c_2}(1-\alpha )$ [4, 19]. Then we have ${\mathcal {E}}\{\delta (t) - \delta _0 \}=0$ and ${\mathcal {E}}\{(\delta (t) -\delta _0)^2 \}=\delta _0(1-\delta _0)$.

Define two functions $\tau _1:{\mathcal {R}}\rightarrow [0,c_1]$ and $\tau _2:{\mathcal {R}}\rightarrow [c_1,c_2]$ such that

$$\begin{aligned} \tau _1 (t) = \left\{ {\begin{array}{c} d_k(t), \delta (t)=1 \\ c_1, \delta (t)=0, \\ \end{array}} \right. \quad \tau _2 (t) = \left\{ {\begin{array}{c} c_1, \delta (t)=1, \\ d_k(t), \delta (t)=0. \\ \end{array}} \right. \end{aligned}$$

(7)

Therefore, the system (4) can be equivalently written by using $\delta (t)$ and $\tau _i(t)(i=1,2)$

$$\begin{aligned} \dot{e}(t)= & {} Ae(t)+Hg(De(t),x(t))+\delta (t)KCe(t-\tau _1(t)) \nonumber \\&+\,(1-\delta (t))KCe(t-\tau _2(t)). \end{aligned}$$

(8)

Remark 2.1

 In [3, 15, 24, 26–28, 37, 38, 41], the sampled-data synchronization of chaotic Lur’e system has been studied. It should be pointed that the sampling period are assumed to be implemented in a deterministic way. However, due to the sudden environment changes, random sampler failures, etc., it is necessary to investigated the stochastic sampling (the sampling periods may vary in a probabilistic way) case. Hence, the sampled-data synchronization of chaotic Lur’e systems with stochastic sampling is studied in this paper. And the random variables $\delta (t)$ are employed to model the probability distribution of the stochastic sampling. Such a description originated from [4, 19] has never been considered in Lur’e systems.

Definition 2.1

The system (8) is said to be exponentially mean-square stable if there exist two constants $\alpha >0$ and $\beta > 0$ such that

$$\begin{aligned} {\mathcal {E}}{\Vert e(t)\Vert ^2} \le \alpha e ^{-\beta t}\text {sup}_{-2c_2\le \eta \le 0}{\mathcal {E}}{\Vert \phi (t)\Vert ^2}, \end{aligned}$$

where $\phi (\cdot )$ is the initial function of system (8) defined as $e(t)=\phi (t), t\in [-c_2,0]$.

Definition 2.2

The master system (1) and the slave system (2) are said to be exponentially mean-square synchronized if system (8) is exponentially mean-square stable.

The main purpose of this paper is to design a controller with the stochastic sampling to achieve exponentially mean-square synchronization of the master system (1) and slave systems (2). In other words, we are interested in finding a gain matrix $K$ such that the error system (8) is exponentially mean-square stable.

The following lemmas will be used for providing the main results.

Lemma 2.1

(Lower bounds lemma [16]) Let $f_1,f_2,\ldots ,f_N: {\mathcal {R}}^m \rightarrow {\mathcal {R}}$ have positive values in an open subset $D \in {\mathcal {R}}^m$. Then, the reciprocally convex combination of $f_i$ over $D$ satisfies

$$\begin{aligned} \mathop {\min }\limits _{\{ {\alpha _i}\left| {{\alpha _i} > 0,\sum \nolimits _i {{\alpha _i}} = 1\} } \right. } \sum \limits _i {\frac{1}{{{\alpha _i}}}} {f_i}(t) = \sum \limits _i {{f_i}(t)} + \mathop {\max }\limits _{{g_{ij}}} \sum \limits _{i \ne j} {{g_{ij}}(t)}, \end{aligned}$$

subject to

$$\begin{aligned} \left\{ {{g_{ij}}:{R^m} \rightarrow R,{g_{j,i}}(t) \buildrel \varDelta \over = {g_{i,j}}(t),\quad \left[ {\begin{array}{cc} {{f_i}(t)} &{}\quad {{g_{i,j}}(t)} \\ {{g_{i,j}}(t)} &{}\quad {{f_j}(t)} \\ \end{array}} \right] \ge 0} \right\} . \end{aligned}$$

3 Main Results

In this section, sufficient conditions will be established to the control synthesis assuring the synchronization between the master system (1) and slave system (2). First rewrite system (8) as the following

$$\begin{aligned} \dot{e}(t)= & {} Ae(t)+Hg(De(t),x(t))+\delta _0KCe(t-\tau _1(t))+(1-\delta _0)KCe(t-\tau _2(t)) \nonumber \\&+\,(\delta (t)-\delta _0)(KCe(t-\tau _1(t))-KCe(t-\tau _2(t))). \end{aligned}$$

(9)

Theorem 3.1

For the given constants $c_1>0, c_2>0, \delta _0$, the system (8) is exponentially mean-square stable if there exist matrices $P>0, Q_1>0,Q_2>0,R_1>0,R_2>0$, symmetric matrix $T_1,T_2$ and any appropriate dimensional matrix $G,L$ such that the following LMIs hold

$$\begin{aligned}&\varOmega = \left[ \begin{array}{ccccc} \varOmega _{11} &{} \varOmega _{12} &{} T_1 &{} (1-\delta _0)LC &{} \\ * &{} \varOmega _{22} &{} R_1-T_1 &{} 0 &{} 0 \\ * &{} * &{} \varOmega _{33} &{} R_2-T_2 &{} T_2 \\ * &{} * &{} * &{} \varOmega _{44} &{} R_2-T_2 \\ * &{} * &{} * &{}* &{} -Q_2-R_2 \\ * &{} * &{} * &{}* &{} * \\ * &{} * &{} * &{}* &{} * \\ \end{array}\right. \nonumber \\&\qquad \qquad \qquad \qquad \qquad \left. \begin{array}{cc} \varOmega _{16} &{} P-G+A^\mathrm{{T}}G^\mathrm{{T}}\\ 0 &{} \delta _0C^\mathrm{{T}}L^\mathrm{{T}}\\ 0 &{} 0\\ 0 &{} (1-\delta _0)C^\mathrm{{T}}L^\mathrm{{T}}\\ 0 &{} 0\\ -2S &{} H^\mathrm{{T}}G^\mathrm{{T}}\\ * &{} c_1^2R_1+(c_2-c_1)^2R_2-G-G^\mathrm{{T}} \end{array}\right] <0, \end{aligned}$$

(10)

$$\begin{aligned}&\left[ {\begin{array}{cc} {{R_1}} &{} {{T_1}} \\ * &{} {{R_1}} \\ \end{array}} \right] \ge 0, \left[ {\begin{array}{cc} {{R_2}} &{} {{T_2}} \\ * &{} {{R_2}} \\ \end{array}} \right] \ge 0, \end{aligned}$$

(11)

$$\begin{aligned} \varOmega _{11}= & {} GA+A^\mathrm{{T}}G^\mathrm{{T}}+Q_1-R_1-2D^\mathrm{{T}}K_1SK_2D, \\ \varOmega _{12}= & {} R_1-T_1+\delta _0LC,\\ \varOmega _{16}= & {} D^\mathrm{{T}}(K_1+K_2)S+GH,\\ \varOmega _{22}= & {} -2R_1+T_1+T_1^\mathrm{{T}}, \\ \varOmega _{33}= & {} -Q_1+Q_2-R_1-R_2,\\ \varOmega _{44}= & {} -2R_2+T_2+T_2^\mathrm{{T}}. \end{aligned}$$

Moreover, the sampled-data controller gain is given by $K=G^{-1}L$.

Proof

Choose the following Lyapunov–Krasoskii functionals

$$\begin{aligned} ~ V(e_t)=\sum \limits _{i=1}^3V_i, \end{aligned}$$

(12)

where

$$\begin{aligned} V_1= & {} e^\mathrm{{T}}(t)Pe(t),\\ V_2= & {} \int _{t-c_1}^{t}e^\mathrm{{T}}(s)Q_1e(s){\text {d}}s+\int _{t-c_2}^{t-c_1}e^\mathrm{{T}}(s)Q_2e(s){\text {d}}s,\\ V_3= & {} c_1\int _{-c_1}^0\int _{t+\alpha }^t\dot{e}^\mathrm{{T}}(s)R_1\dot{e}(s)\text {d}s\text {d}\alpha +(c_2-c_1)\int _{-c_2}^{-c_1}\int _{t+\alpha }^t\dot{e}^\mathrm{{T}}(s)R_2\dot{e}(s)\text {d}s\text {d}\alpha , \end{aligned}$$

Define the infinitesimal operator ${\mathcal {L}}$ of $V(e_t)$ as follows:

$$\begin{aligned} {\mathcal {L}}V(e_t)= \mathop {\lim }\limits _{\mathrm{{h}} \rightarrow \infty } \frac{1}{h} {{\mathcal {E}}\left\{ {{\mathcal {V}}(e_{t+h}|e_t)-{\mathcal {V}}(e_t)} \right\} }. \end{aligned}$$

(13)

Calculating ${\mathcal {E}}\{{\mathcal {V}}(e_t)\}$ along the trajectory of system (9) yields

$$\begin{aligned} {\mathcal {E}}\{{\mathcal {L}}V_1\}= & {} {\mathcal {E}}\{2e^\mathrm{{T}}(t)P \dot{e}(t)\}, \end{aligned}$$

(14)

$$\begin{aligned} {\mathcal {E}}\{{\mathcal {L}}V_2\}= & {} {\mathcal {E}} \left\{ e^\mathrm{{T}}(t)Q_1e(t)+e^\mathrm{{T}}(t-c_1)(Q_2-Q_1)e(t-c_1)) \right. \nonumber \\&\left. -e^\mathrm{{T}}(t-c_2)Q_2e(t-c_2))\right\} ,\end{aligned}$$

(15)

$$\begin{aligned} {\mathcal {E}}\{{\mathcal {L}}V_3\}= & {} {\mathcal {E}} \left\{ \dot{e}^\mathrm{{T}}(t)(c_1^2R_1+(c_2-c_1)^2R_2)\dot{e}(t) -c_1\int _{t - c_1 }^t \dot{e}^\mathrm{{T}}(s)R_1\dot{e}(s){\text {d}}s \right. \nonumber \\&\left. -(c_2-c_1)\int _{t - c_2 }^{t-c_1} \dot{e}^\mathrm{{T}}(s)R_2\dot{e}(s){\text {d}}s \right\} . \end{aligned}$$

(16)

According to Lemma 2.1 we get

$$\begin{aligned}&{\mathcal {E}}\left\{ -c_1\int _{t - c_1 }^t \dot{e}^T(s)R_1 \dot{e}(s) \right\} \nonumber \\&\quad = {\mathcal {E}}\left\{ -c_1\int _{t-c_1}^{t-\tau _1(t)}\dot{e}^\mathrm{{T}}(s)R_1\dot{e}(s){\text {d}}s -c_1\int _{t-\tau _1(t)}^{t}\dot{e}^\mathrm{{T}}(s)R_1\dot{e}(s){\text {d}}s \right\} \nonumber \\&\quad \le {\mathcal {E}}\left\{ -\left( {\frac{ c_1}{c_1-\tau _1(t)}} \right) {\left( {\int _{t - c_1}^{t-\tau _1(t)} {\dot{e}(s)}{\text {d}}s } \right) ^\mathrm{{T}}}{R_1}{\left( {\int _{t - c_1}^{t-\tau _1(t)} {\dot{e}(s)}{\text {d}}s }\right) } \right. \nonumber \\&\qquad -\left. \left( {\frac{ c_1}{\tau _1(t)}} \right) {\left( {\int _{t -\tau _1(t)}^{t} {\dot{e}(s)}{\text {d}}s } \right) ^\mathrm{{T}}}{R_1}{\left( {\int _{t - \tau _1(t)}^{t} {\dot{e}(s)}{\text {d}}s } \right) }\right\} \nonumber \\&\quad \le {\mathcal {E}} \left\{ - {\left[ {\begin{array}{c} {e(t-\tau _1(t)) - e(t - c_1)} \\ {e(t) - e(t - \tau _1(t))} \\ \end{array}} \right] ^\mathrm{{T}}}\left[ {\begin{array}{cc} {{R_1}} &{} {{T_1}} \\ * &{} {{R_1}} \\ \end{array}} \right] \left[ {\begin{array}{c} {e(t-\tau _1(t)) - e(t - c_1)} \\ {e(t) - e( t- \tau _1(t))} \\ \end{array}} \right] \right\} \!.\nonumber \\ \end{aligned}$$

(17)

and

$$\begin{aligned}&{\mathcal {E}}\left\{ -(c_2-c_1)\int _{t - c_2 }^{t-c_1} \dot{e}^\mathrm{{T}}(s)R_2e(s){\text {d}}s \right\} \nonumber \\&\quad = {\mathcal {E}}\left\{ -(c_2-c_1)\int _{t-c_2}^{t-\tau _2(t)} \dot{e}^\mathrm{{T}}(s)R_2\dot{e}(s){\text {d}}s -(c_2-c_1)\int _{t-\tau _2(t)}^{t-c_1}\dot{e}^\mathrm{{T}}(s)R_2\dot{e}(s){\text {d}}s \right\} \nonumber \\&\quad \le {\mathcal {E}}\left\{ -\left( {\frac{ c_2-c_1}{c_2-\tau _2(t)}} \right) {\left( {\int _{t - c_2}^{t-\tau _2(t)} {\dot{e}(s)}{\text {d}}s } \right) ^\mathrm{{T}}}{R_2}{\left( {\int _{t - c_2}^{t-\tau _2(t)} {\dot{e}(s)}{\text {d}}s } \right) } \right. \nonumber \\&\qquad -\left. \left( {\frac{ c_2-c_1}{\tau _2(t)-c_1}} \right) {\left( {\int _{t -\tau _2(t)}^{t-c_1} {\dot{e}(s)}{\text {d}}s } \right) ^\mathrm{{T}}}{R_2}{\left( {\int _{t - \tau _2(t)}^{t-c_1} {\dot{e}(s)}{\text {d}}s } \right) }\right\} \nonumber \\&\quad \le {\mathcal {E}} \left\{ - {\left[ {\begin{array}{cc} {e(t-\tau _2(t)) - e(t - c_2)} \\ {e(t-c_1) - e(t - \tau _2(t))} \\ \end{array}} \right] ^\mathrm{{T}}}\left[ {\begin{array}{cc} {{R_2}} &{} {{T_2}} \\ * &{} {{R_2}} \\ \end{array}} \right] \left[ {\begin{array}{c} {e(t-\tau _2(t)) - e(t - c_2)} \\ {e(t-c_1) - e(t - \tau _2(t))} \\ \end{array}} \right] \right\} \!.\nonumber \\ \end{aligned}$$

(18)

It should be noted that when $\tau _1(t)=0$ or $\tau _1(t) =c_1$, we have $\int _{t-\tau _1(t)}^{t}\dot{e}(s){\text {d}}s=0$ or $\int _{t-c_1}^{t-\tau _1(t)}\dot{e}(s){\text {d}}s=0$, respectively. So, the relation (17) still holds. When $\tau _2(t) =c_1$ or $\tau _2(t) =c_2$, we have $\int _{t-\tau _2(t)}^{t-c_1}\dot{e}(s){\text {d}}s=0$ or $\int _{t-c_2}^{t-\tau _2(t)}\dot{e}(s){\text {d}}s=0$, respectively. Thus, the relation (18) is also satisfied.

According to the Eq. (5), we obtain the following inequality for any $S=diag\{ s_1,s_2,\ldots ,s_m\}>0$,

$$\begin{aligned} -{\mathcal {E}}\left\{ 2\sum \limits _{i = 1}^ns_i\left[ g_i(d_{i}e(t),x(t))-k_i^-d_{i}e(t)\right] \left[ g_i(d_{i}e(t),x(t)) -k_i^+d_{i}e(t)\right] \right\} \ge 0,\nonumber \\ \end{aligned}$$

(19)

This can be written as

$$\begin{aligned}&{\mathcal {E}}\left\{ -2g^\mathrm{{T}}(De(t),x(t)) S g(De(t),x(t)) +2e^\mathrm{{T}}(t)D^\mathrm{{T}}(K_1+K_2) S g(De(t),x(t))\right. \nonumber \\&\qquad \left. -2e^\mathrm{{T}}(t)D^\mathrm{{T}}K_1S K_2D e(t)\right\} \ge 0. \end{aligned}$$

(20)

According to the error system (9), the following equation holds for any appropriate dimensions matrix $G$

$$\begin{aligned}&{\mathcal {E}}\left\{ 2\left[ e^\mathrm{{T}}(t)G+\dot{e}(t)G\right] \left[ -\dot{e}(t)+Ae(t)+Hg(De(t),x(t))\right. \right. \nonumber \\&\qquad \left. \left. +\,\delta _0KCe(t-\tau _1(t))+(1-\delta _0)KCe(t-\tau _2(t)) \right] \right\} =0 \end{aligned}$$

(21)

Let

$$\begin{aligned} \xi ^\mathrm{{T}}(t)= & {} \left[ e^\mathrm{{T}}(t),e^\mathrm{{T}}(t-\tau _1(t)),e^\mathrm{{T}}(t-c_1),e^\mathrm{{T}}(t-\tau _2(t)),\right. \nonumber \\&\left. e^\mathrm{{T}}(t-c_2), g^\mathrm{{T}}(De(t),x(t)), \dot{e}(t)\right] \end{aligned}$$

and considering (14)–(21), we have

$$\begin{aligned} {\mathcal {E}}\left\{ {\mathcal {L}}(e_t)\right\} \le {\mathcal {E}}\left\{ \xi ^\mathrm{{T}}(t)\varOmega \xi (t) \right\} . \end{aligned}$$

We obtain immediately from (10) that ${\mathcal {E}}\left\{ {\mathcal {L}}V(e_t)\right\} <0$, which implies a sufficient small constant $\epsilon >0$ such that

$$\begin{aligned} {\mathcal {E}}\{{\mathcal {L}}V(e_t)\} < -\epsilon {\mathcal {E}}\left\{ \Vert e(t)\Vert ^2\right\} . \end{aligned}$$

Then, using a similar method to the proof of Lemma 1 in [19], it easy to know that the augmented system (8) is exponentially mean-square stable, which completes the proof. $\square$

Remark 3.1

In the proof of Theorem 3.1, a similar Lyapunov functional [4, 19] is constructed. However, instead of using the Jenson integral inequality and free-weighting matrix method in [4, 19], the lower bound lemma is employed to derive a stability criteria for the system (8). As pointed out in [16], the usage of the lower bound lemma can provide less conservative results than Jenson integral inequality and can also reduce the calculation than by using free-weighting matrix method.

4 Numerical Examples

In this section, two numerical examples are given to show the validity and effectiveness of the proposed design method.

Example 4.1

Consider the master–slave synchronization of two identical Chua’s circuits via stochastic sampling control. We take the following representation of Chua’s circuit system:

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_1&=a(x_2(t)-h(x_1(t)) \\ \dot{x}_2&=x_1(t)-x_2(t)+x_3(t) \\ \dot{x}_3&= -bx_2(t) \\ \end{aligned} \right. \end{aligned}$$

(22)

with the nonlinear characteristics of Chua’s diode

$$\begin{aligned} h(x)=m_1x_1(t)+\frac{1}{2}(m_0-m_1)\left( |(x_1(t)+1|-|x_1(t)-1|\right) \end{aligned}$$

and parameters $m_0=-1/7,m_1=2/7,a=9,b=14.28$.

It can be found that the system can be represented in Lur’e form with

$$\begin{aligned} A= & {} \left[ {\begin{array}{ccc} -am_1 &{} a &{} 0 \\ 1 &{} -1 &{} 1 \\ 0 &{} -b &{} 0 \\ \end{array}} \right] ,\quad H= \left[ {\begin{array}{c} -a(m_0-m_1) \\ 0 \\ 0 \\ \end{array}} \right] , \nonumber \\ C= & {} D=[ 1 ~~ 0 ~~0], \end{aligned}$$

with $f(x_1(t))=(1/2)(|x_1(t)+1|-|x_1(t)-1|)$ belongs to the sector $[0,1]$.

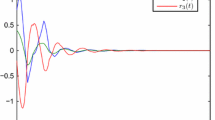
It is well-known that this system is unstable [27]. Our purpose is to design a state-feedback controller such that the closed-loop system is exponentially mean-square stable. It is assumed that $\alpha =0.8$, based on Theorem 3.1, we can obtain the upper bound of $c_2$ for different $c_1$, which is shown in Table 1. When $c_1=0.05$, for various $\alpha$, the upper bound of $c_2$ was given in Table 2. Assume that the initial values of the master system and the slave system are $x(0)=[0.1~ 0.5 ~-0.3]^\mathrm{{T}}$ and $y(0)=[-0.1~ 0.4 ~0.2]^\mathrm{{T}}$, the response curves of the uncontrolled error signals are shown in Fig. 1.

Table 1 The maximum allowable bound $c_2$ for different values of $c_1$ (where $\alpha =0.8$ )

Table 2 The maximum allowable bound $c_2$ for different values of $\alpha$ (where $c_1=0.05$ )

Fig. 1

The uncontrolled error signals in Example 4.1

In order to show the effectiveness of this method, taking $c_1=0.1, c_2=0.38$. Fig. 2 displays the stochastic parameters $\delta (t)$. By solving the LMI given by Theorem 3.1, we obtain the parameter of the desired controller gain matrix as follows

$$\begin{aligned} K=[ -4.2336 ~~ -1.0953 ~~ 3.2528]^\mathrm{{T}}. \end{aligned}$$

For the above gain matrix $K$, the response curves of the controlled error signals are given in Fig. 3, which shows that the synchronization error is tending to zero. It means that the slave system can be synchronized successfully to the master system by control inputs, which are shown in Fig. 4.

Fig. 2

The stochastic parameter $\delta (t)$ in Example 4.1

Fig. 3

The controlled error signals in Example 4.1

Fig. 4

The control input $u(t)$ in Example 4.1

Example 4.2

Consider the master–slave systems (1–3) with the following parameters:

$$\begin{aligned} A= & {} \left[ {\begin{array}{ccc} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -1 \\ \end{array}} \right] , H= \left[ {\begin{array}{ccc} 1.2 &{} -1.6 &{}0 \\ 1.24 &{} 1 &{} 0.9\\ 0 &{} 2.2 &{} 1.5 \\ \end{array}} \right] , \nonumber \\ C= & {} D=\left[ {\begin{array}{ccc} 1 &{} 0 &{}0 \\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \\ \end{array}} \right] , \end{aligned}$$

which implies the Lur’e system reduces to a neural network with three neurons. Furthermore, the neuron activation functions are $f(x_1(t))=\frac{1}{2}(|x_i(t)+1|-|x_i(t)-1|), i=1,2,3$. From Theorem 3.1, the maximum sampling interval $c_2$, can be obtained for a variety of cases, as listed in Tables 3 and 4. Based on Theorem 3.1, when $\alpha =0.9,c_1=0.01$ and $c_2=3.78$, the corresponding controller is

$$\begin{aligned} K=\left[ {\begin{array}{ccc} -1.3941 &{} 0.2297 &{} 0.8098 \\ -0.6147 &{} -1.4445 &{} -0.8466 \\ 0.5984 &{} -1.4366 &{} -2.0750 \\ \end{array}} \right] , \end{aligned}$$

Table 3 The maximum allowable bound $c_2$ for different values of $c_1$ (where $\alpha =0.9$ )

Table 4 The maximum allowable bound $c_2$ for different values of $\alpha$ (where $c_1=0.05$ )

The initial states of the master and slave system are chosen as $x(0)=[0.1 ~~0.2-0.1]^\mathrm{{T}}$ and $y(0)=[0~~0.2 ~~0]^\mathrm{{T}}$, respectively. For the above gain matrix $K$, the response curves of the controlled error signals are given in Fig. 5, which implies the error system is tending to zero. It means that the slave system can be synchronized successfully to the master system by control inputs, which are shown in Fig. 6. And the stochastic parameters $\delta (t)$ is shown in Fig. 7.

Fig. 5

The controlled error signals in Example 4.2

Fig. 6

The control input $u(t)$ in Example 4.2

Fig. 7

The stochastic parameter $\delta (t)$ in Example 4.2

5 Conclusion

In this paper, the master–slave synchronization problem of Lur’e systems with probabilistic sampled-data control has been investigated via a input-delay approach. Based on Lyapunov–Krasosvkii stability theory, mean-square exponential synchronization criteria has been derived by using lower bounds lemma. Furthermore, the sampled-data controller can be derived by solving a set of LMIs. Finally, the effectiveness of the proposed method has been demonstrated via two numerical examples.