Stabilization of a fractional-order chaotic brushless DC motor via a single input

Abstract

A fractional-order brushless DC motor (BLDCM) system is proposed in this paper. By computer simulations, we find that the fractional-order BLDCM system exhibits a chaotic attractor for fractional order $0.96 < q \le 1$, and that the largest Lyapunov exponent varies depending on fractional-order q. Furthermore, in order to stabilize the fractional-order chaotic BLDCM system, two control strategies are presented via single input, based on the generalized Gronwall inequality and the Mittag–Leffler function. Numerical simulations are presented to verify the validity and feasibility of the proposed control schemes.

1 Introduction

Many real-world physical systems such as dielectric polarization, viscoelasticity, electrode–electrolyte polarization, electromagnetic waves, diffusion wave, super-diffusion, and heat conduction can be accurately described by fractional differential equations [1–3]. Complex chaotic behaviors exist in many physical fractional-order systems, e.g., fractional-order gyroscopes [4], fractional-order micro-electro-mechanical system [5], and fractional-order electronic circuits [6, 7]. Meanwhile, more and more attention has been paid on fractional-order chaotic system control, for instance in chaotic communications [8], authenticated encryption schemes [9], etc.

On the other hand, since BLDCM has many advantages over brushed DC motor [10–13], such as more torque per weight and per watt, high reliability, longer lifetime, and reduced noise, BLDCM has been used widely in manufacturing engineering and industrial automation design, e.g., heating and ventilations, motion control systems, positioning and actuation systems, and radio-controlled cars. However, BLDCM exhibits undesirable chaotic phenomena (as shown in [11–13]), which can destroy the stable operation of the motor and can lead to collapse of industrial drive system. Up to now, many researchers have paid more and more attention to find new ways to suppress and control chaos more efficiently, and many schemes for chaos control in BLDCM have been put forward, such as the nonlinear feedback controller, multiple state variables, and multiple controllers. However, these control strategies require heavy computational efforts and difficult to use in practice.

Motivated by the above considerations, in this paper, we introduce a BLDCM model with fractional order, which exhibits the chaotic behavior too. To this end, the maximum Lyapunov exponent and chaotic attractors are obtained by numerical calculation. Furthermore, two control schemes for the stabilization of the fractional-order chaotic BLDCM are proposed via single state variable and linear scalar controller. The numerical simulations show the validity and feasibility of the proposed scheme.

2 The fractional-order BLDCM

The mathematical model of BLDCM [13] under no loading conditions can be described as

$$\begin{aligned}&\left\{ {\begin{array}{l} \dot{x}_\mathrm{d} =-\sigma x_\mathrm{d} +x_\mathrm{q} x_\mathrm{a} \\ \dot{x}_\mathrm{q} =-x_\mathrm{q} -x_\mathrm{d} x_\mathrm{a} +\beta x_\mathrm{a} \\ \dot{x}_\mathrm{a} =\gamma (x_\mathrm{q} -x_\mathrm{a} ) \\ \end{array}} \right. \end{aligned}$$

(1)

where $x_\mathrm{d} , x_\mathrm{q}$, and $x_\mathrm{a}$ denote direct axis current, quadrature axis current, and angular velocity of the motor, respectively. System parameters $\sigma , \beta$, and $\gamma$ are determined by the type of brushless DC motor. As shown in Fig. 1, the BLDCM system (1) exhibits a chaotic attractor for $\sigma =0.875, \beta =55$, and $\gamma =4$.

Fig. 1

The chaotic attractor in the BLDCM

We notice that Vanecek and Celikovsky [14] classified a system family by a condition on its linear part $A=[a_{ij} ]$ in 1996, and the generalized Lorenz chaotic system family satisfies $a_{12} a_{21} >0$. In 1999, Chen and Ueta [15] proposed the Chen chaotic system, which satisfies $a_{12} a_{21} <0$. In 2002, Lu and Chen [16] presented the Lu chaotic system, which satisfies $a_{12} a_{21} =0$. According to the BLDCM system (1), we have $a_{12} =\gamma =4, a_{21} =\beta =55$, and $a_{12} a_{21} >0$. So, the BLDCM system (1) belongs to the generalized Lorenz chaotic system family.

Fig. 2

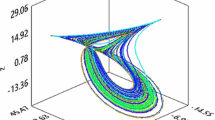
The chaotic attractor in the fractional-order BLDCM (2) when $q=0.97$

Based on the BLDCM system (1), a fractional-order BLDCM system is constructed as

$$\begin{aligned}&\left\{ {\begin{array}{l} D^{q}x_\mathrm{d} =-0.875x_\mathrm{d} +x_\mathrm{q} x_\mathrm{a} \\ D^{q}x_\mathrm{q} =-x_\mathrm{q} -x_\mathrm{d} x_\mathrm{a} +55x_\mathrm{a} \\ D^{q}x_\mathrm{a} =4(x_\mathrm{q} -x_\mathrm{a} ) \\ \end{array}} \right. \end{aligned}$$

(2)

where $0<q<1$ is the fractional order. The Caputo derivative of fractional order $0<q<1$ for function x(t) and is defined as follows,

$$\begin{aligned}&D^{q}x(t)=\Gamma ^{-1}(n-q)\int _0^t {x^{(n)}(\tau ) (t-\tau )^{-(q+1-n)}\,\hbox {d}\tau },\\&n-1 \leqq q <n \end{aligned}$$

herein n is the first integer that is not less than $q, x^{(n)}(t)=d^{n}x(t)/\hbox {d}t^{n}$, and

$$\begin{aligned} \Gamma (n-q)=\int _0^{+\infty } {t^{(n-q)-1}e^{-t}\hbox {d}t} \end{aligned}$$

(3)

is the Gamma function.

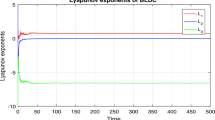
Now, to deal with the fractional-order BLDCM system (2), we propose to use an improved version of Adams–Bashforth–Moulton numerical algorithm [17], which has been applied by many researchers [17–20]. By numerical calculation, we can obtain that the largest Lyapunov exponent of fractional-order BLDCM system (2) is larger than zero for $0.96<q\le 1$. For example, the largest Lyapunov exponent is 0.8760 when $q=0.97$, and its chaotic attractor is shown as Fig. 2, while largest Lyapunov exponent is 0.8908 when $q=0.98$, and its chaotic attractor is shown as Fig. 3. The behavior of the largest Lyapunov exponent of fractional-order BLDCM system (2) with respect to the fractional-order q is shown in Fig. 4.

Fig. 3

The chaotic attractor in the fractional-order BLDCM (2) when $q=0.98$

Fig. 4

The largest Lyapunov exponent varies as fractional-order q

According to Figs. 2, 3, and 4, the fractional-order BLDCM system (2) exhibits chaotic behavior if and only if $0.96<q\le 1$. Conversely, for $q \le 0.96$, the fractional-order BLDCM system (2) is stable, as shown in Fig. 5 for $q=0.96$.

Fig. 5

The fractional-order BLDCM system (2) is stable for $q=0.96$

To the best of our knowledge, the above results are not present in the existing literature.

3 Stabilization of the fractional-order chaotic BLDCM

In this section, we discuss how to stabilize the fractional-order chaotic BLDCM system that can be obtained via single state variable and linear scalar controller. First, we report some preliminary results.

Definition

[1] The Mittag–Leffler function is,

$$\begin{aligned} M_{q,p} (x)=\sum _{n=0}^\infty {\frac{x^{n}}{\Gamma (qn+p)}} (q>0,p>0) \end{aligned}$$

where $\Gamma (qn+p)$ is the Gamma function given in Eq. (3).

Lemma 1

[21] Let $A\in R^{n\times n}$ be a real matrix, $\lambda _i (A)(i=1,2,{\ldots },\hbox {n})$ are its eigenvalues. If $q\pi /2<\left| {\arg \lambda _i (A)} \right| \le \pi (i=1,2,\ldots ,n)$ holds, then

$$\begin{aligned} \left\| {M_{q,p} (A)} \right\| \le N(1+\left\| A \right\| )^{-1} \end{aligned}$$

(4)

where $\left\| A \right\|$ is the $l_2$-norm for matrix A, and $N>0$.

Lemma 2

[22] (Generalized Gronwall inequality) Giving a real time interval $t\in [t_1 ,t_2 ]$, let g(t), h(t) and j(t) be real-valued piecewise continuous functions, and let j(t) be nonnegative. For all $t\in [t_1 ,t_2 ]$, if $g(t)\le h(t)+\int _{t_1 }^t {j(\tau )g(\tau )\,\hbox {d}\tau }$, then

$$\begin{aligned} g(t)\le h(t)+\int _{t_1 }^t {j(\tau )h(\tau )\exp \left[ \int _\tau ^t {j(\zeta )\hbox {d}\zeta } \right] \,\hbox {d}\tau } \end{aligned}$$

(5)

Now, the following results are given.

Theorem 1

Consider the controlled fractional-order chaotic BLDCM system

$$\begin{aligned} \left\{ {\begin{array}{l} D^{q}x_\mathrm{d} =-0.875x_\mathrm{d} +x_\mathrm{q} x_\mathrm{a} \\ D^{q}x_\mathrm{q} =-x_\mathrm{q} -x_\mathrm{d} x_\mathrm{a} +55x_\mathrm{a} +u(x_\mathrm{a} ) \\ D^{q}x_\mathrm{a} =4(x_\mathrm{q} -x_\mathrm{a} ) \\ \end{array}} \right. \end{aligned}$$

(6)

for $0.96<q\le 1$ and $u(x_\mathrm{a} )=(m-55)x_\mathrm{a}$ be a linear scalar controller determined by single state variable $x_\mathrm{a}$, i.e., single input. If $m<1$, then $x_\mathrm{d} (t)=0, x_\mathrm{q} (t)=0$, and $x_\mathrm{a} (t)=0$ $(t>0)$ is a stable solution of the controlled fractional-order BLDCM system (6).

Proof

Using $u(x_\mathrm{a} )=(m-55)x_\mathrm{a}$, the controlled system (6) can be rewritten as

$$\begin{aligned} D^{q}x(t)=A(m)x(t)+f(x(t)) \end{aligned}$$

(7)

where

$$\begin{aligned}&x(t)=({\begin{array}{lll} {x_\mathrm{d} }&{} \quad {x_\mathrm{q} }&{} \quad {x_\mathrm{a} } \\ \end{array} })^{\mathbf{T}},\\&A(m)=\left( {{\begin{array}{ccc} {-0.875}&{} \quad 0&{} \quad 0 \\ 0&{} \quad {-1}&{} \quad m \\ 0&{} \quad 4&{} \quad {-4} \\ \end{array} }} \right) , \end{aligned}$$

and

$$\begin{aligned} f(x(t))=\left( {{\begin{array}{c} {x_\mathrm{q} x_\mathrm{a} } \\ {-x_\mathrm{d} x_\mathrm{a} } \\ 0 \\ \end{array} }} \right) \end{aligned}$$

First, it is easy to obtain that,

$$\begin{aligned} \left. {f(x(t))} \right| _{x(t)=0} =0 \end{aligned}$$

(8)

and

$$\begin{aligned}&\left\| {f(x(t))} \right\| /\left\| {x(t)} \right\| \\&\quad =\sqrt{(x_\mathrm{q} x_\mathrm{a} )^{2}+(x_\mathrm{d} x_\mathrm{a} )^{2}}\Big /\sqrt{x_\mathrm{d}^2 +x_\mathrm{q}^2 +x_\mathrm{a}^2 } \\&\quad \le \sqrt{x_\mathrm{q}^2 +x_\mathrm{d}^2 } \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim }\limits _{x(t)\rightarrow 0} \left\| {f(x(t))} \right\| /\left\| {x(t)} \right\| \le \mathop {\lim }\limits _{x(t)\rightarrow 0} \sqrt{x_\mathrm{q}^2 +x_\mathrm{d}^2 }=0 \end{aligned}$$

(9)

According to Eqs. (8)–(9), there exists a constant $N>0$ and $\varepsilon >0$ such that

$$\begin{aligned} \left\| {f(x(t))} \right\| <N^{-1}\left\| {x(t)} \right\| \end{aligned}$$

(10)

for $\left\| {x(t)} \right\| <\varepsilon$ and $t\ge 0$.

Second, we can obtain the eigenvalues of matrix A(m) as follows,

$$\begin{aligned} \lambda _1 =-0.875, \quad \lambda _{2,3} =-2.5\pm 0.5\sqrt{25-16(1-m)} \end{aligned}$$

According to the assumption $m<1$, it is easy to obtain,

$$\begin{aligned} Re(\lambda _i )<0 \quad (i=1,2,3), \end{aligned}$$

and

$$\begin{aligned} \sigma (A(m))=\max (\left| {\lambda _1 } \right| ,\left| {\lambda _2 } \right| ,\left| {\lambda _3 } \right| )\ge 2.5. \end{aligned}$$

With condition $0.96<q\le 1$, we have

$$\begin{aligned} q\sigma (A(m))>1 \end{aligned}$$

(11)

and

$$\begin{aligned} \left| {\arg \lambda _i (A(m))} \right| >\pi /2>q\pi /2, \quad (i=1,2,3) \end{aligned}$$

(12)

where $\sigma (A)$ denotes the spectral radius of matrix A(m). According to (11) and (12), one gets

$$\begin{aligned} q\left\| {A(m)} \right\| \ge q\sigma (A(m))>1 \end{aligned}$$

(13)

and

$$\begin{aligned} \left| {\arg \lambda _i (t^{q}A(m))} \right| >q\pi /2, \quad (i=1,2,3) \end{aligned}$$

(14)

Now, we discuss the solution x(t) of the fractional-order system (7). Taking Laplace transform $\ell [.]$ on system (7), it can be rewritten as

$$\begin{aligned} s^{q}\ell [(x(t)]-s^{q-1}x(0)\!=\!A(m)\ell [(x(t)]\!+\!\ell [f(x(t))]\nonumber \\ \end{aligned}$$

(15)

where x(0) is the initial condition. So we have

$$\begin{aligned} \ell [(x(t)]=\frac{s^{q-1}}{s^{q}-A(m)}x(0)+\frac{\ell [f(x(t))]}{s^{q}-A(m)} \end{aligned}$$

(16)

Taking Laplace inverse transform for Eq. (16) yield to,

$$\begin{aligned}&x(t)=M_{q,1} [A(m)t^{q}]\,x(0) \nonumber \\&\quad +\,\mathop {\int }\limits _{0}^{t} {(t-\tau )^{q-1}M_{q,q} [A(m)(t-\tau )^{q}]} f(x(\tau ))\,\hbox {d}\tau \nonumber \\ \end{aligned}$$

(17)

Let $\varepsilon _0 (0<\varepsilon _0 <\varepsilon )$ arbitrarily small, and consider the solution x(t) for which $\left\| {x(0)} \right\| <\varepsilon _0$. Using the inequality (4), (10), and (14), Eq. (17) gives

$$\begin{aligned}&\left\| {x(t)} \right\| \le N\varepsilon _0 [1+t^{q}\left\| {A(m)} \right\| ]^{-1} \nonumber \\&\quad +\,\mathop {\int }\limits _{0}^{t} {(t-\tau )^{q-1}[1+(t-\tau )^{q}\left\| {A(m)} \right\| ]^{-1}\left\| {x(\tau )} \right\| } \,\hbox {d}\tau \nonumber \\ \end{aligned}$$

(18)

By means of the generalized Gronwall inequality (5), inequality (18) becomes

$$\begin{aligned}&\left\| {x(t)} \right\| \le N\varepsilon _0 [1+t^{q}\left\| {A(m)} \right\| ]^{-1}\nonumber \\&\quad +\mathop {\int }\limits _{0}^{t} {\frac{N\varepsilon _0 (t-\tau )^{q-1} (1+\tau ^{q}\left\| {A(m)} \right\| )^{-1}}{[1+(t-\tau )^{q} \left\| {A(m)} \right\| ]^{1-\left( q\left\| {A(m)} \right\| \right) ^{-1}}}} \,\hbox {d}\tau \nonumber \\&\quad =N\varepsilon _0 \left\{ {\begin{array}{l} \left[ 1+t^{q}\left\| {A(m)} \right\| \right] ^{-1}+\displaystyle \int \limits _{0}^{t/2} {\frac{(t-\tau )^{q-1}(1+\tau ^{q}\left\| {A(m)} \right\| )^{-1}}{\left[ 1+(t-\tau )^{q}\left\| {A(m)} \right\| \right] ^{1-\left( q\left\| {A(m)} \right\| \right) ^{-1}}}} \,\hbox {d}\tau \\ +\displaystyle \int \limits _{t/2}^{t} {\frac{(t-\tau )^{q-1}\left( 1+\tau ^{q}\left\| {A(m)} \right\| \right) ^{-1}}{\left[ 1+(t-\tau )^{q}\left\| {A(m)} \right\| \right] ^{1-\left( q\left\| {A(m)} \right\| \right) ^{-1}}}} \,\hbox {d}\tau \\ \end{array}} \right\} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{aligned}$$

(19)

Since $t-\tau \ge \tau$ for $\tau \in [0,t/2], t-\tau \le \tau$ for $\tau \in [t/2,t]$, and $q\left\| {A(m)} \right\| \ge q\sigma (A(m))>1$. Hence, from inequality (19), one has

(20)

Since $q\left\| {A(m)} \right\| \ge q\sigma (A(m))>1$ and $\varepsilon _0 (0<\varepsilon _0 <\varepsilon )$ is a arbitrarily small. Therefore, when time $t>0$ is large enough, inequality (20) implies that the zero solution $x_\mathrm{d} (t)=0, x_\mathrm{q} (t)=0$, and $x_\mathrm{a} (t)=0 (t>0)$ is a stable solution of the controlled fractional-order BLDCM system (6), which allows concluding the proof. $\square$

Theorem 1 indicates that the fractional-order chaotic BLDCM system (2) can be stabled via single input $u(x_\mathrm{a} )=(m-55)x_\mathrm{a}$. For example, we display in Fig. 6 the simulative results obtained with $m=-20$ and $q = 0.97$, in which we set initial conditions as $(x_\mathrm{d} ,x_\mathrm{q} ,x_\mathrm{a} )=(10,10,10)$.

Fig. 6

Stabilization of the fractional-order chaotic BLDCM system (2) for $q=0.97$

Theorem 2

Consider the controlled fractional-order BLDCM system

$$\begin{aligned} \left\{ {\begin{array}{l} D^{q}x_\mathrm{d} =-0.875x_\mathrm{d} +x_\mathrm{q} x_\mathrm{a} \\ D^{q}x_\mathrm{q} =-x_\mathrm{q} -x_\mathrm{d} x_\mathrm{a} +55x_\mathrm{a} \\ D^{q}x_\mathrm{a} =4(x_\mathrm{q} -x_\mathrm{a} )+u(x_\mathrm{q} ) \\ \end{array}} \right. \end{aligned}$$

(21)

for $0.96 <q \le 1$ and $u(x_\mathrm{q} )=(n-4)x_\mathrm{q}$ be a linear scalar controller determined by single state variable $x_\mathrm{q}$. If $n<4/55$, then $x_\mathrm{d} (t)=0, x_\mathrm{q} (t)=0$, and $x_\mathrm{a} (t)=0 \, (t>0)$ is a stable solution of the controlled fractional-order BLDCM system (21).

Proof

Using $u(x_\mathrm{q} )=(n-4)x_\mathrm{q}$, the controlled system (21) can be rewritten as

$$\begin{aligned} D^{q}x(t)=A(m)x(t)+f(x(t)) \end{aligned}$$

where

$$\begin{aligned}&x(t)=({\begin{array}{ccc} {x_\mathrm{d} }&{} {x_\mathrm{q} }&{} {x_\mathrm{q} } \\ \end{array} })^{\mathbf{T}},\\&A(m)=\left( {{\begin{array}{ccc} {-0.875}&{} 0&{} 0 \\ 0&{} \quad {-1}&{} \quad {55} \\ 0&{} \quad n&{} \quad {-4} \\ \end{array} }} \right) , \end{aligned}$$

and

$$\begin{aligned} f(x(t))=\left( {{\begin{array}{c} {x_\mathrm{q} x_\mathrm{a} } \\ {-x_\mathrm{d} x_\mathrm{a} } \\ 0 \\ \end{array} }} \right) . \end{aligned}$$

Now, the proof can be completed in a similar way of that for Theorem 1, and it is omitted here. $\square$

Theorem 2 indicates that the fractional-order chaotic BLDCM system (2) can be stabilized through single input $u(x_\mathrm{q} )=(n-4)x_\mathrm{q}$. For example, we display in Fig. 7 the simulative results obtained with $n=-6$ and $q=0.97$, in which we set initial conditions as $(x_\mathrm{d} ,x_\mathrm{q} ,x_\mathrm{a} )=(10,10,10)$.

Fig. 7

Stabilization of the fractional-order chaotic brushless DC motor system (2) for $q=0.97$

Recently, Wei et al. [13] reported some results about stabilization of integer-order chaotic BLDCM system, and two state variables were used in their controller. We notice that stabilization for the fractional-order chaotic BLDCM system with single state variable is discussed in our paper, and our result can be seen as the generalization of the result reported by Wei et al. [13]. Meanwhile, our control scheme is efficient as well for integer-order BLDCM system.

4 Conclusions

This paper presents a fractional-order chaotic BLDCM system, which exhibits chaos for fractional order $0.96 < q \le 1$, the evidence of which is shown by using computer simulations for $q =0.97$ and $q = 0.98$. We also computed the largest Lyapunov exponent on varying the fractional-order q. Two control schemes are proposed via single state variable and linear scalar controller, to stabilize the fractional-order chaotic BLDCM system. Up to now, to the best of our knowledge, there are no similar results on fractional-order chaotic BLDCM system.