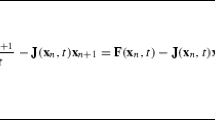1 Introduction

The harmonic balance method (HB), applied within an appropriate period of the periodic solution is popularly applied to solve the Duffing equation with large nonlinearity [4–6, 16, 18, 19]. Unfortunately, large numbers of symbolic operations are inevitable due to tedious Fourier expansions of the nonlinear terms.

To remedy this drawback, Thomas [17] developed a high dimensional harmonic balance method (HDHB), which has been successfully applied in aeroelastic problems [10], time delay problems [11], Duffing oscillators [7], Van der Pol’s oscillators [9], etc. However, the HDHB may produce additional nonphysical solutions [7, 12], which make the solutions of the HDHB sometimes unreliable.

Recently, Dai [2] proposed a time domain collocation method (TDC), and applied it to solve the harmonic and 1/3 subharmonic solutions of the Duffing oscillator. They demonstrated that the TDC was equivalent to the HDHB, and pointed out that the HDHB is not a modified harmonic balance method, but a time domain collocation method (TDC) in disguise. The TDC works in terms of the frequency domain variables while the HDHB works in the time domain variables. Thus, the time domain collocation method (TDC) is believed simpler than the HDHB in the framework of solving the Duffing equation. Nevertheless, the TDC also suffers from the generation of nonphysical solutions as existed in the HDHB approach. In the mentioned work [2], using a frequency marching procedure to generate initial values for the collocation resulting nonlinear algebraic equations (NAEs) successfully avoids the occurrence of the nonphysical solutions in finding the response curves.

Following the previous study, we apply the TDC approach to find the superharmonic responses to the Duffing equation in this study. In addition, we extend the original TDC to a new version by collocating at more points. Both the two versions are labeled as TDC hereafter without distinction, unless otherwise needed. We find that the probability of the attraction to physical solutions increases as more collocation points are chosen. The extended TDC with more collocation points significantly relieves the nonphysical solution phenomenon.

The third superharmonic oscillations of the Duffing equation have been widely analyzed in literature. In the classical book by Nayfeh [14], the harmonic, subharmonic, and superharmonic resonances have been extensively investigated by various versions of perturbation methods. Moriguchi [13] studied the superharmonic resonances of the Duffing equation by numerical integration method, and a large variety of superharmonic resonances have been detected in their model. Rahman [15] and Hassan [3] applied the perturbation methods to explore the bifurcation, and stability property of the third superharmonic solution of the Duffing equation. Herein, we apply the newly developed semianalytical time domain collocation method (TDC) to solve the periodic solutions of the Duffing equation. Moreover, we give a further description of the property of the third superharmonic responses.

The paper is organized as follows. In Sect. 2, we nondimensionalize a general Duffing equation to a simpler form. In Sect. 3, the time domain collocation method is formulated to find periodic solutions of harmonic and third superharmonic oscillations. The equivalence between the TDC method and the HDHB method is proved. In Sect. 4, we extend the TDC, and investigate the nonphysical solution phenomenon. Section 5 provides initial values to the NAEs solver. We investigate various properties of the harmonic and superharmonic responses of the Duffing equation in Sect. 6, among which some properties are believed to be first examined. In Sect. 7, the accuracy of time domain collocation method is verified by comparing with the harmonic balance method. Finally, we come to some conclusions in Sect. 8.

2 The dimensionless Duffing equation

The general form of the Duffing equation is

$$ \ddot{x}+\xi\dot{x}+\alpha x+\beta x^3=F\cos{\omega t}. $$
(1)

In Eq. (1), ξ is the damping parameter, \(\sqrt{\alpha}\) is the natural frequency (denoted by ω 0) of the linear system, and β reflects the nonlinearity. By making the transformations,

Equation (1) is transformed into

$$ \frac{d^2x^*}{dt{^*}^2}+\xi^*\frac{dx^*}{dt^*}+ x^*+\beta^* {x^*}^3=\cos{\omega^* t^*}. $$
(2)

Therefore, ξ ∗, ω ∗, and β ∗ are the control parameters except for the case where β ∗=βF 2/α 3=0. Specifically, F=0, β≠0; F≠0, β=0; and F=0, β=0 correspond to nonlinear free oscillation, linear forced oscillation, and linear free oscillation, respectively. In order to distinguish the three types of possibilities, we investigate the Duffing equation having the following form:

$$ \frac{d^2x^*}{dt{^*}^2}+\xi^*\frac{dx^*}{dt^*}+ x^*+\beta^* {x^*}^3=F^*\cos{\omega^* t^*}. $$
(3)

For simplicity, all ∗ notation will be omitted in the remainder of this paper.

It is worth noting that ω ∗ in Eq. (3) is actually the ratio of the frequency of the impressed force ω to the natural frequency ω 0 of the linear system.

3 The formulation of the time domain collocation method

In this section, we apply the time domain collocation method (TDC) within a period of oscillation, for the periodic solutions to the Duffing equation:

$$ \ddot{x}+\xi \dot{x}+x+\beta x^3=F\cos{\omega t}. $$
(4)

The periodic solution of Eq. (4) is sought in the form:

$$ x(t)=A_0+\sum^{N}_{n=1}A_n \cos{n\omega t}+B_n\sin{n\omega t}. $$
(5)

The assumed form of x(t) can be simplified by considering the symmetrical property of the nonlinear restoring force. First, Hayashi [6] pointed out that under circumstances when the nonlinearity is symmetric, A 0 can be discarded. Second, it was demonstrated by Urabe [20] both numerically and theoretically that the even harmonic components in Eq. (5) are zero. Therefore, the approximate solution is simplified to

(6)

where N is the number of harmonics used in the desired approximation. x(t) in Eq. (6) is called the N harmonic approximation (or labeled as the Nth order approximation in the present paper).

It should be noted that, Eq. (6) is capable of capturing a mth order superharmonic solution, where m=2n−1 (n=1,2,…,N). When the fundamental harmonic component, i.e., n=1, dominates x(t), the periodic solution is referred to as a harmonic solution. When a superharmonic component, i.e., n>1, is significant, the solution is called a superharmonic solution.

In using the collocation method, we obtain the residual error function R(t) by substituting the approximate solution, Eq. (6), into the following equation:

$$ R(t)=\ddot{x}+\xi \dot{x}+ x+\beta x^3 -F \cos{ \omega t}\neq0. $$
(7)

For obtaining the harmonic/superharmonic solution, the collocation method is performed over a period of oscillation. Upon enforcing R(t) to be zero at 2N equidistant points t i =(i−1)π/(Nω)∈[0,2π/ω], we obtain a system of 2N nonlinear algebraic equations:

(8)

where

(9a)
(9b)
(9c)

where i is an index value ranging from 1 to 2N. Equation (8) is the collocation-resulting NAEs. It is also referred to as the TDC algebraic system for the harmonic/superharmonic solutions. The Jacobian matrix B to this system can be readily derived upon differentiating R i with respect to A j and B j .

$$ \mathbf{B}= \biggl[\frac{\partial{R_i}}{\partial{A_j}},\ \frac{\partial{R_i}}{\partial{B_j}} \biggr]_{2N\times2N}, $$
(10)

where

Consequently, the coefficient variables A n , B n in Eq. (8) can be determined by the Newton–Raphson method.

3.1 Equivalence between the HDHB and the TDC

The equivalence between HDHB and TDC was found and demonstrated in Dai [2] in detail. For the paper’s integrity, we herein derive the HDHB system from the TDC system to demonstrate their equivalence. A detailed investigation of the HDHB method can be found in Liu [12].

In accordance with [12], the Duffing equation takes the form: \(m\ddot{x}+d\dot{x}+k x+\alpha x^{3}=F\sin{\omega t}\), and the trial solution is chosen as

$$ x(t)=\hat{x}_0+\sum_{n=1}^{N} [\hat{x}_{2n-1}\cos{n\omega t}+\hat{x}_{2n}\sin{n\omega t} ]. $$
(11)

To formulate the TDC algebraic system, we enforce the residual-error function \(R(t)=m\ddot{x}+d\dot{x}+k x+\alpha x^{3}-F\sin{\omega t}\) to be zero at 2N+1 equidistant points t i =2iπ/[(2N+1)ω] (i=0,1,…,2N). Then we obtain the TDC algebraic system:

(12)

The HDHB system can be derived from the TDC system equivalently. We treat each term in the above equation separately. Firstly, collocating x(t) at points t i , we have

$$ x(t_i)=\hat{x}_0+\sum _{n=1}^N [\hat{x}_{2n-1}\cos{n\omega t_i}+\hat{x}_{2n}\sin{n\omega t_i} ]. $$
(13)

Considering θ i =ωt i , Eq. (13) can be rewritten in a matrix form

(14)

Therefore,

$$ \tilde{\mathbf{Q}}_x\equiv \left [\begin{array}{c} x(t_0)\\ x(t_1)\\ \vdots\\ x(t_{2N})\\ \end{array} \right ] = \mathbf{E}^{-1}\hat{\mathbf{Q}}_x, $$
(15)

where E −1 is a transformation matrix, i.e., the square matrix in Eq. (14), and \(\hat{\mathbf{Q}}_{x}=[\hat{x}_{0},\hat{x}_{1},\ldots,\hat{x}_{2N}]^{T}\).

Similarly, collocating \(\dot{x}(t)\) at t i , we have

(16)

Interestingly, we observe that the above equation can be written in a matrix form by existing quantities:

(17)

where

$$ \mathbf{A}=\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0& & & & & & &\\ & 0&1& & & & &\\ &-1&0& & & & &\\ & & &0&2& & &\\ & & &-2&0& & &\\ & & & & &\ddots& &\\ & & & & & &0&N\\ & & & & & &-N&0\\ \end{array} \right ]. $$
(18)

In the same manner, collocating \(\ddot{x}(t)\) at t i , we have

(19)

Encouragingly, Eq. (16) can be written compactly as

$$ \left [\begin{array}{c} \ddot{x}(t_0)\\ \ddot{x}(t_1)\\ \vdots\\ \ddot{x}(t_{2N})\\ \end{array} \right ] =\omega^2 \mathbf{E}^{-1}\mathbf{A}^2\hat{\mathbf{Q}}_x. $$
(20)

The nonlinear part \(\tilde{\mathbf{R}}_{x}\) is defined as

(21)

Plus,

$$ \left [ \begin{array}{c} \sin{\omega t_0}\\ \sin{\omega t_1}\\ \vdots \\ \sin{\omega t_{2N}}\\ \end{array} \right ]=\mathbf{E}^{-1}\mathbf{H}, \quad\text{where } \mathbf{H}\equiv \left [ \begin{array}{c} 0\\ 0\\ 1 \\ \vdots\\ 0\\ \end{array} \right ]. $$
(22)

Now, substituting Eqs. (15), (17), (20)–(22) into the TDC system (12), we obtain

$$ \mathbf{E}^{-1} \bigl(m\omega^2\mathbf{A}^2+d \omega \mathbf{A}+k\mathbf{I} \bigr)\hat{\mathbf{Q}}_x+\alpha\tilde{ \mathbf{R}}_x =F\tilde{\mathbf{H}}. $$
(23)

According to Eq. (15) \(\hat{\mathbf{Q}}_{x}=\mathbf{E} \tilde{\mathbf{Q}}_{x}\), the above equation can be written as

$$ \bigl(m\omega^2\mathbf{D}^2+d\omega \mathbf{D}+k\mathbf{I} \bigr)\tilde{\mathbf{Q}}_x+\alpha\tilde{ \mathbf{R}}_x=F\tilde{\mathbf{H}}, $$
(24)

where D=E −1 AE and I is identity matrix. The algebraic system (24) is equivalent to the TDC system (12), since no approximation is adopted during derivation. We point out that system (24) is exactly the same as the HDHB algebraic system in [12]. We therefore conclude that the HDHB method is the TDC method in disguise.

4 An extended time domain collocation method

4.1 The extended time domain collocation method

In the previous section, we have demonstrated that the HDHB system is equivalent to the original TDC system. In the framework of the solving Duffing equation, however, the TDC is simpler than the conventional HDHB, since it works in terms of Fourier coefficient variables, instead of transforming into the time domain variables as in HDHB. In fact, Liu [10] provided another version of HDHB to avoid the transformation procedure. Nevertheless, both the TDC and the HDHB produce nonphysical solutions. Therefore, the TDC method is to be improved to deal with this limitation.

In the TDC, as the number N of the harmonics is small in the trial solution, e.g., Eq. (6), it may not be sufficient to collocate the residual error function, Eq. (7), only at 2N points in a period. One may have to use M collocation points, M>2N, to obtain a reasonable solution [1]. As M→∞ one develops a method of least-squared error, wherein one seeks to minimize a scalar function \(J(A_{n},B_{n})=\int^{T}_{0}R^{2}(t)\,dt\) [T is the period of the periodic solution] with respect to the coefficient variables A n , B n .

We herein propose the extended time domain collocation method in the model of the Duffing equation. In the previous section, we have obtained the determining algebraic system (8) of the original TDC. For simplicity, the algebraic system \(\mathbf{R}(\bar{\mathbf{A}},\bar{\mathbf{B}})\) Footnote 1 is expressed by R(x). In order to obtain the extended TDC system, we collocate the residual function (7) at M points leading to an over-determined system of equations

$$ R_i(x_j)=0,\quad i=1,2,\ldots,M;\ j=1,2,\ldots,2N, $$
(25)

where M>2N. Since the number of equations outnumbers the number of the unknowns, we can use least square method to find an approximate solution.

We seek an approximate solution \(x^{*}_{j}\) for x j ,

$$ R_i\bigl(x^*_j\bigr)=\epsilon_i\neq0, $$
(26)

so that \(x^{*}_{j}\) minimize the square error, ϵ i ϵ i . The Einstein summation convention applies herein.

To minimize ϵ i ϵ i , we require

$$ \frac{\partial}{\partial x^*_k}(\epsilon_i\epsilon_i)= \frac{\partial R_i}{\partial x^*_k}R_i=B_{ik}R_i=0_k. $$
(27)

The above formula can be written in a matrix form:

$$ \textbf{B}^\text{T}\textbf{R}=\textbf{0}. $$
(28)

The size of the Jacobian matrix B of the collocation resulting system is M×2N, and R is M×1. The number of equations of the well-determined system is 2N. To the end, we have transformed the over-determined system into a well-determined system.

In addition, the explicit expression for the Jacobian matrix of the well-determined system can be readily obtained:

$$ \frac{\partial}{\partial x^*_p}\bigl(B_{ik}R_i\bigl(x^*_j \bigr)\bigr)=B_{ik}\frac{\partial R_i}{\partial x^*_p}=B_{ik}B_{ip}. $$
(29)

Thus, the Jacobian matrix of the well-determined system, denoting by B L, is

$$ \mathbf{B}_\text{L}=\textbf{B}^\text{T} \textbf{B}, $$
(30)

where B L is 2N×2N.

In Sect. 3, we have obtained the algebraic system R and Jacobian matrix B for the original TDC method. Considering Eqs. (28) and (30), we can conveniently extend the original TDC to the new TDC by modifying the codes by multiplying B T on the left of R and B.

4.2 Elimination of the nonphysical solutions

The HDHB has been demonstrated to produce nonphysical solutions in solving the nonlinear problems [7, 12]. The time domain collocation method (TDC) suffers from the same drawback, since they have been proved equivalent [2].

4.2.1 The nonphysical solution phenomenon in response curves

In this section, the nonphysical solution phenomenon is exhibited by comparing amplitude-frequency response curves in the frequency domain. Using the Newton–Raphson method (NR), the algebraic system arising from the HDHB or the TDC will converge to a solution, provided the initial conditions are within a certain radius of convergence. Since the NR is sensitive to initial values, we apply the globally optimally iterative algorithm (GOIA) [8], in the case that the NR fails to converge. The amplitude-frequency response curve can be obtained by incrementally increasing or decreasing the frequency. At each step, the previous solution is employed as the initial conditions for the next step. This procedure is called a frequency marching procedure. For the Duffing oscillator, the response curves will have regions of hysteresis when the nonlinearity is large. In the hysteresis region, there are three branches. Typically, the upper branch and the lower branch are stable, which correspond to stable periodic motions. The middle branch is unstable, it cannot be reached practically.

Figure 1 plots the response curves of the Duffing equation by the harmonic balance method, the HDHB method and the collocation method. Specifically, the model \(\ddot{x}+0.2 \dot{x}+x+x^{3}=1.25 \sin{\omega t}\) is investigated in this section. The solid line is the response curve computed by the tenth-order harmonic balance method named HB10, which is applied herein as the benchmark. It can be seen from the solid line that when the frequency increases beyond the turning point near ω=2.40, the peak amplitude will drop down and continue on the lower branch. Similarly, an oscillator that begins on the lower branch will jump to the upper branch as the frequency decreases beyond the turning frequency near ω=1.75.

Fig. 1
figure 1

The response curves of the Duffing equation: \(\ddot{x}+0.2\dot{x}+x+x^{3}=1.25\sin{\omega t}\), by HDHB method and time domain collocation method, via frequency marching procedure. The solid lines are the results by HB10

Full size image

Figure 1(a) shows two sets of response curves by the HDHB4 (fourth-order HDHB): one by marching the frequency from 0.1 to 3, and another by marching the frequency from 3 to 0.1, both at an increment of Δω=0.1. The HDHB4 with an increasing frequency marching procedure generates the upper curve similar to the one generated by the HB10 until near ω=1.9. Beyond that, it goes up with the increase of the frequency, and does not drop down to the lower branch. The HDHB4 with an decreasing frequency marching procedure accurately predicts the lower branch. However, at the turning point ω=1.75, it does not jump up to the upper branch until reaching the frequency near 1.2. It is demonstrated that the HDHB4 may produce nonphysical solutions.

Figure 1(b) displays the response curves by the collocation methods. The collocation method with 2 harmonics in the trial function and 4 collocation points is referred to as TDC2. The collocation method with 2 trial harmonics and 20 collocation points is an extended TDC denoted by TDCn2m20. We see from Fig. 1(b) that the TDC2 cannot give a reasonable prediction of the response curve, for both forward marching and backward marching. All the results by TDC2 far away from the benchmark are nonphysical solutions. Note that the TDC2 with the backward frequency marching fails to converge near ω=1.5 by either NR or GOIA. Hence, the amplitude of the rest part is plotted to zero.

The TDCn2m20 with the forward marching can capture the upper branch of the response curve. However, it does not drop down to the lower branch beyond the turning point, ω=2.40. The TDCn2m20 with the backward marching captures the lower branch of the response curve very well. Similarly, it does not jump up to the upper branch at the turning point at ω=1.75.

Thereby, with only two harmonics included, the extended TDC successfully predicts the upper and lower branches of the response curve which the original TDC cannot. And also, we see that the extended TDC with two harmonics yields a better result than the HDHB with four harmonics by comparing the two figures.

4.2.2 Monte Carlo simulation

In addition to the frequency marching procedure, we can employ other methods for initial condition generation. Here, the nature of the solutions generated by the TDC system is studied from a statistical perspective by generating initial conditions through Monte Carlo simulation. That is, initial conditions are randomly generated for a large number of computations in order to determine the probability of converging to any particular solution. For each simulation, 10,000 sample initial conditions are specified. The coefficient variables A n , B n of the resulting NAEs are randomly specified within the range of [−2,2]. The forcing frequency is set to ω=2.0 to produce the three solutions on the three branches of the hysteresis curve. In Fig. 2, Monte Carlo histograms are presented for the solution convergence of the TDC2, TDCn2m6, TDCn2m10, and TDCn2m20.

Fig. 2
figure 2

Monte Carlo histograms for the solutions of the TDC system at ω=2. (a) Results for TDC2. (b) Results for TDCn2m6. (c) Results for TDCn2m10. (d) Results for TDCn2m20

Full size image

For the TDC systems, the probability of converging to any particular solution is highly sensitive to initial conditions. Figure 2(a) displays that the TDC2 yields 7244 unique solutions out of 10,000 trials. This means that the TDC2 algebraic system accommodates a large number of solutions computationally. Physically, almost all of them are fake solutions for the Duffing oscillator. In this case, the TDC2 has very slim possibility to converge to the physical solutions. Figures 2(b)–(d) show that the TDCn2m6, TDCn2m10, and TDCn2m20 simulations generate 15, 9, and 3 unique solutions respectively, where the three true solutions are labeled. Concretely, in the TDCn2m6 simulation, the probability of converging to the lower, unstable, and upper branches are 3.83, 25.97, and 19.98 %, respectively. In the TDCn2m10 simulation, the probability of converging to the lower, unstable, and upper branches are 0.18, 23.51, and 69.73 %, respectively. In the TDCn2m20 simulation, the probability of converging to the lower, unstable, and upper branches are 5.98, 28.13, and 65.89 %, respectively. In sum, the probability of converging to a physical solution is 49.78 % for the TDCn2m6 simulation, and 93.42 % for the TDCn2m10 simulation, and 100 % for the TDCn2m20 simulation.

In general, the probability of the attraction to physical solutions increases as more collocation points are chosen. To sum up, the extended time domain collocation method (TDC) with more collocation points can relieve or eliminate the nonphysical solution phenomenon. Theoretical investigations of the dealiasing function of the extended TDC is undergoing and will be done in another paper.

5 Initial values for the Newton–Raphson method

In Sect. 3, the time domain collocation method (TDC) has been formulated. The algebraic system accounting for harmonic/superharmonic solutions was given in Eq. (8). In order to solve the resulting NAEs, one has to give initial values for the Newton iterative process to start. It is known that the system may have multiple solutions, viz, multiple steady states under a given set of parameters. Hence, it is expected to provide the deterministic initial values to direct the algebraic system to the desired solutions. In this section, we provide the appropriate initial values by using the second-order harmonic balance method (HB2). The initial values for undamped and damped systems are considered separately.

5.1 Initial values for the NAE system, for the undamped Duffing oscillator

In this subsection, we consider the undamped system:

$$ \ddot{x}+x+\beta x^3=F\cos{\omega t}. $$
(31)

Because the damping is absent, the trial function to Eq. (31) can be simplified to [20]

$$ x(t)=\sum^{N}_{n=1}A_n \cos{(2n-1)\omega t}. $$
(32)

We simply consider the second-order harmonic balance method (HB2). The approximate solution is chosen as

$$ x(t)=A^{(2)}_1\cos{\omega t}+A^{(2)}_2 \cos{3\omega t}. $$
(33)

The superscript (2) is introduced, on one hand, to distinguish from the coefficients A 1, A 2 in the Nth order approximation in Eq. (32), and on the other hand to denote the order of approximation. For brevity, however, we omit the superscript unless needed.

Substitution of Eq. (33) in Eq. (31) and balancing the coefficients of cosωt and cos3ωt, leads to two simultaneous nonlinear algebraic equations

(34a)
(34b)

Equations (34a) and (34b) can be solved immediately by Mathematica, to obtain coefficient variables of HB2. We set the initial values of the coefficients of the Nth order approximation in Eq. (32) as

(35)

Then we can solve the collocation resulting NAEs, similar to Eq. (8), by the Newton–Raphson method.

We note that Eqs. (34a) and (34b) may have multiple sets of solutions at a certain frequency. Since in Eq. (33) we included the first and the third harmonic (i.e., third superharmonic) in it, the multiple sets of solutions can be either harmonic solution or third superharmonic solution, by HB2. Each set of solutions of Eqs. (34a) and (34b), may direct the collocation-resulting NAEs to its corresponding high order approximation as will be verified later.

5.2 Initial values for the NAEs arising from the damped system

The second-order approximation for the damped system as Eq. (4) is

(36)

Substitution of Eq. (36) into the Duffing equation (4) and then collecting coefficients of cosωt, sinωt, cos3ωt, and sin3ωt, leads to a system of NAEs as follows:

$$ \left \{ \begin{array}{l} A_1 \bigl[4-4\omega^2+3\beta\bigl(A_1^2+A_1A_2+2A_2^2+B_1^2\\[5pt] \quad{}+2B_1B_2+2B_2^2\bigr)\bigr]\\[5pt] \qquad{}=4F+B_1(3\beta A_2B_1-4\xi\omega)\\[5pt] B_1 \bigl[4-4\omega^2+3\beta\bigl(A_1^2-2A_1A_2+2A_2^2+B_1^2\\[5pt] \quad{}-B_1B_2+2B_2^2\bigr)\bigr]\\[5pt] \qquad{}=4\xi\omega A_1-3\beta A_1^2B_2\\[5pt] A_2 \bigl[4-36\omega^2+3\beta\bigl(2A_1^2+A_2^2+2B_1^2+B_2^2\bigr)\bigr]\\[5pt] \quad{}=\beta A_1\bigl(3B_1^2-A_1^2\bigr)-12\xi\omega B_2\\[5pt] B_2 \bigl[4-36\omega^2+3\beta\bigl(2A_1^2+A_2^2+2B_1^2+B_2^2\bigr)\bigr]\\[5pt] \quad{}=12\xi\omega A_2+\beta B_1\bigl(B_1^2-3 A_1^2\bigr). \end{array} \right . $$

This system of NAEs determines the coefficients of the second order approximation by HB2. It may have multiple sets of solutions under a given system of parameters, which may be either fundamental harmonic or third superharmonic solutions. The initial values of the harmonic solution by HB2 lead to the corresponding harmonic solution by TDCN. Similarly, the initial values of the superharmonic solution by HB2 lead to the corresponding superharmonic solution by TDCN. The initial values for the Nth order approximation can be chosen as:

(37)

Consequently, the collocation-resulting NAEs can be solved. Then we can obtain the Nth order approximation by inserting the coefficient variables into the trial function in Eq. (6).

6 Numerical simulation

In this section, we apply the original time domain collocation method (TDC) to investigate the response curves of the Duffing equation. Specifically, we focus on examining the properties of the accurate third superharmonic response curves, and discuss some peculiar behaviors.

6.1 Undamped system

We apply the time domain collocation method (TDC) to solve an undamped Duffing equation. Moriguchi [13] investigated the undamped Duffing equation having the form

$$ \ddot{x}+x+\beta x^3=F\cos{\omega t} $$
(38)

by numerical integration method.

They found various orders of resonances in this system. Now we apply the time domain collocation method to solve both the fundamental harmonic and third superharmonic solutions. In accordance with the current topic, we concentrate on the frequency range where the third superharmonic may occur. In this case, the parameters β and F are specified to be 4 and 1, respectively.

6.1.1 Initial values, and response curves by HB2

We solve Eqs. (34a) and (34b), arising from HB2, to obtain the initial values for the higher order approximation. Because of the simplicity of the system, we can plot the A 1 vs. ω and A 2 vs. ω curves. Figure 3 indicates that the Duffing equation has one periodic solution, denoted by SOL1, when the frequency is below ω c . If ω>ω c , there exist three solutions, namely SOL1, SOL2, SOL3 marked in Fig. 3. For SOL1, it can be seen from Fig. 3 that the fundamental harmonic dominates the oscillation where ω<0.4. The third harmonic component can be regarded to be significant after about ω=0.55. Thus, SOL1 may be either fundamental harmonic solutions or third superharmonic solutions, depending on the frequency range. There exists a handover region or transitional region for the harmonic and third superharmonic oscillations.

Fig. 3
figure 3

The coefficient-frequency relationship of the Duffing equation: \(\ddot{x}+x+4x^{3}=\cos{\omega t}\), by HB2. Since B 1 and B 2 are zero, thus |A 1| is the amplitude of the fundamental harmonic component, and |A 2| is the amplitude of the third superharmonic component

Full size image

For SOL2, the third harmonic amplitude, |A 2|, is always larger than the fundamental amplitude, |A 1|. Hence, SOL2 is always a third superharmonic solution.

For SOL3, the third harmonic can be comparable with the fundamental harmonic from the onset ω c to a certain frequency. As the frequency increases, the fundamental harmonic finally dominates the oscillation. Therefore, there exists a transitional region between the two modes of oscillations.

In order to solve Eqs. (34a) and (34b), we need to choose a frequency ω g , where by the response curves can be obtained. Therefore, ω g is called the generating frequency. Once the second-order approximation by HB2 has been obtained, we apply Eq. (35) to generate the initial values for the higher order approximation. The collocation resulting NAEs can be solved by the Newton–Raphson method. The main principle of choosing a proper ω g is to select a frequency where there exist as many solutions as possible, so that more response curves can be obtained. It can be seen that at a frequency greater than ω c , the system has three solutions. Hence, we chose the ω g >ω c so that all three response curves can be generated from ω g .

6.1.2 High order approximation by collocation method

In this case, the ω g is chosen to be 0.6. The initial values are tabulated in Table 1. Using the initial values, we can solve the collocation-resulting NAEs to obtain a high order approximation. Throughout the paper, we set the convergence criterion ϵ of the Newton–Raphson solver to be 10−10.

Table 1 Initial values, by HB2, at ω g =0.6
Full size table

The results by TDC12 are tabulated in Table 2. There are three sets of solutions at ω g =0.6, so that we can apply the frequency marching procedure, marching from ω g back and forth to find the three frequency-response curves, which are plotted in Fig. 4(a). In computation, the initial values given by HB2 are used only at the generating frequency.

Fig. 4
figure 4

The response curves and the three x versus t curves (at ω=0.6) of the Duffing equation: \(\ddot{x}+x+4x^{3}=\cos{\omega t}\), by TDC12

Full size image
Table 2 Results by TDC12, at ω g =0.6
Full size table

The comparison of Tables 1 and 2 shows that each of the three sets of initial values by HB2 successfully directs the NAEs, arising from twelfth-order approximation of TDC12, to its corresponding solution. It confirms the validity of using the HB2 to supply the initial values.

Now we investigate the three solutions at the frequency ω g . The x versus t curves in one cycle are provided in Fig. 4. Figures 4(b), (c), and (d) correspond to the solutions of SOL2, SOL1, and SOL3 in Table 2, respectively. It can be seen that Figs. 4(b), (c) have three local peaks in one period, while Fig. 4(d) has only one. This can be explained by Table 2. In SOL2 and SOL1, the third harmonic is more significant than the first harmonic, so the third harmonic component plays a more important role in x(t). In SOL3, the fundamental harmonic component is more significant than others, so it displays more like a simple harmonic oscillation. However, the third harmonic components of the three solutions are comparable with the fundamental ones. Thus, all the three solutions can be regarded as third superharmonic oscillations.

6.1.3 Amplitudes of each harmonic

The amplitudes of each harmonic are given in Fig. 5, in order to explore the significance of each harmonic. In accordance with the notations in Eq. (32), the amplitudes of the first, third, and fifth harmonic are |A 1|, |A 2|, and |A 3|, respectively. The peak amplitude, e.g., max |x|, is plotted by heavy lines in figures. We investigate the three curves (marked by SOL1, SOL2, and SOL3) in Fig. 5(a) separately.

Fig. 5
figure 5

The amplitude/harmonic amplitudes versus frequency curves of the Duffing equation: \(\ddot{x}+x+4x^{3}=\cos{\omega t}\), by TDC12

Full size image

Figure 5(b) shows that SOL1 is a third superharmonic solution in the region from about ω=0.5 to infinity, since the third harmonic component is significant compared with the first harmonic component. The amplitude of the fifth harmonic, i.e., |A 3|, can be comparable with that of the third harmonic in [0.35,0.5]. Therefore, the onset of the third superharmonic solution of SOL1 is blurry. It should be some value around 0.5. It depends on how one defines a third superharmonic solution, that is, how significant should the third superharmonic component be, comparing with the harmonic and fifth superharmonic parts, so as to regard the solution as a third superharmonic solution.

The onset frequency of the multiple valued response is ω B , predicted by TDC12. Figure 5(c) plots the curve associated with SOL2. It displays that the fifth superharmonic is very weak. The third superharmonic component is larger than the first harmonic at the onset, and keeps being so with the increase of the frequency. Thus, SOL2 is the third superharmonic solution in the whole branch.

The response curve associated with SOL3 is plotted in Fig. 5(d). The first and third harmonic components are comparable from the onset ω B to a certain value. Thus, in this region, the solution can be regarded as a third superharmonic solution. As the frequency increases to a large enough value, the solution becomes a harmonic one, where all higher harmonics are weak. Overall, there exists a transitional region between the harmonic solution and the third superharmonic solution for SOL3.

6.2 Damped system

6.2.1 Multiple valued response

In this section, the system: \(\ddot{x}+\xi \dot{x}+x+\beta x^{3}=F\cos{\omega t}\) is considered. Herein, we specify the parameters as: ξ=0.01, β=4, and F=1. In order to see the contributions of each harmonic, we evaluate the amplitudes of the lowest few harmonics separately. The peak/harmonic amplitude-frequency response curves are given in Fig. 6, where the solid and dashed curves are corresponding to the stable and unstable periodic solutions, respectively. We see that the multivalued response curves (from ω C to ω D ) constitute a loop, which is in contrast to the undamped system. The amplitudes of the first, third, and fifth harmonic are denoted by |a 1|, |a 3|, and |a 5|, respectively.

Fig. 6
figure 6

The peak/harmonic amplitude-frequency response curves of the Duffing equation: \(\ddot{x}+0.01\dot{x}+x+4x^{3}=\cos{\omega t}\), by TDC12

Full size image

Figure 6(b), shows that in the region of about ω∈[0.45,ω D ], the first harmonic and third harmonic are significant and comparable. Thus, the oscillation in this region can be regarded as a third superharmonic one. Also, we notice that |a 5| can be comparable with |a 3| in about [0.35,0.45], where the fifth superharmonic solution exists. Therefore, SOL1 has a transitional region between the third and the fifth superharmonic oscillations.

In Fig. 6(c), |a 5| is weak; |a 3| is larger than |a 1|. Therefore, the oscillations belonging to this curve are the third superharmonic oscillations in the entire branch.

In Fig. 6(d), the third harmonic components are significant from ω C to a blurry value (it depends on how to define “significant”). In this region, the solution can be regarded as a third superharmonic solution. As the frequency increases, the fundamental harmonic component finally dominates others. The oscillation becomes a fundamental harmonic oscillation. Thus, there is a transitional region for the two modes of oscillations.

In sum, we conclude that the two stable curves (SOL1, SOL3) experience a transitional region, wherein two modes of oscillations hand over continuously. For the unstable curve, SOL2, it is a third superharmonic oscillation in the entire branch, i.e., [ω C ,ω D ]. The defined transitional region is believed to be first examined in literature.

6.2.2 Single valued response

We now turn to study a strongly damped Duffing equation: \(\ddot{x}+0.2\dot{x}+x+4x^{3}=\cos{\omega t}\). The peak amplitude, and the amplitudes of up to the seventh harmonic, are plotted in Fig. 7, wherein the amplitudes of the first, third, fifth, and seventh harmonic are denoted by |a 1|, |a 3|, |a 5|, and |a 7|, respectively. It shows that the response curve is a single valued one in this case.

Fig. 7
figure 7

The peak/harmonic amplitude-frequency response curves of the Duffing equation: \(\ddot{x}+0.2\dot{x}+x+4x^{3}=\cos{\omega t}\), by TDC12. E: the seventh superharmonic response region. F: the fifth superharmonic response region. G: the third superharmonic response region

Full size image

Figure 7 displays that the peak amplitude versus frequency curve has three local maximum values in the marked areas E, F, and G, arising from the local maximum values of |a 7|, |a 5|, and |a 3|, respectively. Therefore, the regions of E, F, and G are corresponding to the seventh, fifth, and third superharmonic solutions, respectively. Similar to the multiple valued case, the regions for different modes of oscillations are indefinite. Different modes of oscillations hand over continuously in the transitional region.

6.2.3 The effects of parameters: ξ, β and F

Figure 8 plots the frequency response curves for various values of damping, nonlinearity, and external force in the region where the third superharmonic response occurs. Figure 8(a) indicates that a smaller damping can locally enhance the upper branch of the loop. As the damping goes to zero, the loop will approach to infinity as the case of the undamped system. Conversely, the multivalued region shrinks as the damping increases. The multivalued response ceases to occur when the damping is increased to a certain value. Figure 8(a) shows that the response curve is single valued when the damping is raised up to 0.2.

Fig. 8
figure 8

The amplitude versus frequency curves for the Duffing equation \(\ddot{x}+\xi\dot{x}+x+\beta x^{3}=F\cos{\omega t}\), with various values of ξ, β and F, by TDC12

Full size image

Figure 8(b) provides the response curves with a varying β. We see that a larger nonlinearity bends and shifts the response curves to the right. Also, it lowers the response amplitude in the considered region.

The effect of the amplitude of the impressed force is shown in Fig. 8(c). It displays that when F increases, the response amplitude increases globally. Besides, a larger force enlarges and shifts the multivalued region to the right.

6.2.4 Jump phenomena

To give a whole understanding of the response of the Duffing equation, Fig. 9 plots the 1/3 subharmonic [2], the fundamental harmonic, and the third superharmonic response curves of the Duffing equation.

Fig. 9
figure 9

The one third subharmonic, fundamental harmonic and third superharmonic response curves of the Duffing equation: \(\ddot{x}+0.01\dot{x}+x+4x^{3}=\cos{\omega t}\)

Full size image

It reveals that the jump phenomena occur in both harmonic and third superharmonic responses. To explain this, letting the amplitude of the external force be fixed, we vary the forcing frequency slowly up and down. For the superharmonic response, the frequency starts at about 0.4. As the frequency is increased, the amplitude increases through point A until point D is reached. As the frequency is increased further, a jump-down from D to B takes place. Let the frequency start at ω=0.7. As the frequency is decreased, the amplitude increases through point B until point C is reached. As the frequency is decreased further, a jump-down from C to A takes place. Thus, there are two jump-downs in the third superharmonic response; see Fig. 9(b). For the harmonic response, there is a jump-down from E to F on the increasing road, and a jump-up from G to H on the decreasing road; see Fig. 9(a).

It needs to be noted that the third superharmonic response curve is attached to the fundamental response curve, while the 1/3 subharmonic response curve is isolated. It means that if the forcing frequency is increased or decreased through their existing regions slowly, the superharmonic response appears. The 1/3 subharmonic response, however, does not appear. This stresses the importance of exploring the superharmonic solutions.

7 The accuracy of the time domain collocation method

The x versus t curves and the phase portraits of SOL3 of the Duffing equation: \(\ddot{x}+x+4x^{3}=\cos{t}\), by TDC12 and HB12 are given in Fig. 10. It indicates that the TDC12 and the HB12 agree very well with each other.

Fig. 10
figure 10

Comparisons of the x vs. t and phase portraits on the lower branch response curve of the Duffing equation: \(\ddot{x}+x+4x^{3}=\cos{t}\), by TDC12 and HB12

Full size image

Furthermore, Fig. 11 plots the absolute differences of x between the two methods. We can see that maximum differences between the two methods of order N=5,8,10 and 12 are about 5.54×10−6, 1.21×10−9, 5.67×10−12 and 2.68×10−14, respectively. It indicates that a higher order time domain collocation method can be more accurate. In sum, Figs. 10 and 11 verify the high accuracy of the TDC.

Fig. 11
figure 11

The absolute differences of the displacement x by the time domain collocation method (TDC) and the harmonic balance method (HB) with various orders of approximations

Full size image

8 Conclusions

In this paper, the time domain collocation method (TDC) was applied to find the third superharmonic solutions of the Duffing equation. The collocation of the residual error in the ODE, at discrete time intervals, was performed on a whole period of the considered oscillation. The collocation-resulting nonlinear algebraic equations were solved by the Newton–Raphson method. Based on the proposed scheme, the effects of each parameter on the amplitude-frequency response were examined. The multivaluedness, jump phenomenon and transitional region [which to the authors’ best knowledge has never been discussed in literature] of the third superharmonic response were explored. The HDHB method was demonstrated to be the TDC method in disguise. In addition, the TDC was also extended to a new version by collocating at more points. It was demonstrated that the extended TDC method remarkably relieved or even eliminated the nonphysical solution phenomenon upon comparing with the original TDC and the HDHB method. Finally, numerical examples confirmed that the time domain collocation method (TDC) was simple and accurate in obtaining the periodic solutions of the Duffing equation. Also, this simple approach can be readily applied to solve other nonlinear oscillatory problems.