1 Introduction

The absolute nodal coordinate formulation (ANCF) has been widely used in the large deformation analysis of flexible multibody systems [16, 38]. This flexible body formulation uses global position vectors and their gradients as element degrees of freedom [36–38], and it leads to the constant mass matrix for fully nonlinear dynamics problems while ensuring the exact modeling of rigid body dynamics. The use of three gradient vectors as degrees of freedom allows for the parameterization of both finite rotation and deformation field of the infinitesimal volume within the element, and it leads to the general motion description of a deformable body in the three-dimensional space. This, however, necessitates introducing high-order polynomials, and the ANCF elements have a large number of degrees of freedom per node. Furthermore, as in existing displacement-based finite elements, ANCF elements suffer from element locking caused by the inconsistent strain field obtained directly by the differentiation of the assumed global displacement field, exhibiting the lower rate of convergence of numerical solutions than expected. For this reason, substantial efforts have been made in addressing the element locking problems of various types of ANCF elements. It has been demonstrated that the use of only transverse gradient nodal vectors allows for defining a consistent strain field by employing various techniques for the element locking alleviation [30, 31].

Despite the successful development of shear deformable ANCF beam elements [30, 31], there still exist open issues regarding the element locking remedies for shear deformable ANCF plate/shell elements. Various types of plate/shell elements have been proposed in the context of the absolute nodal coordinate formulation [9, 11, 12, 21, 22, 26, 28, 29, 32, 33, 48]. The fully parameterized quadrilateral ANCF shell element was proposed by Mikkola and Shabana [28], in which each node has the global position vector coordinates and a set of three gradient vector coordinates. Since the element parameterization with the gradient vector coordinates allows for modeling stretches of the cross section along the gradient vectors, use of lower-order polynomials for displacement field in the transverse direction leads to the thickness locking [25, 27, 42]. The plate element that has only transverse gradient vector coordinates can be developed by removing the two tangential gradient vectors, allowing for retaining the transverse shear and normal deformation of the cross section. The quadrilateral shear deformable ANCF plate element based on the transverse gradient parameterization was first proposed by Dmitrochenko et al. using the selective reduced integration for the in-plane shear locking and the modified Gaussian integration for the transverse shear locking [10]. This element was further enhanced to the initially curved shell element with the continuum mechanics approach which allows for considering various nonlinear material models by Yamashita et al. [47]. The lockings of the continuum mechanics-based shear deformable ANCF shell element are addressed using the assumed natural strain (ANS) and enhanced assumed strain (EAS) methods [47]. In particular, it is demonstrated that the element exhibits a severe locking problem associated with the transverse normal strain due to the linear interpolation of the transverse gradient vector in the transverse direction. While the continuum mechanics-based shear deformable ANCF shell element is capable of solving a wide variety of challenging problems that involve nonlinear material models as well as thick shell structures, the elastic forces can be evaluated efficiently with the plane stress assumption for thin to moderately thick shell structures while keeping the same element parameterization as shown in the literature [10]. However, further generalization needs to be made in terms of the elastic force formulation for an initially curved shell element and its thickness locking remedies. It is, therefore, the objective of this study to generalize the bilinear shear deformable ANCF plate element to the locking-free initially curved shell element using the elastic middle surface approach for the large deformation analysis of thin to moderately thick shell structures. Furthermore, the shear deformable ANCF shell elements based on the continuum mechanics approach [47] and the elastic middle surface approach developed in this study are compared to shed light on the nature of the thickness locking exhibited in the bilinear ANCF shell element and its locking remedies. Since the shell element has no element discretization in transverse direction, the thickness lockings are fundamental and crucial problems of the shear deformable shell element of the absolute nodal coordinate formulation that need to be properly addressed. For this reason, this issue is discussed with particular emphasis on the way the transverse gradient vectors are interpolated in the absolute nodal coordinate formulation, and it is shown that locking remedies presented in study allow for developing the new locking-free 24-DOF shear deformable shell element.

Fig. 1
figure 1

Kinematics of the bilinear ANCF shell element

Full size image

2 Kinematics of bilinear ancf shell element

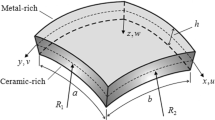
As shown in Fig. 1, the shell element of the absolute nodal coordinate formulation in this study consists of four nodes. Each node has three position coordinates and three coordinates associated with the transverse position vector gradient. The global position vector \(\mathbf{r}^{i}\) of a material point \(\mathbf{x}^{i}=[{\begin{array}{lll} {x^{i}}&{} {y^{i}}&{} {z^{i}} \\ \end{array} }]^{T}\) in element \(i\) can be defined as [47]

$$\begin{aligned} \mathbf{r}^{i}=\mathbf{r}_m^i (x^{i},y^{i})+z^{i}\frac{\partial \mathbf{r}^{i}}{\partial z^{i}}(x^{i},y^{i}) \end{aligned}$$
(1)

where \(\mathbf{r}_m^i (x^{i},y^{i})\) is the global position vector of the middle surface of the element, and \(\partial \mathbf{r}^{i}/\partial z^{i}\) is the transverse position vector gradient. The global position field is interpolated using the following polynomial:

$$\begin{aligned} r^{i}&= a_0 + a_1 x^{i}+a_2 y^{i}+a_3 x^{i}y^{i}+z^{i}(a_4 +a_5 x^{i}\nonumber \\&+a_6 y^{i}+a_7 x^{i}y^{i}) \end{aligned}$$
(2)

from which the global position vector of an arbitrary material point in the shell element can be defined using the bilinear shape function matrix \(\mathbf{S}_m^i (x^{i},y^{i})\) as follows [47]:

$$\begin{aligned} \mathbf{r}^{i}(x^{i},y^{i},z^{i})=\mathbf{S}_m^i (x^{i},y^{i})\mathbf{e}_p^i +z^{i} \mathbf{S}_m^i (x^{i},y^{i})\mathbf{e}_g^i \end{aligned}$$
(3)

where \(\mathbf{S}_m^i =\left[ {{\begin{array}{llll} {S_1^i \mathbf{I}}&{} {S_2^i \mathbf{I}}&{} {S_3^i \mathbf{I}}&{} {S_4^i \mathbf{I}} \\ \end{array} }} \right] \), I is a \(3\times 3\) identity matrix; and the vectors \(\mathbf{e}_p^i \) and \(\mathbf{e}_g^i \) are the element nodal coordinate vectors associated with the global position and the transverse gradient, respectively. The preceding equation can be re-expressed in the following simpler form:

$$\begin{aligned} \mathbf{r}^{i}(x^{i},y^{i},z^{i})=\mathbf{S}^{i}(x^{i},y^{i},z^{i})\mathbf{e}^{i} \end{aligned}$$
(4)

where the shape function matrix \(\mathbf{S}^{i}\) and the element nodal coordinate vector \(\mathbf{e}^{i}\) are defined as [47]

$$\begin{aligned} \mathbf{S}^{i}=\left[ {\mathbf{S}_m^i } \quad {z^{i}\mathbf{S}_m^i } \right] ,\quad \quad \quad \mathbf{e}^{i}= [{(\mathbf{e}_p^i )^{T}} \quad {(\mathbf{e}_g^i )^{T}}]^{T} \end{aligned}$$
(5)

It is important to notice here that the element parameterization and the assumed global displacement field defined in the ANCF shell element are essentially different from those of the degenerated shell elements [1]. For more details on the difference between the ANCF and degenerated shell elements, one can refer to the literature [39], in which a fully parameterized ANCF shell element [28] is used for comparison. The difference between the fully parameterized shell element [28] and the gradient deficient shear deformable bilinear shell element considered in this study lies in the order of polynomials introduced to the global position field of the middle surface. The traverse position gradient vector is interpolated with the same bilinear polynomial in the fully parameterized shell element as can be seen by comparing the Eq. 2 to the following:

$$\begin{aligned} r^{i}&= a_0 +a_1 x^{i}+a_2 y^{i}+a_3 x^{i}y^{i}+a_4 (x^{i})^{2}\nonumber \\&\quad +\,a_5 (y^{i})^{2}+a_6 (x^{i})^{3}+a_7 (y^{i})^{3}+a_8 (x^{i})^{2}y^{i}\nonumber \\&\quad +\,a_9 x^{i}(y^{i})^{2}+a_{10} (x^{i})^{3}y^{i}+a_{11} x^{i}(y^{i})^{3}\nonumber \\&\quad +\,z^{i}\left( {a_{12} +a_{13} x^{i}+a_{14} y^{i}+a_{15} x^{i}y^{i}} \right) \end{aligned}$$
(6)

In the fully parameterized shell element, two additional gradient vectors tangent to the middle surface are introduced as nodal coordinates, which ensures \(C^{1}\) continuity at the nodal points, while \(C^{0}\) continuity is fulfilled in the bilinear shell element considered in this study.

3 Formulation of generalized elastic forces with elastic middle surface approach

Using the kinematic description introduced for the shear deformable ANCF shell element, the generalized elastic forces are derived in this section. For modeling shell structures with nonlinear material models, the general continuum mechanics approach has been introduced to the bilinear shear deformable ANCF shell element in the previous study, and it has been shown that severe thickness locking is exhibited [47]. The plane stress assumption, on the other hand, has been applied to the same element for modeling thin to moderately thick plate element in the literature [10] with the selective reduced integration for the in-plane shear locking and the modified Gaussian integration for the transverse shear locking. However, it is well known that use of one point selective integration leads to an extra zero energy mode, which is not desirable for general multibody dynamics applications. Furthermore, the formulation is restricted to a flat plate element. For this reason, in this section, the elastic forces are generalized to those of the initially curved shell element using the elastic middle surface approach.

Using the Green–Lagrange strain tensor, the six strain components in the middle surface of the shell element \(i\) can be defined as follows:

$$\begin{aligned} {\hat{\mathbf{E}}}_m^i (x^{i},y^{i},0)=\frac{1}{2}\left( {(\mathbf{F}_m^i )^{T}\mathbf{F}_m^i -\mathbf{I}} \right) \end{aligned}$$
(7)

where \(\mathbf{F}_m^i \) is the global position vector gradient tensor at a material point in the middle surface of the shell element \(i\) and is given as

$$\begin{aligned} \mathbf{F}_m^i (x^{i},y^{i},0)=\frac{\partial \mathbf{r}^{i}}{\partial \mathbf{X}^{i}}={\bar{\mathbf{J}}}_m^i (\mathbf{J}_m^i )^{-1} \end{aligned}$$
(8)

where \({\bar{\mathbf{J}}}_m^i \) and \(\mathbf{J}_m^i \) are covariant base tensors of the material point in the middle surface at the deformed and reference configurations, respectively. These tensors are defined as

$$\begin{aligned} {\bar{\mathbf{J}}}_m^i =\left. {\frac{\partial \mathbf{r}^{i}}{\partial \mathbf{x}^{i}}} \right| _{z^{i}=0} =\left[ {{\begin{array}{lll} {\mathbf{g}_1^i }&{} {\mathbf{g}_2^i }&{} {\mathbf{g}_3^i } \\ \end{array} }} \right] \end{aligned}$$
(9)

where \(\mathbf{g}_1^i =\partial \mathbf{r}_m^i /\partial x^{i},\quad \mathbf{g}_2^i =\partial \mathbf{r}_m^i /\partial y^{i},\quad \mathbf{g}_3^i =\partial \mathbf{r}^{i}/\partial z^{i}\) and

$$\begin{aligned} \mathbf{J}_m^i =\left. {\frac{\partial \mathbf{X}^{i}}{\partial \mathbf{x}^{i}}} \right| _{z^{i}=0} =\left[ {{\begin{array}{lll} {\mathbf{G}_1^i }&{} {\mathbf{G}_2^i }&{} {\mathbf{G}_3^i } \\ \end{array} }} \right] \end{aligned}$$
(10)

where the vector \(\mathbf{X}^{i}\) represents the global position vector of element \(i\) at the reference configuration and one can define \(\mathbf{G}_1^i =\partial \mathbf{X}_m^i /\partial x^{i},\quad \mathbf{G}_2^i =\partial \mathbf{X}_m^i /\partial y^{i}\) and \(\mathbf{G}_3^i =\partial \mathbf{X}^{i}/\partial z^{i}\), where \(\mathbf{X}_m^i =\mathbf{X}^{i}(x^{i},y^{i},0)\) defined in the middle surface. Substituting Eq. 8 into Eq. 7, one can obtain [47]

$$\begin{aligned} {\hat{\mathbf{E}}}_m^i (x^{i},y^{i},0)=(\mathbf{J}_m^i )^{-T}{\tilde{\mathbf{E}}}_m^i (\mathbf{J}_m^i )^{-1} \end{aligned}$$
(11)

where

$$\begin{aligned} {\tilde{\mathbf{E}}}_m^i (x^{i},y^{i},0)=\frac{1}{2}\left( {({\bar{\mathbf{J}}}_m^i )^{T}{\bar{\mathbf{J}}}_m^i -(\mathbf{J}_m^i )^{T}\mathbf{J}_m^i } \right) \end{aligned}$$
(12)

The Green–Lagrange strains given by Eq. 11 are transformed to those defined with respect to the orthogonal frame \(\mathbf{A}_m^i \) defined at the reference configuration as follows:

$$\begin{aligned}&\mathbf{E}_m^i (x^{i},y^{i},0)=(\mathbf{B}_m^i )^{-T}{\tilde{\mathbf{E}}}_m^i (\mathbf{B}_m^i )^{-1}\equiv \varepsilon _{rs}^i,\nonumber \\&r,s=x,y,z \end{aligned}$$
(13)

where

$$\begin{aligned} \mathbf{B}_m^i =(\mathbf{A}_m^i )^{T}\mathbf{J}_m^i \equiv B_{rs}^i,\quad r,s=1,2,3 \end{aligned}$$
(14)

The tensor transformation given by Eq. 13 can be re-expressed in terms of the engineering strain vector \(\varvec{\upvarepsilon }_m^i \) and the covariant strain vector \({\tilde{\varvec{\upvarepsilon }}}_m^i \) as [47]

$$\begin{aligned} \varvec{\upvarepsilon }_m^i =(\mathbf{T}_m^i )^{-T}{\tilde{\varvec{\upvarepsilon }}}_m^i \end{aligned}$$
(15)

where \(\mathbf{T}_m^i \) is a 6 by 6 matrix is defined as

$$\begin{aligned} \mathbf{T}_m^i =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {(B_{11}^i )^{2}}&{} {(B_{12}^i )^{2}}&{} {2B_{11}^i B_{12}^i }&{} {(B_{13}^i )^{2}}&{} {2B_{11}^i B_{13}^i }&{} {2B_{12}^i B_{13}^i } \\ {(B_{21}^i )^{2}}&{} {(B_{22}^i )^{2}}&{} {2B_{21}^i B_{22}^i }&{} {(B_{23}^i )^{2}}&{} {2B_{21}^i B_{23}^i }&{} {2B_{22}^i B_{23}^i } \\ {B_{11}^i B_{21}^i }&{} {B_{12}^i B_{22}^i }&{} {B_{11}^i B_{22}^i +B_{12}^i B_{21}^i }&{} {B_{13}^i B_{23}^i }&{} {B_{11}^i B_{23}^i +B_{13}^i B_{21}^i }&{} {B_{12}^i B_{23}^i +B_{13}^i B_{22}^i } \\ {(B_{31}^i )^{2}}&{} {(B_{32}^i )^{2}}&{} {2B_{31}^i B_{32}^i }&{} {(B_{33}^i )^{2}}&{} {2B_{31}^i B_{33}^i }&{} {2B_{32}^i B_{33}^i } \\ {B_{11}^i B_{31}^i }&{} {B_{12}^i B_{32}^i }&{} {B_{11}^i B_{32}^i +B_{12}^i B_{31}^i }&{} {B_{13}^i B_{33}^i }&{} {B_{11}^i B_{33}^i +B_{13}^i B_{31}^i }&{} {B_{12}^i B_{33}^i +B_{13}^i B_{32}^i } \\ {B_{21}^i B_{31}^i }&{} {B_{22}^i B_{32}^i }&{} {B_{21}^i B_{32}^i +B_{22}^i B_{31}^i }&{} {B_{23}^i B_{33}^i }&{} {B_{21}^i B_{33}^i +B_{23}^i B_{31}^i }&{} {B_{22}^i B_{33}^i +B_{23}^i B_{32}^i } \\ \end{array} }} \right] \end{aligned}$$
(16)

The orthogonal frame \(\mathbf{A}_m^i \) is defined using the cross-sectional frame [43]. In the cross-sectional frame, the unit vector along the \(Z\)-axis of the orthogonal frame \(\mathbf{A}_m^i \) is parallel to the third covariant base vector \(\mathbf{G}_3^i \), thus the orthogonal frame describes the orientation of the cross section of the shell. That is, the unit vector \(\mathbf{k}_s^i \) along the \(Z\)-axis of the cross-sectional frame is defined as

$$\begin{aligned} \mathbf{k}_s^i =\frac{\mathbf{G}_3^i }{\left| {\mathbf{G}_3^i } \right| } \end{aligned}$$
(17)

Two other axes are defined using Gram–Schmidt orthogonalization procedure as follows:

$$\begin{aligned} \mathbf{j}_s^i =\frac{\mathbf{G}_2^i -((\mathbf{G}_2^i )^{T}\mathbf{k}_s^i )\mathbf{k}_s^i }{\left| {\mathbf{G}_2^i -((\mathbf{G}_2^i )^{T}\mathbf{k}_s^i )\mathbf{k}_s^i } \right| }\quad \hbox {and}\quad \mathbf{i}_s^i =\mathbf{j}_s^i \times \mathbf{k}_s^i \end{aligned}$$
(18)

from which, one has

$$\begin{aligned} \mathbf{A}_m^i =\left[ {{\begin{array}{lll} {\mathbf{i}_s^i }&{} {\mathbf{j}_s^i }&{} {\mathbf{k}_s^i } \\ \end{array} }} \right] \end{aligned}$$
(19)

Since the orthogonal frame \(\mathbf{A}_m^i \) is defined at the reference configuration, the orientation matrix is an identity matrix if the element is initially flat.

Since the six strain components are defined in the middle surface, the bending and twisting deformations of the shell element need to be introduced. To this end, the three curvature components defined with respect to the orthogonal frame \(\mathbf{A}_m^i \) are defined as

$$\begin{aligned}&{\mathbf{K}}_m^i (x^{i},y^{i},0)=(\mathbf{C}_m^i )^{-T}{\tilde{\mathbf{K}}}_m^i (\mathbf{C}_m^i )^{-1}\equiv \kappa _{rs}^i,\nonumber \\&r,s = x,y \end{aligned}$$
(20)

where \(\mathbf{C}_m^i \) is a 2 by 2 matrix that can be extracted from the matrix \(\mathbf{B}_m^i \) and is defined by \(\mathbf{C}_m^i \equiv C_{rs}^i =B_{rs}^i \) for \(r,s=1,2\). In the preceding equation, the matrix \({\tilde{\mathbf{K}}}_m^i \) is defined as

$$\begin{aligned} {\tilde{\mathbf{K}}}_m^i =\left[ {{\begin{array}{c@{\quad }c} {\tilde{\kappa }_{xx}^i -\tilde{\kappa }_{0xx}^i }&{}\quad {\tilde{\kappa }_{xy}^i -\tilde{\kappa }_{0xy}^i } \\ {\tilde{\kappa }_{xy}^i -\tilde{\kappa }_{0xy}^i }&{}\quad {\tilde{\kappa }_{yy}^i -\tilde{\kappa }_{0yy}^i } \\ \end{array} }} \right] \end{aligned}$$
(21)

where

$$\begin{aligned} \left. {\begin{array}{l} \tilde{\kappa }_{xx}^i \!=\!-\!\left( {\frac{\partial }{\partial x^{i}}\left( {\frac{\partial \mathbf{r}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{r}_m^i }{\partial x^{i}},\quad \tilde{\kappa }_{yy}^i \!=\!-\!\left( {\frac{\partial }{\partial y^{i}}\left( {\frac{\partial \mathbf{r}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{r}_m^i }{\partial y^{i}}\quad \\ \tilde{\kappa }_{xy}^i \!=\!\frac{1}{2}\left( {\!-\!\left( {\frac{\partial }{\partial x^{i}}\left( {\frac{\partial \mathbf{r}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{r}_m^i }{\partial y^{i}}\!-\!\left( {\frac{\partial }{\partial y^{i}}\left( {\frac{\partial \mathbf{r}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{r}_m^i }{\partial x^{i}}} \right) \\ \end{array}} \right\} \nonumber \\ \end{aligned}$$
(22)

and

$$\begin{aligned} \left. {\begin{array}{l} \tilde{\kappa }_{0xx}^i \!\!=\!-\!\left( {\frac{\partial }{\partial x^{i}}\left( {\frac{\partial \mathbf{X}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{X}_m^i }{\partial x^{i}},\,\, \tilde{\kappa }_{0yy}^i \!=\!-\!\left( {\frac{\partial }{\partial y^{i}}\left( {\frac{\partial \mathbf{X}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{X}_m^i }{\partial y^{i}} \\ \tilde{\kappa }_{0xy}^i \!=\!\frac{1}{2}\left( {\!-\!\left( {\frac{\partial }{\partial x^{i}}\left( {\frac{\partial \mathbf{X}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{X}_m^i }{\partial y^{i}}\!-\!\left( {\frac{\partial }{\partial y^{i}}\left( {\frac{\partial \mathbf{X}^{i}}{\partial z^{i}}} \right) } \right) ^{T}\frac{\partial \mathbf{X}_m^i }{\partial x^{i}}} \right) \end{array}}\!\!\right\} \nonumber \\ \end{aligned}$$
(23)

Using Eqs. 15 and 20, the generalized elastic forces \(\mathbf{Q}_k^i \) for the initially curved shell element can be defined using the virtual work as follows:

$$\begin{aligned} \delta W^{i}&= -h^{i}\int \!\! {(\delta \varvec{\upvarepsilon }_p^i )^{T}\mathbf{D}_p \varvec{\upvarepsilon }_p^i dA_0^i } \!-\!h^{i}\!\!\int \!\! {(\delta \varvec{\upgamma }_t^i )^{T}\mathbf{D}_\gamma \varvec{\upgamma }_t^i dA_0^i } \nonumber \\&\quad -\,h^{i}\int {\delta \varepsilon _{zz}^i E\varepsilon _{zz}^i dA_0^i } -\int {(\delta \varvec{\upkappa }^{i})^{T}\mathbf{D}_\kappa \varvec{\upkappa }^{i} dA_0^i } \nonumber \\&= (\delta \mathbf{e}^{i})^{T} {\mathbf{Q}_k^i } \end{aligned}$$
(24)

where \( dA _0^i \) is the infinitesimal area of element \(i\) in the reference configuration, and the following engineering strain and curvature vectors are defined:

$$\begin{aligned} \varvec{\upvarepsilon }_p^i \!&= \![{\varepsilon _{xx}^i }\quad {\varepsilon _{yy}^i }\quad {2\varepsilon _{xy}^i }]^{T},\quad \varvec{\upgamma }_t^i =[{2\varepsilon _{xz}^i }\quad {2\varepsilon _{yz}^i }]^{T},\nonumber \\ \varvec{\upkappa }^{i}&= [{\kappa _{xx}^i }\quad {\kappa _{yy}^i }\quad {2\kappa _{xy}^i}]^{T} \end{aligned}$$
(25)

where \(\varvec{\upvarepsilon }_p^i \) represents the vector of the in-plane strains, \(\varvec{\upgamma }_t^i \) the vector of transverse shear strains and \(\varvec{\upkappa }^{i}\) the vector of curvatures. For a linear Hookean material model in plane stress condition with constant shell thickness \(h\), the following matrices of elasticity are defined:

$$\begin{aligned} \mathbf{D}_p&= \frac{E}{1-\nu ^{2}} \left[ {{\begin{array}{ccc} 1&{}\quad \nu &{}\quad 0 \\ \nu &{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad {(1-\nu )/2} \\ \end{array} }} \right] ,\nonumber \\ \mathbf{D}_\gamma&= \frac{E}{2(1+\nu )} \left[ {{\begin{array}{cc} {c_{xz} }&{}\quad 0 \\ 0&{}\quad {c_{yz} } \\ \end{array} }} \right] ,\quad \mathbf{D}_\kappa =\frac{h^{3}}{12}\mathbf{D}_p \end{aligned}$$
(26)

where \(E\) is Young’s modulus; \(\nu \) Poisson’s ratio; \(c_{xz} \) and \(c_{yz} \) the transverse shear strain distribution correction factors. The integration is performed over the middle surface of the element, and the stress distribution along the thickness of the shell is assumed constant in this model. This assumption can be considered a reasonable approximation for thin shell structures with linear Hookean material model. Since the elastic forces are evaluated only in the middle surface, the total number of integration points is less than that of the continuum mechanics-based shell element [47].

4 Element locking and remedies

The bilinear interpolation of the middle surface and transverse position vector gradient leads to several element locking problems. Numerous approaches have been proposed to remedy the poor elastic energy description for the displacement-based finite elements in the past. Reduced integration or selective reduced integration [20, 50] is one of the simplest methods to improve element performance. However, the rank deficiency may occur if uniform reduced integration is applied [5, 34]. The methods based on incompatible modes [4, 44], Hellinger–Reissner two field principle [17] and Hu–Washizu three-field principle [19], and discrete shear gap [7] can be considered as more general approaches which do not require special numerical integration schemes to alleviate the element locking phenomena. These formulations have been categorized and reviewed by Yang et al. [49] and locking remedies by Sze [24]. In this section, remedies for the element lockings of the bilinear ANCF shell element based on the elastic middle surface approach are discussed.

4.1 In-plane normal/shear locking

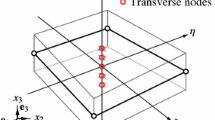
The bilinear interpolation of the global position field in the middle surface is not able to describe pure in-plane bending without shear strains (see Fig. 2) [8]. An enhancement of the middle surface strain field leads to better approximation of shear strain distribution in the middle surface. Using the enhanced assumed strain (EAS) approach, the compatible in-plane strains in the middle surface \(\varvec{\upvarepsilon }_p^{i c} \) obtained by differentiating the assumed global position vector are modified as follows [2, 40, 41]:

$$\begin{aligned} \varvec{\upvarepsilon }_p^i =\varvec{\upvarepsilon }_p^{i c} +\varvec{\upvarepsilon }_p^{i \mathrm{EAS}} \end{aligned}$$
(27)

where \(\varvec{\upvarepsilon }_p^{i \mathrm{EAS}} \) is the enhanced assumed strain vector defined by

$$\begin{aligned} \varvec{\upvarepsilon }_p^{i \mathrm{EAS}} (\varvec{\upxi }^{i})=\mathbf{G}^{i}(\varvec{\upxi }^{i}){\varvec{\upalpha }}^{i} \end{aligned}$$
(28)

In the preceding equation, \({\varvec{\upalpha }}^{i}\) is the vector of internal parameters that defines the assumed strain field of element \(i\), and the matrix \(\mathbf{G}^{i}(\varvec{\upxi }^{i})\) is defined as [2, 40, 41]

$$\begin{aligned} \mathbf{G}^{i}(\varvec{\upxi }^{i})=\frac{\left| {\mathbf{J}_0^i } \right| }{\left| {\mathbf{J}^{i}(\varvec{\upxi }^{i})} \right| }(\mathbf{T}_{0mp}^i )^{-T}\mathbf{N}^{i}(\varvec{\upxi }^{i}) \end{aligned}$$
(29)

where \(\mathbf{J}^{i}(\varvec{\upxi }^{i})\) and \(\mathbf{J}_0^i \) are, respectively, the position vector gradient tensor at the reference configuration evaluated at the Gauss integration point \(\varvec{\upxi }^{i}\) and that evaluated at the center of the element (\(\varvec{\upxi }^{i}=\mathbf{0})\). \(\mathbf{T}_{0mp}^i \) is the 3 by 3 transformation matrix defined by the sub-matrix of the 6 by 6 transformation matrix given by Eq. 16 associated with the in-plane strain vector \(\varvec{\upvarepsilon }_p^i \), and this matrix has to be evaluated at the center of the element [2, 40, 41]. The explicit form of the transformation matrix is given as follows:

$$\begin{aligned}&\mathbf{T}_{mp0}^i \!=\!\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {(B_{11}^i )^{2}}&{} {(B_{12}^i )^{2}}&{} {2B_{11}^i B_{12}^i } \\ {(B_{21}^i )^{2}}&{} {(B_{22}^i )^{2}}&{} {2B_{21}^i B_{22}^i } \\ {B_{11}^i B_{21}^i }&{} {B_{12}^i B_{22}^i }&{} {B_{11}^i B_{22}^i +B_{12}^i B_{21}^i } \\ \end{array} }} \right] _{\varvec{\upxi }^{i}=\mathbf{0}}\nonumber \\ \end{aligned}$$
(30)

where \(B_{rs}^i =(\mathbf{B}_m^i )_{rs} =((\mathbf{A}_m^i )^{T}\mathbf{J}_m^i )_{rs},\quad r,s=1,2\) as defined by Eq. 14. The matrix \(\mathbf{N}^{i}(\varvec{\upxi }^{i})\) consists of polynomial terms of the enhanced strain field in parametric domain. The simplest enhancement which introduces four internal parameters \({\varvec{\upalpha }}^{i}\) is given as follows:

$$\begin{aligned} \mathbf{N}^{i}(\varvec{\upxi }^{i})=\left[ {{\begin{array}{cccc} {\xi ^{i}}&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\eta ^{i}}&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\xi ^{i}}&{}\quad {\eta ^{i}} \\ \end{array} }} \right] \end{aligned}$$
(31)

The effect of the number of internal parameters on the elastic force accuracy is discussed in literature [2]. It is important to notice here that the matrix \(\mathbf{N}^{i}(\varvec{\upxi }^{i})\) should fulfill the following condition

$$\begin{aligned} \int {\mathbf{N}^{i}(\varvec{\upxi }^{i})d\varvec{\upxi }^{i}} =\mathbf{0} \end{aligned}$$
(32)

such that the assumed stress vanishes over the reference volume of the element, and it passes the patch test [41].

Fig. 2
figure 2

Middle surface of the shell subjected to pure bending (left) depicting expected pure bending without shear strain and element response (right) depicting artificial shear strain

Full size image

4.2 Transverse shear locking

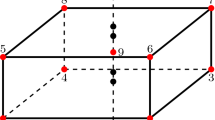
Finite elements that are not able to describe pure bending without vanishing transverse shear strains will store excessive shear strain energy. This makes the elements especially for thin structures behave stiffer than expected. The absolute nodal coordinate formulation-based finite elements are no exception to this rule. The transverse shear locking can be avoided by the use of reduced integration. However, in most cases, this leads to extra zero energy modes [8]. Alternatively, a more robust remedy without extra zero energy modes is achieved by using a method of assumed strains which was originally proposed by MacNeal for small displacement analysis for the tri- and quadrilateral plate as well as membrane elements [23]. Later, Bathe and Dvorkin generalized this method for continuum shell element [13] and for general mixed interpolation of tensorial components (MITC) shell elements [3]. This method is known as assumed natural strain method (ANS). In this approach, the covariant strains evaluated at Barlow points are tied to assumed natural strain interpolation points through the use of Lagrange multipliers. The Barlow points are unique points where the strain field terms are exactly correct. These sampling points for different plate elements are presented in the literature [18]. In the bilinear shell element, the covariant shear strain \(\tilde{\gamma }_{yz}^i \) for the element \(i\) is zero where the coordinate \(y^{i}\) is zero, and the covariant shear strain \(\tilde{\gamma }_{xz}^i \) is zero where the coordinate \(x^{i}\) is zero. The extra zero energy modes can be avoided by using a linear interpolation for the assumed natural shear strains which will retain the correct rank of the stiffness matrix. The linear interpolation requires tying points that are located at the positions \(A, B, C\) and \(D\) as shown in the Fig. 3. The assumed covariant natural transverse shear strain field can be defined as follows:

$$\begin{aligned} \left. {\begin{array}{l} \tilde{\gamma }_{xz}^{i \mathrm{ANS}} =\frac{1}{2}\left( {1-\eta ^{i}} \right) \tilde{\gamma }_{xz}^{iC} +\frac{1}{2}\left( {1+\eta ^{i}} \right) \tilde{\gamma }_{xz}^{iD} \\ \\ \tilde{\gamma }_{yz}^{i \mathrm{ANS}} =\frac{1}{2}\left( {1-\xi ^{i}} \right) \tilde{\gamma }_{yz}^{iA} +\frac{1}{2}\left( {1+\xi ^{i}} \right) \tilde{\gamma }_{yz}^{iB} \quad \\ \end{array}} \right\} \end{aligned}$$
(33)

where \(\tilde{\gamma }_{xz}^{iC}, \tilde{\gamma }_{xz}^{iD}, \tilde{\gamma }_{yz}^{iA} \) and \(\tilde{\gamma }_{yz}^{iB} \) are the covariant transverse shear strains at the tying points.

Fig. 3
figure 3

Tying points for the assumed natural stain method applied to remedy transverse shear and curvature thickness lockings

Full size image

4.3 Poisson’s thickness locking

The use of a linear interpolation of the global position field along the shell thickness leads to thickness locking in the element. This is called Poisson’s thickness locking because it is the Poisson’s ratio that introduces the coupling of the in-plane strains to the transverse normal strain. In the case of pure bending, the axial strains due to bending are linearly distributed along the thickness, and it leads to the linearly varying transverse normal strain due to the coupling induced by Poisson’s ratio. However, the use of the linear interpolation along the thickness leads to constant thickness strains which make the element behave overly stiff since the thickness strain does not vanish on the neutral axis as shown in Fig. 4. It is demonstrated in the previous study on the continuum mechanics-based shear deformable shell element that use of EAS allows for incorporating the linearly varying transverse normal strain to alleviate the Poisson’s thickness locking effectively [45–47]. On the other hand, due to the plane stress assumption made in the shell element discussed in this study, the in-plane strains and the transverse normal strain are decoupled, thus the Poisson’s thickness locking is not essentially exhibited. This is one of the most economical ways of treating the Poisson’s locking for applications where the plane stress assumption is fulfilled. For thick shell structures with nonlinear material models, this assumption is no longer valid, and the continuum mechanics approach needs to be used [47].

Fig. 4
figure 4

Shell subjected to pure bending (left) depicting expected through thickness strain and element response (right) depicting Poisson’s thickness locking

Full size image

4.4 Curvature thickness locking

The transverse gradient vectors can be erroneously elongated when the shell element is subjected to bending and twisting deformation. Remedies for the artificial elongation have been proposed by Gebhard and Schweizerhof [14]. In the ANCF beam elements [15, 30, 31], this artificial thickness strain have been avoided by using Lobatto numerical integration for the transverse direction strain components. Lobatto integration includes the integration interval boundaries which coincide with nodal points of the ANCF elements in the parametric domain. Therefore, the use of Lobatto numerical integration points leads to same thickness strain field evaluation as what is achieved by the ANS method. However, ANS method is more general and has been successfully applied to the shell element by Betch and Stein [6]. As shown in the Fig. 3, the covariant transverse normal strains at the four nodal points are interpolated by the Lagrange polynomial as follows [6]:

$$\begin{aligned} \tilde{\varepsilon }_{zz}^{i\mathrm{ANS}} =S_1^{i\mathrm{ANS}} \tilde{\varepsilon }_{zz}^{i1} +S_2^{i\mathrm{ANS}} \tilde{\varepsilon }_{zz}^{i2} +S_3^{i\mathrm{ANS}} \tilde{\varepsilon }_{zz}^{i3} +S_4^{i\mathrm{ANS}} \tilde{\varepsilon }_{zz}^{i4}\nonumber \\ \end{aligned}$$
(34)

where \(\tilde{\varepsilon }_{zz}^k \) indicates the compatible transverse normal strain at node \(k\) and \(S_k^\mathrm{ANS} \) is the shape function associated with it.

4.5 Modified generalized elastic forces

The enhancement of the in-plane strains using the EAS method as well as the application of the ANS method to the transverse normal and transverse shear strains leads to the following modified expression of the virtual work of the elastic forces:

$$\begin{aligned} \delta W^{i}&= -h^{i}\int {(\delta \varvec{\upvarepsilon }_p^i )^{T}\mathbf{D}_p (\varvec{\upvarepsilon }_p^{i c} +\varvec{\upvarepsilon }_p^{i \mathrm{EAS}} ) dA_0^i }\nonumber \\&\quad -\,h^{i}\int {(\delta \varvec{\upgamma }_t^{i \mathrm{ANS}} )^{T}\mathbf{D}_\gamma \varvec{\upgamma }_t^{i \mathrm{ANS}} dA_0^i } \nonumber \\&\quad -\,h^{i}\int {\delta \varepsilon _{zz}^{i \mathrm{ANS}} E\varepsilon _{zz}^{i \mathrm{ANS}} dA_0^i }\nonumber \\&\quad -\,\int {(\delta \varvec{\upkappa }^{i})^{T}\mathbf{D}_\kappa \varvec{\upkappa }^{i} dA_0^i }\nonumber \\&= (\delta \mathbf{e}^{i})^{T} {\mathbf{Q}_k^i } \end{aligned}$$
(35)

The internal parameters \({\varvec{\upalpha }}^{i}\) introduced for the enhanced assumed strain are determined iteratively such that the following condition is fulfilled for each element [41]:

$$\begin{aligned}&\int _{A_0^i } {\left( {\frac{\partial \varvec{\upvarepsilon }_p^{i \mathrm{EAS}} }{\partial {\varvec{\upalpha }}^{i}}} \right) ^{T}\mathbf{D}_p(\varvec{\upvarepsilon }_p^{i c} +\varvec{\upvarepsilon }_p^{i \mathrm{EAS}} ) dA_0^i } =\mathbf{0},\nonumber \\&\quad i=1,\ldots ,ne \end{aligned}$$
(36)

The equations of motion can be expressed as follows:

$$\begin{aligned} \mathbf{M}^{i}{\ddot{\mathbf{e}}}^{i}=\mathbf{Q}_k^i (\mathbf{e}^{i},{\varvec{\upalpha }}^{i})+\mathbf{Q}_e^i (\mathbf{e}^{i},{\dot{\mathbf{e}}}^{i},t) \end{aligned}$$
(37)

where the vectors \(\mathbf{Q}_k^i \) and \(\mathbf{Q}_e^i \) are, respectively, the element elastic and external force vectors; and the matrix \(\mathbf{M}^{i}\) is the constant element mass matrix [47]. The preceding equations of motion are solved at each time step together with Eq. 36 to determine the nodal coordinates and the internal parameters. For details on the solution procedure, one can refer to the literature [47].

5 Numerical examples

In this section, several numerical examples are presented in order to demonstrate the use of the shear deformable ANCF shell element based on the elastic middle surface approach.

5.1 Cantilevered square plate subjected to distributed transverse force

In the first example, the basic element performance is evaluated using linear static problems. As shown in Fig. 5, a cantilevered plate is subjected to the distributed transverse load. The length \(L\) and width \(W\) of the plate are assumed to be 1.0 and 1.0 m, while the Young’s modulus \(E\) and Poisson’s ratio \(\upnu \) are assumed to be \(2.1\times 10^{11}\) Pa and 0.3, respectively. In order to discuss the effect of the slenderness ratio on the numerical solutions obtained using the moderately thick shell element developed in this investigation, the following three scenarios are considered:

  1. (A)

    Thin plate (\(L/H =1{,}000\)); thickness \(H=10^{-3}\) m and distributed load \(q_z =5\times 10^{-2}\) N/m

  2. (B)

    Moderately thick plate (\(L/H=100\)); thickness \(H=10^{-2}\) m and distributed load \(q_z =5\times 10^{1}\) N/m

  3. (C)

    Thick plate (\(L/H =10\)); thickness \(H=10^{-1}\) m and distributed load \(q_z =5\times 10^{4}\) N/m

The linear analytical solution of the free-end transverse deflection based on thin plate theory is given as [35]

$$\begin{aligned} {(\delta _z )}_\mathrm{exact} =\frac{q_z L^{3}}{3D} \end{aligned}$$
(38)
Fig. 5
figure 5

Cantilevered square plate subject to distributed transverse force

Full size image
Table 1 Deflection of the cantilever thin plate (\(L/H=1{,}000\)) subjected to transverse distributed load with mesh refinement of \({\mathbf {n}} \times {\mathbf {n}}= \mathbf 2 ^{{\mathbf {m}}}\times \mathbf 2 ^{{\mathbf {m}}},\) \( {\mathbf {m}}=\mathbf 0 \ldots \mathbf 5 \)
Full size table
Table 2 Deflection of the cantilever moderately thick plate (\(L/H=100\)) subjected to transverse distributed load with mesh refinement of \({\mathbf {n}}\times {\mathbf {n}}=\mathbf 2 ^{{\mathbf {m}}}\times \mathbf 2 ^{{\mathbf {m}}}, {\mathbf {m}}=\mathbf 0 \ldots \mathbf 5 \)
Full size table

where \(q_z \) is the distributed transverse load, and \(D\) is the plate stiffness constant defined by \(D=EH^{3}/12(1-\nu ^{2})\). In the preceding three different scenarios, the distribution loads are chosen such that the transverse deflections in the analytical solution based on the thin plate theory become \((\delta _z )_\mathrm{exact} =8.667\times 10^{-4}\) m to ensure small deformation. The numerical solutions for the thin, moderately thin and thick plates are summarized in Tables 1, 2 and 3, respectively. The numerical results of the proposed ANCF shell element based on the elastic middle surface approach (denoted as ANCF EMS shell in the tables) are compared with those obtained using the continuum mechanics-based ANCF shell element (denoted as ANCF CM shell in the tables) proposed in the literature [47] and ANSYS SHELL181 based on the mixed interpolation of tensorial components (MITC) shell element. As observed from Tables 1 and 2, the numerical results and the rate of convergence for the three different models are the same, and the element locking is not exhibited. On the other hand, numerical results of the continuum mechanics ANCF shell model in the thick shell problem shown in Table 3 differ from those of the elastic middle surface shell element and SHELL181. This is attributed to the fact that the slenderness ratio of the shell is small (i.e., the shell is thick), and the plane stress assumption made in the EMS ANCF shell element and SHELL181 is no longer valid in this problem. The numerical results of ANCF CM shell element are compared with those of the solid shell element in ANSYS (SOLSH190) which consists of layers of translational nodal coordinates at the top and bottom surfaces of the element to capture the thickness deformation of the shell structure in Table 3. It is observed that the numerical results of ANCF CM shell element agree well with those of the solid shell element SOLSH190 which allows for modeling thick shell structures, while ANCF EMS shell is equivalent to MITC shear deformable shell element SHELL181 which leads to efficient solutions to moderately thick shell problems. It is important to notice here that the number of Gaussian integration points per EMS element presented in this study is 4 (\(2\times 2)\), while that of CM element is 8 (\(2\times 2\times 2)\), which is two times greater than that of EMS element. This allows the EMS element to provide efficient solutions to problems involving thin to moderately thick shell structures with linear material models.

Table 3 Deflection of the cantilever thick plate (\(L/H=10\)) subjected to transverse distributed load with mesh refinement of \({\mathbf {n}}\times {\mathbf {n}}=\mathbf 2 ^{{\mathbf {m}}}\times \mathbf 2 ^{{\mathbf {m}}},\) \( {\mathbf {m}}=\mathbf 0 \ldots \mathbf 5 \)
Full size table

5.2 Cantilevered quarter cylinder subjected to transverse point force

In the next problem, an initially curved shell structure is considered as discussed in literature [47]. The radius of curvature and the thickness are, respectively, assumed to be 1.0 and 0.01 m, while Young’s modulus and Poisson’s ratio are assumed to be \(2.1\times 10^{8}\) Pa and 0.3, respectively. The vertical point force \(F_{z}\) defined at the corner of the shell is assumed to be 20 N. As shown in Fig. 6, the quarter cylinder shell is subjected to large deformation at the static equilibrium state. To measure the accuracy, the error is defined by a deviation of the vertical deflection at the force application point on the plate from that of the reference solution obtained by ANSYS SHELL181 with \(100\times 100\) elements. The numerical convergence of the solution is presented in Fig. 7. In the moderately thick shell problems, numerical results obtained by the proposed EMS ANCF shell element agree well with those of ANCF CM shell, and the linear rate of convergence is ensured, which implies that the element locking is not exhibited in the large deformation problem of the initially curved shell structure.

Fig. 6
figure 6

Initial and deformed configurations of cantilevered quarter cylinder subjected to a transverse tip load

Full size image
Fig. 7
figure 7

Numerical convergence of the vertical deflection error at the force application point of the quarter cylinder shell

Full size image

5.3 Natural frequencies of free interface (FFFF) square plate

The eigenfrequency analysis of a square plate with completely free boundaries analyzed in the literature [35] is discussed. The eigenfrequency analysis is a simple and effective way to verify that lockings are removed without leading to spurious zero eigenmodes. The dimensionless natural frequencies defined by \(\Omega =\omega /\omega _0 \) with \(\omega _0 =\pi ^{2}\sqrt{D/\rho HL^{4}}\) are used, where \(D=EH^{3}/12(1-\nu ^{2}), \rho , H\) and \(L\) are the plate stiffness constant, material density, height and length of the plate, respectively. The first ten nonzero dimensionless natural frequencies are summarized in Table 4. In all of the cases, six rigid body modes with zero natural frequencies are obtained in the analysis, and spurious modes are not exhibited. The numerical results are compared with the analytical solutions [35]. The proposed shell element leads to better rate of convergence in eigenfrequencies in comparison to the higher-order fully parameterized ANCF element which suffers from element lockings [26].

Table 4 First ten dimensionless eigenfrequencies \(\varOmega =\omega /\omega _0 \) with \(\omega _0 =\pi ^{2}\sqrt{D/\rho HL^{4}}\) and \(D=EH^{3}/12\left( {1-\nu ^{2}} \right) \) of the free (FFFF) square plate elements and mesh refinement of \(n\times n=2^{m}\times 2^{m},m=0\ldots 4\)
Full size table

5.4 Quarter cylinder pendulum

The nonlinear dynamics of an initially curved shell is analyzed in the last numerical example to demonstrate the performance of the ANCF EMS shell element. A quarter cylinder that has the same dimension as the one in Sect. 5.2 is used. The total mass, Young’s modulus and Poisson’s ratio are assumed to be 5 kg, \(2.1\times 10^{7}\) Pa and 0.3, respectively. Newmark-\(\upbeta \) method is used for time integration with automatic time stepping, and an error tolerance of 1E\(-\)5 is assumed. One corner of the quarter cylinder is connected to the ground by a spherical joint. The global \(X, Y\) and \(Z\)-positions at the corner of the shell are shown in Figs. 8, 9 and 10 for different number of elements (\(16\times 16, 32\times 32\) and \(64\times 64)\). The reference solution is obtained using ANSYS SHELL181 with \(100\times 100\) elements. It is observed from these figures that the results obtained using the ANCF EMS shell element agree well with the reference solution obtained using ANSYS SHELL181.

Fig. 8
figure 8

Global \(X\)-position of quarter-cylindrical shell pendulum

Full size image
Fig. 9
figure 9

Global \(Y\)-position of quarter-cylindrical shell pendulum

Full size image
Fig. 10
figure 10

Global \(Z\)-position of quarter-cylindrical shell pendulum

Full size image

6 Summary and conclusions

In this investigation, a shear deformable ANCF shell element is developed based on the elastic middle surface approach for the large deformation analysis of thin to moderately thick shell structures. To this end, the bilinear ANCF plate element is generalized to the locking-free initially curved shell element using the elastic middle surface approach. The developed element is compared with the continuum mechanics-based shear deformable ANCF shell element to shed light on the nature of the thickness locking exhibited in the bilinear shell element and its locking remedies. The use of transverse position vector gradients and its interpolation with low-order polynomials leads to thickness lockings which makes the element behave overly stiff, leading to the lower rate of convergence of numerical solutions. Since the shell element has no element discretization in transverse direction, the thickness lockings are fundamental and crucial problems of the shear deformable shell element of the absolute nodal coordinate formulation. The thickness lockings can be categorized into Poisson’s locking and curvature locking. Poisson’s locking is caused by the erroneous transverse normal strain distribution induced by the coupling with the in-plane strains. While it has been shown that the enhanced assumed strain is required to incorporate the linearly varying transverse normal strain in the continuum mechanics approach, the Poisson’s locking can be automatically removed with the use of plane stress assumption in the elastic middle surface approach for thin to moderately thick shell structures. The curvature locking, on the other hand, is caused by erroneous elongation of the transverse gradient vectors when the shell element is in bending and twisting. This locking can be alleviated by the assumed natural strain as has been applied to the continuum mechanics-based shell element [47]. In this approach, the covariant transverse normal strains at the four nodal points are interpolated to better approximate the transverse normal strain distribution. The developed element leads to an efficient finite element solution due to no requirement of integration in the transverse direction in the large deformation analysis of moderately thick multibody shell structures. Numerical examples indicate expected linear rate convergence of numerical solutions.