1 Introduction

Numerical simulations for sheet forming using the finite element method can be classified by two types of elements. One is a solid (or continuum) element, and the other is a structural element. Continuum elements are widely used, because they are capable of modeling the complex behaviors of the sheet forming process. However, they require huge computational costs, which include pre-processing for mesh generation and solving a linear system of equations. On the other hand, structural elements are more efficient than continuum elements regarding computational costs. Structural elements can only be employed to predict simple bending behavior accurately if the thickness of the simulation model is small, because the plane stress condition is assumed. However, conventional shell elements are not sufficient for simulating some situations involved in sheet forming, such as the change in thickness of the sheet and the contact force applied at the sheet-die interface. For the purpose of obtaining more accurate results from shell elements in sheet forming simulations, it is necessary to develop a shell element in which thickness–stretch can be considered.

The development of shell elements for general shell structures that are based on either the degenerated solid approach [1] or the stress resultant shell theory [2] has represented an attractive research field for several decades. The kinematic assumptions are essentially the same for both formulations. However, the procedure of evaluating the resultant stress is carried out numerically in the former and analytically in the latter. The common kinematic assumptions of inextensibility in the transverse direction and the zero transverse normal stress condition apply in both formulations. The shell element based on the degenerated solid approach, which was originally presented by Ahmad, Irons, and Zienkiewicz (A–I–Z), has been the basis of the finite element analysis of shell structures for many years. The A–I–Z shell element is an isoparametric element, for which translations and rotations are interpolated independently with common shape functions that have only \(C^{0}\) continuity. The A–I–Z shell element has also been extended to nonlinear analysis by Hughes and Liu [3, 4], Hughes and Carnoy [5], Liu et al. [6], and others. In nonlinear analysis, the formulations are constrained by the requirement of infinitesimal strains, owing to the assumption of a constant thickness during the deformation. Furthermore, the A–I–Z element suffers from the locking phenomena, and much research effort has been dedicated to the development of shell elements based on the A–I–Z formulation that circumvent this problem. Dvorkin and Bathe presented the MITC4 shell element [7] to avoid the locking phenomena of the A–I–Z shell element. The MITC4 shell element is one of the most popular elements in engineering applications. However, the formulation of the MITC4 shell element is also constrained by the limitation of infinitesimal strains. In developing shell elements for modeling large strain ranges, changes in thickness must be introduced to formulate the geometry and kinematics.

Shell elements that are developed for application to finite strain problems can roughly be classified into three groups. One is a class of elements that assume the plane stress state in the transverse direction, such as the degenerated shell element and the MITC4 shell element. The MITC4 shell element has been extended to large strain problems in the studies [8,9,10,11,12,13]. These elements are capable of dealing with large strains, but thickness–stretch is based on the plane stress assumption, which is only valid for thin structures. In contrast, the second group is a class of elements that assume the distribution of the transverse strains. Parisch [14] presented a shell formulation with seven degrees of freedom per midsurface node, called a seven-parameter shell element. However, the seven-parameter shell element does not have the capability of representing a state of pure bending, owing to the constant transverse normal strain. This feature is called thickness locking [15, 16]. El-Abbasi and Meguid [17] proposed a seven-parameter shell element in which a quadratic displacement function is employed to avoid thickness locking. Pimenta et al. [18] also applied a quadratic displacement function in the transverse direction to a triangular shell element. Büchter et al. [19] developed an alternative formulation that considers a linear variation of strains through the thickness. In this formulation, they introduced a thickness variable and a linear strain term based on the enhanced assumed strain (EAS) formulation, which was originally introduced by Simo and Rifai [20] to improve the in-plane behavior of displacement-based elements; see also Andelfinger and Ramm [21]. Betsch and Stein [22] and Betsch et al. [23] also presented a similar shell formulation, and Huttel and Matzenmiller [24] extended the element developed by Betsch and Stein [22]. In cases where the EAS formulation is employed, numerical schemes exhibit severe instabilities in large strain ranges; see [25]. These instabilities encountered with the EAS formulation can be suppressed by introducing artificial numerical parameters that can change the deformation response of the simulation model. In fact, the use of these numerical parameters is quite undesirable, because the solutions can be unreliable and inaccurate. The final group of shell elements for finite strain problems is a class of elements that represent the displacement field, similarly to the hexahedral solid elements. In the solid-shell concept [26], the kinematic description consists of only displacement degrees of freedom at the top and bottom surfaces of the shell. That is, the nodes of the solid-shell element are placed on the top and bottom surfaces instead of the rotational degrees of freedom. Thus, a low order solid-shell element suffers from the locking phenomena, similarly to solid elements. In order to avoid the transverse shear and membrane locking phenomena, either the assumed strain technique [7] or the EAS formulation [20] is employed for most solid-shell elements. In addition, thickness locking is avoided by introducing a quadratic displacement field [27], assuming the plane stress condition in the transverse direction [26, 28], or imposing the EAS formulation [29,30,31,32,33,34]. Because solid-shell elements that do not assume the plane stress state exhibit volumetric locking, either the EAS formulation or the selective reduced integration technique is adopted [35, 36]. Solid-shell elements that employ the EAS formulation have the same disadvantage as mentioned above. In contrast, Reese [37] devised a formulation of solid-shell element based on a reduced integration technique with hourglass stabilization. In this approach, artificial numerical parameters must be included in a numerical simulation.

As a basis for the concept of solid elements, multilayered shell elements have been developed in the research field of composites and laminates. Elements based on the multilayered model are constructed by introducing independent degrees of freedom for each shell layer. Formulations have been devised by Epstein and Huttelmaier [38] and Huttelmaier and Epstein [39]. These formulations have been extended with multi-director fields by Pinsky and Kim [40], and have been applied to anisotropic laminated plates by Owen and Li [41], sandwich shells by Vu-Quoc et al. [42] and Vu-Quoc and Ebcioğlu [43], and multilayered plates by Chinosi et al. [44]. Braun et al. [45] and El-Abbasi and Meguid [46] devised multilayered shell elements by employing the concept of the seven-parameter shell element. Tan and Vu-Quoc [47] and Rah et al. [48] proposed solid-shell elements using the multilayered concepts. In the general formulation of multilayered shell elements, the number of degrees of freedom at one side in an element increases in response to the number of layers in the element. As the number of degrees of freedom of a multilayered shell element increases, the solutions are improved. However, the numerical costs increase dramatically in such situations.

In recent years, new types of shell elements have been developed for the numerical simulation of shell structures in large strain states. Kim and Bathe [49] devised an MITC4 shell element with some variables for considering thickness–stretch, for which the plane stress condition is not imposed. Sussman and Bathe [50] proposed conventional shell elements with two extensible vectors introduced at each node. These elements have the capability to model the stress distribution through the thickness flexibly. However, these formulations are more complicated than those of the shell elements developed by other researchers, because the additional degrees of freedom have special properties compared with those of other shell elements. Furthermore, there have been some approaches proposed that are specialized to sheet forming. To predict the springback of the sheet, Yoon et al. [51] presented a three dimensional hybrid membrane/shell method, and Iwata et al. [52] proposed a shell element coupled with numerical results obtained using solid elements or experimental results. In these approaches, the numerical solutions are obtained with the shell element and an additional scheme. That is, the simulation models are not solved by using the shell element only.

Our proposed shell element incorporates three features for the purpose of applying it to sheet forming simulations. One is the use of the three dimensional constitutive equation without any additional assumptions. Thus, a plane stress state in the transverse direction is not assumed in this study. The second is to exhibit no numerical instabilities in the formulation and not to include any artificial numerical parameters. Hence, neither the EAS formulation nor reduced integration technique is employed. The final feature is to avoid extreme increases in the degrees of freedom at an element, as far as possible. As a key technique of this study, additional degrees of freedom are introduced to the MITC4 shell element for the evaluation of thickness–stretch. The thickness–stretch can be discretized at each element, and hence the additional degrees of freedom are independent of each element. Thus, discontinuities of the thickness between elements are allowed in the proposed formulation. Furthermore, by virtue of this discretization of thickness–stretch, static condensation can be employed to construct the element stiffness matrix. Hence, the number of unknowns in the resulting linear system of equations is same as for conventional shell elements. Mesh generation in this approach is the same procedure as that for conventional four node shell elements. Additional work is only input of the number of additional nodes, which express the change in thickness. This task is similar to prescribe the number of layers through the thickness for conventional shell elements.

Because the proposed shell element exhibits the locking phenomena when a full integration technique is employed for numerical integration, some techniques are proposed to avoid the locking phenomena. Transverse shear strains are interpolated using the same technique as for the MITC4 shell element, in order to circumvent transverse shear locking. In addition, volumetric locking may occur for (nearly) incompressible material, because the additional degrees of freedom are displacement variations. As a basis for the selective reduced integration technique [53], we propose a technique to alleviate volumetric locking.

Some representative numerical examples are presented to verify the capabilities of the proposed shell element in elastic and elastoplastic deformation problems. We also focus on the eigenvalues of a single element, in order to gain further insight into the case of incompressibility. In small and large deformation ranges, the behavior of the proposed shell element is compared with that of solid elements.

2 Kinematics

This section describes the formulation of the proposed shell element, in terms of geometry and kinematics. After assuming a constant thickness in each element for the formulation of the conventional four-node shell element, we introduce a displacement variation in the thickness direction to evaluate the change in thickness. Considering the definition of the displacement field with thickness–stretch, a constraint condition for the displacement variation must be imposed in this formulation. An important feature in the discretized equation is illustrated by expressing the external virtual work applied in terms of the surface traction for an element. Because the equilibrium equation in the transverse direction is defined explicitly, the stiffness equation for an element can be expanded in response to the additional degrees of freedom. By virtue of the proposed formultion, static condensation can be employed to construct the element stiffness matrix.

Fig. 1
figure 1

Four-node shell element with five transverse nodes

Full size image

2.1 Kinematic description

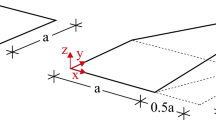
In the conventional four-node quadrilateral shell element, the geometry and kinematics are described in a Cartesian coordinate system. The element is mapped to the local coordinates \(\xi \), \(\eta \), and \(\zeta \). As shown in Fig. 1, \((\xi , \eta )\) are the in-plane coordinates corresponding to the tangential directions to the midsurface, while \(\zeta \) denotes the thickness coordinate. The position of a point inside an element in the initial configuration is described by the interpolation equation

$$\begin{aligned} \mathbf X (\xi , \eta , \zeta ) = \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf X _{a} +\sum _{a=1}^{4} Z_{a}(\zeta ) N_{a} (\xi , \eta ) \mathbf V _{a}, \end{aligned}$$
(1)

where \(\mathbf X _{a}\) and \(\mathbf V _{a}\) are the initial coordinates and director vector at the midsurface node a, respectively, and \(N_{a}\) is the shape function described in the local coordinates. The initial thickness function \(Z_{a}\) at the midsurface node a is defined in terms of the nodal thickness \(h_{a}\) and the thickness coordinate \(\zeta \) by

$$\begin{aligned} Z_{a}(\zeta ) = \zeta \frac{h_{a}}{2}. \end{aligned}$$
(2)

In this study, we assume a constant shell thickness for each element, hence discontinuities of the thickness between elements are allowed in this formulation. Thus, the initial geometry is defined by

$$\begin{aligned} \mathbf X (\xi , \eta , \zeta ) = \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf X _{a} +Z(\zeta ) \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf V _{a}, \end{aligned}$$
(3)

where the initial thickness function Z can be expressed in terms of the initial thickness of the element \(h_{e}\) and the thickness coordinate \(\zeta \) as

$$\begin{aligned} Z(\zeta ) = \zeta \frac{h_{e}}{2}. \end{aligned}$$
(4)

In the same way, the position of a point inside an element in the deformed configuration is descrived as

$$\begin{aligned} \mathbf x (\xi , \eta , \zeta ) = \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf x _{a} +z(\zeta ) \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf v _{a}, \end{aligned}$$
(5)

where \(\mathbf x _{a}\) and \(\mathbf v _{a}\) are the deformed coordinates and director vector at the midsurface node a, respectively. The deformed thickness function z in (5) is not always equal to the initial thickness function Z. A key technique of this work involves introducing a thickness variation for the evaluation of thickness–stretch. The deformed thickness function z in (5) can be expressed in terms of the initial thickness function Z and the thickness variation w as

$$\begin{aligned} z(\zeta ) = Z(\zeta ) +w(\zeta ), \end{aligned}$$
(6)

where the thickness variation is also assumed to be constant on the \(\xi -\eta \) plane in each element.

As shown in Fig. 1, additional nodes are introduced to the conventional four-node shell element. These additional nodes are designated as transverse nodes, while the midsurface nodes construct a general shell element (see Fig. 2). The thickness variation w is described by the movement of transverse nodes and evaluated at \((\xi , \eta ) = (0,0)\). The degree of freedom for each transverse node is a translation in the thickness direction, which is defined using the director vectors at the midsurface nodes and \(C^{0}\) shape functions [54] as

$$\begin{aligned} \displaystyle \mathbf v _{\mathrm{td}} = \frac{\displaystyle \sum \nolimits _{a=1}^{4} N_{a} (0,0) \mathbf v _{a}}{\displaystyle \left| \sum \nolimits _{a=1}^{4} N_{a} (0,0) \mathbf v _{a} \right| }. \end{aligned}$$
(7)

The transverse nodes are introduced to the degenerated shell element along the vector \(\mathbf v _{\mathrm{td}}\) (see Fig. 3). The thickness–stretch is simply expressed by the movement of a successive series of transverse nodes (for example, the five nodes in Fig. 3) in the thickness direction. Thus, the movement of transverse nodes is independent of that of midsurface nodes. Substituting (6) and the thickness variation along the transverse vector (7) into (5), the deformed geometry is described as

$$\begin{aligned} \mathbf x (\xi , \eta , \zeta ) =&\sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf x _{a} +Z(\zeta ) \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf v _{a} \nonumber \\&+ w(\zeta ) \mathbf v _{\mathrm{td}}. \end{aligned}$$
(8)
Fig. 2
figure 2

Degrees of freedom of midsurface nodes

Full size image
Fig. 3
figure 3

Introduction of transverse nodes

Full size image
Fig. 4
figure 4

Displacement variation of transverse nodes for layer i

Full size image

For the purpose of the discretization of displacement variations, we set M nodes in the transverse direction, and the shell element is devided into \((M-1)\) layers in thickness by transverse nodes. In the thickness coordinate \(\zeta \), \(\zeta _{i}\) and \(\zeta _{i+1}\) represent the positions of the bottom and top surfaces of the layer i, respectively, as shown in Fig. 4. At the layer i \((\zeta _{i} \le \zeta \le \zeta _{i+1})\), the thickness variation \(w(\zeta )\) is linearly interpolated using \(C^{0}\) shape functions with the translations of the transverse nodes \(w_{i}\) and \(w_{i+1}\), as

$$\begin{aligned} w(\zeta )&= \frac{\zeta _{i+1} -\zeta }{\zeta _{i+1} -\zeta _{i}} w(\zeta _{i}) +\frac{\zeta -\zeta _{i}}{\zeta _{i+1} -\zeta _{i}} w(\zeta _{i+1}) \nonumber \\&= \frac{\zeta _{i+1} -\zeta }{\zeta _{i+1} -\zeta _{i}} w_{i} +\frac{\zeta -\zeta _{i}}{\zeta _{i+1} -\zeta _{i}} w_{i+1}. \end{aligned}$$
(9)

From above definitions, the displacement of the shell element undergoing a large deformation can be expressed as

$$\begin{aligned} \mathbf u (\xi , \eta , \zeta )&= \mathbf x (\xi , \eta , \zeta ) -\mathbf X (\xi , \eta , \zeta ) \nonumber \\&= \sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf u _{a} \nonumber \\&\quad + Z(\zeta ) \sum _{a=1}^{4} N_{a} (\xi , \eta ) \left( \mathbf v _{a} -\mathbf V _{a} \right) \nonumber \\&\quad + w(\zeta ) \mathbf v _{\mathrm{td}}, \end{aligned}$$
(10)

where \(\mathbf u _{a} = \mathbf x _{a} -\mathbf X _{a}\) denotes the nodal displacements at the midsurface node a. The first and second terms on the top right hand side of (10) correspond to the formulation of the degenerated shell elements, whose shell thickness is constant and defined at each element. Thus, these terms are described using the degrees of freedom for midsurface nodes. On the other hand, the third term on the top right hand side of (10) describes the thickness–stretch, using the degrees of freedom for transverse nodes. From the displacement field (10), the proposed shell element has a multiple layers in an element. As a similar manner to express the displacement field, multilayered shell elements have been developed. In the multilayered shell elements [15, 16, 55,56,57], additional degrees of freedom for expressing thickness–stretch are introduced along the director vectors at midsurface nodes. Thus, the number of degrees of freedom of multilayered shell elements increases four times in an element depending on the number of layers. On the other hand, additional degrees of freedom are translations along the thickness direction (7) for transverse nodes in the proposed approach.

2.2 Constraint condition on the transverse displacement variation

Because additional displacement variations are defined with transverse nodes independently of the displacement field on the midsurface, the constraint condition must be imposed on transverse nodes. Even if a Dirichlet boundary condition is applied to midsurface nodes, displacement variations with transverse nodes are not determined uniquely. Thus, the proposed approach results in a lack of uniqueness in the discrete problem. Therefore, a constraint condition must be introduced to the transverse displacement variation.

The constraint condition for transverse nodes is derived from the definition of the displacement field (10) in the proposed formulation. The geometry, other than for the thickness–stretch, is represented with midsurface nodes, while the thickness–stretch is described with transverse nodes. The displacement in the thickness direction for midsurface nodes \(\bar{U}_{\mathrm{td}}\) is obtained from the inner product of the first and second terms on the top right hand side of (10) and the transverse vector (7) as

$$\begin{aligned} \bar{U}_{\mathrm{td}} =&\sum _{a=1}^{4} N_{a} (\xi , \eta ) \mathbf u _{a} \cdot \mathbf v _{\mathrm{td}} \nonumber \\&+Z(\zeta ) \sum _{a=1}^{4} N_{a} (\xi , \eta ) \left( \mathbf v _{a} -\mathbf V _{a} \right) \cdot \mathbf v _{\mathrm{td}}. \end{aligned}$$
(11)

Similarly, the displacement in the thickness direction for transverse nodes \(\hat{u}_{\mathrm{td}}\) is expressed by the inner product of the third term on the top right hand side of (10) and the transverse vector (7) as

$$\begin{aligned} \hat{u}_{\mathrm{td}}&= w(\zeta ) \mathbf v _{\mathrm{td}} \cdot \mathbf v _{\mathrm{td}} \nonumber \\&= w(\zeta ). \end{aligned}$$
(12)

Thus, the total amount of displacement in the thickness direction is given by the inner product of displacement vector (10) and the transverse vector (7) as

$$\begin{aligned} u_{\mathrm{td}}&= \mathbf u \cdot \mathbf v _{\mathrm{td}} \nonumber \\&= \bar{U}_{\mathrm{td}} +\hat{u}_{\mathrm{td}}. \end{aligned}$$
(13)

Here, \(\hat{u}_{\mathrm{td}}\) is the displacement variation in terms of transverse nodes in (12), and hence \(\hat{u}_{\mathrm{td}}\) can be defined by the variation of \(u_{\mathrm{td}}\). In (13), \(u_{\mathrm{td}}\) may be regarded as the sum of the average and the variation. Thus, \(\bar{U}_{\mathrm{td}}\) can be recognized as the average of \(u_{\mathrm{td}}\). The average displacement \(\bar{U}_{\mathrm{td}}\) is also described in terms of the total amount of displacement \(u_{\mathrm{td}}\), as

$$\begin{aligned} \bar{U}_{\mathrm{td}}&= \frac{1}{h_{e}} \int _{-\frac{h_{e}}{2}}^{\frac{h_{e}}{2}} u_{\mathrm{td}} dz \nonumber \\&= \frac{1}{h_{e}} \int _{-\frac{h_{e}}{2}}^{\frac{h_{e}}{2}} \left( \bar{U}_{\mathrm{td}} +\hat{u}_{\mathrm{td}} \right) dz \nonumber \\&= \bar{U}_{\mathrm{td}} +\frac{1}{h_{e}} \int _{-\frac{h_{e}}{2}}^{\frac{h_{e}}{2}} \hat{u}_{\mathrm{td}} dz. \end{aligned}$$
(14)

From (12) and (14), the constraint condition for the transverse displacement variation is obtained as

$$\begin{aligned} \int _{-\frac{h_{e}}{2}}^{\frac{h_{e}}{2}} \hat{u}_{\mathrm{td}} dz = 0, \end{aligned}$$
(15)

which can be applied to transverse nodes as the constraint condition.

The constraint condition for transverse nodes is introduced to the node that has no involvement in the Neumann boundary condition. In sheet forming, a blank captures the surface traction at a top or a bottom surface, or both. In a numerical simulation of this situation, an external force (e.g. distributed load, pressure, or contact force) is applied to the surfaces of the element as a Neumann boundary condition. Thus, a Dirichlet boundary condition (15) should be imposed on the transverse node that is initially placed on the midsurface, because its position is separated from the surfaces where the external force is applied. As a result, a transverse node must be placed on the midsurface in the initial configuration. Therefore, the number of transverse nodes must be odd in order to impose the constraint condition (15).

The constraint condition (15) is described by translations of transverse nodes. Thus, the movement of the transverse node that is initially placed on the midsurface can be expressed using translations of other transverse node. Hence, the rigid body motion of each transverse node is prevented.

2.3 Strain field

In a total Lagrangian framework, the covariant components of the Green–Lagrange strain can be written as

$$\begin{aligned} \tilde{E}_{ij} = \frac{1}{2} \left( \mathbf g _{i} \cdot \mathbf g _{j} -\mathbf G _{i} \cdot \mathbf G _{j} \right) , \end{aligned}$$
(16)

where \(\mathbf g _{i}\) and \(\mathbf G _{i}\) are the respective covariant base vectors associated with local coordinates \((\xi , \eta , \zeta )\) defined by

$$\begin{aligned} \mathbf G _{i} = \frac{\partial \mathbf X }{\partial r_{i}},\quad \mathbf g _{i} = \frac{\partial \mathbf x }{\partial r_{i}} = \mathbf G _{i} +\frac{\partial \mathbf u }{\partial r_{i}}\quad \mathrm{for}\ { i} =1,2,3, \end{aligned}$$
(17)

with \(r_{1} = \xi \), \(r_{2} = \eta \), and \(r_{3} = \zeta \).

2.4 Discretized equation

From the principle of virtual work, the linearized incremental variational formulation at time \(t +{\varDelta }t\) in the element e is shown to be

$$\begin{aligned}&\int _{{}^{0} {{\Omega }}_{{ e}}} {}^{t} \tilde{C}^{ijkl} {\varDelta }\tilde{e}^{\mathrm{l}}_{kl} \delta \left( {\varDelta }\tilde{e}^{\mathrm{l}}_{ij} \right) \ d{\varOmega }\nonumber \\&\qquad + \int _{{}^{0} {{\Omega }}_{{ e}}} {}^{t} \tilde{S}^{ij} \delta \left( {\varDelta }\tilde{\eta }^{\mathrm{l}}_{ij} \right) \ d{\varOmega }\nonumber \\&\qquad + \int _{{}^{0} {{\Omega }}_{e}} {}^{t} \tilde{S}^{ij} \delta \left( {\varDelta }\tilde{e}^{\mathrm{q}}_{ij} \right) \ d{\varOmega }\nonumber \\&\quad = {}^{t+{\varDelta }t}\delta W^{\mathrm{ext}}_{e} -\int _{{}^{0} {{\Omega }}_{{ e}}} {}^{t} \tilde{S}^{ij} \delta \left( {\varDelta }\tilde{e}^{\mathrm{l}}_{ij} \right) \ d{\varOmega }, \end{aligned}$$
(18)

where \({}^{t} \tilde{C}^{ijkl}\) is the tangent moduli tensor at time t, \({}^{t} \tilde{S}^{ij}\) are the contravariant components of the second Piola–Kirchhoff stress tensor at time t, \({\varDelta }\tilde{e}_{ij}\) and \({\varDelta }\tilde{\eta }_{ij}\) are the increments in the linear and nonlinear components of the covariant components for the Green–Lagrange strain tensor, respectively, and \(W^{\mathrm{ext}}\) is the external work. Here, the superscripts \(\mathrm{l}\) and \(\mathrm{q}\) denote linear and quadratic displacement terms, respectively, and the subscript e indicates quantities evaluated in the element e. Appendices “Principle of virtual work” and “Variational formulation” provide the details regarding the derivation of (18). Within the proposed formulation of the displacement field (10), the virtual displacement vector in the element e is defined by

$$\begin{aligned} \delta \mathbf u _{e} = \delta \mathbf u _{\mathrm{m}} +\delta \mathbf u _{\mathrm{t}}, \end{aligned}$$
(19)

where \(\delta \mathbf u _{\mathrm{m}}\) and \(\delta \mathbf u _{\mathrm{t}}\) are the virtual displacement vectors expressed with midsurface nodes and transverse nodes in the element e, respectively. Thus, the strain tensors in (18) are described as follows:

$$\begin{aligned}&\left. {\varDelta }\tilde{e}^{\mathrm{l}}_{ij} \right| _{{{\Omega }}_{e}} = {}^{t} \mathbf B ^{\mathrm{l}}_{\mathrm{m}} {\varDelta }\mathbf u _{\mathrm{m}} + {}^{t} \mathbf B ^{\mathrm{l}}_{\mathrm{t}} {\varDelta }\mathbf u _{\mathrm{t}}, \end{aligned}$$
(20)
$$\begin{aligned}&\left. \delta \left( {\varDelta }\tilde{e}^{\mathrm{l}}_{ij} \right) \right| _{{{\Omega }}_{e}} = {}^{t} \mathbf B ^{\mathrm{l}}_{\mathrm{m}} \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) + {}^{t} \mathbf B ^{\mathrm{l}}_{\mathrm{t}} \delta \left( {\varDelta }\mathbf u _{\mathrm{t}} \right) , \end{aligned}$$
(21)
$$\begin{aligned}&\left. \delta \left( {\varDelta }\tilde{e}^{\mathrm{q}}_{ij} \right) \right| _{{{\Omega }}_{e}} = \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) \right\} ^{\mathrm{t}}\ {}^{t} \mathbf L _{\mathrm{m}}\ {\varDelta }\mathbf u _{\mathrm{m}}, \end{aligned}$$
(22)
$$\begin{aligned}&\left. \delta \left( {\varDelta }\tilde{\eta }^{\mathrm{l}}_{ij} \right) \right| _{{{\Omega }}_{e}} = \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) \right\} ^{\mathrm{t}}\ {}^{t} \mathbf L ^{\mathrm{n}}_{\mathrm{mm}}\ {\varDelta }\mathbf u _{\mathrm{m}} \nonumber \\&\quad \quad + \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{t}} \right) \right\} ^{\mathrm{t}}\ {}^{t} \mathbf L ^{\mathrm{n}}_{\mathrm{tm}}\ {\varDelta }\mathbf u _{\mathrm{m}} \nonumber \\&\quad \quad + \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) \right\} ^{\mathrm{t}}\ {}^{t} \mathbf L ^{\mathrm{n}}_{\mathrm{mt}}\ {\varDelta }\mathbf u _{\mathrm{t}} \nonumber \\&\quad \quad + \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{t}} \right) \right\} ^{\mathrm{t}}\ {}^{t} \mathbf L ^{\mathrm{n}}_{\mathrm{tt}}\ {\varDelta }\mathbf u _{\mathrm{t}}. \end{aligned}$$
(23)

Appendix “Discretization of variational formulation” can be referred to for the details regarding the derivation of (20), (21), (22), and (23).

The proposed approach is capable of assessing the surface traction at the surface where the traction is subjected. For example, the surface traction \(\mathbf f ^{\mathrm{top}}_{e}\) is applied at the top surface of the element e. In this situation, the external virtual work can be expressed by using the virtual displacement \(\delta \mathbf u ^{\mathrm{top}}_{e}\) at the top surface and the top surface area \(A^{\mathrm{top}}_{e}\) of the element e as

$$\begin{aligned} {}^{t+{\varDelta }t} \delta W^{\mathrm{ext}}_{e} = \int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \delta \left( {\varDelta }\mathbf u ^{\mathrm{top}}_{e} \right) \ dA. \end{aligned}$$
(24)

From (19), the virtual displacement \(\delta \left( {\varDelta }\mathbf u ^{\mathrm{top}}_{e} \right) \) at the top surface is defined using the virtual displacements \(\delta \left( {\varDelta }\mathbf u _{a} \right) \) of the midsurface node a, \(\delta \left( {\varDelta }w \right) |_{\zeta =1}\) of the transverse node initially placed on the top surface, and the transverse vector \(\mathbf v _{\mathrm{td}}\) of the element e, as

$$\begin{aligned} \delta \left( {\varDelta }\mathbf u ^{\mathrm{top}}_{e} \right)&= \left. \delta \left( {\varDelta }\mathbf u _{e} \right) \right| _{\zeta = 1} \nonumber \\&= \left. \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) +\delta \left( {\varDelta }\mathbf u _{\mathrm{t}} \right) \right\} \right| _{\zeta = 1} \nonumber \\&= \sum _{a=1}^{4} N_{a} (\xi , \eta ) \delta \left( {\varDelta }\mathbf u _{a} \right) + \left. \delta \left( {\varDelta }w \right) \right| _{\zeta =1} \ \mathbf v _{\mathrm{td}}. \end{aligned}$$
(25)

By substituting (25) into (24), the external virtual work is given by

$$\begin{aligned} {}^{t+{\varDelta }t} \delta W^{\mathrm{ext}}_{e}&= \int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \left. \left\{ \delta \left( {\varDelta }\mathbf u _{\mathrm{m}} \right) + \delta \left( {\varDelta }\mathbf u _{\mathrm{t}} \right) \right\} \right| _{\zeta = 1}\ dA \nonumber \\&= \int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \left\{ \sum _{a=1}^{4} N_{a} (\xi , \eta ) \delta \left( {\varDelta }\mathbf u _{a} \right) \right\} \ dA \nonumber \\&\quad +\int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \left\{ \left. \delta \left( {\varDelta }w \right) \right| _{\zeta =1} \ \mathbf v _{\mathrm{td}} \right\} \ dA. \end{aligned}$$
(26)

In this study, the displacement variation of transverse nodes is described as the translation along the transverse vector \(\mathbf v _{\mathrm{td}}\), as denoted in (7). The thickness–stretch in an element is homogeneous in the in-plane directions. Thus, the second term on the top right hand side of (26) can be rewritten as

$$\begin{aligned}&\int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \left\{ \left. \delta \left( {\varDelta }w \right) \right| _{\zeta =1} \ \mathbf v _{\mathrm{td}} \right\} \ dA \nonumber \\&\quad = \left. \delta \left( {\varDelta }w \right) \right| _{\zeta =1} \int _{A^{\mathrm{top}}_{e}} {}^{t+{\varDelta }t} \mathbf f ^{\mathrm{top}}_{e} \cdot \mathbf v _{\mathrm{td}}\ dA \nonumber \\&\quad = {}^{t+{\varDelta }t} f_{\mathrm{td}}\ A^{\mathrm{top}}_{e} \left. \delta \left( {\varDelta }w \right) \right| _{\zeta =1}, \end{aligned}$$
(27)

where \(f_{\mathrm{td}}\) is the component along the transverse vector \(\mathbf v _{\mathrm{td}}\) of the surface traction \(\mathbf f ^{\mathrm{top}}_{e}\). From (26) and (27), the surface traction is applied to both midsurface nodes and transverse nodes.

The discretized equation can be described as

$$\begin{aligned} \left[ \begin{array}{cc} \mathbf k _{\mathrm{mm}} &{} \mathbf k _{\mathrm{mt}} \\ \mathbf k _{\mathrm{tm}} &{} \mathbf k _{\mathrm{tt}} \end{array} \right] \left\{ \begin{array}{c} \mathbf u _{\mathrm{m}} \\ \mathbf u _{\mathrm{t}} \end{array} \right\} = \left\{ \begin{array}{c} \mathbf r _{\mathrm{m}} \\ \mathbf r _{\mathrm{t}} \end{array} \right\} . \end{aligned}$$
(28)

Appendix “Element stiffness equation” can be referred to for the details regarding the derivation of (28). Within the proposed approach, the additional degrees of freedom describing the displacement variations of transverse nodes are independent of each element. In constructing the element stiffness matrix, static condensation [58] is applied to (28). Thus, the element stiffness equation is obtained as follows:

$$\begin{aligned} \mathbf k \mathbf u _{\mathrm{m}} = \mathbf f , \end{aligned}$$
(29)

where

$$\begin{aligned} \mathbf k= & {} \mathbf k _{\mathrm{mm}} -\mathbf k _{\mathrm{mt}} \mathbf k _{\mathrm{tt}}^{-1} \mathbf k _{\mathrm{tm}}, \end{aligned}$$
(30)
$$\begin{aligned} \mathbf f= & {} \mathbf r _{\mathrm{m}} -\mathbf k _{\mathrm{mt}} \mathbf k _{\mathrm{tt}}^{-1} \mathbf r _{\mathrm{t}}, \end{aligned}$$
(31)

which is further processed by the conventional assembly procedure. It should be noted that the element stiffness Eq. (29) takes a similar form to that of conventional shell elements. Thus, the number of unknowns in the resulting linear system of equations is same as that of conventional shell elements.

3 Techniques for avoiding locking phenomena

This section describes some techniques for avoiding the locking phenomena exhibited by the proposed shell element when a full integration technique is employed in numerical integration. In addition to transverse shear locking, the proposed shell element results in thickness locking and volumetric locking when a plane stress state in the transverse direction is not assumed. Transverse shear locking can be alleviated using the same technique as for the MITC4 shell element [7]. To circumvent thickness locking, we improve the distribution of the transverse normal strain through the thickness. Further, volumetric locking can be avoided by employing a selective reduced integration technique [53].

3.1 Mixed interpolation of strain field

The degenerated shell element exhibits a transverse shear locking phenomenon. In order to avoid this locking for the degenerated shell element, Dvorkin and Bathe [7] developed the MITC4 shell element. In the MITC4 shell element, transverse shear strains are assumed by interpolating the covariant components of transverse shear strains evaluated at the sampling points shown in Fig. 5 as follows:

$$\begin{aligned} \begin{array}{l} \displaystyle \tilde{E}_{13} = \frac{1}{2} (1+\eta ) \tilde{E}_{13} |_{\xi =0,\ \eta =1,\ \zeta =0} \\ \displaystyle \quad +\,\,\frac{1}{2} (1-\eta ) \tilde{E}_{13} |_{\xi =0,\ \eta =-1,\ \zeta =0}, \\ \displaystyle \tilde{E}_{23} = \frac{1}{2} (1+\xi ) \tilde{E}_{23} |_{\xi =1,\ \eta =0,\ \zeta =0} \\ \displaystyle \quad +\,\,\frac{1}{2} (1-\xi ) \tilde{E}_{23} |_{\xi =-1,\ \eta =0,\ \zeta =0}. \end{array} \end{aligned}$$
(32)

The proposed shell element exhibits a transverse shear locking phenomenon because the geometric and kinematic descriptions involving the midsurface nodes are expressed in a similar manner to the degenerated shell elements. Thus, transverse shear locking can be avoided by using the interpolations in (32). In this study, we assume that the degrees of freedom for additional nodes are constant on the \(\xi -\eta \) plane in each element. Thus, the additional degrees of freedom do not affect to transverse shear strains (32). It should be noted that the proposed shell element is suitable for bending analyses of thin structures, even for large bending strains.

Fig. 5
figure 5

Sampling points for transverse shear strains

Full size image

3.2 Interpolation to alleviate thickness locking

Thickness locking may occur when the displacement in the thickness direction is interpolated by a linear function [15, 16]. Specifically, this locking results from the assumption of a constant strain in the thickness direction. Concerning bending deformation, the transverse normal strain varies linearly through the thickness, owing to the coupling between the linear in-plane strains and the normal stress in the thickness direction if Poisson’s ratio is not equal to zero. In the proposed formulation, the displacement variations are interpolated using the nodal values of transverse nodes that are placed on the top and bottom surfaces in each layer, see (9), and hence the transverse normal strain is constant at each layer. Thus, the proposed shell element exhibits thickness locking.

This thickness locking can be avoided by introducing multiple layers through the thickness in the proposed formulation. From the constraint condition (15) for transverse nodes, a transverse node must be placed on the midsurface in the initial configuration. Therefore, the proposed shell element has multiple layers in an element, and the distribution of the transverse normal strain is expressed in terms of the value at each layer. Considering these properties, thickness locking can be alleviated by introducing more than three transverse nodes (the minimum number of transverse nodes for imposing the constraint condition).

3.3 Extension to nearly incompressible media

For nearly incompressible material, such as metal plasticity, standard displacement-based elements often suffer from a so-called volumetric locking phenomenon. In general, a degenerated shell element does not exhibit volumetric locking, because of the plane stress assumption. However, volumetric locking occurs in the proposed shell element, in which the three dimensional constitutive equation is employed without assuming the plane stress condition.

This volumetric locking can be alleviated by employing the techniques developed for solid elements when the displacement interpolation of the element is similar to that of solid elements [31, 36]. However, the displacement interpolation of the proposed shell element is expressed in a similar manner to the degenerated shell element, see Fig. 1. Thus, a new technique for avoiding volumetric locking must be developed in this study.

A selective reduced integration (SRI) technique is applied to the volumetric part to avoid the volumetric locking phenomenon [53]. In trilinear hexahedral elements that incorporate the SRI technique to alleviate volumetric locking, isochoric strain is evaluated at \(2 \times 2 \times 2\) Gauss integration (full integration) points, while volumetric strain is assessed at the center of an element.

Let \(\mathbf F \) be the deformation gradient, and let \(J \equiv \mathrm{det}\ \mathbf F \) be the Jacobian of the deformation gradient. Then, the basic kinematic split of the deformation gradient [59] into volumetric and isochoric parts, which was proposed by Simo et al. [60], may be formulated as

$$\begin{aligned} \mathbf F = \mathbf F _{\mathrm{vol}} \mathbf F _{\mathrm{iso}}, \end{aligned}$$
(33)

where the volumetric part \(\mathbf F _{\mathrm{vol}}\) can be written as

$$\begin{aligned}&{} \mathbf F _{\mathrm{vol}} = J^{\frac{1}{3}} \mathbf I , \end{aligned}$$
(34)
$$\begin{aligned}&\mathrm{det}\ \mathbf F _{\mathrm{vol}} = { J}, \end{aligned}$$
(35)

and the isochoric part \(\mathbf F _{\mathrm{iso}}\) can be represented as

$$\begin{aligned}&{} \mathbf F _{\mathrm{iso}} = J^{-\frac{1}{3}} \mathbf F , \end{aligned}$$
(36)
$$\begin{aligned}&\mathrm{det}\ \mathbf F _{\mathrm{iso}} = 1. \end{aligned}$$
(37)

If the deformation gradient \(\mathbf F \) is evaluated at Gauss integration points, volumetric locking occurs in the proposed shell element. Therefore, the volumetric part of the deformation gradient is evaluated at the center of a layer, see Fig. 6.

Fig. 6
figure 6

Evaluation point shown on proposed shell element at each layer for avoiding volumetric locking

Full size image

Volumetric locking can be avoided by evaluating the volumetric strain at each layer in the proposed shell element. Layer coordinates are introduced and denoted by \(\xi _{l}\), \(\eta _{l}\), and \(\zeta _{l}\) in each layer, as shown in Fig. 6. The evaluation point for the volumetric part of the deformation gradient is defined at \((\xi _{l}, \eta _{l}, \zeta _{l}) = (0,0,0)\). Let \({\bar{\mathbf{F }}}^{(i)}_{\mathrm{vol}}\), which is computed at \((\xi _{l}, \eta _{l}, \zeta _{l}) = (0,0,0)\) in layer i, be replaced as the volumetric part of the deformation gradient by \(\mathbf F _{\mathrm{vol}}\) in (33). Thus, the modified deformation gradient \({\bar{\mathbf{F }}}^{(i)}\) can be defined by

$$\begin{aligned} {\bar{\mathbf{F }}}^{(i)} = {\bar{\mathbf{F }}}^{(i)}_{\mathrm{vol}} \mathbf F ^{(i)}_{\mathrm{iso}}, \end{aligned}$$
(38)

where \(\mathbf F ^{(i)}_{\mathrm{iso}}\) is the isochoric part of the deformation gradient, which is assessed at the Gauss integration points in layer i. Associated with the deformation gradient \({\bar{\mathbf{F }}}^{(i)}\), the corresponding right Cauchy-Green tensor is described by

$$\begin{aligned} {\bar{\mathbf{C }}}^{(i)} = \left( {\bar{\mathbf{F }}}^{(i)} \right) ^{\mathrm{t}} {\bar{\mathbf{F }}}^{(i)}, \end{aligned}$$
(39)

in which the superscript \(\mathrm{t}\) denotes the transpose.

4 Constitutive equation

In this section, a hyperelastic–plastic constitutive equation, which is developed by Simo and Ortiz [61], Moran et al. [62], and Betsch and Stein [63], is summarized briefly. Within the proposed formulation, the three dimensional constitutive law is employed without any modification.

The major application supposed in this work is sheet forming, in which blank materials are metals such as steel modelled as elastoplasticity. Due to the property of metals, the elastic strain is expected to be small. Thus, the St. Venant–Kirchhoff material is adopted for elastic response.

4.1 Hyperelastic response model

It is necessary to express the elastic stress–strain relationship in the convected coordinates. For a hyperelastic material, the appropriate constitutive relations are given by

$$\begin{aligned} \tilde{\mathbf{S }} = \tilde{\mathbf{C }} \tilde{\mathbf{E }}, \end{aligned}$$
(40)

where \(\tilde{\mathrm{C}}\) is the fourth-order contravariant tangent moduli tensor in the convected coordinates and can be expressed as

$$\begin{aligned} \tilde{\mathbf{C }} = \tilde{C}^{ijkl} \mathbf G _{i} \otimes \mathbf G _{j} \otimes \mathbf G _{k} \otimes \mathbf G _{l}. \end{aligned}$$
(41)

For the isotropic St. Venant–Kirchhoff material, the contravariant components \(\tilde{C}^{ijkl}\) is written as

$$\begin{aligned} \tilde{C}^{ijkl} = \lambda G^{ij} G^{kl} +\mu \left( G^{ik} G^{jl} +G^{il} G^{jk} \right) , \end{aligned}$$
(42)

where

$$\begin{aligned} G^{ij} = \mathbf G ^{i} \cdot \mathbf G ^{j}, \end{aligned}$$
(43)

and \(\lambda \) and \(\mu \) are Lamé’s constants. The second Piola–Kirchhoff stress and Green–Lagrange strain tensors can be described as

$$\begin{aligned} \tilde{\mathbf{S }}= & {} \tilde{S}^{ij} \mathbf G _{i} \otimes \mathbf G _{j}, \end{aligned}$$
(44)
$$\begin{aligned} \tilde{\mathbf{E }}= & {} \tilde{E}_{ij} \mathbf G ^{i} \otimes \mathbf G ^{j}, \end{aligned}$$
(45)

where \(\tilde{S}^{ij}\) is the contravariant components of the second Piola–Kirchhoff stress tensor and \(\tilde{E}_{ij}\) denotes the covariant components of the Green–Lagrange strain tensor. Since the three dimensional constitutive law is used without modification, the constitutive Eq. (40) can be directly substituted to other hyperelastic constitutive laws.

4.2 Modeling of plastic response

In the finite deformation range, the deformation gradient tensor \(\mathbf F \) is expressed by using the elastic part \(\mathbf F ^{e}\) and the plastic part \(\mathbf F ^{p}\) as

$$\begin{aligned} \mathbf F = \mathbf F ^{e} \mathbf F ^{p}, \end{aligned}$$
(46)

where the plastic part \(\mathbf F ^{p}\) denotes the transformation matrix from the initial configuration to the virtual intermediate stress free configuration, which is obtained by unloading elastic deformation from the current configuration [64].

In the virtual intermediate stress free configuration, the plastic Green–Lagrange strain tensor \(\tilde{\mathbf{E }}^{p}\) in a covariant formulation is defined by using the plastic right Cauchy-Green tensor \(\mathbf C ^{p}\) and the covariant metric tensor \({\mathbf{G }}\) as

$$\begin{aligned} \tilde{\mathbf{E }}^{p} = \frac{1}{2} \left( \mathbf C ^{p} -\mathbf G \right) , \end{aligned}$$
(47)

where

$$\begin{aligned} \mathbf C ^{p} = \left( \mathbf F ^{p} \right) ^{\mathrm{t}} \mathbf F ^{p}. \end{aligned}$$
(48)

Thus, the elastic Green–Lagrange strain tensor \(\tilde{\mathbf{E }}^{e}\) in a covariant formulation is obtained by

$$\begin{aligned} \tilde{\mathbf{E }}^{e} = \tilde{\mathbf{E }} -\tilde{\mathbf{E }}^{p}. \end{aligned}$$
(49)

For a plasticity model, the von Mises yield criterion with isotropic hardening is employed. The von Mises yield function is defined by

$$\begin{aligned} {\varPhi }(\tilde{\mathbf{S }}, \mathbf C , \sigma _{y} ) = \frac{1}{2} \left( \tilde{S}'^{ij} \tilde{S}'^{kl} C_{ik} C_{jl} \right) -\sigma _{y}^{2} = 0, \end{aligned}$$
(50)

where the deviatoric part \(\tilde{\mathbf{S }}'\) of the stress tensor \(\tilde{\mathbf{S }}\) is expressed as

$$\begin{aligned} \tilde{\mathbf{S }}'&= \tilde{S}'^{ij} \mathbf G _{i} \otimes \mathbf G _{j} \nonumber \\&= \left\{ \tilde{S}^{ij} -\frac{1}{3} ( \tilde{S}^{kl} C_{kl} ) (C^{-1})^{ij} \right\} \mathbf G _{i} \otimes \mathbf G _{j}, \end{aligned}$$
(51)

and \(\sigma _{y}\) is the yield stress in shear [65]. Further, \({\mathbf{C }}\) and \({\mathbf{C }}^{-1}\) are the covariant and contravariant components of the right Cauchy-Green tensors, respectively, as follows:

$$\begin{aligned}&{} \mathbf C = \mathbf F ^{\mathrm{t}} \mathbf F , \end{aligned}$$
(52)
$$\begin{aligned}&{} \mathbf C ^{-1} = \left( \mathbf F ^{\mathrm{t}} \mathbf F \right) ^{-1}, \end{aligned}$$
(53)

which are identified with the metric tensors of the current configuration in the material descriptions. Note that \(\sigma _{y}\) is a function of stress history. The hardening law is described as

$$\begin{aligned} \dot{\sigma _{y}} = h \dot{\bar{\gamma }}, \end{aligned}$$
(54)

where \(h=h (\bar{\gamma })\) is the hardening modulus and \(\bar{\gamma }\) is the equivalent plastic strain. In this study, for the purpose of calculating the equivalent plastic strain rate \(\dot{\bar{\gamma }}\), the flow rule associated with the von Mises yield criterion is used. In the incremental procedure, \(\mathbf E ^{p}\) may be calculated through the elastic predictor-return mapping scheme proposed by Simo and Ortiz [61].

5 Numerical examples

Several numerical examples are chosen to verify the capabilities of the proposed shell element in elastic and elastoplastic deformation problems. Its performance is demonstrated in small and large deformation ranges by comparing the behavior of the proposed shell element with that of solid elements and/or the MITC4 shell element. In the visualization of calculation results, we plot shell elements as if they were solid elements.

5.1 Investigation of eigenvalues

For the purpose of examining the element behavior concerning zero energy modes and possible locking tendencies, the eigenvalues of a single element are computed using the proposed shell element (with a selective reduced integration (SRI) technique and with a full integration (FI) technique) and the MITC4 shell element. The element shape is typical for an element contained in a regular mesh of a square plate (see Fig. 7) with thickness to length ratios of \(h/l = 1/50\) and 1.

The eigenvalues of these models are computed using Poisson’s ratios \(\nu = 0\), 0.3, and 0.499, and are displayed in Tables 1 and 2. These results show that the proposed shell element includes no spurious zero energy mode. In addition, the more important conclusion is that the proposed shell element with the SRI technique does not show a serious tendency to lock, even if Poisson’s ratio becomes close to 0.5. On the other hand, it is obvious that the proposed shell element with the FI technique exhibits a volumetric locking phenomenon for nearly incompressible material.

5.2 In-plane tensile deformation

The most simple model incorporating in-plane tensile deformation is computed to evaluate thickness–stretch. A numerical investigation is conducted to verify the element behavior of the proposed shell element concerning the three dimensional effects for the in-plane tensile deformation, as shown in Fig. 8. This model is studied using a single mesh and a hyperelastic material, such as the St. Venant–Kirchhoff model. The material has Young’s modulus \(E=100\ \mathrm{[N/mm^{2}]}\) and Poisson’s ratio \(\nu =0.3\).

Fig. 7
figure 7

Geometry and material data for the eigenvalue analysis

Full size image
Table 1 Eigenvalues of a thin square plate; \(h / l = 1 / 50\)
Full size table
Table 2 Eigenvalues of a thick square plate; \(h / l = 1\)
Full size table
Fig. 8
figure 8

Geometry of initial and deformed configuration of in-plane tensile deformation

Full size image
Fig. 9
figure 9

Movement of the top surface with in-plane deformation in elastic case

Full size image

Figure 9 illustrates the position of the top surface corresponding to the displacement in the x direction of the free edge. The proposed shell element is capable of evaluating the thickness–stretch with the in-plane deformation due to the effect of Poisson’s ratio, similarly to the hexahedral solid element. It is also obvious that its behavior is based on the three dimensional constitutive equation.

5.3 Transverse compressive deformation

Now, we examine a model that is compressed in the transverse direction for a single element, as shown in Fig. 10. This simple model is the most attractive example for comparing the behavior of the proposed shell element with that of conventional shell elements. It is not possible to compute this situation using the conventional shell elements, because the traction is cancelled out on account of the evaluation of the traction at the midsurface. In contrast, the proposed shell element is capable of capturing the surface traction at the surface where the traction is imposed. Thus, a numerical solution can be obtained for this model using the proposed shell element, similarly to solid elements. The behavior of the material follows the St. Venant–Kirchhoff material model, and it has Young’s modulus \(E=100\ \mathrm{[N/mm^{2}]}\) and Poisson’s ratio \(\nu = 0.499\).

The position of the top surface corresponding to the surface traction is depicted in Fig. 11, and the load displacement diagram at the free edge is illustrated in Fig. 12. These results show that the proposed shell element has the property that it can capture the surface traction in this situation and evaluate the thickness–stretch and in-plane deformation due to the effect of Poisson’s ratio.

Fig. 10
figure 10

Geometry of initial and deformed configuration of transverse compressive deformation

Full size image
Fig. 11
figure 11

Movement of the top surface with traction in transverse compressive deformation

Full size image
Fig. 12
figure 12

Load displacement diagram at the free edge in transverse compressive deformation

Full size image
Fig. 13
figure 13

Geometry and material data of a square plate with pure bending

Full size image
Fig. 14
figure 14

Relative error for Poisson’s ratio \(\nu =0.3\) in pure bending

Full size image

5.4 Pure bending in a small deformation

Now, the situation of a square plate that is subjected to a bending moment is investigated, as shown in Fig. 13. The geometry and material data for the numerical simulation are also described in Fig. 13, and this model is discretized with a single element. We compare the angles of bending and warpage between the initial configuration and the deformed configuration (see Fig. 13) obtained using the proposed shell element with analytical solutions.

Figures 14 and 15 show that the differences between numerical solutions and analytical solutions become larger as the number of transverse nodes becomes smaller. In the case of Poisson’s ratio \(\nu =0.499\), the proposed shell element with the FI technique exhibits severe locking phenomena, mainly in the form of the volumetric locking phenomenon. These tendencies can be explained by the transverse normal strain distribution through the thickness, as shown in Figs. 16 and 17. Within the proposed approach, the translations of transverse nodes are interpolated linearly, and hence thickness locking occurs because the transverse normal strain is constant at each layer. Figures 16 and 17 illustrate that the SRI technique (see Sect. 3.3) also has the property of alleviating thickness locking.

Fig. 15
figure 15

Relative error for Poisson’s ratio \(\nu =0.499\) in pure bending

Full size image
Fig. 16
figure 16

Transverse normal strain distributions for Poisson’s ratio \(\nu =0.3\) in pure bending (eleven transverse nodes)

Full size image
Fig. 17
figure 17

Transverse normal strain distributions for Poisson’s ratio \(\nu =0.499\) in pure bending (eleven transverse nodes)

Full size image
Fig. 18
figure 18

Patch test mesh

Full size image

5.5 Patch tests

Here, patch tests are examined using a mesh, as illustrated in Fig. 18. The models above that are investigated in Sects. 5.2, 5.3, and 5.4 are simulated using this mesh, and the same results are obtained as those calculated with a single element. In addition, if the loading condition of the in-plane shear is imposed, the same results are computed with both this mesh and a single element. Thus, it should be noted that the proposed shell element passes the patch tests.

5.6 Cantilever beam with line load

Next, a cantilever beam subjected to a line load is examined to verify the performance of the proposed shell element in a large deformation range. The geometry, material data, and boundary conditions are given in Fig. 19. This model is discretized with \(10 \times 1\) elements.

The numerical results obtained with the proposed shell element (with the SRI technique) are compared with those calculated using the MITC4 shell element, which does not exhibit any locking phenomenon. The load displacement diagrams with ten equal load steps are presented in Figs. 20, 21 and 22. A comparison of the tip deflection in the deformed configuration is illustrated in Fig. 23. The effectiveness of the SRI technique for nearly incompressible material is proved in Sects. 5.1 and 5.4. In this example, the good agreement demonstrated between both elements indicates that the SRI technique is valid for geometrically nonlinear analysis.

5.7 Inflation of a cylinder subjected to internal pressure

Here, a simulation model is chosen to demonstrate the predictive capabilities of the proposed shell element in the analysis of a thick-walled structure for tube hydroforming process. In the studies of shell elements in which nodes are placed on the midsurface [17, 18], formulations of the external work are derived using the surface traction applied at the top and bottom surfaces. However, numerical results included the effect of the surface traction were not illustrated.

The geometric and material properties are given in Fig. 24. The material behavior is described by the St. Venant–Kirchhoff model for the elastic part with von Mises plasticity [61], where \(\sigma _{y}\) is the initial yield stress and H is the linear hardening modulus. On account of symmetry, one eighth of the cylinder is modeled using 50,000 hexahedral elements and 200 shell elements with 10 layers.

Figure 25 indicates the plastic zones of the cylinder in the deformed configuration. As can be seen from this figure, the proposed shell element is capable of evaluating the pressure that is applied to the internal surface. The computational costs of this model are shown in Table 3. The cost of elastic or plastic range is calculated as the average per load step of the total cost of each range. In the elastic range, the cost of the proposed shell element is higher than that of the MITC4 shell element, because static condensation is employed for additional degrees of freedom of transverse nodes. In the plastic range of the proposed shell element, the cost increases for elastic predictor-return mapping scheme in addition to the operation of static condensation. On the other hand, the cost of the MITC4 shell element increases because the plane stress condition is enforced by the internal iterative algorithm at each quadrature point together with the return-mapping scheme [9]. Figure 25 and Table 3 illustrate that the proposed shell element can be more efficient than conventional shell elements in this situation.

Fig. 19
figure 19

Geometry and material data of a cantilever beam

Full size image
Fig. 20
figure 20

Load displacement diagram for Poisson’s ratio \(\nu =0\) in bending of a cantilever beam (eleven transverse nodes)

Full size image
Fig. 21
figure 21

Load displacement diagram for Poisson’s ratio \(\nu =0.3\) in bending of a cantilever beam (eleven transverse nodes)

Full size image
Fig. 22
figure 22

Load displacement diagram for Poisson’s ratio \(\nu =0.499\) in bending of a cantilever beam (eleven transverse nodes)

Full size image
Fig. 23
figure 23

Relative error in bending of a cantilever beam

Full size image

5.8 Square plate undergoing large elastoplastic deformations

Here, a square plate with a uniform loading is employed to examine the behavior of the model when subjected to surface traction in a large deformation range, see Fig. 26. The geometry and material data for the numerical simulation are also given in Fig. 26. The material behavior is described by the St. Venant–Kirchhoff model for the elastic part with von Mises plasticity. At the edges of the plate, the displacements in the tangential directions to the plate are fixed, and the displacement in the vertical direction is fixed at the midsurface in the initial configuration only. On account of symmetry, only one quarter is modeled. In the proposed shell element, the model is discretized with 11 transverse nodes over the thickness and \(10 \times 10\) elements in the tangential directions to the plane. On the other hand, a \(100 \times 100 \times 10\) mesh of the trilinear hexahedral solid element is used to represent a symmetric one quarter portion.

Figure 27 shows the load-displacement curves at the center of the square plate. The result obtained by the proposed shell element indicates a good performance, similar to the hexahedral solid element in this deformation range. In contrast, a large disparity between the MITC4 shell element and the proposed shell element is indicated in Fig. 27. These results reveal that the surface traction is applied and evaluated at the bottom surface in the proposed shell element and the hexahedral solid element, whereas this takes place at the midsurface in the MITC4 shell element. It should be noted that the proposed shell element is capable of capturing the surface traction accurately in a large deformation range.

Fig. 24
figure 24

Geometry and material data of the cylinder

Full size image
Fig. 25
figure 25

Equivalent plastic strain distributions of the cylinder: a Hexahedral solid; b Proposed shell; c MITC4 shell

Full size image
Table 3 Computational costs of the cylinder
Full size table
Fig. 26
figure 26

Geometry and material data of the square plate

Full size image
Fig. 27
figure 27

Load displacement diagram at center point of the square plate

Full size image
Fig. 28
figure 28

Displacement variation in the transverse direction across the section at the center of the square plate

Full size image
Fig. 29
figure 29

Stress distribution of \(\sigma _{xx}\) through the thickness at the center of the square plate

Full size image
Fig. 30
figure 30

Stress distribution of \(\sigma _{zz}\) through the thickness at the center of the square plate

Full size image
Fig. 31
figure 31

Strain distribution of \(E_{xx}\) through the thickness at the center of the square plate

Full size image

The thickness–stretch across the section at the center of the square plate is illustrated in Fig. 28. To consider the displacement of the node that is placed on the midsurface in the initial configuration, we compare the the nodal displacements in the transverse direction, which are indicated by the transverse nodes of the proposed shell element or by the nodes of the hexahedral solid element. Thus, at the midsurface (or the initial position \(z_{0} = 0\)), the modified displacement variation \(\bar{w}\) is zero. Figure 28 shows that the proposed shell element is effective in estimating the change in thickness when the effect of the surface traction is included, similarly to the hexahedral solid element. In this example, the positions of the top and bottom surfaces can be captured using solid-shell elements. In addition, elements based on the multilayered model are capable of evaluating the deformation on the interior of the model. However, extreme increases in the degrees of freedom are inevitable. In contrast, the proposed shell element has the capability to assess the behavior on the interior of the model by introducing transverse nodes only. Thus, the proposed shell element can be more efficient than the multilayered shell elements. It should be noted that discontinuities of the thickness between elements are allowed in the proposed approach.

The validity of the proposed shell element is assessed to verify the numerical results on the interior of the model. Figures 29, 30, 31 and 32 show the stress and strain distributions through the thickness at the center of the square plate in the deformed configuration. These results confirm that the proposed shell element is capable of evaluating the stress and strain distributions, similarly to the hexahedral solid element. Furthermore, Figs. 33 and 34 illustrate the plastic zones in the deformed configuration near the top and bottom surfaces. The results for the proposed shell element are in good agreement with those of the hexahedral solid element.

Fig. 32
figure 32

Strain distribution of \(E_{zz}\) through the thickness at the center of the square plate

Full size image
Fig. 33
figure 33

Zones of equivalent plastic strain at near top surface of the square plate: a Hexahedral solid; b Proposed shell

Full size image
Fig. 34
figure 34

Zones of equivalent plastic strain at near bottom surface of the square plate: a Hexahedral solid; b Proposed shell

Full size image

6 Concluding remarks

A quadrilateral shell element incorporating a degree of freedom to represent thickness–stretch has been developed, without assuming the plane stress state. A displacement variation is introduced to the MITC4 shell element for the evaluation of thickness–stretch. Because the transverse normal strain is computed using the additional degrees of freedom, the three dimensional constitutive equation can be employed without any modification. Hence, the stress and strain distributions through the thickness can be expressed in a similar manner as for solid elements. In addition, the constitutive equation for the proposed formulation can be directly substituted to other material constitutive laws. One of the most important features is that the equilibrium equation in the transverse direction is defined explicitly. For this formulation, the surface traction can be evaluated at the surface where the traction is applied. Thus, the proposed shell element is capable of assessing the change in thickness and the stress distribution resulting from the effect of the surface traction. In the construction of the element stiffness matrix, the additional degrees of freedom can be condensed out at each element. Thus, the number of unknowns in the resulting linear system of equations for the proposed shell element is same as that for the conventional four-node shell element. It should be noted that the proposed approach is valid when discontinuities of the thickness between elements are allowed. Furthermore, the degrees of freedom for midsurface nodes of the proposed shell element are similar to those of conventional four node shell element. The degrees of freedom for the proposed shell element can be connected with those of conventional shell elements. Hence, the proposed approach is capable of using elements properly only when discontinuities of the thickness between elements are allowed. For example, the proposed shell element can be employed for the part imposing the surface traction and other parts are modeled using conventional shell elements.

Artificial numerical parameters are not included in the proposed formulation, and the proposed shell element does not exhibit any instabilities. In the proposed formulation, transverse shear locking can be avoided using the assumed strain approach, which has previously been applied to the MITC4 shell element. In addition, thickness locking can be alleviated by increasing the number of transverse nodes, and the SRI technique is proposed to circumvent volumetric locking. Some numerical examples were performed to indicate that the SRI technique works effectively to reduce both thickness locking and volumetric locking.

Representative numerical examples demonstrate the applicability and validity of the proposed shell element. The results reveal that the proposed shell element provides an accurate analysis of problems subjected to surface traction.

In future work, we will apply the proposed shell element to practical problems in sheet metal forming. In such problems, the proposed approach should be verified in the situations involving contact between the sheet and the die.