Composite fuzzy control of a class of uncertain nonlinear systems with disturbance observer

Abstract

In this paper, a novel composite control, using fuzzy logic system (FLS) and disturbance observer, is proposed for a class of uncertain nonlinear systems with actuator saturation and external disturbances. FLS is employed to approximate the unknown nonlinearities and a serial–parallel identification model is introduced to construct the composite updating law. The disturbance observer is developed to estimate the unknown compounded disturbance composed of the unknown external disturbance, the unknown fuzzy approximation error and the effect of actuator saturation. The uniformly ultimate boundedness of the closed-loop tracking error can be guaranteed rigorously via Lyapunov stability analysis. Simulation results are presented to demonstrate the effectiveness of the proposed method.

1 Introduction

Owing to the excellent function approximation ability of neural networks (NNs) [25] or FLS [20], intelligent systems are employed for analysis and controller design. The tremendous advantage of designing a control system using NNs or FLS is that it does not require an exact mathematical model of the controlled system [19]. Numerous designs have been proposed for different kinds of systems such as the strict-feedback system [14], single-input–single-output (SISO) pure-feedback system [13], multi-input–multi-output (MIMO) uncertain and perturbed system [9] and the chaotic systems [15, 16].

In practice, systems are subjected to unknown time-varying external disturbance [2, 11, 26]. In [2], linear parameter-varying systems with matched disturbance are studied. For nonlinear systems, in [1, 27, 28], the controller design is with system decomposition and sliding mode. Recently, the disturbance observer-based controller is gaining more and more attention as it is argued [4] that if the observer dynamics is much faster than the system dynamics, to a large extent, the influence of uncertainties can be estimated and compensated for. In [11], a discrete-time fuzzy disturbance observer (FDO) is developed to monitor the total disturbance including the internal parameter uncertainties and the external disturbance. In [6], both state feedback and output feedback designs for the nonaffine system are presented. It is noted that time-varying disturbance cannot be approximated directly by NNs or FLS.

Also physical actuators in control systems have amplitude and rate limitations [8, 30]. The controller ignoring actuator limitations may cause the closed-loop system performance to degenerate or even make the closed-system unstable. Command filter design is proposed for controller design of the related hypersonic flight dynamics with actuator saturation [22, 24]. In [7], adaptive tracking control is proposed for a class of uncertain MIMO nonlinear systems with input constraints. In [29], asymptotic tracking control is investigated for discrete-time MIMO system with nonlinear uncertainties. In [6], the saturation is considered as part of compounded disturbance and the adaptive design is proposed with disturbance observer.

In the above-mentioned methods, most efforts have been directed toward one goal: achieving asymptotic stability and tracking. Little attention has been paid to the accuracy of the desired identified models and to the transparency and the interpretability, whereas there should be the key aspects motivating the use of intelligent approximation in adaptive control. In [10], the fuzzy approximation modeling error is included in the updating law of the parameter estimation where faster state tracking and better parameter convergence were achieved due to the quicker and smoother parameter adaption. However, the method is impractical in real-world applications since the nth derivative of the plant output is required to be known. In [23], the composite design is proposed for a class of strict-feedback systems. Furthermore, similar design is proposed in [17] and applied on Lorenz system [16]. However, in [16, 17], the disturbance is considered as part of uncertainty to be approximated by FLS and the theoretical analysis is not rigorous.

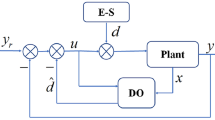
In this paper, we study disturbance observer-based composite fuzzy control (DOBCFC) of a class of uncertain nonlinear systems with both actuator saturation and time-varying disturbance. The external disturbance, the fuzzy approximation errors and actuator saturation effect are integrated as a compounded disturbance. The new serial–parallel identification model is developed with disturbance observer to provide additional approximation error information for FLS weights updating. Semiglobal uniform boundedness stability is rigourously established using Lyapunov approach.

The paper is organized as follows. In Sect. 2, the class of SISO nonlinear systems is characterized and the brief introduction of FLS is given. In Sect. 3, the composite fuzzy control is designed and the stability analysis is presented. The effectiveness of the proposed approach is verified by simulation in Sect. 4. The final conclusion is included in Sect. 5.

2 Problem formulation and preliminaries

2.1 Problem formulation

Consider the nth-order nonlinear system of the controllability canonical form

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{\xi }_i=\xi _{i+1},\quad i=1,2,\ldots ,n-1\\ \dot{\xi }_n=f(\bar{\xi }_n)+g(\bar{\xi }_n)u+d(t)\\ y(t)=\xi _1 \end{array} \right. \end{aligned}$$

(1)

where ${\bar{\xi }}_n=[\xi _1,\xi _2,\ldots ,\xi _n]^\mathrm{T} \in \mathfrak {R}^n$ are system states which are assumed to be available for measurement, $f$ and $g$ are unknown real continuous functions (in general nonlinear), $y \in \mathfrak {R}$ is system output, $u\in \mathfrak {R}$ is system input, $|u|\le u_{\max }, |{\dot{u}}| \le v_{\max }$ and $d(t)\in \mathfrak {R}$ denotes the external disturbance.

For system (1) to be controllable, it requires that $g\ne 0$ for all ${\bar{\xi }}_n$ in a certain controllability region $U_c \subset \mathfrak {R}^n$.

Assumption 1

There exist unknown bound functions ${\bar{f}}({\bar{\xi }}_n), {\bar{g}}({\bar{\xi }}_n)$ and constants ${\underline{g}}, {\bar{d}}$ such that $|f(\bar{\xi }_n)|\le |\bar{f}(\bar{\xi }_n)|, 0<\underline{g}\le |g(\bar{\xi }_n)|\le |\bar{g}(\bar{\xi }_n)|, |d(t)|\le \bar{d}, |\dot{d}(t)|\le \bar{v}_{d}$.

Assumption 2

The system nonlinearities $f$ and $g$ satisfy

$$\begin{aligned}&\hat{f}\left( \bar{\xi }_n|w_f^L\right) \le f\left( \bar{\xi }_n\right) \le \hat{f}\left( \bar{\xi }_n|w_f^U\right) \end{aligned}$$

(2)

$$\begin{aligned}&\hat{g}\left( \bar{\xi }_n|w_g^L\right) \le g\left( \bar{\xi }_n\right) \le \hat{g}\left( \bar{\xi }_n|w_g^U\right) \end{aligned}$$

(3)

where $w_f^L, w_f^u, w_g^L, w_g^u$ are the bounds of fuzzy weight vector.

The control objective is to synthesize an adaptive fuzzy control $u$ for system (1), such that all signals in the closed-loop systems are bounded, and the output $\bar{\xi }_n(t)$ tracks a bounded reference trajectory $\bar{y}_d(t)=[y_d(t), \dot{y}_d(t),\ldots , y^{(n-1)}_d(t)]^\mathrm{T}$.

2.2 Preliminaries

In this paper, the applied FLS [21] is employed to approximate the unknown nonlinearity $f$.

$$\begin{aligned} {\hat{f}}\left( {{X}_\mathrm{in}}\right) ={{\hat{w}}^\mathrm{T}}\theta \left( {{X}_{\text {in}}}\right) \end{aligned}$$

(4)

where ${{X}_{\text {in}}}\in D \subset {{\mathfrak {R}}^{M}}$ is the input vector of the FLS, $D=\varOmega _{x_1}\times \varOmega _{x_2} \times \cdots \times \varOmega _{x_M}$ is a fuzzy approximation region, ${\hat{f}} \in \mathfrak {R}$ is the FLS output, ${\hat{{w}}} \in {{\mathfrak {R}}^{L_N}}$ is the adjustable parameter vector, $\theta (\cdot ):{{\mathfrak {R}}^{M}}\rightarrow {{\mathfrak {R}}^{L_N}}$ is a nonlinear vector function of the inputs and the elements in $\theta ({{X}_\mathrm{in}})$ are given by

$$\begin{aligned} {{\theta }_{l}}\left( {{X}_\mathrm{in}} \right) =\dfrac{\prod _{i=1}^M\mu _{A_i^l}(x_i)}{\Sigma _{l=1}^{L_N}\prod _{i=1}^M\mu _{A_i^l}(x_i)} \end{aligned}$$

(5)

where ${{A}_{i}^l}$ is the fuzzy partitions on $\varOmega _{x_i}$ and $\mu _{A_i^l}$ is the membership function of ${{A}_{i}^l}$. In this paper, we select the Gaussian functions with the form

$$\begin{aligned} \mu _{A_i^l}(x_i)=\exp \left[ -\left( \dfrac{x_i-a_i^l}{\sqrt{2}b_i^l}\right) ^2\right] \end{aligned}$$

(6)

where $a_i^l$ and $b_i^l$ denote the centers and widths of $\mu _{A_i^l}$, respectively.

For any given real continuous function $f$ on a compact set ${{\varOmega }_{{{X}_\mathrm{in}}}}\in {{\mathfrak {R}}^{M}}$ and an arbitrary ${\varepsilon }_{M}>0$, there exist FLS in the form of (7) and an optimal parameter vector ${{w}^{*}}$ such that

$$\begin{aligned}&f\left( X_\mathrm{{in}}\right) = {w^*}^\mathrm{T} \theta \left( X_\mathrm{{in}} \right) + \varepsilon \end{aligned}$$

(7)

$$\begin{aligned}&\sup \limits _{{\mathrm{{X}}_{\mathrm{{in}}}} \in {\varOmega _{{\mathrm{{X}}_{\mathrm{{in}}}}}}} \mid \varepsilon \mid < {\varepsilon _{{M}}} \end{aligned}$$

(8)

where ${{\varepsilon }_{M}}>0$ denotes the supremum value of the reconstruction error $\varepsilon$ that is inevitably generated.

3 Composite fuzzy controller design

Considering system (1), if the nonlinearities $f$ and $g$ are known, the constraints on control inputs can be ignored, and there is no disturbance, then based on dynamic inversion algorithm, the control law is designed as

$$\begin{aligned} u^{*}=\dfrac{1}{g}\left[ -f+y_d^{(n)}(t)+{\bar{k}} {\bar{e}}\right] \end{aligned}$$

(9)

where $e=e(t)\,\triangleq \,y_d(t)-y(t)\in \mathfrak {R}$ is the tracking error, ${\bar{e}}={\bar{e}}(t)\,\triangleq \,[e, {\dot{e}}, \ldots , e^{(n-1)}]^\mathrm{T} \in \mathfrak {R}^n$ and $\bar{k}=[k_n, \ldots , k_2, k_1]^\mathrm{T} \in \mathfrak {R}^n$ is chosen such that the polynomial $s^n+k_1 s^{n-1}+ \cdots + k_n=0$ is Hurwitz.

The error dynamics can be derived as

$$\begin{aligned} e^{(n)}+k_1 e^{(n-1)} + \cdots +k_n e=0 \end{aligned}$$

(10)

This implies that starting from any initial conditions, the asymptotically stable tracking is achieved.

Since the nonlinear functions $f,g$ are unknown while there exists time-varying disturbance $d(t)$ , the controller (9) cannot be implemented.

The last equation of (1) can be written as

$$\begin{aligned} {\dot{\xi }}_n&= f\left( \bar{\xi }_n\right) +g\left( \bar{\xi }_n\right) u+d(t)\nonumber \\&= w_f^{*^\mathrm{T}} \theta _f\left( \bar{\xi }_n\right) + \varepsilon _f\left( \bar{\xi }_n\right) \nonumber \\&\quad + \left[ w_g^{*^\mathrm{T}} \theta _g\left( \bar{\xi }_n\right) + \varepsilon _g\left( \bar{\xi }_n\right) \right] u+d(t)\nonumber \\&= w_f^{*^\mathrm{T}} \theta _f\left( \bar{\xi }_n\right) + w_g^{*^\mathrm{T}} \theta _g\left( \bar{\xi }_n\right) u \nonumber \\&\quad + \left[ \varepsilon _f\left( \bar{\xi }_n\right) + \varepsilon _g\left( \bar{\xi }_n\right) u\right] +d(t)\nonumber \\&= \hat{f} + \hat{g}u_c + \varpi +D(t) \end{aligned}$$

(11)

where $w_f^{*}, w_g^{*}$ are the optimal FLS weight vectors approximating $f, g$ separately, and $|\varepsilon _f(\bar{\xi }_n)|\le \bar{\varepsilon }_f, |\varepsilon _g(\bar{\xi }_n)|\le \bar{\varepsilon }_g$.

$$\begin{aligned}&\hat{f}=\hat{w}_f^\mathrm{T} \theta _f(\bar{\xi }_n)\\&\hat{g}=\hat{w}_g^\mathrm{T} \theta _g(\bar{\xi }_n)\\&\varpi = \Delta f + \Delta g u\\&\Delta f= w_f^{*^\mathrm{T}} \theta _f(\bar{\xi }_n)-\hat{f}=\tilde{w}_f^\mathrm{T} \theta _f(\bar{\xi }_n)\\&\Delta g= w_g^{*^\mathrm{T}} \theta _g(\bar{\xi }_n)-\hat{g}=\tilde{w}^\mathrm{T}_g \theta _g(\bar{\xi }_n)\\&D(t)=\left[ \varepsilon _f(\bar{\xi }_n) + \varepsilon _g(\bar{\xi }_n)u\right] +\hat{g}\Delta u+d(t)\\&\Delta u= u-u_c \end{aligned}$$

Remark 1

It is easy to see that $D(t)$ is a compounded disturbance with different effects of fuzzy approximation error, actuator saturation and time-varying disturbance. Similar to the analysis in [6], following the boundedness of

$$\begin{aligned}&\left| \dot{\varepsilon }_f(\bar{\xi }_n)\right| \le \nu _f,\quad \left| \dot{\varepsilon }_g(\bar{\xi }_n)\right| \le \nu _g,\quad \left| \dot{u}\right| \le v_{\max },\nonumber \\&\quad \left| {\dot{u}}_c\right| \le v_{c\max } \end{aligned}$$

(12)

where $v_{c\max }$ is an unknown positive constant. From Assumption 1, we know there exists upper bound of the derivative of $D$

$$\begin{aligned} \left| \dot{D}\right| \le v_D \end{aligned}$$

(13)

where $v_D$ is an unknown positive constant.

Assumption 3

[12] The parameter vectors ${\hat{w}}_f$ and ${\hat{w}}_g$ belong to compact $\varOmega _f$ and $\varOmega _g$, respectively, which are defined as $\varOmega _f=\{\hat{w}_f: \Vert \hat{w}_f\Vert \le M_f\}$ and $\varOmega _g=\{\hat{w}_g: \Vert \hat{w}_g\Vert \le M_g\}$, where $M_f, M_g \in \mathfrak {R}^+$ are user-defined finite constants.

Define

$$\begin{aligned} \varLambda =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 1 &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{}0 &{}\cdots &{} 1\\ -k_n &{} -k_{n-1} &{} \cdots &{} -k_1\\ \end{array} \right] \end{aligned}$$

(14)

and $B=[0, \ldots , 0, 1]^\mathrm{T}$.

We propose the following indirect composite fuzzy controller with adaptive item $u_a$ and $H^{\infty }$ term $u_h$

$$\begin{aligned} u_c=u_a+u_h \end{aligned}$$

(15)

where

$$\begin{aligned} u_a=\dfrac{1}{\hat{g}}\left[ -\hat{f}+y_d^{(n)}(t)+\bar{k} \bar{e}-\hat{D}(t)\right] \end{aligned}$$

(16)

with $\hat{D}(t)$ as the estimate of disturbance $D(t)$ to be designed later and

$$\begin{aligned} u_h=-\dfrac{1}{\hat{g}} u_{h0} \end{aligned}$$

(17)

with $u_{h0}=-\dfrac{1}{r}B^\mathrm{T}P\bar{e}, r$ is positive constant and matrix $P=P^\mathrm{T} \ge 0$ is the solution of the following Riccati-like equation

$$\begin{aligned} \varLambda ^\mathrm{T} P + P \varLambda + Q -\dfrac{2}{r}\textit{PBB}^\mathrm{T}P+\dfrac{1}{\rho ^2}\textit{PBB}^\mathrm{T}P =0\qquad \end{aligned}$$

(18)

where $Q$ is an arbitrary $n\times n$ positive definite symmetric matrix to be given.

The real control input $u$ is applied

$$\begin{aligned} u&= \text {sat}(u_c)\nonumber \\&= \left\{ \begin{array}{ll} u_c &{} \quad \text {if}\,|u_c|\le u_{\max }\\ u_{\max }\text {sgn}(u_c) &{} \quad \text {if}\, |u_c|>u_{\max } \end{array} \right. \end{aligned}$$

(19)

where $\text {sgn}(\cdot )$ is the sign function.

Remark 2

The saturation effect is considered as part of $D(t)$. Similar to the idea in [6], the main focus is on the design of disturbance observer and there is no need to construct the auxiliary system as [5, 22].

From (15) and (16), we have

$$\begin{aligned} y_d^{(n)}(t)= - \bar{k} \bar{e} + \hat{D} +\hat{g} u_c + \hat{f} + u_{h0} \end{aligned}$$

(20)

Subtracting (11) from (20), the error dynamics is obtained

$$\begin{aligned} \dot{\bar{e}}&= \varLambda \bar{e} + B \left[ \hat{D} +\hat{g} u_c + \hat{f}+ u_{h0} - f -gu- d\right] \nonumber \\&= \varLambda \bar{e} - B \left[ -u_{h0}+ \varpi + \tilde{D} \right] \end{aligned}$$

(21)

where $\tilde{D}=D-\hat{D}$.

We know $\varLambda$ is a stable matrix from the selection of $\bar{k}$ in (9). Then, there exists a unique positive definite symmetric $n\times n$ matrix $P$ that satisfies the Lyapunov equation

$$\begin{aligned} \varLambda ^\mathrm{T} P + P \varLambda = -Q. \end{aligned}$$

(22)

To achieve the composite adaption, we define the filtered modeling error

$$\begin{aligned} \zeta _f=\hat{\xi }^{(n-1)}-\xi _n \end{aligned}$$

(23)

and introduce the following serial–parallel identification model with a low-pass filter

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{\hat{\xi }}_{i-1}=\hat{\xi }_i,\quad i=2,\ldots ,n\\ \dot{\hat{\xi }}_n=-\alpha _f \zeta _f + \hat{f} + \hat{g}u_c + \hat{D}\\ \end{array} \right. \end{aligned}$$

(24)

where $\hat{\xi }_i$ is the estimation of $\xi _i, \alpha _f \in \mathfrak {R}$ is positive design constant.

The parameter adaptive laws are proposed with both tracking error and filtered modeling error

$$\begin{aligned} \dot{\hat{w}}_f=-\gamma _f\left( \bar{e}^\mathrm{T}\textit{PB}+\gamma _{\xi }\zeta _f\right) \theta _f\end{aligned}$$

(25)

$$\begin{aligned} \dot{\hat{w}}_g=-\gamma _g\left( \bar{e}^\mathrm{T}\textit{PB}+\gamma _{\xi }\zeta _f\right) \theta _g u \end{aligned}$$

(26)

where $\gamma _f, \gamma _g$ and $\gamma _{\xi }$ are positive design parameters.

From (23), the error dynamics of $\zeta _f$ is obtained as

$$\begin{aligned} {\dot{\zeta }}_f&= {\hat{\xi }}^{(n)}-\dot{\xi }_n \nonumber \\&= -\alpha _f \zeta _f - \varpi - \tilde{D} \end{aligned}$$

(27)

For the estimation of $D(t)$, an auxiliary variable is introduced as

$$\begin{aligned} z=D+k_d \zeta _f \end{aligned}$$

(28)

where $k_d>0$ is the design parameter.

Considering (27) and (28), the derivative of $z$ can be written as

$$\begin{aligned} \dot{z}&= \dot{D}+k_d \dot{\zeta }_f\nonumber \\&= \dot{D}-k_d ( \alpha _f \zeta _f + \varpi + \tilde{D}) \end{aligned}$$

(29)

The estimate of intermediate variable $z$ is given by

$$\begin{aligned} \dot{\hat{z}}= -\bar{e}^\mathrm{T}\textit{PB} - k_d \alpha _f \zeta _f - \gamma _{\xi } \zeta _f \end{aligned}$$

(30)

where $\hat{z}$ is the estimation of $z$.

From (28), the estimation of $D(t)$ can be written as

$$\begin{aligned} \hat{D}=\hat{z}- k_d \zeta _f \end{aligned}$$

(31)

Define $\tilde{z}=z-\hat{z}$ and we have

$$\begin{aligned} \tilde{z}=D-\hat{D}=\tilde{D} \end{aligned}$$

(32)

Differentiating (32) and considering (28), (30) yields

$$\begin{aligned} \dot{\tilde{z}}&= \dot{z}-\dot{\hat{z}}\nonumber \\&= \dot{D}+\bar{e}^\mathrm{T}\textit{PB} - k_d \tilde{z}- k_d \varpi +\gamma _{\xi } \zeta _f. \end{aligned}$$

(33)

Remark 3

Since the information of time-varying disturbance is included in (24), the estimate is with information of $\zeta _f$ and there is no need to construct the $\hat{z}$ as [4, 6].

Remark 4

The $H^{\infty }$ fuzzy controller (FC) $u_1^{C}$ in [3] has the following formulation

$$\begin{aligned} u^{C}=u_a^C+u_h^C \end{aligned}$$

(34)

where $u_a^C=\dfrac{1}{\hat{g}}[-\hat{f}+y_d^{(n)}(t)+\bar{k} \bar{e}]$ and $u_h^C=u_h$. The difference between the controller in this paper and $H^{\infty }$ FC (34) lies in the disturbance observer (31) and the updating law (25) and (26).

Remark 5

Recently, disturbance observer-based controller design is commonly studied and the design origins from the dynamics of $\xi _n$. The controller is simply presented as follows:

$$\begin{aligned} u^{D}=u_a^D+u_h^D \end{aligned}$$

(35)

where $u_h^D=u_h, u_a^D=\dfrac{1}{\hat{g}}[-\hat{f}+y_d^{(n)}(t)+\bar{k} \bar{e}-{\hat{D}}_d], {\hat{D}}_d={\hat{z}}_D+k_d^D e^{(n-1)}$, and

$$\begin{aligned} \dot{\hat{z}}_D=-k_d^D\left[ y_d^{(n)}(t)-\hat{f}-\hat{g}u^{D}-\hat{z}_D-k_d^D e^{(n-1)}\right] \nonumber \\ \end{aligned}$$

(36)

with $k_d^D$ as the positive design parameter.

In this paper, the composite design is developed using serial–parallel identification model (24) and the disturbance observer is constructed based on the filtered modeling error $\zeta _f$.

Now, we have the following theorem.

Theorem 1

For the nonlinear system (1), satisfying Assumptions 1–3, select (19) from (15) as the tracking controller, (25) and (26) as updating algorithm and (31) as compounded disturbance observer. Then, all the closed-loop system signals are semiglobally uniformly ultimately bounded (UUB) under the proposed disturbance-based fuzzy controller.

Furthermore, the tracking error and the filtered modeling error remain within the following compact

$$\begin{aligned}&\varOmega _{\bar{e}}=\left\{ \bar{e}:\Vert \bar{e}\Vert \le \bar{\chi } (2k_d \lambda _{\min }(Q))^{-{\dfrac{1}{2}}}\right\} \end{aligned}$$

(37)

$$\begin{aligned}&\varOmega _{\zeta _f}=\left\{ \zeta _f: |\zeta _f|\le \bar{\chi } (4k_d \alpha _f {\gamma _{\xi }})^{-{\dfrac{1}{2}}}\right\} \end{aligned}$$

(38)

and the $H_\infty$ tracking performance can be obtained

$$\begin{aligned}&\int \nolimits _0^T {\bar{e}^\mathrm{T} Q \bar{e}}\mathrm{d}t \le 2 V(0) \!+\! \dfrac{1}{2k_d} \int \nolimits _0^T {(\dot{D}-k_d \varpi )^2}\mathrm{d}t\qquad \end{aligned}$$

(39)

Proof

Consider the following Lyapunov function candidate

$$\begin{aligned} V&= \dfrac{1}{2} \bar{e}^\mathrm{T} P \bar{e} + \dfrac{1}{2}\tilde{D}^2 + \dfrac{1}{2\gamma _f}\tilde{w}_f^\mathrm{T}\tilde{w}_f\nonumber \\&\quad + \dfrac{1}{2\gamma _g} \tilde{w}_g^\mathrm{T}\tilde{w}_g + \dfrac{\gamma _{\xi }}{2}{\zeta _f}^2 \end{aligned}$$

(40)

The time derivative of $V$ is

$$\begin{aligned} \dot{V}&= \dfrac{1}{2}\left( {\dot{\bar{e}}^\mathrm{T} P \bar{e}+ \bar{e}^\mathrm{T} P \dot{\bar{e}}}\right) \nonumber \\&\quad +\,\dot{\tilde{D}}\tilde{D}+\left( \bar{e}^\mathrm{T}\textit{PB}+\gamma _{\xi }\zeta _f\right) \theta _f^\mathrm{T} \tilde{w}_f \nonumber \\&\quad +\,\left( \bar{e}^\mathrm{T}\textit{PB}+\gamma _{\xi }\zeta _f\right) \theta _g^\mathrm{T} \tilde{w}_g u + {\gamma _{\xi }}\dot{\zeta }_f{\zeta _f}\nonumber \\&= -\,\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e}+ \bar{e}^\mathrm{T}\textit{PB} u_{h0}\nonumber \\&\quad -\, \bar{e}^\mathrm{T}\textit{PB} \left( \theta _f^\mathrm{T} \tilde{w}_f + \theta _g^\mathrm{T} \tilde{w}_gu + \tilde{z}\right) \nonumber \\&\quad +\,\tilde{z} \left( \dot{D}+\bar{e}^\mathrm{T}\textit{PB} - k_d \tilde{z} - k_d \varpi +\gamma _{\xi } \zeta _f\right) \nonumber \\&\quad +\,\left( \bar{e}^\mathrm{T}\textit{PB}\!+\!\gamma _{\xi }\zeta _f\right) \!\theta _f^\mathrm{T} \tilde{w}_f \!+\!\left( \bar{e}^\mathrm{T}\textit{PB}\!+\!\gamma _{\xi }\zeta _f\right) \!\theta _g^\mathrm{T} u \tilde{w}_g \nonumber \\&\quad +\,{\gamma _{\xi }}\left( -\alpha _f \zeta _f - \theta _f^\mathrm{T} \tilde{w}_f - \theta _g^\mathrm{T} \tilde{w}_gu - \tilde{z}\right) {\zeta _f} \end{aligned}$$

(41)

Furthermore, we know

$$\begin{aligned} \dot{V}&= -\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e} - \alpha _f {\gamma _{\xi }} {\zeta _f^2} - \dfrac{\left( \bar{e}^\mathrm{T}\textit{PB}\right) ^2}{2\rho ^2} \nonumber \\&\quad +\,\tilde{z}\left( \dot{D}-k_d\tilde{z}-k_d\varpi \right) \nonumber \\&= -\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e} - \alpha _f {\gamma _{\xi }} {\zeta _f^2} - \dfrac{\left( \bar{e}^\mathrm{T}\textit{PB}\right) ^2}{2\rho ^2} \nonumber \\&\quad -\, k_d \left( \tilde{z}-\dfrac{\dot{D}-k_d \varpi }{2k_d}\right) ^2 + \dfrac{1}{4k_d} \left( \dot{D}-k_d \varpi \right) ^2 \nonumber \\&\le -\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e} - \alpha \!_{f} {\gamma _{\xi }} {\zeta _f^2}+ \dfrac{1}{4k_d} \left( \dot{D}-k_d \varpi \right) ^2 \end{aligned}$$

(42)

Similar to the analysis of the proof [18], we know

$$\begin{aligned} \dot{V}\le -k_{\min }V+k_{\min }V_r \end{aligned}$$

(43)

where $k_{\min }=\dfrac{\lambda _{\min }(Q)}{\lambda _{\max }(P)}$ and $V_r \in \mathfrak {R}^+$ is a finite constant. Then, we know all the signals are UUB.

From the bound of $\dot{D}$ and Assumption 2, we know

$$\begin{aligned} \chi =|\dot{D}-k_d \varpi | \le \bar{\chi } \end{aligned}$$

(44)

Furthermore, $\bar{e}$ and $\zeta _f$ converge to the compact

$$\begin{aligned}&\varOmega _{\bar{e}}=\left\{ \bar{e}:\Vert \bar{e}\Vert \le \bar{\chi } \left( 2k_d\lambda _{\min }(Q)\right) ^{-{\dfrac{1}{2}}}\right\} \\&\varOmega _{\zeta _f}=\left\{ \zeta _f: |\zeta _f|\le \bar{\chi } \left( 4k_d \alpha _f {\gamma _{\xi }}\right) ^{-{\dfrac{1}{2}}}\right\} \end{aligned}$$

Similarly, we can prove the disturbance estimation error $\tilde{D}$ and the error of FLS weights $\tilde{w}_f, \tilde{w}_g$ are bounded.

From (42), we know

$$\begin{aligned} \dot{V}&\le -\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e} - \alpha _f {\gamma _{\xi }} {\zeta _f^2}+ \dfrac{1}{4k_d} (\dot{D}-k_d \varpi )^2\nonumber \\&\le -\dfrac{1}{2} \bar{e}^\mathrm{T} Q \bar{e} + \dfrac{1}{4k_d} \left( \dot{D}-k_d \varpi \right) ^2 \end{aligned}$$

(45)

Integrating both sides of the above inequality (45) from 0 to $T$ yields

$$\begin{aligned} V(T)-V(0)&\le \frac{1}{4k_d} \int \nolimits _0^T {(\dot{D}-k_d \varpi )^2}\hbox {d}t\nonumber \\&\quad -\,{\frac{1}{2} \int \nolimits _0^T \bar{e}^\mathrm{T} Q \bar{e}}\hbox {d}t \end{aligned}$$

(46)

Then, the conclusion of (39) could be obtained. This completes the proof.$\square$

Remark 6

Since there exist input saturation and time-varying disturbance, the compensating design for $D(t)$ is employed, while the composite learning with modeling error is designed.

Remark 7

The disturbance observer design (31) with (30) is different from the design in [6] because the filtered modeling error (23) is incorporated.

Remark 8

The composite learning (25) and (26) is different from the design in [18] since the disturbance is estimated and included in the identification model (24).

Remark 9

It is obvious that the controller can be applied without any change for the case free of actuator saturation.

Remark 10

From the derivative of the Lyapunov function $V$ in (42), if without the item $u_a$, the conclusion of Theorem 1 still exists. However, with the item $u_{h0}$, one item $\dfrac{(\bar{e}^\mathrm{T}\textit{PB})^2}{2\rho ^2}$ is subtracted from $\dot{V}$ and it makes the Lyapunov function decreasing faster.

4 Simulation

In this section, the following second-order nonlinear inverted pendulum system [3] is used for simulation

$$\begin{aligned} \dot{\xi }_1&= \xi _2\nonumber \\ \dot{\xi }_2&= f(\bar{\xi }_2)+g(\bar{\xi }_2)u +d(t) \end{aligned}$$

(47)

where

$$\begin{aligned} f&= \dfrac{g_\mathrm{e}\sin \xi _1 -\dfrac{ml \xi _2^2\cos \xi _1 \sin \xi _1}{m_\mathrm{c}+m}}{l\left( \dfrac{4}{3}-\dfrac{m\cos ^2 \xi _1}{m_\mathrm{c}+m}\right) }\\ g&= \dfrac{\dfrac{\cos \xi _1}{m_\mathrm{c}+m}}{{l\left( \dfrac{4}{3}-\dfrac{m\cos ^2 \xi _1}{m_\mathrm{c}+m}\right) }}\\ d&= 5\sin t \end{aligned}$$

and $\xi _1$ is the angular position of the pendulum, $\xi _2$ is the corresponding angular velocity, $g_\mathrm{e}=9.8$ m/s$^{2}$ is the acceleration due to gravity, $m_\mathrm{c}$ is the mass of the cart, $m$ is the mass of the pole and $l$ is the half length of the pole.

Fig. 1

Tracking of $y_d$

Fig. 2

Reference signal $\xi _{2d}$ and system output $\xi _{2}$

Fig. 3

Tracking errors

The controller in this paper is denoted as DOBCFC, while the design in (34) is marked as $H^{\infty }$FC, and the controller (35) is named as disturbance observer-based fuzzy control (DOB-FC). For simulation, $m_\mathrm{c}=1$ kg, $m=0.1$ kg, $l=0.5$ m, $\bar{\xi }_2(0)=[0,\pi /12]^\mathrm{T}$.

Let $k_1=2, k_2=1, \gamma _f=30, \gamma _g=1.5, \gamma _\xi =10$. Select $Q=\left[ \begin{array}{cc} 10 &{} 0\\ 0&{} 10 \\ \end{array} \right] , \rho =0.1, r=2\rho ^2, P=\left[ \begin{array}{cc} 15 &{} 5\\ 5&{} 5 \\ \end{array}\right]$.

Fig. 4

Estimation of the compound disturbance

Fig. 5

Components of control input

For the FLS, $\hat{w}_f(0)=[0,\ldots ,0]^\mathrm{T}, \hat{w}_g(0)=[0.5,\ldots ,0.5]^\mathrm{T}, a_i^l, i=1,2$ is selected as $[-\pi /6; -\pi /12;0;\pi /12;\pi /6], b_i^l=0.1, L_{N}=25, M_f=10, M_g=1$.

4.1 Period signal tracking without input saturation

The control objective is to ensure that the output $y$ tracks $y_d=\pi /6\sin t$ with $d(t)=5\sin t$. Accordingly, we know $\xi _{2d}=\dot{y}_d=\pi /6\cos t$. The parameter is $k_d=0.1$, $\alpha _f = 2$ and in this example, to clearly show the difference between DOBCFC and $H^{\infty }$FC, the input saturation is not considered.

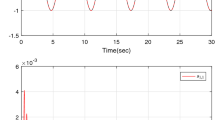
The simulation results are shown in Figs. 1, 2, 3, 4 and 5. From the system tracking depicted in Fig. 1, it is observed that both controllers can follow the reference trajectory $y_d$, but the result of DOBCFC is with higher tracking precision. From the tracking of $x_{2d}$ in Fig. 2 similar conclusion can be obtained. The deduction could be further confirmed from the tracking errors shown in Fig. 3. The estimation of disturbance observer is presented in Fig. 4. In Fig. 5, the robust item $u_h(t)$ of DOBCFC is with smaller value compared with $H^{\infty }$FC. It means that $H^{\infty }$FC is mainly relying on the $H^{\infty }$ term, while for DOBCFC, the basic adaptive fuzzy controller $u_a(t)$ plays more important roles. It indicates that the more controller could adapt to the system uncertainty and disturbance, the higher precision could be obtained.

4.2 Square signal tracking with input saturation

The control objective is to ensure that the output $y$ tracks the square command with period 60 s and magnitude $\pi /6$. The saturation is considered as $|u|\le 6.5$, and control parameters are selected as $k_d=0.2, \alpha _f = 15, k_d^D=0.5$. In this example, three methods are tested on the same scenario and the disturbance is set with a sudden change during the steady state

$$\begin{aligned} d(t) = \left\{ \begin{array}{l l} 0.1\sin (t) &{} \quad \text {if}\, t \le 20\\ 0.1\sin (t)-5 &{} \quad \text {if}\, t > 20 \end{array} \right. \end{aligned}$$

(48)

The filter (49) is used to derive the reference signals $y_d, \dot{y}_d$ and $\ddot{y}_d$.

$$\begin{aligned} \dfrac{{{y_d}}}{{{y_c}}} = \dfrac{{w_n^2}}{{ s^2 + 2 \varepsilon _c w_n s + w_n^2}} \end{aligned}$$

(49)

where $w_n=0.9, \varepsilon _c=0.9$.

Fig. 6

Tracking of $y_d$

Fig. 7

Tracking error of $y_d$

Fig. 8

Reference signal $\xi _{2d}$ and system output $\xi _2$

Fig. 9

Tracking error of $\xi _{2d}$

Fig. 10

Control input

Fig. 11

Estimation of the compound disturbance

The simulation results are shown in Figs. 6, 7, 8, 9, 10 and 11. From the system response depicted in Figs. 6 and 8, under DOBCFC the tracking errors in Figs. 7 and 9 converge to the neighborhood of zero faster with higher precision. It is obvious that compared with the other two methods, DOBCFC exhibits better performance even with sudden disturbance (at $t=20$ s) or reference command change (at $t=30$ s). It is observed that initially since the system is not at trim state, there exists large variation for system tracking, while for steady state, the amplitude of tracking error is smaller when there comes sudden disturbance or new tracking command. Due to the compounded disturbance estimation and effect of the input saturation, it is interesting to find that the control input of DOBCFC exhibits quite different response from $H^{\infty }$FC and DOB-FC as shown in Fig. 10. Also from the response shown in Figs. 10 and 7, in case of reference command change, DOBCFC is with smaller control input and better transient performance. Though DOBCFC and DOB-FC are both equipped with disturbance observer, the estimation in Fig. 11 is quite different and the reason is discussed as in Remark 5.

5 Conclusion

In this paper, a novel composite fuzzy control is proposed for a class of uncertain nonlinear systems with actuator saturation and external disturbances. FLS is employed to approximate the unknown nonlinearities and a serial–parallel identification model is introduced to construct the composite fuzzy updating law. The disturbance observer is developed to estimate the unknown compounded disturbance composed of the unknown external disturbance, the unknown fuzzy approximation error and the actuator saturation effect. The uniformly ultimate boundedness of the closed-loop tracking error can be guaranteed rigorously via Lyapunov stability analysis. The simulation results verify the philosophy of the controller design in this paper using composite design with disturbance observer to enhance the tracking performance.