Theoretical and practical applications of fuzzy fractional integral sliding mode control for fractional-order dynamical system

Abstract

This paper proposes a fuzzy fractional integral sliding mode control for synchronizing fractional-order dynamical systems with mismatched fractional orders. It is applied to synchronize the fractional-order modified coupled dynamos chaotic systems. Synchronization between two identical fractional order, different fractional orders, integer order and fractional-order modified coupled dynamos chaotic systems have been demonstrated. For practical applications, these derived synchronized fractional-order chaotic systems are utilized to develop a novel cryptosystem for an image encryption and decryption. Numerical simulations are provided to verify the significance of theoretical analysis.

1 Introduction

Fractional calculus is an area of mathematics that handles with derivatives and integrals of non integer orders. It can be traced to the work of Leibniz and L’Hospital in 1695, which has almost the same long history as integer order calculus. In general, many real objects are of fractional order, so fractional calculus opens broad ways to describe a real object more accurately and more adequately than the classical integer calculus method. Recently, fractional calculus have been dominated by modern examples of applications which involve integral equations, ordinary and partial differential equations in physics, fluid mechanics, fractals, mathematical biology, electrochemistry, automatic control, robotics, secure communication or signal processing. Therefore, fractional calculus has become an exciting new mathematical method of solution of various problems in applied mathematics, science and engineering.

Synchronization is the dynamical process by which two or more oscillators adjust their rhythms due to a weak interaction [1]. In 1990, a method to synchronize two identical chaotic systems with different initial conditions has been introduced by Pecora and Carroll [2]. Synchronization of fractional-order chaotic systems is increasing interest among researchers in the past few years. Also, it has been growing continuously due to its potential applications in cryptography or secure communication, signal and control processing [3–8]. Latterly, several techniques and methods have been improved and applied for chaos control and synchronization. Two adaptive synchronization schemes have been analyzed for the fractional-order memristor-based Chua’s circuit in [9]. Robust fractional order sliding mode control technique [10] has been applied for synchronization of two fractional-order chaotic systems with external disturbance. An active sliding mode controller has been proposed to synchronize two different fractional-order systems in [11]. Synchronization between two classes of fractional-order new hyperchaotic system and Chen system has been investigated in [12] via new nonlinear control technique. In [13], chaos synchronization of variable order fractional financial system based on active control method has been studied. A new criterion of synchronization of fractional-order chaotic systems based on the stability theory of impulsive fractional-order systems has been proposed in [14]. Phase synchronization has been studied for synchronizing fractional-order chaotic systems in [15] by using an active nonlinear feedback control technique, and so on. Especially, the fractional-order controller plays an important role in controlling robots, robotic manipulator and tip position of a lightweight flexible manipulator, for more details see [16–19] and references therein.

Nowadays, the sliding mode control (SMC) has been proven to be an effective robust control strategy and provides high faithfulness performance in different control problems for nonlinear systems. The principal of SMC is to apply a discontinuous control to force the system state trajectories to some predefined sliding surfaces. The main advantages of the SMC are the fast response, low sensitivity to external disturbances, robustness to the plant uncertainties, and easy realization. Due to these advantages, the SMC strategy has been successfully applied to control and synchronize the fractional order dynamical systems, see [10, 20–30]. However, one major drawback of the conventional SMC approach is the high frequency of control action called chattering. In 1992, a fuzzy sliding mode approach has been designed by Palm [31] to avoiding the chattering in the SMC. This fuzzy sliding mode design can contribute to stable closed-loop system by avoiding the chattering problem in the SMC. Therefore, the stability is ensured for the systems with the combination of SMC and fuzzy logic control. Further, fuzzy fractional-order sliding mode controller for nonlinear systems has been investigated in [32]. Chaos synchronization between two different uncertain fractional-order chaotic systems has been studied based on adaptive fuzzy sliding mode control in [33]. In [34], integer order and fractional-order chaotic systems have been synchronized by using fuzzy sliding mode control. Fuzzy logic controller has been addressed for controlling fractional-order Liu system in [35]. An adaptive fuzzy sliding mode strategy has been developed for the generalized projective synchronization of fractional-order chaotic system in [36]. Recently, fuzzy fractional differential equation has attracted increasing attention among researchers. For instance, the existence and uniqueness of the solution for a class of fractional differential equation with fuzzy initial value have been studied in [37]. A fuzzy fractional integral equation has been investigated in [38]. Fuzzy fractional Volterra–Fredholm integro-differential equations has been introduced in [39]. The exact and approximate solutions have been constructed for fuzzy fractional differential equations in [40].

In this paper, a fuzzy fractional integral sliding mode (FFISM) control is designed for synchronizing mismatched fractional-order dynamical systems. Different possibilities of fractional orders of the drive system and the response system are analyzed and achieved the synchronization between these systems by using the proposed control. It is shown that the proposed FFISM control is the generalization of existing fuzzy sliding mode control. The validity and the performance of the proposed FFISM control are verified by analytically and numerically. For real-life applications, a new cryptosystem is formulated for an image encryption and decryption based on synchronized fractional-order modified coupled dynamos chaotic systems. The experimental results are provided to validate the efficiency and security of the proposed cryptosystem. Finally, we conclude that the proposed cryptosystem is more secure than existing cryptosystem according to the experimental results.

The paper is organized as follows: In Sect. 2, some basic definitions, properties and theorems of fractional calculus are given. The FFISM control law is designed for the fractional-order dynamical system in Sect. 3. Theoretical and practical applications of the proposed FFISM control are presented in Sects. 4 and 5, respectively. Numerical simulations are given to demonstrate the proposed theory. The conclusions are finally drawn in Sect. 6.

2 Preliminaries for fractional calculus

In this section, basic definition of fractional derivative, important theorems and properties of the operators of fractional calculus will be presented.

The fractional derivatives have many nonequivalent definitions. One of the commonly used definition is the Caputo fractional derivative [41], which is defined as follows:

Definition 1

The $\alpha$-order fractional derivative of function $f(t)$ with respect to $t$ is defined by

$$\begin{aligned} D^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\int _a^t (t-\tau )^{-\alpha +n-1}f^{(n)}(\tau )d\tau ,\nonumber \\ \end{aligned}$$

(1)

where $n=[\alpha ]+1$, $[\alpha ]$ is the integer part of $\alpha$, $\varGamma (\cdot )$ is the gamma function, and $D^\alpha$ is called the $\alpha$-order Caputo differential operator. Especially $D^{\alpha }0=0$.

The fractional-order Caputo differential operator also satisfies the following general properties of fractional-order derivative.

Property 1

The additive index law

$$\begin{aligned} D^{\alpha }D^{\beta }x(t)=D^{\beta }D^{\alpha }x(t)=D^{\alpha +\beta }x(t)=D^{\beta +\alpha }x(t).\nonumber \\ \end{aligned}$$

(2)

Property 2

The Caputo differential operator is a linear operator

$$\begin{aligned} {D^{\alpha }(ux_1(t)+vx_2(t))=uD^{\alpha }x_1(t)+vD^{\alpha }x_2(t)}, \end{aligned}$$

(3)

where $u,v$ are real constants.

Property 3

The Caputo fractional-order nonlinear system $D^{\alpha }x(t)=f(x(t))$, satisfies Lipschitz condition with respect to $x$. That is

$$\begin{aligned} \Vert f(x_1(t))-f(x_2(t))\Vert \le l\Vert x_1(t)-x_2(t)\Vert , \end{aligned}$$

(4)

where $l$ is a positive constant. Without loss of generality, we assume that $f(x)$ satisfies $f(x)=0$ at $x=0$. Then,

$$\begin{aligned} \Vert f(x_1(t))\Vert \le l\Vert x_1(t)\Vert \end{aligned}$$

That is,

$$\begin{aligned} \Vert D^{\alpha }x_1(t)\Vert \le l\Vert x_1(t)\Vert \end{aligned}$$

Theorem 1

[42] Consider the following fractional-order system

$$\begin{aligned} D^{\alpha }x(t)=Ax, \ x(0)=x_0{,} \end{aligned}$$

(5)

where $0<\alpha \le 1$, $x\in \mathbb {R}^n$ and $A\in \mathbb {R}^{n\times n}$ with fractional-order $\alpha$. It is asymptotically stable if and only if

$$\begin{aligned} |arg(eig (A))|>\frac{\alpha \pi }{2}, \end{aligned}$$

(6)

In this case, the components of the state decay to $0$ like $t^{-\alpha }$.

Theorem 2

[42] Consider a system given by the following linear state-space form with finite inner dimension $n$:

$$\begin{aligned} \begin{aligned}&D^{\alpha }x(t)=Ax+Bu,\\&y=Cx,\ x(0)=x_0 \end{aligned} \end{aligned}$$

(7)

where $0<\alpha \le 1$, $x\in \mathbb {R}^n$ is the state, $y\in \mathbb {R}^p$ is the observation, and $u$ is the control. Assume that, the triplet $(A,B,C)$ is minimal and then the system (7) is bounded input bounded-output if and only if $|arg(eig (A))|>\frac{\alpha \pi }{2}$.

3 Design of fuzzy fractional integral sliding mode control

In this section, a new FFISM control will be designed for controlling fractional-order dynamical system. Further, the necessary condition will be derived to achieve the synchronization between two fractional-order dynamical systems.

3.1 System description

Consider the following fractional-order dynamical system as a drive system

$$\begin{aligned} D^{\alpha }X(t)=AX+F(X), \end{aligned}$$

(8)

and the corresponding response system is described by

$$\begin{aligned} D^{\beta }Y(t)=BY+G(Y)+U(X,Y), \end{aligned}$$

(9)

where $\alpha ,\beta$ are fractional orders of the states of the systems (8) and (9), respectively, such that $0<\alpha ,\beta \le 1$. $X,Y\in \mathbb {R}^n$ are the state variables, $A,B\in \mathbb {R}^{n\times n}$ are the coefficient of the linear parts, and $F,G$ are nonlinear parts such that $F,G:\mathbb {R}^n\rightarrow \mathbb {R}^n$ of the systems (8) and (9), respectively. $U(X,Y)$ is the control input to be determined later. It can be added to the response system (9), to realize the synchronization between the systems (8) and (9).

Define the error variable

$$\begin{aligned} E=Y-X. \end{aligned}$$

(10)

The ultimate aim is to construct a suitable FFISM control such that

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\Vert E(t)\Vert =\lim \limits _{t\rightarrow \infty }\Vert Y(t)-X(t)\Vert =0. \end{aligned}$$

(11)

If (11) is satisfied, then the synchronization between the drive system (8) and the response (9) will be achieved and realized.

3.2 Control design

The synchronization error $E=Y-X$ as defined in (10) between the drive system (8) and the response system (9) of the fractional-order dynamical systems involve the nonlinear parts $F(X)$ and $G(Y)$. To overcome this situation, we will construct the control input $U(X,Y)$ to remove the nonlinear parts from the error system. At this point of view, $U(X,Y)$ can be defined as follows.

Define the control input,

$$\begin{aligned} U(X,Y)=D^{\beta }X-G(Y)-BX+u(t), \end{aligned}$$

(12)

where $u\in \mathbb {R}^{n\times 1}$ is a new supportive control input to be evaluated later.

Substitute (12) into (9), one can obtain that

$$\begin{aligned}&D^{\beta }Y(t)=BY+G(Y)+D^{\beta }X-G(Y)\nonumber \\&\qquad \qquad \quad -BX+u(t)\nonumber \\&\quad \quad \quad \,\,\, =B(Y-X)+D^{\beta }X+u(t)\nonumber \\&D^{\beta }Y(t)-D^{\beta }X(t)=B(Y-X)+u(t) \end{aligned}$$

(13)

Since by Property 2, (13) becomes

$$\begin{aligned}&D^{\beta }(Y(t)-X(t))=B(Y-X)+u(t)\nonumber \\&D^{\beta }E(t) = BE+u(t) \end{aligned}$$

(14)

3.3 Formation of fuzzy integral sliding mode control

Two steps are needed to design a sliding mode control. In the first step, we construct a sliding surface that represents the desired system dynamics. In the second step, we develop a switching control law such that the sliding mode exist at every point in the sliding surface, and any states outside the surface are driven to reach the surface swiftly.

A fractional-order integral sliding surface is chosen as

$$\begin{aligned} s(t)&= CD^{\beta -1}E(t)-D^{-1}[(A+M)E(t)]\nonumber \\&= CD^{\beta -1}E(t)-\int _0^t(A+M)E(\tau )d\tau , \end{aligned}$$

(15)

where $C$ and $M$ are parameter matrices and whose entries are in the real line.

When the system operates in the sliding mode, the sliding surface $s$ and its derivative $\dot{s}$ must satisfy the following condition

$$\begin{aligned} s(t)=\dot{s}(t)=0. \end{aligned}$$

Differentiating (15) and using (14) one can have

$$\begin{aligned} \dot{s}(t)&= \frac{d}{dt}s(t)\nonumber \\&= \frac{d}{dt}\left[ CD^{\beta -1}E(t)-\int _0^t(A+M)E(\tau )d\tau \right] \nonumber \\&= CD^{\beta }E(t)-\frac{d}{dt}\int _0^t(A+M)E(\tau )d\tau \nonumber \\&= CD^{\beta }E(t)-(A+M)E(t) \nonumber \\&= C[BE+u(t)]-(A+M)E. \end{aligned}$$

(16)

Since $\dot{s}(t)=0$, one can obtain that

$$\begin{aligned} C[BE+u(t)]=(A+M)E. \end{aligned}$$

According to the sliding mode control theory, the equivalent control law is calculated as

$$\begin{aligned} u_{eq}(t)=[C^{-1}(A+M)-B]E. \end{aligned}$$

(17)

To satisfy the sliding mode condition, the discontinuous reaching law should be selected as

$$\begin{aligned} \dot{s}(t)=-K.FFISM\left( \frac{s}{s_\epsilon }\right) , \end{aligned}$$

(18)

where $K\in \mathbb {R}^{n\times 1}$ and $s_\epsilon$ are positive constants. Here, $\frac{s}{s_\epsilon }$ is an input linguistic, and $FFISM(\bullet )$ denotes the fuzzy features of the decision strategy at $\bullet$. The membership functions of input linguistic $\frac{s}{s_\epsilon }$ and the output $FFISM(\bullet )$ are decomposed with decolorized seven fuzzy segments, which are represented by Negative Big (NB), Negative Medium (NM), Negative Small (NS), Zero (ZE), Positive Small (PS), Positive Medium (PM) and Positive Big (PB). The fuzzy logic control rules of $FFISM(\bullet )$ are defined as follows:

• $R_1:$ If $\frac{s}{s_\epsilon }$ is NB, then $FFISM(\bullet )$ is NB.

• $R_2:$ If $\frac{s}{s_\epsilon }$ is NM, then $FFISM(\bullet )$ is NM.

• $R_3:$ If $\frac{s}{s_\epsilon }$ is NS, then $FFISM(\bullet )$ is NS.

• $R_4:$ If $\frac{s}{s_\epsilon }$ is ZE, then $FFISM(\bullet )$ is ZE.

• $R_5:$ If $\frac{s}{s_\epsilon }$ is PS, then $FFISM(\bullet )$ is PS.

• $R_6:$ If $\frac{s}{s_\epsilon }$ is PM, then $FFISM(\bullet )$ is PM.

• $R_7:$ If $\frac{s}{s_\epsilon }$ is PB, then $FFISM(\bullet )$ is PB.

By a weighted average defuzzification method, the crisp of $FFISM(\bullet )$ is evaluated as

$$\begin{aligned} FFISM(\bullet )&= \frac{\sum _{i=1}^{7}\mu _{R_i}u_{R_i}}{\sum _{i=1}^{7}u_{R_i}}, \end{aligned}$$

(19)

where $\mu _{R_i}$ is the premise membership function value of the $i$th rule, and $u_{R_i}$ is the control value in the $i$th rule. The membership function of input linguistic $\frac{s}{s_\epsilon }$ is shown in Fig. 1, and the membership function of $FFISM(\bullet )$ is depicted in Fig. 2.

Fig. 1

Membership function of $\frac{s}{s_\epsilon }$

Fig. 2

Membership function of $FFISM(\bullet )$

Since $\dot{s}(t)=0$, we have

$$\begin{aligned} \dot{s}(t)=-K.FFISM\left( \frac{s}{s_\epsilon }\right) =0. \end{aligned}$$

According to sliding mode control theory, the switching control law is calculated as

$$\begin{aligned} u_{sw}(t)=-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right) . \end{aligned}$$

(20)

Now, the new supportive input control $u(t)$ can be defined as

$$\begin{aligned} u(t)&= u_{eq}(t)+u_{sw}(t). \end{aligned}$$

(21)

Substitute (21) into (12), the total control input is obtained as

$$\begin{aligned} U(X,Y)\!&= \!D^{\beta }X\!-\!G(Y)\!-\!BX\!+\! \left( C^{-1}(A\!+\!M)\!-\!B\right) E\nonumber \\&-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right) . \end{aligned}$$

(22)

Thus, the fractional-order error dynamical system (14) can be written as

$$\begin{aligned} D^{\beta }E(t)&= BE+\left( C^{-1}(A+M)-B\right) E\nonumber \\&-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right) \nonumber \\&= C^{-1}\left[ (A+M)E-K.FFISM\left( \frac{s}{s_\epsilon }\right) \right] .\nonumber \\ \end{aligned}$$

(23)

Theorem 3

On the sliding surface, the fractional-order error dynamical system (23) is a linear fractional-order dynamical system with bounded input $-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right)$. Also, the fractional-order error dynamical system (23) is asymptotically stable.

Proof

Consider the fractional-order error dynamical system (23) and note that, the values of input linguistic $\frac{s}{s_\epsilon }$ and their corresponding output values $FFISM(\bullet )$ are defined in $[-1,1]$, see Figs. 1 and 2. Thus, the function $FFISM\left( \frac{s}{s_\epsilon }\right)$ is bounded. Since any constant multiple of a bounded function is bounded, then $-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right)$ is also bounded.

In (23), $A$ is a coefficient matrix of linear parts of the fractional-order system (8), and $C$ and $M$ are parameter matrices whose entries are in the real line. Hence, the fractional order error dynamical system (23) has no nonlinear terms.

According to Theorem 2 in the sliding surface, the fractional-order error system (23) is a linear fractional order system with bounded input $-C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right)$.

Choose the appropriate values of the matrices $C$ and $M$ such that $|arg(eig(C^{-1}(A+M)))|>\frac{\beta \pi }{2}$, then the fractional order error dynamical system (23) is asymptotically stable by Theorem 1.

Theorem 4

Consider the proposed control input (22). If $K>0$ and $s_\epsilon >0$, then the state trajectories of the fractional-order error dynamical system (23) will converge to the sliding surface $s=0$. That is, the synchronization between the fractional order dynamical systems (8) and (9) is globally asymptotically stable.

Proof

Choose a Lyapunov candidate function as

$$\begin{aligned} V=s^2. \end{aligned}$$

(24)

The time derivative of (24) is given by

$$\begin{aligned} \dot{V}&= 2s\dot{s}\nonumber \\&= 2s\left[ C(BE+u(t))-(A+M)E\right] \nonumber \\&= 2s\left[ C(BE+u_{eq}(t)+u_{sw}(t))-(A+M)E\right] \nonumber \\&= 2s\left[ C\left( BE+C^{-1}(A+M)E-BE\right. \right. \nonumber \\&\left. \left. -C^{-1}K.FFISM\left( \frac{s}{s_\epsilon }\right) \right) -(A+M)E\right] \nonumber \\&= 2s\left[ -K.FFISM\left( \frac{s}{s_\epsilon }\right) \right] \nonumber \\&= -2s.K.FFISM\left( \frac{s}{s_\epsilon }\right) \end{aligned}$$

(25)

Thus, outside the boundary layer (that is, $|s|>s_\epsilon$), we have

$$\begin{aligned} \dot{V}&= -2K.s.FFISM(s)\nonumber \\&= -2K.|s|<0. \end{aligned}$$

(26)

Since $K>0$ and $|s(0)|>s_\epsilon$, then $|s|$ will strictly be decreased until it reaches the set $|s|\le s_\epsilon$ in a finite time and remains inside thereafter.

On the other hand, inside the boundary layer (that is, $|s|\le s_\epsilon$), we have

$$\begin{aligned} \dot{V}&= -2K.s.FFISM\left( \frac{s}{s_\epsilon }\right) =-2K.\frac{|s|}{s_\epsilon }<0. \end{aligned}$$

(27)

Thus, the Lyapunov candidate function $V$ is positive definite and its derivative $\dot{V}$ is negative definite. By Lyapunov stability theory, inside the boundary layer the synchronization between the fractional-order dynamical systems (8) and (9) is globally asymptotically stable.

Remark 1

Apart from the existing fuzzy sliding mode control for fractional systems in [33–36], the proposed FFISM control is fully suitable for synchronizing two identical and different fractional-order dynamical systems. Also, it is worthy for synchronizing integer order and fractional-order dynamical systems. Therefore, the proposed FFISM control is the generalization of the existing fuzzy sliding mode control presented in [33–36]. It will be easily visualized in the following section.

4 Theoretical application of the proposed FFISM control

In this section, the proposed FFISM control will be applied to synchronize two identical fractional order, two different fractional order, integer order and fractional-order modified coupled dynamos chaotic systems.

Consider the fractional-order modified coupled dynamos system [43], which is described by

$$\begin{aligned} \begin{aligned}&D^{\alpha }x_1(t)=-\mu x_1+x_2(x_3+\gamma ), \\&D^{\alpha }x_2(t)=-\mu x_2+x_1(x_3-\gamma ),\\&D^{\alpha }x_3(t)=x_3-x_1x_2, \end{aligned} \end{aligned}$$

(28)

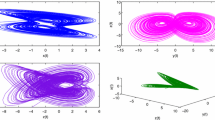
where $0<\alpha \le 1$, $D^{\alpha }$ is the $\alpha$-order differential operator in the sense of Caputo [41]. Here, $X=(x_1,x_2,x_3)^T\in \mathbb {R}^3$ is the state variable, and $\mu$ and $\gamma$ are the parameters of fractional-order system (28). The system (28) exhibits chaos when the fractional-order $\alpha \ge 0.87$ for the parameters $\mu =2$ and $\gamma =1$, for more details see [43]. The chaotic attractor corresponding to the system (28) when $\alpha =0.87$ is depicted in Fig. 3.

Fig. 3

Different portraits of the system (28) when $\alpha =0.87$ for $\mu =2$ and $\gamma =1$

Consider the fractional-order modified dynamos chaotic system (28) as the drive system and the following fractional-order modified dynamos chaotic system with control input as the response system.

$$\begin{aligned} \begin{aligned}&D^{\beta }y_1(t)=-\mu y_1+y_2(y_3+\gamma )+U_1, \\&D^{\beta }y_2(t)=-\mu y_2+y_1(y_3-\gamma )+U_2,\\&D^{\beta }y_3(t)=y_3-y_1y_2+U_3, \end{aligned} \end{aligned}$$

(29)

where $0<\beta \le 1$, $D^{\beta }$ is the $\beta$-order differential operator in the sense of Caputo [41]. Here, $Y=(y_1,y_2,y_3)^T\in \mathbb {R}^3$ is the state variable, $U=(U_1,U_2,U_3)^T$ and $E=Y-X=(e_1,e_2,e_3)^T$.

Assume that the fractional orders $\alpha ,\beta \ge 0.87$, the parameters $\mu =2,\gamma =1$ and the initial conditions of the drive system (28) and the response system (29) are $(x_1(0),x_2(0),x_3(0))=(1,2,-3)$ and $(y_1(0),y_2(0),y_3(0))=(-1,-2,0)$, respectively.

From (28) and (29),

$$\begin{aligned}&A=B=\left( \begin{array}{ccc} -\mu &{} \gamma &{} 0 \\ -\gamma &{} -\mu &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right) ,\ F(X)=\left( \begin{array}{c} x_2x_3 \\ x_1x_3\\ -x_1x_2 \end{array} \right) ,\\&G(Y)=\left( \begin{array} {c} y_2y_3 \\ y_1y_3\\ -y_1y_2 \end{array} \right) . \end{aligned}$$

Now, we fix the constants $K=(K_1,K_2,K_3)^T=(5,3,4)^T$ and $s_\epsilon =0.05$. The parameter matrices $C$ and $M$ are selected as

$$\begin{aligned} C=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right) , \ M=\left( \begin{array}{ccc} \mu -c_1 &{} -\gamma &{} 0\\ \gamma &{} \mu -c_2 &{} 0\\ 0 &{} 0 &{} -(c_3+1) \end{array} \right) . \end{aligned}$$

where $c_i>0$ for $i=1,2,3$.

By (22), the total control input can be written as

$$\begin{aligned} \left( \begin{array} {c} U_1\\ U_2\\ U_3 \end{array} \right)&= D^{\beta }\left( \begin{array} {c} x_1\\ x_2\\ x_3 \end{array} \right) -\left( \begin{array} {c} y_2y_3 \\ y_1y_3\\ -y_1y_2 \end{array} \right) -\left( \begin{array} {ccc} -\mu &{} \gamma &{} 0 \\ -\gamma &{} -\mu &{} 0\\ 0 &{} 0 &{} 1 \end{array} \right) \nonumber \\&\left( \begin{array} {c} y_1\\ y_2\\ y_3 \end{array} \right) +\left( \begin{array} {ccc} -c_1 &{} 0 &{} 0 \\ 0 &{} -c_2 &{} 0\\ 0 &{} 0 &{} -c_3 \end{array} \right) \left( \begin{array} {c} y_1-x_1\\ y_2-x_2\\ y_3-x_3 \end{array} \right) \nonumber \\&-\left( \begin{array} {c} K_1.FFISM\left( \frac{s_1}{s_\epsilon }\right) \\ K_2.FFISM\left( \frac{s_2}{s_\epsilon }\right) \\ K_3.FFISM\left( \frac{s_3}{s_\epsilon }\right) \end{array} \right) \end{aligned}$$

(30)

According to (23), the fractional-order error dynamical system can be written as

$$\begin{aligned} D^{\beta }\left( \begin{array} {c} e_1\\ e_2\\ e_3 \end{array} \right) (t)&= C^{-1}(A+M)\left( \begin{array} {c} e_1\\ e_2\\ e_3 \end{array} \right) \nonumber \\&-\,C^{-1}\left( \begin{array} {c} K_1.FFISM\left( \frac{s_1}{s_\epsilon }\right) \\ K_2.FFISM\left( \frac{s_2}{s_\epsilon }\right) \\ K_3.FFISM\left( \frac{s_3}{s_\epsilon }\right) \end{array} \right) \nonumber \\&= \left( \begin{array} {ccc} -\,c_1 &{} 0 &{} 0 \\ 0 &{} -c_2 &{} 0\\ 0 &{} 0 &{} -c_3 \end{array} \right) \left( \begin{array} {c} e_1\\ e_2\\ e_3 \end{array} \right) \nonumber \\&\quad -\left( \begin{array} {c} K_1.FFISM\left( \frac{s_1}{s_\epsilon }\right) \\ K_2.FFISM\left( \frac{s_2}{s_\epsilon }\right) \\ K_3.FFISM\left( \frac{s_3}{s_\epsilon }\right) \end{array} \right) . \end{aligned}$$

(31)

The eigenvalues of the matrix $C^{-1}(A+M)$ are $\lambda _1=-c_1,\lambda _2=-c_2$ and $\lambda _3=-c_3$. Hence, $|arg(\lambda _i)|>\frac{\beta \pi }{2}$ for every $i=1,2,3$. By Theorem 3, the fractional-order error dynamical system (31) is asymptotically stable. According to Theorem 4, the state trajectories of the fractional-order error dynamical system (31) are converging to the sliding surface $s=0$. Hence, the synchronization between the systems (28) and (29) is achieved for every fractional-order $\alpha ,\beta \ge 0.87$.

4.1 Numerical simulations

In this subsection, the synchronization between the systems (28) and (29) will be numerically demonstrated with different possibilities of fractional orders $\alpha$ and $\beta$. Assume that the values $c_1, c_2$ and $c_3$ are 15, 10 and $10$, respectively.

• Case (i): Identical fractional orders ($\alpha =\beta$ and $\alpha \ne 1\ne \beta$).

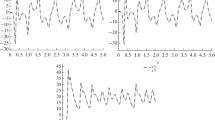
  If $\alpha =\beta =0.97$, then the projection of the synchronized attractors of the drive system (28) and response system (29) are depicted in Fig. 4. Further, the time response between the states of (28) and (29) and their synchronization errors are depicted in Fig. 5. Hence, the synchronization between two identical fractional-order systems is realized.

• Case (ii): Two different fractional orders ($\alpha \ne \beta \ne 1$).

  If $\alpha =0.91$ and $\beta =0.97$, then the projection of the attractors between the synchronized systems (28) and (29) are depicted in Fig. 6. The time response between their states and synchronization errors are depicted in Fig. 7. Hence, the synchronization between two different fractional-order systems is realized.

• Case (iii): Integer order and fractional-order (either $\alpha =1$ or $\beta =1$).

  If $\alpha =1$ and $\beta =0.91$, then the projection of the synchronized attractors of the systems (28) and (29) are depicted in Fig. 8. The time response between their states and synchronization errors are depicted in Fig. 9. Hence, the synchronization between integer order and fractional-order systems is realized. Further, the Remark 1 is numerically conformed by the above three cases.

Fig. 4

Projection of the synchronized attractors of the drive system (28) when $\alpha =0.90$ and the response system (29) when $\beta =0.90$

Fig. 5

The time response when $\alpha =\beta =0.90$: a $x_i$ and $y_i$ and b synchronization errors $e_i$, $i=1,2,3$

Fig. 6

Projection of the synchronized attractors of the drive system (28) when $\alpha =0.91$ and the response system (29) when $\beta =0.97$

Fig. 7

The time response when $\alpha =0.91, \beta =0.97$: a $x_i$ and $y_i$ and b synchronization errors $e_i$, $i=1,2,3$

Fig. 8

Projection of the synchronized attractors of the drive system (28) when $\alpha =1$ and the response system (29) when $\beta =0.91$

Fig. 9

The time response when $\alpha =1,\beta =0.91$: a $x_i$ and $y_i$ and b synchronization errors $e_i$, $i=1,2,3$

5 Practical application of the proposed FFISM control

In this section, a new cryptosystem for an image encryption and decryption will be developed based on the derived synchronized fractional-order modified coupled dynamos chaotic systems.

Proposed cryptosystem:

In the proposed cryptosystem, we assume that Alice as a sender and Bob as a receiver. Consider the fractional-order drive system (28) as a sender system and the fractional-order response system (29) with the proposed FFISM control (30) as a receiver system. Both Alice and Bob agree on the fractional orders $\alpha ,\beta$ such that $\alpha ,\beta \ge 0.87$. Assume that, the synchronization errors between the systems (28) and (29) tend to zero after a time $t_0$. The details of the proposed cryptosystem are given in Table 1, which include key generation, encryption and decryption phase. The following steps are needed to understand the encryption and decryption phase easily.

• 1. Alice and Bob compute the solutions of the fractional order systems (28) and (29), respectively, at time $t\ge t_0$.

• 2. The secret keys $\left\{ KA_R,KA_G,KA_B\right\}$ and $\{KB_R,KB_G,KB_B\}$ are generated by Alice and Bob, respectively, by using key generation phase given in Table 1.

• 3. Alice wants to send a RGB image $I$ with size $m\times n$ to Bob secretly. For encryption, she decomposes $I$ into Red, Green and Blue color components.

• 4. Each color component of the image $I$ is encrypted separately by Alice and let it be $E_R, E_G$ and $E_B$. The encrypted images $E_R,E_G$ and $E_B$ are converted into a single encrypted RGB image and let it be $E$. Alice sends $E$ to Bob. The details of the encryption process are presented in Table 1.

• 5. Bob receives $E$ from Alice. For decryption, he decomposes $E$ into their color components $E_R,E_G$ and $E_B$.

• 6. Each color component of the $E$ is decrypted separately by Bob and let it be $D_R, D_G$ and $D_B$. The decrypted images $D_R,D_G$ and $D_B$ are converted into a single decrypted RGB image and let it be $D$. The details of the decryption process are presented in Table 1.

• 7. Finally, Bob recovers an original image $D=I$ successfully.

Table 1 Proposed cryptosystem

5.1 Numerical example

In order to demonstrate the proposed cryptosystem, we assume that $\alpha =\beta =0.90$ and $t=4.5$. For these fractional orders, the synchronization errors between the drive system (28) and the response system (29) are zero after a time $t\ge t_0=0.3$ since by Fig. 5. Alice finds $x_1(t)=0.8880,\ x_2(t)=0.7168, \ x_3(t)=4.6260$ and generates on her own secret keys

$$\begin{aligned} KA_{R}&=\hbox {floor}\left( (x_1(t)x_2(t))*10^3\right) =124 \, \hbox {mod}\,256\\ KA_{G}&=\hbox {floor}\left( (x_2(t)x_3(t))*10^3\right) =243 \, \hbox {mod}\,256\\ KA_{B}&=\hbox {floor}\left( (x_1(t)x_3(t))*10^3\right) =11 \, \hbox {mod}\,256 \end{aligned}$$

Similarly, Bob solves the fractional-order system (29) and generates on his own secret keys $KB_{R},KB_{G},KB_{B}$. Alice wants to send a RGB image $I$ with size $650\times 487$ to Bob, which is visualized in Fig. 10a. The Red, Green and Blue color components of $I$ are depicted in Fig. 11a–c, respectively. Then, Alice encrypts the color components of $I$. The encrypted color components $E_R, E_G$ and $E_B$ are depicted in Fig. 12a–c, respectively. Alice converts $E_R, E_G$ and $E_B$ into a single encrypted RGB image $E$ and sends to Bob, which is depicted in Fig. 10b.

Fig. 10

a An original RGB image $I$, b encrypted image $E$ and c decrypted image $D$

Fig. 11

Color components of $I$: a Red, b Green and c Blue

Fig. 12

Color components of $E$: a Red $(E_R)$, b Green $(E_G)$ and c Blue $(E_B)$

Bob receives $E$ and decomposes into Red, Green and Blue color components, respectively, equivalent to $E_R, E_G$ and $E_B$. Then, he decrypts the color components of $E$. The decrypted color components $D_R,D_E$ and $D_B$ are depicted in Fig. 13a–c, respectively. Bob converts $D_R,D_E$ and $D_B$ into a single decrypted RGB image $D$, which is depicted in Fig. 10c. Hence, Bob decrypts an original image $I$ without loss of any information from $I$.

Fig. 13

Color components of $D$: a Red $(D_R)$, b Green $(D_G)$ and c Blue $(D_B)$

5.2 Performance analysis of the proposed cryptosystem

In this subsection, the key sensitivity of proposed cryptosystem will be analyzed. Also, three major statistical analysis of an image, namely histogram, entropy and the correlation will be analyzed to prove the efficiency of the proposed cryptosystem.

5.2.1 Key sensitivity analysis

In the proposed cryptosystem, the sender and receiver keys are generated based on the solutions of fractional-order chaotic systems. Naturally, chaotic systems are very sensitive depends on initial conditions. But the fractional-order chaotic system is a generalization of integer order chaotic system, which is more sensitive depends on initial conditions and the fractional order of state variables. The proposed cryptosystem have some secret elements: $(i)$ initial conditions of the drive system $x_i(0)$ and the response system $y_i(0)$, $(ii)$ parameters $\mu$ and $\gamma$, $(iii)$ fractional orders $\alpha$ and $\beta$, $(iv)$ time $t$ and $(v)$ solutions $x_i(t)$ and $y_i(t)$ of the fractional-order drive system (28) and response system (29), respectively. Therefore, the keys are highly sensitive due to the hardness of $(i)-(v)$. These high sensitivity keys are used in the proposed cryptosystem for encryption and decryption. Therefore, original image cannot be decrypted correctly except by the receiver.

5.2.2 Histogram analysis

Histogram analysis indicates the distribution of pixel value, and it can represent how pixels in an RGB image are spread by marking out the number of pixels at each intensity level. The histogram of an original RGB image $I$ (Fig. 10a), encrypted RGB image $E$ (Fig. 10b) and decrypted RGB image $D$ (Fig. 10c) are depicted in Fig. 14a–c, respectively. To keep the attacker from receiving any useful statistical information, the histogram of the encrypted image should be uniform. Note that, the histogram of an encrypted image $E$ is always uniform, and it is entirely different from the histogram of $I$, see Fig. 14b. Comparing the histograms of the encrypted image showed in [44] and [45], the encrypted image histogram of the proposed cryptosystem is completely uniformly distributed. Hence, through the proposed cryptosystem, one can achieve high-level security for image encryption and decryption.

Fig. 14

Histogram: a original image $I$ , b encrypted image $E$ and c decrypted image $D$

From the visualization of histograms of the original and decrypted images, we conclude that an original image is completely recovered by decryption. Further, the histograms of Red, Green and Blue color components of $I$ are depicted in Fig. 15a–c, respectively. The histograms of encrypted Red, Green and Blue color components of $I$ are depicted in Fig. 16a–c, respectively.

Fig. 15

Histogram of color components of $I$: a Red, b Green and c Blue

Fig. 16

Histogram of color components of $E$: a Red $(E_R)$, b Green $(E_G)$ and c Blue $(E_B)$

5.2.3 Information entropy analysis

Information entropy is an important quantitative measure of the randomness and the unpredictability of an information source. It can be computed by the following formula

$$\begin{aligned} H(X)=-\sum _{i=0}^{2^N-1}P_r(x_i)\log _2P_r(x_i), \end{aligned}$$

(32)

where $P_r(X=x_i)=1/F$, $F$ is the number of intensity scales associated with the image format. $X$ is the source, and $x_i$ denotes the $i$th possible value in $X$, and $P_r(x_i)$ is the probability of $x_i$.

In the proposed cryptosystem, RGB image is used for encryption and decryption, therefore $F=256$ and the upper bound of an information entropy is 8. A good encrypted image has entropy very close to 8. Information entropy value of the original RGB image $I$ (Fig. 10a), encrypted RGB image $E$ (Fig. 10b) and decrypted RGB image $D$ (Fig. 10c) are displayed in Table 2. The calculated information entropy value of encrypted image $E$ is 7.9998, and it is very close to the upper bound of the information entropy value. This entropy value is higher than the entropy value of existing encryption algorithms analyzed in [44–46]. Further, the original image is completely decrypted only by the receiver because the entropy value is same for an original image $I$ and the decrypted image $D$, see Table 2. Hence, the proposed cryptosystem is a good cryptosystem for an image encryption and decryption.

Table 2 Results of information entropy

5.2.4 Correlation coefficient analysis

In an ordinary image, each pixel is highly correlated with its adjacent pixel in horizontal, vertical and diagonal direction. A good encryption scheme should produce an encrypted image with very low correlation in the adjacent pixels. To test the correlation between horizontally, vertically and diagonally adjacent pixels of the original image $I$ and encrypted image $E$, we calculate the correlation coefficient $r_{xy}$ of each pair in each direction by the following formula

$$\begin{aligned} r_{xy}=\frac{cov(x,y)}{\sqrt{D(x)}\sqrt{D(y)}}, \end{aligned}$$

(33)

where $cov(x,y)=\frac{1}{N}\sum _{i=1}^{n} (x_i-E(x))(y_i-E(y))$, $E(x)\!=\!\frac{1}{N}\sum _{i=1}^{n} (x_i)$ and $D(x)\!=\!\frac{1}{N}\sum _{i=1}^{n} (x_i-E(x))^2$.

The outcomes of correlation coefficients of images $I$ and $E$ are shown in Table 3. The result indicates that the correlation of two adjacent pixels in horizontal, vertical and diagonal directions of the original RGB image $I$ is significant, whenever the encrypted RGB image $E$ is very small and close to zero. Hence, the proposed encryption scheme is effect rather well than the encryption algorithms demonstrated in [44–46].

Table 3 Correlation coefficients for original image and encrypted image

Remark 2

The experimental results show that the proposed cryptosystem is more secure than other existing algorithms proposed in [44–46].

6 Conclusions

A new fuzzy fractional integral sliding mode control has been designed which unites the fuzzy logic control and sliding mode control for synchronizing fractional-order dynamical systems with mismatched fractional orders. The stability condition of synchronization between fractional-order dynamical systems has been derived and guaranteed based on Lyapunov stability theory. The proposed control has been applied in fractional-order modified coupled dynamos chaotic system. We have proven that, it has been easily adapted for synchronizing two distinct, alike fractional order dynamical systems, integer order and fractional-order dynamical systems. A new cryptosystem has been proposed for an image encryption and decryption by using synchronized fractional-order modified coupled dynamos chaotic systems. The proposed cryptosystem has been producing high-level security and it has been verified through experimental results. Finally, numerical simulations have been provided to verify the effectiveness of the proposed control scheme and cryptosystem.