Sliding mode control of fractional order nonlinear differential inclusion systems

Abstract

In this paper, variable structure control is utilized for stabilization of a particular class of nonlinear polytopic differential inclusion systems with fractional-order-0 < q < 1. By defining a sliding surface with fractional integral formula and obtaining sufficient conditions for stability of the sliding surface, a special feedback law is presented which enables the system states to reach the sliding surface and consequently creates a sliding mode control. Finally, the performance of the proposed method is illustrated with examples and related numerical simulations results.

1 Introduction

Differential inclusion (DI) is an effective tool for analysis of uncertain, nonlinear and hybrid as well as switching and time-variant systems. DI has been developed based on the absolute stability theory (Aizerman and Gantmacher 1964). Many practical systems contain uncertainties which may lead to a suddenly change of a trajectory of a differential equation that can be described more properly by differential inclusions. Numerous practical systems have been reported in the literature which employ equations described by differential inclusion (Boyd et al. 1994; Leine and van de Wouw 2008). On the other hand, fractional calculus, which dates back to 1695, has been the focus of much attention in recent years. This is due to the applicability of equations based on fractional derivatives in modeling various practical and engineering systems (Arena et al. 2000; Baleanu et al. 2010; Ferreira et al. 2004; Sabatier et al. 2007; Valerio and Sa da Costa 2004; Ortigueira 2008). Some of these systems include electromagnetic waves, fractal electrical networks, electrical machines, visco-elastic materials and systems, quantum evolution of complex systems, heat conduction, and robotics.

Consequently, the study of fractional-order polytopic differential inclusion (FOPDI) instead of PDI seems indispensable. In general, FOPDI systems are a more generalized form of fractional differential equations and systems, and have been studied in various research articles, including (Chang et al. 2009; Ouahab 2008; Benchohra et al. 2008; Ahn and Chen 2008). This paper deals with the sliding mode control of FOPDI systems. Variable structure controllers (VSCs) with sliding mode proposed by Utkin (1977) are used to achieve an effective closed loop control of these systems. The main advantage of the VSC approach is that the variable structure can potentially be exploited to improve the control performance criterions such as the robustness and fast time response. The VSC strategy is based on the concept of an attractive manifold, upon which the underlying state of vector space and the desired dynamic is assured. During sliding motion, the system has invariance properties and is independent of parameter uncertainty and disturbance. Therefore, design of the sliding manifold determines the performance of the system. It is well known that sliding mode control is capable of tracking various trajectories for nonlinear systems with modeling uncertainty, when the upper bound of the inaccuracies is known. Sliding mode controller design for system of fractional orders was also developed and discussed in research papers. Variable structure control that defined the sliding surface for linear time invariant fractional order systems (LTI-FOS) was introduced in (El-Khazali et al. 2004a) and further developed in (El-Khazali et al. 2006). Variable structure control systems for LTI-FOS with time delay using specification of sliding surface without any limitations on input controls is considered in (El-Khezali and Ahmad 2006c). Authors in (Si-Ammour et al. 2009) have considered the design of sliding control for LTI-FOS with time delay in control input. The linear matrix inequality (LMI) approach is used in (Rubio et al. 2011; Cao and Frank 2000). In (Balochian et al. 2011) definition of the sliding sector based on the LMI approach in fractional order system has been presented. Then, design of a VSC for the LTI-FOS using a finite number of control gains with the aim of obtaining a decreasing Lyapunov function was introduced. Also, in (Tavazoei and Haeri 2008) has proposed a controller based on active sliding mode theory to synchronize chaotic fractional order systems in a master–slave structure.

First, we will review the advancements made in control and stabilization of integer order PDI systems. In (Cai et al. 2009), a saturated control design for LDIs subject to disturbance has been presented. (Liu et al. 2010) has focused on robust stabilization of delayed linear differential inclusion systems with nonlinear feedback law. In (Hu et al. 2007), a nonlinear control design method for LDIs has been presented by using quadratic Lyapunov functions of their convex hull. In (Sun 2009), a frequency domain approach has been proposed to analyze the globally asymptotic stability of DI systems with discrete and distributed time-delays. (Gao et al. 2007) has focused on delay-dependent and parameter-dependent robust stability criterion for linear continuous-time systems with polytopic parameter uncertainties and time-varying delay in the state. In (Chen 2001), the problem of tracking control of nonlinear uncertain dynamical systems described by DIs has been studied. In (Wu 2006), the control Lyapunov function method has been used to solve the stabilizing problem for single-input polytopic DI systems. In (Chen et al. 2006), the viable control problem for a class of uncertain nonlinear dynamical systems described by DI has been presented.

The main objective of this paper is to extend PDI stabilization concepts to FOPDI systems using sliding mode control and to extend the method used in (Salarieh and Alasty 2009) for FOPDI systems with fractional order of 0 < q < 1. The proposed sliding mode control in this paper is the first attempt in the control of nonlinear FOPDI systems with input disturbance. The paper is organized as follows. In Sect. 2, a review of fractional calculus and FOPDI systems is presented. Section 3, presents the problem formulation and the main results of this paper which includes a definition of the sliding surface for FOPDI systems and the design of a new state feedback law for convergence of the state of the FOPDI systems to stabilize the sliding surface in finite time. Finally, simulation results are provided in Sect. 4 to illustrate the main results of the paper.

2 Preliminaries

Fractional order derivative and integral:

Let f: [0, +∞) → (−∞, +∞) be a real-valued function. The Riemann–Liouville fractional integral and derivative operators of order q are defined as

$$ \begin{aligned} {}_{0}D_{t}^{q} f(t) &=& \frac{1}{\Upgamma (n - q)}\left( \frac{d}{dt} \right)^{n} \int\limits_{0}^{t} {\frac{f(\tau )}{{(t - \tau )^{q - n + 1} }}d\tau }\\ & \quad (n - 1) \le q < n \\ \end{aligned}$$

(1)

where n is an integer and q is a real number. Γ(.) is the Gamma function generalizing factorial for non-integer arguments.

$$ \Upgamma (q) = \int\limits_{0}^{\infty } {e^{ - t} t^{q - 1} dt} $$

If 0 < q < 1, the Riemann–Liouville fractional derivative and integral operators of order q are defined as

$$ {}_{0}D_{t}^{q} f(t) = \frac{1}{\Upgamma (1 - q)}\frac{d}{dt}\int\limits_{0}^{t} {(t - \tau )^{ - q} f(\tau )d\tau } $$

and

$$ {}_{0}I_{t}^{q} f(t) = \frac{1}{\Upgamma (q)}\int\limits_{0}^{t} {(t - \tau )^{q - 1} f(\tau )d\tau } $$

respectively. From the above definition, note that (Si-Ammour et al. 2009)

$$ _{0} D_{t}^{q} = \frac{d}{dt}({}_{0}I_{t}^{1 - q} ) $$

Another definition for the fractional derivative is the

Grünwald–Letnikov definition:

$$ {}_{0}D_{t}^{q} f(t) = \mathop {\lim }\limits_{N \to \infty } \left[ \frac{t}{N} \right]^{ - q} \sum\limits_{j = 0}^{N - 1} {( - 1)^{j} } \left( \begin{gathered} q \hfill \\ j \hfill \\ \end{gathered} \right)f(t - j\left[ \frac{t}{N} \right]) $$

This paper adopts the Grünwald–Letnikov definition and Riemann–Liouville definition of the fractional differ-integration operators (Podlubny 1999).

A Fractional Order Differential Inclusion (FODI) system is described by ${}_{0}D_{t}^{q} x(t) \in F\left( {x(t),t} \right),\quad x(0) = x_{0}$ where F is a set-valued function on R ⁿ × R ₊. Any x: R ₊ → R ⁿ that satisfies the above FODI is called a solution or trajectory of the FODI.

A fractional order linear differential inclusion (FOLDI) is given by:

$$ {}_{0}D_{t}^{q} x(t) \in \Upomega x(t),\quad x(0) = x_{0} $$

where Ω is a subset of R ^n×n.

Some specific classes of the FOLDI systems are the fractional order linear time invariant systems and the polytopic FOLDI systems.

In the case that Ω is a singleton, the FOLDI system reduces to a fractional order linear time invariant (FOLTI) system. FOLTI systems can be represented in the following state space form:

$$ \left\{ \begin{gathered} {}_{0}D_{t}^{q} X(t) = AX(t) + BU(t) + B_{w} W(t),\quad x(0) = x_{0} \hfill \\ y(t) = CX(t) + DU(t) + D_{w} W(t) \hfill \\ \end{gathered} \right. $$

where

$$ \Upomega = \left\{ {\left[ {\begin{array}{*{20}c} A & B & {B_{w} } \\ C & D & {D_{w} } \\ \end{array} } \right]} \right\}, $$

and $X(t) \in R^{n} ,\quad U(t) \in R^{{n_{u} }} ,\quad W(t) \in R^{{n_{w} }} ,\quad y(t) \in R^{p}$ are the state, the control input, the exogenous input, and the output vectors of the system, respectively and ${A} \in R^{n \times n} ,\,\quad {B} \in R^{{n \times n_{u} }} ,\,\quad B_{w} \in R^{{n \times n_{w} }} ,\;C \in R^{p \times n} ,\quad \,D_{w} \in R^{{p \times n_{w} }} ,\quad \,D \in R^{{p \times n_{u} }}$, and q is the fractional commensurate order. It has been shown that the system D ^q X(t) = AX(t) is asymptotically stable if the following condition is satisfied (Matignon 1998)

$$ \left| {\arg (eig(A))} \right| > \frac{q\pi }{2} $$

where 0 < q < 2, and eig(A) are eigenvalues of the matrix A.

In the case that Ω is a polytope, the FOLDI is called polytoic FOLDI or FOPLDI. Most of our results require that Ω be described by a list of its vertices, i.e., in the form

$$ Conv\left\{ {\left[ {\begin{array}{*{20}c} {A_{1} } & {B_{1} } & {B_{w,1} } \\ {C_{1} } & {D_{1} } & {D_{w,1} } \\ \end{array} } \right], \ldots ,\left[ {\begin{array}{*{20}c} {A_{L} } & {B_{L} } & {B_{w,L} } \\ {C_{L} } & {D_{L} } & {D_{w,L} } \\ \end{array} } \right]} \right\}. $$

or,

$$ \Upomega \in Conv\left\{ {A_{i} ,B_{i} ,B_{w,i} ,C_{i} ,D_{i} ,D_{w,i} } \right\},\quad i = 1, \ldots ,L $$

where the above matrices are given.

In the case that F is a polytope, the FODI is called polytoic FODI or FOPDI. Most of our results require that F be described by a list of its vertices, i.e., in the form conv{f ₁,…, f _L }or,

$$ F \in conv\left\{ {f_{i} } \right\},\,\quad i = 1, \ldots ,L $$

where f _i are given.

3 Main results

Consider the following fractional order polytopic nonlinear differential inclusion (FO-PNDI):

$$ _{0} D_{t}^{q} x\left( t \right) \in Conv\left\{ {f_{i} \left( x \right) + h_{i} \left( x \right)\left( {u\left( t \right) + w\left( t \right)} \right)} \right\},\quad i = 1,2, \ldots ,N $$

(2)

where 0 < q < 1, x(t), and u(t) ∈ R ⁿ are, respectively, the state and input of the system, w(t) is a bounded disturbance, i.e., ‖w(t)‖ < γ, with a positive constant γ. Conv{.} denotes the convex hull of a set, f _i (x) ∈ R ⁿ is smooth vector-valued function. h _i (x) ∈ R ^n×n,  are vector-valued functions that can be decomposed as h _i (x) = g _i (x)B where g _i (x) > 0 are smooth function and B ∈ R ^n×n is a full rank matrix. The main objective of this paper is stabilization of the FOPDI systems Eq. 2 using sliding mode control.

Using the results of convex analysis, a differential inclusion system can be described using convex combination as an uncertainty system (Smironov 2002). Accordingly, system (2) can be equivalently written as an uncertainty system:

$$ _{0} D_{t}^{q} x\left( t \right) = \sum\limits_{i = 1}^{N} {\alpha_{i} \left( {f_{i} \left( x \right) + g_{i} \left( x \right)B\left( {u\left( t \right) + w\left( t \right)} \right)} \right)} $$

(3)

where α _i are indeterminate parameters which satisfy α _i  ≥ 0 and $\sum\nolimits_{i = 1}^{N} {\alpha_{i} = } 1$.

Let us assume the following definition of the sliding surface and use it to stabilize the system (2)

$$ S(x,t) = I^{1 - q} X(t), $$

(4)

After calculating the derivative of the sliding surface and substituting (3) in it, we have:

$$ \dot{S} = \frac{d}{dt}I^{1 - q} x(t) = {}_{0}D_{t}^{q} x(t) = \sum\limits_{i = 1}^{N} {\alpha_{i} f_{i} (x)} + \sum\limits_{i = 1}^{N} {\alpha_{i} g_{i} (x)Bu(t)} + \sum\limits_{i = 1}^{N} {\alpha_{i} g_{i} (x)Bw(t)} . $$

(5)

Lemma 1 The nonlinear fractional order differential inclusion system (2) with control input u(t) as

$$ u(t) = \frac{{ - B^{ - 1} }}{a(x)}\left( {k\frac{S(t)}{{\left\| {S(t)} \right\|}}} \right) $$

(6)

converges to the sliding surface in (4) in finite time and remains on it, where

$$ \begin{gathered} a(x) = Min\left\{ {\left| {g_{1} (x)} \right|,\left| {g_{2} (x)} \right|, \ldots ,\left| {g_{N} (x)} \right|} \right\} \hfill \\ b(x) = Max\left\{ {\left| {g_{1} (x)} \right|,\left| {g_{2} (x)} \right|, \ldots ,\left| {g_{N} (x)} \right|} \right\} \hfill \\ d(x) = Max\left\{ {\left\| {f_{1} (x)} \right\|,\left\| {f_{2} (x)} \right\|, \ldots \left\| {f_{N} (x)} \right\|} \right\} \hfill \\ k = d(x) + b(x)\left\| B \right\|\gamma + \eta e^{ - \lambda t} \left\| {S(t)} \right\|^{1 - \delta } \hfill \\ \end{gathered} $$

and η > 0, λ > 0, 0 < δ ≤ 1.

Proof In order to show that u(t) in (6) leads to stabilization of system (2), we determine a Lyapunov candidate function and show that the Lyapunov candidate function variation is negative in the direction of the given system. If we consider the Lyapunov candidate function as

$$ V(t) = \frac{1}{2}S^{T} (t)S(t). $$

(7)

Using (5), its derivative satisfies

$$ \dot{V}(t) = S^{T} (t)\dot{S}(t) = S^{T} (t)\left( {\sum\limits_{i = 1}^{N} {\alpha_{i} f_{i} (x)} + \sum\limits_{i = 1}^{N} {\alpha_{i} g_{i} (x)Bu(t)} + \sum\limits_{i = 1}^{N} {\alpha_{i} g_{i} (x)Bw(t)} } \right) $$

(8)

Substituting (6) in (8), we have

$$ \dot{V}\left( t \right) = S^{T} \left( t \right)\dot{S}\left( t \right) = S^{T} \left( t \right)\left[ {\sum\limits_{i = 1}^{N} {\alpha_{i} f_{i} \left( x \right) - \frac{S\left( t \right)}{{\left\| {S\left( t \right)} \right\|}}\left( k \right)\frac{{\sum\nolimits_{i = 1}^{N} {\alpha_{i} g_{i} \left( x \right)} }}{a\left( x \right)} + \sum\limits_{i = 1}^{N} {\alpha_{i} g_{i} \left( x \right)Bw\left( t \right)} } } \right] $$

(9)

which results in,

$$ \dot{V}(t) < - \eta e^{ - \lambda t} \left\| {S(t)} \right\|^{2 - \delta } . $$

(10)

Consequently, the fractional differential inclusion system (2) will be stable with the controller given by Eq. 6. On the other hand,

$$ \dot{V}(t) = S^{T} (t)\dot{S}(t) = \frac{1}{2}\frac{d}{dt}\left\| {S(t)} \right\|^{2} = \left\| {S(t)} \right\|\frac{{d\left\| {S(t)} \right\|}}{dt} $$

(11)

According to (10) and (11), we have

$$ \frac{{d\left\| {S(t)} \right\|}}{dt} \le - \eta e^{ - \lambda t} \left\| {S(t)} \right\|^{1 - \delta } $$

(12)

Setting the time of reaching to the sliding surface as S(T) = 0 and integrating Eq. 12 from 0 to T gives

$$ \int\limits_{t = 0}^{T} {\frac{{d\left\| {S(t)} \right\|}}{dt}\left\| {S(t)} \right\|^{\delta - 1} dt} \le \int\limits_{t = 0}^{T} { - \eta e^{ - \lambda t} dt} $$

(13)

therefore according to integral formulas

$$ \left. {\frac{{\left\| {S(t)} \right\|^{\delta } }}{\delta }} \right|_{t = 0}^{t = T} \le \left. {\frac{{\eta e^{ - \lambda t} }}{\lambda }} \right|_{t = 0}^{t = T} \Rightarrow \left\| {S(T)} \right\|^{\delta } - \left\| {S(0)} \right\|^{\delta } \le \frac{\delta \eta }{\lambda }\left( {e^{ - \lambda T} - 1} \right) $$

(14)

substituting S(T) = 0

$$ 1 - \frac{\lambda }{\delta \eta }\left\| {S(0)} \right\|^{\delta } \le e^{ - \lambda T} $$

(15)

calculating T from Eq. 15, we have

$$ T \le \frac{ - 1}{\lambda }\ln \left( {1 - \frac{\lambda }{\delta \eta }\left\| {S(0)} \right\|^{\delta } } \right) $$

(16)

Since T is the time of reaching to the sliding surface and is positive, it is enough that the selected constants η, δ, and λ satisfy this condition:

$$ T \le \frac{ - 1}{\lambda }\ln \left( {1 - \frac{\lambda }{\delta \eta }\left\| {S(0)} \right\|^{\delta } } \right) . $$

(17)

Therefore, it is required to choose the constants η, δ, and λ such that the following condition be satisfied:

$$ 0 \le \frac{\lambda }{\delta \eta }\left\| {S(0)} \right\|^{\delta } < 1 $$

(18)

Consequently, with the controller given by (6), system (2) converges to the sliding surface and remains on it.

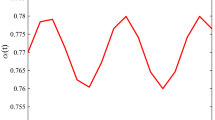
Remark a(x), b(x), and d(x) are functions of the states and the states change respect to time (t), therefore a(x(t)), b(x(t)), and d(x(t)) in each time can be calculated from Min{|g ₁(x(t))|, |g ₂(x(t))|,…, |g _N (x(t))|}, Max{|g ₁(x(t))|, |g ₂(x(t))|,…, |g _N (x(t))|}, and Max{‖f ₁(x(t))‖, ‖f ₂(x(t))‖,…‖f _N (x(t))‖} respectively. At the result u(t) can be calculated in each time from (6).

4 Simulation results

Example 1Consider the system in (2)

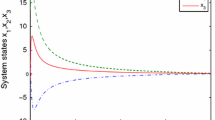
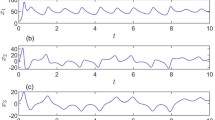
where i = 1, 2 and $f_{1} (x) = \left[ {\begin{array}{*{20}c} {\sin (x_{1} )} \\ {x_{2}^{2} } \\ \end{array} } \right],\,f_{2} (x) = \left[ {\begin{array}{*{20}c} {\left| {x_{2} } \right|} \\ {x_{1}^{2} } \\ \end{array} } \right],\,B = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\,g_{1} (x) = 1 + x_{2}^{2} ,\,g_{2} (x) = 1,\,q = 0.5,\,h = 0.001$, and the disturbance is in the form of, and the parameters η = 2, δ = 0.4, γ = 1, λ = 2. The simulation results with the proposed sliding mode controller, the above parameters and the initial condition $[x_{1} (0)\,x_{2} (0)]^{T} = [\begin{array}{*{20}c} 2 & { - 1} \\ \end{array} ]^{T}$ are shown in Figs. 1 and 2 for the different parameters α ₁, α ₂. Figures 1a and 2a are the time responses where the continuous state x(t) converges to the origin. Figures 1b and 2b give the control input u ₁(t) and Figs. 1c and 2c are the control input u ₂(t).

Fig. 1

Sliding mode control α ₁ = 1, α ₂ = 0 (sampling interval, h = 0.001 s)

Fig. 2

Sliding mode control α ₁ = 0.5, α ₂ = 0.5 (sampling interval, h = 0.001 s)

Example 2Consider the system in (2)

where i = 1, 2, 3 and $f_{1} (x) = \left[ {\begin{array}{*{20}c} {e^{{x_{1} }} } \\ {x_{2}^{2} } \\ \end{array} } \right],\,f_{2} (x) = \left[ {\begin{array}{*{20}c} {\left| {x_{2} } \right|} \\ {x_{1}^{2} } \\ \end{array} } \right],\,f_{3} (x) = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{1}^{2} + x_{2} } \\ \end{array} } \right],\;B = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\,g_{1} (x) = 1 + x_{2}^{2} ,\,g_{2} (x) = 2,\,g_{3} (x) = 1 + x_{1}^{2} ,\,q = 0.7,\,h = 0.002$, and the disturbance is in the form of $w(t) = \left[ {\begin{array}{*{20}c} 0 \\ {\sin (t)} \\ \end{array} } \right]$, and the parameters η = 2, δ = 0.4, γ = 1, λ = 2. The simulation results with the proposed sliding mode controller, the above parameters and the initial condition $[x_{1} (0)\,x_{2} (0)]^{T} = [ - \begin{array}{*{20}c} 1 & 2 \\ \end{array} ]^{T}$ are shown in Figs. 3 and 4 for the different parameters α ₁, α ₂, α ₃. Figures 3a and 4a are the time responses where the continuous state x(t) converges to the origin. Figures 3b and 4b give the control input u ₁(t) and Figs. 3c and 4c are the control input u ₂(t).

Fig. 3

Sliding mode control α ₁ = 1, α ₂ = 0, α ₃ = 0 (sampling interval, h = 0.002 s)

Fig. 4

Sliding mode control α ₁ = 0.3, α ₂ = 0.5, α ₃ = 0.2 (sampling interval, h = 0.002 s)

5 Conclusion

As it was mentioned, DI is one of the methods for modeling uncertainty and on the other hand, many practical and physical systems with exact coefficients cannot be modeled using fractional derivatives. As a result, this paper studies a special class of nonlinear FOPDI systems, and considers an important class of variable structure controls, i.e. sliding mode controls for stabilization of these systems. In fact, the concepts of sliding mode control are extended to these systems and simulation results are provided for illustrate the effectiveness of the proposed methodology.