Iterative identification of nonlinear dynamic systems with output backlash using three-block cascade models

Abstract

The paper deals with the parameter identification of nonlinear dynamic systems with both actuator and sensor nonlinearities using three-block cascade models with nonlinear static, linear dynamic and nonlinear dynamic blocks. Multiple application of a decomposition technique provides special expressions for the corresponding nonlinear model description that are linear in parameters. A least-squares-based iterative technique allows estimation of all the model parameters based on measured input/output data. Illustrative examples of nonlinear systems identification with two-segment polynomial input block and backlash output block characteristics are included.

1 Introduction

Cascade models are a popular type of block-oriented models in system identification. These models are used in mathematical modeling of nonlinear dynamic systems not only for their relative simplicity but also for their ability to approximate closely more general nonlinear systems, which are not necessarily of this form.

The simplest types of cascade nonlinear models consist of two blocks. The so-called Hammerstein model consists of a static nonlinear block followed by a linear dynamic block, and the so-called Wiener model consists of a linear dynamic block followed by a static nonlinear block. Generally, the Wiener model is supposed to represent sensor nonlinearities, while the Hammerstein model is supposed to represent actuator nonlinearities. These models appear in many engineering applications, and therefore, the identification of nonlinear dynamic systems using Hammerstein and Wiener models has been an active research area for many years. Some recent works dealing with the Hammerstein models can be found in [1–14], while the Wiener models are used e.g., in [15–24].

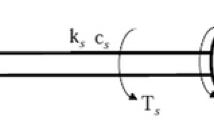
If the systems to be identified contain nonlinearities with memory such as backlash or hysteresis [25], the choice of Hammerstein or Wiener models is not appropriate, because the nonlinear static blocks cannot characterize these dynamic nonlinearities. Therefore, a special case of two-block models consisting of the cascade of linear dynamic and nonlinear dynamic blocks has to be used for modeling and identification of nonlinear dynamic systems with backlash or hysteresis. In analogy with the Wiener model, the cascade model structure consisting of a linear dynamic block followed by a nonlinear dynamic block (Fig. 1) was often used for the identification of nonlinear dynamic systems with output dynamic nonlinearities [26–29].

Fig. 1

Two-block cascade system

However, in some cases of more complex nonlinear dynamic systems with both input and output nonlinearities, the two-block cascade model may be not precise enough and it is appropriate to choose a three-block cascade model with combination of nonlinear static, linear dynamic, and nonlinear dynamic blocks (Fig. 2). It means, compared with the well-known structure of Hammerstein–Wiener model, that the output block contains dynamic nonlinearities, e.g., backlash or hysteresis. Actually, this form of three-block cascade model can be considered as a cascade of Hammerstein model and a dynamic nonlinearity block and significantly extends the applicability for more precise modeling and identification of real systems with both actuator and sensor nonlinearities. While more approaches to the identification of nonlinear dynamic systems using the structurally similar Hammerstein–Wiener model have been presented [30–34], up to now no results were published on the three-block cascade models with both static and dynamic nonlinearities.

Fig. 2

Three-block cascade system

In this paper, the three-block cascade model is used to the parameter identification of nonlinear dynamic systems with a complicated input nonlinearity and a backlash output nonlinearity (Fig. 3). The previous results on the decomposition of compound operators [35] are effectively applied to simplify the mathematical description of this complex system. The resulting model equation is without cross-multiplication of parameters; nevertheless, it contains more internal variables, which are generally unmeasurable. Application of a least-squares-based iterative algorithm enables estimation of all the model parameters on the basis of measured input/output data. Illustrative examples of three-block cascade systems identification with two-segment polynomial and backlash characteristics are included.

2 Three-block cascade model with output backlash

Let the three-block cascade model be given by the cascade connection of a nonlinear static block followed by a linear dynamic block, which is followed by a nonlinear dynamic block according to Fig. 3. Nonlinear static characteristics can be approximated by polynomials of appropriate degree. In some cases, the required accuracy of approximation and the type of nonlinearity can lead to polynomials with rather high degrees, e.g., if the characteristics are strongly/extremely asymmetric. The offset between the accuracy of approximation and the lowest possible degrees of approximating polynomials can be solved by considering two-segment polynomial approximations [36].

Fig. 3

Three-block cascade system with output backlash

Fig. 4

Two-segment nonlinearity

Let us assume the output of nonlinear static block $v(t)$ according to Fig. 4 significantly depends on the sign of input $u(t)$ and can be written as

$$\begin{aligned} v(t)=\left\{ {{\begin{array}{l} {\alpha (u(t))\quad \hbox { if }u(t)\ge 0} \\ {\beta (u(t))\quad \hbox { if }u(t)<0} \\ \end{array} }} \right. \end{aligned}$$

(1)

Introducing the following switching function

$$\begin{aligned} h(s)=\left\{ {{\begin{array}{l} {0\quad \hbox { if }s\ge 0} \\ {1\quad \hbox { if }s<0} \\ \end{array} }} \right. \end{aligned}$$

(2)

the relation between the inputs and outputs of assumed nonlinearity can be written as follows:

$$\begin{aligned} v(t) = \alpha (u(t)) + (\beta (u(t)) - \alpha (u(t))) h(u(t)). \end{aligned}$$

(3)

Let the nonlinear maps $f(.)$ and $g(.)$ be approximated by polynomials

$$\begin{aligned} \alpha (u(t))&= \sum _{k=1}^n {\alpha _k u^{k}(t)} \end{aligned}$$

(4)

$$\begin{aligned} \beta (u(t))&= \sum _{k=1}^n {\beta _k u^{k}(t)} \end{aligned}$$

(5)

Then, the nonlinear static block can be described by the following equation

$$\begin{aligned} v(t) = \sum _{k=1}^n {\alpha _k u^{k}(t)} + \sum _{k=1}^n {\gamma _k u^{k}(t)} h(u(t)) \end{aligned}$$

(6)

where

$$\begin{aligned} \gamma _k = \beta _k - \alpha _{k}. \end{aligned}$$

(7)

The linear dynamic block LD can be described by the difference equation

$$\begin{aligned} x(t)=\sum _{i=1}^r {a_i v(t-i)} -\sum _{j=1}^p {b_j x(t-j)} \end{aligned}$$

(8)

where $v(t)$ and $x(t)$ are the inputs and outputs of LD, respectively. It is assumed that $r$ and $p$ are known.

Let the nonlinear dynamic block ND be a backlash with inputs $x(t)$ and outputs $y(t)$ shown in Fig. 5. The backlash is a dynamic nonlinearity and can be described by the following first-order nonlinear difference equation [37]

$$\begin{aligned} y(t)&= m_L (x(t)+c_L )f_1 (t)+m_R (x(t)-c_R )f_2 (t)\nonumber \\&\quad +\,y(t-1)(1-f_1(t))(1-f_2 (t)) \end{aligned}$$

(9)

where $f_{1}(t)$ and $f_{2}(t)$ are auxiliary internal variables defined as:

$$\begin{aligned} f_1 (t)&= h(m_L x(t)+m_L c_L -y(t-1)) \end{aligned}$$

(10)

$$\begin{aligned} f_2 (t)&= h(y(t-1)-m_R x(t)+m_R c_R ) \end{aligned}$$

(11)

and $h(.)$ is the above-defined switching function.

Fig. 5

Backlash

The mathematical description of this cascade system resulting from direct substitutions of the corresponding variables from (6) into (8) and then into (9) is

$$\begin{aligned} y(t)&= m_L \left( \sum _{i=1}^r a_i \left( \sum _{k=1}^n {\alpha _k u^{k}} (t-i)\right. \right. \nonumber \\&\quad +\,\left. \sum _{k=1}^n {\gamma _k u^{k}(t-i)} h(u(t-i))\right) \nonumber \\&\quad -\,\left. \sum _{j=1}^p{b_j x(t-j)} +c_L \right) f_1 (t)\nonumber \\&\quad +\,m_R \left( \sum _{i=1}^r a_i \left( \sum _{k=1}^n {\alpha _k u^{k}} (t-i)\right. \right. \nonumber \\&\quad +\,\left. \sum _{k=1}^n {\gamma _k u^{k}(t-i)}h(u(t-i))\right) \nonumber \\&\quad -\,\left. \sum _{j=1}^p {b_j x(t-j)} -c_R \right) f_2 (t)\nonumber \\&\quad +\,y(t-1)(1-f_1(t))(1-f_2 (t)) \end{aligned}$$

(12)

The input–output Eq. (12) is strongly nonlinear both in the variables and in the parameters, hence not very suitable for the parameter estimation. To find a simpler form of this description, the so-called key-term separation principle will be applied [35]. Because of the cascade connection of three blocks, the parameterization of model (12) is not unique; many combinations of parameters can be found. Therefore, in at least two blocks, one parameter has to be fixed. Choosing $m_{L}\,=\,1$, we rewrite (9) as follows:

$$\begin{aligned} y(t)&= x(t)f_1 (t)+c_L f_1 (t)+m_R x(t)f_2 (t)\nonumber \\&\quad -\,m_R c_R f_2 (t)\!+\!y(t{-}1)(1{-}f_1 (t))(1{-}f_2 (t))\nonumber \\ \end{aligned}$$

(13)

and we half-substitute (8) into (13), i.e., only for $x(t)$ in the first term

$$\begin{aligned} y(t)&= \sum _{i=1}^r {a_i v(t-i)f_1 (t)} -\sum _{j=1}^p {b_j x(t-j)} f_1 (t)\nonumber \\&\quad +\,c_L f_1 (t)+ m_R x(t)f_2 (t)-cf_2 (t)\nonumber \\&\quad +\,y(t-1)(1-f_1 (t))(1-f_2 (t)) \end{aligned}$$

(14)

where

$$\begin{aligned} c= c_R m_{R}. \end{aligned}$$

(15)

Then, we can choose $a_{1}\,=\,1$, and half-substitute (6) into (14), i.e., only for the term with variable $v(t-1)$. This will lead to the three-block cascade model output equation

$$\begin{aligned} y(t)&= \sum _{k=1}^n {\alpha _k u^{k}} (t-1)f_1 (t)\nonumber \\&\quad +\,\sum _{k=1}^n {\gamma _k u^{k}(t-1)} h(u(t-1))f_1 (t)\nonumber \\&\quad +\,\sum _{i=2}^r {a_i v(t-i)f_1 (t)} -\sum _{j=1}^p {b_j x(t-j)} f_1 (t) \nonumber \\&\quad +\,c_L f_1 (t)+ m_R x(t)f_2 (t)-cf_2 (t)\nonumber \\&\quad +\,y(t-1)(1-f_1 (t))(1-f_2 (t)) \end{aligned}$$

(16)

This equation is linear in all the cascade model block parameters, but nonlinear in some variables. The model inputs $u(t)$ and outputs $y(t)$ are available, while the internal variables $v(t)$, $x(t)$, $f_{1}(t)$ and $f_{2}(t)$ are not.

3 Parameter estimation

The three-block cascade model equation can be written in the following concise form

$$\begin{aligned} y_c (t)=y(t)-y(t-1)(1-f_1 (t))(1-f_2 (t))=\varphi ^{T}(t)\;\theta \nonumber \\ \end{aligned}$$

(17)

where

$$\begin{aligned} \varphi (t)&= [u(t-1)f_1 (t),{\ldots },u^{n}(t-1)f_1 (t),\nonumber \\&\quad u(t-1)h(u(t-1))f_1 (t),\ldots ,\nonumber \\&\quad u^{n}(t-1)h(u(t-1))f_1 (t), v(t-2)f_1 (t),{\ldots },\nonumber \\&\quad v(t-r)f_1 (t),-x(t-1)f_1 (t),{\ldots },\nonumber \\&\quad -\,x(t-p)f_1 (t),f_1 (t),x(t)f_2 (t),\quad -f_2 (t)]^{T}\nonumber \\ \end{aligned}$$

(18)

is the vector of data and

$$\begin{aligned} \theta&= [\alpha _{1},{\ldots },\alpha _{n}, \gamma _{1},{\ldots },\gamma _n , a_{2},{\ldots },a_{r},b_{1},{\ldots },\nonumber \\&\quad b_{p}, c_{L},m_R, c]^{T} \end{aligned}$$

(19)

is the vector of parameters and $y_{c}(t)$ is the so-called corrected output.

Considering N observations of input $u(t)$ and output $y(t)$ and assuming that $u(t)\,=\,0$ and $y(t)\,=\,0$ for t $\le \,0$, we can define the stacked corrected output vector $Y_{c}(N)$, the stacked information matrix $\Phi (N)$ as

$$\begin{aligned} Y_c (N)&= [y_c (1),y_c (2), \ldots ,y_c (N)]^{T} \end{aligned}$$

(20)

$$\begin{aligned} \Phi (N)&= [\varphi (1),\varphi (2), \ldots ,\varphi (N)]^{T} \end{aligned}$$

(21)

and from (17), we have

$$\begin{aligned} Y_c (N)=\Phi (N)\theta \end{aligned}$$

(22)

Minimizing the least-squares criterion function

$$\begin{aligned} J(\theta )=\left\| {Y_c (N)-\Phi (N)\theta } \right\| ^{2} \end{aligned}$$

(23)

with respect to $\theta$ and assuming that the information matrix $\Phi (N)$ is persistently exciting, that is, $\Phi ^{T}(N)\Phi (N)$ is an invertible matrix, we can obtain the least-squares estimate of the parameter vector as

$$\begin{aligned} \hat{{\theta }}=[\Phi ^{T}(N)\Phi (N)]^{-1}\Phi ^{T}(N)Y_c (N) \end{aligned}$$

(24)

However, the information matrix $\Phi (N)$ and the corrected output vector $Y_{c}(N)$ contain unknown internal variables, therefore an iterative algorithm must be applied for estimation of model parameters.

The technique presented in [36–38], which is based on the use of the preceding estimates of model parameters for the estimation of internal variables and vice-versa, can be easily extended to this three-block model. We replace the internal variables in (20) and (21) by their estimates defined as

$$\begin{aligned} { }^sv(t)&= \sum _{k=1}^n {{ }^s\alpha _k u^{k}(t)} + \sum _{k=1}^n {{ }^s\gamma _k u^{k}(t)} h(u(t)) \end{aligned}$$

(25)

$$\begin{aligned} { }^sx(t)&= { }^sv(t-1)+\sum _{i=2}^r {{ }^sa_i { }^sv(t-i)}\nonumber \\&\quad -\,\sum _{j=1}^p {{ }^sb_j { }^sx(t-j)} \end{aligned}$$

(26)

$$\begin{aligned} { }^{s}f_1 (t)&= h\left( { }^sx(t)+{ }^sc_L -y(t-1)\right) \end{aligned}$$

(27)

$$\begin{aligned} { }^{s}f_2 (t)&= h\left( y(t-1)-{ }^sm_R { }^sx(t)+{ }^sm_R { }^sc_R \right) \end{aligned}$$

(28)

$$\begin{aligned} { }^{s}y_c (t)&= y(t)-y(t-1)\left( 1-{ }^sf_1 (t)\right) \left( 1-{ }^sf_2 (t)\right) \nonumber \\ \end{aligned}$$

(29)

using the s-th estimates of corresponding parameters and variables and rewrite (25) as follows

$$\begin{aligned} { }^{s+1}\hat{{\theta }}=[{ }^s\Phi ^{T}(N){ }^s\Phi (N)]^{-1}{ }^s\Phi ^{T}(N){ }^sY_c (N) \end{aligned}$$

(30)

where the information matrix $\Phi (N)$ and the corrected output vector $Y_{c}(N)$ are replaced by their estimates.

Then, the iterative algorithm consists of the following steps:

• (a) The s-th estimates of internal variables, i.e., $^{s }v(t),$ $\,^{s } x(t),\,^{s }f_{1}(t),\,^{s} f_{2}(t)$ and the corrected output $y_{c}(t)$ are computed using (25)–(29);

• (b) The s-th estimates of information matrix $^{s}$ $\Phi (N)$ and the corrected output vector $^{s}Y_{c}(N)$ are generated using the estimates computed in the step (a);

• (c) The ($\hbox {s}+1$)-st estimates of the three-block model parameters are computed using (30);

• (d) If the mean square error is less than a predetermined value, the procedure ends, else it continues by repeating steps (a)–(c).

In the first iteration, only the parameters of nonlinear static block and the linear dynamic block are estimated where $^{1}v(t-i)$ is approximated by $u(t-i)$ and $^{1}x(t-j)$ is approximated by $y(t-j)$. The initial values of the parameter estimates can be chosen zero for all the parameters in the nonlinear static and the linear dynamic blocks. Nonzero initial values have to be chosen only for the backlash parameters, i.e., ${m}_{R},\,{c}_{L}$ and ${c}_{R}$, which are required for the first estimation of internal variables $f_{1}(t)$ and $f_{2}(t)$. Sufficiently small values can be chosen for $^{1}{c}_{L}$ and $^{1}{c}_{R}$ (i.e., 0.01–0.001). As the left slope of backlash is $m_{L}\,=\,1$, it is advantageous to choose the same value for the initial value of the right slope of backlash $^{1}{m}_{R}$.

4 Examples

The following examples of simulated three-block cascade systems with two-segment polynomial input block and output backlash illustrate the feasibility of proposed identification method.

Example 1

The input static nonlinearity of the three-block cascade system was characterized by the two-segment polynomial

$$\begin{aligned} v(t)=\left\{ {{\begin{array}{l} {1.3u(t)-0.2u^{2}(t)-0.3u^{3}(t)\quad \hbox { if }u(t)\ge 0} \\ {0.3u(t)+0.5u^{2}(t)+0.6u^{3}(t)\quad \hbox { if }u(t)<0} \\ \end{array} }} \right. \end{aligned}$$

and is depicted in Fig. 6. The linear dynamic system was given by the difference equation

$$\begin{aligned} x(t)&= v(t-1)+0.15v(t-2)\nonumber \\&\quad +\,0.2x(t-1)-0.35x(t-2) \end{aligned}$$

followed by the output backlash (Fig. 7) characterized by the parameters ${m}_{L}\,=\,1.0,\,{c}_{L}\,=\,0.3,\, {m}_{R}\,=\,1.2,\,{c}_{R}\, =\,0.2$. The identification was performed on the basis of 6,000 samples of uniformly distributed random inputs with ${\vert }u(t){\vert }\,<\,1.5$ and simulated outputs. To make the simulation more realistic, a zero mean random disturbance uncorrelated with $u(t)$ was added to the outputs. Normally distributed random noise was chosen with zero mean and signal-to-noise ratio—SNR $=$ 50 (the square root of the ratio of output and noise variances). The iterative estimation algorithm was applied with the initial values $^{1}{c}_{L}=^{1}{c}_{R}\,$=$\,0.001$. However, the initial value for the right slope was chosen $^{1}{m}_{R} = 0.5,$ to show that the convergence is also good for the initial value of ${m}_{R}$ being more distant from its real value. The process of parameter estimation is shown in Fig. 8 for the nonlinear block (the top-down order of parameters is $\alpha _{1},\,\beta _{3},\,\beta _{2},\,\beta _{1},\,\alpha _{2},\,\alpha _{3}$), in Fig. 9 for the linear block and in Fig. 10 for the backlash. The estimates meet the values of real parameters after about 7 iterations.

Fig. 6

Example 1—input nonlinearity

Fig. 7

Example 1—output backlash

Fig. 8

Example 1—the process of parameter estimation for the nonlinear block

Fig. 9

Example 1—the process of parameter estimation for the linear block

Fig. 10

Example 1—the process of parameter estimation for the backlash

Example 2

The input static nonlinearity of the three-block cascade system was characterized by the two-segment polynomial

$$\begin{aligned} v(t)=\left\{ {{\begin{array}{l} {0.3u(t)-0.3u^{2}(t)+0.5u^{3}(t)\quad \hbox { if }u(t)\ge 0} \\ {0.9u(t)-0.1u^{2}(t)-0.4u^{3}(t)\quad \hbox { if }u(t)<0} \\ \end{array} }} \right. \end{aligned}$$

and is depicted in Fig. 11. The linear dynamic system was given by the difference equation

$$\begin{aligned} x(t)&= v(t-1)+0.15v(t-2)\nonumber \\&\quad +\,0.2x(t-1)-0.35x(t-2) \end{aligned}$$

followed by the output backlash (Fig. 12) characterized by the parameters ${m}_{L}\,=\,1.0,\,{c}_{L}\,=\,0.1,\,{m}_{R}\,=\, 1.2,\,{c}_{R}\,=\,0.2$. The identification was performed under the same conditions as in Example 1. The process of parameter estimation is shown in Fig. 13 for the nonlinear block (the top-down order of parameters is $\beta _{1},\,\alpha _{3},\,\alpha _{1},\,\beta _{2},\,\alpha _{2},\,\beta _{3}$), in Fig. 14 for the linear block and in Fig. 15 for the backlash. The estimates meet the values of real parameters after about 7 iterations.

Fig. 11

Example 2—input nonlinearity

Fig. 12

Example 2—output backlash

Fig. 13

Example 2—the process of parameter estimation for the nonlinear block

Fig. 14

Example 2—the process of parameter estimation for the linear block

Fig. 15

Example 2—the process of parameter estimation for the backlash

Example 3

The input static nonlinearity of the three-block cascade system was characterized by the two-segment polynomial

$$\begin{aligned} v(t)=\left\{ {{\begin{array}{l} {0.03u(t)-0.27u^{2}(t)+1.27u^{3}(t)\quad \hbox { if }u(t)\ge 0} \\ {-0.02u(t)-0.17u^{2}(t)+0.07u^{3}(t)\quad \hbox { if }u(t)<0} \\ \end{array} }} \right. \end{aligned}$$

and is depicted in Fig. 16. The linear dynamic system was given by the difference equation

$$\begin{aligned} x(t)&= v(t-1)+0.5v(t-2)\\&\quad +\,0.5x(t-1)-0.4x(t-2) \end{aligned}$$

followed by the output backlash (Fig. 17) characterized by the parameters ${m}_{L}\,=\,1.0,\,{c}_{L}\,=\,0.2,\,{m}_{R}\,=\,0.8,\, {c}_{R}\,=\,0.3$. The identification was performed under the same conditions as in Example 1. The process of parameter estimation is shown in Fig. 18 for the nonlinear block (the top-down order of parameters is $\alpha _{3},\,\beta _{3},\,\alpha _{1},\,\beta _{1},\,\beta _{2},\,\alpha _{2})$, in Fig. 19 for the linear block and in Fig. 20 for the backlash. The estimates meet the values of real parameters after about 12 iterations.

Fig. 16

Example 3—input nonlinearity

Fig. 17

Example 3—output backlash

Fig. 18

Example 3—the process of parameter estimation for the nonlinear block

Fig. 19

Example 3—the process of parameter estimation for the linear block

Fig. 20

Example 3—the process of parameter estimation for the backlash

5 Conclusion

The presented approach to the identification of nonlinear dynamic systems with output backlash is based on three-block cascade models with both static and dynamic nonlinearities. These models are appropriate for control systems with both actuator and sensor nonlinearities. The identification is based on a special form of model description resulting from more consecutive decompositions of compound mappings describing this block-oriented model. An iterative least-squares-based parameter estimation algorithm with internal variables estimations has been proposed and illustrated in examples of simulated nonlinear dynamic systems with two-segment polynomial nonlinearities in the input block and with the backlash in the output block. Although a general proof of convergence for the iterative algorithm with internal variable estimation is not available, the simulation results show good convergence.

As the proposed three-block cascade models are linear in parameters, they can also be applied for on-line identification of nonlinear dynamic systems with static input nonlinearity and output backlash using the known recursive least-squares algorithm [39, 40]. They can be used for nonlinear systems with other estimation techniques, e.g., based on scarce measurements [41] or dual-rate sampled-data [42]. Finally, note that also other types of static and dynamic nonlinearities can be considered in the input block and/or in the output block of presented three-block cascade models.