Identification of Wiener–Hammerstein nonlinear systems with backlash operators

Abstract

In this paper, a new identification method is developed for Wiener–Hammerstein systems that contain memory nonlinearity of backlash type. The latter is flanked by two linear transfer functions that may be parametric or not. The proposed identification method is carried out in two stages. Firstly, the parameters (the lateral borders) of memory operator are identified using a set of constant inputs. In the second stage, an identification method based on Fourier analysis is developed to determine the frequency responses of both transfer functions. The performances of the proposed identification method are highlighted by simulation results. Finally, experimental application has been established to show the effectiveness of this method.

1 Introduction

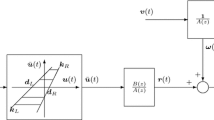
Nonlinear system identification has been a hot research field over the past two decades [1, 2]. A substantial portion of the research works has been carried out on the basis of block-structured models. The simplest structures are Hammerstein model, consisting of a static nonlinear block followed in series by a linear time invariant dynamic system, and Wiener model composed of a linear subsystem followed by a static nonlinearity. Hammerstein (resp. Wiener) model structure proved to be useful in the presence of actuator (resp. sensor) nonlinearity. In the case of systems with strong nonlinearities, these models might not be sufficient to provide an accurate approximation of the system dynamics. Then, system identification must be carried out using more complex structures, e.g., Hammerstein–Wiener and Wiener–Hammerstein models. In this work, the identification problem of Wiener–Hammerstein nonlinear system is addressed. The latter consists of series connection of a linear block ${G}_{1}(s)$, a static nonlinearity $F[.]$, and another linear block ${G}_{2}(s)$ (Fig. 1). This structure has proved to be suitable for modeling a wide range of real systems [3]. In this study, the considered system nonlinearity $F[.]$ is a backlash operator (Fig. 2). Most of available works addressing the issue of backlash effect focus on Wiener or Hammerstein systems. These models can be viewed as special cases of Wiener–Hammerstein nonlinear systems.

Fig. 1

Wiener–Hammerstein model having backlash nonlinearity $H[.]$. $u$ is the input, $y$ is the output, $(v,w,x)$ are inaccessible inner signals, and $\xi$ is the noise. ${G}_{1}(s)$ is transfer function of the front block, and ${G}_{2}(s)$ is transfer function of the back block

Fig. 2

Backlash having straight borders. ${S}_{\text{L}}$ and ${S}_{\text{U}}$ are the slope of loading and unloading borders, respectively; ${D}_{\text{L}}$ (respectively, ${D}_{\text{U}}$) is the value of $v\left(t\right)$ where the loading (respectively, unloading) border crosses the $x$-axis. ${v}_{m}$ and ${v}_{M}$ are the minimum and maximum values of $v\left(t\right)$, respectively

Various methods have been proposed to deal with system identification based on Wiener–Hammerstein model, see, e.g., [31, 35, 34, 35]. The identification issue of Wiener–Hammerstein model having a memory operator has not yet been studied. The available works considering a memory operator in the case of Wiener or Hammerstein models that cannot be generalized to Wiener–Hammerstein systems. In [5], an identification method using standard support vector machines (SVM) has been developed. The method only applies to nonlinear finite impulse response (NFIR) systems. The aim is to estimate a function approximating the input–output relationship using the input/output measurement data. Furthermore, this method suffers from high computational time and memory usage, making it not suitable in the presence of large amount of data. This solution is approximate and can be considered in the case of smooth nonlinearity. An identification method was proposed, but it was only applicable to case of FIR linear subsystems [6]. This solution is considered in the case of linear model and cannot be applied to Wiener–Hammerstein models. Furthermore, the transfer function is a ratio of coprime polynomials having known degrees. The used input signal is a zero-mean stationary ergodic random signal and is persistently exciting of sufficiently high order.

In Falck et al. [7], an identification method involving model overparameterization was proposed that combines least-squares method and SVM (LS-SVM). The input linear block ${G}_{1}(s)$ and the output linear block ${G}_{2}(s)$ (Fig. 1) are parameterized as a FIR and an ARX (autoregressive exogenous) model, respectively. Then, the linear blocks are parametric of known structure. In [8], the (discrete) impulse responses of the linear elements are estimated using stochastic approximation. Then, the numerators and denominators of the two linear subsystems are polynomials with known orders.

In [9], a recursive identification method involving recursive least-squares is proposed. In this work, the used system nonlinearity is a dead-zone function, which can be viewed as a special case of memory operator. This method is applied in discrete time domain, and the linear dynamic subsystems are parametric of known structure.

In [10], an identification method using the best linear approximation (BLA) technique is developed. The main identification challenge in the BLA techniques resides in separating the linear subsystem parameters. The partition of poles and zeros of resulting filter to form the input linear block ${G}_{1}(s)$ and the output linear block ${G}_{2}(s)$ is unique. Furthermore, the considered system nonlinearity is a static and monotonic function. In [11], an identification method of Wiener–Hammerstein systems is proposed. This method is developed assuming the static nonlinearity is Lipschitz function, and the linear blocks are FIR filters of known orders. In [12], the problem of Wiener–Hammerstein identification is addressed making use of Volterra series and ℓ1-constrained least squares. The linear subsystem blocks are characterized by the impulse responses. Then, the system nonlinearity is assumed to be smooth, and all its derivatives are bounded. Furthermore, the input signal $\left\{{u}_{\text{n}}\right\}$ is a sequence of bounded i.i.d. (independently and identically distributed) random signal satisfying $\left|{u}_{\text{n}}\right|\le 1$. In [13], an identification method is proposed that applies to the case the linear block ${G}_{2}(\text{s})$ is a FIR filter. In [14], an identification method using the second-order Volterra kernel and reduced order linear dynamic blocks was presented. A method based on the fractional approach was proposed in [15] that applies to the case of static nonlinearity.

In most of these works, the linear blocks are supposed of FIR types (e.g., in [11]). Furthermore, some of the previous papers have considered parametric linear blocks of known order.

Quite a few existing works dealt with system identification of systems with backlash. The works [16, 17, 22, 23, 28,29,30] are some exceptions, but none of them was focused on Wiener–Hammerstein models. In [24], the identification of Wiener–Hammerstein systems with backlash was considered in discrete time and dealt with using multi-innovation stochastic gradient method. In the present study, we develop a frequency identification method for Wiener–Hammerstein systems that contain a backlash operator (Fig. 2) and continuous time linear subsystems.

Note that backlash effect is widely present in practical systems, especially in electric servomotors and mechanical systems [16]. Analytically, backlash can be seen as a gap (offset) between the input and output of the nonlinearity (e.g., Fig. 3). Examples of mechanical systems containing backlash nonlinearity are given in [25, 26, 33]. The considered model is representative of e.g., mechanical systems composed by a DC motor (linear system), with a gear on its rotor shaft, and a load (that might be a motor) coupled to the driven gear. Such a system is well represented by a Wiener–Hammerstein model with backlash.

Fig. 3

The play between the teeth of the driving gear and those of the driven gear is a backlash; the latter is symmetric, i.e., ${D}_{\text{L}}={D}_{\text{U}}=b$ and ${S}_{\text{L}}={S}_{\text{U}}$

Presently, the system backlash operator may be symmetric or not and the linear blocks, ${G}_{1}(\text{s})$ and ${G}_{2}(\text{s})$, may be parametric or not. In this proposed solution, a step signal and a sine signal are used to excite the Wiener–Hammerstein system, which constitutes one of the innovations of this method. We present a two-stage identification method that provides estimates of the various parts of the system. In the first stage, the system nonlinearity is identified using a set of constant inputs. In the second stage, Fourier expansion-based method is developed to obtain a set of points of the frequency response of the system transfer functions. Of course, the obtained points can be used to get parameter estimates of the transfer functions in case these are parametric. Then, the order of linear elements ${G}_{1}(\text{s})$ and ${G}_{2}(\text{s})$ is not necessarily known and the latter can be of unknown structure. Both stages of the identification method involve deterministic input signals (step or sine signals) that can be easily generated, unlike in several previous papers requiring complex input signals that may be hard to realize practically (e.g., Gaussian or/ and persistent excitation).

Recall that, the main issue in the identification problem of Wiener–Hammerstein nonlinear system lies in the separation of the dynamics over the linear blocks ${G}_{1}(\text{s})$ and ${G}_{2}(\text{s})$ [4]. Unlike several previous works, in this study, the separation of the dynamics over the front and the back linear blocks can be is easily accomplished without any further assumptions or experiments.

This method can be applied to physical system of feedback loop structure and having stable linear block is in the forward loop [27].

The nonlinear system to be identified is described by Wiener–Hammerstein model, where the system nonlinearity is a memory operator given in Fig. 2.

For convenience, the main contributions of this paper are summarized as follows:

2 Summary of main contributions

Before describing the organization of the paper, let us summarize the novelty of the contribution, in comparison with existing works:

• Identification approach for Wiener–Hammerstein nonlinear system is presented.

• Most previous works have been focused on Wiener or Hammerstein systems.

• The linear blocks can be parametric or not. The blocks ${G}_{1}(\text{s})$ and ${G}_{2}(\text{s})$ can be of unknown structure.

• The considered system nonlinearity is a backlash operator which can be symmetric or not.

• The proposed identification approach is new based on Fourier technique.

• Experimental test using electronic components has been conducted.

• The separation of the dynamics over the front and the back linear blocks is easily accomplished, without any further assumptions or experiments.

Outline of the paper

The rest of the paper is organized as follows: The system identification problem under study is formulated in Sect. 2; Sect. 3 is devoted to identification method design; simulation results are presented in Sect. 4; and concluding remarks end the paper.

3 Problem formulation

We consider the identification problem for Wiener–Hammerstein systems depicted in Fig. 1. Accordingly, the system is a series connection of linear block with transfer function ${G}_{1}\left(\text{s}\right)$, a nonlinear block $F\left[ \cdot \right]$, and again a linear block ${G}_{2}(\text{s})$. It turns out that the Wiener–Hammerstein system can be analytically described as follows:

$$v\left(t\right)={g}_{1}\left(t\right)*u(t)$$

(1)

where * stands for the convolution product, ${g}_{i}\left(t\right)={L}^{-1}\left({G}_{i}(\text{s})\right)$, $i=1$ or $2$, denotes the inverse Laplace transform of the input linear block. Then, the inner signals $v\left(t\right)$ and $w\left(t\right)$ are related by the following expression:

$$w\left(t\right)=F\left[v(t)\right]=F\left[{g}_{1}\left(t\right)*u(t)\right]$$

(2)

where $F\left[ \cdot \right]$ is a backlash nonlinearity having affine lateral borders (Fig. 2). Accordingly, the undisturbed output $x\left(t\right)$ can be written as:

$$ x\left( t \right) = g_{2} \left( t \right){*}w\left( t \right) = g_{2} \left( t \right){*}F\left[ {g_{1} \left( t \right){*}u\left( t \right)} \right] $$

(3)

Finally, the system output can be expressed as:

$$y\left(t\right)={g}_{2}\left(t\right)*F\left[{g}_{1}\left(t\right)*u(t)\right]+\xi (t)$$

(4)

The unmeasurable noise $\xi (t)$ is presently supposed to be a zero-mean ergodic stochastic process and is independent on the system input. The noise zero-mean is denoted $\lambda_{\xi } = 0$ and its variance $\sigma_{\xi }^{2} < \infty$.

Presently, we seek the development of a new identification method that provides estimates of the system components $\left( {G_{1} \left( {\text{s}} \right),{ }F\left[ \cdot \right],G_{2} \left( {\text{s}} \right)} \right)$.

Assumptions A1

Since the identification is carried out in open loop, the dynamic linear blocks ${G}_{1}(s)$ and ${G}_{2}(s)$ are assumed to be asymptotically stable. Further, both linear elements are supposed to have a nonzero DC gain (i.e., ${G}_{1}(0)\ne 0$ and ${G}_{2}(0)\ne 0$).

A2. The nonlinearity $F\left[ \cdot \right]$ is a backlash operator bordered by straight lines.

In the sequel, except of assumptions A1–A2, no other condition is required.

Remark 1

• 1. Let us consider the identification problem of Wiener–Hammerstein system described by (1)–(4). Clearly, this problem does not have a unique solution [19]. Indeed, if the triplet $\left({G}_{1}(s),F\left[v\right],{G}_{2}(s)\right)$ is solution of the above identification problem, then any triplet of the form:

  $$\left(\frac{{G}_{1}\left(s\right)}{{k}_{1}},{k}_{2}F\left[{k}_{1}v\right],\frac{{G}_{2}\left(s\right)}{{k}_{2}}\right)$$

  (5a)

  is also a solution of this identification problem, for any nonzero reals $({k}_{1},{k}_{2})$. Now the question is which particular model should we be focused on? This will be discussed in the next remarks.

• 2. Let us consider the Heaviside function $\upsigma \left(t\right)$ defined as:

  $$ {\upsigma }\left( t \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{for }}t < 0} \hfill \\ 1 \hfill & {{\text{for }}t \ge 0} \hfill \\ \end{array} } \right.. $$

Let ${V}_{\text{p}}$ denotes the peak (maximal) value of the step response $v\left(t\right)$ that results from a unitary step input signal, i.e., when $u\left(t\right)=\upsigma \left(t\right)$ (Heaviside function). Note that the maximum value ${V}_{\text{p}}$ is either equal to the steady-state value (i.e., the static gain ${V}_{\text{p}}={G}_{1}(0)$), for linear system without overshoot, or ${V}_{\text{p}}\ne {G}_{1}(0)$ for linear block with overshoot.

• 3. Let ${V}_{j}$ denotes the peak of $v(t)$ when an arbitrary step input $u\left(t\right)={u}_{j}(t)$ with ${u}_{j}\left(t\right)={U}_{j}\upsigma \left(t\right)$ is applied, where ${U}_{j}>0$ is arbitrary. It is readily seen that:

  $${V}_{j}={U}_{j} {V}_{p}$$

  (5b)

• 4. In view of Parts 1 and 2 of this remark, it is judicious to set the constants $\left({k}_{1}{,k}_{2}\right)$ in (5a) as follows:

  $${k}_{1}={V}_{p} \, \text{And } \, {k}_{2}={G}_{2}\left(0\right)$$

  (5c)

Doing so, we make the model (5a) satisfy two key properties:

(P1) The peak value ${V}_{\text{p}}$ of the intermediary signal $v(t)$, in response to a step input ${u}_{j}\left(t\right)={U}_{j}\upsigma \left(t\right)$, is known. Specifically, we have ${V}_{j}={U}_{j}$.

(P2) The transfer function located at the output side has a unitary static gain. □

From Remark 1, it follows that there is a unique model of the form (5a) that enjoys properties (P1) and (P2) stated in Part 3. In order to avoid multiple notations, the model to be identified will be still noted $\left( {G_{1} \left( {\text{s}} \right),F\left[ \cdot \right],G_{2} \left( {\text{s}} \right)} \right)$ and this satisfies properties (P1)–(P2). Accordingly, we have:

$${G}_{2}\left(0\right)=1 \, \text{and} \, {V}_{j}={U}_{j}$$

(5d)

where ${V}_{j}$ denotes the peak value of the intermediary signal $v(t)$, in response to a step input ${u}_{j}\left(t\right)={U}_{j}\upsigma \left(t\right)$. Using the assumptions A1, an identification method is developed in the first stage to determine the system nonlinearity $F\left[ \cdot \right]$. In the second stage, a sine signal $u\left(t\right)$ of frequency $\omega$ is applied to the input of the Wiener–Hammerstein nonlinear system. Bearing in mind that $u\left(t\right)$ is a periodic signal of the period $T=2\pi /\omega$, the steady state of system output $y(t)$ is thus also T-periodic. Then, using the relationship between the input and output system, the frequency gains ${G}_{1}\left(\text{s}\right)$ and ${G}_{2}\left(\text{s}\right)$ can be estimated using Fourier analysis. It is interesting to note in this respect that, when a linear block is excited by a sine signal of frequency $\omega$, its output (after the transient response) becomes sine signal of the same frequency $\omega$, but the amplitude and the phase change according to the linear block parameters. Conversely, when a nonlinear block is excited by a sine signal, it generates harmonic of frequencies $k\omega$, $k=\text{1,2},\dots$ [21, 22].

So far, the identification problem of nonlinear system having backlash operator has been addressed only in the case of Wiener or Hammerstein systems. Presently, the backlash operator is considered in the more general case of Wiener–Hammerstein system. It turns out that the present identification method is quite different from those developed for Wiener or Hammerstein systems, which are particular simpler cases of the Wiener–Hammerstein system.

Remark 2

Figure 4 shows example of mechanical system where a backlash bordered by two straight line curves occurs. After the establishment of the contact between the drive and driven gears, the latter follows linearly the move of the input (drive gear). If the contact between the drive and driven gears is lost, the working point $(v\left(t\right),w\left(t\right))$ moves horizontally between the lateral borders.

Fig. 4

Example of static backlash nonlinearity bordered by straight line

Then, for a step input less than the minimal horizontal distance between the lateral borders of backlash, the working point moves horizontally (Fig. 5).

Fig. 5

Example of cycle performed by the working point

4 System nonlinearity identification

For convenience, we first introduce the following terminology:

Definition 1

• 1. The lateral borders of backlash operator are called loading and unloading curves, respectively [23, 28].

• 2. A signal $u\left(t\right)$ is called loading signal in any time interval $\left[\begin{array}{cc}{t}_{m}& {t}_{M}\end{array}\right]$, where ${t}_{m}<{t}_{M}$, if it is nondecreasing in $\left[\begin{array}{cc}{t}_{m}& {t}_{M}\end{array}\right]$, i.e.,

  its derivative $\dot{u}\left(t\right)\ge 0 \forall t\in \left[\begin{array}{cc}{t}_{m}& {t}_{M}\end{array}\right]$

• 3. Similarly, $u\left(t\right)$ is called unloading signal in the time interval $\left[\begin{array}{cc}{t}_{m}& {t}_{M}\end{array}\right]$ if it is nonincreasing, i.e.,

Its derivative $\dot{u}\left(t\right)\le 0 \forall t\in \left[\begin{array}{cc}{t}_{m}& {t}_{M}\end{array}\right]$

In the sequel, the abbreviations L and U stand for loading and unloading, respectively. In this section, the problem at hand is to identify the system nonlinearity $F\left[ \cdot \right]$. The latter is a backlash nonlinearity having straight-line lateral borders (Fig. 2). To this end, it is sufficient to determine a set of points $N$ of the nonlinearity $F\left[ \cdot \right]$ borders. These lateral borders, denoted $\left({f}_{L},{f}_{U}\right)$, are represented by the equations:

$${f}_{\text{L}}\left(v\left(t\right)\right)={S}_{\text{L}}\left(v\left(t\right)-{D}_{\text{L}}\right)$$

(6a)

$${f}_{\text{U}}\left(v\left(t\right)\right)={S}_{\text{U}}\left(v\left(t\right)-{D}_{\text{U}}\right)$$

(6b)

where ${S}_{\text{L}}$ and ${S}_{\text{U}}$ are the slope of loading and unloading borders, respectively; ${D}_{\text{L}}$ (respectively, ${D}_{\text{U}}$) is the value of $v\left(t\right)$ where the loading (respectively, unloading) border crosses the $x$-axis.

4.1 Backlash operation principle

Let us suppose that the initial backlash working point $(v\left(t\right),w\left(t\right))$ belongs to the increasing lateral border ${f}_{L}\left(.\right)$ (respectively ${f}_{U}\left(.\right)$). Then, the point $(v\left(t\right),w\left(t\right))$ keeps moving along ${f}_{L}\left(.\right)$ (respectively, ${f}_{U}\left(.\right)$) as long as $v\left(t\right)$ is monotonic. When the derivative $\dot{v}\left(t\right)$ changes sign, the backlash working point $(v\left(t\right),w\left(t\right))$ leaves one border and starts moving horizontally toward the opposite border. When the point $(v\left(t\right),w\left(t\right))$ intersects the lateral border, it keeps moving along this one as long as $v\left(t\right)$ is monotonic.

Then, the backlash nonlinearity can be analytically described as:

$$ w\left( t \right) = \left\{ {\begin{array}{*{20}l} {f_{{\text{L}}} \left( {v\left( t \right)} \right) = S_{{\text{L}}} \left( {v\left( t \right) - D_{{\text{L}}} } \right) } \hfill & {{\text{if}} v\left( t \right) \ge f_{{\text{L}}}^{ - 1} \left( {w\left( {t - 1} \right)} \right)} \hfill \\ {f_{{\text{U}}} \left( {v\left( t \right)} \right) = S_{{\text{U}}} \left( {v\left( t \right) - D_{{\text{U}}} } \right)} \hfill & {{\text{if}} v\left( t \right) \le f_{{\text{U}}}^{ - 1} \left( {w\left( {t - 1} \right)} \right)} \hfill \\ {F\left[ {v\left( {t - 1} \right)} \right] } \hfill & {\text{else }} \hfill \\ \end{array} } \right. $$

(7)

where ${f}^{-1}\left(.\right)$ stands for the inverse function, and $\left(v\left(t-1\right),w(t-1)\right)$ denote the last values of $v$ and $w$ before time $t$.

Remark 3

For convenience, an example of path carried out by the working point $(v\left(t\right),w\left(t\right))$, for the studied backlash nonlinearity, is shown in Fig. 6. As given in Fig. 4, let consider the initial position of working point is placed between the lateral borders of backlash, e.g., position ① in Fig. 6. For increasing signal $v\left(t\right)$, the working point $(v\left(t\right),w\left(t\right))$ moves along a horizontal path, i.e., positions ② and ③ (Fig. 6).

Fig. 6

_{Example of cycle performed by the working point}

When the working point $(v\left(t\right),w\left(t\right))$ reaches the ascending lateral border ${f}_{L}\left(.\right)$ (position ④ in Fig. 6), it moves along this ascending border until $v\left(t\right)$ changes monotonicity. For instance, the working point $(v\left(t\right),w\left(t\right))$ takes the positions ⑤ and ⑥ in Fig. 6. Then, when $\dot{v}\left(t\right)$ changes sign, the working point $(v\left(t\right),w\left(t\right))$ leaves the ascending border and moves horizontally (positions ⑦ and ⑧ in Fig. 6).

When the working point $(v\left(t\right),w\left(t\right))$ reaches the descending lateral border, it remains moving along this border as long as $\dot{v}\left(t\right)$ does not change sign (position ⑨ in Fig. 6).

4.2 Input signal design

The input signal used to identify $F\left[ \cdot \right]$ should include an ascending part, called loading stage, and a descending phase, called unloading stage (Definition 1). Example of signal having loading and unloading stages is shown in Fig. 7. Therefore, we let the Wiener–Hammerstein nonlinear system (Fig. 1) be excited by a signal $u\left(t\right)$ featured by loading and unloading stages. Presently, we use a piecewise constant signal, i.e., $u\left(t\right)$ steps from one constant value to another and stay constant at each value (Fig. 7). Let ${d}_{\text{max}}$ denote the maximal distance between the lateral borders of the backlash. To ensure that all obtained points in loading (respectively, unloading) stage belong to the same lateral border of the backlash, an initialization step is used. This consists of applying an input ${U}_{\text{L}0}$ before the first value ${U}_{\text{L}1}$ in loading stage such that ${U}_{\text{L}1}-{U}_{\text{L}0}>{d}_{\text{max}}$. Similarly, the difference between the first value in unloading stage ${U}_{\text{U}1}$ and ${U}_{\text{U}0}$ should be less than ${-d}_{\text{max}}$. Figure 8a illustrates the initialization step that can be used; the resulting backlash working points is illustrated in Fig. 8b. In the case where this initialization step is not used, the backlash working points can move along horizontal lines before following the later border (Fig. 8c).

Fig. 7

Signal including loading and unloading stages

Fig. 8

a Loading stage of input signal with initialization step, b Example of obtained backlash working points using initialization step, c Example of obtained backlash working points without initialization step

Let ${t}_{r}$ denote the settling time of the system. The design of the input signal must meet two requirements. First, the duration of each constant stage of the input must be greater than ${t}_{r}$. This assumes that the estimation of system settling time is obtained. Second, the step size (between two successive constant values of the input signal) should be not too large so that to prevent the operation point $(v\left(t\right),w\left(t\right))$ skipping from one lateral border of the hysteresis operator $F\left[ \cdot \right]$ to the other. This problem arises in the case of oscillating systems (i.e., ${G}_{1}\left(\text{s}\right)$). To keep simpler the presentation, the case of oscillating block ${G}_{1}\left(\text{s}\right)$ is ruled out. Then, the backlash working point either moves horizontally or moves along one lateral border.

Let ${v}_{1}$ and ${v}_{2}$ denote arbitrary values within the domain interval $\left[\begin{array}{cc}{v}_{m}& {v}_{M}\end{array}\right]$ of the inner signal $v(t)$ such that:

$${f}_{\text{L}}\left({v}_{1}\right)={f}_{\text{U}}\left({v}_{2}\right) \, \text{or} \, {S}_{\text{L}}\left({v}_{1}-{D}_{\text{L}}\right)={S}_{\text{U}}\left({v}_{2}-{D}_{\text{U}}\right)$$

where $\left({S}_{\text{L}},{D}_{\text{L}}\right)$ and $\left({S}_{\text{U}},{D}_{\text{U}}\right)$ are the parameters of the increasing and decreasing lateral borders (straight lines), respectively. Referring to Fig. 9, this second requirement can be expressed by the inequality $D<{d}_{\text{min}}$, where $D$ denotes the overshoot of step response of internal signal $v(t)$ and ${d}_{\text{min}}$ is the minimal horizontal distance between the lateral borders. From (6a–b), it follows that:

Fig. 9

Shape of step response of subsystem G₁(s)

$${d}_{\text{min}}=\underset{{{v}_{m}\le v}_{1}<{v}_{2}\le {v}_{M}}{\text{min}}\left|{v}_{1}-{v}_{2}\right|$$

Remark 4

• 1. For monotonic input, using the condition $D<{d}_{\text{min}}$ and Remark 1, the value of backlash output ${W}_{j}$, in steady state, will remain equal to $F\left[{U}_{j}{V}_{p}\right]=F\left[{U}_{j}\right]$ regardless the response type (oscillatory or not).

• 2. Step inputs with multiple excitation levels can be easily generated using electronic or electrical equipment. An example of mechanical system generating step inputs, with multiple excitation levels, is shown in Fig. 10. The corresponding relationship (backlash) between input and output motions is given at the bottom of this figure.

• 3. The condition ${U}_{\text{L}1}-{U}_{\text{L}0}>{d}_{\text{max}}$ (respectively, ${U}_{\text{U}1}-{U}_{\text{U}0}>{d}_{\text{max}}$) considered in loading (respectively, unloading) stage is not necessary in the identification process. This condition is considered to ensure that all obtained points in loading (respectively, unloading) stage remain on the same lateral border. If this condition is not satisfied, the backlash working point moves along a horizontal path before reaching the lateral border.

Fig. 10

Example of backlash operator in mechanical systems

4.3 Estimation of the lateral border of backlash operator ${\mathbf{F}}\left[ \cdot \right]$

Using an input signal $u\left(t\right)$ as explained above results in an internal signal $v(t)$ that includes loading and unloading stages. Furthermore, $v(t)$ itself steps from a steady-state value to another. Let $N$ denotes the number of different constant values in the input signal $u\left(t\right)$. Using this (loading and unloading) property, a set of points ($\le N/2$) belonging to the loading curve and other set of points ($\le N/2$) belonging to the unloading curve can be determined. Accordingly, an estimate of the hysteresis (backlash) nonlinearity can be easily obtained. In this respect, note that the number of points corresponding to the ascending and unloading curves should be greater than $2$. Let ${U}_{1}<\dots <{U}_\frac{N}{2}$ be the selected abscissas of the wave $u\left(t\right)$ describing the increasing stage. The input values referred to the unloading curve should satisfy ${U}_{\frac{N}{2}+1}>\dots >{U}_{N}$. Let ${V}_{j}$ and ${W}_{j}$, for $j=1\dots N$, denote the steady-state values of $v\left(t\right)$ and $w\left(t\right)$, respectively, corresponding to the input ${U}_{j}$.

The set of selected abscissas ${U}_{j}$, for $j=1\dots \frac{N}{2}$ (respectively, for $j=\frac{N}{2}+1,\frac{N}{2}+2,\dots ,N$), are chosen such that the working point $\left({V}_{j},F\left[{V}_{j}\right]\right)$ belongs to the increasing stage (resp. decreasing stage). The choice of the abscissas ${U}_{j}$ can be done practically [16, 17, 20, 28]. To make the explanation of the hysteresis identification method easier, let us suppose that the increasing stage of $u\left(t\right)$ corresponds to the increasing stage of the sequence $\left\{{V}_{j};j=1,\dots ,\frac{N}{2}\right\}$ and the decreasing stage of $u\left(t\right)$ corresponds to the decreasing stage of the sequence $\left\{{V}_{j};j=\frac{N}{2}+1,\frac{N}{2}+2,\dots ,N\right\}$, i.e., the static gain ${G}_{1}\left(0\right)$ is positive. Note that it will be no problem if ${G}_{1}\left(0\right)<0$, because of Remark 1 (in this case ${k}_{1}<0$). Let us suppose that ${V}_{j}$ (for any $j\in \left\{1,\dots ,\frac{N}{2}\right\})$, is the first abscissa such that the working point $\left({V}_{j},F\left[{V}_{j}\right]\right)$ reaches the increasing lateral border. Accordingly, it follows from (6a) that:

$${W}_{j}={S}_{\text{L}}\left({V}_{j}-{D}_{\text{L}}\right)$$

(8)

When $u(t)$ steps from ${U}_{j}$ to a greater value ${U}_{j+1}$ the inner signal $v\left(t\right)$ is increasing (because ${G}_{1}\left(0\right)>0$). Then, the working point $\left(v\left(t\right),w\left(t\right)\right)=\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ will remain in the increasing lateral border, i.e.:

$$w\left(t\right)={S}_{\text{L}}\left(v\left(t\right)-{D}_{\text{L}}\right)$$

for $t>{t}_{r1}$ and $u\left(t\right)={U}_{j+1}$ (where ${t}_{r1}$ denotes the response time of ${G}_{1}\left(\text{s}\right)$), until the input $u(t)$ steps again. For $t>{t}_{r1}$ and $u\left(t\right)={U}_{j+1}$, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves horizontally (i.e., $w\left(t\right)$ remains constant). In the case where the input linear block is not oscillatory nature, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves on the increasing lateral border all the time after $u\left(t\right)={U}_{j+1}$. In light of the above observations, it turns out that letting $u\left(t\right)={U}_{j+1}$ results in steady-state values of the inner signals $v\left(t\right)={V}_{j+1}$ and $w\left(t\right)={W}_{j+1}$ that are related by the expression:

$${W}_{j+1}=F\left[{V}_{j+1}\right]={S}_{\text{L}}\left({U}_{j+1}{G}_{1}\left(0\right)-{D}_{\text{L}}\right)$$

(9)

In this case, the maximum value ${V}_{\text{p}}$ of $v\left(t\right)$ for a step response is ${G}_{1}\left(0\right)$. In the other case (i.e., the input linear block presents oscillations for a step response), it is seen that the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves on the increasing lateral border until the first maximum of $v\left( t \right)$ ($= V_{{\text{p}}} U_{j + 1}$) will be achieved. At this moment, one has the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)=\left({V}_{\text{p}}{U}_{j+1},F\left[{V}_{\text{p}}{U}_{j+1}\right]\right)$. Therefore, $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves horizontally for the rest of time. This means that $w\left(t\right)$ remains constant during this time and takes thus the following value:

$$w\left(t\right)={W}_{j+1}=F\left[{V}_{\text{p}}{U}_{j+1}\right]={S}_{\text{L}}\left({V}_{\text{p}}{U}_{j+1}-{D}_{\text{L}}\right)$$

(10)

Note that in the case where ${G}_{1}\left(\text{s}\right)$ does not present oscillations, ${V}_{\text{p}}$ equals to the static gain ${G}_{1}\left(0\right)$. Then, (9) can be viewed as a particular case of (10). Using (3) and (10), the steady state of the undisturbed output $x\left(t\right)$ corresponding to the input ${U}_{j+1}$, noted ${X}_{j+1}$, can be written as:

$${X}_{j+1}={G}_{2}\left(0\right)F\left[{V}_{\text{p}}{U}_{j+1}\right]={G}_{2}\left(0\right){S}_{\text{L}}\left({V}_{\text{p}}{U}_{j+1}-{D}_{\text{L}}\right)$$

(11)

By combining (11) and the properties (5c) (Remark 1) of system to be identified, one immediately gets:

$${X}_{j+1}=F\left[{U}_{j+1}\right]={S}_{\text{L}}\left({U}_{j+1}-{D}_{\text{L}}\right)$$

(12)

Finally, it follows from (4) and (11), one has:

$$y\left(t\right)={X}_{j+1}+\xi (t)={S}_{\text{L}}\left({U}_{j+1}-{D}_{\text{L}}\right)+\xi (t)$$

(13)

This result shows that the system output (for $u\left(t\right)={U}_{j+1})$) is constant up to noise and the point of couple $\left({U}_{j+1},{X}_{j+1}\right)$ belongs to the increasing lateral border ${f}_{\text{L}}(.)$. Let ${\widehat{X}}_{j}$ denotes the estimate of ${X}_{j}$ for $j=1\dots N$. Then, the estimate ${\widehat{f}}_{\text{L}}\left({U}_{j+1}\right)$ of ${f}_{\text{L}}\left({U}_{j+1}\right)={X}_{j+1}$ can be obtained by averaging a number M of measures of (steady-state) $y(t)$, where M is arbitrarily large just as suggested in [2] and [17, 20]. Specifically, we suggest the following estimator of ${f}_{\text{L}}\left({U}_{j+1}\right)$:

$${\widehat{f}}_{\text{L}}\left({U}_{j+1}\right)={\widehat{X}}_{j+1}=\frac{1}{M}\sum_{t=1}^{M}y(t)$$

(14)

with $M\gg 1$.

Remark 5. 1

• 1. The present method can be generalized to other types of nonlinearities, e.g., polynomial or smooth functions. Specifically, in the case of polynomial function of degree $n$, a set of at least $n+1$ points belonging to the nonlinearity is required [21]. Using the same method described in this section and choosing $N\ge n+1$, the nonlinearity parameters can be determined.

• 2. The value of the number $M$ can be chosen based on the levels of noise amplitudes. For instance, in the case of free noise system, the number $M$ is not necessarily of large value and can be set to 1 (for step input). Specifically, one unique measure of $y(t)$, in steady state, is sufficient to determine a point belonging to the backlash nonlinearity.

It is easily shown that the estimator (14) is consistent in the sense that the nonlinearity parameters converge to their true value. Indeed, it follows from (13) and (14) that:

$${\widehat{f}}_{\text{L}}\left({U}_{j+1}\right)= {f}_{\text{L}}\left({U}_{j+1}\right)+\frac{1}{M}\sum_{t=1}^{M}\xi (t)$$

(15)

Bearing in mind that the noise $\left\{\xi (t)\right\}$ is presently supposed to be a zero-mean ergodic stochastic process, which leads to the following result:

$$\frac{1}{M}\sum_{t=1}^{M}\xi (t)\underset{M\to \infty }{\to }E\left[\xi (t)\right]=0 \, (\text{w}.\text{p}.1)$$

(16)

Accordingly, it follows from (15) and (16) that the following convergence can be derived:

$${\widehat{f}}_{\text{L}}\left({U}_{j+1}\right)\underset{M\to \infty }{\to }{f}_{\text{L}}\left({U}_{j+1}\right) \, (\text{w}.\text{p}.1)$$

(17)

Furthermore, the increasing lateral border ${f}_{\text{L}}(.)$ is featured by the parameters $\left({S}_{\text{L}},{D}_{\text{L}}\right)$. Then, using the same experiment to estimate another point in ${\widehat{f}}_{\text{L}}\left(.\right)$, e.g., for ${U}_{j+2}$, the parameters $\left({S}_{\text{L}},{D}_{\text{L}}\right)$ can be determined. Therefore, using (17) one immediately gets:

$$\left({\widehat{S}}_{\text{L}},{\widehat{D}}_{\text{L}}\right)\underset{M\to \infty }{\to }\left({S}_{\text{L}},{D}_{\text{L}}\right) \, \text{(w.p.1)}$$

(18)

Let us show how the estimation accuracy depends on the noise variance. In this respect, it follows (14) that, for any constant input ${U}_{j}$:

$$E\left[{\widehat{X}}_{j}\right]={X}_{j}+\frac{1}{M}E\left[\sum_{t=1}^{M}\xi (t)\right]={X}_{j}+\frac{M}{M}{\lambda }_{\xi }={X}_{j}$$

Then, the variance or mean square error is given as:

$$E\left[{\left({\widehat{X}}_{j}-{X}_{j}\right)}^{2}\right]=E\left[{{\widehat{X}}_{j}}^{2}\right]-2{X}_{j}E\left[{\widehat{X}}_{j}\right]+{{X}_{j}}^{2}$$

where

$${{\widehat{X}}_{j}}^{2}={{X}_{j}}^{2}+2\frac{{X}_{j}}{M}\sum_{t=1}^{M}\xi (t)+\frac{1}{{M}^{2}}{\left(\sum_{t=1}^{M}\xi (t)\right)}^{2}$$

For independent and identically distributed (i.i.d) variables of $\xi (t)$ (i.e., $\left[\xi (s)\xi (t)\right]=0$ $\forall s\ne t$), one gets:

$$E\left[{{\widehat{X}}_{j}}^{2}\right]={{X}_{j}}^{2}+\frac{1}{{M}^{2}}\left(M{{\sigma }_{\xi }}^{2}\right)={{X}_{j}}^{2}+\frac{{{\sigma }_{\xi }}^{2}}{M}$$

Accordingly, the mean square error becomes:

$$E\left[{\left({\widehat{X}}_{j}-{X}_{j}\right)}^{2}\right]={{X}_{j}}^{2}+\frac{{{\sigma }_{\xi }}^{2}}{M}-2{{X}_{j}}^{2}+{{X}_{j}}^{2}=\frac{{{\sigma }_{\xi }}^{2}}{M}$$

which is inversely proportional to $M$.

Similarly, (8)–(13) will be applied to a set of inputs ${U}_{j}$ in the decreasing stage ($j=\frac{N}{2}+1,\frac{N}{2}+2,\dots ,N$). Then, let consider that ${V}_{j}$ is the first abscissa such that the working point $\left({V}_{j},F\left[{V}_{j}\right]\right)$ belongs to the decreasing lateral border, where $j\in \left\{\frac{N}{2}+1,\frac{N}{2}+2,\dots ,N\right\}$. Accordingly, the steady-state system output $y\left(t\right)$ can written as:

$$y\left(t\right)={S}_{\text{U}}\left({U}_{j}-{D}_{\text{U}}\right)+\xi \left(t\right)$$

(19)

Accordingly, the decreasing lateral border ${f}_{\text{U}}(.)$ can be determined using at least two points in the decreasing stage and the estimator (14). These results show that an accurate estimate of hysteresis (backlash or backlash operators) nonlinearity $F\left[ \cdot \right]$ can be obtained.

To ensure that the first point in loading stage belongs to the increasing lateral border of the backlash, the initialization step like (Fig. 8a) is applied. Accordingly, an input ${U}_{0}$ is applied, before the first value ${U}_{1}$ with ${U}_{1}-{U}_{0}>{d}_{\text{max}}$ (maximum distance between the lateral borders). Similarly, to ensure that the value ${U}_{\frac{N}{2}+1}$ belongs to the decreasing lateral border of the backlash, the condition ${U}_{\frac{N}{2}+1}-{U}_\frac{N}{2}{<-d}_{\text{max}}$ must be satisfied.

For convenience, the main steps of system nonlinearity identification are summarized in Table 1.

Table 1 Identification of backlash nonlinearity

Remark 6

• 1. As the value of ${d}_{\text{max}}$ is not a priori known, the condition ${U}_{1}-{U}_{0}>0$ (respectively, ${U}_{\frac{N}{2}+1}-{U}_\frac{N}{2}<0$) must be satisfied. If the system output remains constant (up to noise), after ${U}_{1}$ is applied (for $t\ge 0$), the quantity ${U}_{1}-{U}_{0}$ must be increased (by reducing the value of ${U}_{0}$). A similar remark applies to the tuning of ${U}_{\frac{N}{2}+1}-{U}_\frac{N}{2}$.

• 2. To estimate the increasing and decreasing lateral borders $\left({f}_{\text{L}}\left(.\right),{f}_{\text{U}}(.)\right)$, the determination of two points in each stage (increasing and decreasing) is sufficient. However, to improve the estimate accuracy, it is better to use several points in both (loading and unloading) stages.

• 3. To reduce the vibration effects in real mechanical systems, the difference between two successive inputs must be small to ensure that the working point $\left({V}_{j},F\left[{V}_{j}\right]\right)$ moves along the lateral border of the hysteresis operator $F\left[ \cdot \right]$.

• 4. In this study, the frequency band of the measurement noise is not necessarily bounded and not necessarily of high frequencies, i.e., a low pass filter cannot be used. Presently, the frequency decomposition of the measurement noise can spread over the entire frequency space, e.g., a white noise.

5 Identification of linear blocks

In this section, we aim to develop an identification method that provides the estimates of the frequency gains ${G}_{1}\left({\omega }_{i}\right)$ and ${G}_{2}\left({\omega }_{i}\right)$ ($i=\text{1,2},\dots$), where the set of frequencies ${\omega }_{i}$ is arbitrarily chosen by the designer. Accordingly, the objective is to estimate the gain module and phase of the frequency gains ${G}_{1}\left({\omega }_{i}\right)$ and ${G}_{2}\left({\omega }_{i}\right)$. Interestingly, the linear blocks ${G}_{1}\left(s\right)$ and ${G}_{2}\left(s\right)$ can be parametric or nonparametric. It is worth mentioning that, if $v\left(t\right)$ is of small amplitude, the backlash working point will move horizontally. The proposed frequency identification method relies on Fourier analysis of signals. Then, it involves system excitation with sine signal:

$$u\left(t\right)=U\text{cos}\left({\omega }_{i}t\right)$$

(20)

Let $\left|{G}_{l}\left({j\omega }_{i}\right)\right|$ and ${\varphi }_{l}\left({\omega }_{i}\right)=\text{arg}\left({G}_{l}\left({j\omega }_{i}\right)\right)$ ($l=\text{1,2}$) denote, respectively, the gain module and the phase of the linear element $l$ for the frequency ${\omega }_{i}$. Accordingly, one immediately gets using (1) and (20) that the inner signal $v\left(t\right)$ (in the steady state) can be expressed as:

$$v\left(t\right)=U\left|{G}_{1}\left({j\omega }_{i}\right)\right|\text{cos}\left({\omega }_{i}t+{\varphi }_{1}\left({\omega }_{i}\right)\right)$$

(21)

Let ${d}_{\text{max}}$ denote the maximal horizontal distance between the lateral borders ${f}_{\text{L}}\left(.\right)$ and ${f}_{\text{U}}\left(.\right)$ of the backlash, i.e.

$${d}_{\text{max}}=\underset{{{v}_{m}\le v}_{1}<{v}_{2}\le {v}_{M}}{\text{max}}\left|{v}_{1}-{v}_{2}\right|$$

(22)

where ${f}_{\text{L}}\left({v}_{1}\right)={f}_{\text{U}}\left({v}_{2}\right)$. Let the input amplitude $U$ be sufficiently large so that $U\left|{G}_{1}\left({j\omega }_{i}\right)\right|>{d}_{\text{max}}$. Then, the resulting signal $w\left(t\right)$ is periodic (but not necessarily sine wave signal) of period ${T=2\pi /\omega }_{i}$. For small input amplitudes, the inequality $U\left|{G}_{1}\left({j\omega }_{i}\right)\right|>{d}_{\text{max}}$ is not satisfied and the backlash output becomes constant in steady state. This phenomenon can also be observed when the linear block ${G}_{1}\left(s\right)$ is a selective filter and the input frequency of $u\left(t\right)$ is outside its passband. Practically, the system output $y\left(t\right)$ becomes (in steady state) constant up to noise [17, 20, 28].

The requirement $U\left|{G}_{1}\left({j\omega }_{i}\right)\right|>{d}_{\text{max}}$ makes the hysteresis output $w\left(t\right)$ changing in time. Then, any interval $[\begin{array}{cc}{t}_{1}& {t}_{1}+T\end{array})$ (in steady state) can be divided into four subintervals as shown in Fig. 11a. For $t\in [\begin{array}{cc}{t}_{2}& {t}_{3}\end{array})$, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves along one lateral border. For $t\in [\begin{array}{cc}{t}_{4}& {t}_{1}+T\end{array})$, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ moves along the opposite lateral border. For $t\in [\begin{array}{cc}{t}_{1}& {t}_{2}\end{array})\cup [\begin{array}{cc}{t}_{3}& {t}_{4}\end{array})$, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$ takes a horizontal path (the curves linking the lateral border $\left({f}_{\text{L}}\left(.\right),{f}_{\text{U}}(.)\right)$). Accordingly, the working point $\left(v\left(t\right),F\left[v\left(t\right)\right]\right)$, for $t\in [\begin{array}{cc}{t}_{1}& {t}_{1}+T\end{array})$, describes a backlash cycle (Fig. 11b).

Fig. 11

a Shapes of inner signals $v\left(t\right)$ and $w\left(t\right)$, b example of obtained cycle for sufficient large $U$

The time ${t}_{1}$ is related to ${\varphi }_{1}\left({\omega }_{i}\right)$ by the expression:

$${t}_{1}=-{\varphi }_{1}\left({\omega }_{i}\right)/{\omega }_{i}$$

(23a)

Also, it is readily seen that:

$${t}_{3}={t}_{1}+\frac{T}{2}=\left(\pi -{\varphi }_{1}\left({\omega }_{i}\right)\right)/{\omega }_{i}$$

(23b)

In the case of symmetrical hysteresis nonlinearity, the times ${t}_{2}$ and ${t}_{4}$ are related as follows:

$${t}_{4}={t}_{2}+\frac{T}{2}$$

(23c)

Then, the inner signal $w\left(t\right)$ can be analytically described by the following equation system:

$$ w\left( t \right) = \left\{ {\begin{array}{*{20}l} {f_{{\text{L}}} \left( {U\left| {G_{1} \left( {j\omega_{i} } \right)} \right|} \right) = S_{{\text{L}}} \left( {U\left| {G_{1} \left( {j\omega_{i} } \right)} \right| - D_{{\text{L}}} } \right),} \hfill & {{\text{for}}\;\;t \in [\begin{array}{*{20}c} {t_{1} } & {t_{2} } \\ \end{array} )} \hfill \\ {S_{{\text{U}}} \left( {U\left| {G_{1} \left( {j\omega_{i} } \right)} \right|{\text{cos}}\left( {\omega_{i} t + \varphi_{1} \left( {\omega_{i} } \right)} \right) - D_{{\text{U}}} } \right),} \hfill & {{\text{for}}\;\;t \in [\begin{array}{*{20}c} {t_{2} } & {t_{3} } \\ \end{array} )} \hfill \\ {f_{{\text{U}}} \left( { - U\left| {G_{1} \left( {j\omega_{i} } \right)} \right|} \right) = S_{{\text{U}}} \left( { - U\left| {G_{1} \left( {j\omega_{i} } \right)} \right| - D_{{\text{U}}} } \right),} \hfill & {t \in [\begin{array}{*{20}c} {t_{3} } & {t_{4} } \\ \end{array} )} \hfill \\ {S_{{\text{L}}} \left( {U\left| {G_{1} \left( {j\omega_{i} } \right)} \right|{\text{cos}}\left( {\omega_{i} t + \varphi_{1} \left( {\omega_{i} } \right)} \right) - D_{{\text{L}}} } \right),} \hfill & {t \in [\begin{array}{*{20}c} {t_{4} } & {t_{1} + T} \\ \end{array} )} \hfill \\ \end{array} } \right. $$

(24)

Furthermore, note that this signal is periodic with the same period ${T=2\pi /\omega }_{i}$ as the input $u\left(t\right)$. Fourier series expansion of $w\left(t\right)$ writes as follows:

$$w\left(t\right)=\sum_{n=0}^{\infty }{s}_{n}\text{cos}\left(n{\omega }_{i}t+{\psi }_{n}({\omega }_{i})\right)$$

(25)

It is readily shown from Equation (24) that the parameters $\left({s}_{n},{\psi }_{n}\left({\omega }_{i}\right)\right)$ of Fourier series expansion in (25) depend only on the complex gain of the input linear block $\left(\left|{G}_{1}\left(j{\omega }_{i}\right)\right|,{\varphi }_{1}\left({\omega }_{i}\right)\right)$ and the times $\left({t}_{1},{t}_{2},{t}_{3},{t}_{4}\right)$. These times also depend on the parameters $\left(\left|{G}_{1}\left(j{\omega }_{i}\right)\right|,{\varphi }_{1}\left({\omega }_{i}\right)\right)$ (using (23a–c)).

At this stage, the parameters of the hysteresis nonlinearity $\left({S}_{\text{L}},{D}_{\text{L}},{S}_{\text{U}},{D}_{\text{U}}\right)$ are available. Then, the only unknown parameters in Fourier expansion of $w\left(t\right)$ are the parameters of linear block $\left(\left|{G}_{1}\left(j{\omega }_{i}\right)\right|,{\varphi }_{1}\left({\omega }_{i}\right)\right)$. Combining (3) and (25), the undistubed system output $x\left(t\right)$ can be expressed (in steady state) as follows:

$$x\left(t\right)=\sum_{n=0}^{\infty }{s}_{n}\left|{G}_{2}\left({jn\omega }_{i}\right)\right|\text{cos}\left(n{\omega }_{i}t+{\psi }_{n}({\omega }_{i})+{\varphi }_{2}\left(n{\omega }_{i}\right)\right)$$

(26)

Finally, it follows from (4) and (26) that the system output $y\left(t\right)$ can be written as:

$$y\left(t\right)=\sum_{n=0}^{\infty }{s}_{n}\left|{G}_{2}\left({jn\omega }_{i}\right)\right|\text{cos}\left(n{\omega }_{i}t+{\psi }_{n}({\omega }_{i})+{\varphi }_{2}\left(n{\omega }_{i}\right)\right)+\xi (t)$$

(27)

One the other hand, bearing in mind that the signal $x\left(t\right)$ is also periodic of the same period ${T=2\pi /\omega }_{i}$ as $u\left(t\right)$, then $x\left(t\right)$ can also be described by Fourier expansion series:

$$x\left(t\right)=\sum_{n=0}^{\infty }{X}_{n}\text{cos}\left(n{\omega }_{i}t+{\theta }_{n}\right)$$

(28)

where the parameters $\left({X}_{n},{\theta }_{n}\right)$ in (28) can be determined using the following expressions:

$${X}_{n}=\sqrt{{{a}_{n}}^{2}+{{b}_{n}}^{2}}$$

(29a)

$${\theta }_{n}=-{\text{tan}}^{-1}\left({b}_{n}/{a}_{n}\right)$$

(29b)

where

$${a}_{n}=\frac{2}{T}{\int }_{0}^{T}x\left(t\right)\text{cos}\left(n{\omega }_{i}t\right)\text{d}t$$

(29c)

$${b}_{n}=\frac{2}{T}{\int }_{0}^{T}x\left(t\right)\text{sin}\left(n{\omega }_{i}t\right)\text{d}t$$

(29d)

At this stage, the problem is how to get the estimate of the inner (not accessible) signal $x\left(t\right)$. This difficulty can be overcome by getting benefit from the periodicity property of $x\left(t\right)$. Then, an accurate estimate for the signal $x\left(t\right)$ can be obtained using the following estimator [18,19,20,21]:

$$ \left\{ {\begin{array}{*{20}l} {\hat{x}_{M} \left( t \right) = \frac{1}{M}\mathop \sum \limits_{l = 0}^{M - 1} x\left( {t + lT} \right), } \hfill & {{\text{for}}\;\; t \in \left[ {\begin{array}{*{20}c} 0 & T \\ \end{array} } \right)} \hfill \\ {\hat{x}_{M} \left( {t + T} \right) = \hat{x}_{M} \left( t \right), } \hfill & {{\text{else}}} \hfill \\ \end{array} } \right. $$

(30)

where $M$ is any integer preferably of large value. Practically, one can check whether the values of $M$ are suitable by comparing the output of the true system with the estimated model. Specifically, by combining (4) and (30), one immediately gets:

$${\widehat{x}}_{M}\left(t\right)=\frac{1}{M}\sum_{l=0}^{M-1}x\left(t+lT\right)+\frac{1}{M}\sum_{l=0}^{M-1}\xi (t+lT)$$

(31)

Bearing in mind that $x\left(t\right)$ is T-periodic, this implies that the first term in the right side of (31) can be reduced to:

$$\frac{1}{M}\sum_{l=0}^{M-1}x\left(t+lT\right)=x\left(t\right)$$

(32)

On the other hand, the external noise $\left\{\xi (t)\right\}$ is presently supposed to be a zero-mean stochastic process and ergodic. The stationarity property of $\left\{\xi (t)\right\}$ means that:

$$E\left[\xi (t+lT)\right]=E\left[\xi (t)\right] \, \text{for } \, \text{all } \, \left(t,l\right)$$

(33)

Accordingly, the last term in the right side of (31) vanishes with probability 1:

$$ \frac{1}{M}\mathop \sum \limits_{l = 0}^{M - 1} \xi \left( {t + lT} \right)\to _{M \to \infty } 0 $$

(34)

Then, it readily follows by combining (31), (32) and (34) that the estimated signal ${\widehat{x}}_{M}\left(t\right)$ in (30) converges with probability 1 to $x\left(t\right)$:

$$ \hat{x}_{M} \left( t \right)\to _{M \to \infty } x\left( t \right) $$

(35)

This result is a quite interesting achievement as it shows that, the frequency parameters of the linear blocks can be determined, for any frequency ${\omega }_{i}$, using the estimate ${\widehat{x}}_{M}\left(t\right)$ of $x\left(t\right)$ and capturing the Fourier transform spectra of $x\left(t\right)$. Specifically, the linear block identification can be carried as follows:

Firstly, the estimate $\left({\widehat{X}}_{n}(M),{\widehat{\theta }}_{n}(M)\right)$ of Fourier expansion parameters $\left({X}_{n},{\theta }_{n}\right)$ in (28) can be obtained by replacing $x\left(t\right)$ in (29c–d) by its estimate ${\widehat{x}}_{M}\left(t\right)$, given by (30). Accordingly, by referencing the correspondence between $\left({\widehat{X}}_{n}(M),{\widehat{\theta }}_{n}(M)\right)$ with the analytical expression of $x\left(t\right)$ given by (26), one immediately gets:

$$ \left\{ {\begin{array}{*{20}c} {s_{n} \left( {\omega_{i} } \right)\left| {G_{2} \left( {jn\omega_{i} } \right)} \right| = \hat{X}_{n} \left( M \right) } \\ {\psi_{n} \left( {\omega_{i} } \right) + \varphi_{2} \left( {n\omega_{i} } \right) = \hat{\theta }_{n} \left( M \right)} \\ \end{array} } \right.n = 0,1,2, \ldots ; $$

(36)

where $\left({s}_{n},{\psi }_{n}\right)$ depend on the parameters of the input linear block $\left(\left|{G}_{1}\left(j{\omega }_{i}\right)\right|,{\varphi }_{1}\left({\omega }_{i}\right)\right)$. For any $n$ frequency components and using the properties (5c) (Remark 1), one has the $2n+2$ following unknown parameters: $\left(\left|{G}_{1}\left(j{\omega }_{i}\right)\right|,{\varphi }_{1}\left({\omega }_{i}\right)\right)$ and $\left\{\left(\left|{G}_{2}\left(jk{\omega }_{i}\right)\right|,{\varphi }_{2}\left({k\omega }_{i}\right)\right); k=1\dots n\right\}$. It follows from these $n$ frequency components, $2n+1$ equations are involved, i.e., the amplitude ${\widehat{X}}_{k}\left(M\right)$, the phase ${\widehat{\theta }}_{k}(M)$ of the frequency component $k$ (for $k=1\dots n$) and the DC component. At this stage, the number of unknowns is large compared to the number of equations. Then, the last experiment is repeated for a frequency ${2\omega }_{i}$. It follows from (20)–(31) and by capturing the frequency components belonging to the band $\big[\begin{array}{cc}0& {n\omega }_{i}\end{array}\big]$ that $2n+1$ equations can be involved and two new unknown parameters: $\left(\left|{G}_{1}\left(j{2\omega }_{i}\right)\right|,{\varphi }_{1}\left({2\omega }_{i}\right)\right)$. It is readily seen that the number of equations is sufficient to obtain all the involved parameters. This experiment can be repeated for other frequencies ${k\omega }_{i}$, e.g., $k=\text{3,4},\dots$ if necessarily. This result is quite interesting, for convenience let us summarize this identification method:

By capturing the spectrum of the estimate of $x\left(t\right)$, the values of the amplitudes ${s}_{n}\left({\omega }_{i}\right)\left|{G}_{2}\left({jn\omega }_{i}\right)\right|$ and the phases ${\psi }_{k}\left({\varphi }_{1}\left({\omega }_{i}\right)\right)+{\varphi }_{2}\left(k{\omega }_{i}\right)$, for $k=0\dots n$, can be obtained. By repeating this experiment for the frequency ${2\omega }_{i}$, all the frequency parameters of linear blocks can be determined.

The main steps of the identification of linear blocks are summarized in Table 2.

Table 2 Identification of linear blocks

Remark 7

Following the previously described method, the identification of the Wiener–Hammerstein system can be performed using one-step method, i.e., the parameters of linear blocks and those of the hysteresis nonlinearity can be determined simultaneously. To make easy the identification method, we have proposed to separate the identification of the linear blocks from that of the nonlinearity (two-step identification method).

Remark 8

• 1. So far, the complex gains ${G}_{1}\left(j\omega \right)$ and ${G}_{2}\left(j\omega \right)$ have been assumed to be nonparametric. Then, making use of the method presented in this section, one obtains accurate estimates of ${G}_{1}\left({j\omega }_{i}\right)$ and ${G}_{2}\left({jk\omega }_{i}\right)$, for $k=1\dots n$ and for a set of frequencies ${\omega }_{i}\in \left\{{\omega }_{1},{\omega }_{2},\dots \right\}$ arbitrarily chosen by the designer. It may happen that one of the linear subsystems is parametric, i.e., ${G}_{l}\left({j\omega }_{i}\right)={G}_{l}\left({j\omega }_{i},\theta \right)$ ($l=1, 2$) for some vector $\theta$ including the unknown coefficients of the transfer function ${G}_{l}\left({j\omega }_{i}\right)$ ($l=1, 2$). Then, one can get estimates of $\theta$ using various well-known techniques [1, 2], including the weighted nonlinear least squares technique. Then, the estimate is given by:

  $$\widehat{\theta }=\text{arg}\underset{\theta }{\text{min}}\left[{\frac{1}{P}\sum_{i=1}^{P}\left|{\widehat{G}}_{l}\left({j\omega }_{i}\right)-{G}_{l}\left({j\omega }_{i},\theta \right)\right|}^{2}{\delta }_{P}\right]$$

  (37)

where ${\widehat{G}}_{l}\left({j\omega }_{i}\right)$ denotes the estimate of transfer function ${G}_{l}\left({j\omega }_{i},\theta \right)$ ($l=1, 2$), provided by the above method, and ${\delta }_{P}$ is the weighting function. The number $P$ in (37) should be greater than the dimension of $\theta$. The optimization problem can be carried out using iterative search techniques, e.g., Gauss–Newton, Levenberg–Marquardt, and others [1, 2].

• 2. The backlash identification stage requires an input signal satisfying the loading and unloading properties, but not necessarily periodic.

6 Simulation

To highlight the applicability and robustness of the proposed identification method, the system transfer functions of the considered system (Fig. 1) are subjected to higher-order dynamics errors. Specifically, the input transfer function is of the form:

$${G}_{1}\left(s\right)=\frac{1}{\left(s+1\right)\left(s+0.5\right)}\left(1+\mu \Delta (s)\right)$$

(38a)

where $\Delta \left(s\right)=\frac{1}{\left(s+5\right)}$ and $\mu$ is a scaling parameter that is let to be $\mu =0.01$. To make the system more complex, the output transfer function contains a delay time:

$${G}_{2}\left(s\right)=\frac{0.1}{\left(s+0.2\right)\left(s+0.4\right)\left(s+1\right)}{e}^{-5s}$$

(38b)

The system nonlinearity $F\left[ \cdot \right]$ is a backlash operator featured by the following loading and unloading functions:

$${f}_{\text{L}}\left(v\right)={S}_{\text{L}}\left(v-{D}_{\text{L}}\right)=0.75\left(v-0.75\right)$$

(39a)

$${f}_{\text{U}}\left(v\right)={S}_{\text{U}}\left(v-{D}_{\text{U}}\right)=0.75\left(v+3.57\right)$$

(39b)

Figure 12 shows the complete backlash cycle of operator $F\left[ \cdot \right]$ when applying to the letter a periodic input belonging to the interval $[-4 4]$. The stochastic process noise $\left\{\xi (t)\right\}$ is zero-mean ergodic, with normally random numbers belonging to $\left[\begin{array}{cc}-0.2& 0.2\end{array}\right]$ and standard deviation $\sigma =0.07$. Getting benefit from model multiplicity (Remark 1), the linear block transfer functions of the system to be identified are $\frac{{G}_{1}\left(s\right)}{{G}_{1}\left(0\right)}$ and $\frac{{G}_{2}\left(s\right)}{{G}_{2}\left(0\right)}$, respectively. To avoid excessive notation, this system will still be noted $\left( {G_{1} \left( s \right),F\left[ \cdot \right],G_{2} \left( s \right)} \right)$ and is defined by the following blocks:

Fig. 12

System nonlinearity $F\left[ \cdot \right]$ considered in simulation

$${G}_{1}\left(s\right)=\frac{0.499}{\left(s+1\right)\left(s+0.5\right)}\left(1+\frac{0.01}{s+5}\right)$$

(40a)

$${G}_{2}\left(s\right)=\frac{0.08}{\left(s+0.2\right)\left(s+0.4\right)\left(s+1\right)}{e}^{-5s}$$

(40b)

$${f}_{L}\left(v\right)=1.76\left(v-0.36\right); \, {f}_{U}\left(v\right)=1.76\left(v+1.78\right)$$

(40c)

It readily seen from (40a–b) that the linear subsystems of the system to be identified satisfy the properties: ${G}_{1}\left(0\right)={G}_{2}\left(0\right)=1$.

Following the nonlinearity identification method described in Sect. 3, the Wiener–Hammerstein nonlinear system is excited by an input signal $u\left(t\right)$, of loading and unloading nature (Fig. 13). In the proposed simulation, the system is excited by an enough number of constant inputs $\left\{{U}_{k}; \, k=1\dots N\right\}$, with $N=26$. In this experiment, the signal-to-noise ratio (SNR) for the chosen ergodic additive noise is:

$$\text{SNR}=10 \text{log}\left(\frac{{P}_{x}}{{P}_{\xi }}\right)\approx 32 \text{dB}$$

(41)

where ${P}_{x}$ is the signal power (of $x\left(t\right)$), and ${P}_{\xi }$ is the noise power.

Fig. 13

The loading and unloading input $u\left(t\right)$

The used input signal is composed by a set of constant value ${U}_{k}$, for $k=1\dots 26$ (Fig. 13), where the duration of each constant (here $100s$) is greater than ${t}_{r}$. It is shown from Fig. 13 that:

• For $t\in \left[\begin{array}{cc}0& 1300s\end{array}\right]$, the input $u\left(t\right)$ satisfies the loading property, i.e., $\dot{u}\left(t\right)\ge 0 \forall t$.

• For $t\in \left[\begin{array}{cc}1300s& 2600s\end{array}\right]$, the input $u\left(t\right)$ satisfies the unloading property, i.e., $\dot{u}\left(t\right)\le 0 \forall t$.

The corresponding system output $y\left(t\right)$ is plotted in Fig. 14. Using the estimator (14), we get the estimates $\widehat{F}\left[{U}_{k}\right]$, for $k=1\dots 26$, providing the set of points $\left\{\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right); k=1\dots 26\right\}$. For convenience, these points are plotted in Fig. 15. To appreciate the estimation quality, the estimated points $\left\{\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right); k=1\dots 26\right\}$ are plotted together with those of the true backlash $F\left[ \cdot \right]$ in Fig. 16. Clearly, the estimated points are close to their true values. Furthermore, examples of input values ${U}_{k}$, the true values ${X}_{k}$, and the corresponding estimates ${\widehat{X}}_{k}$ for $\text{SNR}1\approx 32 \text{dB}$ and $M=200$, are given in Table 3. To better evaluate the identification accuracy, the relative errors ${e}_{k}=\left({\widehat{X}}_{k}-{X}_{k}\right)/{X}_{k}$ are estimated and are given in Table 3. To show the robustness of the method, a comparison for different values of the SNR is performed. Specifically, for the same value of $M$ ($M=200$), the estimates ${\widehat{X}}_{k}$ and the relative errors ${e}_{k}$ are determined for $\text{SNR}2=64.6 \text{dB}$ and $\text{SNR}3\approx 11\text{ dB}$. The results of this comparison are summarized in Table 3.

Fig. 14

The system output $y\left(t\right)$

Fig. 15

Set of estimated points $\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right)$, for $k=1\dots 26$

Fig. 16

True $F\left[ \cdot \right]$ and the identified points $\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right)$

Table 3 The inputs ${U}_{k}$ and the estimates $\widehat{F}\left[{U}_{k}\right]={\widehat{X}}_{k}$

For a fixed value of $M$ in the estimator (14), it is shown that the estimation accuracy can be degraded for low values of $\text{SNR}$. To improve the estimation accuracy, the number $M$ should be increased. For convenience, these simulations have been done for low $\text{SNR}$. The latter is set to $\text{SNR}4=10 \text{dB}$. The obtained estimate results are given in Table 3.

To estimate the quantified measure of accuracy, the best fit rate (BFR) defined by:

$$ {\text{BFR}}\left( \% \right): = \max \left( {1 - \frac{{\left\| {F\left( {U_{k} } \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} _{k} } \right\|_{2} }}{{\left\| {F\left( {U_{k} } \right) - F\left( {\bar{U}_{k} } \right)} \right\|_{2} }},0} \right) $$

(42)

is determined in loading and unloading stages, noted ${\text{BFR}}_{\text{L}}$ and ${\text{BFR}}_{\text{U}}$, respectively. Here, we have ${\overline{U} }_{k}=0$. One gets:

$${\text{BFR}}_{\text{L}}=99\% \, \text{and} \, {\text{BFR}}_{\text{L}}=97.8\%$$

(43)

On the other hand, the frequency identification of the linear block is performed following Stage 2 of Sect. 4. First, the Wiener–Hammerstein system is excited by the sine input $u\left(t\right)=U\text{cos}\left({\omega }_{1}t\right)$ with $U=3.5$ and ${\omega }_{1}=0.01 (\text{rad}/\text{s})$. Then, the value of signal-to-noise ratio in this experiment is:

$$\text{SNR}1\approx 34.45 \text{dB}$$

(44)

The steady-state output signal $y(t)$ is plotted in Fig. 17. The measurements of $y(t)$ are collected on the interval $0\le t\le {M2\pi /\omega }_{1}$ (here $M=100$). The collected sample is used to generate the estimate of the inner signal $x(t)$ using (30). The obtained estimate ${\widehat{x}}_{M}\left(t\right)$ is plotted in Fig. 18 over one period.

Fig. 17

The output y(t) for $U=3.5$ and ${\omega }_{1}=0.01 (\text{rad}/\text{s})$

Fig. 18

The inner signal estimate ${\widehat{x}}_{M}\left(t\right)$ over one period

The spectrum corresponding to the estimate ${\widehat{x}}_{M}\left(t\right)$, for ${T=2\pi /\omega }_{1}$, is given in Fig. 19. This result shows that the system power is concentrated on frequencies ${\omega }_{1},2{\omega }_{1},{3\omega }_{1},\dots$. Estimates of the coefficients $\left({X}_{n},{\theta }_{n}\right)$ (of Fourier expansion) are determined by replacing $x\left(t\right)$ by ${\widehat{x}}_{M}\left(t\right)$ in (29a–d).

Fig. 19

Magnitude spectrum of inner signal estimate ${\widehat{x}}_{M}\left(t\right)$

Let $\left[\begin{array}{cc}0& {\omega }_{\text{Max}}\end{array}\right[$ denotes the chosen frequency band (the measurement band). Using the spectrum of the estimate ${\widehat{x}}_{M}\left(t\right)$ and (36), a set of equations involving $\left(\left|{G}_{1}\left(j{\omega }_{1}\right)\right|,{\varphi }_{1}\left({\omega }_{1}\right)\right)$ and $\big\{\left(\left|{G}_{2}\left(jk{\omega }_{1}\right)\right|,{\varphi }_{2}\left({k\omega }_{1}\right)\right); k=1\dots n\big\}$ can be obtained, where ${n\omega }_{1}<{\omega }_{Max}$. If necessary, this experiment can be repeated for other frequencies ${k\omega }_{1}$ (e.g., $k=\text{2,3},\dots$), until we get enough equations. Examples of obtained results (spectrum of the estimate ${\widehat{x}}_{M}\left(t\right)$) are given in Fig. 20 and Fig. 21, where the input signal is of frequency ${5\omega }_{1}$ and ${10\omega }_{1}$, respectively. Finally, for $p$ experiments (of frequency ${l\omega }_{1}$, $l=1\dots p$), the estimates $\left(\left|{\widehat{G}}_{1}\left({l\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left({l\omega }_{1}\right)\right)$ and $\left(\left|{\widehat{G}}_{2}\left({jkl\omega }_{1}\right)\right|,{ \widehat{\varphi }}_{2}\left({kl\omega }_{1}\right)\right)$, for $l=1\dots p$ and $k=\text{1,2},\dots$ such as ${kl\omega }_{1}<{\omega }_{\text{Max}}$, can be determined.

Fig. 20

Magnitude spectrum of inner signal estimate ${\widehat{x}}_{M}\left(t\right)$

Fig. 21

Magnitude spectrum of inner signal estimate ${\widehat{x}}_{M}\left(t\right)$

Presently, three experiments have been carried out. Then, the estimates $\left(\left|{\widehat{G}}_{1}\left({l\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left({l\omega }_{1}\right)\right)$ and $\left(\left|{\widehat{G}}_{2}\left({jkl\omega }_{1}\right)\right|,{ \widehat{\varphi }}_{2}\left({kl\omega }_{1}\right)\right)$, for $l=1\dots 3$ and $k=\text{1,2},\dots$ can be easily obtained. Samples of estimate results corresponding to $\left(\left|{G}_{1}\left({l\omega }_{1}\right)\right|,{\varphi }_{1}\left({l\omega }_{1}\right)\right)$, where $l=1$, $5$, and $10$, are shown in Table 4. Similarly, samples of the estimates of $\left(\left|{G}_{2}\left({jk\omega }_{1}\right)\right|,{ \varphi }_{2}\left({k\omega }_{1}\right)\right)$ are given in Table 5. These results are obtained for $\text{SNR}1=34.45 \text{dB}$.

Table 4 Estimates of ${G}_{1}\left({jl\omega }_{1}\right)$, for $l=1, 5$ and $10$, and their true values for 3 values of SNR

Table 5 Estimates of ${G}_{2}\left({jk\omega }_{1}\right)$ $(k=1\dots 5)$ and their true values for 4 values of SNR

To show the influence of noise on the simulation results, the estimates $\left(\left|{\widehat{G}}_{1}\left({l\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left({l\omega }_{1}\right)\right)$ and $\left(\left|{\widehat{G}}_{2}\left({jk\omega }_{1}\right)\right|,{ \widehat{\varphi }}_{2}\left({k\omega }_{1}\right)\right)$, for $l=1\dots 3$ and $k=1\dots 5$, are given for two other values of $\text{SNR}$: $\text{SNR}2=71.6\text{ dB}$, and $\text{SNR}3=9.9\text{ dB}$, where the number $M$ is set to $100$. The obtained estimate results are summarized in Tables 4 and 5. For convenience, these simulations have been carried out for low value of $\text{SNR}$. Then, for $\text{SNR}4=9\text{ dB}$, one gets:

$\left(\left|{\widehat{G}}_{1}\left({\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left({\omega }_{1}\right)\right)=\left(1.31,-0.16\right)$ and $\big(\left|{\widehat{G}}_{1}\left(5{\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left(5{\omega }_{1}\right)\big)=\left(0.43,- 0.36\right)$. The estimates of $\big(\left|{\widehat{G}}_{2}\left({jk\omega }_{1}\right)\right|,{ \widehat{\varphi }}_{2}\left({k\omega }_{1}\right)\big)$, for $k=1\dots 5$, are given in Table 5.

Finally, it is seen that the linear blocks parameter estimates are close to their true values, a result confirmed by several simulations. Furthermore, the estimate results given in Tables 4 and 5 show that the estimation quality deteriorates for small values of the signal-to-noise ratio ($\text{SNR}$), while keeping the same number $M$ (in the estimator (30)).

To complete the simulation study, a comparison is performed between the actual system output and simulated output of identified model. Firstly, using the estimated points $\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right)$ ($k=1\dots N$) (Fig. 15), the estimates of backlash lateral borders are determined. Furthermore, using Remark 8, the estimates ${\widehat{G}}_{1}\left(s\right)$ and ${\widehat{G}}_{2}\left(s\right)$ of transfer functions ${G}_{1}\left(s\right)$ and ${G}_{2}\left(s\right)$, respectively, are obtained. To this end, the following multisine is applied as input signal:

$$u\left(t\right)=\sum_{k=1}^{3}{U}_{k}\text{cos}\left({\omega }_{k}t\right)$$

(45)

where ${\omega }_{1}=0.01\text{ rad}/\text{s}$, ${\omega }_{2}=0.05 \text{rad}/\text{s}$, ${\omega }_{3}=0.5 \text{rad}/\text{s}$, and ${U}_{1}={U}_{2}={U}_{3}=1$. The actual system output and its estimate are plotted and are given in Fig. 22. Clearly, the two signals are close to each other.

Fig. 22

Comparison between the simulated and actual system outputs

7 Experimental application

To highlight the applicability and robustness of the proposed identification approach, an experimental evaluation is established by applying the method to a real system (Fig. 23). The latter is built up with electronic components. Referring to Fig. 1, the linear blocks are defined by the following transfer functions:

Fig. 23

Photo of the experimental setup

$${G}_{1}\left(s\right)=\frac{1000}{1000+ 20s+ {{10}^{-4}s}^{2}}$$

(46a)

$${G}_{2}\left(s\right)=\frac{1000}{1000+ 2s+ {{10}^{-6}s}^{2}}$$

(46b)

The loading and unloading functions $\left({f}_{L}\left(.\right),{f}_{U}\left(.\right)\right)$ of the backlash operator are as follows:

$${f}_{\text{L}}\left(v\right)={S}_{\text{L}}\left(v-{D}_{\text{L}}\right)=8\left(v-1.25\right)$$

(47a)

$${f}_{\text{U}}\left(v\right)={S}_{\text{U}}\left(v-{D}_{\text{U}}\right)=8\left(v+1.25\right)$$

(47b)

A saturation effect is added to the backlash by using operational amplifiers of $\pm {V}_{\text{sat}}=\pm 10\text{V}$ saturation value. Simulation of the theoretical backlash operator $F[.]$ leads to the backlash cycle shown in Fig. 24a. The experimental backlash cycle provided by the real backlash is shown in Fig. 24b.

Fig. 24

a Simulation of the theoretical backlash operator F[.] with saturation effect, b experimental cycle of the real backlash operator with saturation effect

The input wave $u\left(t\right)$, given in Fig. 13, is experimentally generated. Samples of the resulting system output $y\left(t\right)$, in loading and unloading stages, are shown in Fig. 25a–b. The experimentally collected points $\left\{\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right);k=1\dots N\right\}$ are plotted in Fig. 26, together with the true nonlinearity $F\left[.\right]$.

Fig. 25

a System output $y\left(t\right)$ in loading stage, b system output $y\left(t\right)$ in descending stage

Fig. 26

Samples of identified points $\left({U}_{k},\widehat{F}\left[{U}_{k}\right]\right)$ and true $F\left[.\right]$

The linear block identification is performed using a sine signal $u\left(t\right)=U\text{cos}\left({\omega }_{i}t\right)$. For instance, for $U=10$ and ${\omega }_{i}={\omega }_{1}=100\pi (\text{rad}/\text{s})$, the experimentally obtained system output $y(t)$ in steady-state is given in Fig. 27.

Fig. 27

Input $u\left(t\right)$ and the experimental measured output $y\left(t\right)$ for $U=10$ and ${\omega }_{1}=100\pi (\text{rad}/\text{s})$

The spectrum of system output $y(t)$, for ${T=2\pi /\omega }_{1}$, is plotted in Fig. 28. This shows that the spectral power is concentrated on frequencies ${\omega }_{1},2{\omega }_{1},{3\omega }_{1},\dots$. Then, using (29a–d), the estimate $\left({\widehat{X}}_{n}(M),{\widehat{\theta }}_{n}(M)\right)$ of Fourier expansion parameters can be obtained (Step 4 of Table 2).

Fig. 28

Magnitude spectrum of the experimentally measured output $y\left(t\right)$

Then, the estimates $\left(\left|{\widehat{G}}_{1}\left({l\omega }_{1}\right)\right|,{\widehat{\varphi }}_{1}\left({l\omega }_{1}\right)\right)$ of $\big(\left|{G}_{1}\left({l\omega }_{1}\right)\right|,{\varphi }_{1}\left({l\omega }_{1}\right)\big)$, for $l=1,\boldsymbol{ }2$, and 5 are given in Table 6. Similarly, the estimates $\left(\left|{\widehat{G}}_{2}\left({jkl\omega }_{1}\right)\right|,{ \widehat{\varphi }}_{2}\left({kl\omega }_{1}\right)\right)$, for $k=1\dots 4$, are shown in Table 7. Finally, it is observed that the estimates of linear block parameters are close to the true parameters.

Table 6 Estimates of ${G}_{1}\left({jl\omega }_{1}\right)$ for $l=1, 2$, and 5

Table 7 Estimates of ${G}_{2}\left({jk\omega }_{1}\right)$ $(k=1\dots 4)$

8 Conclusion

In this paper, the identification problem of Wiener–Hammerstein systems is addressed in the case of a memory nonlinearity of backlash type. The identification method presented in Sects. 3 and 4 provides estimates of the backlash operator and the system transfer functions, which can be parametric or not. It involves Fourier series expansion and makes use of simple input signals, specifically step-like loading/unloading signal and sine signals. The simulation study shows that the estimated values are close to their true values. In this study, the influence of noise (SNR) and the quantity of data acquisition on the simulation results has been addressed. It is seen that, for a fixed quantity of data acquisition, the quality of the estimation can deteriorate for small values of SNR.

This work can be pursued in many directions. One of them is to investigate the possibility of estimating extra values of the transfer function ${G}_{1}$ without repeating the whole method, presented in this paper, with different input frequencies ${\omega }_{i}$. One interesting idea would be to get benefit from the fact that $f(.)$ and (several points of the function) ${G}_{2}$ become available (after one experiment involving the $u\left(t\right)=U\text{cos}\left({\omega }_{i}t\right)$). Then, one seeks only the identification of ${G}_{1}$ considering a multisine input $u\left(t\right)=\sum_{i=1}^{m}{U}_{i}\text{cos}\left({\omega }_{i}t\right)$, making use of the estimates of $f$ and ${G}_{2}$, applying some nonlinear least squares iterative method. Another possible perspective of this work is to investigate the case of backlash of arbitrarily nonlinear borders.

The identification problem of this nonlinear system using only harmonic signals and decomposition can be considered as perspective of this work.